Adaptive Waveform Design with Multipath Exploitation Radar in Heterogeneous Environments

Abstract

The problem of detecting point like targets over a glistening surface is investigated in this manuscript, and the design of an optimal waveform through a two-step process for a multipath exploitation radar is proposed. In the first step, a non-adaptive waveform is transmitted and a constrained Generalized Likelihood Ratio Test (GLRT) detector is deduced at reception which exploits multipath returns in the range cell under test by modelling the target echo as a superposition of the direct plus the multipath returns. Under the hypothesis of heterogeneous environments, thus by assuming a compound-Gaussian distribution for the clutter return, this latter is estimated in the range cell under test through the secondary data, which are collected from the out-of-bin cells. The Fixed Point Estimate (FPE) algorithm is applied in the clutter estimation, then used to design the adaptive waveform for transmission in the second step of the algorithm, in order to suppress the clutter coming from the adjacent cells. The proposed GLRT is also used at the end of the second transmission for the final decision. Extensive performance evaluation of the proposed detector and adaptive waveform for various multipath scenarios is presented. The performance analysis prove that the proposed method improves the Signal-to-Clutter Ratio (SCR) of the received signal, and the detection performance with multipath exploitation.

1. Introduction

The detection of radar signals from targets on time-varying surfaces is challenging due to the low Signal-to-Clutter Ratio (SCR), yet an active field of study in statistical signal processing. Many early adaptive detection and waveform design algorithms have offered solutions in homogeneous environments, where the signal of interest is embedded in a Gaussian noise. However, target detection over a glistening surface, such as the sea surface, requires disturbance models which take the inhomogeneous characteristics of the environment into account. Robust and reliable target detection in rich and dynamic clutter background such as in heterogeneous environments is of wide interest to radar community. Once we consider the sea surface, the traits of sea clutter returns viewed by high-resolution radars are non-Gaussian [1]. A proper disturbance model, which reflects the characteristics of heterogeneous environment, is pivotal to develop coherent detection and waveform optimization algorithms. Thus, several non-Gaussian disturbance model have been devised in the last decades [2,3,4,5,6,7]. Among these disturbance models, Spherically Invariant Random Vector (SIRV) is the most widely used one. Moreover, with real radar clutter, the Spherically Invariant Random Processes (SIRPs) are proven to be suitable for the correct clutter modelling [8].

The radar signal backscattered from a target over a glistening surface, contains not only a line of sight component but also multipath returns via many propagation paths. Thus, return signal needs to be properly modeled, as much as disturbance. Otherwise, ultimate performance degradation occurs in target detection, localization, and tracking in such environments [9,10,11,12]. In this respect, multipath exploitation techniques, which use a priori information in order to predict the multipath structure of target return, are resorted to tackle the performance degradation in the receiver side [13,14,15,16].

However, multipath returns, which are present in the signal backscattered from the target on a glistening surface, have characteristics (e.g., direction of arrival, echo strength and phase) that are dynamic due to time-varying nature of the reflecting environment. A sample geometry of the problem showing this phenomenon, which is referred as diffuse multipath, is presented in Figure 1, that at the bottom right shows also the specular reflection phenomenon. It makes the problem more challenging in particular to predict the target subspace and the characteristics of multipath returns. A remarkable adaptive detector, which model multipath echoes as random variables so that enable us to model the effect of multipath returns on disturbance model, has been proposed as Tunable Adaptive Matched Filter (T-AMF) in [17,18]. It models the radar target echo as the superposition of a deterministic signal, representing the direct path component, plus a zero-mean complex normal vector, which is to represent the multipath returns. Thus, it can tackle the covariance matrix mismatch between the range cell under test (referring as primary data) and reference data cells (referring as secondary data) in the estimation of primary data covariance matrix due to diffuse multipath. Note that, the range cell under test may contain target returns whereas the reference cells are assumed free of useful signal components. Later, the approach in [17] is extended to partially homogeneous environments by introducing an unknown power scaling factor to represent the covariance matrix mismatch between the disturbance component of the cell under test and secondary data [19,20]. Here in this article, the adopted approach is also based on the idea that covariance matrix is affected due to the multipath, but, while the existing solutions refer to the case of homogeneous and partially homogeneous environments, our proposal considers the problem in heterogeneous environments.

There are also several studies in literature, which targets the radar signal detection in non-Gaussian and heterogeneous clutter. Although these studies do not consider the multipath exploitation, instead examined in our work, it is worth mentioning their valuable contribution on the technical content of the subject. In particular, target detection with multiple-input–multiple-output radar in non Gaussian and heterogeneous clutter was carried out in [21], by using the generalized likelihood ratio test-linear quadratic (GLRT-LQ) detector. In [22], the authors specified and demonstrated a practical technique for characterizing non-Gaussian clutter using Over The Horizon Radar (OTHR) data. A priori knowledge of non-Gaussian clutter has been used in [23] in order to improve the detection performance when the secondary data are limited. The inverse Gaussian distribution is used in this case to model the clutter texture in order to characterize the non-Gaussian characteristics of the clutter.

In addition, adaptive coherent radar detection in non-Gaussian environment is also investigated in other relevant papers [3,24,25,26]. In [26], the authors have shown how a sub-optimal detector, which does not require information about the specific nature of the non-Gaussian clutter, may be implemented to obtain quasi-optimal performance. This problem is studied in [3] with a two-step procedure. In the first step, the structure of the amplitude and the multivariate probability density functions (PDFs) describing the statistical properties of the clutter is derived. The end product of the first step is a multidimensional PDF in the form of a Gaussian mixture, which is then used in order to derive both the optimal and a sub-optimal detection structure for detecting radar targets in non-Gaussian clutter.

The waveform design is another important issue to be considered in adaptive radar signal detection, and particularly in radar target environments with time-varying behaviour, in order to have a fully adaptive approach [27,28,29,30]. The adaptive waveform design has therefore received much attention from the radar community in the modern era of radar signal processing [31,32,33]. In [34], an algorithm based on an adaptive waveform design is proposed for space-based radar, by which targets can be detected effectively in complicated heavy fast-varying sea clutter. Lately, new paradigms have been derived through the introduction of cognition inside the radar systems [27,28,35,36]. As a result, new cognitive architectures, which are able to exploit the design of optimized waveforms, through a coordinated and continuous feedback between transmitter and receiver, have been proposed as well [37,38].

Hereafter the organization of the manuscript. After a brief notation paragraph, in Section 2, we briefly explain our approach and proposed solution towards the problem. In Section 3, the assumptions are described with the model adopted for the target and the disturbance parameters. The statistics of the clutter and their estimation are presented in Section 4, for adaptive radars. Section 5 describes the detection strategy. The design of the adaptive waveform for sub-dwell two is presented in Section 6, while Section 7 assesses the performance of the devised detector with an adaptive waveform. Lastly, conclusions are highlighted in Section 8.

Notation

In this article we adopt the following notation: We use upper case boldface for matrices A, and lower case boldface for vectors a. The symbol ${(·)}^{†}$ is for the complex conjugate transpose, and $|·|$ symbol is for the determinant of the square matrix argument. I denotes the identity matrix, and reader can determine its size from the context. diag a represents the diagonal matrix whose diagonal entries are the elements of a. ${\mathbb{C}}^N,{\mathbb{C}}^N,K,{\mathbb{H}}^N$ are the sets of N-dimensional complex value vectors, $NxK$ dimensional complex matrices and $NxN$ Hermitian matrices, respectively. $\mathit{\lambda }\left(\mathit{X}\right)$ is the eigenvalue vector of $\mathit{X}\in {\mathbb{H}}^N$. The curled inequality symbol denotes generalized matrix inequality, i.e., $\mathit{A}\succ 0$ means that A is a positive definite matrix, where $\mathit{A}\in {\mathbb{H}}^N$. $\parallel \mathit{x}\parallel$ is for the Euclidean norm of vector x. ${\parallel \mathit{A}\parallel }_2$ denotes the spectral norm of matrix A, where $\mathit{A}\in {\mathbb{C}}^{N,M}$. Last, $\mathbb{E}\left[·\right]$ is for statistical expectation. Finally, $\mathcal{P}$ represents the optimization problem.

2. Proposed Solution

In this study, with respect to the work present in the literature, an adaptive waveform design in the case of multipath, and for heterogeneous environments, is introduced. A cognitive architecture is conceived for improving the SCR in the range bin under test by not only exploiting the multipath returns of useful target echo but also suppressing the clutter coming from the adjacent radar cells. While the former is achieved using the constrained GLRT detector, the latter is accomplished by the adaptive waveform design. In order to do these, a radar system which transmits $N_p$ pulses from $N_a$ uniformly spaced and identical sensors is considered. The transmitted waveform consists of two sub-dwells, where each sub-dwell is represented by $N_p/2$ number of pulses. During the sub-dwell one, $N_p/2$ number of pulses are transmitted and received back through $N_a$ sensors. At the end of sub-dwell one, the clutter in the range cell under test is estimated via the Fixed Point Estimate (FPE) algorithm [39,40], which utilizes the data collected from the out-of-bin cells (referring as secondary data). Then, a constrained GLRT detector [41,42,43,44] is deduced which exploits diffuse multipath returns of target [17,20]. Later, an adaptive waveform is constructed based on the clutter statistics previously obtained in the sub-dwell one and transmitted at the second sub-dwell in order to suppress the unwanted signal coming from the out-of-bin cells. Finally, the deduced GLRT detector is used for final decision at the end of sub-dwell two. The block diagram of the proposed algorithm, as above described, is presented in Figure 2, where, as we will see later, r and $r_k$ are respectively the primary data and the secondary dataset, y and $y_k$ are the matched-filtered output, $\overline{M}$ is the estimated speckle covariance matrix of the primary data and ${\tau }_k$ represents texture components of adjacent cells.

An initial implementation of this algorithm has been analyzed in [45]. Yet, in this manuscript, a great extension of our study is presented with a more detailed derivation and analysis of the detector optimization problem, and through a deep performance evaluation of the proposed detector and the derived adaptive waveform in the case of various multipath scenarios. Namely, we can summarize the main novel contributions of the present manuscript as below:

• the introduction section has been extended to provide the interested reader a better understanding of the state of the art in the research field of adaptive detection and waveform design;
• the contribution on adaptive target detection in heterogeneous environments with multipath exploitation radar and an optimal waveform, designed through a two-step process for the deduced detector, has been emphasized;
• the GLRT detection section includes a very detailed derivation and proof of the optimization problem and decision rules, so to allow interested readers to follow the derivation of the receiver thoroughly;
• a more detailed performance analysis has been carried out in terms of waveform and adaptive detectors, in particular:

  –

  both non-adaptive Linear Frequency Modulation (LFM) and Phase Modulated (PM) waveform cases in the sub-dwell one have been included;

  –

  in addition to the performance analysis for the case of LFM waveform in sub-dwell one and Adaptive PM waveform in sub-dwell two, the performance analysis with LFM waveform in both sub-dwell one and two has been included, in order to show the performance improvement of the adaptive waveform clearly;

  –

  the performance comparison of the proposed detector with the Adaptive Matched Filter (AMF) [46] has been discussed, in addition to Adaptive Coherence Estimator (ACE) [47], in order to show the performance improvement with multipath exploitation in heterogeneous environments.

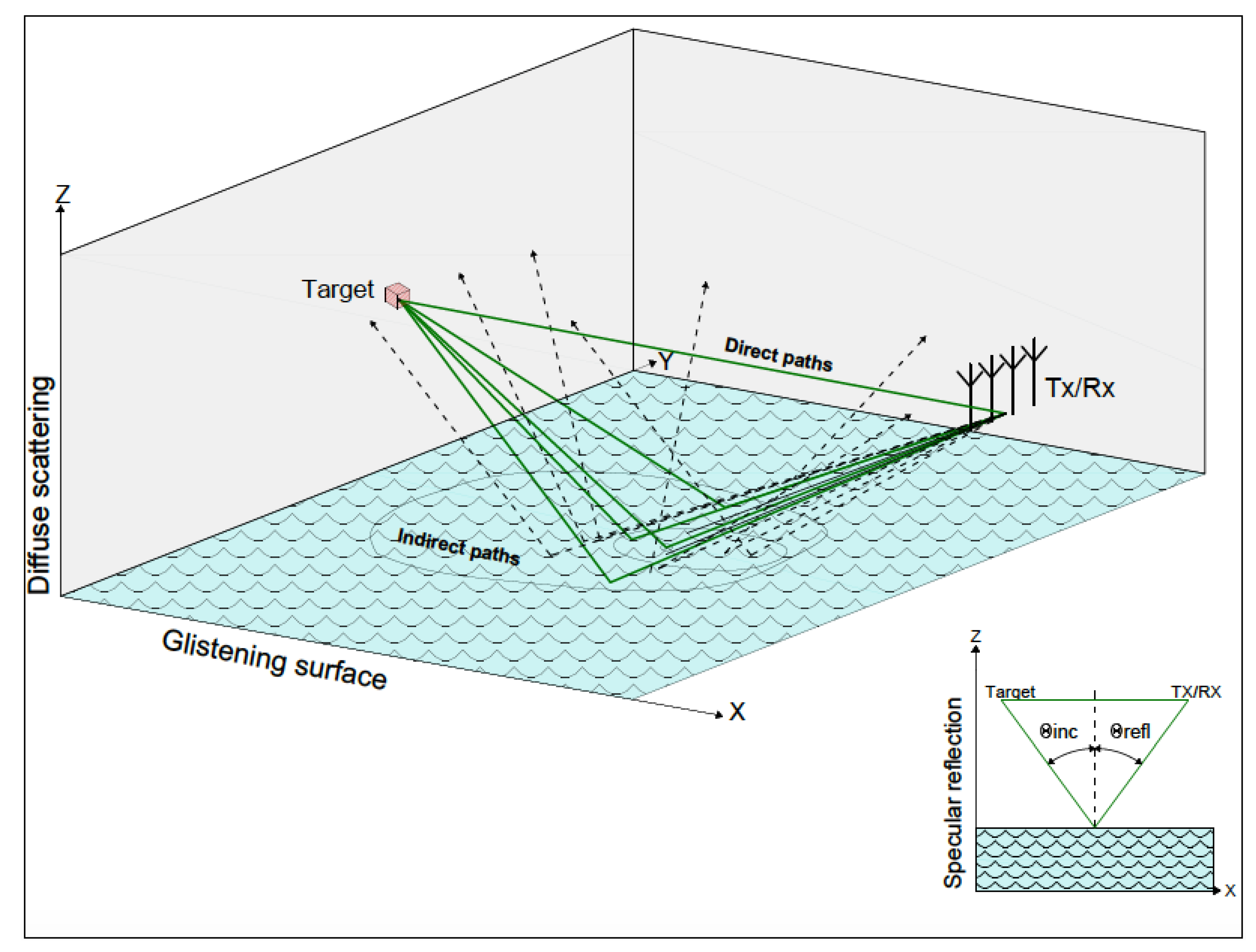
3. Theoretical Model and Assumptions

In this section, we formulate the detection problem with the assumption of a radar system, which transmits $N_p$ pulses from $N_a$ identical and uniformly spaced sensors. The proposed model consists of two sub-dwells, where each sub-dwell is represented by $N_p/2$ number of pulses. Thus, the system transmits half of the $N_p$ pulses, and receives them back through $N_a$ sensors during each sub-dwell. As a consequence, the radar receiver has data from N channels during each sub-dwell, where N equals to $(N_p\times N_a)/2$. Accordingly the corresponding detection problem can be formulated as the following hypothesis testing:

$$\left\{\begin{array}{cc}{H}_0:\hfill & \left\{\begin{array}{cc}\mathbf{r}\hfill & =\mathbf{c}+\sum _{k=1}^K{\mathbf{c}}_k\hfill \\ {\mathbf{r}}_k\hfill & ={\mathbf{c}}_k\hfill \end{array}\right.\hfill \\ \\ H_1:\hfill & \left\{\begin{array}{cc}\mathbf{r}\hfill & =\alpha \mathbf{p}+\mathbf{s}+\mathbf{c}+\sum _{k=1}^K{\mathbf{c}}_k\hfill \\ {\mathbf{r}}_k\hfill & ={\mathbf{c}}_k\hfill \end{array}\right.\hfill \end{array}\right.$$

(1)

where

• $\mathbf{r}\in {\mathbb{C}}^N$ is the received signal from the range cell under test (RCUT).
• ${\mathbf{r}}_k\in {\mathbb{C}}^N,k\in [1,K],(K\ge N)$ is the secondary data set which is assumed to be free of target response.
• $\mathbf{p}\in {\mathbb{C}}^N,{\parallel \mathbf{p}\parallel }^2=1$, is the target steering vector, and known for the line of sight path.
• $\alpha \in \mathbb{C}$ is an unknown deterministic parameter accounting for both the line of sight channel propagation factor and target response to the incident wave.
• $\mathbf{c}\mathrm{and}{\mathbf{c}}_k$ represent clutter, which is due to large number of independent scattering centers, in the primary and the secondary data, respectively. They are assumed to zero mean SIRVs, where SIRV is a special case of a compound-Gaussian process. It is defined as the product of independent zero-mean circular complex Gaussian vector, which is called speckle, and a non-negative scalar random variable, which is called texture [4,5]. Their respective covariance matrices are defined below.

  $$\begin{array}{c}\hfill \mathbb{E}\left[c{c}^{†}\right]=\tau \overline{M}\mathrm{and}\mathbb{E}\left[c_k{c}_k^{†}\right]={\tau }_k\overline{M}\end{array}$$

  (2)

  where $\overline{M}$ is the covariance matrix of the speckle. It is assumed to be same for each range cell. Random variables $\tau ,{\tau }_1,\cdots ,{\tau }_k$ are texture components representing relatively slow variations on the surface that can modulate the local mean power of the speckle. These texture components are assumed to be unknown deterministic parameters. Note that, the scattered clutter echoes from secondary data, which are assumed adjacent to and accordingly increase the disturbance power in the interested cell, are also considered while modeling the received signal from RCUT.
• $\mathbf{s}\in {\mathbb{C}}^N$ is i.i.d. zero mean complex Gaussian vector with unknown covariance matrix, $\Sigma \succ 0$, and represents the diffuse multipath component of target response in multipath environment.

In case Doppler and angle processing are not present, one can perceive the match filtered signal at the receiver side as a convolution of the radar received signal with the auto-correlation function of the transmitted signal [31,32,33]. Thus, the output of the matched filter for primary and secondary data are formulated as the following hypothesis testing, including auto-correlation function of the transmitted signal.

$$\left\{\begin{array}{cc}{H}_0:\hfill & {\mathbf{y}}_i={\mathbf{r}}_i{z}_s\left[i\right]+\sum _{k=1}^K{\mathbf{r}}_k{z}_s\left[k\right]\hfill \\ \\ H_1:\hfill & {\mathbf{y}}_i={\mathbf{r}}_i{z}_s[i-i_0]+\sum _{k=1}^K{\mathbf{r}}_k{z}_s\left[k\right]\hfill \end{array}\right.$$

where

• ${\mathbf{y}}_i\in {\mathbb{C}}^N,i=1,\cdots ,N_s$, is the matched-filtered output at the ith range bin.
• $N_s$ is the length of the transmitted signal.
• $i_0$ is the index of the range bin that contains the target if target is present.
• $z_s$ is the auto-correlation function of the transmitted signal at lag m, and it is defined as the following equation.

  $$z_s\left[m\right]=\sum _{n=1}^{N_s}t\left[n\right]t^{\ast }[n-m],\left|m\right|<N_s$$

  (3)

Here, t represents the transmitted signal.

4. The Model for the Clutter

Proper clutter model, which yields the statistical parameters characterizing the heterogeneous environment, is pivotal to develop coherent detection and waveform optimization algorithms. In this study, we use a SIRP, which is also proven to be suitable for clutter modelling [8], in order to model our heterogeneous clutter, where statistical parameters are assumed to be unknown and need to be estimated. In this respect, we utilize the secondary data set, which is defined in Section 3. We resort the FPE algorithm for the secondary data set in order to estimate the clutter covariance of the primary data.

The random texture component of the SIRV model is assumed to be unknown and deterministic for each single element of the secondary data set. Accordingly, PDF of ${\mathit{c}}_k$, where $k=1,\cdots ,K$, in hypothesis testing (1) can be expressed as

$$p({\mathit{c}}_k;{\tau }_k,\overline{\mathit{M}})=\frac{exp\left(\frac{-{\mathit{c}}_k^{†}{\overline{\mathit{M}}}^{-1}{\mathit{c}}_k}{{\tau }_k}\right)}{{\pi }^N{\tau }_k^N\left|\overline{\mathit{M}}\right|}.$$

The clutter covariance in primary data is estimated via maximizing the following likelihood function with respect to $\overline{\mathit{M}}$ and the ${\tau }_k$, for $k=1,\cdots ,K$.

$$\prod _{k=1}^{K}p({\mathit{r}}_k;{\tau }_k,\overline{\mathit{M}})=\prod _{k=1}^K\frac{exp\left(\frac{-{\mathit{r}}_k^{†}{\overline{\mathit{M}}}^{-1}{r}_k}{{\tau }_k}\right)}{{\pi }^N{\tau }_k^N\left|\overline{\mathit{M}}\right|}$$

(4)

The unknown parameters are estimated via FPE algorithm by using an iterative approach. Namely, ${\tau }_1^{(t+1)},\cdots ,{\tau }_k^{(t+1)}$ are obtained by maximizing the likelihood function when $\overline{\mathit{M}}$ equals to ${\overline{\mathit{M}}}^{\left(t\right)}$. Later, ${\overline{\mathit{M}}}^{(t+1)}$ is calculated using the estimated values of ${\tau }_1^{(t+1)},\cdots ,{\tau }_k^{(t+1)}$. Therefore, the recursive formula, which is used to estimate $\overline{\mathit{M}}$, is obtained as

$${\overline{\mathit{M}}}^{(t+1)}=\frac{N}{K}\sum _{k=1}^K\frac{{\mathit{r}}_k{\mathit{r}}_k^{†}}{{\mathit{r}}_k^{†}{\left({\overline{\mathit{M}}}^{\left(t\right)}\right)}^{-1}{\mathit{r}}_k}.$$

(5)

This iterative process continues until the estimates of $\overline{\mathit{M}}$ begin to converge. The rate of convergence depends on the parameters N and K [39]. In this study, we choose the initial value of $\overline{\mathit{M}}$ as the sample covariance matrix of the normalized data (NSCM). At the end of these iterations, having reached convergence, we use the final set of ${\tau }_1^{(t+1)},\cdots ,{\tau }_k^{(t+1)}$ for the adaptive waveform design in the second sub-dwell, which is elaborated in Section 6.

5. A Constrained GLRT Detector

In this section, we devise a constrained GLRT detector, which is capable of exploiting multipath phenomena, for the final decision regime at the end of sub-dwell two. It is assumed that the primary data covariance matrix in the target present case is in the neighborhood of the covariance matrix, which is estimated through the secondary data. Estimating the total covariance matrix of the RCUT from secondary data set may give accurate results when the received signal has only a line of sight component. However, in the case of diffuse multipath, whose direction of arrivals are not predictable, huge performance degradation is expected due to mismatch between two covariance matrices. The degree of mismatch, from the opposite perspective similarity, between the two covariance matrices is up to both multipath and clutter returns [17,20]. Accordingly, received signal $\mathbf{r}$ in hypothesis testing (1) is modeled as including i.i.d. zero mean complex Gaussian vector $\mathbf{s}$, which accounts for the target response with diffuse multipath, and also including ${\mathit{c}}_k$ for clutter returns coming from adjacent cells. In this case, the total covariance matrix of the primary data in the target present case can be represented as

$$\mathit{M}=(\tau |z_s[i-i_0]{|}^2+\beta )\overline{\mathit{M}}+\Sigma |z_s[i-i_0]{|}^2$$

(6)

where $\beta$ represents the clutter returns coming from adjacent cells, and it is given as

$$\beta =\sum _{k=1}^K{\tau }_k{\left|z_s\left[k\right]\right|}^2.$$

In addition, the covariance matrix of the primary data in the target absent case can be expressed as

$$\mathit{M}=(\tau |z_s{\left[i\right]|}^2+\beta )\overline{\mathit{M}}={\tau }_0\overline{\mathit{M}}.$$

(7)

Note that the scattered clutter from adjacent cells $\beta$, which increases the clutter power in RCUT, and the auto-correlation function $z_s$ are both included in Equations (6) and (7) together with the scaling factor of noise covariance $\tau$, since they all affect the overall covariance matrix. In addition, the covariance matrix of the diffuse multipath returns $\mathsf{\Sigma }$ is included in equation (6), since it causes covariance matrix mismatch. Thus, in order to solve the overall detection problem, a constrained GLRT detector as in [19] is deduced by the following decision rule.

$$\begin{array}{c}\hfill \frac{{\displaystyle \underset{\alpha \in \mathbb{C},\mathit{M}\in \Psi }{max}{\displaystyle p_1(\mathit{y};\alpha ,\mathit{M})}}}{{\displaystyle \underset{{\tau }_0=\widehat{{\tau }_0},\overline{\mathit{M}}={\mathit{M}}_{FPE}}{max}{p}_0(\mathit{y};{\tau }_0,\overline{\mathit{M}})}}\begin{array}{c}\stackrel{\stackrel{H_1}{>}}{\stackrel{<}{H_0}}\end{array}{\eta }_1\end{array}$$

(8)

where

$$\begin{array}{ccc}\hfill p_1(\mathit{y};\alpha ,\mathit{M})& =& \frac{1}{\left|\pi \mathit{M}\right|}exp-{(\mathit{y}-\alpha \mathit{p})}^{†}{\mathit{M}}^{-1}(\mathit{y}-\alpha \mathit{p})\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill p_0(\mathit{y};{\tau }_0,\overline{\mathit{M}})& =& \frac{1}{\left|\pi \right({\tau }_0\overline{\mathit{M}}\left)\right|}exp-{\mathit{y}}^{†}{\left({\tau }_0\overline{\mathit{M}}\right)}^{-1}\mathit{y}\hfill \end{array}$$

(10)

Here, $\mathit{y}$ is the matched filter output for RCUT, ${\eta }_1$ is the detection threshold set according to the desired Probability of False Alarm, $P_{fa}$. ${\mathit{M}}_{FPE}$ is the speckle covariance matrix estimate obtained via FPE algorithm, and ${\widehat{\tau }}_0\approx {\sum }_{k=i-K/2}^{i+K/2}{\widehat{\tau }}_k$. Under $H_1$ hypothesis, the following similarity constraint is used with the assumption of M is in the neighborhood of $\widehat{\mathit{M}}$$={\mathit{M}}_{FPE}$.

$$\mathsf{\Psi }=\left\{\begin{array}{c}\parallel {\widehat{\mathit{M}}}^{1/2}{\mathit{M}}^{-1}{\widehat{\mathit{M}}}^{1/2}-{\tau }_x{\mathit{I}\parallel }_2\le ϵ\hfill \\ \mathit{M}\succ \mathbf{0}\hfill \\ {\tau }_x>0\hfill \\ ϵ>0\hfill \end{array}\right.$$

(11)

where ${\tau }_x$ is a substitute parameter, and given as

$${\tau }_x=\frac{1}{\tau |z_s[i-i_0]{|}^2+\beta }.$$

In (11), ${\tau }_x$ and $ϵ$ parameters both control the size of the covariance uncertainty region due to the clutter and the multipath return, respectively. Note that $ϵ$ is a priori information for multipath exploitation whereas ${\tau }_x$ is an unknown parameter which is estimated. The effect of $ϵ$ parameter is investigated in the performance analysis sections of [17,20] in detail.

The decision rule in (8) can be reduced to the following, [17,20].

$${\displaystyle \underset{\tilde{\alpha }\in \mathbb{C},\mathit{M}\in \tilde{\Psi }}{max}\left[logdet\left(\mathit{X}\right)-{(\tilde{\mathit{y}}-\tilde{\alpha }\tilde{\mathit{p}})}^{†}\mathit{X}(\tilde{\mathit{y}}-\tilde{\alpha }\tilde{\mathit{p}})+Nlog\left({\widehat{\tau }}_0\right)+\frac{\parallel \tilde{\mathit{y}}{\parallel }^2}{{\widehat{\tau }}_0}\right]\begin{array}{c}\stackrel{\stackrel{H_1}{>}}{\stackrel{<}{H_0}}\end{array}{\eta }_2}$$

(12)

with the constraint set $\tilde{\mathsf{\Psi }}$, which is defined as

$$\tilde{\mathsf{\Psi }}=\left\{X\succ \mathbf{0},{\tau }_x>0:{\parallel X-{\tau }_{x}I\parallel }_2\le ϵ\right\}$$

where

• $X={\widehat{M}}^{1/2}{M}^{-1}{\widehat{M}}^{1/2}$,
• $\tilde{y}={\widehat{M}}^{-1/2}y,\tilde{p}=\frac{{\widehat{M}}^{-1/2}p}{\parallel {\widehat{M}}^{-1/2}p\parallel },\mathrm{and}\tilde{\alpha }=\alpha \parallel {\widehat{M}}^{-1/2}p\parallel$.

First we fix ${\tau }_x$ to ${\overline{\tau }}_x$. Then, we can find the optimal solution to the given decision statistics in (12) by solving the following optimization problem.

$$\mathcal{P}\left\{\begin{array}{cc}{\displaystyle \underset{\mathit{X},\tilde{\alpha }}{max}}\hfill & \begin{array}{c}{\displaystyle logdet\left(\mathit{X}\right)-{(\tilde{\mathit{y}}-\tilde{\alpha }{\mathit{p}}_1)}^{†}\mathit{X}(\tilde{\mathit{y}}-\tilde{\alpha }{\mathit{p}}_1)}\end{array}\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & \begin{array}{c}\mathit{X}\in \tilde{\Psi }\hfill \end{array}\hfill \\ & \tilde{\alpha }\in \mathbb{C},\hfill \end{array}\right.$$

(13)

An optimal solution $({\mathit{X}}^{🟉}\left(\overline{{\tau }_x}\right),{\tilde{\alpha }}^{🟉})$ to problem $\mathcal{P}$ is given by:

$${\tilde{\alpha }}^{🟉}={\tilde{\mathit{p}}}^{†}\tilde{\mathit{y}}$$

$${\mathit{X}}^{🟉}\left(\overline{{\tau }_x}\right)={\mathit{V}}_0\mathbf{diag}\left({\mathit{\lambda }}^{🟉}\left(\overline{{\tau }_x}\right)\right){\mathit{V}}_0^{†}$$

where ${\mathit{V}}_0$ is a unitary matrix as in [17], and ${\mathit{\lambda }}^{🟉}=[{\lambda }_1^{🟉}\left(\overline{{\tau }_x}\right),\dots ,{\lambda }_N^{🟉}\left(\overline{{\tau }_x}\right)]$ is the eigenvalue vector of X and its optimum value is given as follows [20];

$${\lambda }_i^{🟉}\left(\overline{{\tau }_x}\right)=\left\{\begin{array}{c}\overline{{\tau }_x}+ϵ,0<i<N\hfill \\ min(\overline{{\tau }_x}+ϵ,max(\overline{{\tau }_x}-ϵ,\frac{1}{\gamma })),i=N\hfill \end{array}\right.$$

where $\gamma =\parallel \tilde{\mathit{y}}{\parallel }^2-{\left|{\tilde{\mathit{p}}}^{†}\tilde{\mathit{y}}\right|}^2$.

Next, it remains to maximize the unknown noise level parameter ${\tau }_x$. Resorting to the affine mapping property [48], ${\tau }_x$ can be maximized exactly as in [20], and the detector can be written as the following.

$$\begin{array}{c}\hfill t\left(ϵ\right)=g_{ϵ}\left(\gamma \right)+{\gamma }_0\begin{array}{c}\stackrel{\stackrel{H_1}{>}}{\stackrel{<}{H_0}}\end{array}{\eta }_3.\end{array}$$

(14)

where

• $g_{ϵ}\left(\gamma \right)=(N-1)log({\tau }_x^{🟉}+ϵ)+log({\tau }_x^{🟉}-ϵ)-\gamma ({\tau }_x^{🟉}-ϵ)$
• ${\gamma }_0=Nlog\left({\widehat{\tau }}_0\right)+\frac{\parallel \tilde{y}{\parallel }^2}{{\widehat{\tau }}_0}$.

The optimum solution of ${\tau }_x$, which is represented with ${\tau }_x^{🟉}$, is expressed as in [20].

$${\tau }_x^{🟉}=\frac{N+\sqrt{N^2+4\gamma ϵ(\gamma ϵ-N+2)}}{2\gamma }.$$

6. Design of the Waveform

In this section, a detailed description of the waveform design is given. First the ith range, at the end of sub-dwell one, is considered, since all bins in the range cells contribute to the out-of-bin clutter except the ith bin itself. In order to minimize the clutter effect from out-of-bin cells the waveform in sub-dwell two is designed such that its auto-correlation function takes the values close to zero at those bins where the clutter is estimated to have the highest energy.

The FPE algorithm which estimates the clutter in the primary data, provides also an estimate of the texture ${\tau }_k,\mathit{k}\in [\mathit{i}-[K-1],\mathit{i}+[K-1]]$ that is considered for the waveform design. To create a waveform whose auto-correlation function is negligibly small where ${\tau }_k$ is large, let’s consider an uni-modular phase modulated (PM) waveform [31,32,33,34], given by:

$$s_2\left(t\right)=exp\left(j\psi \left(t\right)\right),0<t<T_s$$

(15)

where the phase modulation is expanded in range in terms of an orthogonal set of basis functions ${\psi }_i$ as

$$\psi \left(t\right)=\sum _{i=1}^{N_s}{\lambda }_i{\psi }_i\left(t\right)$$

(16)

and

$${\psi }_i\left(t\right)=\left\{\begin{array}{c}1,(i-1)∆T_s<t<i∆T_s\hfill \\ 0,otherwise\hfill \end{array}\right.$$

Here, $T_s$ and $∆T_s$ are the pulse duration and the sampling interval, respectively. In order to eliminate the effect of clutter in the RCUT, we need to design the waveform $s_2\left(t\right)$, which will optimize the matched filter output. To do so, we need to solve the following optimization problem which finds the ${\lambda }_i$ values that minimize the auto-correlation function where ${\tau }_k$ is large.

$$\underset{\mathit{\lambda }}{min}\sum _{Z_{\tau }}{\left|z_{s_2}\left[m\right]\right|}^2$$

(17)

where $Z_{\tau }$ is the set of out-of-range bins for which the texture values are large and $z_{s_2}\left[m\right]$ is the auto-correlation function of $s_2\left(t\right)$ given by:

$$z_{s_2}\left[m\right]=\frac{1}{N_s}\sum _{i=1}^{N_s-m}[cos({\lambda }_{m+i}-{\lambda }_i)+jsin({\lambda }_{m+i}-{\lambda }_i)]$$

(18)

The optimization problem as expressed in (17) can be solved through a Newton-Raphson method.

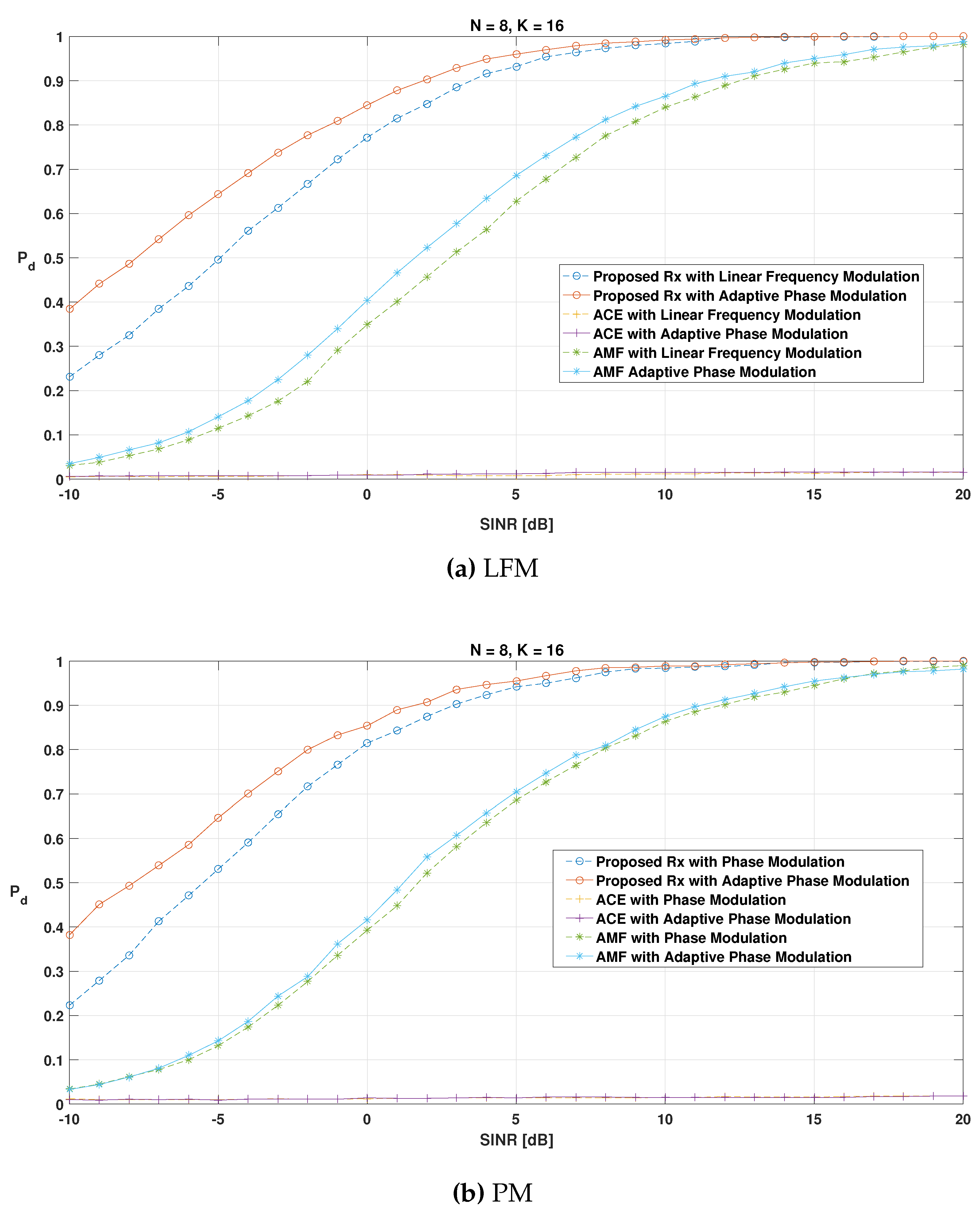
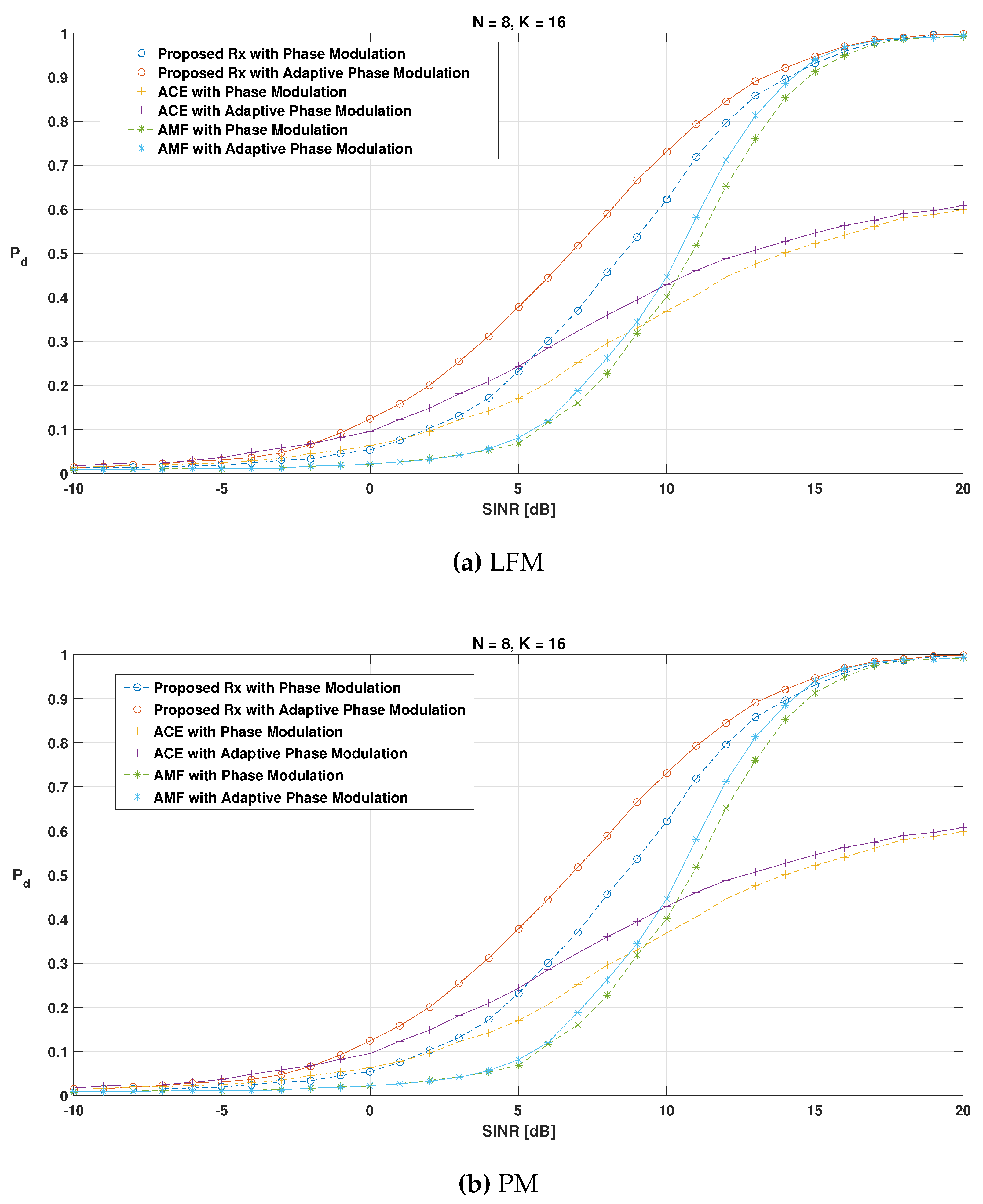
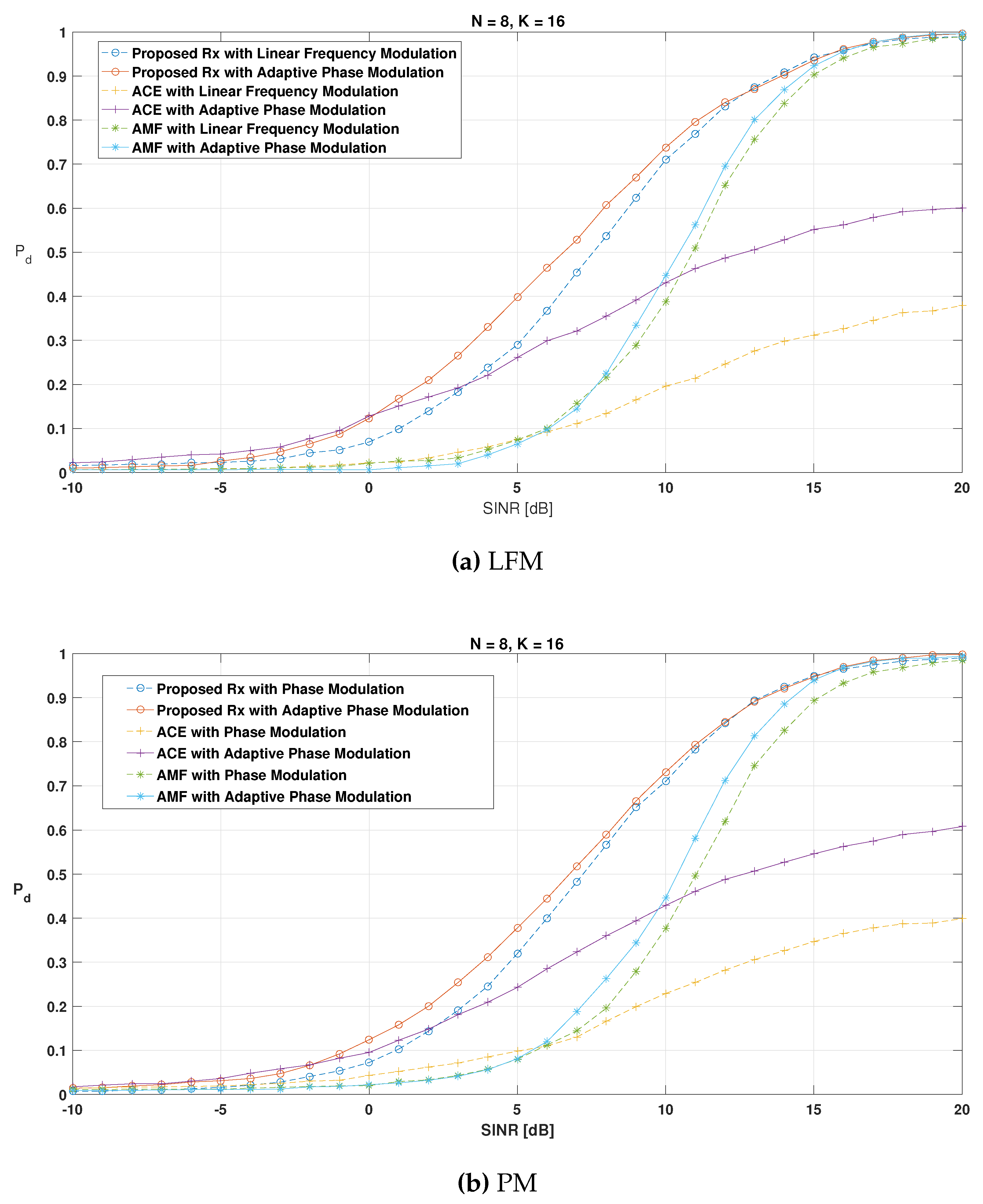
7. Simulation Setup and Performance Analysis

In this section, we present the simulation setup, and later the performance analysis of the proposed adaptive detector along with designed adaptive waveform with probability of detection (Pd) versus signal-to-interference-plus-noise ratio (SINR) graphs. Non-adaptive Linear Frequency Modulated (LFM) and Phase Modulated (PM) waveforms were included in performance comparison to analyze the improvement due to designed adaptive waveform. We also present the performance of the proposed multipath exploited adaptive detector AMF and ACE. Note that the ACE detector is invariant to the scaling of the noise covariance matrix [47]. Hence, it is suitable for the comparison in a heterogeneous environment. On the other hand, AMF is suitable for the comparison in the presence of multipath since it is classified as a robust receiver against steering vector mismatches.

The pulse duration of the waveforms in sub-dwell one and sub-dwell two were chosen as 1 μs. The frequency sweep of LFM is chosen as 100 MHz and bit duration of PM was chosen as 0.01 μs. Additionally, the sampling frequency was set as 100 MHz so that the number of samples for a pulse to be 100. While constructing the adaptive waveform described in Section 6, we used 100 orthogonal set of basis functions (${\psi }_i$) in order to equalize the time bandwidth product of the adaptive waveform to the other two non-adaptive waveforms.

In order to avoid computational burden, $N_p=8$ number of pulses were transmitted in each sub-dwell, and the sensor number was chosen as one. Besides, $K=16$ secondary data were used. For the waveform design in sub-dwell 2, we used the largest eight texture estimates out of K secondary data to define $Z_{\tau }$ in the Equation (17). During the performance analysis of the multipath exploited detection algorithm with the proposed adaptive waveform, we made use of Monte Carlo counting techniques. The $P_{fa}$ value was preassigned to ${10}^{-2}$ and the threshold of the GLRT was evaluated resorting to $100/P_{fa}$ independent trials. In addition, each value of $P_d$ was evaluated by using ${10}^4$ independent realizations of the decision statistics.

The interference covariance matrix $\overline{\mathit{M}}$ of the primary data covariance was calculated as the following, where ${\sigma }_n^2=1$ is the thermal noise power, ${\sigma }_c^2>0$ is the clutter power, and ratio between them, ${\sigma }_c^2/{\sigma }_n^2$, is 24 dB.

$$\overline{\mathit{M}}={\sigma }_c^2\overline{{\mathit{M}}_1}+{\sigma }_n^2\mathit{I}$$

The $(n,m)$-th entry of $\overline{{\mathit{M}}_1}$ is given below, where ${\sigma }_d=0.995$ is the one-lag correlation coefficient [49].

$$\overline{{\mathit{M}}_1}(n,m)=e^{-{(n-m)}^2/\left(2{\sigma }_d^2\right)}$$

In addition, the texture parameter $\tau$ of the compound Gaussian model had gamma distribution with the shape parameter $0.5$ and scale parameter 1. In the simulation of diffuse multipath environment for the cell under test, we assumed $N_{ML}=4$ main lobe and $N_{SL}=4$ sidelobe scatterers were coming from glistening points. The amplitudes of the scattered components were assumed to be dependent on the amplitude of the line of sight component with following equation.

$${\alpha }_i=\alpha \frac{x_i}{\sqrt{L}},i=1,\dots ,N_{ML}+N_{SL}$$

where x is an independent zero-mean circular symmetric complex normal random variable with unit variance, and L represents path loss in decibels.

The path loss was set to several values in the presented figures. The $ϵ$ value, which was used as a priori information about the multipath severity, was set as $0.75$. Moreover, SINR in the simulations was defined as the ratio of the target signal power to the total power of the interference in the range cell under test which is given by

$$\mathrm{SINR}={\left|\alpha \right|}^2{\mathit{p}}^{†}{\mathit{M}}^{-1}\mathit{p}.$$

It is also important to note that we investigated the performance gain of the detectors related to the proposed adaptive waveform, thus we did not make use of techniques like clutter suppression to increase the SINR values.

First, the Pd-SINR curves of the detectors were obtained at the end of sub-dwell 1 with the transmitted non-adaptive LFM and PM waveforms. Later, PD-SINR curves were obtained at the end of sub-dwell 2 after transmitting the adaptive phase modulated (APM) waveform. The performance analysis in Figure 3, Figure 4 and Figure 5 was conducted to observe the performance of detectors under diffuse multipath conditions with arranging severity of the multipath by setting L parameter. In Figure 3, the performance of the detectors was observed when diffuse multipath condition was assumed to have L = 10 dB. Then, in order to make the effects of the multipath less severe, we increased the value of L in Figure 4 and Figure 5, where $L=20$ and $L=30$ respectively.

One can observe that ACE gave lower $P_d$ results compared to the proposed detector and AMF under multipath conditions. This was an expected result since ACE has selective characteristics. It was also observed that performance difference between non-adaptive and adaptive waveforms was quite small during high or low end SINR levels. Besides, the detection performance of AMF was observed as not changing significantly between sub-dwell one and two with L values, namely 10, 20 and 30 dB. On the other hand, the proposed detector and ACE performed better when APM waveform used in the second sub-dwell. The performance improvement of ACE with APM waveform can better be observed in Figure 4. It is also important to note that LFM waveform with the proposed detector showed performance degradation with respect to PM waveform when diffuse multipath was less severe, i.e., $L=30$ in Figure 4.

In order to obtain results in Figure 6a, the Pd-SINR curves for three detectors were calculated by transmitting N = 16 identical non-adaptive LFM pulses first. In other words, the dwell was not divided into two sub-dwells, and no adaptive waveform is used. The results were compared with the performance of the proposed adaptive waveform algorithm which transmitted N = 8 LFM pulses in sub-dwell one followed by N = 8 adaptive phase modulated (APM) pulses in sub-dwell two. In Figure 5b, the same procedure was applied using non-adaptive PM waveform instead of LFM. It was well expected to observe that non-adaptive LFM and PM waveforms with the proposed detector performed better then the non-adaptive waveform results in Figure 3, Figure 4 and Figure 5 due to integration of more pulses, namely two times. However, ACE exhibited performance degradation when N = 16 non-adaptive waveform was transmitted rather than N = 8. The selectivity probability of ACE may have caused this performance loss since much more interference was coming to the reference cell from the adjacent cells when N = 16 pulses were transmitted.

It is evident from the figures that the proposed detector with adaptive waveform had performance improvement than the non-adaptive waveform case of the same detector in each scenario. Besides, the proposed detector with and without adaptive waveform had $P_d$ gain with respect to the ACE and the AMF detectors. The later is because the proposed detector also exploited multipath, and thus had more robust characteristics in diffuse multipath environments.

8. Conclusions

An adaptive detector with an adaptive waveform design has been proposed in order to increase SINR ratio on glistening surfaces. The advantage of the detector is to exploit diffuse multipath returns of the target while suppressing the clutter coming from the adjacent cells. In this respect, a constrained GLRT detector is used for multipath exploitation and an adaptive waveform structure is introduced to suppress clutter. In particular, a radar system that consists of two sub-dwells, where each dwell is represented by the number of pulses, has been considered. At the end of sub-dwell one, the clutter in the range cell under test is estimated via the FPE algorithm while the constrained GLRT detector is used for pre-detection. The FPE algorithm is also used to design the adaptive waveform for the second dwell in order to suppress the clutter. At the end of sub-dwell two, the constrained GLRT detector is used for the final decision. In conclusion, we devise a cognitive architecture improving the SCR in the range bin under test by not only exploiting the multipath returns of useful target echo but also suppressing the clutter coming from the adjacent radar cells. The simulation results indicate that devised cognitive architecture can improve the SINR in the range bin under test by suppressing the clutter coming from the adjacent radar cells. It is also shown that conceived detector is more robust to multipath effect compared to conventional adaptive detectors not exploiting multipath returns.

It is worth adding that we recognize the necessity and importance of using real data to analyze and verify the performance of the proposed technique, but constructing such an experimental study or using real data is outside the scope of this current manuscript. However, it is our future work plan to acquire real data and test the proposed technique. The actual detection strategy presented in this manuscript provides promising results to improve the detection performance via multipath exploitation and waveform design in heterogeneous clutter and diffuse multipath environment. Thus, this current work is a necessary theoretical approach and it represents a starting point towards further experimental studies.