A Fast Back-Projection SAR Imaging Algorithm Based on Wavenumber Spectrum Fusion for High Maneuvering Platforms

Abstract

In this paper, a fast back-projection (BP) synthetic aperture radar (SAR) imaging algorithm based on wavenumber spectrum fusion is proposed for high maneuvering platforms with high squint angles and high dive angles. When the platforms have nonlinear trajectory errors, the trajectory errors will introduce significant spectrum displacement, which varies with the target position. If the influence of trajectory error is not considered, the trajectory’s deviation from the ideal SAR imaging geometry will degrade the focusing performance. The dive angle will further enlarge the influence on SAR focusing. In this paper, the center function of the spatially variable sub-aperture wavenumber spectrum is derived, firstly, which is the basis for reasonably setting the oversampling rate. Then, the accurate spectrum fusion method is proposed, which is efficiently implemented by fast Fourier transform (FFT) and circular shifting. The proposed algorithm is called high-squint and high-dive accelerated factorized back-projection (HSHD-AFBP). Compared to the commonly used spectrum fusion method, HSHD-AFBP not only improves the imaging quality, but also expands the image width. Finally, the effectiveness of the proposed algorithm is verified by simulation data.

1. Introduction

As a powerful microwave imaging system, synthetic aperture radar (SAR) is widely concerned in the military and civil detection fields because of its advantages for all-time and all-weather working ability [1,2]. As is well known, SAR achieves range resolution by transmitting large time-bandwidth product signals, and azimuth resolution by the synthetic aperture, which is formulated by the relative motion of the platform and the target to obtain the azimuth-Doppler bandwidth. The high maneuvering platform has the characteristics of fast flight speed and high maneuverability, which can realize the requirement of advanced observation. With the rapid development of SAR applications, high maneuvering platforms SAR imaging technology has become a hot issue in SAR imaging application [3,4,5,6].

At present, SAR imaging algorithms are usually divided into two categories: frequency domain algorithms and time domain algorithms.

Traditional frequency domain algorithms, such as the range-Doppler algorithm (RDA) [7], chirp scaling algorithm (CSA) [8,9,10], nonlinear chirp scaling algorithm (NCSA) [11], many extensions of the NCSA (ENCSA) [12,13], etc., are widely used and deeply investigated. These methods use the azimuth translation-invariance of echo data to uniformly deal with the spatial variation of echo data in the range of the Doppler domain, so the efficiency of the algorithm is high. However, if the radar platform’s moving trajectory has a large dive angle and squint angle, simultaneously combining with high maneuvering ability, the radar echoes have inherent spatial variation, and the high-squint angle observation mode gives the echo data a serious coupling effect between range and azimuth, as well as Doppler folding. Therefore, the traditional frequency domain algorithms cannot be directly applied to high maneuvering platforms.

The widely used time domain algorithm is the back-projection algorithm (BPA) [14,15,16,17,18], which is suitable for arbitrary platforms and arbitrary trajectories, and adopts the method of point-by-point coherent accumulation to achieve high-precision SAR imaging with accurate motion compensation. The disadvantage of BPA is the intensive computational burden and that the motion trajectory is required to have high accuracy. To improve SAR imaging efficiency, two improved BP algorithms—the fast BP (FBP) [15] algorithm and the fast factorized BP (FFBP) algorithm [17]—have recently been developed. During sub-image fusion, the FFBP often needs two-dimensional image-domain complex interpolation for SAR imaging performance conservation, so it still produces a huge amount of calculation. Considering imaging efficiency and imaging performance, the accelerated fast BP algorithm (AFBP) is developed in [18]. Sub-aperture wavenumber spectrum fusion is carried out in the wavenumber spectrum domain by using a unified polar coordinate system. Compared with the conventional FBP algorithm, the AFBP can precisely focus more efficiently by means of the implementation of fast Fourier transform (FFT) and circular shifting for wavenumber domain SAR fusion. However, AFBP is suitable for a broadside mode, and it fails to correct the sub-image spectrum center accurately in high-squint SAR. Moreover, AFBP cannot deal with a nonlinear trajectory, which limits its practical application in the SAR field. The high-squint AFBP algorithm (HS-AFBP) for airborne SAR processing is proposed in [19], and two spectrum center functions are also given for linear and nonlinear trajectories. In [19], the radar platforms’ motion error is modeled as a linear function for two-dimensional spatial variance. The angular-variant coefficient, generally being a constant, is obtained by first-order fitting of the motion errors in the central range cell. However, the motion errors introduce the displacement of the sub-aperture spectrum centers of point targets for different angular positions even in the same range cell. That is to say, the angular-variant coefficient varies with the target position. Therefore, the linear function model of the two-dimensional spatial variance cannot be used accurately to represent the real motion errors. Moreover, this approximation error of the linear function model will increase with the motion errors and the dive angles’ increment.

In this paper, the high-squint and high-dive AFBP (HSHD-AFBP) is proposed for high maneuvering platforms SAR imaging. The main contributions can be specified as follows. Based on the high maneuvering platforms SAR imaging geometry, the relationship of the sub-aperture wavenumber spectrum centroid position and the target position is firstly derived. It is found that the center position of the sub-aperture wavenumber spectrum varies with the target position if the nonlinear motion errors occur for the high maneuvering platforms. The larger the motion errors and trajectory dive angles, the larger the center position variations. Secondly, an accurate sub-aperture spectrum fusion method is proposed, which eliminates spectrum folding by formulating the accurate spectrum shift function. The proposed spectrum fusion method can overcome the spatial variation influence of the center position of the sub-aperture spectrum, and then the SAR focusing performance can be guaranteed effectively.

This paper is organized as follows. In Section 2, the SAR signal model of high maneuvering platforms is established. In Section 3, the AFBP and HS-AFBP are briefly reviewed, followed by a detailed shortage description of the existed methods. In Section 4, the details of the proposed HSHD-AFBP algorithm are given. Firstly, the more accurate wavenumber spectrum center function of sub-aperture is derived and the constraint of the motion errors for the length of the sub-aperture is discussed. Then, the improved spectrum fusion method is proposed. Next, the integrated implementation process of the HSHD-AFBP algorithm is introduced. Finally, its computation load is discussed. In Section 5, the proposed algorithm is verified based on simulation experiments. Section 6 summarizes this paper.

2. Signal Model

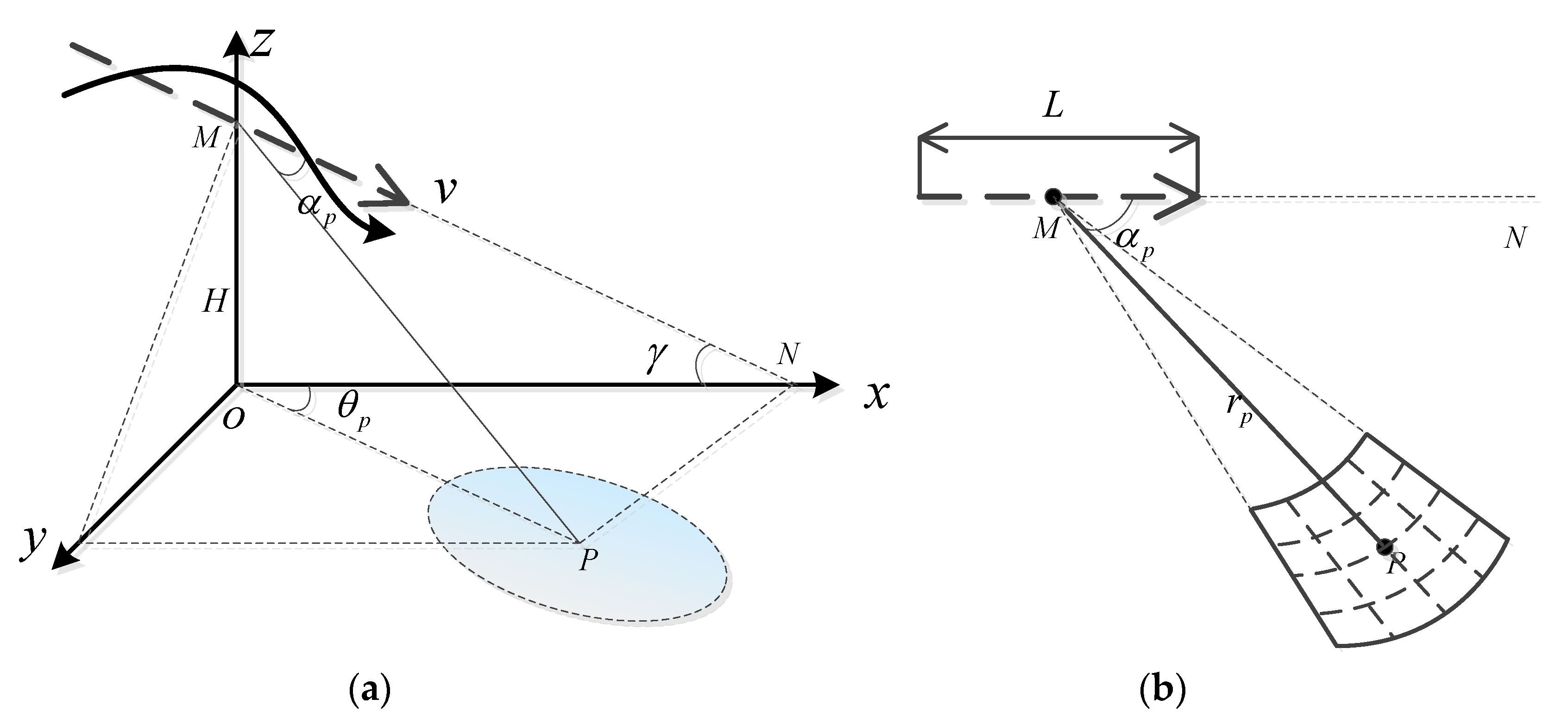
The geometry of high maneuvering platforms SAR is shown in Figure 1. All of the parameters in Figure 1a are defined in the local ground coordinate system. The origin $o$ of the coordinate system is the projection point of the aperture center on the ground. The $xoy$ plane is parallel to the surface of the Earth. The positive direction of the $x$-axis is the projection direction of the platform’s speed in the $xoy$ plane. The solid line with arrow represents a true trajectory, and dashed lines with arrows indicate a nominal trajectory. The ideal trajectory is obtained by one-dimensional fitting of the actual trajectory. The motion speed of the ideal trajectory is $v$. The nominal trajectory intersects the $z$-axis at $M$ and the $x$-axis at $N$. $\gamma$ represents the angle between the speed direction and $x$ axis, i.e., the dive angle. ${\alpha }_p$ represents the angle between the speed direction and the straight line, $\mathrm{MP}$. ${\theta }_p$ represents the angle between the $x$-axis and the straight line, $\mathrm{OP}$. The platform’s height is $H$.

We denote $\tau$ as the slow time. At an arbitrary azimuth time, the ideal antenna phase center position of uniform linear motion can be expressed as $\left[X\left(\tau \right),0,Z\left(\tau \right)\right]$ with $X\left(\tau \right)=v\cdot \cos \gamma \cdot \tau$, $Z\left(\tau \right)=H-v\cdot \mathit{sin}\gamma \cdot \tau$. The actual antenna phase center position can be expressed as $\left[X\left(\tau \right)+\Delta X\left(\tau \right),\Delta Y\left(\tau \right),Z\left(\tau \right)+\Delta Z\left(\tau \right)\right]$. For the convenience of formula derivation, $X\left(\tau \right)$,$Z\left(\tau \right)$,$\Delta X\left(\tau \right)$,$\Delta Y\left(\tau \right)$,$\Delta Z\left(\tau \right)$ will be abbreviated as $X$,$Z$,$\Delta X$,$\Delta Y$, ΔZ, in turn, in the following. The actual instantaneous slant range of an arbitrary point target $P\left(x_p,y_p,0\right)$ in the scene can be expressed as:

$$R\left(\tau ;x_p,y_p\right)=\sqrt{{\left(X+\Delta X-x_p\right)}^2+{\left(\Delta Y-y_p\right)}^2+{\left(Z+\Delta Z\right)}^2}$$

(1)

The $\mathrm{MNP}$ plane is the imaging slant plane of target $P$. Figure 1b shows the polar coordinate system established on the $\mathrm{MNP}$ plane. The whole-aperture length is $L$. The center of the aperture and the origin of the polar coordinate system is $M$. Point target $P$ can be expressed as $\left(r_p,{\Theta }_p\right)$ in the polar coordinate system, denoted as ${\Theta }_p=\cos {\alpha }_p$. Then, the conversion relationship between the point target $P$ in the Cartesian coordinate system and the polar coordinate system can be established:

$$\{\begin{array}{c}{x}_p=\frac{\left(r_p{\Theta }_p-H\cdot \mathit{sin}\gamma \right)}{\mathit{cos}\gamma }\\ y_p=\sqrt{r_p^2-H^2-x_p^2}\end{array}$$

(2)

Substituting Equation (2) into Equation (1), we can get:

$$R\left(\tau ;x_p,r_p\right)=\sqrt{{\left(X+\Delta X-x_p\right)}^2+{\left(\Delta Y-\sqrt{r_p^2-H^2-x_p^2}\right)}^2+{\left(Z+\Delta Z\right)}^2}$$

(3)

Ideally, the platform flies along the linear trajectory with a constant speed, $v$. In the polar coordinate system, the instantaneous slant range between the target $P$ and the ideal trajectory can be expressed as [18]:

$$R\left(r_p,{\Theta }_p;D\right)=\sqrt{r_p^2+D^2-2r_{p}D{\Theta }_p}, -\frac{L}{2}<D\le \frac{L}{2}$$

(4)

where $D=v\tau$.

Assumed that the SAR system transmits a linear frequency modulation (LFM) signal with a bandwidth of $B$ and a wavelength of $\lambda$, the range compressed signal of the target $P$ can be expressed as:

$$S_{rc}\left(t,D\right)=rect\left(\frac{D}{L}\right)\cdot \mathit{sin}c\left[B\cdot \left(t-\frac{2R\left(r_p,{\Theta }_p;D\right)}{c}\right)\right]\cdot \mathit{exp}\left[-j4\pi \frac{R\left(r_p,{\Theta }_p;D\right)}{\lambda }\right]$$

(5)

where

$$\mathit{sin}c\left(x\right)=\frac{\mathit{sin}\left(\pi x\right)}{\pi x}$$

(6)

$$rect\left(\frac{D}{L}\right)=\{\begin{array}{c}1,-\frac{L}{2}<D\le \frac{L}{2}\\ 0,\mathit{else}\end{array}$$

(7)

3. Problem Description

The AFBP algorithm was proposed in [18]. Before that, all of the FBP imaging algorithms adopted an interpolation method for sub-aperture wavenumber spectrum fusion, and the echo data focusing effect was greatly affected by the accuracy of the interpolation function. The AFBP algorithm is realized under the unified polar coordinate system instead of the traditional interpolation fusion method by the wavenumber spectrum fusion. The core of the AFBP algorithm is to establish the Fourier transform relationship between the angular-domain impulse response function and the angular-domain wavenumber spectrum function. The concrete derivation process is as follows.

Since the main energy of point target $P$ is concentrated in the small angle neighborhood with $P$ as the center, the response function of point target $P$ can be obtained by Equation (8). Then, integrating along the range history of $R\left(r_p,\Theta ;D\right)$ to $S_{rc}\left(t,D\right)$ within the small angle range $\Theta$, where $\Theta \in {\Theta }_p+\Delta \Theta$ with ${\Theta }_p$ as the center. The impulse response function of point target $P$ in the $uth$ sub-aperture can be expressed as:

$$I_u\left(r_p,\mathsf{\Theta }\right)={{\displaystyle \int }}_{-\frac{l}{2}+x_u}^{\frac{l}{2}+x_u}{S}_{rc}\left(t=\frac{2R\left(r_p,{\mathsf{\Theta }}_p;D\right)}{c},D\right)·exp\left(j4\pi \frac{2R\left(r_p,\Theta ;D\right)}{\lambda }\right)dD$$

(8)

where $D\in x+x_u, -l/2\le x<l/2$, $x_u$ represents the center of the $uth$ sub-aperture. Substituting Equation (5) into Equation (8), we obtain the following expression:

$$I_u\left(r_p,\mathsf{\Theta }\right)={{\displaystyle \int }}_{-\frac{l}{2}+x_u}^{\frac{l}{2}+x_u}exp\left(-j4\pi \frac{\Delta R\left(r_p,\Theta ;D\right)}{\lambda }\right)dD$$

(9)

where

$$\Delta R\left(r_p,\Theta ;D\right)=R\left(r_p,{\mathsf{\Theta }}_p;D\right)-R\left(r_p,\Theta ;D\right)\approx \left(\Theta -{\mathsf{\Theta }}_p\right)·D$$

(10)

In Equation (10), both the quadratic term and higher-order term can be ignored for the broadside mode [18]. Substituting Equation (10) into Equation (9), the following can be obtained:

$$\begin{array}{ll}{I}_u\left(r_p,\mathsf{\Theta }\right)& ={{\displaystyle \int }}_{-\frac{l}{2}+x_u}^{\frac{l}{2}+x_u}exp\left[-j4\pi \frac{\left(\Theta -{\mathsf{\Theta }}_p\right)·D}{\lambda }\right]dD\\ & ={{\displaystyle \int }}_{-\Delta K_{\alpha }/2+K_{au}}^{\Delta K_{\alpha }/2+K_{au}}exp\left[-j\left(K_{\alpha }+K_{au}\right)\left(\Theta -{\mathsf{\Theta }}_p\right)\right]d{K}_{\alpha }\\ & =l·sinc\left[\frac{2l}{\lambda }\left(\Theta -{\mathsf{\Theta }}_p\right)\right]·exp\left[-j{K}_{au}\left(\Theta -{\mathsf{\Theta }}_p\right)\right], \mathsf{\Theta }\in \left[-\frac{\Delta A_u}{2},\frac{\Delta A_u}{2}\right]\end{array}$$

(11)

where $\Delta A_u$ is the angular domain range of the pre-set sub-aperture SAR image, and $K_{\alpha }$ and $K_{au}$ represent the shape and center of the wavenumber spectrum in the angular domain, respectively.

$$\{\begin{array}{c}{K}_{\alpha }=\frac{4\pi }{\lambda }x\\ K_{au}=\frac{4\pi }{\lambda }{x}_u\end{array}$$

(12)

It can be clearly seen from Equation (11) that $K_{\alpha }$ and $\Theta$ are Fourier transform pairs, and the impulse response function $I_u\left(r_p,\mathsf{\Theta }\right)$ of the $u\mathrm{th}$ sub-aperture image can be abbreviated as $I_u\left(\mathsf{\Theta }\right)$.

$$\begin{gathered} I_u\left(K_{\alpha }\right)={{\displaystyle \int }}_{-\frac{\Delta A_u}{2}+A_{cu}}^{\frac{\Delta A_u}{2}+A_{cu}}{I}_u\left(\mathsf{\Theta }\right)·exp\left(j{K}_a\Theta \right)d\Theta =rect\left(\frac{K_{\alpha }-K_{au}}{\mathsf{\Delta }{K}_{\alpha }}\right)·exp\left(j\left(K_a-K_{au}\right){\Theta }_p\right) \\ {K}_{\alpha }\in (-\frac{\Delta K_{\alpha }}{2},\frac{\Delta K_{\alpha }}{2}]+K_{au} \end{gathered}$$

(13)

where $A_{cu}$ is the initialized angular center of the unified polar coordinate system and $\Delta K_{\alpha }=4\pi /\lambda ·l$ is the wavenumber width.

The AFBP algorithm is derived based on a linear trajectory with a constant speed assumption. When there are nonlinear motion errors in the trajectory of the platforms, spectra centroid displacement will be introduced for different ground targets. When fusing sub-aperture wavenumber spectra, the fusing error will degrade the SAR focusing performance if the influence of trajectory error is not considered. Moreover, the AFBP algorithm is only suitable for the broadside mode, not for the high-squint mode.

To deal with these constraints, the HS-AFBP method is proposed [19]. The linear function is used in the HS-AFBP method to fit the motion errors of the two-dimensional spatial variation, which extends the application range. For point target $P\left(r_p,{\Theta }_p\right)$ with HS-AFBP, the motion errors can be modeled as:

$$R_{error}\left(r_p,{\mathsf{\Theta }}_p;D\right)=c_0+c_1\left(D\right)·r_p+c_2\left(D\right)·{\mathsf{\Theta }}_p$$

(14)

where $c_0$ is a constant, $c_1$ denotes the range-variant coefficient, and $c_2$ represents the angular-variant coefficient. The $R_{error}\left(r_p,{\mathsf{\Theta }}_p;D\right)$ represents the difference between the ideal slant range and the actual slant range of the point target P. Then, the impulse response function of the point target under the nonlinear trajectory is derived as [19]:

$$I_u\left(r,\mathsf{\Theta }\right)={{\displaystyle \int }}_{-\frac{l}{2}+x_u}^{\frac{l}{2}+x_u}exp\left[-j\left(K_{\alpha }+K_{au}\right)\left(\Theta -{\mathsf{\Theta }}_p\right)\right]dx$$

(15)

where

$$\{\begin{array}{c}{K}_{\alpha }=\frac{4\pi }{\lambda }·\left(1+\frac{2{\mathsf{\Theta }}_p{x}_u}{r_p}\right)·x\\ K_{au}=\frac{4\pi }{\lambda }·\left(x_u+\frac{{\mathsf{\Theta }}_p}{r_p}{x}_u^2-c_2\left(x_u\right)\right)\end{array}$$

(16)

The previous HS-AFBP method is only suitable for a small trajectory error and small dive angle, and its imaging performance will deteriorate greatly, even becoming invalid, for a large trajectory error and high dive angle. The specific analysis will be introduced in detail in the next section.

4. HSHD-AFBP Algorithm

4.1. Derivation of HSHD-AFBP Algorithm

According to Equation (3), the slant range difference between point target $P$ and its adjacent angular-domain targets can be expressed as $\Delta R\left(\tau ;x_p,r_p\right)$.

$$\begin{array}{ll}\Delta R\left(\tau ;x_p,r_p\right)& =R\left(\tau ;x_p,r_p\right)-R\left(\tau ;x_p+\Delta x,r_p\right)\\ & =\sqrt{{\left(X+\Delta X-x_p\right)}^2+{\left(\Delta Y-\sqrt{r_p^2-H^2-x_p^2}\right)}^2+{\left(Z+\Delta Z\right)}^2}\\ & -\sqrt{{\left(X+\Delta X-\left(x_p+\Delta x\right)\right)}^2+{\left(\Delta Y-\sqrt{r_p^2-H^2-{\left(x_p+\Delta x\right)}^2}\right)}^2+{\left(Z+\Delta Z\right)}^2}\end{array}$$

(17)

The second-order Taylor expansion of Equation (17) with respect to $\Delta x$ can be obtained as follows:

$$\Delta R\left(\tau ;x_p,r_p\right)=\left[X-\Delta Y\frac{x_p}{y_p}+\Delta X\right]·\frac{1}{r_p}·\Delta x+\frac{1}{2}·\frac{\Delta Y}{r_p}·\frac{r_p^2-H^2}{y_p^3}·\Delta x^2+o\left(\Delta x^3\right)$$

(18)

According to Equation (2), we obtain

$$\Delta x=\frac{r_p}{cos\gamma }\left(\Theta -{\mathsf{\Theta }}_p\right)=\frac{r_p}{cos\gamma }·\Delta \Theta$$

(19)

Substituting Equation (19) into Equation (18), $\Delta R\left(\tau ;x_p,r_p\right)$ can be re-expressed as:

$$\begin{array}{l}\Delta R\left(\tau ;x_p,r_p\right)\approx \left[X-\Delta Y\frac{x_p}{y_p}+\Delta X\right]·\frac{1}{cos\gamma }·\Delta \Theta +\frac{1}{2}·\frac{\Delta Y}{r_p}·\frac{r_p^2-H^2}{y_p^3}·{\left(\frac{r_p}{cos\gamma }\right)}^2\Delta {\Theta }^2+o\left(\Delta {\Theta }^3\right)\\ \approx D·\Delta \Theta +\left[\Delta X-\Delta Y\frac{x_p}{y_p}\right]·\frac{1}{cos\gamma }·\Delta \Theta +\frac{1}{2}·\frac{\Delta Y\left(r_p^2-H^2\right)}{y_p^3}·\frac{r_p}{{\left(cos\gamma \right)}^2}\Delta {\Theta }^2\\ =D·\Delta \Theta +\left[\Delta X-\Delta Y\frac{x_p}{y_p}\right]·\frac{1}{cos\gamma }·\Delta \Theta +\Delta r\end{array}$$

(20)

where $\Delta r=\frac{1}{2}·\frac{\Delta Y\left(r_p^2-H^2\right)}{y_p^3}·\frac{r_p}{{\left(cos\gamma \right)}^2}\Delta {\Theta }^2$.

The term $\Delta r$ causes quadratic phase error (QPE) in BP integration, which is expressed by

$$\begin{gathered} \phi =\frac{4\pi }{\lambda }·\frac{1}{2}·\frac{\Delta Y\left(r_p^2-H^2\right)}{y_p^3}·\frac{r_p}{{\left(cos\gamma \right)}^2}·{\left(\Delta \Theta \right)}^2 \\ =\frac{2\pi }{\lambda }·\frac{\Delta Y}{{\left(cosr\right)}^2·sin{\alpha }_p·{\left(sin{\theta }_p\right)}^2}·{\left(\Delta \Theta \right)}^2 \end{gathered}$$

(21)

For the sub-aperture length $l_u$, the angular resolution can be expressed as $\Delta \Theta =\lambda /\left(2l_u\right)$ [20]. If $\phi$ can be constrained within $\pi /8$, its effect on BP integration can be neglected [20]. Substituting $\Delta \Theta =\lambda /\left(2l_u\right)$ into Equation (21), we can get the constraint of sub-aperture length $l_u$:

$$l_u\ge \frac{1}{cosr·sin{\theta }_p}\sqrt{\frac{4\lambda ·\mathsf{\Delta }Y}{sin{\alpha }_p}}$$

(22)

For typical high maneuvering platform parameters, the constraint is easy to satisfy. Therefore, Equation (20) is rewritten as

$$\Delta R\left(r_p,\Theta ;D\right)\approx D·\Delta \Theta +\left[\Delta X-\Delta Y\frac{x_p}{y_p}\right]·\frac{1}{cos\gamma }·\Delta \Theta$$

(23)

For an ideal linear trajectory, $\Delta \mathrm{X}=\Delta \mathrm{Y}=0$. In this case, Equation (20) can be simplified as

$$\Delta R\left(r_p,\Theta ;D\right)\approx D·\Delta \Theta$$

(24)

Comparing Equations (23) and (24), the slant range difference between point target $P$ and its adjacent angular-domain targets caused by motion error can be expressed as:

$$\Delta R_{error}\left(r_p,{\mathsf{\Theta }}_p;D\right)=R_{error}\left(r_p,{\mathsf{\Theta }}_p;D\right)-R_{error}\left(r_p,\mathsf{\Theta };D\right)=\left[\Delta X-\Delta Y\frac{x_p}{y_p}\right]·\frac{1}{cos\gamma }·\Delta \Theta$$

(25)

Equation (16) can be rewritten as:

$$\{\begin{array}{c}{K}_{\alpha }=\frac{4\pi }{\lambda }·\left(1+\frac{2{\mathsf{\Theta }}_p{x}_u}{r_p}\right)·x\\ K_{au}=\frac{4\pi }{\lambda }·\left(x_u+\frac{{\mathsf{\Theta }}_p}{r_p}{x}_u^2+\left[\Delta X-\Delta Y\frac{x_p}{y_p}\right]·\frac{1}{cos\gamma }\right)\end{array}$$

(26)

It can be seen from Equation (26) that the error component of the nonlinear motion trajectory causes the center position deviation of the target azimuth wavenumber spectrum; the displacement is related to motion error, the target position and the dive angle.

The impulse response function of the $uth$ sub-aperture can be expressed as:

$$\begin{gathered} I_u\left(r_p,\mathsf{\Theta }\right)={{\displaystyle \int }}_{-\frac{l_u}{2}+x_u}^{\frac{l_u}{2}+x_u}exp\left[-j\left(K_{\alpha }+K_{au}\right)\left(\Theta -{\mathsf{\Theta }}_p\right)\right]dD \\ =l_u·sinc\left[\frac{2l_u}{\lambda }\left(\Theta -{\mathsf{\Theta }}_p\right)\right]·exp\left[-j{K}_{au}\left(\Theta -{\mathsf{\Theta }}_p\right)\right] \end{gathered}$$

(27)

Since $K_{au}$ is related to the position of target point $P$, $I_u\left(r_p,\mathsf{\Theta }\right)$ cannot be abbreviated as $I_u\left(\mathsf{\Theta }\right)$. By executing an inverse Fourier transform of $I_u\left(r_p,\mathsf{\Theta }\right)$, the wavenumber spectrum function of the sub-aperture image can be obtained.

$$\begin{array}{ll}{I}_u\left(r_p,K_{\alpha }\right)=& {{\displaystyle \int }}_{-\frac{\Delta A_u}{2}+A_{cu}}^{\frac{\Delta A_u}{2}+A_{cu}}{I}_u\left(r_p,\mathsf{\Theta }\right)·exp\left(j{K}_a\Theta \right)d\Theta \\ & =rect\left(\frac{K_{\alpha }-K_{au}}{\mathsf{\Delta }{K}_{\alpha }}\right)·exp\left(j\left(K_a-K_{au}\right){\Theta }_p\right),K_{\alpha }\in (-\frac{\Delta K_{\alpha }}{2},\frac{\Delta K_{\alpha }}{2}]+K_{au}\end{array}$$

(28)

where $\Delta K_{\alpha }=4\pi /\lambda ·l_u$.

From Equations (26) and (28), it is found that the motion error along the x-axis causes a consistent spectral displacement, $K_C$, and the motion error along the y-axis causes a spectral displacement, $K_V$, that varies with the target’s position.

$$\{\begin{array}{c}{K}_C=\frac{4\pi }{\lambda }·\frac{\Delta X}{cos\gamma }\\ K_V=-\frac{4\pi }{\lambda }·\frac{x_p}{y_p}·\frac{\Delta Y}{cos\gamma }\end{array}$$

(29)

4.2. Sub-Aperture Spectrum Fusion

To achieve accurate spectrum fusion, we propose an improved sub-aperture wavenumber spectrum fusion method.

Step 1: Sub-aperture spectrum shift calculation

Calculate the integral number of the central position shift of the sub-aperture wavenumber spectrum caused by motion error. The error component of the $uth$ sub-aperture center along the x axis is denoted as $\Delta X_u$, the error component along the y axis is denoted as $\Delta Y_u$, and the scene center point is marked as $\left(x_0,y_0,0\right)$ in the Cartesian coordinate system and $\left(r_0,{\Theta }_0\right)$ in the polar coordinate system. The whole-aperture data after range compression are divided into sub-aperture data with the same azimuth sampling number, and each sub-aperture contains $N_0$ pulses. Taking the center point target of the angular domain as a reference, the integral number of the $uth$ sub-aperture wavenumber spectrum center position shift caused by motion error is calculated as follows:

$${\Delta }_u=\mathrm{floor}\left(\left(x_u+\frac{{\Theta }_0}{r_0}{x}_u^2+\left[\Delta X_u-\Delta Y_u\frac{x_p}{y_p}\right]·\frac{1}{cos\gamma }\right)/\frac{l_u}{N_0}\right)$$

(30)

where $\mathrm{floor}(·)$ means the operation of taking the nearest integer toward negative infinity.

Assuming that $G\left(r_p,{\Theta }_p\right)=x_p/y_p$, $\Delta G\left(r_p,{\Theta }_p\right)=x_p/y_p-x_0/y_0$, the minimum oversampling rate $k_0$ is expressed as:

$$k_0\ge \frac{2·\Delta Y_u}{cos\gamma ·l_u}·{\left[\Delta G\left(r_p,{\Theta }_p\right)\right]}_{\max }+1$$

(31)

To improve computational efficiency, $k_0$ generally takes the power of 2.

Step 2: Wavenumber spectrum shifting

The wavenumber spectrum center of the $uth$ sub-aperture is shifted to the zero frequency, and the shift function H₁ can be formulated as:

$$H_1=exp\left(j\frac{4\pi }{\lambda }·\left({\Delta }_u·\frac{l_u}{N_0}\right)\left({\Theta }_p-{\Theta }_0\right)\right)$$

(32)

Then the $uth$ sub-aperture SAR image after centroid shifting denoted as

$$I_u^{’}\left(r_p,\Theta \right)=I_u\left(r_p,\Theta \right)·H_1$$

(33)

Step 3: Sub-aperture spectrum fusion

Since the sub-aperture wavenumber spectrum center is shifted by the integral number, no interpolation operation is additionally needed in the sub-aperture wavenumber spectrum fusion procedure. The actual position of each sub-aperture center can be calculated according to ${\Delta }_u$, and then a simple sub-aperture spectrum superposition can be performed. Figure 2 and Figure 3 show the traditional and improved spectra fusion methods, respectively. In Figure 2 and Figure 3, each sub-aperture wavenumber spectrum has been moved to the zero frequency. Assuming that the oversampling factor of the sub-aperture wavenumber spectrum is $k$, the traditional method of spectra fusion is to simply overlap the adjacent sub-aperture wavenumber spectra by $\left(k-1\right)/k$ to obtain the whole-aperture wavenumber spectrum. When the platform moves along a uniform straight line, the correct wavenumber spectrum with whole-aperture can be obtained in this way. However, when the platform moves at a varying speed and along a curved trajectory, the sub-aperture width is different and the corresponding sub-aperture wavenumber spectrum width is also different. If the spectrum fusion is performed in the traditional way, gaps and overlaps between adjacent sub-apertures cannot be avoided. Considering the variation of spectrum width, the improved spectra fusion method effectively avoids the situation of spectrum gaps and overlaps.

4.3. Algorithm Implementation

Figure 4 shows the processing flow chart of the proposed method. The implementation process of the HSHD-AFBP algorithm is the same as that for the HS-AFBP algorithm [19], but their sub-aperture wavenumber spectrum center correction and sub-aperture spectrum fusion are different, as marked in Figure 4 with the blue color. The implementation process of the HSHD-AFBP algorithm is divided into two stages: (1) the prepare phase and (2) the process phase.

The prepare phase stage includes three steps:

(1)

Range interpolation. Interpolation operation is carried out on the range compressed data, so that the echo data can be coherently accumulated.

(2)

Sub-aperture division. The whole-aperture data after range compression are divided into N_s sub-apertures. Each sub-aperture contains the same number of pulses.

(3)

SAR imaging grid construction. The angle interval ΔΘ, established in the unified polar coordinate system, depends on the length of the sub-aperture [20].

$$\Delta \Theta \le \frac{\lambda }{2l_u}$$

(34)

The process phase stage includes four steps:

(1)

Sub-image generation. Sub-images $I_u\left(r_p,\Theta \right),u=1,2,\cdots ,N_s$, where $N_s$ is the number of sub-apertures, will be focused by the sub-apertures’ radar echoes with low resolution by using the BP integral.

(2)

Sub-aperture wavenumber spectrum center correction. Firstly, the correction of each sub-aperture wavenumber spectrum is performed by Equation (33) to obtain $I_u^{’}\left(r_p,\Theta \right)$. Then, the angular inverse Fourier transform is applied to $I_u^{’}\left(r_p,\Theta \right)$ to obtain the wavenumber spectrum $I_u\left(r_p,K_{\alpha }\right)$ of each sub-image.

(3)

Spectrum fusion. The whole-aperture wavenumber spectrum can be obtained by a simple sub-aperture spectrum superposition.

(4)

Full-resolution image generation. The angular Fourier transform of the fusion wavenumber spectrum $I\left(r_p,K_{\alpha }\right)$ is applied to obtain the full-resolution SAR image.

4.4. Computational Complexity Analysis

For simplicity, it is assumed that the size of the imaging scene is $N\times N$ and the whole aperture contains $N$ pulses. The computational burden of the proposed algorithm mostly includes four aspects: sub-image generation ($N^3/N_s$), sub-aperture wavenumber spectrum center correction ($N^2/N_s$), sub-image angular inverse Fourier transform ($N^2·lo{g}_2^{N/N_s}$), and the whole-aperture wavenumber spectrum angular Fourier transform ($N^2·lo{g}_2^N$). Hence, why the computational complexity is approximated as $\left(N/N_s+1/N_s+lo{g}_2^{N/N_s}+lo{g}_2^N\right)·N^2$. Comparing HSHD-AFBP and HS-AFBP, the main difference in computational complexity is in the processing steps of sub-aperture wavenumber spectrum center correction and sub-aperture spectrum fusion. The computational complexity of these two steps is much less than the complexity of sub-image generation. Therefore, HSHD-AFBP and HS-AFBP have almost the same computational complexity.

5. Experiments and Analysis

In this section, we will use the point targets and simulated nature scene to verify the effectiveness of the proposed method, as well as by comparing the focused SAR image performance of the HS-AFBP method.

5.1. Point Targets’ Simulation Results

Table 1. Main system parameters.

Parameter	Value
Wave band	Ku
Bandwidth	100 M
Center line of scene	20.89 km
Squint angle	${70}^{\circ }$
Dive angle	${60}^{\circ }$
Whole-aperture length	446.9 m

lists the main simulation parameters. Nine point targets are placed in the scene, as is shown in Figure 5. The coordinates of the nine point targets are shown in

Table 2. Point targets’ coordinates.

Target	(x,y,z)/km	(r/km, Θ)
${\mathrm{P}}_1$	(10.22, 7.90, 0)	(20.56, 0.9224)
${\mathrm{P}}_2$	(10.93, 6.88, 0)	(20.56, 0.9397)
${\mathrm{P}}_3$	(11.64, 5.60, 0)	(20.56, 0.9570)
${\mathrm{P}}_4$	(10.82, 7.95, 0)	(20.89, 0.9224)
${\mathrm{P}}_5$	(11.54, 6.86, 0)	(20.89, 0.9397)
${\mathrm{P}}_6$	(12.26, 5.47, 0)	(20.89, 0.9570)
${\mathrm{P}}_7$	(11.42, 7.97, 0)	(21.22, 0.9224)
${\mathrm{P}}_8$	(12.16, 6.80, 0)	(21.22, 0.9397)
${\mathrm{P}}_9$	(12.89, 5.28, 0)	(21.22, 0.9570)

. The number of azimuth pulses is 2048. The whole aperture length is 446.9 m. The synthetic aperture is divided into 64 sub-apertures. Therefore, each sub-aperture contains 32 pulses. Figure 6 shows us the trajectory deviations in the corresponding coordinate-axis between the actual trajectory and the ideal trajectory, i.e., the fitting trajectory.

According to Equation (31) and the simulation parameters, we obtain $k_0=2$ if the first sub-aperture is taken as an example. Figure 7 shows the first sub-aperture two-dimensional wavenumber spectrum of three point targets in sequence. It can be seen that the spectra displacement of targets at different angles in the same slant range unit is different in the polar coordinate system.

Table 3. The spectrum center azimuth unit.

Method	Spectrum Center Azimuth Unit
	${\mathbf{P}}_4$	${\mathbf{P}}_5$	${\mathbf{P}}_6$
HS-AFBP	0.66 1	0.66	0.66
HSHD-AFBP	60.46	63.85	5.78
Truth value	60.44	0.18	5.28

¹ The values indicate the azimuth units where the center of the spectrum is folded multiple times.

lists the first sub-aperture wavenumber spectrum center positions of the three point targets obtained by the method of HS-AFBP, HSHD-AFBP, and the true values of the center positions of the sub-aperture wavenumber spectrum of the three point targets. HS-AFBP estimates the first sub-aperture wavenumber spectrum center positions according to Equation (16). HSHD-AFBP estimates the sub-aperture wavenumber spectrum center positions according to Equation (26). The true values of the center positions of the sub-aperture wavenumber spectrum of the three point targets can be obtained according to Figure 7. The values in Table 3 indicate the azimuth units where the center of the spectrum is folded multiple times. It can be seen from Table 3 that, whether the target is in the center of the angular-dimensional or on the edge of the angular-dimensional, HSHD-AFBP can accurately calculate wavenumber spectra displacement.

Taking the target ${\mathrm{P}}_4$ as an example, the whole-aperture wavenumber spectrum is obtained by fusing the wavenumber spectra of 64 sub-apertures, as is shown in Figure 8. Figure 8a is the result obtained by HSHD-AFBP. Figure 8b is the result obtained by HS-AFBP. Figure 8a,b are whole-aperture wavenumber spectra. Figure 8c,d are the results of local position amplification of the whole-aperture wavenumber spectra. HS-AFBP first uses (16) to correct the center of the sub-aperture spectrum, and then uses the traditional spectra fusion method to obtain the whole-aperture wavenumber spectrum. Because the influence of trajectory error on the spectral width is not considered, there will be gaps and overlaps in the spectrum fusion result. It can be seen that there are obvious spectra gaps between adjacent sub-aperture spectra, as is shown in Figure 8d. The spectra gaps and overlaps introduce additional phase errors, which will lead to target defocusing. HSHD-AFBP uses (23) to correct the center of the sub-aperture spectrum, and then uses an accurate sub-aperture spectra fusion method to obtain the whole-aperture wavenumber spectrum. As can be seen from Figure 8c, the whole-aperture wavenumber spectrum is well fused.

Figure 9 shows the imaging results of the point targets. To prove the imaging efficiency of the proposed algorithm, the processing time of the two algorithms is measured in the same condition. They are programmed in the Matlab on a computer with a 2.80 GHz Central Processing Unit and 24 GB Random Access Memory. The processing times of HSHD-AFBP and HS-AFBP are 47.40 s and 46.26 s, respectively.

To compare the 2D focusing performance of HSHD-AFBP and HS-AFBP, the contour images of targets are shown in Figure 10. Figure 10a is the result obtained by HSHD-AFBP. Figure 10b is the result obtained by HS-AFBP. The contour image of each target in Figure 10 is centered on its own location. It can be clearly seen that, for the targets on the edge of the angular-dimensional, HS-AFBP can focus well, but HS-AFBP will cause serious defocusing. The resolution, peak side lobe radio (PSLR), and integral side lobe radio (ISLR) in the range and azimuth directions are listed in

Table 4. Focusing performance evaluation of the nine point targets when using HSHD-AFBP.

Target	Resolution (m)		PSLR (dB)		ISLR (dB)
	Range	Azimuth	Range	Azimuth	Range	Azimuth
${\mathrm{P}}_1$	1.32	0.98	−13.32	−13.19	−11.07	−9.99
${\mathrm{P}}_2$	1.32	1.10	−13.29	−13,23	−11.05	−10.12
${\mathrm{P}}_3$	1.32	1.35	−13.27	−13.30	−11.00	−10.32
${\mathrm{P}}_4$	1.32	0.99	−13.29	−13.16	−11.04	−9.76
${\mathrm{P}}_5$	1.32	1.12	−12.89	−13.16	−11.05	−9.73
${\mathrm{P}}_6$	1.32	1.32	−13.29	−13.21	−11.03	−9.77
${\mathrm{P}}_7$	1.32	1.03	−13.31	−13.24	−11.04	−10.21
${\mathrm{P}}_8$	1.32	1.18	−13.28	−13.27	−11.02	−10.22
${\mathrm{P}}_9$	1.32	1.39	−13.30	−13.28	−11.03	−10.20

. It can be clearly seen that HSHD-AFBP has the ability to obtain well-focused SAR images for all of the nine point targets.

The simulation results reflect the following facts: (1) the trajectory errors cause different spectrum center shifts with different target locations, which will lead to SAR images’ focusing performance deterioration. These offsets must be calculated accurately to set the oversampling rate reasonably and ensure that spectral ambiguity does not occur. (2) Sub-aperture spectra fusion should consider the effect of trajectory errors on spectrum width, otherwise, spectrum gaps and overlaps will occur inevitably, which will affect the amplitude and phase of the whole-aperture spectrum, and then the SAR images will be defocused.

5.2. Nature Scene Simulation Results

To future-proof the feasibility of the proposed algorithm, a set of simulated nature scene data are processed by HSHD-AFBP and HS-AFBP. As is shown in [21], according to the point scattering model, the single look data of the SAR image can be regarded as nature scene targets’ electromagnetic backscattering coefficient in substance. Here, we use a high-resolution real airborne SAR image in X-band to simulate the high maneuvering platforms’ echo signal of the natural scene. The size of the natural scene is 820 m × 820 m (range × azimuth). The system parameters are shown in

Table 5. Main system parameters.

Parameter	Value
Wave band	Ku
Bandwidth	100 M
Center line of scene	24.9 km
Squint angle	${70}^{\circ }$
Dive angle	${25}^{\circ }$
Whole-aperture length	446.9 m

. The slant range of the scene’s center is 24.9 km. The plane flies at a speed of 1000 m/s. The pulse repetition frequency (PRF) is 4582 Hz. Figure 11 shows the raw signal of the nature scene.

Figure 12 shows the reconstructed images of the simulated nature scene by HSHD-AFBP and HS-AFBP. From Figure 12, we can see that the natural scene reconstructed by HSHD-AFBP demonstrates a better focusing effect than that of HS-AFBP. The processing times of HSHD-AFBP and HS-AFBP are 62.07 s and 60.36 s, respectively. For better comparison, we give the range and azimuth profiles of a point-like scatterer in Figure 13. The scatterer is circled in red in Figure 12. From Figure 13, one can see that, compared to those of HS-AFBP, the profiles of HSHD-AFBP have higher resolutions and lower sidelobes. All of the above results effectively prove that the proposed method can focus well on the SAR image of a high maneuvering platform.

6. Conclusions

In this paper, the HSHD-AFBP method was proposed for high squint angle and high dive angle SAR imaging, which is suitable for the nonlinear motion trajectory of high maneuvering platforms. The HSHD-AFBP can calculate the wavenumber spectra displacement of targets at different angles, while the HS-AFBP can only estimate the wavenumber spectrum displacement of the target located at the angle center. Therefore, the HSHD-AFBP can accurately calculate the oversampling rate required for sub-aperture SAR focusing and avoid sub-aperture spectrum blurring. In addition, this paper proposed an accurate sub-aperture spectra fusion method to deal with the influence of the nonlinear trajectory on spectrum width. Compared to the traditional spectrum fusion method, the proposed method improves the SAR’s focusing quality and enlarges the imaging scene’s width. Simulation experiments verified the effectiveness of the proposed method. However, a SAR image application, such as image matching and target recognition, requires the SAR image in the ground plane. Therefore, we will focus on how to quickly and accurately achieve SAR image focusing in the ground plane in future research, to extend the scope of the proposed HSHD-AFBP.