An Improved Phase-Derived Range Method Based on High-Order Multi-Frame Track-Before-Detect for Warhead Detection
Abstract
:1. Introduction
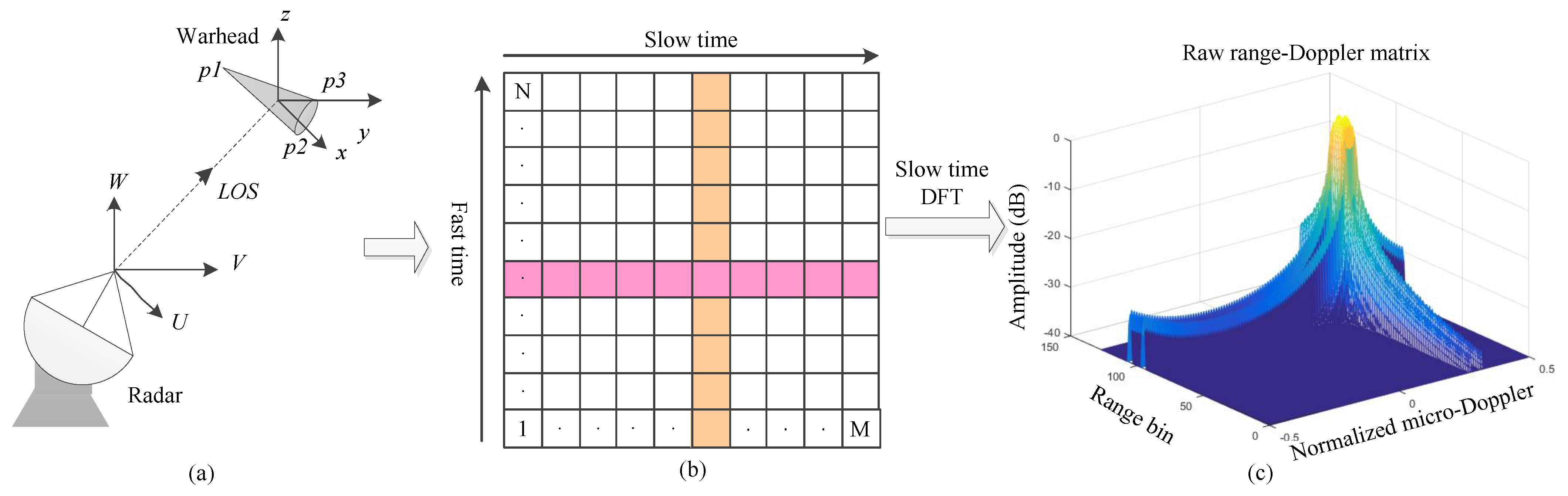
2. Geometric Model and Signal Model
2.1. Geometric Model
2.2. Signal Model
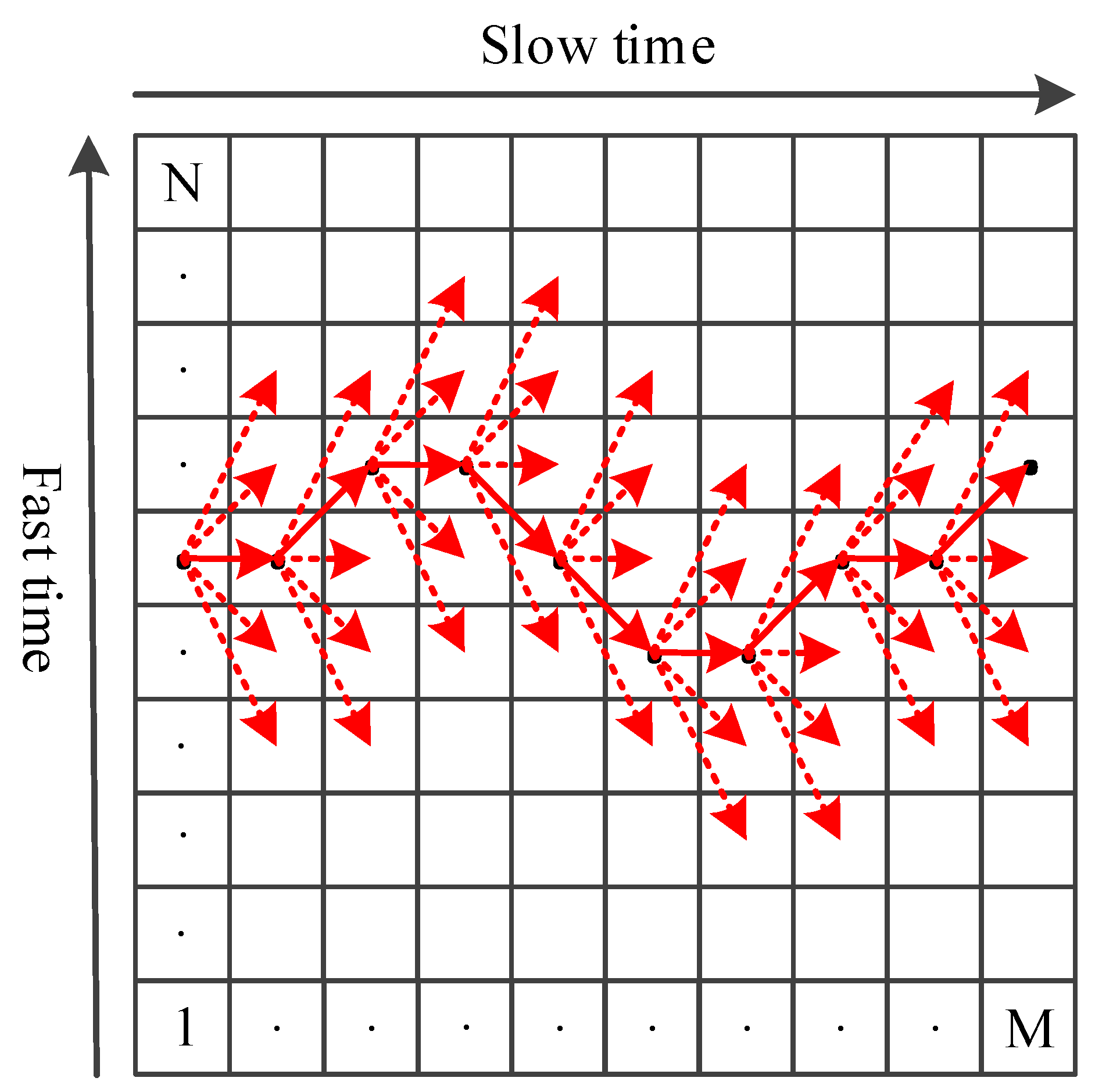
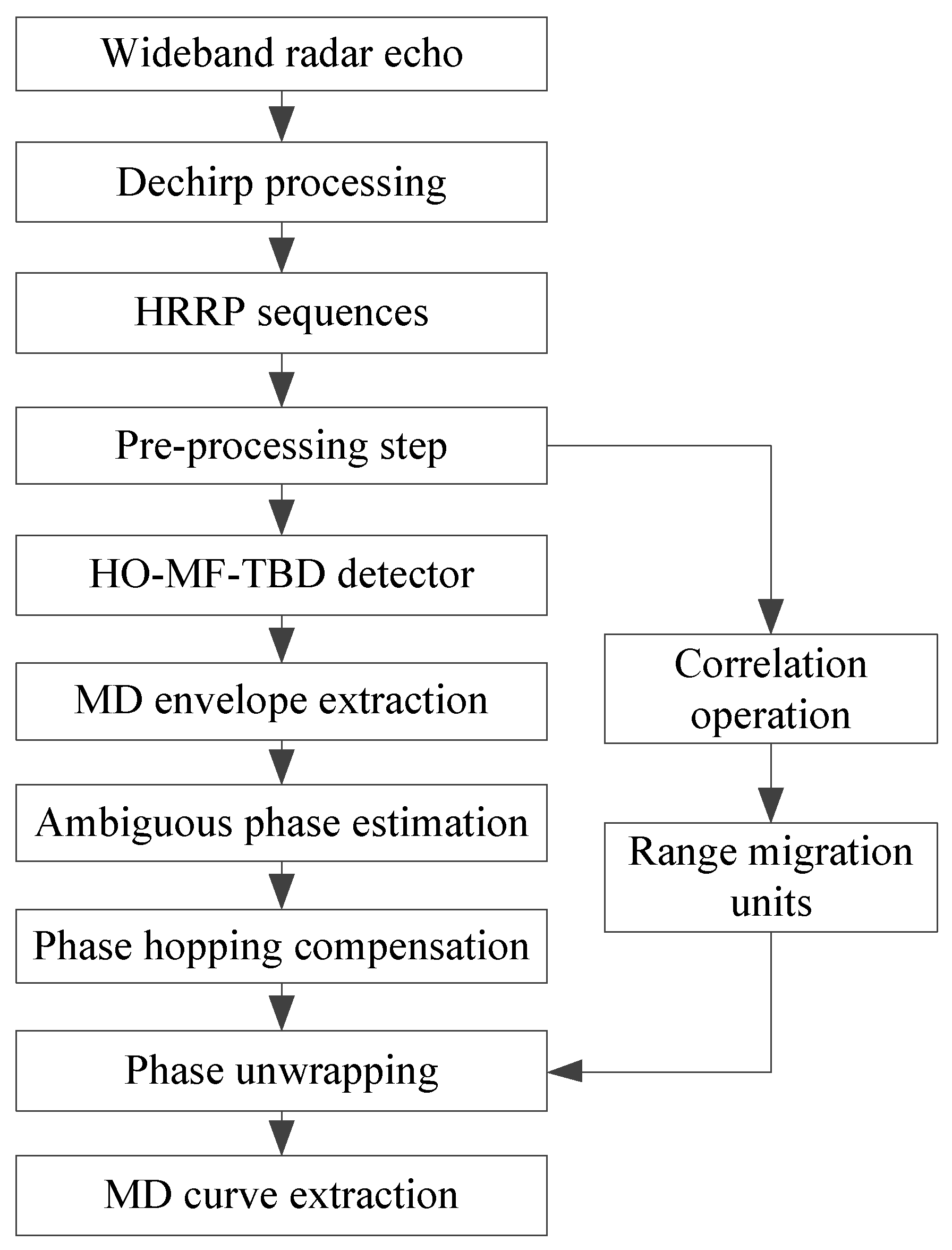
3. Micro-Doppler Envelope Extraction Using HO-MF-TBD
3.1. Measurement Model
3.2. Target Model
3.3. HO-MF-TBD Method
4. Phase Unwrapping
5. Simulations and Discussion
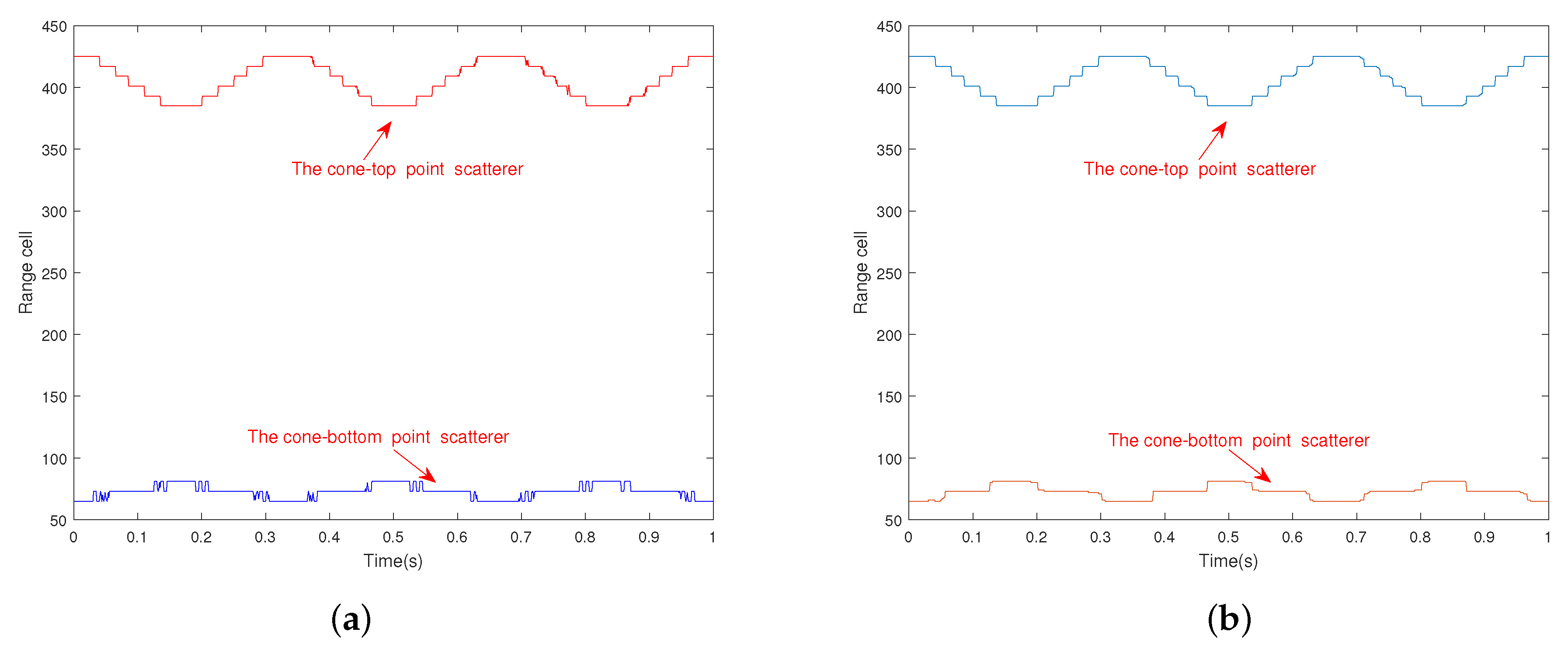
5.1. Micro-Doppler Envelope Extraction Using HO-MF-TBD Method
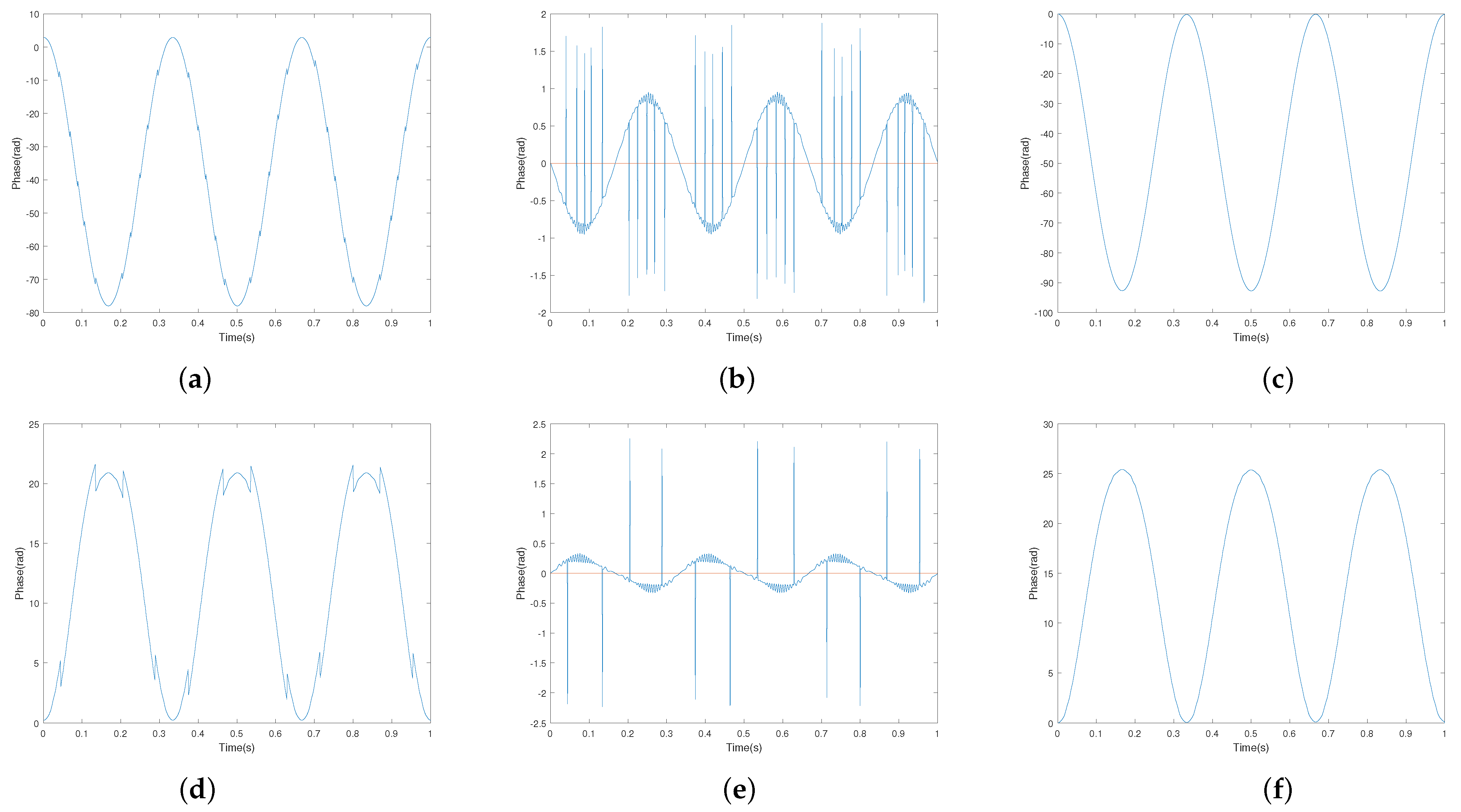
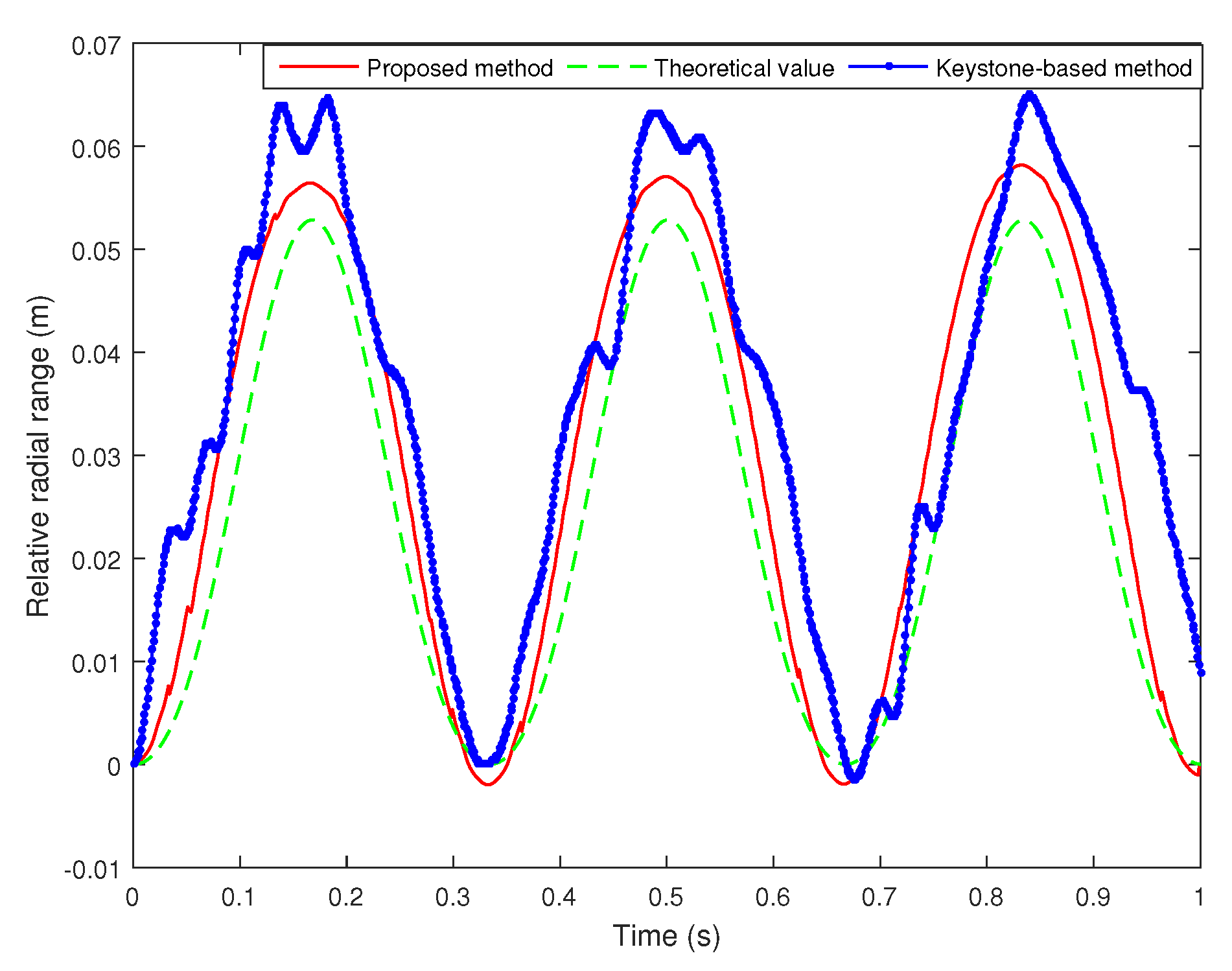
5.2. Phase Unwrapping
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, V.C.; Li, F.; Ho, S.S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Feng, C.Q.; Hu, X.W.; Zhang, Y.S. Classification of Space Micromotion Targets With Similar Shapes at Low SNR. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Choi, I.O.; Park, S.H.; Kang, K.B.; Lee, S.H.; Kim, K.T. Efficient parameter estimation for cone-shaped target based on distributed radar networks. IEEE Sens. J. 2019, 19, 9736–9747. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.Y.; Chen, Z.P. Convolutional neural network for classifying space target of the same shape by using RCS time series. IET Radar Sonar Navig. 2018, 12, 1268–1275. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Zhang, Q.; Kang, L.; Zhang, L. End-to-End Recognition of Similar Space Cone-Cylinder Targets Based on Complex-Valued Coordinate Attention Networks. IEEE Trans. Geosci. Remote Sens. 2021, 1–14. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, Q.; Luo, Y.; Sun, L. Micromotion feature extraction and distinguishing of space group targets. IEEE Geosci. Remote Sens. Lett. 2017, 14, 174–178. [Google Scholar] [CrossRef]
- Zhu, N.N.; Hu, J.; Xu, S.Y.; Wu, W.Z.; Zhang, Y.F.; Chen, Z.P. Micro-Motion Parameter Extraction for Ballistic Missile with Wideband Radar Using Improved Ensemble EMD Method. Remote Sens. 2021, 13, 3545. [Google Scholar] [CrossRef]
- Shi, Y.C.; Jiu, B.; Liu, H.W. Optimization-Based Discontinuous Observation Strategy for Micro-Doppler Signature Extraction of Space Cone Targets. IEEE Access 2019, 7, 58915–58929. [Google Scholar] [CrossRef]
- Delisle, G.Y.; Zebbani, Z.; Charrier, C.; Cote, F. A novel approach to complex target recognition using RCS wavelet decomposition. IEEE Antennas Propag. Mag. 2005, 47, 35–55. [Google Scholar] [CrossRef]
- Wang, T.; Bi, W.; Zhao, Y.; Xue, W. Target recognition algorithm based on RCS observation sequence—Set-valued identification method. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014. [Google Scholar]
- Xiong, X.; Liu, H.; Deng, Z.M.; Fu, M.; Qi, W.; Zhang, Y. Micro-Doppler Ambiguity Resolution with Variable Shrinkage Ratio Based on Time-Delayed Cross Correlation Processing for Wideband Radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1906–1917. [Google Scholar] [CrossRef]
- Zhang, L.; Xing, M.; Qiu, C.; Bao, Z. Two-Dimensional Spectrum Matched Filter Banks for High-Speed Spinning-Target Three-Dimensional ISAR Imaging. IEEE Trans. Geosci. Remote Sens. 2009, 6, 368–372. [Google Scholar] [CrossRef]
- He, X.Y.; Tong, N.N.; Hu, X.W. High-Resolution Imaging and 3-D Reconstruction of Precession Targets by Exploiting Sparse Apertures. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1212–1220. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X.S.; Chang, Y.L.; Liu, J.; Xiao, S.P. Estimation of Precession Parameters and Generation of ISAR Images of Ballistic Missile Targets. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1983–1995. [Google Scholar] [CrossRef]
- Persico, A.R.; Clemente, C.; Gaglione, D.; Ilioudis, C.V. On Model, Algorithms, and Experiment for Micro-Doppler-Based Recognition of Ballistic Targets. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1088–1108. [Google Scholar] [CrossRef] [Green Version]
- Guo, K.Y.; Li, Q.; Sheng, Q. A Precise Recognition Method of Missile Warhead and Decoy in Multi-Target Scene. J. Electromagn. Wave Appl. 2012, 24, 641–652. [Google Scholar] [CrossRef]
- Yi, W.; Fang, Z.C.; Li, W.J.; Hoseinnezhad, R.; Kong, L.J. Multi-Frame Track-Before-Detect Algorithm for Maneuvering Target Tracking. IEEE Trans. Veh. Technol. 2020, 69, 4104–4118. [Google Scholar] [CrossRef]
- Hong, L.; Wang, X.; Liu, S. Micro-Doppler curves extraction based on high-order particle filter track-before detect. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1550–1554. [Google Scholar] [CrossRef]
- Bai, X.; Bao, Z. Imaging of rotation-symmetric space targets based on electromagnetic modeling. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1680–1689. [Google Scholar]
- Wei, J.Q.; Zhang, L.; Liu, H.W.; Zhou, Y.J. Micro-motion and gemetric parameters estimation of wide-band radar cone-shaped targets based on phase-derived range. J. Electr. Inf. Technol. 2018, 40, 2227–2234. [Google Scholar]
- Ren, K.; Du, L.; Lu, X.F.; Zhuo, Z.Y.; Li, L. Instantaneous Frequency Estimation Based on Modified Kalman Filter for Cone-Shaped Target. Remote Sens. 2020, 12, 2766. [Google Scholar] [CrossRef]
- Zhuo, Z.Y.; Zhou, Y.; Du, L.; Ren, K.; Li, Y. A Noise Robust Micro-Range Estimation Method for Precession Cone-Shaped Targets. Remote Sens. 2021, 13, 1820. [Google Scholar] [CrossRef]
- Zeng, C.; Li, D.; Luo, X.; Song, D.W.; Liu, H.Q.; Su, J. Ground Maneuvering Targets Imaging for Synthetic Aperture Radar Based on Second-Order Keystone Transform and High-Order Motion Parameter Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4486–4501. [Google Scholar] [CrossRef]
- Bellantoni, J.F.; Dodge, K.W. A square root formulation of the Kalman-Schmidt filter. AIAA J. 1967, 5, 1309–1314. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, L. Pseudo-spectrum based speed square filter for track-before-detect in range-doppler domain. IEEE Trans. Signal Process. 2019, 67, 5596–5610. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Pham, N.T.; Suter, D. Joint detection and estimation of multiple objects from image observations. IEEE Trans. Signal Process. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Hoseinnezhad, R.; Vo, B.N.; Vo, B.T. Visual tracking in background subtracted image sequences via multi-bernoulli filtering. IEEE Trans. Signal Process. 2013, 61, 392–397. [Google Scholar] [CrossRef]
- Yi, W.; Fu, L.; García-Fernández, A.F.; Xu, L.; Kong, L. Particle filtering based track-before-detect method for passive array sonar systems. Signal Process. 2019, 165, 303–314. [Google Scholar] [CrossRef]
- Davey, S.J. Efficient histogram PMHT via single target chip processing. IEEE Signal Process. Lett. 2015, 22, 569–572. [Google Scholar] [CrossRef]
- Orlando, D.; Venturino, L.; Lops, M.; Ricci, G. Track-before-detect strategies for STAP radars. IEEE Trans. Signal Process. 2010, 58, 933–938. [Google Scholar] [CrossRef]
- Moyer, L.R.; Spak, J.; Lamanna, P. A multi-dimensional Hough transform-based track-before-detect technique for detecting weak targets in strong clutter backgrounds. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 3062–3068. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Willett, P.K.; Bar-Shalom, Y. Tracking the tracker from its passive sonar ML-PDA estimates. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 573–590. [Google Scholar] [CrossRef] [Green Version]
- Thayaparan, T.; Abrol, S.; Riseborough, E.; Stankovic, L.; Lamothe, D.; Duff, G. Analysis of radar micro-Doppler signatures from experimental helicopter and human data. IET Radar Sonar Navig. 2007, 1, 289–299. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Math. Phys. Eng. Sci. 1988, 454, 903–995. [Google Scholar] [CrossRef]


| Notations | Meanings |
|---|---|
| the radar coordinate | |
| target coordinate system | |
| fast time | |
| slow time | |
| pulse duration | |
| carrier frequency | |
| slope frequency modulation | |
| reference distance | |
| m | frame index |
| number of measurement cells | |
| resolution of cell | |
| cell index | |
| D-dimensional different state | |
| K | number of total frames of patch processing |
| measurement matrix in frame m | |
| state matrix in frame m | |
| measurement set | |
| state set | |
| ambiguous phase | |
| unambiguous phase |
| Parameters | Values | |
|---|---|---|
| Warhead height | 0.96 m | |
| Bus length | 0.99 m | |
| Distance from the warhead center to the top | 0.64 m | |
| Warhead | Base radius of warhead | 0.25 m |
| Spin frequency | 4 Hz | |
| Conic rotation frequency | 2 Hz | |
| Precession angle | ||
| Carrier frequency | 10 GHz | |
| Bandwidth | 2 GHz | |
| Radar | Pulse width | 10 us |
| Pulse repetition period | 1 kHz | |
| Dwell time | 1 s |
| Scatterers | Methods | 10 dB | 5 dB | 0 dB | −5 dB | −10 dB | −15 dB |
|---|---|---|---|---|---|---|---|
| Cone-top | Proposed | 129 | 129 | 130 | 130 | 130 | 143 |
| EKF | 134 | 136 | 136 | 140 | 153 | 183 | |
| DP-TBD | 133 | 133 | 133 | 134 | 139 | 162 | |
| EMD | 124 | 124 | 124 | 136 | 136 | 179 | |
| Cone-bottom | Proposed | 77 | 81 | 82 | 82 | 99 | 99 |
| EKF | 99 | 107 | 107 | 113 | 117 | 139 | |
| DP-TBD | 90 | 90 | 93 | 95 | 101 | 117 | |
| EMD | 67 | 84 | 83 | 84 | 105 | 183 |
| Methods | 10 dB | 5 dB | 0 dB | −5 dB | −10 dB | −15 dB |
|---|---|---|---|---|---|---|
| Proposed | 1.5151 | 1.5422 | 1.5838 | 1.6514 | 1.8108 | 2.0903 |
| EKF | 1.0068 | 1.0121 | 1.0456 | 1.0586 | 1.0692 | 0.9812 |
| DP-TBD | 7.8596 | 7.2235 | 6.9757 | 7.0007 | 7.8432 | 7.0104 |
| EMD | 2.2864 | 2.3421 | 2.2532 | 2.4274 | 2.5885 | 2.5948 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, N.; Xu, S.; Li, C.; Hu, J.; Fan, X.; Wu, W.; Chen, Z. An Improved Phase-Derived Range Method Based on High-Order Multi-Frame Track-Before-Detect for Warhead Detection. Remote Sens. 2022, 14, 29. https://doi.org/10.3390/rs14010029
Zhu N, Xu S, Li C, Hu J, Fan X, Wu W, Chen Z. An Improved Phase-Derived Range Method Based on High-Order Multi-Frame Track-Before-Detect for Warhead Detection. Remote Sensing. 2022; 14(1):29. https://doi.org/10.3390/rs14010029
Chicago/Turabian StyleZhu, Nannan, Shiyou Xu, Congduan Li, Jun Hu, Xinlan Fan, Wenzhen Wu, and Zengping Chen. 2022. "An Improved Phase-Derived Range Method Based on High-Order Multi-Frame Track-Before-Detect for Warhead Detection" Remote Sensing 14, no. 1: 29. https://doi.org/10.3390/rs14010029
APA StyleZhu, N., Xu, S., Li, C., Hu, J., Fan, X., Wu, W., & Chen, Z. (2022). An Improved Phase-Derived Range Method Based on High-Order Multi-Frame Track-Before-Detect for Warhead Detection. Remote Sensing, 14(1), 29. https://doi.org/10.3390/rs14010029






