Mid-Term Monitoring of Glacier’s Variations with UAVs: The Example of the Belvedere Glacier
Abstract
:1. Introduction
- 1.
- Document yearly changes of the Belvedere Glacier in terms of volume variations and ice flow velocity during the timespan 2015–2020 by using UAV-based photogrammetry and geomatics techniques;
- 2.
- Prove the effectiveness of low-cost UAV-based photogrammetry for periodical alpine glacier monitoring with high geometrical accuracy (i.e., decimetric).
2. Area of Study
- 1.
- Upper sector (labelled as S1 in Figure 1a): it consists in the accumulation zone. It is located at about 2250 m a.s.l., at the feet of the steep Monte Rosa and the North Locce Glaciers, from which recurrent ice and snow avalanches feed the Belvedere Glacier. This sector is also the main deposition area for rocks and debris [37,44];
- 2.
- Central sector (S2 in Figure 1a): it is the transfer zone and it is enclosed by two sinuous moraines. It starts from an altitude of ∼2250 m a.s.l. and it extends downwards for . This sector shows the highest ice flow velocities and the most irregular surfaces, with the presence of several crevasses;
- 3.
- Lower sector (S3 in Figure 1a): it is the low relief sector. Here, in proximity of the Belvedere hill, the glacier splits in two different tongues: the north-west tongue is the largest and it reaches the lowest altitude of about 1800 m a.s.l. From the north-west tongue, the Anza River springs. A smaller tongue extends from the Belvedere hill towards East and reaches an altitude of about 1850 m a.s.l.
3. UAV-Based Monitoring Campaign on Belvedere Glacier
3.1. Instruments and Surveys Setup
3.2. SfM-MVS Workflow
3.3. Problems Arisind during the Surveys of 2017 and 2020
4. Glacier Flow Velocity
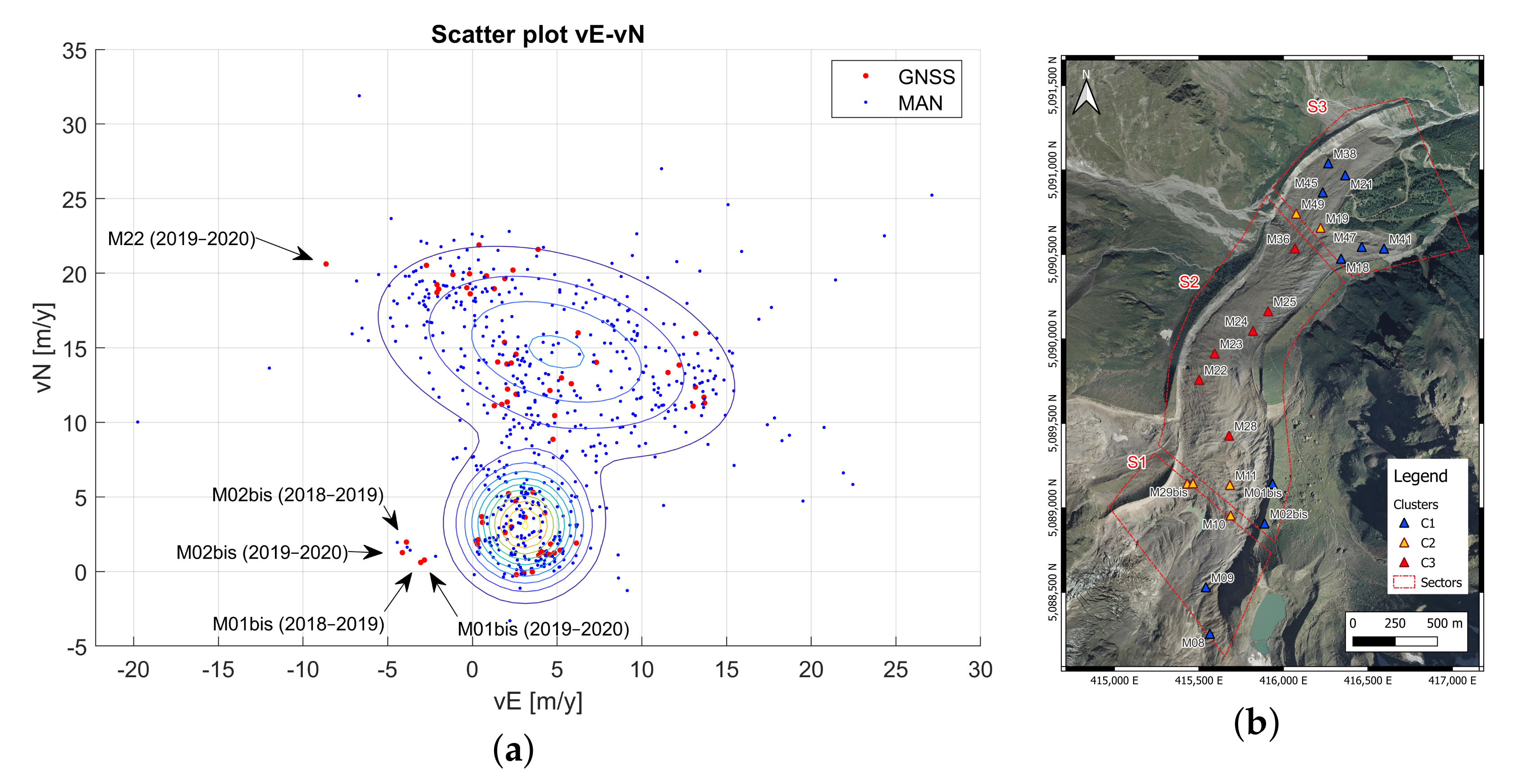
4.1. GNSS Velocity Measurements
4.2. MAN Velocity Measurements
4.3. Average Surface Velocity of the Belvedere Glacier during the Period 2015–2020
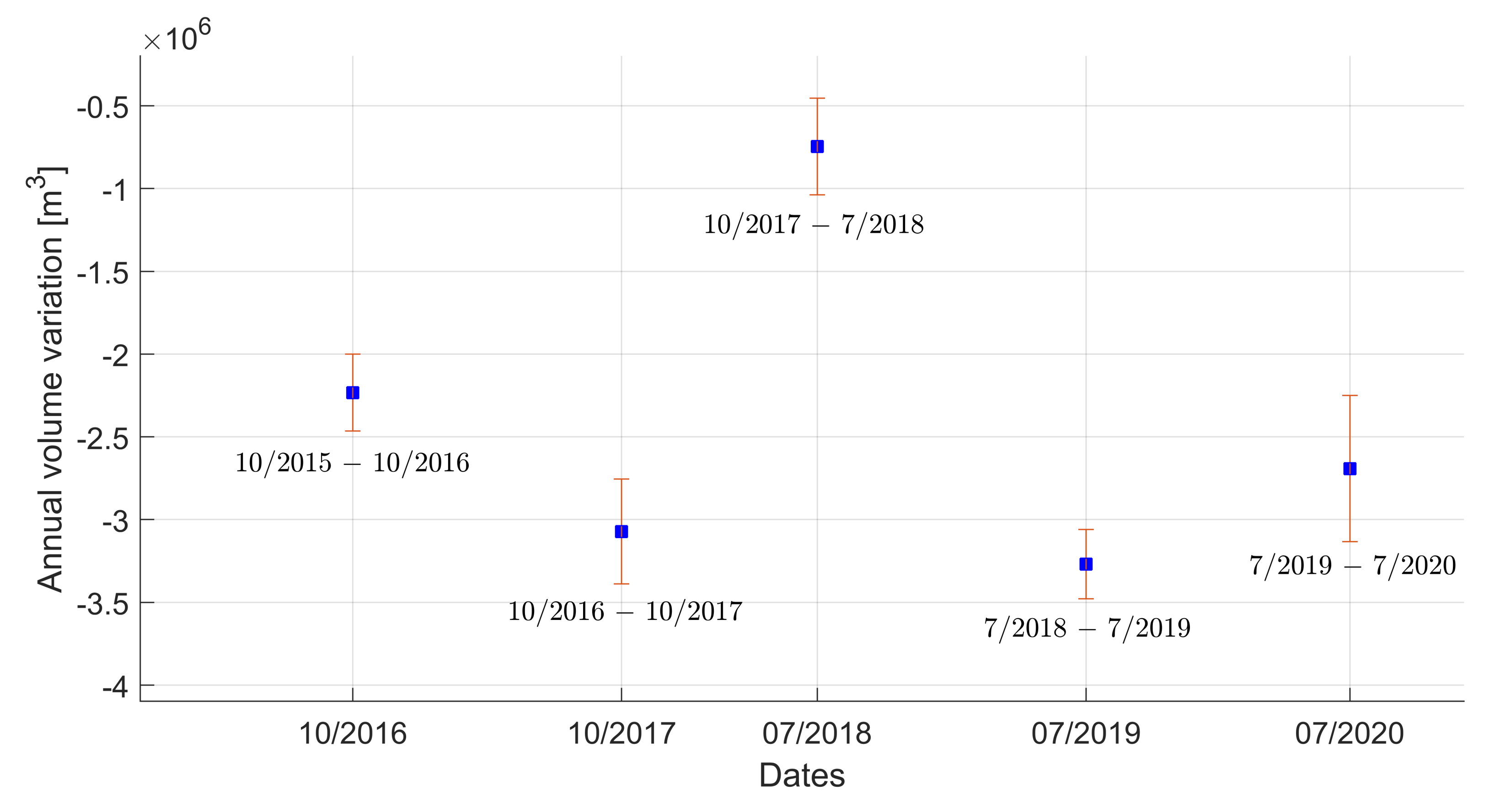
5. Ice Volume Variations
6. Comparison with Previous Studies
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oerlemans, J. Extracting a Climate Signal from 169 Glacier Records. Science 2005, 308, 675–677. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barry, R.G. The status of research on glaciers and global glacier recession: A review. Prog. Phys. Geog. Earth Environ. 2016, 30, 285–306. [Google Scholar] [CrossRef]
- Zemp, M.; Haeberli, W.; Hoelzle, M.; Paul, F. Alpine glaciers to disappear within decades? Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Sommer, C.; Malz, P.; Seehaus, T.C.; Lippl, S.; Zemp, M.; Braun, M.H. Rapid glacier retreat and downwasting throughout the European Alps in the early 21st century. Nat. Commun. 2020, 11, 3209. [Google Scholar] [CrossRef] [PubMed]
- Zekollari, H.; Huss, M.; Farinotti, D. Modelling the future evolution of glaciers in the European Alps under the EURO-CORDEX RCM ensemble. Cryosphere 2019, 13, 1125–1146. [Google Scholar] [CrossRef] [Green Version]
- Roethlisberger, H.; Haeberli, W.; Schmid, W.; Biolzi, M.; Pika, J. Studi Sul Comportamento Del Ghiacciao Del Belvedere; Report 97.3; Comunità montana della Valle Anzasca: Macugnaga, VB, Italy, 1985. [Google Scholar] [CrossRef]
- Kääb, A.; Funk, M. Modelling mass balance using photogrammetric and geophysical data: A pilot study at Griesgletscher, Swiss Alps. J. Glaciol. 1999, 45, 575–583. [Google Scholar] [CrossRef] [Green Version]
- Eder, K.; Würländer, R.; Rentsch, H. Digital photogrammetry for the new Glacier Inventory Of Austria. Int. Arch. Photogramm. Remote Sens. 2000, XXXIII, 254–261. [Google Scholar]
- Scambos, T.A.; Dutkiewicz, M.J.; Wilson, J.C.; Bindschadler, R.A. Application of image cross-correlation to the measurement of glacier velocity using satellite image data. Remote Sens. Environ. 1992, 42, 177–186. [Google Scholar] [CrossRef]
- Kääb, A.; Huggel, C.; Fischer, L.; Guex, S.; Paul, F.; Roer, I.; Salzmann, N.; Schlaefli, S.; Schmutz, K.; Schneider, D.; et al. Remote sensing of glacier-and permafrost-related hazards in high mountains: An overview. Nat. Hazard Earth Sys. 2005, 5, 527–554. [Google Scholar] [CrossRef]
- Heid, T.; Kääb, A. Evaluation of existing image matching methods for deriving glacier surface displacements globally from optical satellite imagery. Remote Sens. Environ. 2012, 118, 339–355. [Google Scholar] [CrossRef]
- Altena, B.; Kääb, A. Ensemble matching of repeat satellite images applied to measure fast-changing ice flow, verified with mountain climber trajectories on Khumbu icefall, Mount Everest. J. Glaciol. 2020, 66, 905–915. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Cheng, X. Glacier Velocity Changes in the Himalayas in Relation to Ice Mass Balance. Remote Sens. 2021, 13, 3825. [Google Scholar] [CrossRef]
- Strozzi, T.; Kouraev, A.; Wiesmann, A.; Wegmüller, U.; Sharov, A.; Werner, C. Estimation of Arctic glacier motion with satellite L-band SAR data. Remote Sens. Environ. 2008, 112, 636–645. [Google Scholar] [CrossRef]
- Fang, L.; Xu, Y.; Yao, W.; Stilla, U. Estimation of glacier surface motion by robust phase correlation and point like features of SAR intensity images. ISPRS J. Photogramm. Remote Sens. 2016, 121, 92–112. [Google Scholar] [CrossRef]
- Strozzi, T.; Caduff, R.; Jones, N.; Barboux, C.; Delaloye, R.; Bodin, X.; Kääb, A.; Mätzler, E.; Schrott, L. Monitoring Rock Glacier Kinematics with Satellite Synthetic Aperture Radar. Remote Sens. 2020, 12, 559. [Google Scholar] [CrossRef] [Green Version]
- Fieber, K.D.; Mills, J.P.; Miller, P.E.; Clarke, L.; Ireland, L.; Fox, A.J. Rigorous 3D change determination in Antarctic Peninsula glaciers from stereo WorldView-2 and archival aerial imagery. Remote Sens. Environ. 2018, 205, 18–31. [Google Scholar] [CrossRef]
- Giulio Tonolo, F.; Cina, A.; Manzino, A.; Fronteddu, M. 3D glacier mapping by means of satellite stereo images: The Belvedere Glacier case study in the Italian Alps. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, 43, 1073–1079. [Google Scholar] [CrossRef]
- Westoby, M.; Brasington, J.; Glasser, N.; Hambrey, M.; Reynolds, J. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–526. [Google Scholar] [CrossRef]
- Cook, K.L. An evaluation of the effectiveness of low-cost UAVs and structure from motion for geomorphic change detection. Geomorphology 2017, 278, 195–208. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Proc. Land. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Detert, M.; Johnson, E.D.; Weitbrecht, V. Proof-of-concept for low-cost and non-contact synoptic airborne river flow measurements. Int. J. Remote Sens. 2017, 38, 2780–2807. [Google Scholar] [CrossRef]
- Ioli, F.; Pinto, L.; Passoni, D.; Nova, V.; Detert, M. Evaluation of Airborne Image Velocimetry Approaches Using Low-Cost UAVs in Riverine Environments. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, 43, 597–604. [Google Scholar] [CrossRef]
- De Michele, C.; Avanzi, F.; Passoni, D.; Barzaghi, R.; Pinto, L.; Dosso, P.; Ghezzi, A.; Gianatti, R.; Vedova, G.D. Using a fixed-wing UAS to map snow depth distribution: An evaluation at peak accumulation. Cryosphere 2016, 10, 511–522. [Google Scholar] [CrossRef] [Green Version]
- Buhler, Y.; Adams, M.S.; Bosch, R.; Stoffel, A. Mapping snow depth in alpine terrain with unmanned aerial systems (UASs): Potential and limitations. Cryosphere 2016, 10, 1075–1088. [Google Scholar] [CrossRef] [Green Version]
- Avanzi, F.; Bianchi, A.; Cina, A.; De Michele, C.; Maschio, P.; Pagliari, D.; Passoni, D.; Pinto, L.; Piras, M.; Rossi, L. Centimetric accuracy in snow depth using unmanned aerial system photogrammetry and a multistation. Remote Sens. 2018, 10, 765. [Google Scholar] [CrossRef] [Green Version]
- Pagliari, D.; Rossi, L.; Passoni, D.; Pinto, L.; Michele, C.D.; Avanzi, F. Measuring the volume of flushed sediments in a reservoir using multi-temporal images acquired with UAS. Geomat. Nat. Haz. Risk 2016, 8, 150–166. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Sam, L.; Akanksha; Martín-Torres, F.J.; Kumar, R. UAVs as remote sensing platform in glaciology: Present applications and future prospects. Remote Sens. Environ. 2016, 175, 196–204. [Google Scholar] [CrossRef]
- Whitehead, K.; Moorman, B.J.; Hugenholtz, C.H. Brief Communication: Low-cost, on-demand aerial photogrammetry for glaciological measurement. Cryosphere 2013, 7, 1879–1884. [Google Scholar] [CrossRef] [Green Version]
- Immerzeel, W.W.; Kraaijenbrink, P.D.; Shea, J.M.; Shrestha, A.B.; Pellicciotti, F.; Bierkens, M.F.; de Jong, S.M. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.; Meijer, S.W.; Shea, J.M.; Pellicciotti, F.; de Jong, S.M.; Immerzeel, W.W. Seasonal surface velocities of a Himalayan glacier derived by automated correlation of unmanned aerial vehicle imagery. Ann. Glaciol. 2016, 57, 103–113. [Google Scholar] [CrossRef] [Green Version]
- Gindraux, S.; Boesch, R.; Farinotti, D. Accuracy Assessment of Digital Surface Models from Unmanned Aerial Vehicles’ Imagery on Glaciers. Remote Sens. 2017, 9, 186. [Google Scholar] [CrossRef] [Green Version]
- Jouvet, G.; van Dongen, E.; Lüthi, M.P.; Vieli, A. In situ measurements of the ice flow motion at Eqip Sermia Glacier using a remotely controlled unmanned aerial vehicle (UAV). Geosci. Instrum. Meth. 2020, 9, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Cao, B.; Guan, W.; Li, K.; Pan, B.; Sun, X. High-Resolution Monitoring of Glacier Mass Balance and Dynamics with Unmanned Aerial Vehicles on the Ningchan No. 1 Glacier in the Qilian Mountains, China. Remote Sens. 2021, 13, 2735. [Google Scholar] [CrossRef]
- Benoit, L.; Gourdon, A.; Vallat, R.; Irarrazaval, I.; Gravey, M.; Lehmann, B.; Prasicek, G.; Gräff, D.; Herman, F.; Mariethoz, G. A high-resolution image time series of the Gorner Glacier – Swiss Alps – derived from repeated unmanned aerial vehicle surveys. Earth Syst. Sci. Data 2019, 11, 579–588. [Google Scholar] [CrossRef] [Green Version]
- Diolaiuti, G.; D’Agata, C.; Smiraglia, C. Belvedere Glacier, Monte Rosa, Italian Alps: Tongue Thickness and Volume Variations in the Second Half of the 20th Century. Arct. Antarct. Alp. Res. 2003, 35, 255–263. [Google Scholar] [CrossRef]
- Haeberli, W.; Kääb, A.; Paul, F.; Chiarle, M.; Mortara, G.; Mazza, A.; Deline, P.; Richardson, S. A surge-type movement at Ghiacciaio del Belvedere and a developing slope instability in the east face of Monte Rosa, Macugnaga, Italian Alps. Nor. Geogr. Tidsskr. 2002, 56, 104–111. [Google Scholar] [CrossRef]
- Monterin, U. Il Ghiacciaio di Macugnaga dal 1870 al 1922. Bolletino Com. Glaciol. Ital. 1923, 5, 12–40. [Google Scholar]
- Mazza, A. Evolution and dynamics of Ghiacciaio Nord delle Locce (Valle Anzasca, Western Alps) from 1854 to the present. Geogr. Fis. Din. Quat. 1998, 21, 233–243. [Google Scholar]
- Kääb, A.; Huggel, C.; Barbero, S.; Chiarle, M.; Cordola, M.; Epifani, F.; Haeberli, W. Glacier Hazards At Belvedere Glacier and the Monte Rosa East Face, Italian Alps: Processes and Mitigation. Int. Symp. Interpraevent–Riva/Trient 2004, 1, 67–78. [Google Scholar]
- Noferini, L.; Mecatti, D.; Macaluso, G.; Pieraccini, M.; Atzeni, C. Monitoring of Belvedere Glacier using a wide angle GB-SAR interferometer. J. Appl. Geophys. 2009, 68, 289–293. [Google Scholar] [CrossRef]
- De Gaetani, C.I.; Ioli, F.; Pinto, L. Aerial and UAV Images for Photogrammetric Analysis of Belvedere Glacier Evolution in the Period 1977–2019. Remote Sens. 2021, 13, 3787. [Google Scholar] [CrossRef]
- Mölg, N.; Ferguson, J.; Bolch, T.; Vieli, A. On the influence of debris cover on glacier morphology: How high-relief structures evolve from smooth surfaces. Geomorphology 2020, 357, 107092. [Google Scholar] [CrossRef]
- Mortara, G.; Tamburini, A.; Ercole, G.; Semino, P.; Chiarle, M.; Godone, F.; Guiliano, M.; Haeberli, W.; Kääb, A.; Huggel, C.; et al. Il Ghiacciaio del Belvedere e L’emergenza del Lago Effimero; Regione Piemonte; Societa’ Meteorologica Subalpina: Moncalieri, TO, Italy, 2009. [Google Scholar]
- Agisoft Metashape. Available online: https://www.agisoft.com (accessed on 25 October 2021).
- Fraser, C.S. Automatic camera calibration in close range photogrammetry. Photogramm. Eng. Remote. Sens. 2013, 79, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Cramer, M.; Przybilla, H.J.; Zurhorst, A. UAV cameras: Overview and geometric calibration benchmark. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Dall’asta, E.; Roncella, R. A comparison of semiglobal and local dense matching algorithms for surface reconstruction. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2014, XL-5, 187–194. [Google Scholar] [CrossRef] [Green Version]
- Debella-Gilo, M.; Kääb, A. Sub-pixel precision image matching for measuring surface displacements on mass movements using normalized cross-correlation. Remote Sens. Environ. 2011, 115, 130–142. [Google Scholar] [CrossRef] [Green Version]
- McLachlan, G.; Peel, D. Finite Mixture Models; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Sibson, R. A Brief Description of Natural Neighbor Interpolation; John Wiley & Sons: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- CloudCompare. Available online: https://www.cloudcompare.org (accessed on 25 October 2021).
- Arpa Piemonte. Available online: https://www.arpa.piemonte.it/rischinaturali/accesso-ai-dati/annali_meteoidrologici/annali-meteo-idro/banca-dati-meteorologica.html (accessed on 25 October 2021).
- Gerbaux, M.; Genthon, C.; Etchevers, P.; Vincent, C.; Dedieu, J. Surface mass balance of glaciers in the French Alps: Distributed modeling and sensitivity to climate change. J. Glaciol. 2005, 51, 561–572. [Google Scholar] [CrossRef] [Green Version]
- Machguth, H.; Paul, F.; Hoelzle, M.; Haeberli, W. Distributed glacier mass-balance modelling as an important component of modern multi-level glacier monitoring. Ann. Glaciol. 2006, 43, 335–343. [Google Scholar] [CrossRef] [Green Version]
- Bavera, D.; De Michele, C.; Pepe, M.; Rampini, A. Melted snow volume control in the snowmelt runoff model using a snow water equivalent statistically based model. Hydrol. Process. 2012, 26, 3405–3415. [Google Scholar] [CrossRef]
- Armstrong, R.; Rittger, K.; Brodzik, M.; Racoviteanu, A.; Barrett, A.; Singh Khalsa, S.; Raup, B.; Hill, A.; Khan, A.; Wilson, A.; et al. Runoff from glacier ice and seasonal snow in High Asia: Separating melt water sources in river flow. Reg. Environ. Chang. 2019, 19, 1249–1261. [Google Scholar] [CrossRef] [Green Version]
- Gaudard, L.; Avanzi, F.; De Michele, C. Seasonal aspects of the energy-water nexus: The case of a run-of-the-river hydropower plant. Appl. Energy 2018, 210, 604–612. [Google Scholar] [CrossRef]
- Patro, E.; De Michele, C.; Avanzi, F. Future perspectives of run-of-the-river hydropower and the impact of glaciers’ shrinkage: The case of Italian Alps. Appl. Energy 2018, 231, 699–713. [Google Scholar] [CrossRef]


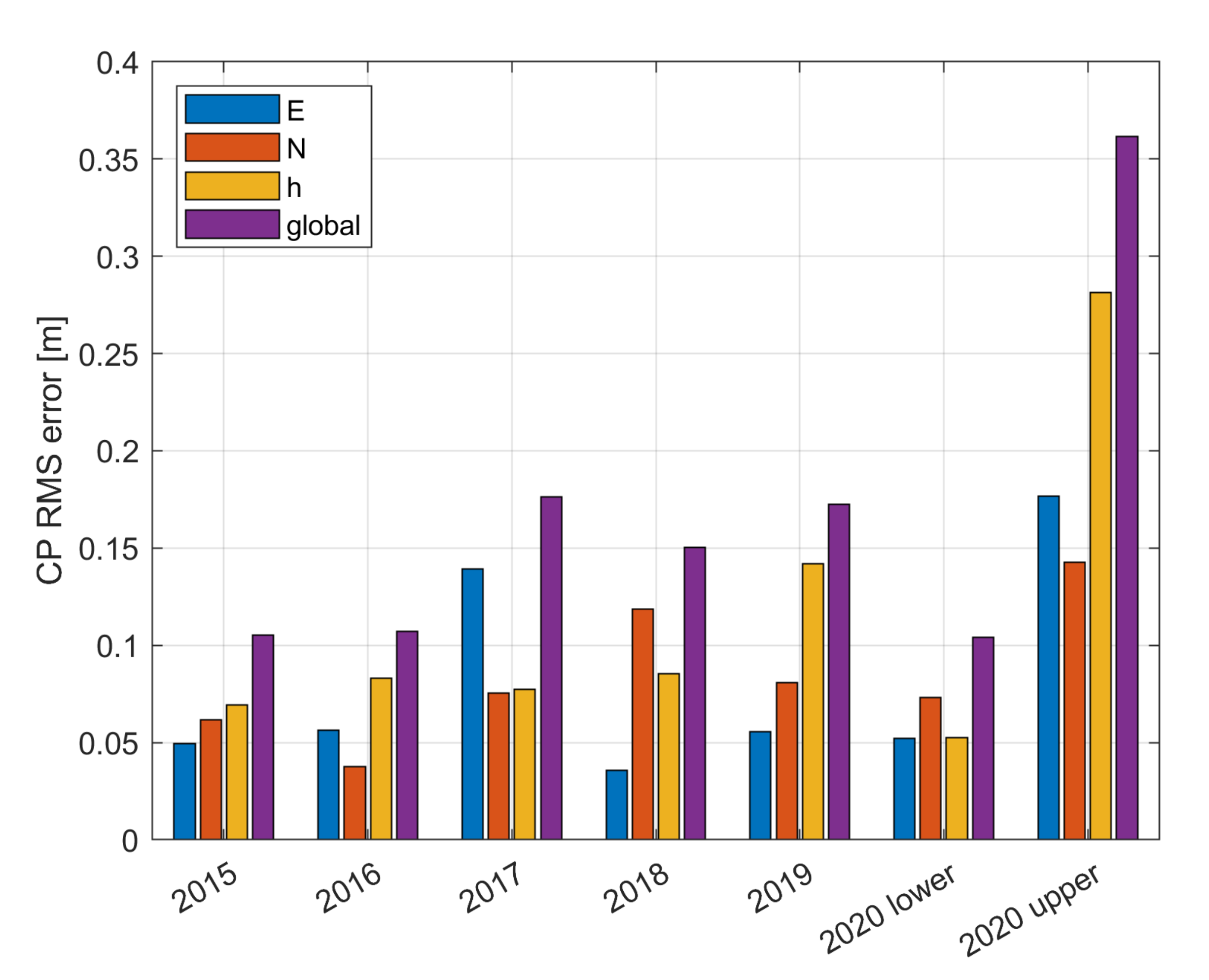



| Year | Date | UAV | Camera | GSD | GCP | CP |
|---|---|---|---|---|---|---|
| [m/px] | [#] | [#] | ||||
| 2015 | A. 8.10 | SenseFly eBee | Canon PowerShot S110 | 0.07 | 24 | 11 |
| B. 23.10 | ||||||
| 2016 | 20.10 | SenseFly eBee | Canon PowerShot S110 | 0.09 | 31 | 15 |
| 2017 | A. 5.10 | A. SenseFly eBee | A. Canon PowerShot S110 | 0.06 | 27 | 8 |
| B. 15.11 | B. SenseFly eBee Plus | B. SenseFly S.O.D.A | ||||
| C. 16.11 | C. DJI Phantom 4 Pro | C. DJI FC6310 | ||||
| 2018 | 23–25.07 | Parrot Disco | Hawkeye Firefly 8S | 0.05 | 27 | 13 |
| 2019 | 29.07–2.08 | Parrot Disco | Hawkeye Firefly 8S | 0.06 | 26 | 10 |
| 2020 | A. 26–27.07 | A. Parrot Disco | A. Hawkeye Firefly 8S | 0.05 | 29 | 12 |
| B. 9.08 | B. DJI Phantom 4 Pro | B. DJI FC6310 |
| Canon PowerShot | SenseFly | DJI FC6310 | Hawkeye | |
|---|---|---|---|---|
| S110 | S.O.D.A | Firefly 8S | ||
| Sensor | 1/1.7 CMOS | 1 CCD | 1 CMOS | 1/2.3 CMOS |
| Sensor Size [] | ||||
| Focal length [] | 5.2 | 10.6 | 8.8 | 3.8 |
| Image size [] | ||||
| Pixel size [] | 1.9 | 2.4 | 2.4 | 1.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ioli, F.; Bianchi, A.; Cina, A.; De Michele, C.; Maschio, P.; Passoni, D.; Pinto, L. Mid-Term Monitoring of Glacier’s Variations with UAVs: The Example of the Belvedere Glacier. Remote Sens. 2022, 14, 28. https://doi.org/10.3390/rs14010028
Ioli F, Bianchi A, Cina A, De Michele C, Maschio P, Passoni D, Pinto L. Mid-Term Monitoring of Glacier’s Variations with UAVs: The Example of the Belvedere Glacier. Remote Sensing. 2022; 14(1):28. https://doi.org/10.3390/rs14010028
Chicago/Turabian StyleIoli, Francesco, Alberto Bianchi, Alberto Cina, Carlo De Michele, Paolo Maschio, Daniele Passoni, and Livio Pinto. 2022. "Mid-Term Monitoring of Glacier’s Variations with UAVs: The Example of the Belvedere Glacier" Remote Sensing 14, no. 1: 28. https://doi.org/10.3390/rs14010028
APA StyleIoli, F., Bianchi, A., Cina, A., De Michele, C., Maschio, P., Passoni, D., & Pinto, L. (2022). Mid-Term Monitoring of Glacier’s Variations with UAVs: The Example of the Belvedere Glacier. Remote Sensing, 14(1), 28. https://doi.org/10.3390/rs14010028










