Estimation of the All-Wave All-Sky Land Surface Daily Net Radiation at Mid-Low Latitudes from MODIS Data Based on ERA5 Constraints
Abstract
:1. Introduction
2. Data and Pre-Processing
2.1. Ground Measurements
2.1.1. Radiation Measurements
2.1.2. Clearness Index Calculation
2.2. Remotely Sensed Products
2.2.1. MODIS Products for Modeling
2.2.2. Products Providing for Comparison
- GLASS
- 2.
- CERES4A
- 3.
- FLUXCOM_RS
2.3. ERA5 Reanalysis Products
3. Methodology
3.1. Estimation Model Development
3.1.1. MODIS TOA Data Selection for Modeling
3.1.2. Modeling with Random Forest
- RF-based ins model
- 2.
- RF-based model
- 3.
- RF-based model with ERA5
3.1.3. Look-Up Table (LUT-Based) Model
3.2. Model Performance Evaluation
4. Results and Analysis
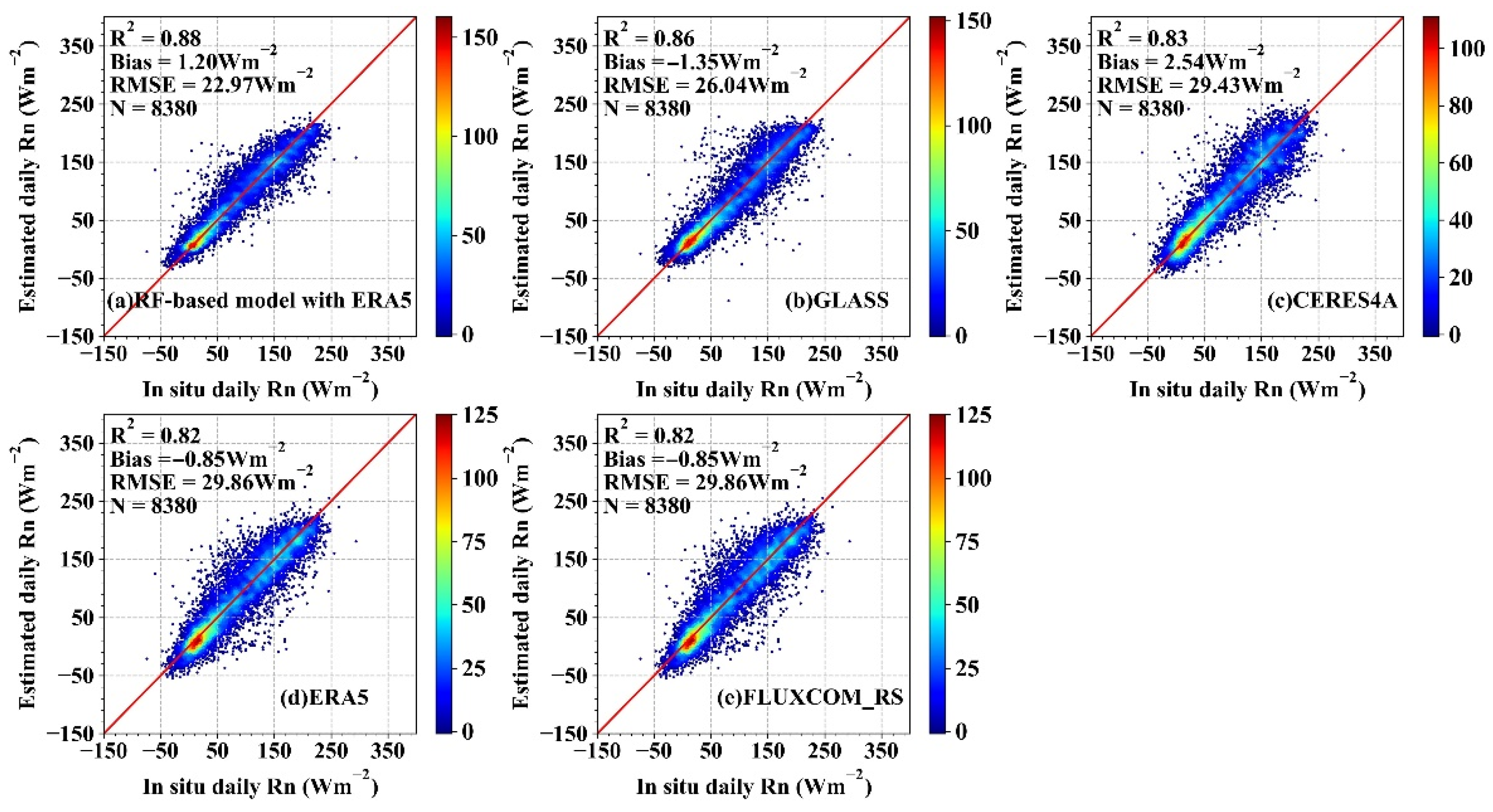
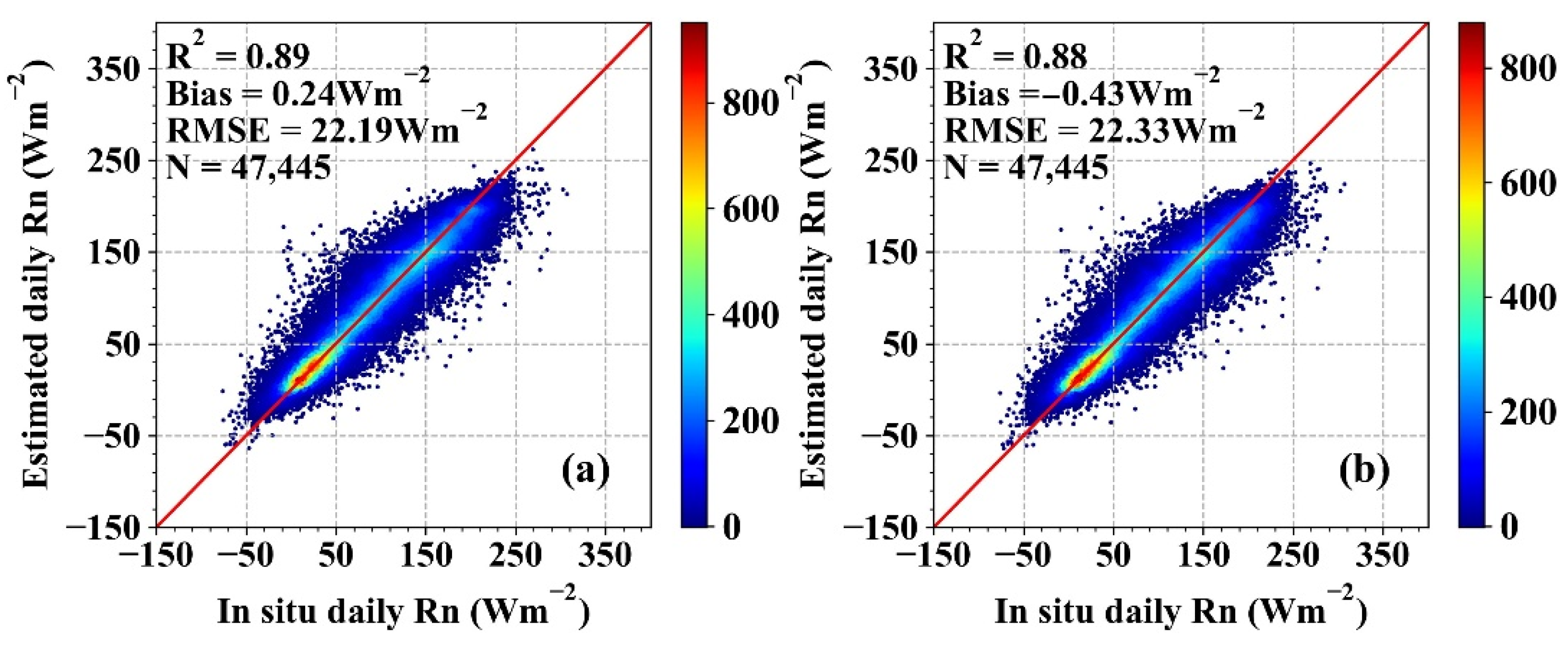
4.1. Proposed Model Performance Evaluation
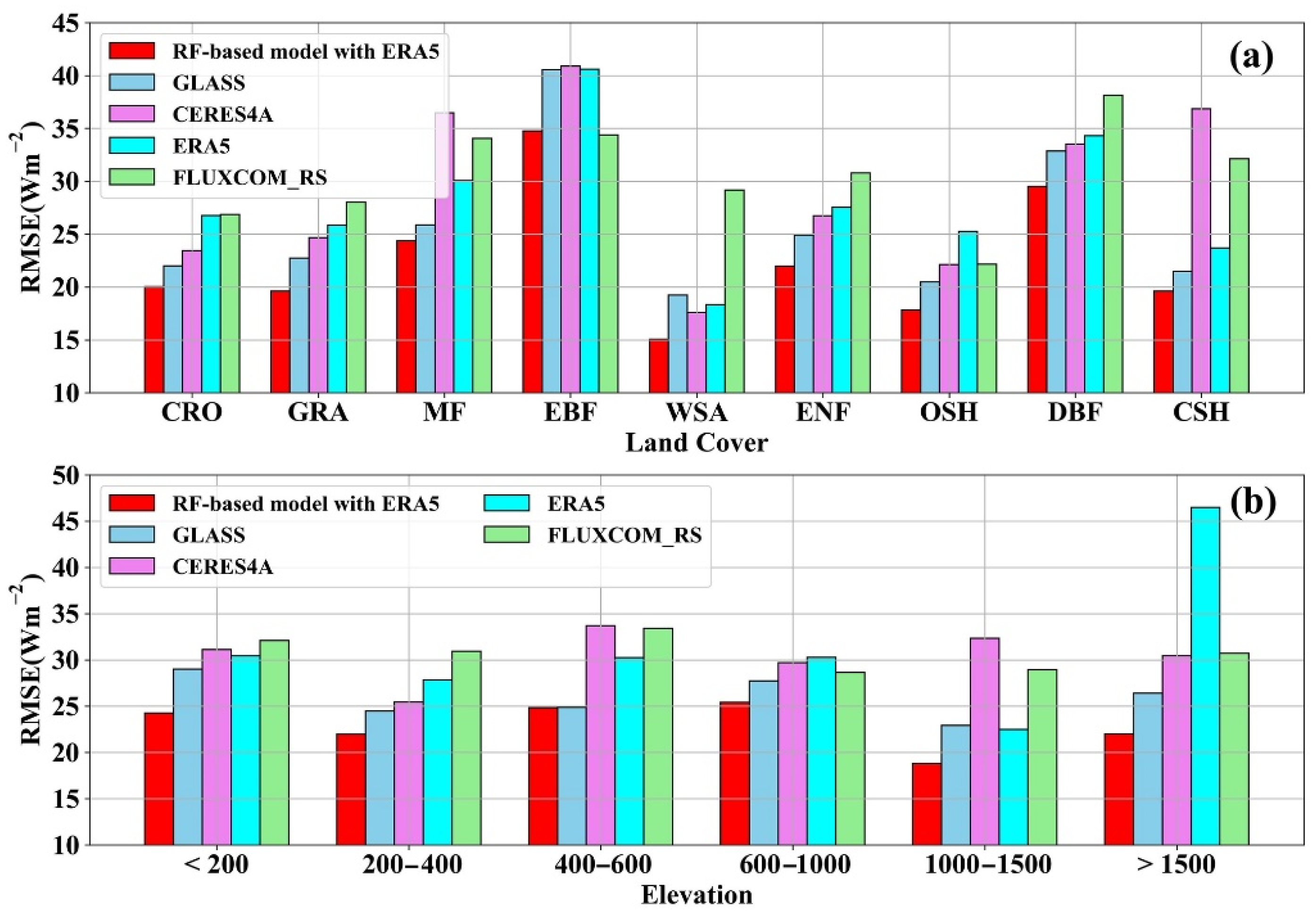
4.2. Further Analysis with RF-Based Model with ERA5
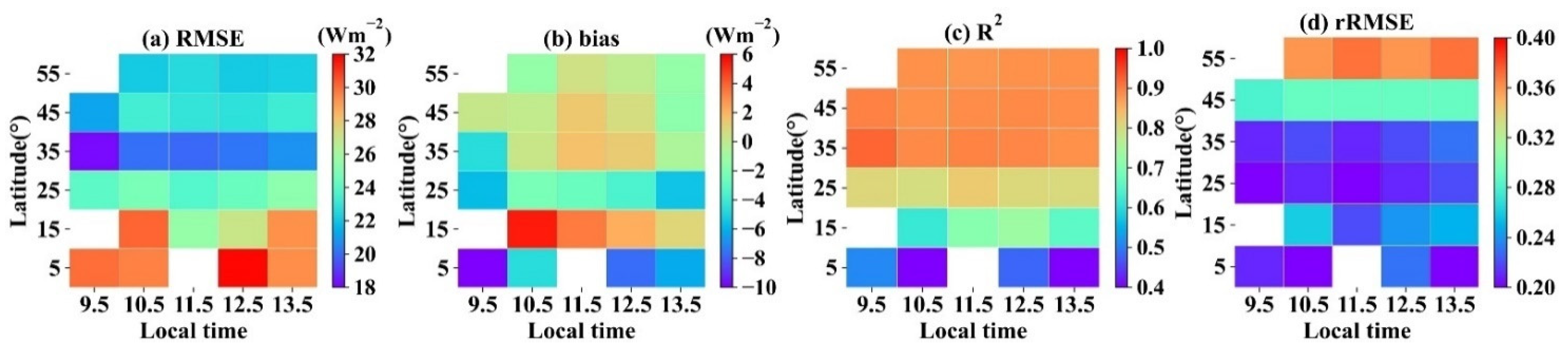
4.2.1. Comparison with Other Products at the Site Scale
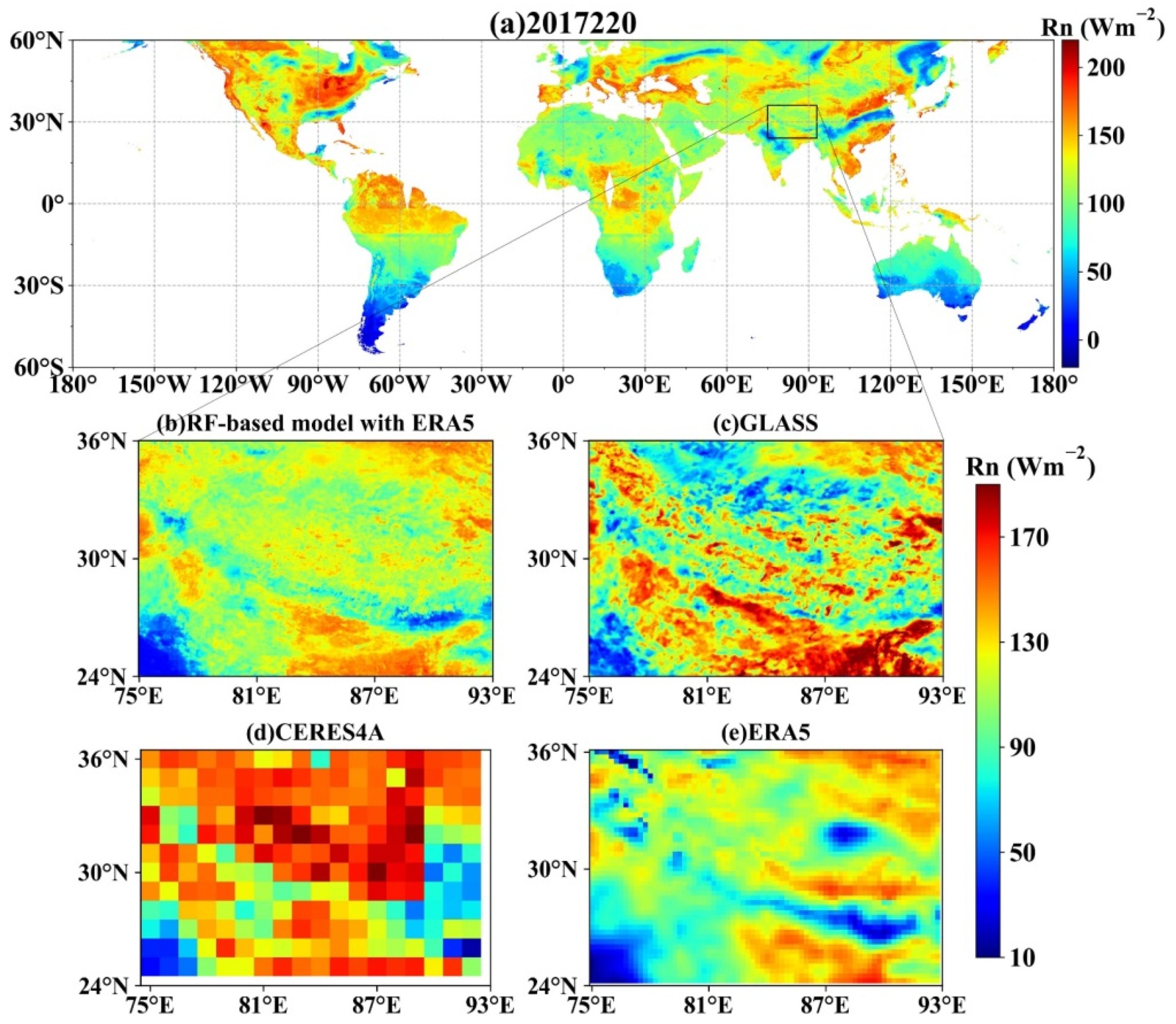
4.2.2. Mapping Using the RF-Based Model with ERA5
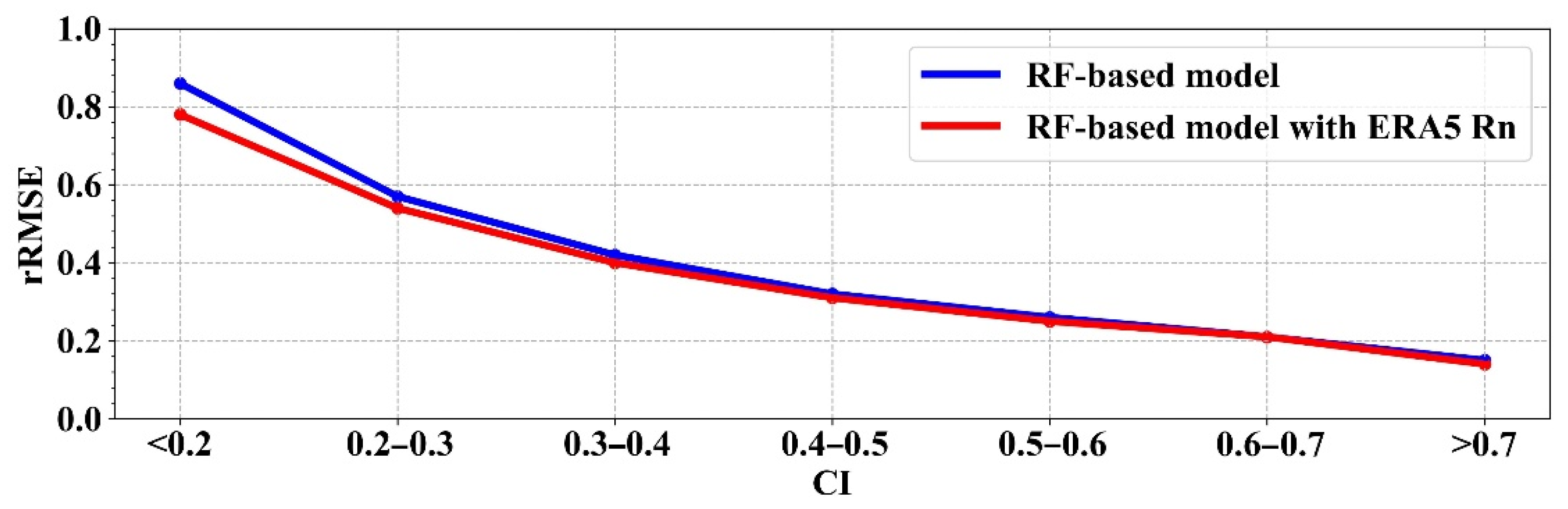
5. Discussion of the RF-Based Model with ERA5
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, S.; Wang, D.; He, T.; Yu, Y. Remote sensing of earth’s energy budget: Synthesis and review. Int. J. Digit. Earth 2019, 12, 737–780. [Google Scholar] [CrossRef] [Green Version]
- Alados, I.; Foyo-Moreno, I.; Olmo, F.; Alados-Arboledas, L. Relationship between net radiation and solar radiation for semi-arid shrub-land. Agric. For. Meteorol. 2003, 116, 221–227. [Google Scholar] [CrossRef]
- Kalthoff, N.; Fiebig-Wittmaack, M.; Meißner, C.; Kohler, M.; Uriarte, M.; Bischoff-Gauß, I.; Gonzales, E. The energy balance, evapo-transpiration and nocturnal dew deposition of an arid valley in the andes. J. Arid Environ. 2006, 65, 420–443. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Oleson, K.W.; Bonan, G.; Hoffman, F.; Thornton, P.; Vertenstein, M.; Yang, Z.-L.; Zeng, X. The community land model and its climate statistics as a component of the community climate system model. J. Clim. 2006, 19, 2302–2324. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using modis (moderate resolution imaging spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Jia, A.; Jiang, B.; Liang, S.; Zhang, X.; Ma, H. Validation and spatiotemporal analysis of ceres surface net radiation product. Remote Sensi. 2016, 8, 90. [Google Scholar] [CrossRef] [Green Version]
- Shi, Q.; Liang, S. Characterizing the surface radiation budget over the tibetan plateau with ground-measured, reanalysis, and remote sensing data sets: 1. Methodology. J. Geophys. Res. Atmos. 2013, 118, 9642–9657. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The era-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Kratz, D.P.; Gupta, S.K.; Wilber, A.C.; Sothcott, V.E. Validation of the ceres edition-4a surface-only flux algorithms. J. Appl. Meteorol. Climatol. 2020, 59, 281–295. [Google Scholar] [CrossRef]
- Decker, M.; Brunke, M.A.; Wang, Z.; Sakaguchi, K.; Zeng, X.; Bosilovich, M.G. Evaluation of the reanalysis products from gsfc, ncep, and ecmwf using flux tower observations. J. Clim. 2012, 25, 1916–1944. [Google Scholar] [CrossRef]
- Jia, A.; Liang, S.; Jiang, B.; Zhang, X.; Wang, G. Comprehensive assessment of global surface net radiation products and uncertainty analysis. J. Geophys. Res. Atmos. 2018, 123, 1970–1989. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Schär, C.; Loeb, N.; Dutton, E.; König-Langlo, G. The global energy balance from a surface perspective. Clim. Dyn. 2012, 40, 3107–3134. [Google Scholar] [CrossRef] [Green Version]
- Trenberth, K.; Fasullo, J. Simulation of present-day and twenty-first-century energy budgets of the southern oceans. J. Clim. 2010, 23, 440–454. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, Y.; Liang, S.; Wohlfahrt, G.; Arain, A.; Cescatti, A.; Georgiadis, T.; Jia, K.; Kiely, G.; Lund, M.; et al. Empirical estimation of daytime net radiation from shortwave radiation and ancillary information. Agric. For. Meteorol. 2015, 211–212, 23–36. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; He, T.; Jiang, B.; Liang, S. Estimation of all-sky all-wave daily net radiation at high latitudes from modis data. Remote Sens. Environ. 2020, 245, 111842. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; He, T.; Shi, Q. Estimating clear-sky all-wave net radiation from combined visible and shortwave infrared (vswir) and thermal infrared (tir) remote sensing data. Remote Sens. Environ. 2015, 167, 31–39. [Google Scholar] [CrossRef]
- Wu, H.; Ying, W. Benchmarking machine learning algorithms for instantaneous net surface shortwave radiation retrieval using remote sensing data. Remote Sens. 2019, 11, 2520. [Google Scholar] [CrossRef] [Green Version]
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the earth’s radiant energy system (ceres) energy balanced and filled (ebaf) top-of-atmosphere (toa) edition-4.0 data product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; He, T.; Shi, Q. Estimation of daily surface shortwave net radiation from the combined modis data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5519–5529. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the modis data under all sky conditions: Southern great plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Xu, X.; Du, H.; Zhou, G.; Mao, F.; Li, P.; Fan, W.; Zhu, D. A method for daily global solar radiation estimation from two instantaneous values using modis atmospheric products. Energy 2016, 111, 117–125. [Google Scholar] [CrossRef]
- Silber, I.; Verlinde, J.; Wang, S.-H.; Bromwich, D.H.; Fridlind, A.M.; Cadeddu, M.; Eloranta, E.W.; Flynn, C.J. Cloud influence on era5 and amps surface downwelling longwave radiation biases in west antarctica. J. Clim. 2019, 32, 7935–7949. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; He, T.; Liang, S.; Wang, D.; Yu, Y. Estimation of all-sky instantaneous surface incident shortwave radiation from moderate resolution imaging spectroradiometer data using optimization method. Remote Sens. Environ. 2018, 209, 468–479. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The era5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Martens, B.; Schumacher, D.L.; Wouters, H.; Muñoz-Sabater, J.; Verhoest, N.E.C.; Miralles, D.G. Evaluating the land-surface energy partitioning in era5. Geosci. Model Dev. 2020, 13, 4159–4181. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from era5 and cosmo-rea6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Babar, B.; Graversen, R.; Boström, T. Solar radiation estimation at high latitudes: Assessment of the cmsaf databases, asr and era5. Solar Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The fluxcom ensemble of global land-atmosphere energy fluxes. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef] [Green Version]
- Phillips, T.J.; Klein, S.A.; Ma, H.Y.; Tang, Q.; Xie, S.; Williams, I.N.; Santanello, J.A.; Cook, D.R.; Torn, M.S. Using arm observations to evaluate climate model simulations of land-atmosphere coupling on the us southern great plains. J. Geophys. Res. Atmos. 2017, 122, 524–548. [Google Scholar] [CrossRef]
- Zo, I.-S.; Jee, J.-B.; Kim, B.-Y.; Lee, K.-T. Baseline surface radiation network (bsrn) quality control of solar radiation data on the gangneung-wonju national university radiation station. Asia-Pac. J. Atmos. Sci. 2017, 53, 11–19. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.B.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Fu, B.; Li, S.; Yu, X.; Yang, P.; Yu, G.; Feng, R.; Zhuang, X. Chinese ecosystem research network: Progress and perspectives. Ecol. Complex. 2010, 7, 225–233. [Google Scholar] [CrossRef]
- Xin, L.; Shaomin, L.; Mingguo, M.; Qing, X.; Qinhuo, L.; Rui, J.; Tao, C.; Weizhen, W.; Yuan, Q.; Hongyi, L. Hiwater: An integrated remote sensing experiment on hydrological and ecological processes in the heihe river basin. Adv. Earth Sci. 2012, 27, 481–498. [Google Scholar]
- Yi, C.; Ricciuto, D.; Li, R.; Wolbeck, J.; Xu, X.; Nilsson, M.; Aires, L.; Albertson, J.D.; Ammann, C.; Arain, M.A. Climate control of terrestrial carbon exchange across biomes and continents. Environ. Res. Lett. 2010, 5, 034007. [Google Scholar] [CrossRef]
- Tóta, J.; Fitzjarrald, D.R.; Staebler, R.M.; Sakai, R.K.; Moraes, O.M.; Acevedo, O.C.; Wofsy, S.C.; Manzi, A.O. Amazon rain forest subcanopy flow and the carbon budget: Santarém lba-eco site. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Swap, R.J.; Annegarn, H.J.; Suttles, J.T.; King, M.D.; Platnick, S.; Privette, J.L.; Scholes, R.J. Africa burning: A thematic analysis of the southern african regional science initiative (safari 2000). J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. Surfrad–a national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2358. [Google Scholar] [CrossRef] [Green Version]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the köppen-geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.; Liang, S.; Tian, X.; Jia, K.; Yao, Y.; Jiang, B. Reconstruction of long-term temporally continuous ndvi and surface reflectance from avhrr data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5551–5568. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Empirical models for estimating net radiative flux: A case study for three mid-latitude sites with orographic variability. Astrophys. Space Sci. 2000, 273, 313–330. [Google Scholar] [CrossRef]
- Irmak, S.; Irmak, A.; Jones, J.; Howell, T.; Jacobs, J.; Allen, R.G.; Hoogenboom, G. Predicting daily net radiation using minimum climatological data. J. Irrig. Drain. Eng. 2003, 129, 256–269. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, B.; Liang, S.; Wang, D.; He, T.; Wang, Q.; Zhao, X.; Xu, J. Surface shortwave net radiation estimation from landsat tm/etm+ data using four machine learning algorithms. Remote Sens. 2019, 11, 2847. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Yao, Y.; Zhang, Y.; Lin, Y.; Jiang, B.; Jia, K.; Zhang, X.; Xie, X.; Zhang, L.; Shang, K.; et al. Discrepancies in the simulated global terrestrial latent heat flux from glass and merra-2 surface net radiation products. Remote Sens. 2020, 12, 2763. [Google Scholar] [CrossRef]
- Brown, P.T.; Caldeira, K. Greater future global warming inferred from earth’s recent energy budget. Nature 2017, 552, 45–50. [Google Scholar] [CrossRef]
- Yu, Y.; Shi, J.; Wang, T.; Letu, H.; Yuan, P.; Zhou, W.; Hu, L. Evaluation of the himawari-8 shortwave downward radiation (swdr) product and its comparison with the ceres-syn, merra-2, and era-interim datasets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 519–532. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.N. Parameterization of the radiative properties of cirrus clouds. J. Atmos. Sci. 1993, 50, 2008–2025. [Google Scholar] [CrossRef] [Green Version]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B.; Smith, G.L.; Cooper, J.E. Clouds and the earth’s radiant energy system (ceres): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the era5 reanalysis as a potential reference dataset for hydrological modelling over north america. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Babar, B.; Luppino, L.T.; Boström, T.; Anfinsen, S.N. Random forest regression for improved mapping of solar irradiance at high latitudes. Sol. Energy 2020, 198, 81–92. [Google Scholar] [CrossRef]
- Carmona, F.; Rivas, R.; Caselles, V. Development of a general model to estimate the instantaneous, daily, and daytime net radiation with satellite data on clear-sky days. Remote Sens. Environ. 2015, 171, 1–13. [Google Scholar] [CrossRef]
- Ying, W.; Wu, H.; Li, Z.-L. Net surface shortwave radiation retrieval using random forest method with modis/aqua data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2252–2259. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Global estimates for high-spatial-resolution clear-sky land surface upwelling longwave radiation from modis data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4115–4129. [Google Scholar] [CrossRef]
- Zhou, W.; Shi, J.; Wang, T.; Peng, B.; Zhao, R.; Yu, Y. Clear-sky longwave downward radiation estimation by integrating modis data and ground-based measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 450–459. [Google Scholar] [CrossRef]
- Wenhui, W.; Shunlin, L.; Augustine, J.A. Estimating high spatial resolution clear-sky land surface upwelling longwave radiation from modis data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1559–1570. [Google Scholar] [CrossRef]
- Xiong, X.; Angal, A.; Twedt, K.A.; Chen, H.; Link, D.; Geng, X.; Aldoretta, E.; Mu, Q. Modis reflective solar bands on-orbit calibration and performance. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6355–6371. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Yu, P.-S.; Yang, T.-C.; Chen, S.-Y.; Kuo, C.-M.; Tseng, H.-W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Verma, M.; Fisher, J.; Mallick, K.; Ryu, Y.; Kobayashi, H.; Guillaume, A.; Moore, G.; Ramakrishnan, L.; Hendrix, V.; Wolf, S.; et al. Global surface net-radiation at 5 km from modis terra. Remote Sens. 2016, 8, 739. [Google Scholar] [CrossRef] [Green Version]
- Doggett, L.; Kaplan, G. An almanac for computers. Bull. Am. Astron. Soc. 1976, 8, 299. [Google Scholar]
- Zhou, Y.; Yan, G.; Zhao, J.; Chu, Q.; Liu, Y.; Yan, K.; Tong, Y.; Mu, X.; Xie, D.; Zhang, W. Estimation of daily average downward shortwave radiation over antarctica. Remote Sens. 2018, 10, 422. [Google Scholar] [CrossRef] [Green Version]
- King, M.D.; Platnick, S.; Menzel, W.P.; Ackerman, S.A.; Hubanks, P.A. Spatial and temporal distribution of clouds observed by modis onboard the terra and aqua satellites. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3826–3852. [Google Scholar] [CrossRef]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Kim, H.-Y.; Liang, S. Development of a hybrid method for estimating land surface shortwave net radiation from modis data. Remote Sens. Environ. 2010, 114, 2393–2402. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, B.; Liang, S.; Li, X.; Wang, Y.; Peng, J.; Chen, H.; Liang, H.; Li, S. Generating a high-resolution time-series ocean surface net radiation product by downscaling j-ofuro3. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2794–2809. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Processing Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. In Rectified linear units improve restricted boltzmann machines. In Proceedings of the ICML, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- He, T.; Liang, S.; Wang, D.; Shi, Q.; Goulden, M.L. Estimation of high-resolution land surface net shortwave radiation from aviris data: Algorithm development and preliminary results. Remote Sens. Environ. 2015, 167, 20–30. [Google Scholar] [CrossRef] [Green Version]
- Sianturi, Y.; Marjuki; Sartika, K. Evaluation of era5 and merra2 reanalyses to estimate solar irradiance using ground observations over indonesia region. In Proceedings of the International Energy Conference Astechnova 2019, Yogyakarta, Indonesia, 30–31 October 2019. [Google Scholar]
- Jiang, H.; Lu, N.; Huang, G.; Yao, L.; Qin, J.; Liu, H. Spatial scale effects on retrieval accuracy of surface solar radiation using satellite data. Appl. Energy 2020, 270, 115178. [Google Scholar] [CrossRef]

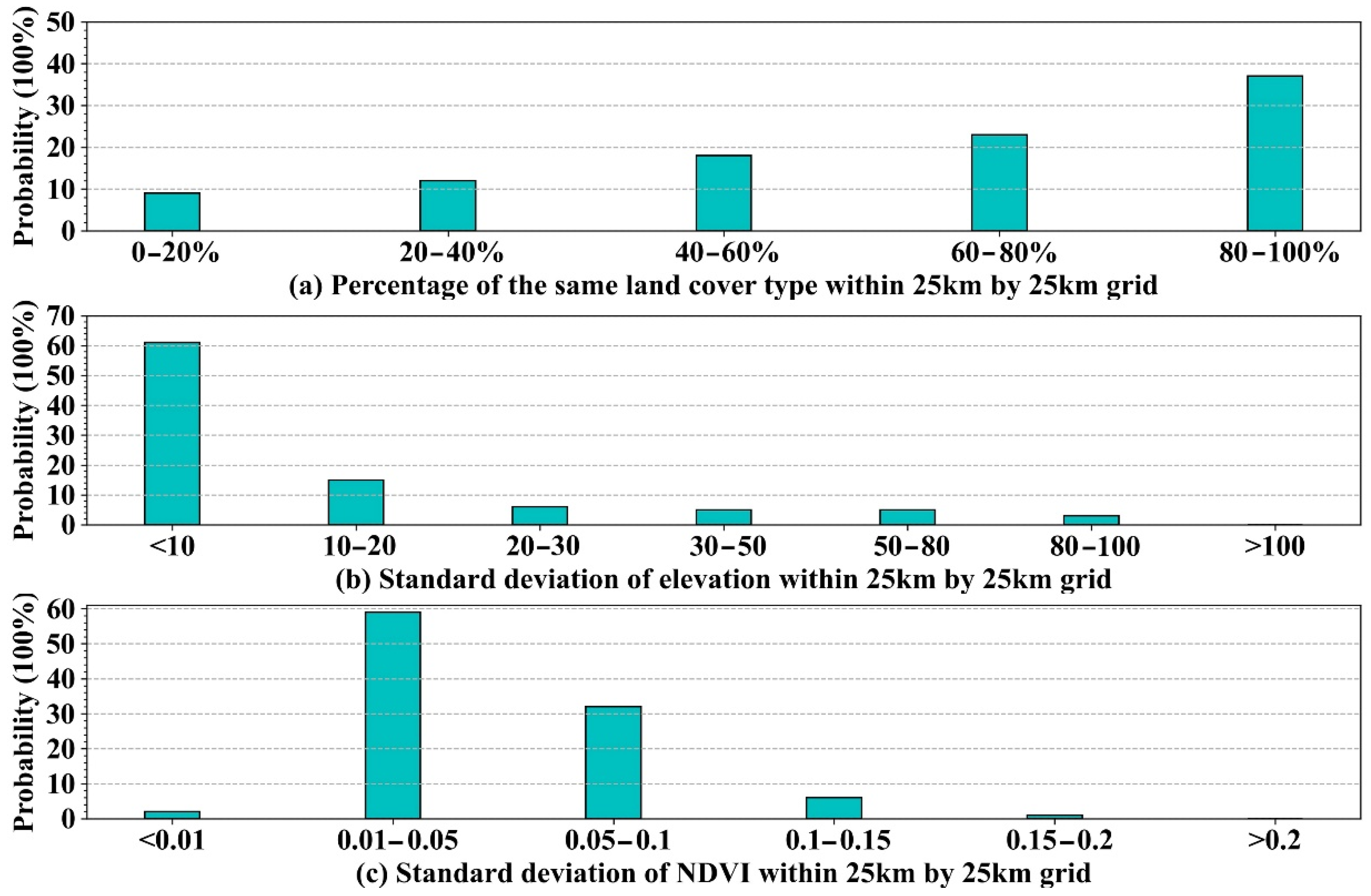


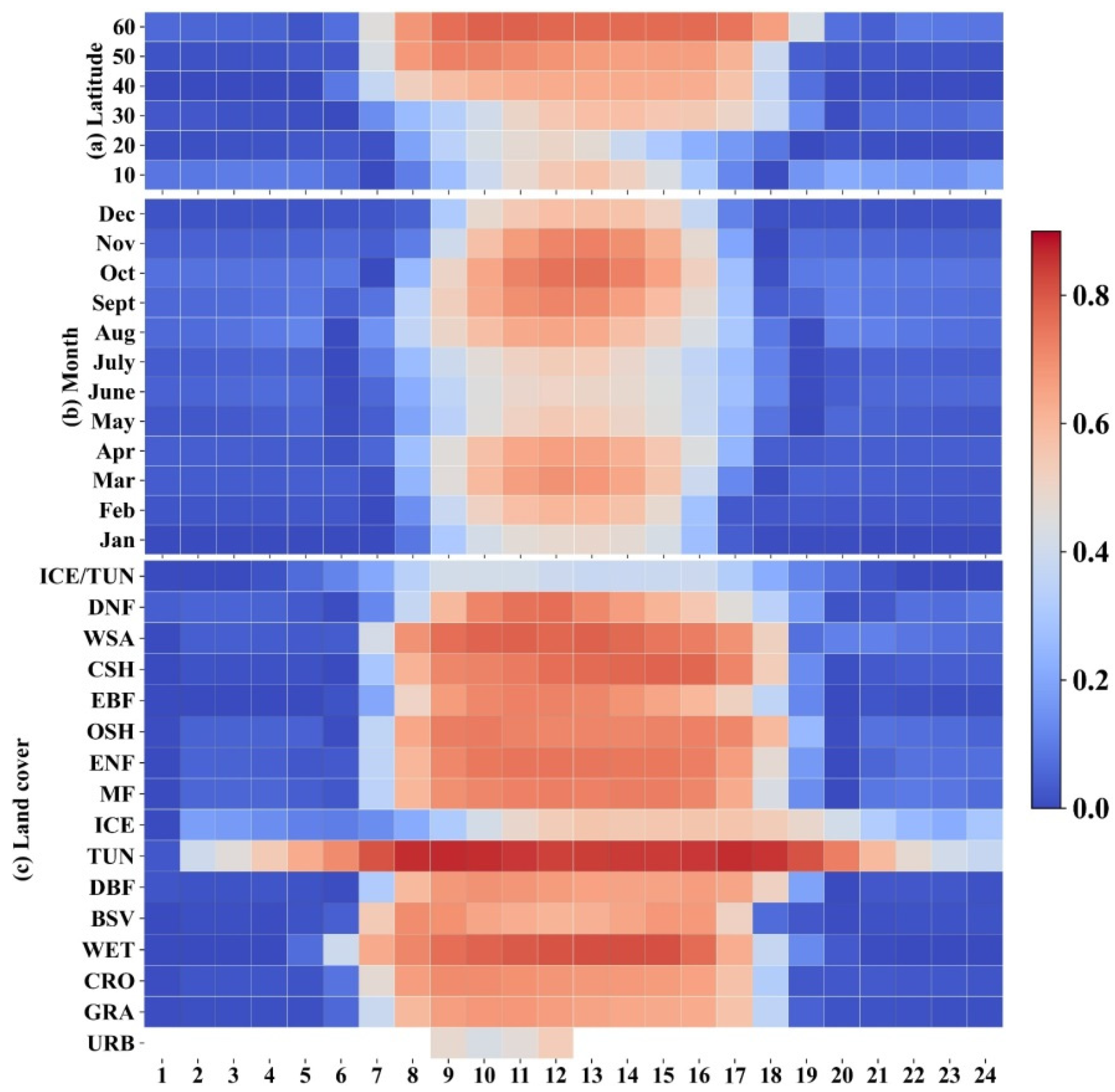
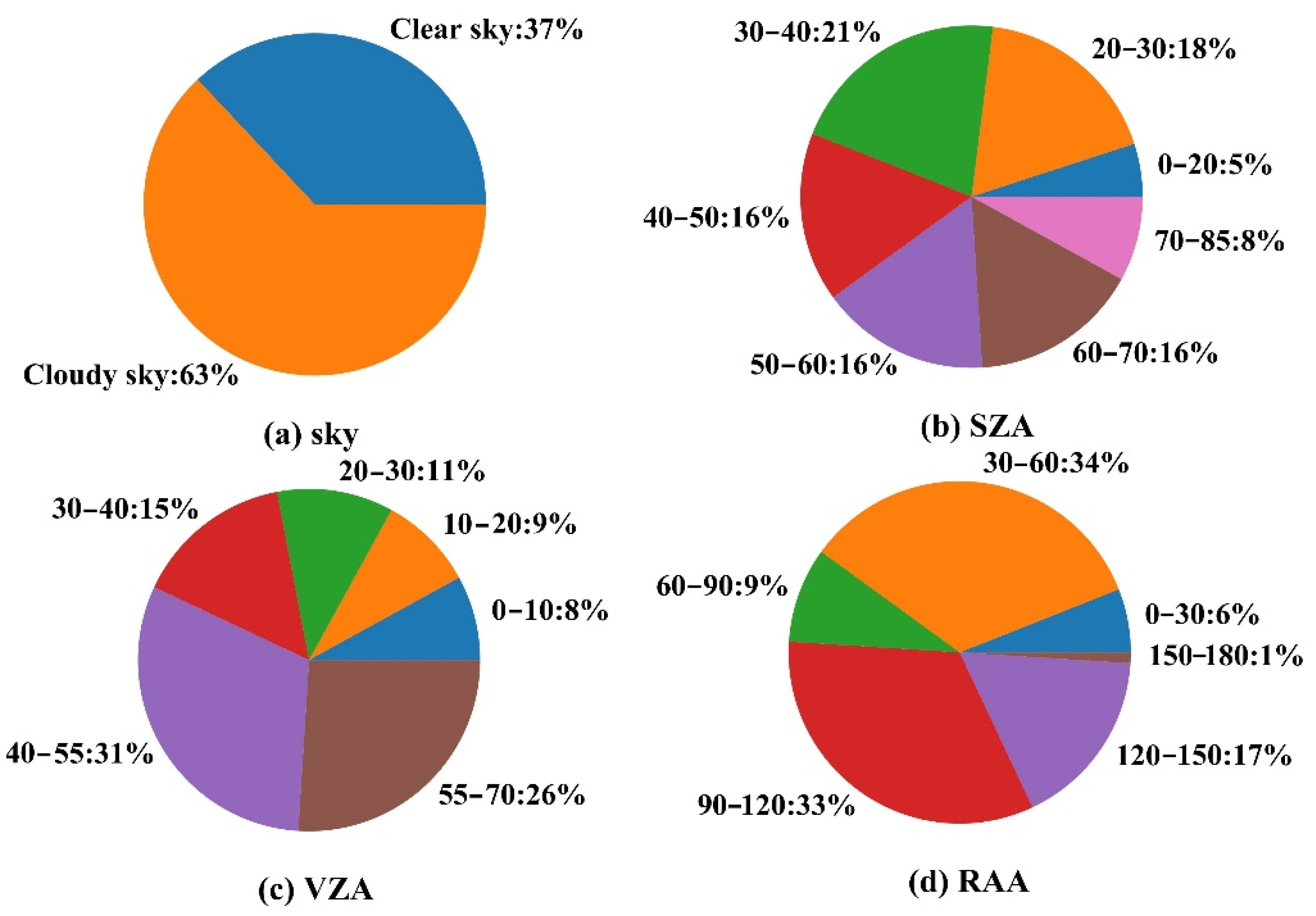

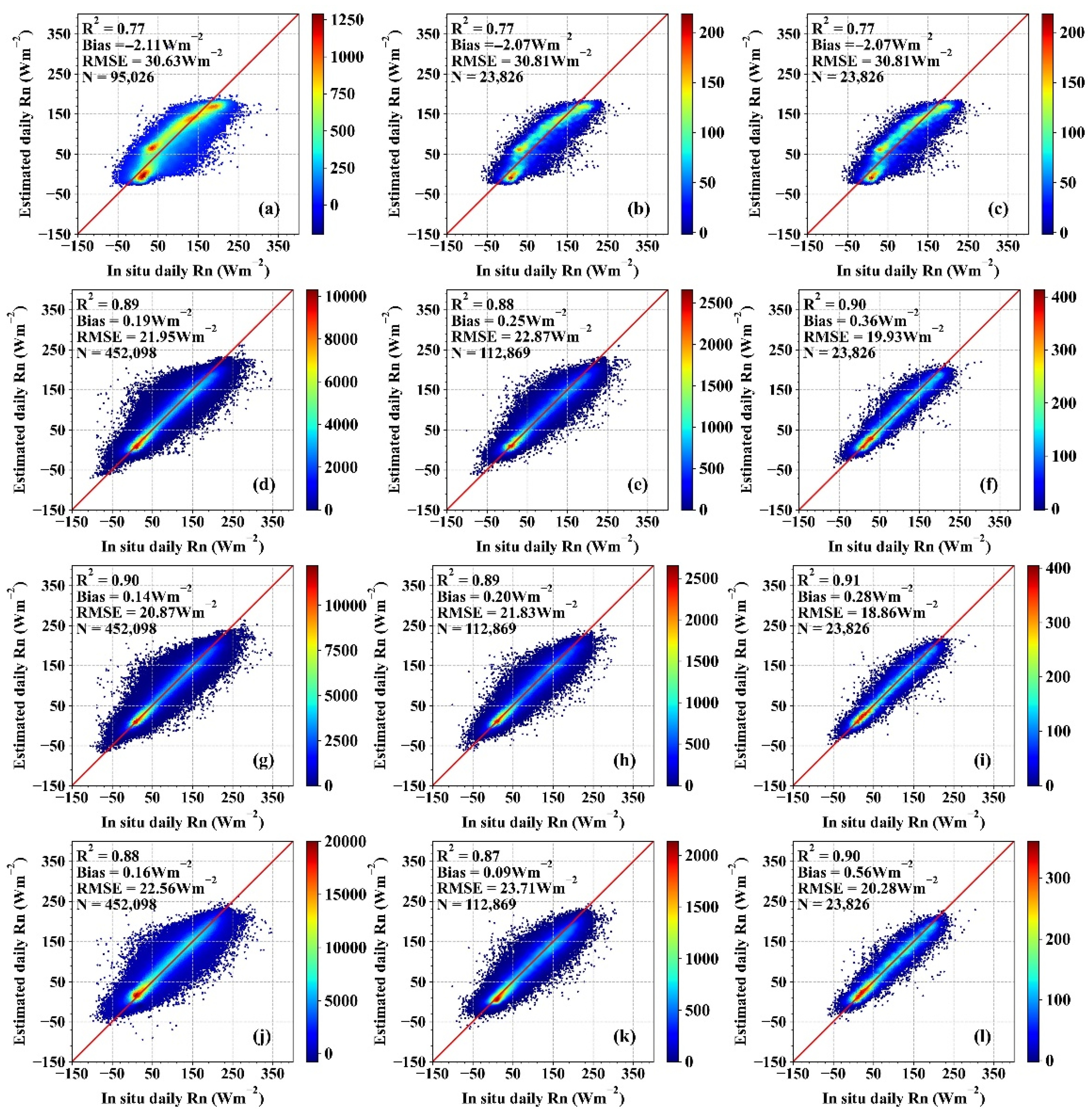



| Abbreviation | No. of Sites | Time Span | Instrument | Temporal Resolution | URL |
|---|---|---|---|---|---|
| ARM 1 | 33 | 2001–2017 | Kipp&Zonen Pyrgeometer | 1 min | [30] |
| AsiaFlux | 26 | 2001–2015 | Kipp&Zonen, CM-6F | 30 min | [7] |
| BSRN 2 | 7 | 2001–2017 | Eppley, PIR/Kipp&Zonen CG4 | 1 or 3min | [31] |
| CEOP 3 | 8 | 2008–2009 | Eppley PIR, CG4 | 30 min | [32] |
| CEOP_Int | 5 | 2002–2019 | QMN101 | 30 min | \ |
| CERN 4 | 1 | 2007–2014 | - | 30 min | [33] |
| ChinaFlux | 3 | 2003–2016 | - | 30 min | \ |
| GAME.ANN | 2 | 2001–2003 | EKO MS0202F | 30 min | \ |
| HiWATER | 16 | 2012–2012 | CNR-4 | 10 min | [34] |
| LaThuile 5 | 227 | 2001–2017 | Kipp&ZonenCNR- 1,etc | 30 min | [35] |
| LBA-ECO 6 | 4 | 2001–2006 | REBS Q*7.1 | 1 h | [36] |
| SAFARI 7 | 1 | 2001–2017 | Kipp&Zonen Pyrgeometer | 30 min | [37] |
| SURFRAD | 7 | 2001–2017 | Eppley, PIR | 3 min | [38] |
| MODIS Product | Temporal Resolution | Spatial Resolution | Parameters Used |
|---|---|---|---|
| MOD/MYD02 | 5 min | 1 km | 1 km_RefSB,1 km_Emissive |
| MOD/MYD03 | 5 min | 1 km | SolarZenith(SZA),SolarAzimuth (SAA), SensorZenith(VZA),SensorAzimuth (VAA), Height |
| MOD/MYD35 | 5 min | 1 km | Cloud Mask |
| Model | Description | No. of Training Samples | No. of Validation Samples | No. of Inter-Comparison Samples |
|---|---|---|---|---|
| RF-based ins model | with Sine model | 95,026 | 23,826 | 23,826 |
| RF-based model | from MODIS TOA observations | 452,098 | 112,869 | 23,826 |
| RF-based model with ERA5 | from ERA5 | 452,098 | 112,869 | 23,826 |
| LUT-based model | from MODIS TOA observations with different conditional models for various conditions | 452,098 | 112,869 | 23,826 |
| Hyper-Parameter | Threshold | Intervals |
|---|---|---|
| n-estimators | 30–100 | 10 |
| max depth | 2–15 | 1 |
| min samples split | 2–10 | 1 |
| min samples leaf | 2–10 | 1 |
| View Geometry/Sky Condition | Values |
|---|---|
| SZA | |
| VZA | |
| RAA | |
| Cloud mask | Clear, cloudy |
| Input | RMSE (Wm−2) | Bias (Wm−2) |
|---|---|---|
| Original | 22.87 | 0.25 |
| 22.63 | 0.33 | |
| Original + T + SP + CC + TCL + RH + TCW | 22.60 | 0.25 |
| + T + SP + CC + TCL + RH + TCW | 22.40 | 0.34 |
| 22.39 | 0.20 | |
| + T + SP + CC + TCL + RH + TCW | 22.27 | 0.23 |
| (ERA5) | 21.83 | 0.20 |
| Overpass Times | Bias (Wm−2) | RMSE (Wm−2) | ||
|---|---|---|---|---|
| RF-Based Model | RF-Based Model with ERA5 | RF-Based Model | RF-Based Model with ERA5 | |
| One | 0.8 | 0.68 | 24.17 | 22.41 |
| Two | 0.01 | −0.13 | 22 | 21.43 |
| Three | -0.66 | −0.29 | 21.92 | 21.55 |
| Average | 0.25 | 0.2 | 22.87 | 21.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Jiang, B.; Peng, J.; Liang, H.; Han, J.; Yao, Y.; Zhang, X.; Cheng, J.; Zhao, X.; Liu, Q.; et al. Estimation of the All-Wave All-Sky Land Surface Daily Net Radiation at Mid-Low Latitudes from MODIS Data Based on ERA5 Constraints. Remote Sens. 2022, 14, 33. https://doi.org/10.3390/rs14010033
Li S, Jiang B, Peng J, Liang H, Han J, Yao Y, Zhang X, Cheng J, Zhao X, Liu Q, et al. Estimation of the All-Wave All-Sky Land Surface Daily Net Radiation at Mid-Low Latitudes from MODIS Data Based on ERA5 Constraints. Remote Sensing. 2022; 14(1):33. https://doi.org/10.3390/rs14010033
Chicago/Turabian StyleLi, Shaopeng, Bo Jiang, Jianghai Peng, Hui Liang, Jiakun Han, Yunjun Yao, Xiaotong Zhang, Jie Cheng, Xiang Zhao, Qiang Liu, and et al. 2022. "Estimation of the All-Wave All-Sky Land Surface Daily Net Radiation at Mid-Low Latitudes from MODIS Data Based on ERA5 Constraints" Remote Sensing 14, no. 1: 33. https://doi.org/10.3390/rs14010033
APA StyleLi, S., Jiang, B., Peng, J., Liang, H., Han, J., Yao, Y., Zhang, X., Cheng, J., Zhao, X., Liu, Q., & Jia, K. (2022). Estimation of the All-Wave All-Sky Land Surface Daily Net Radiation at Mid-Low Latitudes from MODIS Data Based on ERA5 Constraints. Remote Sensing, 14(1), 33. https://doi.org/10.3390/rs14010033









