Challenges in Diurnal Humidity Analysis from Cellular Microwave Links (CML) over Germany
Abstract
:1. Introduction
2. Methodology
2.1. Study Region and Data
2.2. Humidity Retrievals from Commercial Microwave Links
2.3. Calibration
2.4. Optimization of RSLom Calculation
2.5. Interpolation
2.6. Analysis Methods
3. Results
3.1. Statistical Evaluation
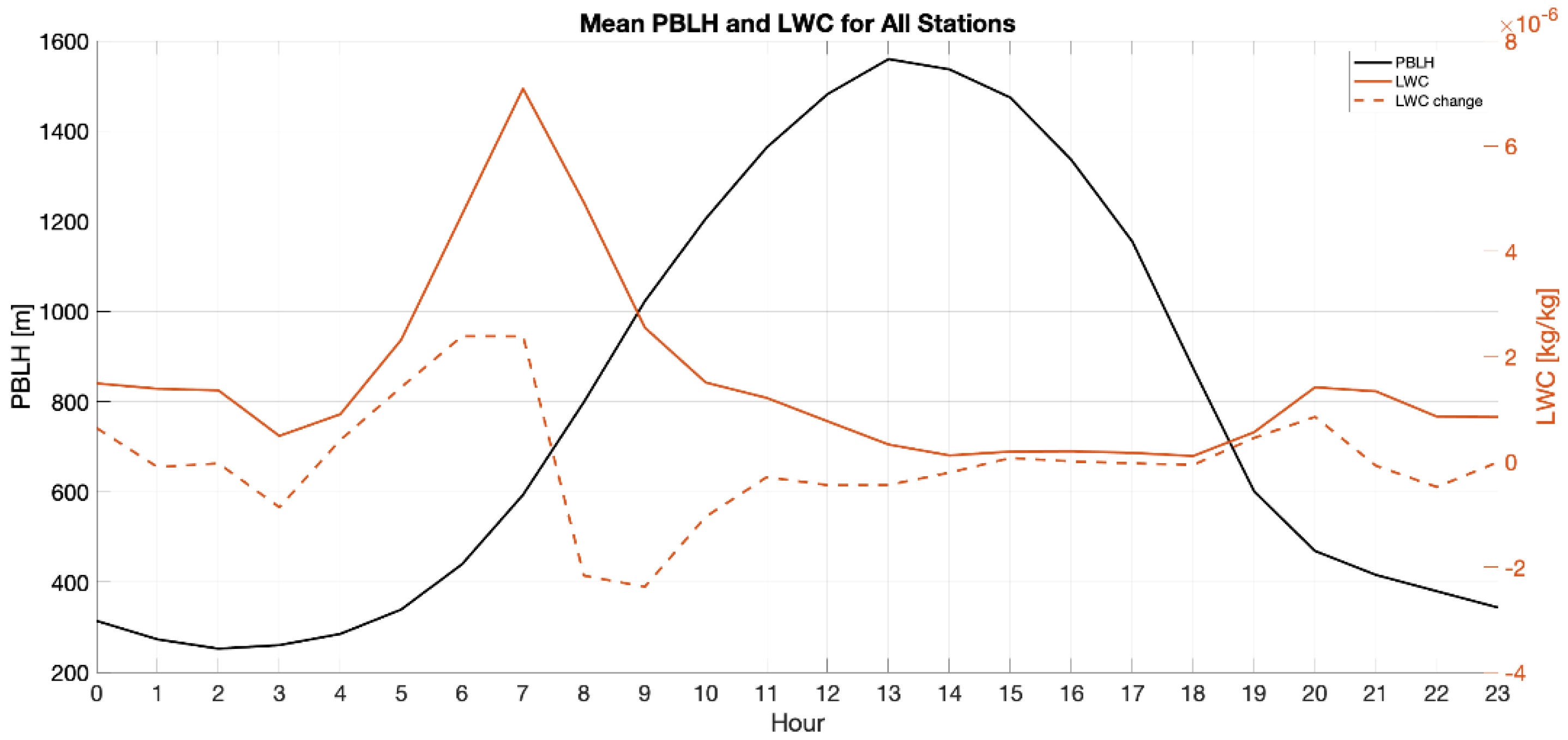
- All sources (WS-HO, CML-HO, and Rea6) show maximum mean values of humidity during nighttime hours and minimum mean values during daylight hours, as expected from the minimum and maximum values of the PBL heights (PBLH), respectively (see Figure 3). The STD values for all sources are of the order of 20% of the mean values.
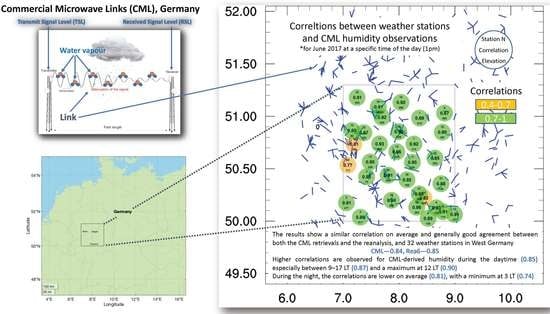
- Focusing on correlations, the WS-HO show high correlations with both CML-HO and Rea6, with average values of about 0.84 and 0.85, respectively. During most hours, the correlation was higher between the Rea6 and the WS-HO (17 out of 24 h) than between CML-HO and WS-HO (7 out of 24 h). Notice, however, that during daylight hours, there is a slight advantage for CML-HO (0.87 vs. 0.84). At night, the correlations between Rea6 and the WS-HO are higher than those between CML-HO and WS-HO (0.86 vs. 0.82, respectively).
- The RMSE is smaller in the case of Rea6 than CML-HO for most of the hours (18 h, with averages of 1.49 vs. 1.58, respectively), except during daylight.
- Mean and STD: The CML-HO mean and the STD values are closer to the WS-HO values, on average, than those of Rea6 (10.12 vs. 10.74 vs. 10.04 and 2.26 vs. 2.21 vs. 2.29, respectively), but during the day light hours, the Rea6 mean and the STD are closer to those of WS-HO, which is just the opposite to the correlation and RMSE behavior.
3.2. Mean Diurnal Cycle
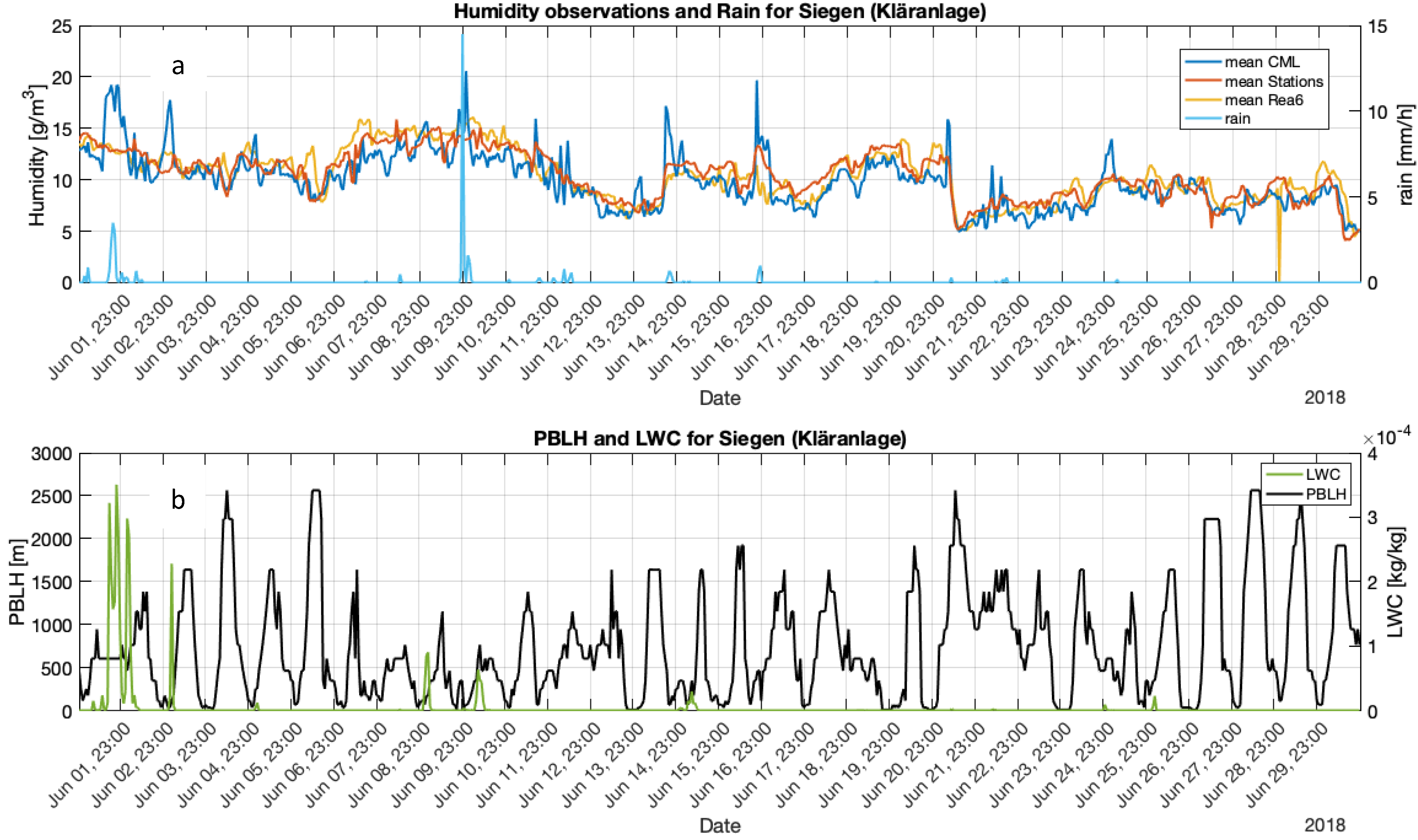
- Low CML-HO values can result from inaccurate WS-HOm values used for the calculation of RSLom at night. When we calculate the WS-HOm at 2 m AGL, it can be quite different from ~30 AGL humidity, especially at night with low inversion. This seems to improve when we used the second method for calibration (cali2). When looking into the calibration equations (Figure S1), we notice that the slope of the equation is higher during the night, which means that for high elevation CMLs, we will observe lower CML-HO values. When we take one diurnal equation instead of the hourly equations, this effect is improved. This conjecture can explain some of the deviations, but not all of them.
- An additional factor contributing to low CML-HO at night is an interference that can be caused by near-surface strong stratification of the atmosphere and the interaction between the electromagnetic waves and the changes in the characteristics of the atmosphere layers at night, when the PBLH is closer to the surface and the inversion is approximately at the CML level. This phenomenon was shown in David et al. [40].
- The strong reduction of the CML-HO at night is observed at many locations and it follows earlier high CML-HO values. For very low inversion layers, the CML could be located within the layer that is characterized by strong gradients of temperature and moisture, and therefore disable the CML-HO retrieval.
3.3. Inter-Daily Variability
- Employ the maximum limit for WV in the air as determined by the Clausius–Clapeyron equation. In the current algorithm, we determined the maximum value for true absolute humidity by the maximum value of the temperature for the whole period. If we choose the maximum temperature for a shorter period or instantaneously from a nearby weather station, or even a model, we expect to reduce the error caused by water on the antenna or in the air.
- Exclude rain events [42,43] and correct wet antenna attenuation (WAA) by the proposed methods for estimate the wet antenna effect [33,34,35,36]. This could be done based on the attenuation itself compared to dry periods, or by additional information from the stations. There are some methods for wet antenna estimation and the results can change between different locations and CMLs characteristics. Alternatively, during the rain events and for several hours afterwards, to allow for complete drying, they can be removed to reduce the errors due to WAA.
4. Discussion and Conclusions
- The best method to retrieve the CML-HO for getting the finest temporal resolution is to calibrate the CMLs calculating RSLm for 24 hour intervals. In addition, when applying one median equation for RSLm for all hours of the day, instead of separate equations for each hour of the day, there is an insignificant improvement, especially in the RMSE at night.
- Some of the most significant differences between CML-HO and WS-HO can be associated with:
- ○
- WAA (water on the antenna) due to rain or condensation.
- ○
- LWC, which might cause significant attenuation due to water in the air or WAA.
- ○
- PBLH, which affects the humidity vertical profile and might create large differences between the weather station (2 m AGL) and the CML (~30 m AGL) when the inversion layer is closer to the surface, especially at night.
- The height differences between stations and CML can be large. Hence, the verification of CML-HO with respect to WS-HO may lead to differences due to true different humidity at the CML and at the station.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| AGL | Above Ground Level |
| AMSL | Above Mean Sea Level |
| BL | Boundary Layer |
| cali1 | Calibration method 1: linear equations were calculated for each hour of the day |
| cali2 | Calibration method 2: a single linear equation was calculated for all hours of the day together |
| CML | Commercial Microwave Links |
| CML-HO | CML humidity observations |
| DWD | Germany’s National Meteorological Service, Deutscher Wetterdienst |
| LC | land cover |
| LWC | Liquid Water Content |
| LT | Local Time |
| NWP | Numerical Weather Prediction |
| PBL | Planetary Boundary Layer |
| PBLH | PBL heights |
| QE | Quantization Error |
| Rea6 | COSMO-REA6 reanalysis |
| RMSE | Root Mean Square Error |
| RSL | Received Signal Level |
| STD | Standard Deviation |
| TSL | Transmit Signal Level |
| WAA | Wet Antenna Attenuation |
| WS-HO | Weather station humidity observations |
| WV | Water Vapor |
References
- Fabry, F. The Spatial Variability of Moisture in the Boundary Layer and Its Effect on Convection Initiation: Project-Long Characterization. Mon. Weather Rev. 2006, 134, 79–91. [Google Scholar] [CrossRef]
- Kunz, M.; Sander, J.; Kottmeier, C. Recent trends of thunderstorm and hailstorm frequency and their relation to atmospheric characteristics in southwest Germany. Int. J. Climatol. 2009, 29, 2283–2297. [Google Scholar] [CrossRef] [Green Version]
- Lilly, D.K.; Gal-Chen, T. Mesoscale Meteorology-Theories, Observations and Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Toporov, M.; Löhnert, U. Synergy of Satellite- and Ground-Based Observations for Continuous Monitoring of Atmospheric Stability, Liquid Water Path, and Integrated Water Vapor: Theoretical Evaluations Using Reanalysis and Neural Networks. J. Appl. Meteorol. Climatol. 2020, 59, 1153–1170. [Google Scholar] [CrossRef] [Green Version]
- Pielke, R.A. Mesoscale Meteorological Modeling, 3rd ed.; International Geophysics Series; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 978-0-12-385237-3. [Google Scholar]
- Messer, H.; Zinevich, A.; Alpert, P. Environmental monitoring by wireless communication networks. Science 2006, 312, 713. [Google Scholar] [CrossRef] [Green Version]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Rainfall measurement using radio links from cellular communication networks. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Zinevich, A.; Alpert, P.; Messer, H. Estimation of rainfall fields using commercial microwave communication networks of variable density. Adv. Water Resour. 2008, 31, 1470–1480. [Google Scholar] [CrossRef]
- Zinevich, A.; Messer, H.; Alpert, P. Frontal rainfall observation by a commercial microwave communication network. J. Appl. Meteorol. Climatol. 2009, 48, 1317–1334. [Google Scholar] [CrossRef]
- Zinevich, A.; Messer, H.; Alpert, P. Prediction of rainfall intensity measurement errors using commercial microwave communication links. Atmos. Meas. Tech. 2010, 3, 1385–1402. [Google Scholar] [CrossRef] [Green Version]
- David, N.; Alpert, P.; Messer, H. Technical note: Novel method for water vapour monitoring using wireless communication networks measurements. Atmos. Chem. Phys. 2009, 9, 2413–2418. [Google Scholar] [CrossRef] [Green Version]
- Alpert, P.; Rubin, Y. First Daily Mapping of Surface Moisture from Cellular Network Data and Comparison with Both Observations/ECMWF Product. Geophys. Res. Lett. 2018, 45, 8619–8628. [Google Scholar] [CrossRef]
- Fencl, M.; Dohnal, M.; Valtr, P.; Grabner, M.; Bareš, V. Atmospheric observations with E-band microwave links–challenges and opportunities. Atmos. Meas. Tech. 2020, 13, 6559–6578. [Google Scholar] [CrossRef]
- Pu, K.; Liu, X.; Liu, L.; Gao, T. Water Vapor Retrieval Using Commercial Microwave Links Based on the LSTM Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4330–4338. [Google Scholar] [CrossRef]
- Song, K.; Liu, X.; Gao, T.; Zhang, P. Estimating Water Vapor Using Signals from Microwave Links below 25 GHz. Remote Sens. 2021, 13, 1409. [Google Scholar] [CrossRef]
- Ducrocq, V.; Ricard, D.; Lafore, J.-P.; Orain, F. Storm-Scale Numerical Rainfall Prediction for Five Precipitating Events over France: On the Importance of the Initial Humidity Field. Weather Forecast. 2002, 17, 1236–1256. [Google Scholar] [CrossRef]
- Rostkier-Edelstein, D.; Hacker, J.P. The Roles of Surface-Observation Ensemble Assimilation and Model Complexity for Nowcasting of PBL Profiles: A Factor Separation Analysis. Weather Forecast. 2010, 25, 1670–1690. [Google Scholar] [CrossRef]
- Ha, S.-Y.; Snyder, C. Influence of Surface Observations in Mesoscale Data Assimilation Using an Ensemble Kalman Filter. Mon. Weather Rev. 2014, 142, 1489–1508. [Google Scholar] [CrossRef] [Green Version]
- Bonafoni, S.; Biondi, R.; Brenot, H.; Anthes, R. Radio occultation and ground-based GNSS products for observing, understanding and predicting extreme events: A review. Atmos. Res. 2019, 230, 104624. [Google Scholar] [CrossRef]
- Ho, S.; Anthes, R.A.; Ao, C.O.; Healy, S.; Horanyi, A.; Hunt, D.; Mannucci, A.J.; Pedatella, N.; Randel, W.J.; Simmons, A.; et al. The COSMIC/FORMOSAT-3 Radio Occultation Mission after 12 Years: Accomplishments, Remaining Challenges, and Potential Impacts of COSMIC-2. Bull. Am. Meteorol. Soc. 2020, 101, E1107–E1136. [Google Scholar] [CrossRef] [Green Version]
- Andersson, E.; Hólm, E.; Bauer, P.; Beljaars, A.; Kelly, G.A.; McNally, A.P.; Simmons, A.J.; Thépaut, J.-N.; Tompkins, A.M. Analysis and forecast impact of the main humidity observing systems. Q. J. R. Meteorol. Soc. 2007, 133, 1473–1485. [Google Scholar] [CrossRef]
- Geer, A.J.; Baordo, F.; Bormann, N.; Chambon, P.; English, S.J.; Kazumori, M.; Lawrence, H.; Lean, P.; Lonitz, K.; Lupu, C. The growing impact of satellite observations sensitive to humidity, cloud and precipitation: Impact of Satellite Humidity, Cloud and Precipitation Observations. Q. J. R. Meteorol. Soc. 2017, 143, 3189–3206. [Google Scholar] [CrossRef]
- Gustafsson, N.; Janjić, T.; Schraff, C.; Leuenberger, D.; Weissmann, M.; Reich, H.; Brousseau, P.; Montmerle, T.; Wattrelot, E.; Bučánek, A.; et al. Survey of data assimilation methods for convective-scale numerical weather prediction at operational centres. Q. J. R. Meteorol. Soc. 2018, 144, 1218–1256. [Google Scholar] [CrossRef] [Green Version]
- Chwala, C.; Kunstmann, H. Commercial microwave link networks for rainfall observation: Assessment of the current status and future challenges. Wiley Interdiscip. Rev. Water 2019, 6, e1337. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Liebe, H.J. An updated model for millimeter wave propagation in moist air. Radio Sci. 1985, 20, 1069–1089. [Google Scholar] [CrossRef] [Green Version]
- van Vleck, J.H. The Absorption of Microwaves by Uncondensed Water Vapor. Phys. Rev. 1947, 71, 425–433. [Google Scholar] [CrossRef]
- Rubin, Y. A Novel Approach for High Resolution Humidity Mapping Based on Cellular Net-Work Data. Master’s Thesis, Tel-Aviv University, Tel-Aviv, Israel, 2018. [Google Scholar]
- David, N.; Sendik, O.; Rubin, Y.; Messer, H.; Gao, H.O.; Rostkier-Edelstein, D.; Alpert, P. Analyzing the ability to reconstruct the moisture field using commercial microwave network data. Atmos. Res. 2019, 219, 213–222. [Google Scholar] [CrossRef]
- Cressman, G.P. An Operational Objective Analysis System. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; International Geophysics Series; Academic Press: Oxford Waltham, MA, USA, 2011; ISBN 978-0-12-385022-5. [Google Scholar]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Microwave link rainfall estimation: Effects of link length and frequency, temporal sampling, power resolution, and wet antenna attenuation. Adv. Water Resour. 2008, 31, 1481–1493. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Raich, R.; Bao, L.; Hansryd, J.; Messer, H. The Wet-Antenna Effect—A Factor to be Considered in Future Communication Networks. IEEE Trans. Antennas Propag. 2018, 66, 315–322. [Google Scholar] [CrossRef]
- Fencl, M.; Valtr, P.; Kvicera, M.; Bares, V. Quantifying Wet Antenna Attenuation in 38-GHz Commercial Microwave Links of Cellular Backhaul. IEEE Geosci. Remote Sens. Lett. 2019, 16, 514–518. [Google Scholar] [CrossRef]
- David, N.; Harel, O.; Alpert, P.; Messer, H. Study of attenuation due to wet antenna in microwave radio communication. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 4418–4422. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Atmospheric Sciences Library; Kluwer Academic Publ: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1988; ISBN 978-90-277-2768-8. [Google Scholar]
- Brümmer, B.; Schultze, M. Analysis of a 7-year low-level temperature inversion data set measured at the 280 m high Hamburg weather mast. Meteorol. Z 2015, 24, 481–494. [Google Scholar] [CrossRef]
- Haikin, N.; Galanti, E.; Reisin, T.G.; Mahrer, Y.; Alpert, P. Inner Structure of Atmospheric Inversion Layers over Haifa Bay in the Eastern Mediterranean. Bound.-Layer Meteorol. 2015, 156, 471–487. [Google Scholar] [CrossRef]
- David, N.; Gao, H.O. Using Cellular Communication Networks To Detect Air Pollution. Environ. Sci. Technol. 2016, 50, 9442–9451. [Google Scholar] [CrossRef] [PubMed]
- Warner, T.T. Numerical Weather and Climate Prediction; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-0-521-51389-0. [Google Scholar]
- Graf, M.; Chwala, C.; Polz, J.; Kunstmann, H. Rainfall estimation from a German-wide commercial microwave link network: Optimized processing and validation for 1 year of data. Hydrol. Earth Syst. Sci. 2020, 24, 2931–2950. [Google Scholar] [CrossRef]
- Polz, J.; Chwala, C.; Graf, M.; Kunstmann, H. Big commercial microwave link data: Detecting rain events with deep learning. In Proceedings of the 22nd EGU General Assembly, Online, 4–8 May 2020. [Google Scholar]
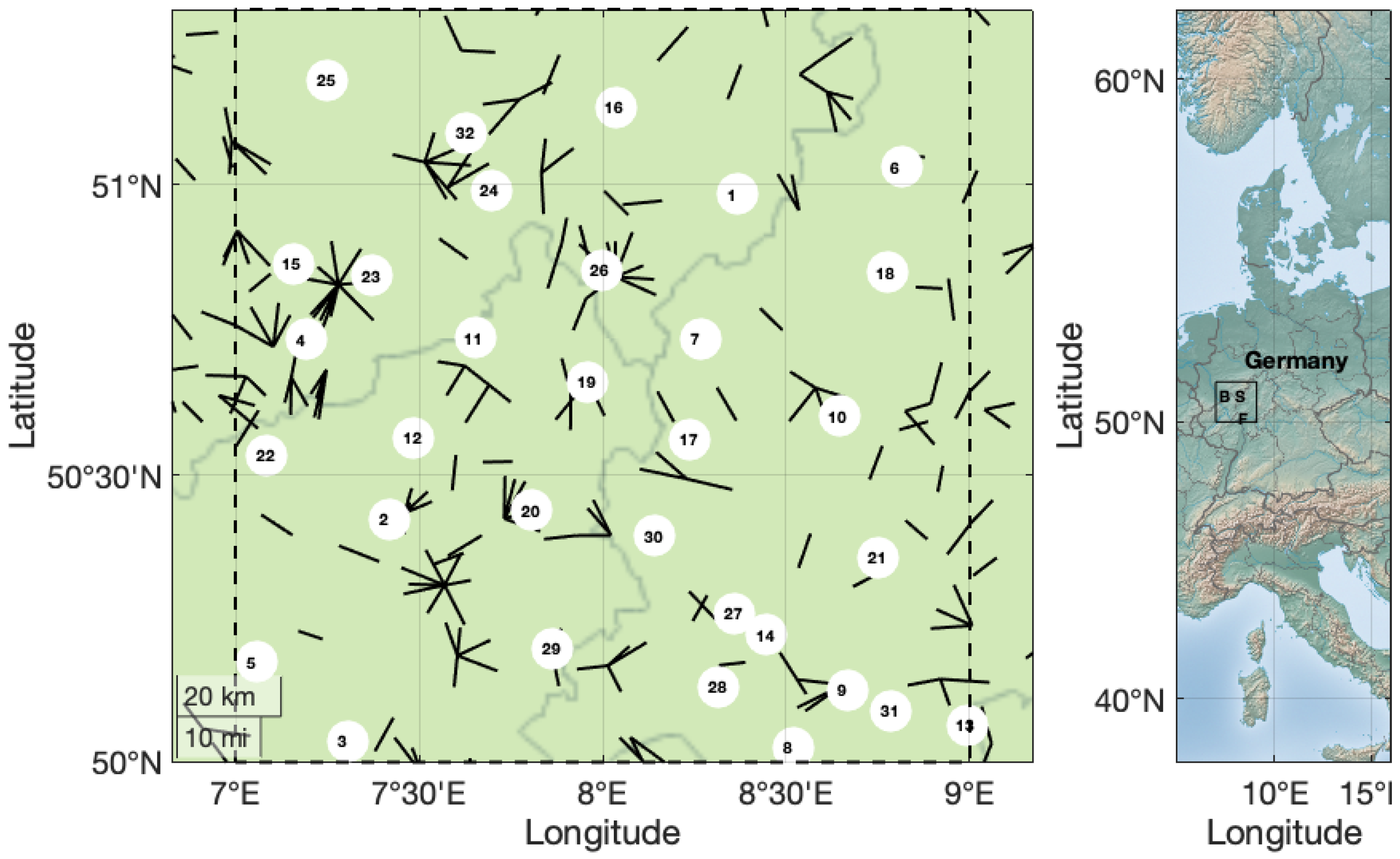


| Number | Name | Elevation [m] |
|---|---|---|
| 1 | Berleburg, Bad-Stenzel | 610 |
| 2 | Andernach | 75 |
| 3 | Blankenrath | 417 |
| 4 | Bonn-Roleber | 159 |
| 5 | Büchel (Flugplatz) | 477 |
| 6 | Burgwald-Bottendorf | 293 |
| 7 | Dillenburg | 314 |
| 8 | Frankfurt/Main | 100 |
| 9 | Frankfurt/Main-Westend | 124 |
| 10 | Gießen/Wettenberg | 203 |
| 11 | Hilgenroth | 295 |
| 12 | Hümmerich | 328 |
| 13 | Kahl/Main | 107 |
| 14 | Kleiner Feldberg/Taunus | 826 |
| 15 | Köln-Bonn | 92 |
| 16 | Lennestadt-Theten | 286 |
| 17 | Löhnberg-Obershausen | 230 |
| 18 | Marburg-Biedenkopf | 187 |
| 19 | Marienberg, Bad | 547 |
| 20 | Montabaur | 265 |
| 21 | Nauheim, Bad | 149 |
| 22 | Neuenahr, Bad-Ahrweiler | 111 |
| 23 | Neunkirchen-Seelscheid-Krawinkel | 195 |
| 24 | Reichshof-Eckenhagen | 350 |
| 25 | Remscheid-Lennep | 345 |
| 26 | Siegen (Kläranlage) | 229 |
| 27 | Waldems-Reinborn | 380 |
| 28 | Wiesbaden-Auringen | 263 |
| 29 | Nastätten | 268 |
| 30 | Runkel-Ennerich | 168 |
| 31 | Offenbach-Wetterpark | 119 |
| 32 | Meinerzhagen-Redlendorf | 380 |
| Hour | Corr_CML_Stations | Corr_Rea6S_Stations | RMSE_CML_Stations | RMSE_Rea6_Stations | Mean_Stations | Mean_CML | Mean_Rea6 | STD_Stations | STD_CML | STD_Rea6 |
|---|---|---|---|---|---|---|---|---|---|---|
| SUM# | 7 | 17 | 6 | 18 | 12 | 12 | 6 | 18 | ||
| MEAN | 0.84 | 0.85 | 1.58 | 1.49 | 10.74 | 10.12 | 10.04 | 2.21 | 2.26 | 2.29 |
| MEAN 9-17 | 0.87 | 0.84 | 1.53 | 1.55 | 10.49 | 9.76 | 9.78 | 2.38 | 2.24 | 2.29 |
| MEAN 18-8 | 0.82 | 0.86 | 1.61 | 1.46 | 10.89 | 10.34 | 10.19 | 2.10 | 2.27 | 2.29 |
| MEAN 6-21 (DAYLIGHT) | 0.853 | 0.852 | 1.59 | 1.54 | 10.67 | 9.85 | 9.89 | 2.31 | 2.25 | 2.30 |
| MEAN 22-5 (NIGHT) | 0.81 | 0.86 | 1.56 | 1.40 | 10.89 | 10.67 | 10.33 | 2.01 | 2.26 | 2.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubin, Y.; Rostkier-Edelstein, D.; Chwala, C.; Alpert, P. Challenges in Diurnal Humidity Analysis from Cellular Microwave Links (CML) over Germany. Remote Sens. 2022, 14, 2353. https://doi.org/10.3390/rs14102353
Rubin Y, Rostkier-Edelstein D, Chwala C, Alpert P. Challenges in Diurnal Humidity Analysis from Cellular Microwave Links (CML) over Germany. Remote Sensing. 2022; 14(10):2353. https://doi.org/10.3390/rs14102353
Chicago/Turabian StyleRubin, Yoav, Dorita Rostkier-Edelstein, Christian Chwala, and Pinhas Alpert. 2022. "Challenges in Diurnal Humidity Analysis from Cellular Microwave Links (CML) over Germany" Remote Sensing 14, no. 10: 2353. https://doi.org/10.3390/rs14102353
APA StyleRubin, Y., Rostkier-Edelstein, D., Chwala, C., & Alpert, P. (2022). Challenges in Diurnal Humidity Analysis from Cellular Microwave Links (CML) over Germany. Remote Sensing, 14(10), 2353. https://doi.org/10.3390/rs14102353