Exploring the Potential of Optical Polarization Remote Sensing for Oil Spill Detection: A Case Study of Deepwater Horizon
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Polarization Satellite Data
2.3. Validation Data
2.4. Random Forest Classifier
3. Results
3.1. Q1. To What Extent Do Polarization Characteristics Help in Optical Remote Sensing for Oil Spill Detection?
3.2. Q2. How Do Different Ways of Expressing Observation Geometry Influence the Result of Oil Spill Detection?
3.3. Q3. Which Combination of Polarization Features Performs Better in Oil Spill Detection?
3.4. Q4. Which Single-Angle Polarization Data Provide Better Oil Spill Detection Performance?
4. Discussion
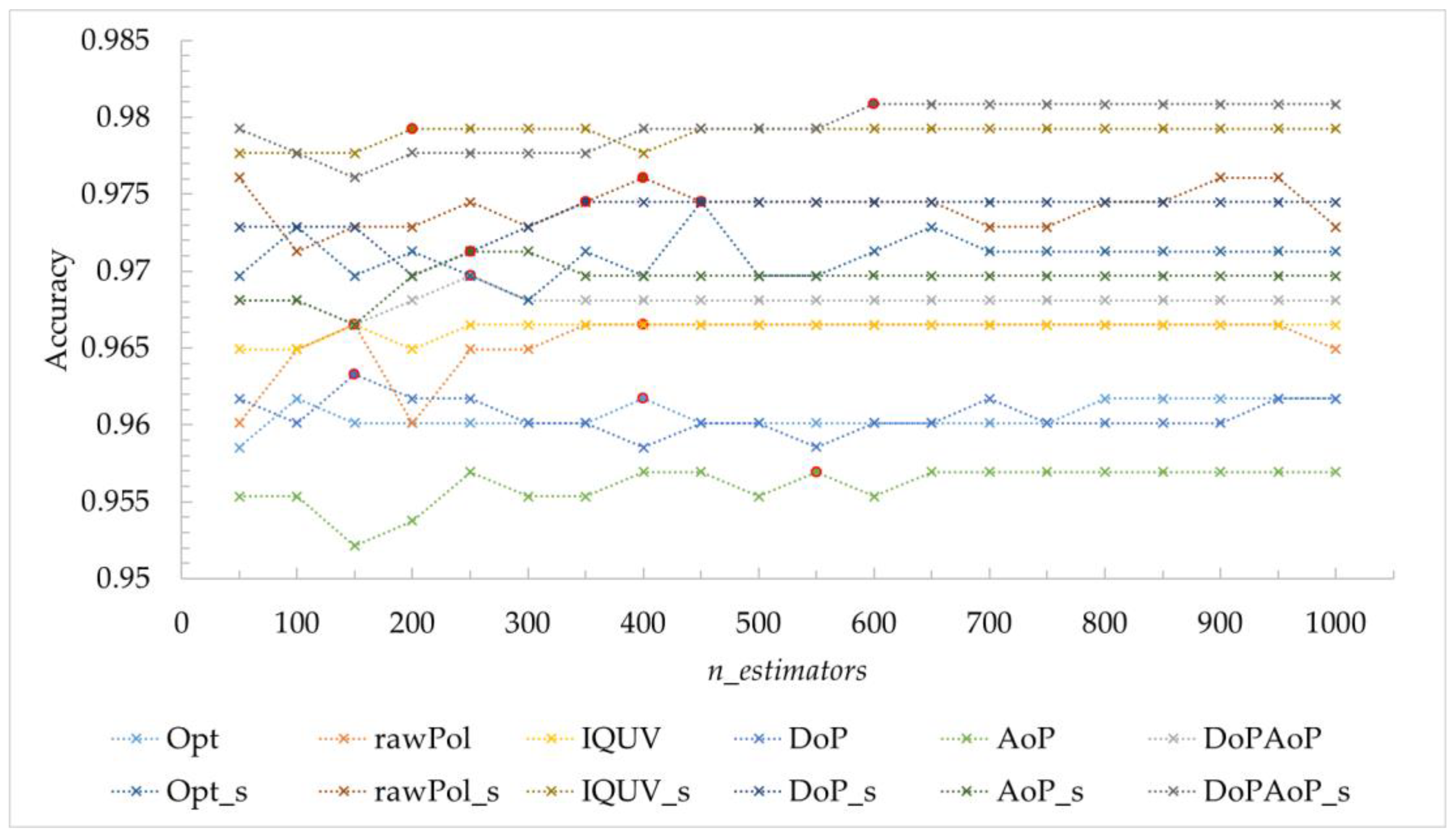
4.1. Determining Random Forest Classifier Parameters
4.2. Coupling between Degree of Polarization and Phase Angle of Polarization
4.3. Sensibility Analysis of Observation Geometry
4.4. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Term | Definition | Formula |
|---|---|---|
| classification tree | Classification trees are tree models where the target variable can take a discrete set of values. | / |
| leaf | In classification trees, leaves refer to the class labels. | / |
| branch | In classification trees, branches refer to the conjunctions of features. | / |
| node | In classification trees, nodes refer to the branch points. | / |
| n_features | The number of features during fit. | / |
| max_feature | The maximum of features when looking for the best split. | max_feature = sqrt(n_features) or max_feature = log2(n_features) |
| criterion | The function to measure the quality of a split. Gini impurity is the recommended function. | / |
| Gini impurity | A function that determines how well a decision tree is split. (D refers to the dataset, and pi refers to the probability of samples belonging to class i at a given node.) | |
| max_depth | The maximum depth of the tree. | / |
| n_estimators | The number of trees in the forest. | / |
| Sensor | Spatial Resolution | Spectral Range | Scheduled Launch Time |
|---|---|---|---|
| 3MI/EPS-SG | 4 km | 410 nm, 443 nm, 490 nm, 555 nm, 670 nm, 865 v, 1370 nm, 1650 nm, 2130 nm | 2022–2023 |
| SPEXone/PACE | 2.5 km | 385–770 nm in 2–4 nm steps | 2023 |
| HARP2/PACE | 3 km | 440 nm, 550 nm, 670 nm, 870 nm | 2023 |
| PolCube | 0.39 km × 0.31 km | 410 nm, 555 nm, 670 nm, 865 nm | 2023 |
| ScanPol/Aerosol-UA | 0.2–0.5 km | 370 nm, 410 nm, 555 nm, 865 nm, 1378 nm, 1610 nm | 2025 |
| MSIP/Aerosol-UA | 0.2–0.5 km | 410 nm, 555 nm, 865 nm | 2025 |
References
- Perrons, R.K. Assessing the damage caused by Deepwater Horizon: Not just another Exxon Valdez. Mar. Pollut. Bull. 2013, 71, 20–22. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Shen, Y. Development of an integrated model system to simulate transport and fate of oil spills in seas. Sci. China Technol. Sci. 2010, 53, 2423–2434. [Google Scholar] [CrossRef]
- Castanedo, S.; Juanes, J.; Medina, R.; Puente, A.; Fernandez, F.; Olabarrieta, M.; Pombo, C. Oil spill vulnerability assessment integrating physical, biological and socio-economical aspects: Application to the Cantabrian coast (Bay of Biscay, Spain). J. Environ. Manag. 2009, 91, 149–159. [Google Scholar] [CrossRef] [PubMed]
- Leifer, I.; Lehr, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef] [Green Version]
- Fingas, M.; Brown, C.E. Oil spill remote sensing: A forensics approach. In Standard Handbook Oil Spill Environmental Forensics; Elsevier: Amsterdam, The Netherlands, 2016; pp. 961–981. [Google Scholar]
- Fingas, M.; Brown, C.E. A review of oil spill remote sensing. Sensors 2018, 18, 91. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fingas, M.; Brown, C. Review of oil spill remote sensing. Mar. Pollut. Bull. 2014, 83, 9–23. [Google Scholar] [CrossRef] [Green Version]
- Brekke, C.; Solberg, A.H. Oil spill detection by satellite remote sensing. Remote Sens. Environ. 2005, 95, 1–13. [Google Scholar] [CrossRef]
- Suo, Z.; Lu, Y.; Liu, J.; Ding, J.; Yin, D.; Xu, F.; Jiao, J. Ultraviolet remote sensing of marine oil spills: A new approach of Haiyang-1C satellite. Opt. Express 2021, 29, 13486–13495. [Google Scholar] [CrossRef]
- Li, Y.; Li, B.; Lin, G.; Huang, Y.; Yang, D.; Ma, Y. Ultraviolet Radiation Characteristic of Oil Spills on Sea Surface. Acta Opt. Sin. 2020, 40, 0801001. [Google Scholar]
- Cong, H. Characteristics of UV Reflection Spectra of Oil Spill Based on Bidirectional Reflectance Distribution Function. Acta Photonica Sin. 2017, 46, 1012002. [Google Scholar] [CrossRef]
- Fang, S.; Huang, X.; Yin, D.; Xu, C.; Feng, X.; Feng, Q. Research on the ultraviolet reflectivity characteristic of simulative targets of oil spill on the ocean. Spectrosc. Spectr. Anal. 2010, 30, 738–742. [Google Scholar]
- Guo, G.; Liu, B.; Liu, C. Thermal infrared spectral characteristics of bunker fuel oil to determine oil-film thickness and API. J. Mar. Sci. Eng. 2020, 8, 135. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Jiang, L.; Lu, Y.; Zhan, W.; Mao, Z.; Qian, W.; Liu, Y. Thermal infrared contrast between different types of oil slicks on top of water bodies. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1042–1045. [Google Scholar] [CrossRef]
- Lu, Y.; Zhan, W.; Hu, C. Detecting and quantifying oil slick thickness by thermal remote sensing: A ground-based experiment. Remote Sens. Environ. 2016, 181, 207–217. [Google Scholar] [CrossRef]
- Xing, Q.; Li, L.; Lou, M.; Bing, L.; Zhao, R.; Li, Z. Observation of oil spills through landsat thermal infrared imagery: A case of deepwater horizon. Aquat. Procedia 2015, 3, 151–156. [Google Scholar] [CrossRef]
- Yang, J.; Ma, Y.; Hu, Y.; Jiang, Z.; Zhang, J.; Wan, J.; Li, Z. Decision Fusion of Deep Learning and Shallow Learning for Marine Oil Spill Detection. Remote Sens. 2022, 14, 666. [Google Scholar] [CrossRef]
- Duan, P.; Xie, Z.; Kang, X.; Li, S. Self-supervised learning-based oil spill detection of hyperspectral images. Sci. China Technol. Sci. 2022, 65, 793–801. [Google Scholar] [CrossRef]
- Caillault, K.; Roupioz, L.; Viallefont-Robinet, F. Modelling of the optical signature of oil slicks at sea for the analysis of multi-and hyperspectral VNIR-SWIR images. Opt. Express 2021, 29, 18224–18242. [Google Scholar] [CrossRef]
- Khanna, S.; Santos, M.J.; Ustin, S.L.; Shapiro, K.; Haverkamp, P.J.; Lay, M. Comparing the potential of multispectral and hyperspectral data for monitoring oil spill impact. Sensors 2018, 18, 558. [Google Scholar] [CrossRef] [Green Version]
- Moon, J.; Jung, M. Geometrical Properties of Spilled Oil on Seawater Detected Using a LiDAR Sensor. J. Sens. 2020, 2020, 5609168. [Google Scholar] [CrossRef]
- Jing, L.; Ying, C.; Shuang, L.; Zhaoxin, W.; Kun, Y. Design of Lidar System Based on Marine Oil Spill Monitoring. In Proceedings of the E3S Web of Conferences, Jilin, China, 20–22 March 2020; p. 03052. [Google Scholar] [CrossRef]
- Alaruri, S.D. Multiwavelength laser induced fluorescence (LIF) LIDAR system for remote detection and identification of oil spills. Optik 2019, 181, 239–245. [Google Scholar] [CrossRef]
- Raimondi, V.; Palombi, L.; Lognoli, D.; Masini, A.; Simeone, E. Experimental tests and radiometric calculations for the feasibility of fluorescence LIDAR-based discrimination of oil spills from UAV. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 46–54. [Google Scholar] [CrossRef]
- Jiao, J.; Lu, Y.; Liu, Y. Optical quantification of oil emulsions in multi-band coarse-resolution imagery using a lab-derived HSV model. Mar. Pollut. Bull. 2022, 178, 113640. [Google Scholar] [CrossRef] [PubMed]
- Seydi, S.T.; Hasanlou, M.; Amani, M.; Huang, W. Oil Spill Detection Based on Multiscale Multidimensional Residual CNN for Optical Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10941–10952. [Google Scholar] [CrossRef]
- Zhao, J.; Temimi, M.; Ghedira, H.; Hu, C. Exploring the potential of optical remote sensing for oil spill detection in shallow coastal waters-a case study in the Arabian Gulf. Opt. Express 2014, 22, 13755–13772. [Google Scholar] [CrossRef]
- Lu, Y.; Li, X.; Tian, Q.; Zheng, G.; Sun, S.; Liu, Y.; Yang, Q. Progress in marine oil spill optical remote sensing: Detected targets, spectral response characteristics, and theories. Mar. Geod. 2013, 36, 334–346. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, B.; Perrie, W.; Lu, Y.; Wang, C. A novel deep learning method for marine oil spill detection from satellite synthetic aperture radar imagery. Mar. Pollut. Bull. 2022, 179, 113666. [Google Scholar] [CrossRef]
- Jafarzadeh, H.; Mahdianpari, M.; Homayouni, S.; Mohammadimanesh, F.; Dabboor, M. Oil spill detection from Synthetic Aperture Radar Earth observations: A meta-analysis and comprehensive review. GIScience Remote Sens. 2021, 58, 1022–1051. [Google Scholar] [CrossRef]
- Cai, Y.; Zou, Y.; Liang, C.; Zou, B. Research on polarization of oil spill and detection. Acta Oceanol. Sin. 2016, 35, 84–89. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, X.; Xu, Q.; Garcia-Pineda, O.; Andersen, O.B.; Pichel, W.G. SAR observation and model tracking of an oil spill event in coastal waters. Mar. Pollut. Bull. 2011, 62, 350–363. [Google Scholar] [CrossRef]
- Ma, X.; Xu, J.; Wu, P.; Kong, P. Oil Spill Detection Based on Deep Convolutional Neural Networks Using Polarimetric Scattering Information From Sentinel-1 SAR Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Naz, S.; Iqbal, M.F.; Mahmood, I.; Allam, M. Marine oil spill detection using Synthetic Aperture Radar over Indian Ocean. Mar. Pollut. Bull. 2021, 162, 111921. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Wu, D.; An, J. Discrimination of oil slicks and lookalikes in polarimetric SAR images using CNN. Sensors 2017, 17, 1837. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Li, Y.; Sun, G.; Zhang, Y. Application of deep networks to oil spill detection using polarimetric synthetic aperture radar images. Appl. Sci. 2017, 7, 968. [Google Scholar] [CrossRef]
- Marghany, M. Automatic Mexico gulf oil spill detection from Radarsat-2 SAR satellite data using genetic algorithm. Acta Geophys. 2016, 64, 1916–1941. [Google Scholar] [CrossRef] [Green Version]
- King, M.D.; Platnick, S.; Menzel, W.P.; Ackerman, S.A.; Hubanks, P.A. Spatial and temporal distribution of clouds observed by MODIS onboard the Terra and Aqua satellites. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3826–3852. [Google Scholar] [CrossRef]
- Hu, C.; Lu, Y.; Sun, S.; Liu, Y. Optical remote sensing of oil spills in the ocean: What is really possible? J. Remote Sens. 2021, 2021, 9141902. [Google Scholar] [CrossRef]
- Sun, S.; Hu, C. The challenges of interpreting oil–water spatial and spectral contrasts for the estimation of oil thickness: Examples from satellite and airborne measurements of the deepwater horizon oil spill. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2643–2658. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, J.; Hu, C.; Zhang, M.; Sun, S.; Liu, Y. Optical interpretation of oil emulsions in the ocean–Part II: Applications to multi-band coarse-resolution imagery. Remote Sens. Environ. 2020, 242, 111778. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, J.; Wen, Y.; Hu, C.; Zhou, Y.; Sun, S.; Zhang, M.; Mao, Z.; Liu, Y. Optical interpretation of oil emulsions in the ocean–Part I: Laboratory measurements and proof-of-concept with AVIRIS observations. Remote Sens. Environ. 2019, 230, 111183. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Leifer, I.; Livo, K.E.; Kokaly, R.; Hoefen, T.; Lundeen, S.; Eastwood, M.; Green, R.O.; Pearson, N. A method for quantitative mapping of thick oil spills using imaging spectroscopy. US Geol. Surv. Open-File Rep. 2010, 1167, 1–51. [Google Scholar]
- Yan, L.; Li, Y.; Chandrasekar, V.; Mortimer, H.; Peltoniemi, J.; Lin, Y. General review of optical polarization remote sensing. Int. J. Remote Sens. 2020, 41, 4853–4864. [Google Scholar] [CrossRef]
- Rozanov, V.; Dinter, T.; Rozanov, A.; Wolanin, A.; Bracher, A.; Burrows, J. Radiative transfer modeling through terrestrial atmosphere and ocean accounting for inelastic processes: Software package SCIATRAN. J. Quant. Spectrosc. Radiat. Transf. 2017, 194, 65–85. [Google Scholar] [CrossRef] [Green Version]
- Chami, M.; Lafrance, B.; Fougnie, B.; Chowdhary, J.; Harmel, T.; Waquet, F. OSOAA: A vector radiative transfer model of coupled atmosphere-ocean system for a rough sea surface application to the estimates of the directional variations of the water leaving reflectance to better process multi-angular satellite sensors data over the ocean. Opt. Express 2015, 23, 27829–27852. [Google Scholar]
- He, X.; Bai, Y.; Zhu, Q.; Gong, F. A vector radiative transfer model of coupled ocean–atmosphere system using matrix-operator method for rough sea-surface. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1426–1448. [Google Scholar] [CrossRef]
- Cheng, T.; Gu, X.; Xie, D.; Li, Z.; Yu, T.; Chen, H. Aerosol optical depth and fine-mode fraction retrieval over East Asia using multi-angular total and polarized remote sensing. Atmos. Meas. Tech. 2012, 5, 501–516. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.; Cheng, T.; Xie, D.; Li, Z.; Yu, T.; Chen, H. Analysis of surface and aerosol polarized reflectance for aerosol retrievals from polarized remote sensing in PRD urban region. Atmos. Environ. 2011, 45, 6607–6612. [Google Scholar] [CrossRef]
- Cheng, T.; Gu, X.; Xie, D.; Li, Z.; Yu, T.; Chen, X. Simultaneous retrieval of aerosol optical properties over the Pearl River Delta, China using multi-angular, multi-spectral, and polarized measurements. Remote Sens. Environ. 2011, 115, 1643–1652. [Google Scholar] [CrossRef]
- Li, C.; Ma, J.; Yang, P.; Li, Z. Detection of cloud cover using dynamic thresholds and radiative transfer models from the polarization satellite image. J. Quant. Spectrosc. Radiat. Transf. 2019, 222, 196–214. [Google Scholar] [CrossRef]
- Goloub, P.; Herman, M.; Chepfer, H.; Riédi, J.; Brogniez, G.; Couvert, P.; Sèze, G. Cloud thermodynamical phase classification from the POLDER spaceborne instrument. J. Geophys. Res. Atmos. 2000, 105, 14747–14759. [Google Scholar] [CrossRef] [Green Version]
- Parol, F.; Buriez, J.-C.; Vanbauce, C.; Riédi, J.; Doutriaux-Boucher, M.; Vesperini, M.; Sèze, G.; Couvert, P.; Viollier, M.; Bréon, F. Review of capabilities of multi-angle and polarization cloud measurements from POLDER. Adv. Space Res. 2004, 33, 1080–1088. [Google Scholar] [CrossRef]
- Chami, M.; Santer, R.; Dilligeard, E. Radiative transfer model for the computation of radiance and polarization in an ocean–atmosphere system: Polarization properties of suspended matter for remote sensing. Appl. Opt. 2001, 40, 2398–2416. [Google Scholar] [CrossRef] [PubMed]
- Chami, M. Importance of the polarization in the retrieval of oceanic constituents from the remote sensing reflectance. J. Geophys. Res. Ocean 2007, 112, C05026. [Google Scholar] [CrossRef]
- Wang, M.; Isaacman, A.; Franz, B.A.; McClain, C.R. Ocean-color optical property data derived from the Japanese Ocean Color and Temperature Scanner and the French Polarization and Directionality of the Earth’s Reflectances: A comparison study. Appl. Opt. 2002, 41, 974–990. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Yang, B.; Zhang, F.; Xiang, Y.; Chen, W. Polarization Remote Sensing Physics; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Yang, F.; Shen, W. Research on polarization detection technology of oil spill on sea surface. In Proceedings of the Seventh Symposium on Novel Photoelectronic Detection Technology and Applications, Kunming, China, 5–7 November 2020; p. 1176364. [Google Scholar]
- Xu, J.; Wang, X.; Qian, W. Optical characteristics of oil spill based on polarization scattering rate. Appl. Opt. 2020, 59, 1193. [Google Scholar] [CrossRef]
- Ren, K.; Lv, Y.; Gu, G.; Chen, Q. Calculation method of multiangle polarization measurement for oil spill detection. Appl. Opt. 2019, 58, 3317–3324. [Google Scholar] [CrossRef]
- Lu, Y.; Zhou, Y.; Liu, Y.; Mao, Z.; Qian, W.; Wang, M.; Zhang, M.; Xu, J.; Sun, S.; Du, P. Using remote sensing to detect the polarized sunglint reflected from oil slicks beyond the critical angle. J. Geophys. Res. Ocean 2017, 122, 6342–6354. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Y.; Shen, Y.; Ding, J.; Zhang, M.; Mao, Z. Polarized Remote Inversion of the Refractive Index of Marine Spilled Oil From PARASOL Images Under Sunglint. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2710–2719. [Google Scholar] [CrossRef]
- Joye, S.B. Deepwater Horizon, 5 years on. Science 2015, 349, 592–593. [Google Scholar] [CrossRef]
- Beyer, J.; Trannum, H.C.; Bakke, T.; Hodson, P.V.; Collier, T.K. Environmental effects of the Deepwater Horizon oil spill: A review. Mar. Pollut. Bull. 2016, 110, 28–51. [Google Scholar] [CrossRef] [Green Version]
- Guard, U.S.C.; Team, N.R. On Scene Coordinator Report: Deepwater Horizon Oil Spill; US Department of Homeland Security, US Coast Guard: Washington, DC, USA, 2011.
- Liu, Y.; Weisberg, R.H.; Hu, C.; Zheng, L. Tracking the Deepwater Horizon Oil Spill: A Modeling Perspective. Eos Trans. Am. Geophys. Union 2011, 92, 45–46. [Google Scholar] [CrossRef]
- Berenshtein, I.; Paris, C.B.; Perlin, N.; Alloy, M.M.; Joye, S.B.; Murawski, S. Invisible oil beyond the Deepwater Horizon satellite footprint. Sci. Adv. 2020, 6, eaaw8863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; MacFadyen, A.; Ji, Z.-G.; Weisberg, R.H. Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record Breaking Enterprise; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 195. [Google Scholar]
- Deschamps, P.; Breon, F.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Bermudo, F.; Fougnie, B.; Bret-Dibat, T. Polder 2 in-flight results and parasol perspectives. In Proceedings of the SPIE, Toulouse, France, 30 March–2 April 2004. [Google Scholar] [CrossRef] [Green Version]
- Lifermann, A.; Proy, C. POLDER on ADEOS-2. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; Volume 21, p. 25. [Google Scholar] [CrossRef]
- Fougnie, B.; Bracco, G.; Lafrance, B.; Ruffel, C.; Hagolle, O.; Tinel, C. PARASOL in-flight calibration and performance. Appl. Opt. 2007, 46, 5435–5451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lier, P.; Bach, M. PARASOL a microsatellite in the A-Train for Earth atmospheric observations. Acta Astronaut. 2008, 62, 257–263. [Google Scholar] [CrossRef]
- Stokes, G.G. On the composition and resolution of streams of polarized light from different sources. Trans. Camb. Philos. Soc. 1851, 9, 399. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Goldstein, D.H. Polarized Light; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Coulson, K.L. Polarization and Intensity of Light in the Atmosphere; A Deepak Pub: Hampton, VA, USA, 1988. [Google Scholar]
- Schott, J.R. Fundamentals of Polarimetric Remote Sensing; SPIE Press: Bellingham, WA, USA, 2009; Volume 81. [Google Scholar]
- Burger, W.; Burge, M.J. Principles of Digital Image Processing: Fundamental Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Streett, D.; Warren, C. Operational Satellite-based Surface Oil Analyses. In Proceedings of the American Geophysical Union Fall Meeting Abstracts, San Francisco, CA, USA, 13–17 December 2010; p. OS41D-01. [Google Scholar]
- Ozigis, M.S.; Kaduk, J.D.; Jarvis, C.H. Mapping terrestrial oil spill impact using machine learning random forest and Landsat 8 OLI imagery: A case site within the Niger Delta region of Nigeria. Environ. Sci. Pollut. Res. 2019, 26, 3621–3635. [Google Scholar] [CrossRef] [Green Version]
- Tong, S.; Liu, X.; Chen, Q.; Zhang, Z.; Xie, G. Multi-feature based ocean oil spill detection for polarimetric SAR data using random forest and the self-similarity parameter. Remote Sens. 2019, 11, 451. [Google Scholar] [CrossRef] [Green Version]
- Baek, W.-K.; Jung, H.-S. Performance Comparison of Oil Spill and Ship Classification from X-Band Dual-and Single-Polarized SAR Image Using Support Vector Machine, Random Forest, and Deep Neural Network. Remote Sens. 2021, 13, 3203. [Google Scholar] [CrossRef]
- Hu, C.; Li, X.; Pichel, W.G.; Muller-Karger, F.E. Detection of natural oil slicks in the NW Gulf of Mexico using MODIS imagery. Geophys. Res. Lett. 2009, 36, L01604. [Google Scholar] [CrossRef]
- Fougnie, B.; Marbach, T.; Lacan, A.; Lang, R.; Schlüssel, P.; Poli, G.; Munro, R.; Couto, A.B. The multi-viewing multi-channel multi-polarisation imager–Overview of the 3MI polarimetric mission for aerosol and cloud characterization. J. Quant. Spectrosc. Radiat. Transf. 2018, 219, 23–32. [Google Scholar] [CrossRef]
- Gorman, E.T.; Kubalak, D.A.; Patel, D.; Mott, D.B.; Meister, G.; Werdell, P.J. The NASA Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission: An emerging era of global, hyperspectral Earth system remote sensing. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIII, Strasbourg, France, 9–12 September 2019; p. 111510G. [Google Scholar]
- Stamnes, S.; Baize, R.; Bontempi, P.; Cairns, B.; Chemyakin, E.; Choi, Y.-J.; Chowdhary, J.; Hu, Y.; Jeong, M.; Kang, K.-I. Simultaneous aerosol and ocean properties from the PolCube CubeSat polarimeter. Front. Remote Sens. 2021, 2, 19. [Google Scholar] [CrossRef]
- Milinevsky, G.; Yatskiv, Y.; Degtyaryov, O.; Syniavskyi, I.; Mishchenko, M.; Rosenbush, V.; Ivanov, Y.; Makarov, A.; Bovchaliuk, A.; Danylevsky, V. New satellite project Aerosol-UA: Remote sensing of aerosols in the terrestrial atmosphere. Acta Astronaut. 2016, 123, 292–300. [Google Scholar] [CrossRef]
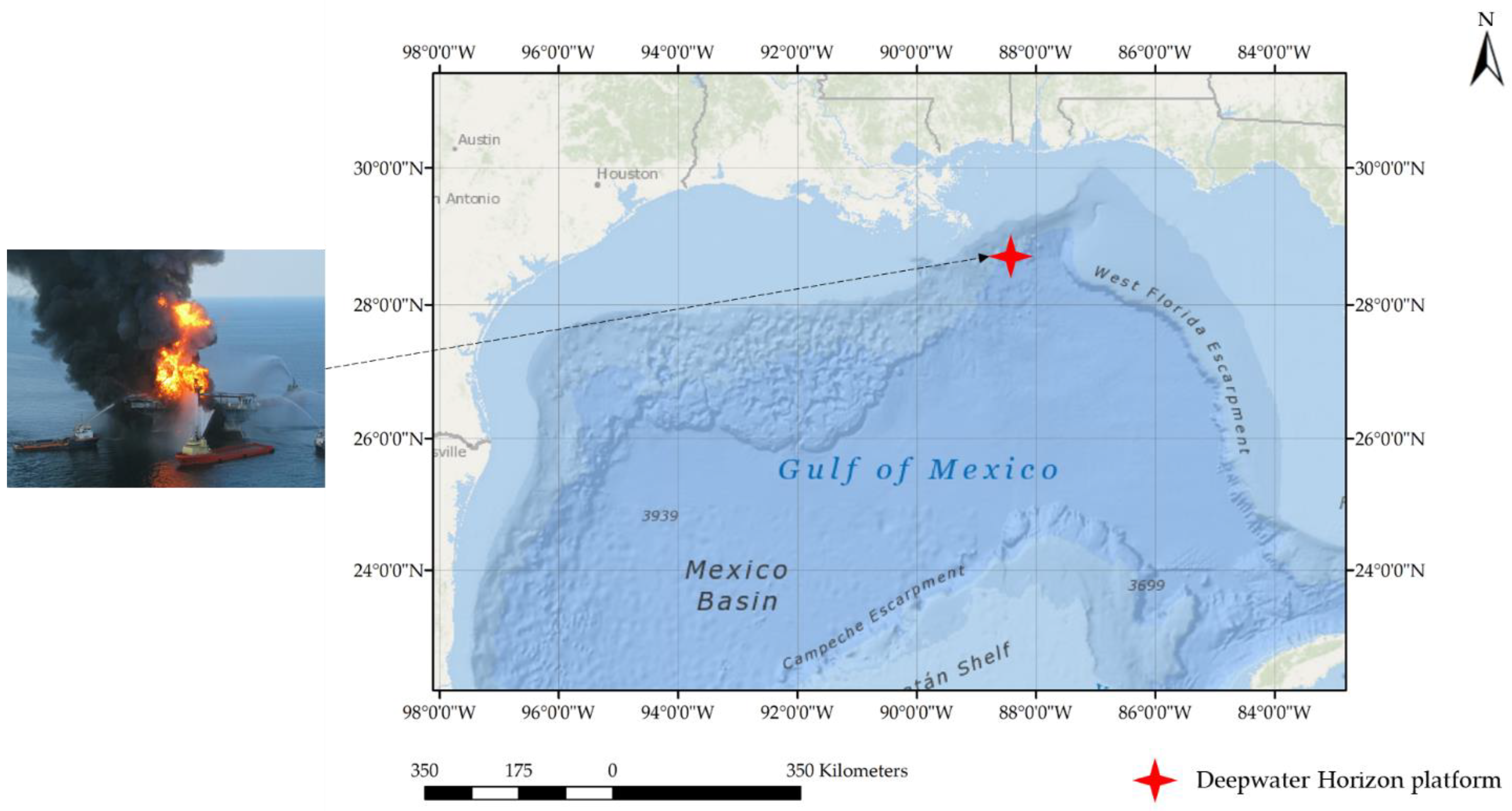



| Sensor | Platform | Duration |
|---|---|---|
| POLDER-1 | ADEOS-1 | November 1996–June 1997 |
| POLDER-2 | ADEOS-2 | April 2003–October 2003 |
| POLDER-3 (POLDER/PARASOL) | PARASOL | December 2004–December 2013 |
| Parasol Band (nm) | Central Wavelength (nm) | Band Width (nm) | Polarization |
|---|---|---|---|
| 443 | 443.9 | 13.5 | Yes |
| 490 | 491.5 | 16.5 | No |
| 565 | 563.9 | 15.5 | No |
| 670 | 669.9 | 15.0 | Yes |
| 763 | 762.8 | 11.0 | No |
| 765 | 762.5 | 38.0 | No |
| 865 | 863.4 | 33.5 | Yes |
| 910 | 906.9 | 21.0 | No |
| 1020 | 1019.4 | 17.0 | No |
| Combination Abbreviation | Feature | Related Questions |
|---|---|---|
| Opt | [θs, θv, φr, L490nm, L670nm, L865nm] (12 angles stacked) | Q1, Q2 |
| rawPol | [θs, θv, φr, (F0°, F60°, F120°)490nm, (F0°, F60°, F120°)670nm, (F0°, F60°, F120°)865nm] (12 angles stacked) | Q1, Q2, Q3 |
| IQUV | [θs, θv, φr, (I, Q, U, V)490nm, (I, Q, U, V)670nm, (I, Q, U, V)865nm] (12 angles stacked) | Q1, Q2, Q3 |
| DoP | [θs, θv, φr, DOP490nm, DOP670nm, DOP865nm] (12 angles stacked) | Q2, Q3 |
| AoP | [θs, θv, φr, AOP490nm, AOP670nm, AOP865nm] (12 angles stacked) | Q2, Q3 |
| DoPAoP | [θs, θv, φr, DOP490nm, DOP670nm, DOP865nm, AOP490nm, AOP670nm, AOP865nm] (12 angles stacked) | Q1, Q2, Q3 |
| Opt_s | [Θ, L490nm, L670nm, L865nm] (12 angles stacked) | Q1, Q2 |
| rawPol_s | [Θ, (F0°, F60°, F120°)490nm, (F0°, F60°, F120°)670nm, (F0°, F60°, F120°)865nm] (12 angles stacked) | Q1, Q2, Q3 |
| IQUV_s | [Θ, (I, Q, U, V)490nm, (I, Q, U, V)670nm, (I, Q, U, V)865nm] (12 angles stacked) | Q1, Q2, Q3 |
| DoP_s | [Θ, DOP490nm, DOP670nm, DOP865nm] (12 angles stacked) | Q2, Q3 |
| AoP_s | [Θ, AOP490nm, AOP670nm, AOP865nm] (12 angles stacked) | Q2, Q3 |
| DoPAoP_s | [Θ, DOP490nm, DOP670nm, DOP865nm, AOP490nm, AOP670nm, AOP865nm] (12 angles stacked) | Q1, Q2, Q3, Q4 |
| DoPAoP_s_anglex (x = 2, 3, …, 13) | [Θ, DOP490nm, DOP670nm, DOP865nm, AOP490nm, AOP670nm, AOP865nm] (angle x only, x = 2, 3, …, 13) | Q4 |
| Combination Abbreviation | Accuracy | Recall | Precision | F1 Score |
|---|---|---|---|---|
| Opt | 0.9617 | 0.6610 | 0.9070 | 0.7647 |
| rawPol | 0.9665 | 0.6780 | 0.9524 | 0.7921 |
| IQUV | 0.9665 | 0.6610 | 0.9750 | 0.7879 |
| DoP | 0.9633 | 0.6271 | 0.9737 | 0.7629 |
| AoP | 0.9569 | 0.6441 | 0.8636 | 0.7379 |
| DoPAoP | 0.9697 | 0.6949 | 0.9762 | 0.8119 |
| Opt_s | 0.9745 | 0.7627 | 0.9574 | 0.8491 |
| rawPol_s | 0.9761 | 0.7966 | 0.9400 | 0.8624 |
| IQUV_s | 0.9793 | 0.7966 | 0.9792 | 0.8785 |
| DoP_s | 0.9745 | 0.7966 | 0.9216 | 0.8545 |
| AoP_s | 0.9713 | 0.7458 | 0.9362 | 0.8302 |
| DoPAoP_s | 0.9809 | 0.8136 | 0.9796 | 0.8889 |
| Combination Abbreviation | Accuracy | Recall | Precision | F1 Score |
|---|---|---|---|---|
| DoPAoP_s | 0.9809 | 0.8136 | 0.9796 | 0.8889 |
| DoPAoP_s_angle2 | 0.9442 | 0.4746 | 0.8750 | 0.6154 |
| DoPAoP_s_angle3 | 0.9378 | 0.4068 | 0.8571 | 0.5517 |
| DoPAoP_s_angle4 | 0.9282 | 0.3390 | 0.7692 | 0.4706 |
| DoPAoP_s_angle5 | 0.9410 | 0.3898 | 0.9583 | 0.5542 |
| DoPAoP_s_angle6 | 0.9442 | 0.5085 | 0.8333 | 0.6316 |
| DoPAoP_s_angle7 | 0.9426 | 0.5085 | 0.8108 | 0.6250 |
| DoPAoP_s_angle8 | 0.9729 | 0.7797 | 0.9200 | 0.8440 |
| DoPAoP_s_angle9 | 0.9681 | 0.7288 | 0.9149 | 0.8113 |
| DoPAoP_s_angle10 | 0.9474 | 0.5254 | 0.8611 | 0.6526 |
| DoPAoP_s_angle11 | 0.9250 | 0.2542 | 0.8333 | 0.3896 |
| DoPAoP_s_angle12 | 0.9250 | 0.2203 | 0.9286 | 0.3562 |
| DoPAoP_s_angle13 | 0.9330 | 0.3729 | 0.8148 | 0.5116 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Yan, L.; Jiang, X.; Ding, J.; Zhang, F.; Jiang, K.; Shang, K. Exploring the Potential of Optical Polarization Remote Sensing for Oil Spill Detection: A Case Study of Deepwater Horizon. Remote Sens. 2022, 14, 2398. https://doi.org/10.3390/rs14102398
Zhang Z, Yan L, Jiang X, Ding J, Zhang F, Jiang K, Shang K. Exploring the Potential of Optical Polarization Remote Sensing for Oil Spill Detection: A Case Study of Deepwater Horizon. Remote Sensing. 2022; 14(10):2398. https://doi.org/10.3390/rs14102398
Chicago/Turabian StyleZhang, Zihan, Lei Yan, Xingwei Jiang, Jing Ding, Feizhou Zhang, Kaiwen Jiang, and Ke Shang. 2022. "Exploring the Potential of Optical Polarization Remote Sensing for Oil Spill Detection: A Case Study of Deepwater Horizon" Remote Sensing 14, no. 10: 2398. https://doi.org/10.3390/rs14102398
APA StyleZhang, Z., Yan, L., Jiang, X., Ding, J., Zhang, F., Jiang, K., & Shang, K. (2022). Exploring the Potential of Optical Polarization Remote Sensing for Oil Spill Detection: A Case Study of Deepwater Horizon. Remote Sensing, 14(10), 2398. https://doi.org/10.3390/rs14102398







