Micro-Doppler Parameters Extraction of Precession Cone-Shaped Targets Based on Rotating Antenna
Abstract
:1. Introduction
2. Micro-Doppler Characteristic Analysis of Precession Cone-Shaped Target
3. Parameters Estimation of Precession Cone-Shaped Target
4. Simulation Results and Discussions
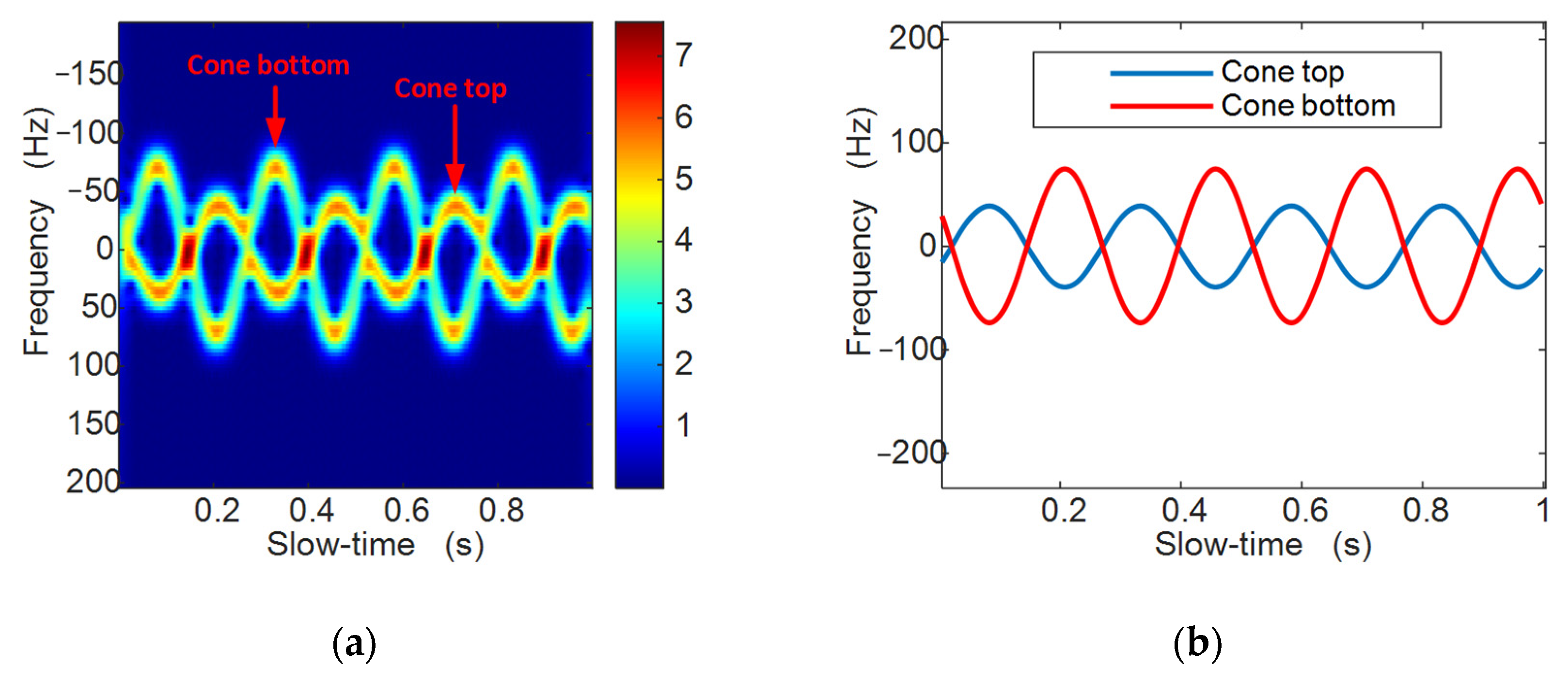
4.1. Validation of the Algorithm
4.2. Performance Analysis of Proposed Algorithm
4.3. Comparison with Other Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, V.C.; Li, F.; Ho, S.S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Liu, N.; Zhou, W.; He, Y. Detection of a Low Observable Sea-Surface Target with Micromotion via the Radon-Linear Canonical Transform. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1225–1229. [Google Scholar] [CrossRef]
- Du, L.; Li, L.; Wang, B.; Xiao, J. Micro-Doppler Feature Extraction Based on Time-Frequency Spectrogram for Ground Moving Targets Classification with Low-Resolution Radar. IEEE Sens. J. 2016, 16, 3756–3763. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Li, X.; He, Y. Effective coherent integration method for marine target with micromotion via phase differentiation and radon-Lv’s distribution. IET Radar Sonar Navig. 2015, 9, 1284–1295. [Google Scholar] [CrossRef]
- Abdullah, R.S.A.R.; Alnaeb, A.; Salah, A.A.; Rashid, N.E.A.; Sali, A.; Pasya, I. Micro-Doppler Estimation and Analysis of Slow Moving Objects in Forward Scattering Radar System. Remote Sens. 2017, 9, 699. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Guan, J.; Huang, Y.; Liu, N.; He, Y. Radon-linear canonical ambiguity function-based detection and estimation method for marine target with micro motion. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2225–2240. [Google Scholar] [CrossRef]
- Amiri, R.; Shahzadi, A. Micro-Doppler based target classification in ground surveillance radar systems. Digit. Signal Process. 2020, 101, 102702. [Google Scholar] [CrossRef]
- Ren, K.; Du, L.; Lu, X.; Zhuo, Z.; Li, L. Instantaneous Frequency Estimation Based on Modified Kalman Filter for Cone-Shaped Target. Remote Sens. 2020, 12, 2766. [Google Scholar] [CrossRef]
- Zhuo, Z.; Zhou, Y.; Du, L.; Ren, K.; Li, Y. A Noise Robust Micro-Range Estimation Method for Precession Cone-Shaped Targets. Remote Sens. 2021, 13, 1820. [Google Scholar] [CrossRef]
- Zhang, W.; Fu, Y.W.; Nie, L.; Zhao, G.H.; Yang, W.; Yang, J. Parameter estimation of micro-motion targets for high-range-resolution radar using high-order difference sequence. IET Signal Process. 2018, 12, 1–11. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Z.Y.; Zhang, L.R.; Xiao, J.G. Micro-doppler curves extraction and parameter estimation for cone-shaped target with occlusion effect. IEEE Sens. J. 2018, 18, 2892–2902. [Google Scholar] [CrossRef]
- Han, L.; Feng, C. Parameter Estimation for Precession Cone-Shaped Targets Based on Range–Frequency–Time Radar Data Cube. Remote Sens. 2022, 14, 1548. [Google Scholar] [CrossRef]
- Bai, X.R.; Bao, Z. High-Resolution 3D Imaging of Precession Cone-Shaped Targets. IEEE Trans. Antennas Propag. 2014, 62, 4209–4219. [Google Scholar] [CrossRef]
- He, X.Y.; Tong, N.N.; Hu, X.W. High-resolution Imaging and Three-dimensional Reconstruction of Precession Targets by Exploiting Sparse Apertures. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1212–1220. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Q.; Yuan, N.; Zhu, F.; Gu, F.F. Three-dimensional precession feature extraction of space targets. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1313–1329. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y.-A.; Sun, Y.; Zhang, Q. Narrowband Radar Imaging and Scaling for Space Targets. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Choi, I.O.; Park, S.H.; Kang, K.B.; Lee, S.H.; Kim, K.T. Efficient parameter estimation for cone-shaped target based on distributed radar networks. IEEE Sens. J. 2019, 19, 9736–9747. [Google Scholar] [CrossRef]
- Choi, I.O.; Park, S.H.; Kim, M.; Kang, K.B.; Kim, K.T. Efficient Discrimination of Ballistic Targets with Micromotions. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1243–1261. [Google Scholar] [CrossRef]
- Persico, A.R.; Clemente, C.; Gaglione, D.; Ilioudis, C.V.; Cao, J.; Pallotta, L.; De Maio, A.; Proudler, I.K.; Soraghan, J.J. On Model, Algorithms, and Experiment for Micro-Doppler-Based Recognition of Ballistic Targets. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1088–1108. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Cheng, Y.Q.; Li, X.; Jiang, Y.W. Passive OAM-Based Radar Imaging with Single-In-Multiple-Out Mode. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 840–842. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cheng, Y.Q.; Liu, K.; Wang, H.Q.; Qin, Y.L. Rotational Doppler Resolution of Spinning Target Detection Based on OAM Beams. IEEE Sens. J. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Wang, J.Q.; Liu, K.; Cheng, Y.Q.; Wang, H.Q. Three-Dimensional Target Imaging Based on Vortex Stripmap SAR. IEEE Sens. J. 2019, 19, 1338–1345. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, K.; Wang, J.Q.; Wang, H.Q. Rotational Doppler detection of a cone-shaped target under the illumination of a vortex electromagnetic wave. Radars. J. 2021, 10, 740–748. [Google Scholar]
- Gong, T.; Cheng, Y.Q.; Li, X.; Chen, D.C. Micromotion Detection of Moving and Spinning Object Based on Rotational Doppler Shift. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 843–845. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, K.; Liu, H.Y.; Wang, J.Q.; Cheng, Y.Q. Detection of Rotational Object in Arbitrary Position Using Vortex Electromagnetic Waves. IEEE Sens. J. 2021, 21, 4989–4994. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y.J.; Zhu, Y.Z.; Li, W.Y.; Zhang, Q. Doppler effect and micro-Doppler effect of vortex-electromagnetic-wave-based radar. IET Radar Sonar Navig. 2019, 14, 2–9. [Google Scholar] [CrossRef]
- Chen, R.; Zhou, H.; Moretti, M.; Wang, X.; Li, J. Orbital Angular Momentum Waves: Generation, Detection, and Emerging Applications. IEEE Commun. Surv. Tutor. 2020, 22, 840–868. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Liu, H.Y.; Qin, Y.L.; Cheng, Y.Q.; Wang, S.N.; Li, X.; Wang, H.Q. Generation of OAM Beams Using Phased Array in the Microwave Band. IEEE Trans. Antennas Propag. 2016, 64, 3850–3857. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Bao, Z.; He, Y. Detection and extraction of target with micro motion in spiky sea clutter via short-time fractional Fourier transform. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1002–1018. [Google Scholar] [CrossRef]
- Zhu, N.; Hu, J.; Xu, S.; Wu, W.; Zhang, Y.; Chen, Z. Micro-Motion Parameter Extraction for Ballistic Missile with Wideband Radar Using Improved Ensemble EMD Method. Remote Sens. 2021, 13, 3545. [Google Scholar] [CrossRef]




















| Category | Parameter | Value | Unit |
|---|---|---|---|
| Radar | Carrier frequency of rotating antenna | 75 | GHz |
| Transmitted bandwidth of wideband radar | 2 | GHz | |
| PRF of rotating antenna | 400 | Hz | |
| Carrier frequency of wideband radar | 10 | GHz | |
| PRF of wideband radar | 1000 | Hz | |
| Antenna’s rotation radius | 10 | m | |
| Antenna’s rotation frequency | 2 | Hz | |
| Observation time | 1 | s | |
| Signal to noise ratio (SNR) | 15 | dB | |
| Target | Coordinates of the centroid | (m, rad, rad) | |
| Cone height | 2 | m | |
| Radius of cone bottom | 0.5 | m | |
| Precession angle | rad | ||
| Coning frequency | 6 | Hz | |
| Distance from centroid to cone bottom | 0.5 | m |
| Parameter | True Value | Estimated Value | MAPE |
|---|---|---|---|
| 6.0 Hz | 6.0 Hz | 0% | |
| 0.5 m | 0.4881 m | 2.38% | |
| 2.0 m | 1.9945 m | 0.28% | |
| rad | 0.2088 rad | 0.31% | |
| 0.5 m | 0.4612 m | 7.76% |
| 6 Hz | 6 Hz | 0.2088 rad | 1.9945 m | 0.4881 m | 0.4612 m |
| 20 Hz | 20.0833 Hz | 0.2088 rad | 1.9965 m | 0.4975 m | 0.4632 m |
| 40 Hz | 40.0228 Hz | 0.2045 rad | 1.9932 m | 0.5005 m | 0.4613 m |
| 60 Hz | 59.8035 Hz | 0.2013 rad | 1.9911 m | 0.5045 m | 0.4602 m |
| −10% | 0.2453 rad | 2.0558 m | 0.5940 m | 0.5095 m |
| −5% | 0.2259 rad | 2.0241 m | 0.5478 m | 0.4850 m |
| 0% | 0.2094 rad | 1.9993 m | 0.5083 m | 0.4658 m |
| 5% | 0.1952 rad | 1.9796 m | 0.4744 m | 0.4506 m |
| 10% | 0.1829 rad | 1.9637 m | 0.4449 m | 0.4382 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Luo, Y.; Li, K.; Yuan, H.; Zhang, Q. Micro-Doppler Parameters Extraction of Precession Cone-Shaped Targets Based on Rotating Antenna. Remote Sens. 2022, 14, 2549. https://doi.org/10.3390/rs14112549
Wang Z, Luo Y, Li K, Yuan H, Zhang Q. Micro-Doppler Parameters Extraction of Precession Cone-Shaped Targets Based on Rotating Antenna. Remote Sensing. 2022; 14(11):2549. https://doi.org/10.3390/rs14112549
Chicago/Turabian StyleWang, Zhihao, Ying Luo, Kaiming Li, Hang Yuan, and Qun Zhang. 2022. "Micro-Doppler Parameters Extraction of Precession Cone-Shaped Targets Based on Rotating Antenna" Remote Sensing 14, no. 11: 2549. https://doi.org/10.3390/rs14112549







