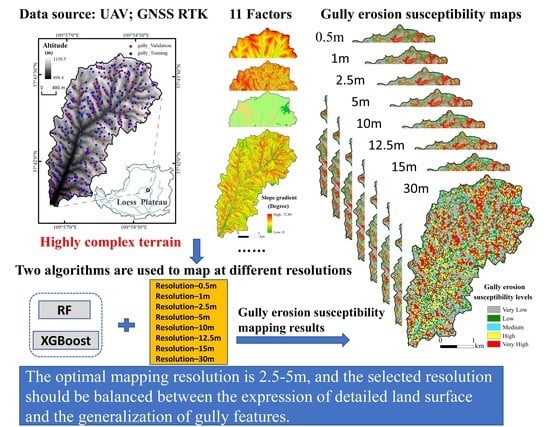
Choosing the Right Horizontal Resolution for Gully Erosion Susceptibility Mapping Using Machine Learning Algorithms: A Case in Highly Complex Terrain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Experimental Procedure
2.3. Base Datasets and Data Processing
2.4. Gully Erosion Inventory Mapping
2.5. Factors That Influence Gully Erosion
2.6. Multicollinearity of the Factors That Influence Gully Erosion
2.7. Description of the Models
2.7.1. Random Forest (RF)
2.7.2. Extreme Gradient Boosting (XGBoost)
2.8. Validation of the Modeling Results
3. Results
3.1. Analysis of the Multicollinearity of Factors
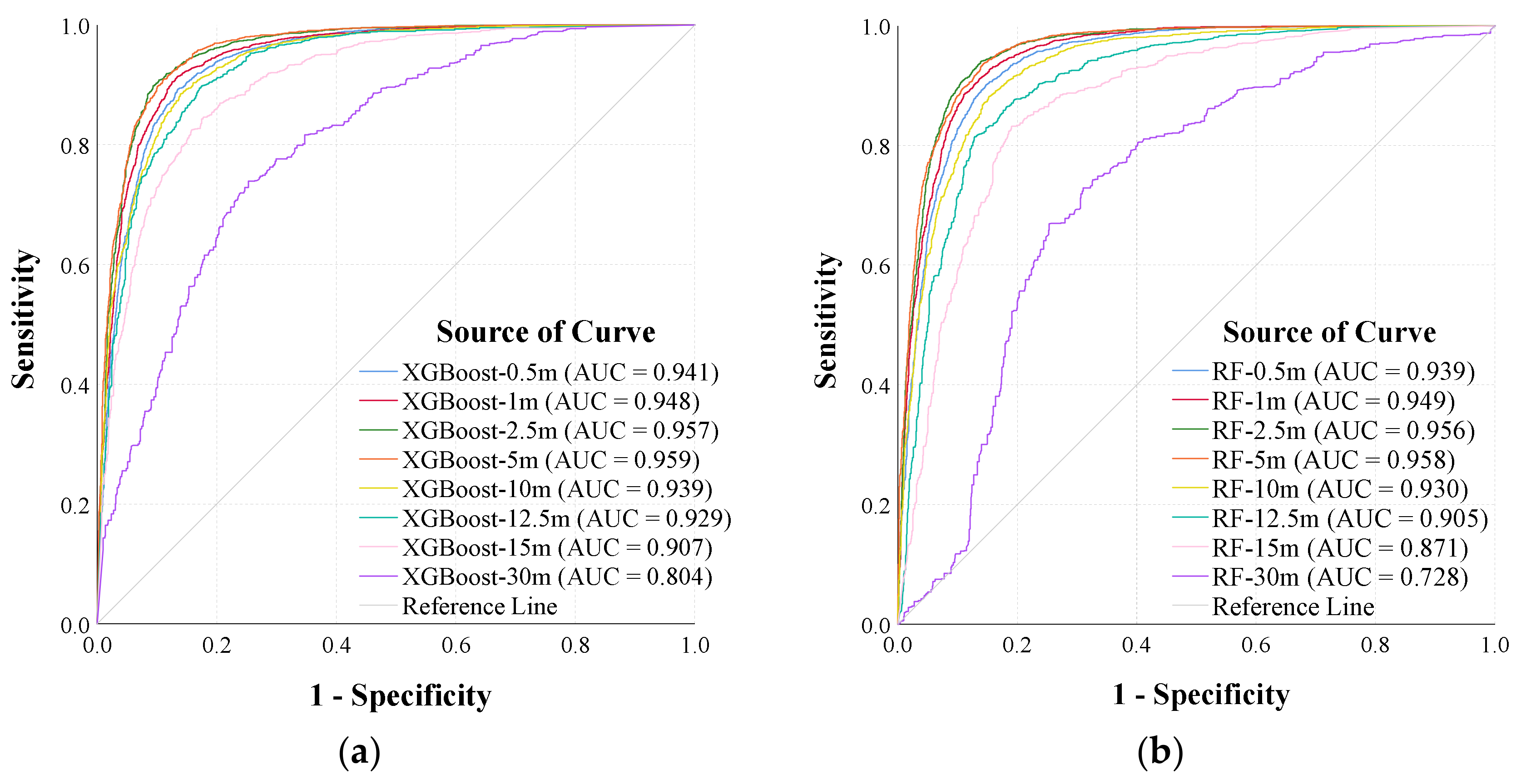
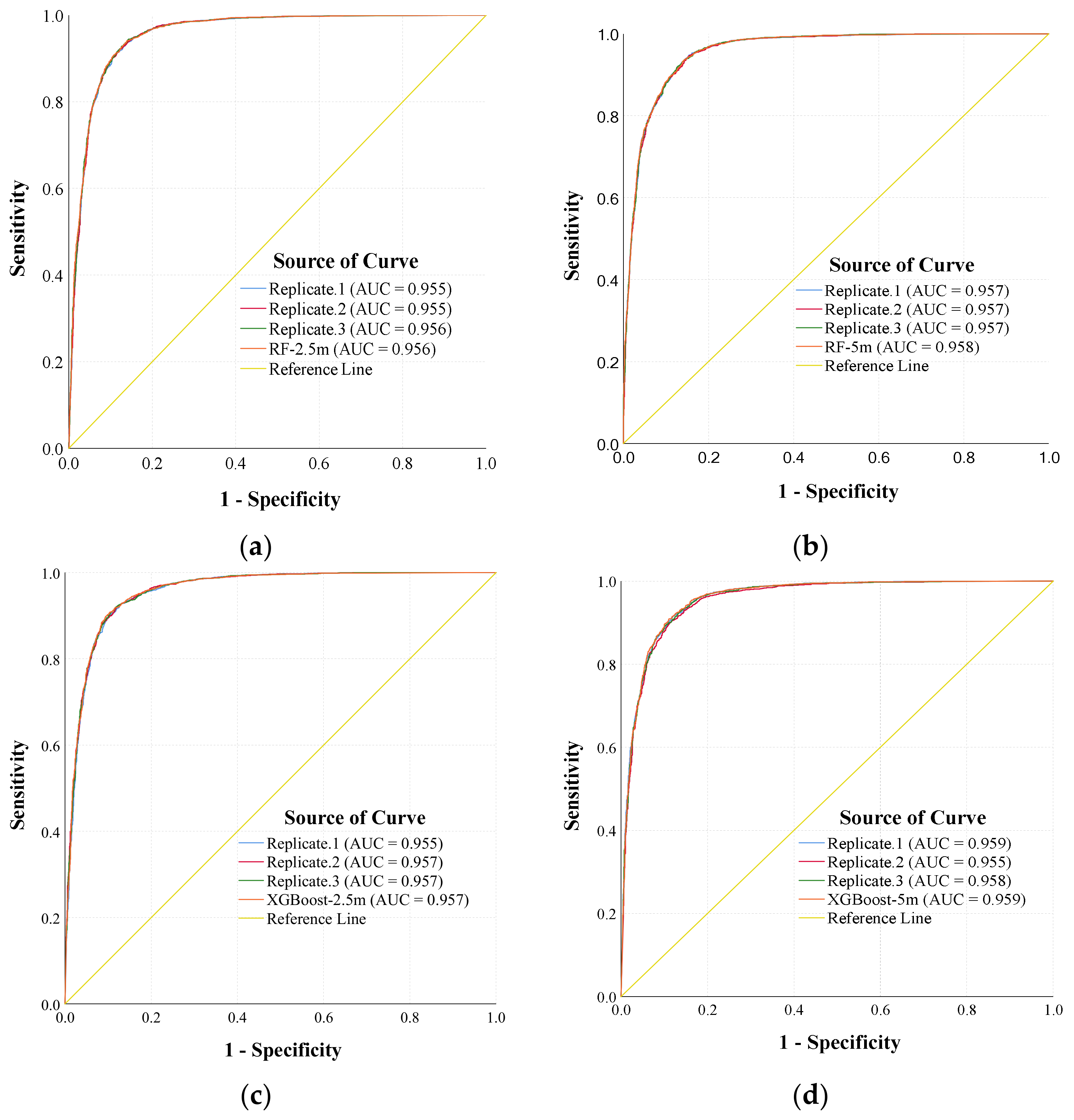
3.2. Impacts of Resolution on Modeling Accuracy
3.3. Impacts of Resolution on GES Map
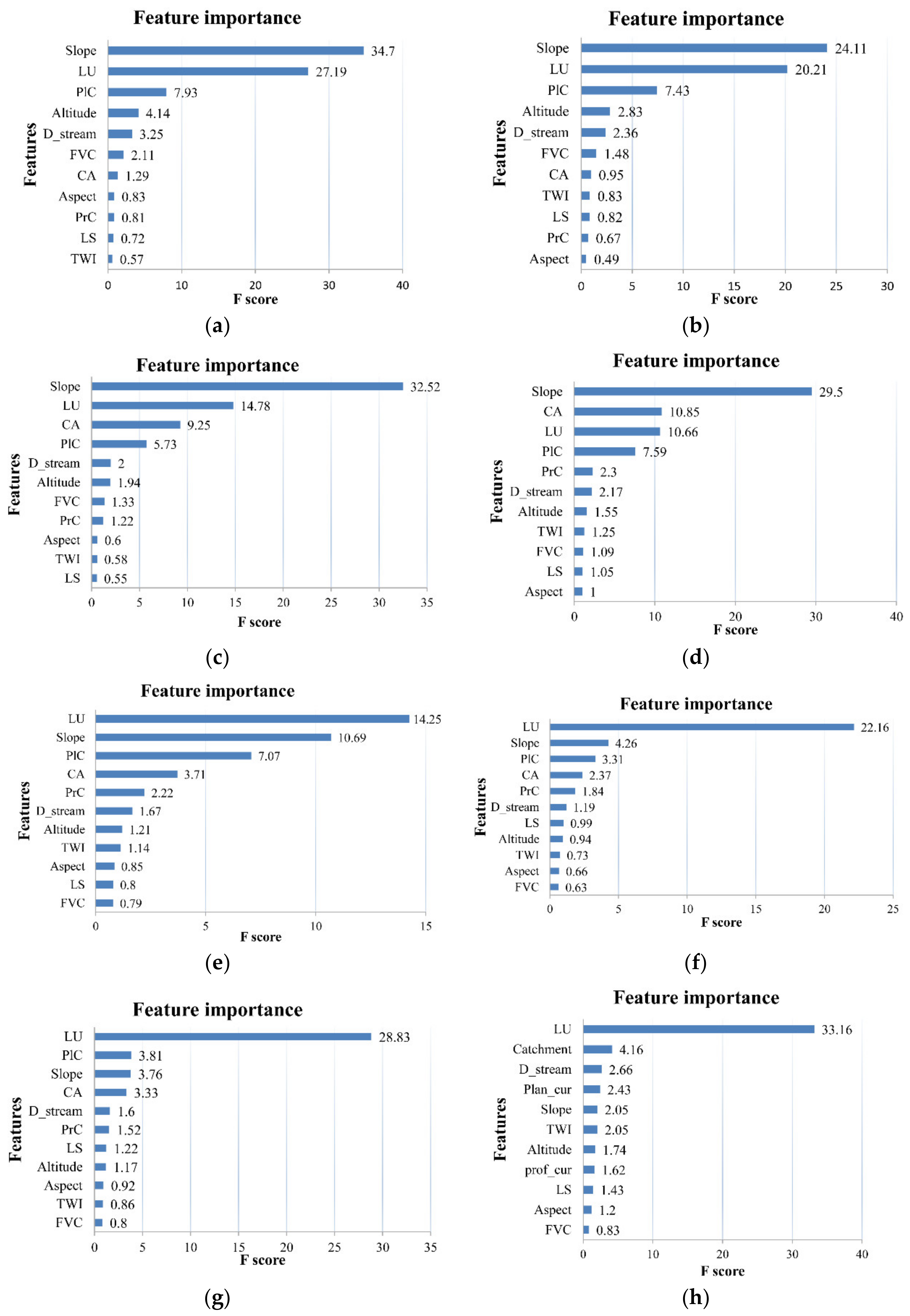
3.4. Impacts of Resolution on Variable Importance
4. Discussion
4.1. Exploration of the Optimal Resolution
4.2. Impacts of Resolution on Variable Importance
4.3. Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kropáček, J.; Schillaci, C.; Salvini, R.; Maerker, M. Assessment of gully erosion in the Upper Awash, Central Ethiopian highlands based on a comparison of archived aerial photographs and very high resolution satellite images. Geogr. Fis. E Din. Quat. 2016, 39, 161–170. [Google Scholar] [CrossRef]
- Zakerinejad, R.; Maerker, M. An integrated assessment of soil erosion dynamics with special emphasis on gully erosion in the Mazayjan basin, southwestern Iran. Nat. Hazards 2015, 79, 25–50. [Google Scholar] [CrossRef]
- Gayen, A.; Pourghasemi, H.R.; Saha, S.; Keesstra, S.; Bai, S. Gully erosion susceptibility assessment and management of hazard-prone areas in India using different machine learning algorithms. Sci. Total Environ. 2019, 668, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Lal, R. Offsetting global CO2 emissions by restoration of degraded soils and intensification of world agriculture and forestry. Land Degrad. Dev. 2003, 14, 309–322. [Google Scholar] [CrossRef]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. CATENA 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; Ahmad, B.B. Modelling gully-erosion susceptibility in a semi-arid region, Iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2019, 655, 684–696. [Google Scholar] [CrossRef]
- Li, H.; Cruse, R.M.; Bingner, R.L.; Gesch, K.R.; Zhang, X. Evaluating ephemeral gully erosion impact on Zea mays L. yield and economics using AnnAGNPS. Soil Tillage Res. 2016, 155, 157–165. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Pourghasemi, H.R.; Rezaei, K.; Kerle, N. Spatial Modelling of Gully Erosion Using GIS and R Programing: A Comparison among Three Data Mining Algorithms. Appl. Sci. 2018, 8, 1369. [Google Scholar] [CrossRef] [Green Version]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 2019, 340, 55–69. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Arabameri, A.; Saha, A.; Chakrabortty, R.; Blaschke, T.; Pradhan, B.; Band, S.S. Implementation of Artificial Intelligence Based Ensemble Models for Gully Erosion Susceptibility Assessment. Remote Sens. 2020, 12, 3620. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluation of different machine learning models for predicting and mapping the susceptibility of gully erosion. Geomorphology 2017, 298, 118–137. [Google Scholar] [CrossRef]
- Saha, S.; Roy, J.; Arabameri, A.; Blaschke, T.; Tien Bui, D. Machine Learning-Based Gully Erosion Susceptibility Mapping: A Case Study of Eastern India. Sensors 2020, 20, 1313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arabameri, A.; Chandra Pal, S.; Costache, R.; Saha, A.; Rezaie, F.; Seyed Danesh, A.; Pradhan, B.; Lee, S.; Hoang, N.-D. Prediction of gully erosion susceptibility mapping using novel ensemble machine learning algorithms. Geomat. Nat. Hazards Risk 2021, 12, 469–498. [Google Scholar] [CrossRef]
- Yang, A.; Wang, C.; Pang, G.; Long, Y.; Wang, L.; Cruse, R.M.; Yang, Q. Gully Erosion Susceptibility Mapping in Highly Complex Terrain Using Machine Learning Models. ISPRS Int. J. Geo-Inf. 2021, 10, 680. [Google Scholar] [CrossRef]
- Chen, W.; Lei, X.; Chakrabortty, R.; Chandra Pal, S.; Sahana, M.; Janizadeh, S. Evaluation of different boosting ensemble machine learning models and novel deep learning and boosting framework for head-cut gully erosion susceptibility. J. Environ. Manag. 2021, 284, 112015. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of GIS-based logistic regression: A case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef] [Green Version]
- Arabameri, A.; Chen, W.; Loche, M.; Zhao, X.; Li, Y.; Lombardo, L.; Cerda, A.; Pradhan, B.; Bui, D.T. Comparison of machine learning models for gully erosion susceptibility mapping. Geosci. Front. 2020, 11, 1609–1620. [Google Scholar] [CrossRef]
- Jiang, C.; Fan, W.; Yu, N.; Liu, E. Spatial modeling of gully head erosion on the Loess Plateau using a certainty factor and random forest model. Sci. Total Environ. 2021, 783, 147040. [Google Scholar] [CrossRef]
- Woolard, J.W.; Colby, J.D. Spatial characterization, resolution, and volumetric change of coastal dunes using airborne LIDAR: Cape Hatteras, North Carolina. Geomorphology 2002, 48, 269–287. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chang, K.-T.; Wu, J. Effects of DEM resolution and source on soil erosion modelling: A case study using the WEPP model. Int. J. Geogr. Inf. Sci. 2008, 22, 925–942. [Google Scholar] [CrossRef]
- Lucà, F.; Conforti, M.; Robustelli, G. Comparison of GIS-based gullying susceptibility mapping using bivariate and multivariate statistics: Northern Calabria, South Italy. Geomorphology 2011, 134, 297–308. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; Conoscenti, C.; Angileri, S.E.; Rotigliano, E.; Schnabel, S. Using topographical attributes to evaluate gully erosion proneness (susceptibility) in two mediterranean basins: Advantages and limitations. Nat. Hazards 2015, 79, 291–314. [Google Scholar] [CrossRef]
- Garosi, Y.; Sheklabadi, M.; Pourghasemi, H.R.; Besalatpour, A.A.; Conoscenti, C.; Van Oost, K. Comparison of differences in resolution and sources of controlling factors for gully erosion susceptibility mapping. Geoderma 2018, 330, 65–78. [Google Scholar] [CrossRef]
- Dai, W.; Yang, X.; Na, J.; Li, J.; Brus, D.; Xiong, L.; Tang, G.; Huang, X. Effects of DEM resolution on the accuracy of gully maps in loess hilly areas. CATENA 2019, 177, 114–125. [Google Scholar] [CrossRef]
- Fu, X.; Shao, M.; Wei, X.; Horton, R. Soil organic carbon and total nitrogen as affected by vegetation types in Northern Loess Plateau of China. Geoderma 2010, 155, 31–35. [Google Scholar] [CrossRef]
- Akturk, E.; Altunel, A.O. Accuracy assessment of a low-cost UAV derived digital elevation model (DEM) in a highly broken and vegetated terrain. Measurement 2019, 136, 382–386. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Lombardo, L. Comparative assessment using boosted regression trees, binary logistic regression, frequency ratio and numerical risk factor for gully erosion susceptibility modelling. CATENA 2019, 183, 104223. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluating the influence of geo-environmental factors on gully erosion in a semi-arid region of Iran: An integrated framework. Sci. Total Environ. 2017, 579, 913–927. [Google Scholar] [CrossRef]
- Conoscenti, C.; Di Maggio, C.; Rotigliano, E. Soil erosion susceptibility assessment and validation using a geostatistical multivariate approach: A test in Southern Sicily. Nat. Hazards 2008, 46, 287–305. [Google Scholar] [CrossRef]
- Arabameri, A.; Asadi Nalivan, O.; Saha, S.; Roy, J.; Pradhan, B.; Tiefenbacher, J.P.; Thi Ngo, P.T. Novel Ensemble Approaches of Machine Learning Techniques in Modeling the Gully Erosion Susceptibility. Remote Sens. 2020, 12, 1890. [Google Scholar] [CrossRef]
- Pal, S.; Arabameri, A.; Blaschke, T.; Chowdhuri, I.; Saha, A.; Chakrabortty, R.; Lee, S.; Band, S. Ensemble of Machine-Learning Methods for Predicting Gully Erosion Susceptibility. Remote Sens. 2020, 12, 3675. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Q.; Li, R.; Liu, Q.; Moore, D.; He, P.; Ritsema, C.J.; Geissen, V. Extension of a GIS procedure for calculating the RUSLE equation LS factor. Comput. Geosci. 2013, 52, 177–188. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrological Processes 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M.; Wang, S.; Wu, Y. Extraction of vegetation information from visible unmanned aerial vehicle images. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2015, 31, 152–159. [Google Scholar] [CrossRef]
- Kuhnert, P.; Kinsey-Henderson, A.; Bartley, R.; Herr, A. Incorporating uncertainty in gully erosion calculations using the random forest modelling approach. Environmetrics 2009, 21, 493–509. [Google Scholar] [CrossRef]
- Messenzehl, K.; Meyer, H.; Otto, J.-C.; Hoffmann, T.; Dikau, R. Regional-scale controls on the spatial activity of rockfalls (Turtmann Valley, Swiss Alps)—A multivariate modeling approach. Geomorphology 2017, 287, 29–45. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Barthold, F.; Blank, B.; Kögel-Knabner, I. Digital mapping of soil organic matter stocks using Random Forest modeling in a semi-arid steppe ecosystem. Plant Soil 2011, 340, 7–24. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Can, R.; Kocaman, S.; Gokceoglu, C. A Comprehensive Assessment of XGBoost Algorithm for Landslide Susceptibility Mapping in the Upper Basin of Ataturk Dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Ding, H.; Na, J.; Jiang, S.; Zhu, J.; Liu, K.; Fu, Y.; Li, F. Evaluation of Three Different Machine Learning Methods for Object-Based Artificial Terrace Mapping—A Case Study of the Loess Plateau, China. Remote Sens. 2021, 13, 1021. [Google Scholar] [CrossRef]
- Park, S.; Choi, C.; Kim, B.; Kim, J. Landslide susceptibility mapping using frequency ratio, analytic hierarchy process, logistic regression, and artificial neural network methods at the Inje area, Korea. Environ. Earth Sci. 2013, 68, 1443–1464. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Lechner, A.M.; Stein, A.; Jones, S.D.; Ferwerda, J.G. Remote sensing of small and linear features: Quantifying the effects of patch size and length, grid position and detectability on land cover mapping. Remote Sens. Environ. 2009, 113, 2194–2204. [Google Scholar] [CrossRef]
- Tang, G.; Zhao, M.; Li, T.; Liu, Y.; Xie, Y. Modeling slope uncertainty derived from DEMs in Loess Plateau. Acta Geogr. Sin. 2003, 58, 824–830. (In Chinese) [Google Scholar]
- Wang, C.; Shan, L.; Liu, X.; Yang, Q.; Cruse, R.M.; Liu, B.; Li, R.; Zhang, H.; Pang, G. Impacts of horizontal resolution and downscaling on the USLE LS factor for different terrains. Int. Soil Water Conserv. Res. 2020, 8, 363–372. [Google Scholar] [CrossRef]
- Yang, X.; Li, M.; Na, J.; Liu, K. Gully boundary extraction based on multidirectional hill-shading from high-resolution DEMs: Trans. GIS 2017, 21, 1204–1216. [Google Scholar] [CrossRef]
- Chang, K.-t.; Tsai, B.-w. The Effect of DEM Resolution on Slope and Aspect Mapping. Cartogr. Geogr. Inf. Syst. 1991, 18, 69–77. [Google Scholar] [CrossRef]
- Wolock, D.; Price, C. Effect of Digital Elevation Model Map Scale and Data Resolution on a Topography-Based Watershed Model. Water Resour. Res. 1994, 30, 3041–3052. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional Development of Streams and Their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. GSA Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef] [Green Version]
- Patton, P.C.; Schumm, S.A. Gully Erosion, Northwestern Colorado: A Threshold Phenomenon. Geology 1975, 3, 88–90. [Google Scholar] [CrossRef]
- Dickie, J.A.; Parsons, A.J. Eco-Geomorphological Processes within Grasslands, Shrublands and Badlands in the Semi-Arid Karoo, South Africa. Land Degrad. Dev. 2012, 23, 534–547. [Google Scholar] [CrossRef] [Green Version]
- Thompson, J.A.; Bell, J.C.; Butler, C.A. Digital elevation model resolution: Effects on terrain attribute calculation and quantitative soil-landscape modeling. Geoderma 2001, 100, 67–89. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Q.; Jupp, D.; Pang, G. Modeling Change of Topographic Spatial Structures with DEM Resolution Using Semi-Variogram Analysis and Filter Bank. ISPRS Int. J. Geo-Inf. 2016, 5, 107. [Google Scholar] [CrossRef] [Green Version]






| Collinearity Statistics with Resolution of | Influencing Factors | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | ||
| 0.5 m | T | 0.69 | 0.39 | 0.99 | 0.57 | 0.56 | 0.96 | 0.45 | 0.47 | 0.71 | 0.88 | 0.98 |
| V | 1.46 | 2.54 | 1.01 | 1.75 | 1.77 | 1.04 | 2.20 | 2.11 | 1.41 | 1.13 | 1.02 | |
| 1 m | T | 0.68 | 0.60 | 0.98 | 0.60 | 0.57 | 0.98 | 0.75 | 0.68 | 0.71 | 0.89 | 0.98 |
| V | 1.47 | 1.66 | 1.02 | 1.68 | 1.75 | 1.02 | 1.33 | 1.48 | 1.42 | 1.13 | 1.03 | |
| 2.5 m | T | 0.67 | 0.49 | 0.99 | 0.60 | 0.51 | 0.97 | 0.44 | 0.45 | 0.16 | 0.17 | 0.98 |
| V | 1.49 | 2.06 | 1.01 | 1.68 | 1.95 | 1.03 | 2.26 | 2.21 | 6.44 | 5.98 | 1.03 | |
| 5 m | T | 0.66 | 0.56 | 0.98 | 0.52 | 0.43 | 0.96 | 0.40 | 0.43 | 0.15 | 0.17 | 0.96 |
| V | 1.51 | 1.80 | 1.02 | 1.92 | 2.31 | 1.04 | 2.54 | 2.32 | 6.49 | 6.02 | 1.04 | |
| 10 m | T | 0.64 | 0.56 | 0.96 | 0.48 | 0.42 | 0.88 | 0.40 | 0.44 | 0.69 | 0.88 | 0.96 |
| V | 1.57 | 1.78 | 1.04 | 2.08 | 2.37 | 1.14 | 2.52 | 2.30 | 1.45 | 1.14 | 1.05 | |
| 12.5 m | T | 0.63 | 0.56 | 0.96 | 0.44 | 0.42 | 0.88 | 0.38 | 0.43 | 0.69 | 0.88 | 0.94 |
| V | 1.59 | 1.78 | 1.04 | 2.27 | 2.39 | 1.14 | 2.61 | 2.35 | 1.45 | 1.14 | 1.06 | |
| 15 m | T | 0.64 | 0.53 | 0.98 | 0.43 | 0.44 | 0.92 | 0.39 | 0.41 | 0.15 | 0.17 | 0.95 |
| V | 1.57 | 1.87 | 1.02 | 2.34 | 2.29 | 1.09 | 2.59 | 2.44 | 6.56 | 6.08 | 1.06 | |
| 30 m | T | 0.57 | 0.52 | 0.93 | 0.41 | 0.58 | 0.89 | 0.40 | 0.40 | 0.67 | 0.89 | 0.97 |
| V | 1.75 | 1.93 | 1.07 | 2.47 | 1.74 | 1.12 | 2.52 | 2.52 | 1.49 | 1.13 | 1.04 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, A.; Wang, C.; Yang, Q.; Pang, G.; Long, Y.; Wang, L.; Yang, L.; Cruse, R.M. Choosing the Right Horizontal Resolution for Gully Erosion Susceptibility Mapping Using Machine Learning Algorithms: A Case in Highly Complex Terrain. Remote Sens. 2022, 14, 2580. https://doi.org/10.3390/rs14112580
Yang A, Wang C, Yang Q, Pang G, Long Y, Wang L, Yang L, Cruse RM. Choosing the Right Horizontal Resolution for Gully Erosion Susceptibility Mapping Using Machine Learning Algorithms: A Case in Highly Complex Terrain. Remote Sensing. 2022; 14(11):2580. https://doi.org/10.3390/rs14112580
Chicago/Turabian StyleYang, Annan, Chunmei Wang, Qinke Yang, Guowei Pang, Yongqing Long, Lei Wang, Lijuan Yang, and Richard M. Cruse. 2022. "Choosing the Right Horizontal Resolution for Gully Erosion Susceptibility Mapping Using Machine Learning Algorithms: A Case in Highly Complex Terrain" Remote Sensing 14, no. 11: 2580. https://doi.org/10.3390/rs14112580
APA StyleYang, A., Wang, C., Yang, Q., Pang, G., Long, Y., Wang, L., Yang, L., & Cruse, R. M. (2022). Choosing the Right Horizontal Resolution for Gully Erosion Susceptibility Mapping Using Machine Learning Algorithms: A Case in Highly Complex Terrain. Remote Sensing, 14(11), 2580. https://doi.org/10.3390/rs14112580