Theoretical Calculations of Directional Scattering Intensities of Small Nonspherical Ice Crystals: Implications for Forward Scattering Probes
Abstract
:1. Introduction
2. The Operating Principle of Forward Scattering Probes to Determine a Size of a Cloud Particle
3. Methodology
3.1. Idealized Models Representing Shapes of Small Cloud Particles
3.2. Single-Scattering Properties and Differential Scattering Cross-Section of Small Cloud Particles
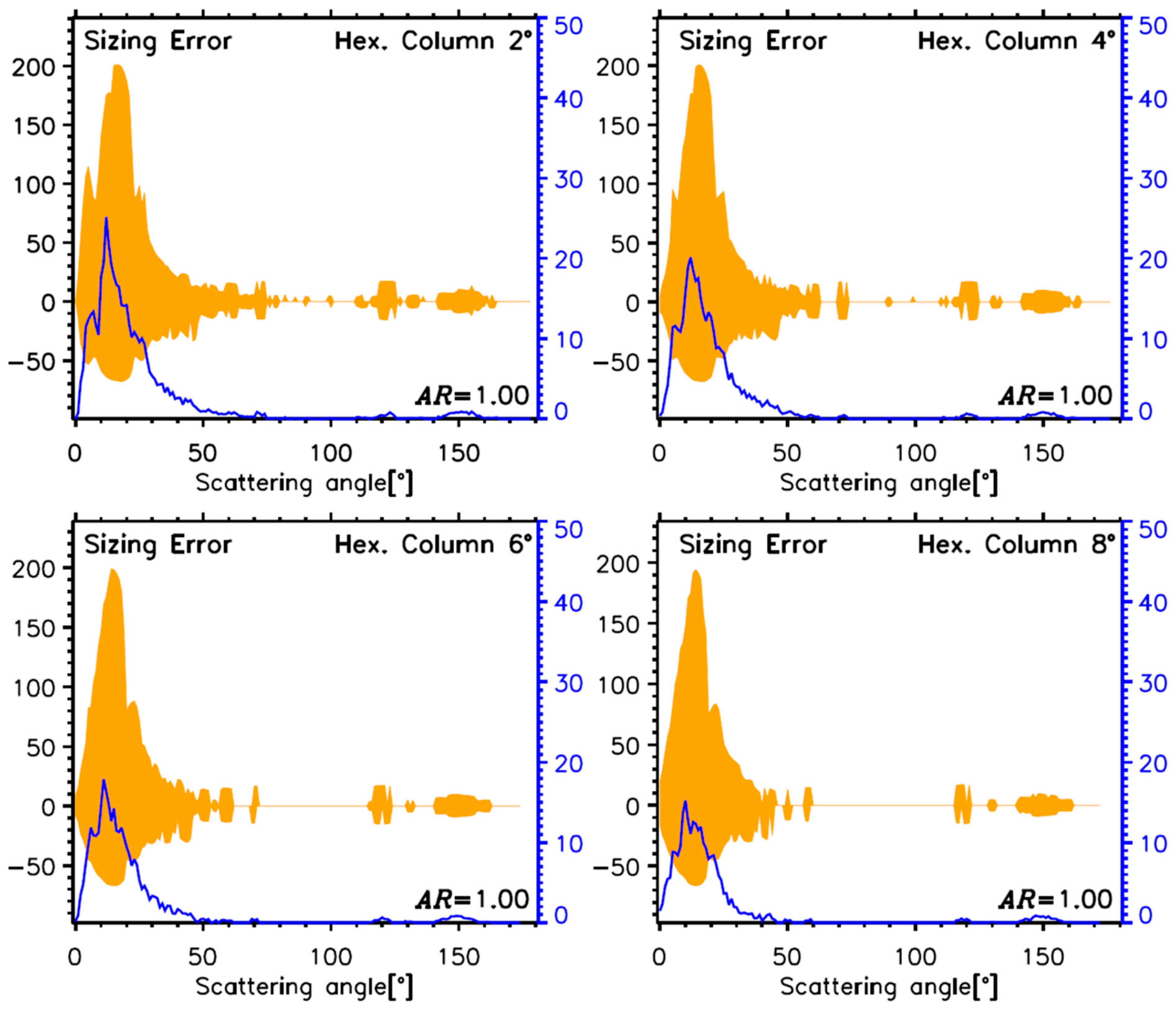
3.3. Quantification of Sizing Errors
4. Sizing Errors Determined for Current Forward Scattering Probes
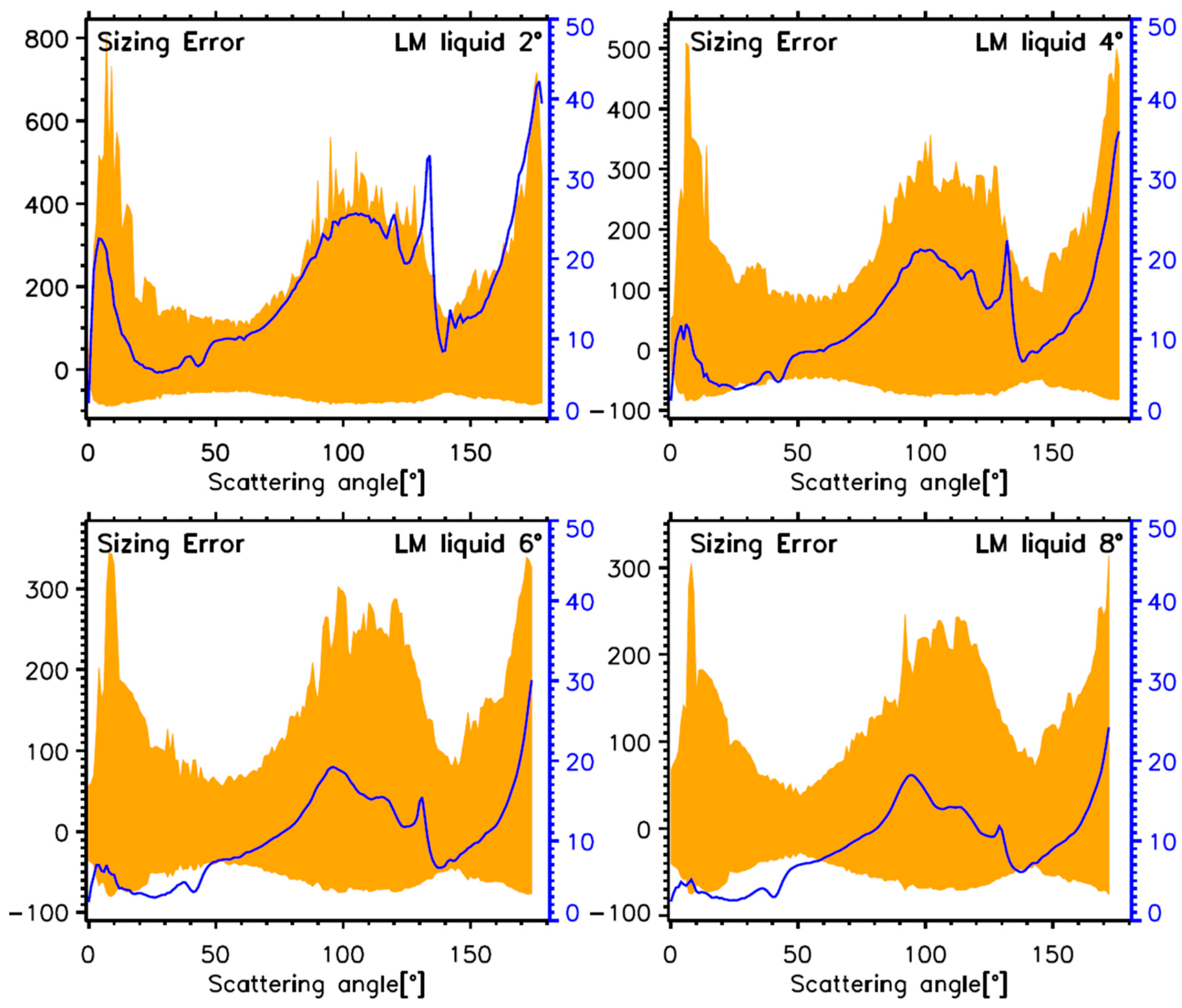
4.1. Measurements of Spherical Liquid Cloud Droplets
4.2. Measurements of Hexagonal Ice Crystals
4.2.1. Determined Sizing Errors Using Spherical Liquid Cloud Droplets
4.2.2. Determined Sizing Errors Using Spherical Ice Crystals
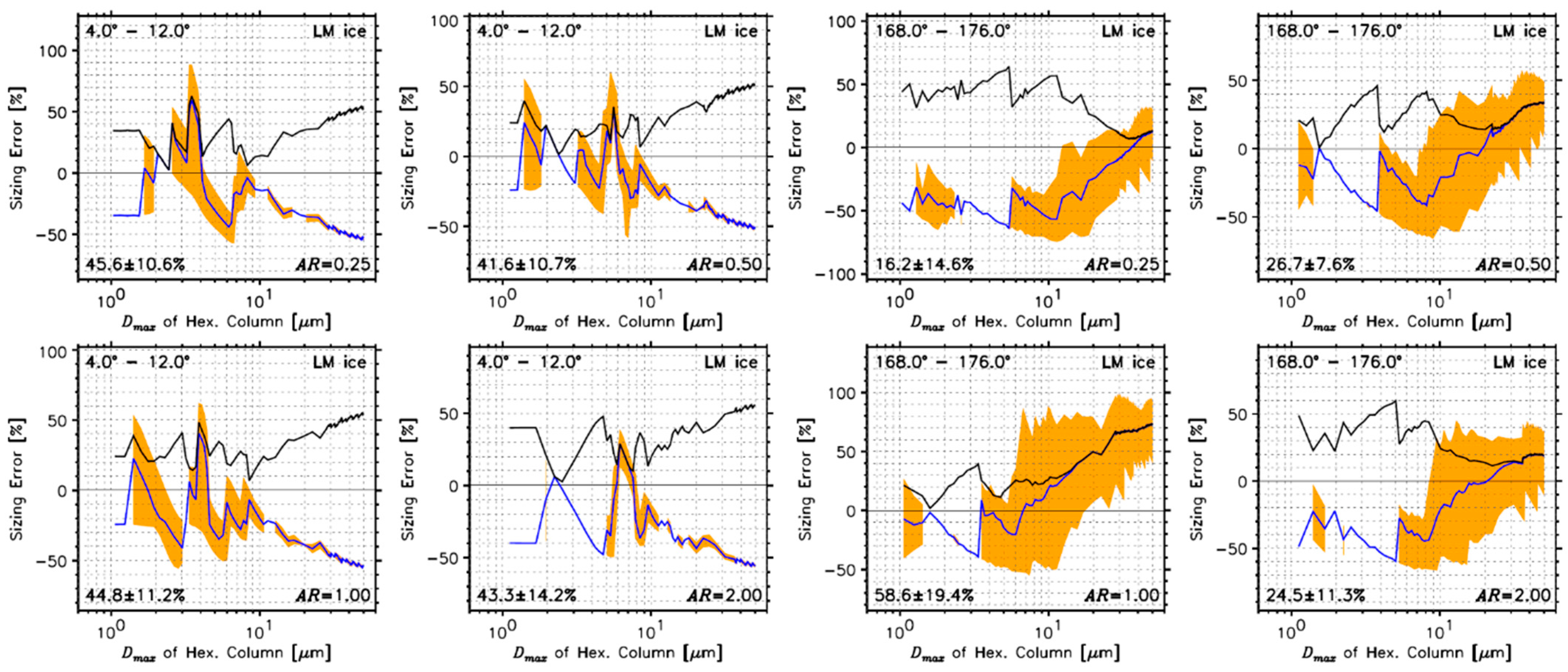
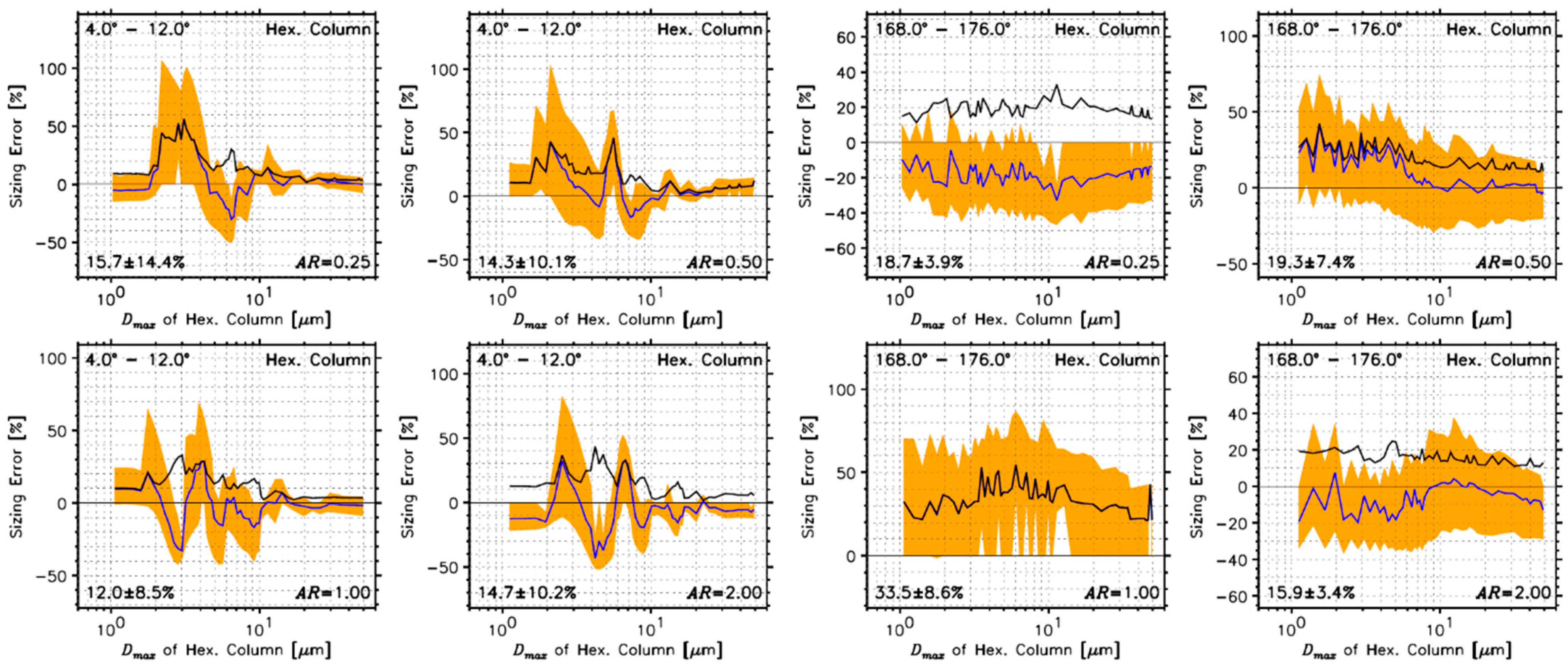
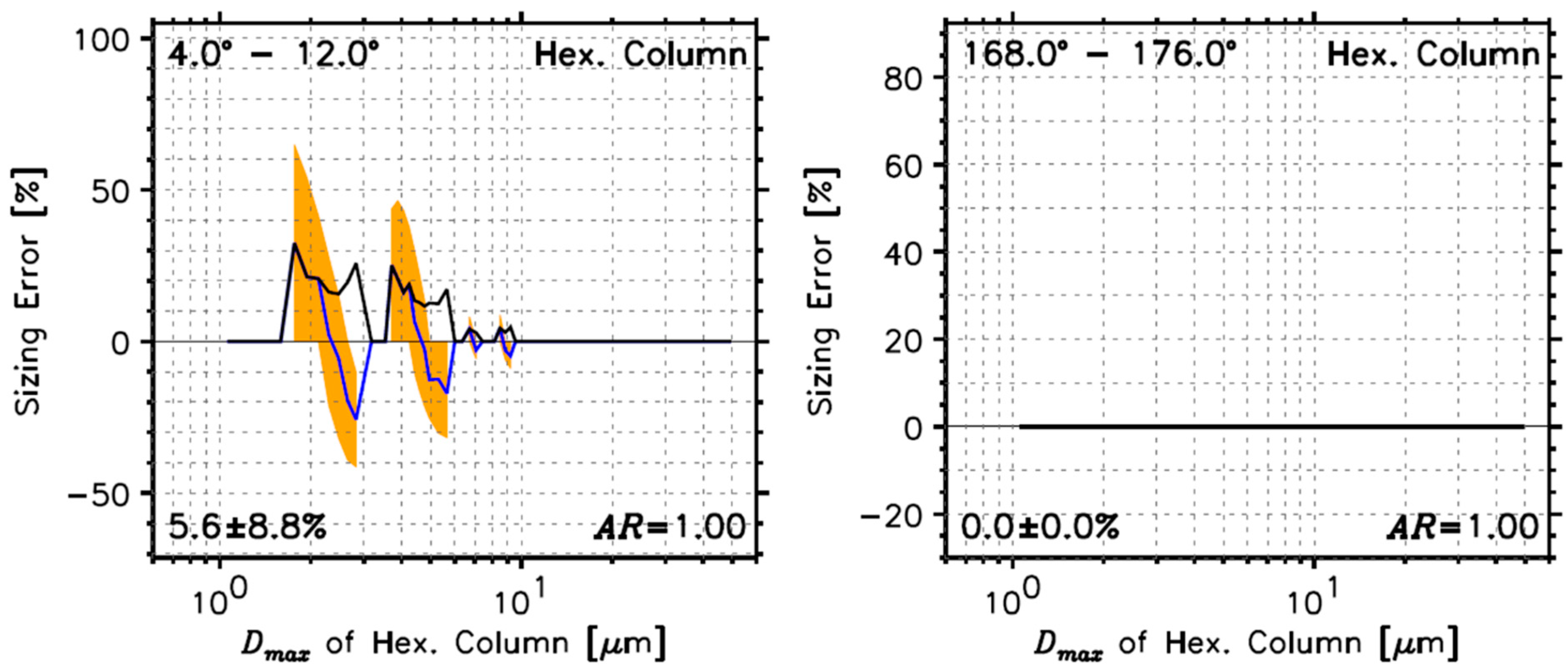
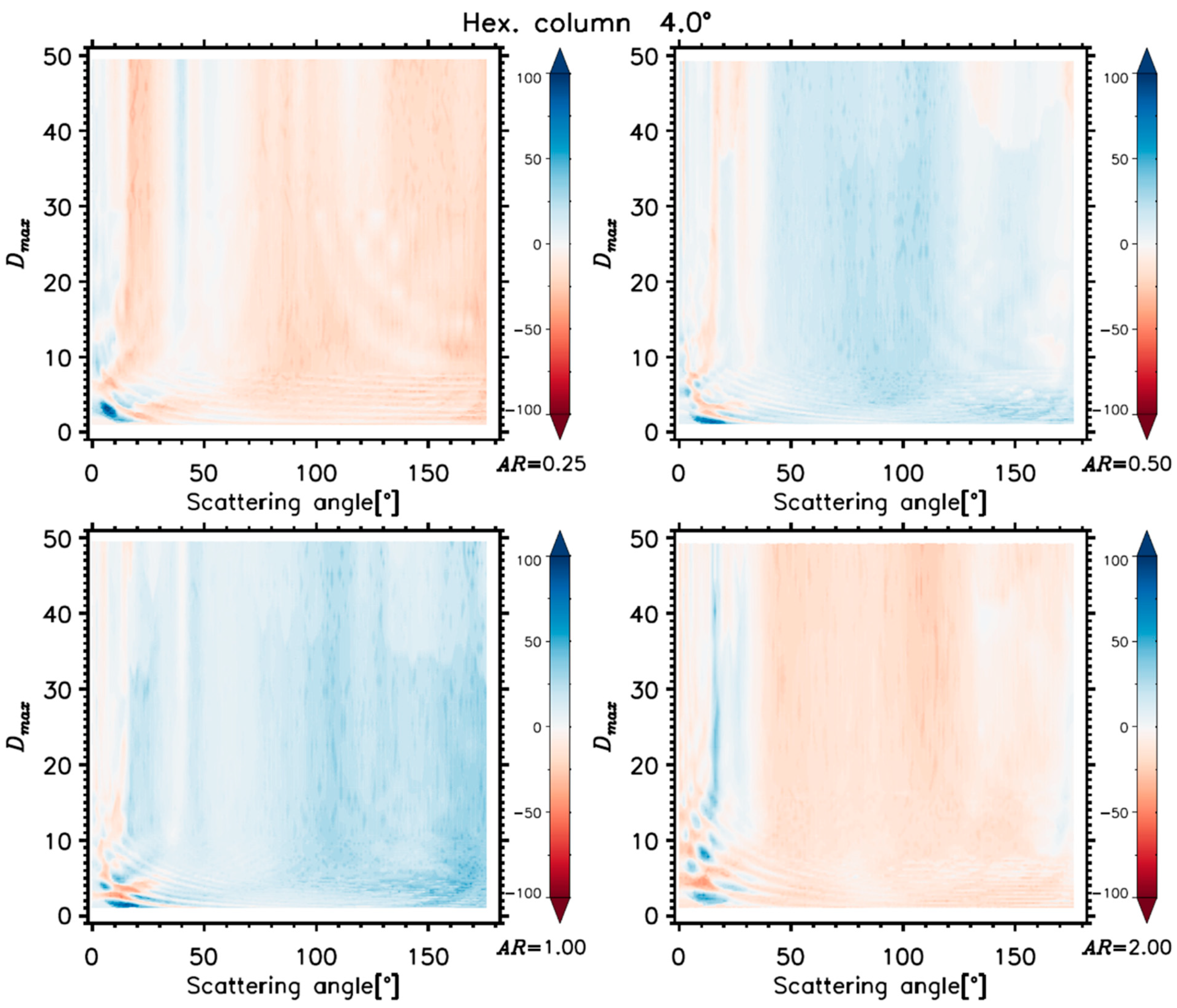
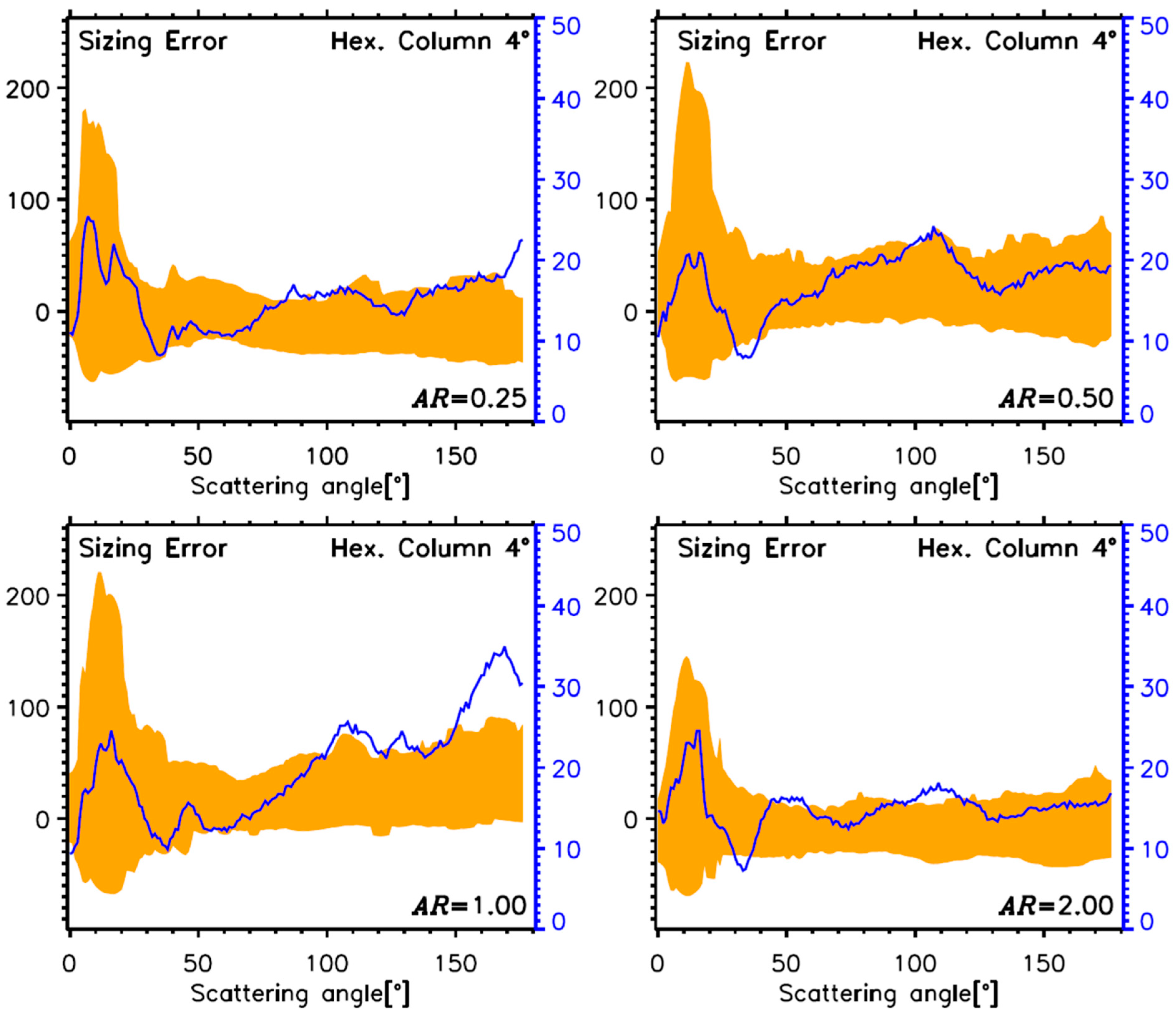
4.2.3. Determined Sizing Errors Using Hexagonal Ice Crystals
5. Determined Optimal Scattering Angles for Forward Scattering Probes
5.1. Optimal Scattering Angles for Spherical Liquid Cloud Droplets
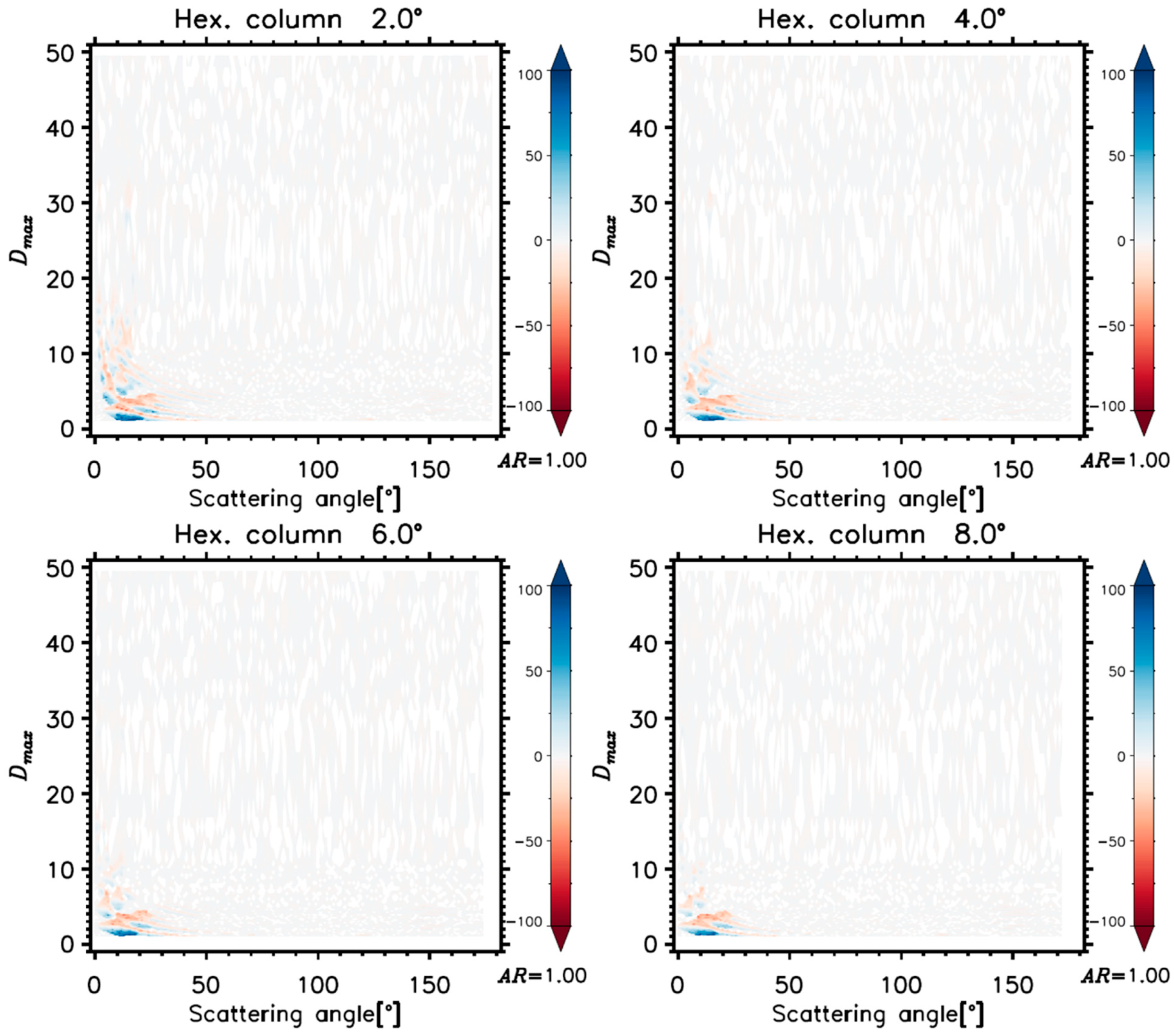
5.2. Optimal Scattering Angles for Hexagonal Ice Crystals
6. Conclusions
- The current forward scattering probes (i.e., CAS) have 5.0 ± 9.7% (121.9%) of average ± standard deviation (maximum) errors in sizing liquid cloud droplets in the forward direction (4–12°), with errors of 17.4 ± 12.8% (229.2%) in the backward direction (168–176°).
- For measurements of hexagonal ice crystals, sizing errors were 44.2 ± 10.1% (91.3%), 40.2 ± 10.1% (58.8%), 43.0 ± 11.7% (59.3%), and 41.1 ± 15.3 (55.4%) for AR = 0.25, 0.50, 1.00, and 2.00, respectively, in the forward direction, and 20.6±16.1% (74.8%), 15.5 ± 9.0% (66.5%), 39.7 ± 10.1% (70.8%), and 19.6 ± 18.2% (67.9%) in the backward direction based on the calculations using a Lorenz–Mie code with assumptions of liquid spherical cloud droplets.
- It was shown that the errors in sizing ice crystals using current forward scattering probes increased almost linearly for Dmax > ~8 μm in the forward direction (4–12°), which implies larger sizing errors for larger ice crystals.
- Replacing spherical liquid cloud droplets with spherical ice cloud droplets did not improve the sizing errors. Thus, the impact of the shape of an ice crystal is larger than that of the thermodynamic phase for measurements of forward scattering probes.
- A newly developed size conversion table based on the ADDA calculations reduced the sizing errors of hexagonal ice crystals to 15.7 ± 14.4% (106.7%), 14.3 ± 10.1% (103.3%), 12.0 ± 8.5% (69.1%), and 14.7 ± 10.2% (82.5%) for AR = 0.25, 0.50, 1.00, and 2.00, respectively, in the forward direction, while those were 18.7 ± 3.9% (46.6%), 19.3 ± 7.4% (74.3%), 33.5 ± 8.6% (86.7%), and 15.9 ± 3.4% (37.5%) in backward direction.
- It was shown that the determined optimal scattering angles were 23–31° (51–59°) to minimize the average (standard deviation) of sizing errors, which provided 2.5 ± 5.2% (7.0 ± 2.6%) of average ± standard deviation errors in sizing liquid cloud droplets.
- Approximately, the 30–40° (60–70°) were suitable selections to reduce the averages (standard deviations) of sizing errors of hexagonal ice crystals with AR = 0.25, 0.50, 1.00, and 2.00 using the ADDA.
- For compact shapes (i.e., AR = 1.00) of hexagonal ice crystals, any selection of scattering angles larger than >~50° would effectively reduce the sizing errors based on the ADDA calculations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bailey, M.; Hallett, J. Growth rates and habits of ice crystals between −20 °C and −70 °C. J. Atmos. Sci. 2004, 61, 514–544. [Google Scholar] [CrossRef]
- Um, J.; McFarquhar, G.M. Dependence of the single-scattering properties of small ice crystals on idealized shape models. Atmos. Chem. Phys. 2011, 11, 3159–3171. [Google Scholar] [CrossRef]
- Um, J.; McFarquhar, G.M. Formation of atmospheric halos and applicability of geometric optics for calculating single-scattering properties of hexagonal ice crystals: Impacts of aspect ratio and ice crystal size. J. Quant. Spectrosc. Radiat. Transf. 2015, 165, 134–152. [Google Scholar] [CrossRef]
- Knollenberg, R.G. The optical array: An alternative to scattering or extinction for airborne particle size determination. J. Appl. Meteor. 1970, 9, 86–103. [Google Scholar] [CrossRef]
- Baumgardner, D.; Jonsson, H.; Dawson, W.; O’Connor, D.; Newton, R. The cloud, aerosol and precipitation spectrometer: A new instrument for cloud investigations. Atmos. Res. 2001, 59–60, 251–264. [Google Scholar] [CrossRef]
- Lawson, R.P.; Stewart, R.E.; Angus, L.J. Observations and numerical simulations of the origin and development of very large snowflakes. J. Atmos. Sci. 1998, 55, 3209–3229. [Google Scholar] [CrossRef]
- Lawson, R.P.; O’Connor, D.; Zmarzly, P.; Weaver, K.; Baker, B.; Mo, Q.; Jonsson, H. The 2DS (stereo) probe: Design and preliminary tests of a new airborne, high speed, high-resolution particle imaging probe. J. Atmos. Ocean. Tech. 2006, 23, 1462–1471. [Google Scholar] [CrossRef]
- Baumgardner, D.; Abel, S.J.; Axisa, D.; Cotton, R.; Crosier, J.; Field, P.; Gurganus, C.; Heymsfield, A.; Korolev, A.; Krämer, M.; et al. Cloud ice properties: In situ measurement challenges. Meteor. Monogr. 2017, 58, 9.1–9.23. [Google Scholar] [CrossRef]
- Gurganus, C.; Lawson, P. Laboratory and Flight Tests of 2D Imaging Probes: Toward a Better Understanding of Instrument Performance and the Impact on Archived Data. J. Atmos. Ocean. Tech. 2018, 35, 1533–1553. [Google Scholar] [CrossRef]
- Wendisch, M.; Brenguier, J.-L. Airborne Measurements for Environmental Research: Methods and Instruments; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- McFarquhar, G.M.; Baumgardner, D.; Bansemer, A.; Abel, S.J.; Crosier, J.; French, J.; Rosenberg, P.; Korolev, A.; Schwarzoenboeck, A.; Leroy, D.; et al. Processing of Ice Cloud In Situ Data Collected by Bulk Water, Scattering, and Imaging Probes: Fundamentals, Uncertainties, and Efforts toward Consistency. Meteor. Monogr. 2017, 58, 11.1–11.33. [Google Scholar] [CrossRef]
- Faber, S.; French, J.R.; Jackson, R. Laboratory and in-flight evaluation of measurement uncertainties from a commercial Cloud Droplet Probe (CDP). Atmos. Meas. Tech. 2018, 11, 3645–3659. [Google Scholar] [CrossRef]
- Pinnick, R.G.; Garvey, D.M.; Duncan, L.D. Calibration of Knollenberg FSSP Light-Scattering Counters for Measurement of Cloud Droplets. J. Appl. Meteor. Climatol. 1981, 20, 1049–1057. [Google Scholar] [CrossRef]
- Dye, J.E.; Baumgardner, D. Evaluation of the forward scattering spectrometer probe. Part I: Electronic and optical studies. J. Atmos. Ocean. Tech. 1984, 1, 329–344. [Google Scholar] [CrossRef]
- Spiegel, J.K.; Zieger, P.; Bukowiecki, N.; Hammer, E.; Weingartner, E.; Eugster, W. Evaluating the capabilities and uncertainties of droplet measurements for the fog droplet spectrometer (FM-100). Atmos. Meas. Tech. 2012, 5, 2237–2260. [Google Scholar] [CrossRef]
- Cox, C.J.; Noone, D.C.; Berkelhammer, M.; Shupe, M.D.; Neff, W.D.; Miller, N.B.; Walden, V.P.; Steffen, K. Supercooled liquid fogs over the central Greenland Ice Sheet. Atmos. Chem. Phys. 2019, 19, 7467–7485. [Google Scholar] [CrossRef]
- Um, J. Calculations of Optical Properties of Cloud Particles to Improve the Accuracy of Forward Scattering Probes for In-Situ Aircraft Cloud Measurements. Atmosphere 2020, 30, 75–89. [Google Scholar]
- Lance, S.; Brock, C.A.; Rogers, D.; Gordon, J.A. Water droplet calibration of the cloud droplet probe (CDP) and in-flight performance in liquid, ice and mixed-phase clouds during ARCPAC. Atmos. Meas. Tech. 2010, 3, 1683–1706. [Google Scholar] [CrossRef]
- Hovenac, E.A.; Hirleman, E.D. Use of Rotating Pinholes and Reticles for Calibration of Cloud Droplet Instrumentation. J. Atmos. Ocean. Tech. 1991, 8, 166–171. [Google Scholar] [CrossRef]
- Rosenberg, P.D.; Dean, A.R.; Williams, P.I.; Dorsey, J.R.; Minikin, A.; Pickering, M.A.; Petzold, A. Particle sizing calibration with refractive index correction for light scattering optical particle counters and impacts upon PCASP and CDP data collected during the Fennec campaign. Atmos. Meas. Tech. 2012, 5, 1147–1163. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Campridge, UK, 2002. [Google Scholar]
- Baumgardner, D.; Strapp, W.; Dye, J.E. Evaluation of the Forward Scattering Spectrometer Probe. Part II: Corrections for Coincidence and Dead-Time Losses. J. Atmos. Ocean. Tech. 1985, 2, 626–632. [Google Scholar] [CrossRef]
- Cooper, W.A. Effects of Coincidence on Measurements with a Forward Scattering Spectrometer Probe. J. Atmos. Ocean. Tech. 1988, 5, 823–832. [Google Scholar] [CrossRef]
- Burnet, F.; Brenguier, J. Comparison between Standard and Modified Forward Scattering Spectrometer Probes during the Small Cumulus Microphysics Study. J. Atmos. Ocean. Tech. 2002, 19, 1516–1531. [Google Scholar] [CrossRef]
- Cotton, R.; Osborne, S.; Ulanowski, Z.; Hirst, E.; Kaye, P.H.; Greenaway, R.S. The Ability of the Small Ice Detector (SID-2) to Characterize Cloud Particle and Aerosol Morphologies Obtained during Flights of the FAAM BAe-146 Research Aircraft. J. Atmos. Ocean. Tech. 2010, 27, 290–303. [Google Scholar] [CrossRef]
- Lance, S. Coincidence Errors in a Cloud Droplet Probe (CDP) and a Cloud and Aerosol Spectrometer (CAS), and the Improved Performance of a Modified CDP. J. Atmos. Ocean. Tech. 2012, 29, 1532–1541. [Google Scholar] [CrossRef]
- Johnson, A.; Lasher-Trapp, S.; Bansemer, A.; Ulanowski, Z.; Heymsfield, A.J. Difficulties in Early Ice Detection with the Small Ice Detector-2 HIAPER (SID-2H) in Maritime Cumuli. J. Atmos. Ocean. Tech. 2014, 31, 1263–1275. [Google Scholar] [CrossRef]
- Gardiner, B.A.; Hallett, J. Degradation of In-Cloud Forward Scattering Spectrometer Probe Measurements in the Presence of Ice Particles. J. Atmos. Ocean. Tech. 1985, 2, 171–180. [Google Scholar] [CrossRef]
- Field, P.R.; Wood, R.; Brown, P.R.A.; Kaye, P.H.; Hirst, E.; Greenaway, R.; Smith, J.A. Ice Particle Interarrival Times Measured with a Fast FSSP. J. Atmos. Ocean. Tech. 2003, 20, 249–261. [Google Scholar] [CrossRef]
- Heymsfield, A.J. On measurements of small ice particles in clouds. Geophys. Res. Lett. 2007, 34, L23812. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Um, J.; Freer, M.; Baumgardner, D.; Kok, G.L.; Mace, G. Importance of small ice crystals to cirrus properties: Observations from the Tropical Warm Pool International Cloud Experiment (TWP-ICE). Geophys. Res. Lett. 2007, 34, L13803. [Google Scholar] [CrossRef]
- Baker, B.; Mo, Q.; Lawson, R.P.; O’Connor, D.; Korolev, A. The Effects of Precipitation on Cloud Droplet Measurement Devices. J. Atmos. Ocean. Tech. 2009, 26, 1404–1409. [Google Scholar] [CrossRef]
- Korolev, A.V.; Emery, E.F.; Strapp, J.W.; Cober, S.G.; Isaac, G.A.; Wasey, M.; Marcotte, D. Small Ice Particles in Tropospheric Clouds: Fact or Artifact? Airborne Icing Instrumentation Evaluation Experiment. Bull. Amer. Meteor. Soc. 2011, 92, 967–973. [Google Scholar] [CrossRef]
- Korolev, A.V.; Emery, E.F.; Strapp, J.W.; Cober, S.G.; Isaac, G.A. Quantification of the Effects of Shattering on Airborne Ice Particle Measurements. J. Atmos. Ocean. Tech. 2013, 30, 2527–2553. [Google Scholar] [CrossRef]
- Baumgardner, D.; Spowart, M. Evaluation of the Forward Scattering Spectrometer Probe, Part III: Time Response and Laser Imhomogeneity Limitations. J. Atmos. Ocean. Tech. 1990, 7, 666–672. [Google Scholar] [CrossRef]
- Brenguier, J.L.; Baumgardner, D.; Baker, B. A Review and Discussion of Processing Algorithms for FSSP Concentration Measurement. J. Atmos. Ocean. Tech. 1994, 11, 1409–1414. [Google Scholar] [CrossRef]
- Brenguier, J.L.; Bourrianne, T.; Coelho, A.A.; Isbert, J.; Peytavi, R.; Trevarin, D.; Weschler, P. Improvements of Droplet Size Distribution Measurements with the Fast-FSSP (Forward Scattering Spectrometer Probe). J. Atmos. Ocean. Tech. 1998, 15, 1077–1090. [Google Scholar] [CrossRef]
- Nagel, D.; Maixner, U.; Strapp, W.; Wasey, M. Advancements in Techniques for Calibration and Characterization of In Situ Optical Particle Measuring Probes, and Applications to the FSSP-100 Probe. J. Atmos. Ocean. Tech. 2007, 24, 745–760. [Google Scholar] [CrossRef]
- Knollenberg, R.G. Three New Instruments for Cloud Physics Measurements: The 2-D Spectrometer Probe, the Forward Scattering Spectrometer Probe, and the Active Scattering Aerosol Spectrometer; Preprints; American Meteorological Society: Boston, MA, USA, 1976; pp. 554–561. [Google Scholar]
- Knollenberg, R.G. Techniques for probing cloud microstructure. In Clouds, Their Formation, Optical Properties and Effects; Hobbs, P.V., Deepak, A., Eds.; Academic Press: Cambridge, MA, USA, 1981; pp. 15–91. [Google Scholar]
- Glen, A.; Brooks, S.D. A new method for measuring optical scattering properties of atmospherically relevant dusts using the Cloud and Aerosol Spectrometer with Polarization (CASPOL). Atmos. Chem. Phys. 2013, 13, 1345–1356. [Google Scholar] [CrossRef]
- Baumgardner, D.; Newton, R.; Krämer, M.; Meyer, J.R.; Beyer, A.; Wendisch, M.; Vochezer, P. The Cloud Particle Spectrometer with Polarization Detection (CPSPD): A next generation open-path cloud probe for distinguishing liquid cloud droplets from ice crystals. Atmos. Res. 2014, 142, 2–14. [Google Scholar] [CrossRef]
- Vali, G.; Politovich, M.K.; Baumgardner, D.; Cooper, W.A. Conduct of Cloud Spectra Measurements Scientific Report 1 to the Air Force Geophysical Laboratory; Contract AFGL-TR-79-025; National Technical Information Service: Springfield, VA, USA, 1979; ADA081127. [Google Scholar]
- Vali, G.; Politovich, M.K.; Baumgardner, D. Conduct of Cloud Spectra Measurements, Final Report to Air Force Geophysics Laboratory; Contract No. AFGL-TR-81-0122; National Technical Information Service: Springfield, VA, USA, 1981; ADA102944. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Borrmann, S.; Beiping, L.; Mishchenko, M. Application of the T-matrix method to the measurement of aspherical (ellipsoidal) particles with forward scattering optical particle counters. J. Aerosol Sci. 2000, 31, 789–799. [Google Scholar] [CrossRef]
- Meyer, J. Ice Crystal Measurements with the New Particle Spectrometer NIXE-CAPS; Forschungszentrum Julich GmbH; Institute for Energy and Climate Research: Jülich, Germany, 2012; 132p. [Google Scholar]
- Schnaiter, M.; Buttner, S.; Mohler, O.; Skrotzki, J.; Vragel, M.; Wagner, R. Influence of particle size and shape on the backscattering linear depolarization ratio of small ice crystals—Cloud chamber measurements in the context of contrail and cirrus microphysics. Atmos. Chem. Phys. 2012, 12, 10465–10484. [Google Scholar] [CrossRef]
- Hirst, E.; Kaye, P.H.; Greenway, R.S.; Field, P.; Johnson, D.W. Discrimination of micrometre-sized ice and super-cooled droplets in mixed-phase cloud. Atmos. Environ. 2001, 35, 33–47. [Google Scholar] [CrossRef]
- Kaye, P.H.; Hirst, E.; Greenway, R.S.; Ulanowski, Z.; Hesse, E.; DeMott, P.; Saunders, C.; Connolly, P. Classifying atmospheric ice crystals by spatial light scattering. Opt. Lett. 2008, 33, 1545–1547. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, G.; Choularton, T.; Bower, K.; Crosier, J.; Gallagher, M.; Flynn, M.; Dorsey, J.; Liu, D.; Taylor, J.W.; Schlenczek, O.; et al. Small ice particles at slightly supercooled temperatures in tropical maritime convection. Atmos. Chem. Phys. 2020, 20, 3895–3904. [Google Scholar] [CrossRef]
- Lawson, R.P.; Woods, S.; Jensen, E.; Erfani, E.; Gurganus, C.; Gallagher, M.; Connolly, P.; Whiteway, J.; Baran, A.J.; May, P.; et al. A review of ice particle shapes in cirrus formed in situ and anvils. J. Geophys. Res. Atmos. 2019, 124, 10049–10090. [Google Scholar] [CrossRef]
- Abdelmonem, A.; Schnaiter, M.; Amsler, P.; Hesse, E.; Meyer, J.; Leisner, T. First correlated measurements of the shape and light scattering properties of cloud particles using the new Particle Habit Imaging and Polar Scattering (PHIPS) probe. Atmos. Meas. Tech. 2011, 4, 2125–2142. [Google Scholar] [CrossRef]
- Gerber, H.; Arends, B.; Ackerman, A. New microphysics sensor for aircraft use. Atmos. Res. 1994, 31, 235–252. [Google Scholar] [CrossRef]
- Gerber, H.; DeMott, P.J. Response of FSSP-100 and PVM-100A to Small Ice Crystals. J. Atmos. Ocean. Tech. 2014, 31, 2145–2155. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Pinnick, R.G.; Auvermann, H.J. Response characteristics of Knollenberg light-scattering aerosol counters. J. Aerosol Sci. 1979, 10, 55–74. [Google Scholar] [CrossRef]
- Gonser, S.G.; Klemm, O.; Griessbaum, F.; Chang, S.C.; Chu, H.S.; Hsia, Y.J. The relation between humidity and liquid water content in fog: An experimental approach. Pure Appl. Geophys. 2012, 169, 821–833. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Um, J.; Jackson, R. Small Cloud Particle Shapes in Mixed-Phase Clouds. J. Appl. Meteor. 2013, 52, 1277–1293. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Heymsfield, A.J.; Macke, A.; Iaquinta, J.; Aulenbach, S.M. Use of observed ice crystal sizes and shapes to calculate mean scattering properties and multi-spectral radiances: CEPEX April 4, 1993 case study. J. Geophys. Res. 1999, 104, 31763–31779. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Yang, P.; Macke, A.; Baran, A.J. A New Parameterization of Single Scattering Solar Radiative Properties for Tropical Anvils Using Observed Ice Crystal Size and Shape Distributions. J. Atmos. Sci. 2002, 59, 2458–2478. [Google Scholar] [CrossRef]
- Yang, P.; Baum, B.A.; Heymsfield, A.J.; Hu, Y.X.; Huang, H.L.; Tsay, S.C.; Ackerman, S. Single-scattering properties of droxtals. J. Quant. Spectrosc. Radiat. Transf. 2003, 79–80, 1159–1169. [Google Scholar] [CrossRef]
- Nousiainen, T.; McFarquhar, G.M. Light Scattering by Quasi-Spherical Ice Crystals. J. Atmos. Sci. 2004, 61, 2229–2248. [Google Scholar] [CrossRef]
- Pauling, L. The structure and entropy of ice and of other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc. 1935, 57, 2680–2684. [Google Scholar] [CrossRef]
- Stith, J.L.; Avallone, L.M.; Bansemer, A.; Basarab, B.; Dorsi, S.W.; Fuchs, B.; Lawson, R.P.; Rogers, D.C.; Rutledge, S.; Toohey, D.W. Ice particles in the upper anvil re- gions of midlatitude continental thunderstorms: The case for frozen-drop aggregates. Atmos. Chem. Phys. 2014, 14, 1973–1985. [Google Scholar] [CrossRef]
- Um, J.; McFarquhar, G.M.; Stith, J.L.; Jung, C.H.; Lee, S.S.; Lee, J.Y.; Shin, Y.; Lee, Y.G.; Yang, Y.I.; Yum, S.S.; et al. Microphysical characteristics of frozen droplet aggregates from deep convective clouds. Atmos. Chem. Phys. 2018, 18, 16915–16930. [Google Scholar] [CrossRef]
- Magee, N.; Boaggio, K.; Staskiewicz, S.; Lynn, A.; Zhao, X.; Tusay, N.; Schuh, T.; Bandamede, M.; Bancroft, L.; Connelly, D.; et al. Captured cirrus ice particles in high definition. Atmos. Chem. Phys. 2021, 21, 7171–7185. [Google Scholar] [CrossRef]
- Järvinen, E.; Schnaiter, M.; Mioche, G.; Jourdan, O.; Shcherbakov, V.N.; Costa, A.; Afchine, A.; Krämer, M.; Heidelberg, F.; Jurkat, T.; et al. Quasi-Spherical Ice in Convective Clouds. J. Atmos. Sci. 2016, 73, 3885–3910. [Google Scholar] [CrossRef]
- Um, J.; McFarquhar, G.M.; Hong, Y.P.; Lee, S.S.; Jung, C.H.; Lawson, R.P.; Mo, Q. Dimensions and aspect ratios of natural ice crystals. Atmos. Chem. Phys. 2015, 15, 3933–3956. [Google Scholar] [CrossRef]
- Warren, S.G.; Brandt, R.E. Optical constants of ice from the ultraviolet to the microwave: A revised compilation. J. Geophys. Res. 2008, 113, D14220. [Google Scholar] [CrossRef]
- Yurkin, M.A.; Hoekstra, A.G. The discrete-dipole-approximation code ADDA: Capabilities and known limitations. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2234–2247. [Google Scholar] [CrossRef]
- Bi, L.; Yang, P. Accurate simulation of the optical properties of atmospheric ice crystals with the invariant imbedding T-matrix method. J. Quant. Spectrosc. Radiat. Transf. 2014, 138, 17–35. [Google Scholar] [CrossRef]
- Okada, Y. Efficient numerical orientation averaging of light scattering properties with a quasi-montecarlo method. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 1719–1742. [Google Scholar] [CrossRef]
- Um, J.; McFarquhar, G.M. Optimal numerical methods for determining the orientation averages of single-scattering properties of atmospheric ice crystals. J. Quant. Spectrosc. Radiat. Transf. 2013, 127, 207–223. [Google Scholar] [CrossRef]
- D’Alessandro, J.J.; McFarquhar, G.M.; Wu, W.; Stith, J.L.; Jensen, J.B.; Rauber, R.M. Characterizing the occurrence and spatial heterogeneity of liquid, ice, and mixed phase low-level clouds over the Southern Ocean using in situ observations acquired during SOCRATES. J. Geophys. Res. 2021, 126, e2020JD034482. [Google Scholar] [CrossRef]
- Atlas, R.; Mohrmann, J.; Finlon, J.; Lu, J.; Hsiao, I.; Wood, R.; Diao, M. The University of Washington Ice–Liquid Discriminator (UWILD) improves single-particle phase classifications of hydrometeors within Southern Ocean clouds using machine learning. Atmos. Meas. Tech. 2021, 14, 7079–7101. [Google Scholar] [CrossRef]
- Ulanowski, Z.; Hesse, E.; Kaye, P.H.; Baran, A.J. Light scattering by complex ice analogue crystal. J. Quant. Spectro. Radiat. Transf. 2006, 100, 382–392. [Google Scholar] [CrossRef]
- Nousiainen, T.; Muñoz, O.; Lindqvist, H.; Mauno, P.; Videen, G. Light scattering by large Saharan dust particles: Comparison of modeling and experimental data for two samples. J. Quant. Spectro. Radiat. Transf. 2011, 112, 420–433. [Google Scholar] [CrossRef]
- Morrison, H.; van Lier-Walqui, M.; Fridlind, A.M.; Grabowski, W.W.; Harrington, J.Y.; Hoose, C.; Korolev, A.; Kumjian, M.R.; Milbrandt, J.A.; Pawlowska, H.; et al. Confronting the challenge of modeling cloud and precipitation microphysics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001689. [Google Scholar] [CrossRef] [PubMed]
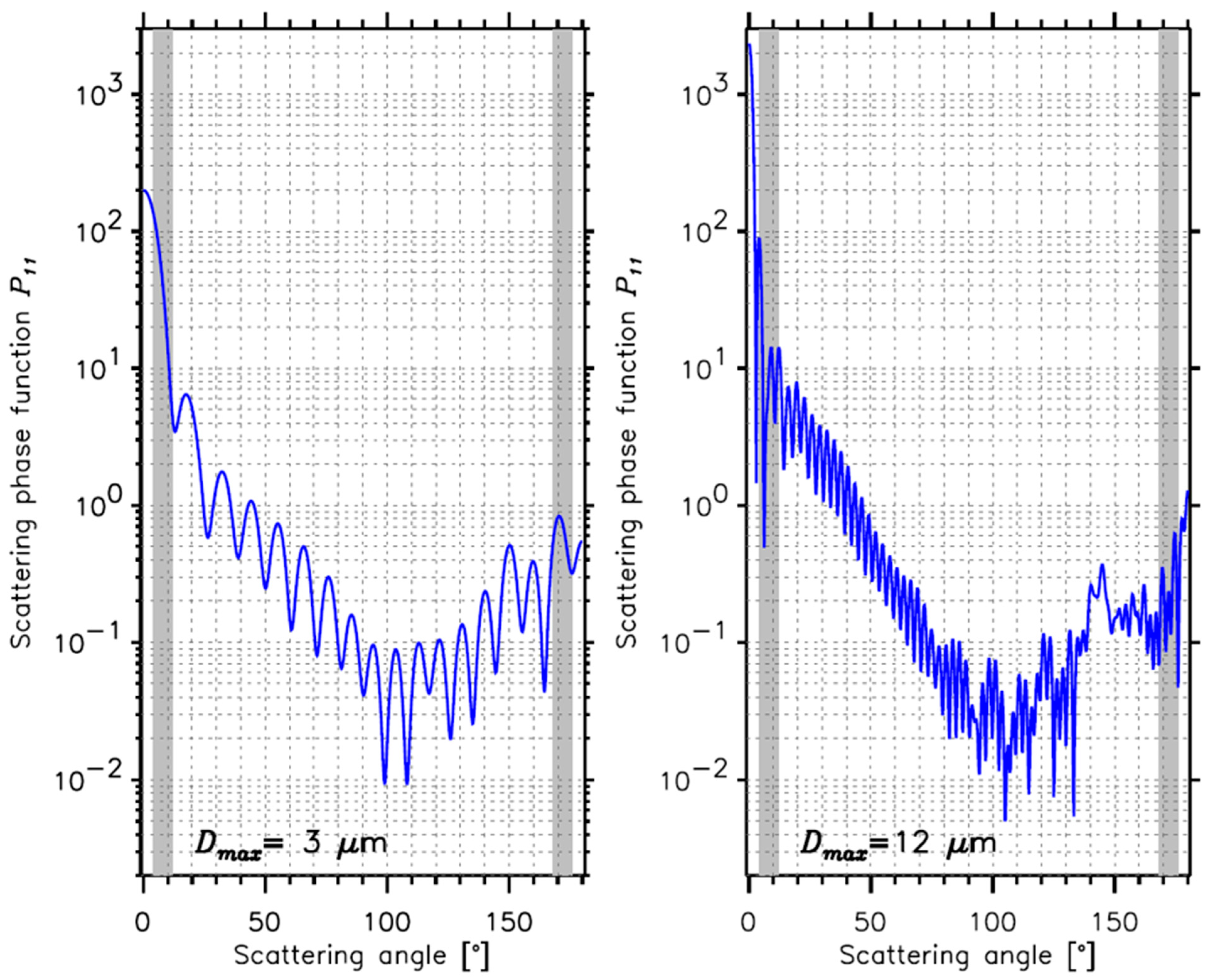


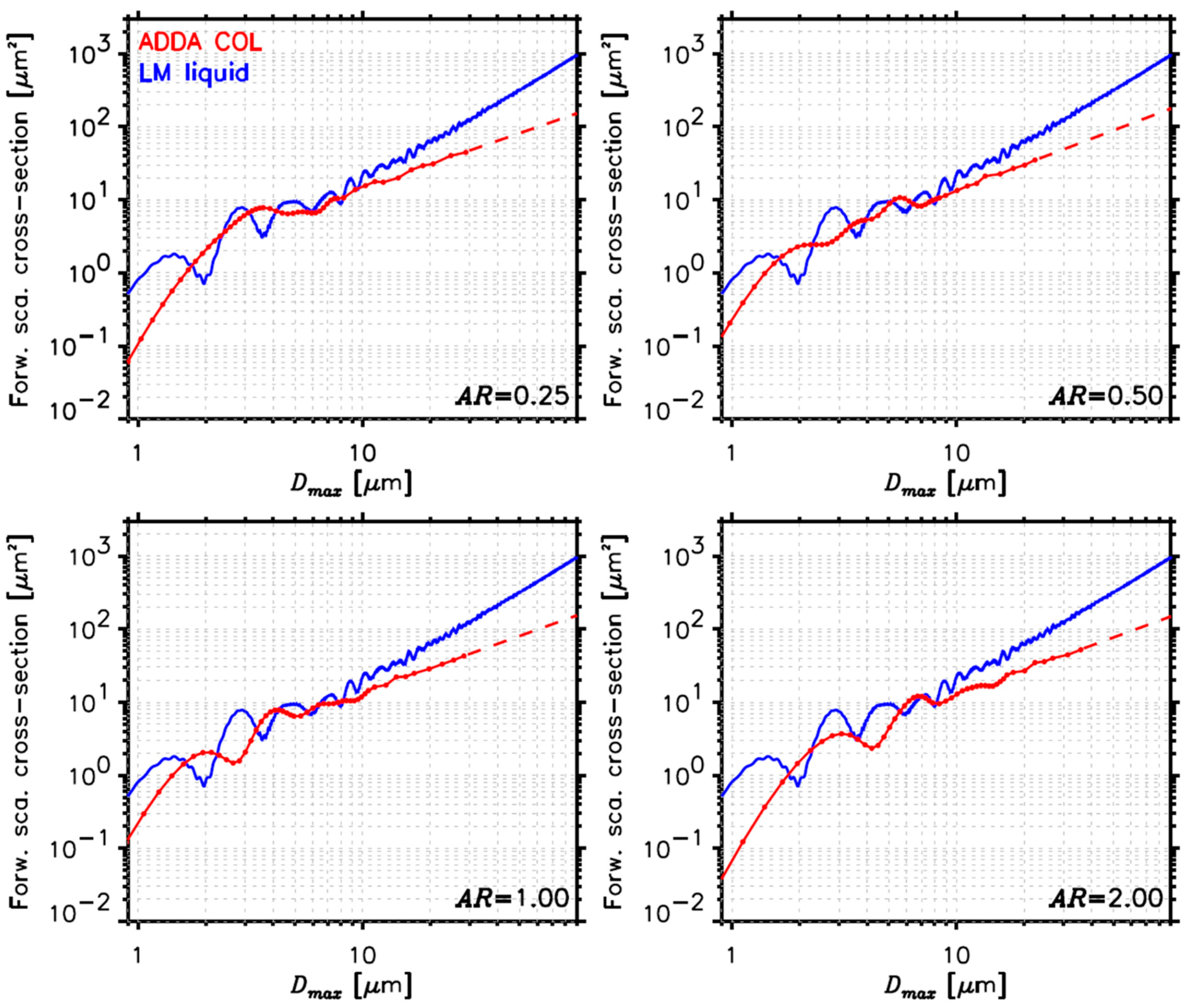
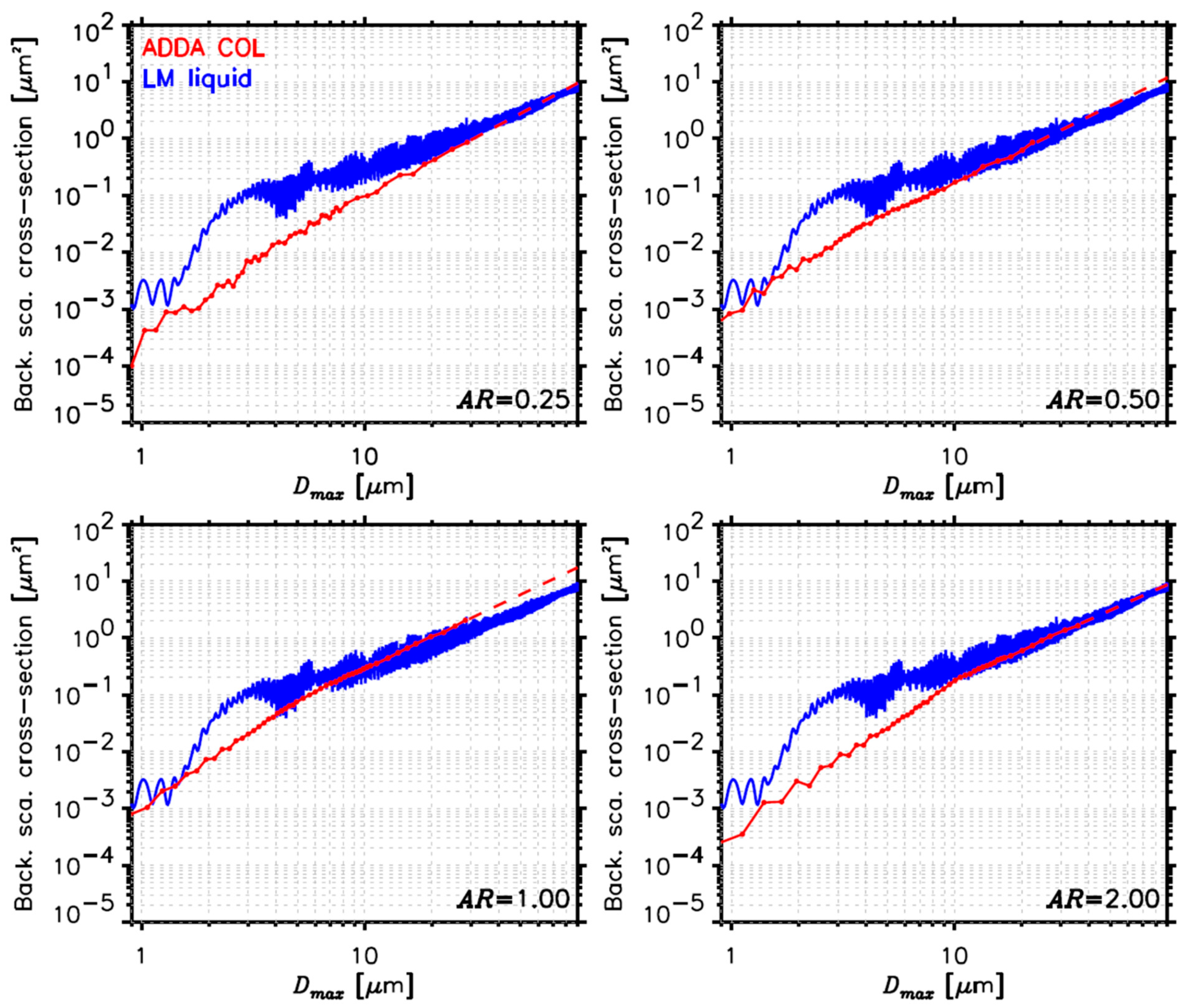


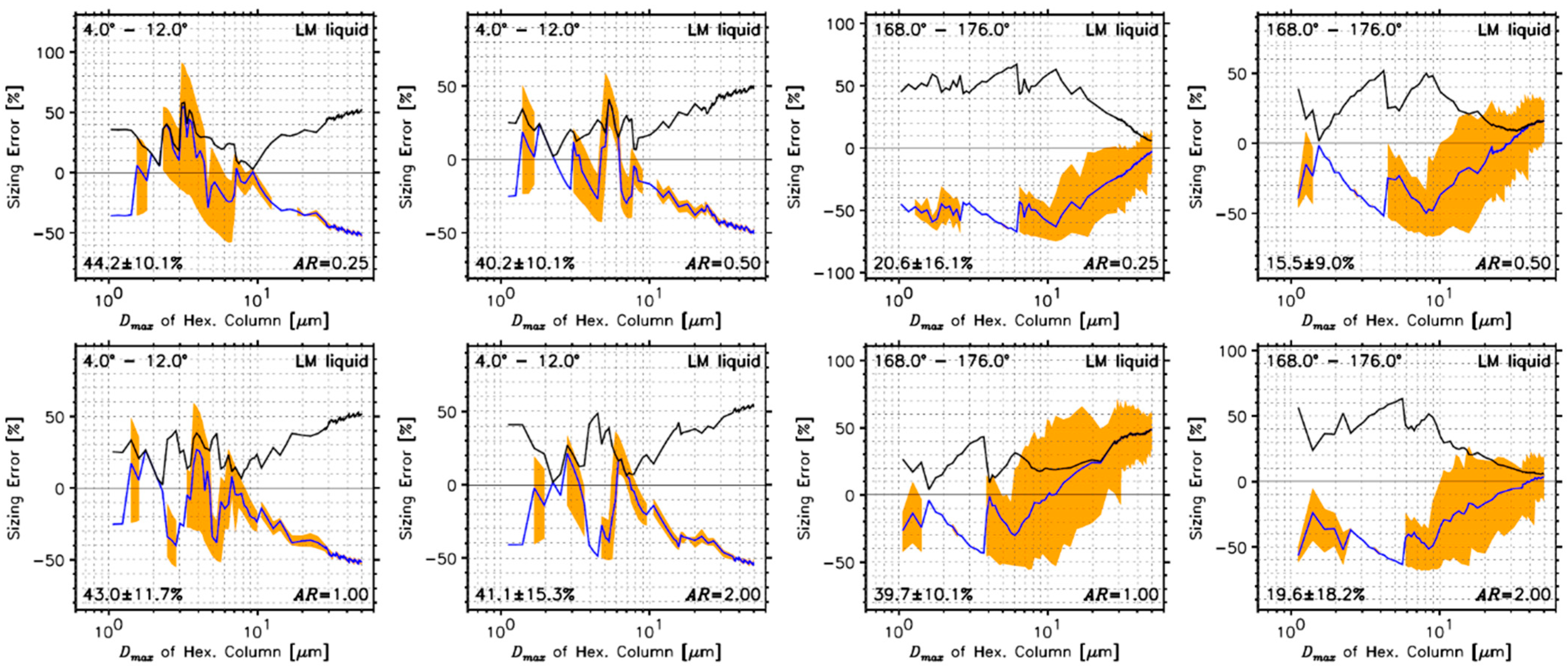

| Probe Name | Measurement Range (µm) | Wavelength (nm) | Light Collection Angles (°) |
|---|---|---|---|
| FSSP | 2–50 | 633 | 3–13° |
| CDP | 2–50 | 658 | 4–12° |
| CAS | 0.5–50 | 658 | 4–12°, 168–176° |
| FFSSP | 1–50 | 632 | 4–12° |
| FCDP | 1–50 | 785 | 4–12° |
| CAS-POL | 0.6–50 | 680 | 4–12°, 168–176° |
| CPSPD | 0.65–30 | 658 | 13–47°, 133–167° |
| AR = 0.25 | AR = 0.50 | AR = 1.00 | AR = 2.00 | |
|---|---|---|---|---|
| L (μm) | 0.0625–7.0 | 0.125–10.0 | 0.25–20.00 | 0.50–32.0 |
| W (μm) | 0.25–28.0 | 0.25–20.0 | 0.25–20.0 | 0.25–16.0 |
| Dmax | 0.26–28.86 | 0.28–22.36 | 0.35–28.28 | 0.56–35.78 |
| χDmax | 1.47–164.86 | 1.60–127.72 | 2.02–161.56 | 3.19–204.36 |
| Target (Measured Particle, Dactual) | Pre-Calculation of Cloud Particle | Section | Determined Average ± Standard Deviation (Maximum) Sizing Errors (%) | ||||
|---|---|---|---|---|---|---|---|
| Assumed Phase | Assumed Shape | Forward (4–12°) | Backward (168–176°) | ||||
| Spherical liquid cloud droplet | Liquid | Sphere | Section 4.1 | 5.0 ± 9.7 (121.9) [6.9 ± 16.1 (113.7)] | 17.4 ± 12.8 (229.2) [14.6 ± 17.9 (128.7)] | ||
| Hexagonal ice crystal | Liquid | Sphere | Section 4.2.1 | AR = 0.25 | 44.2 ± 10.1 (91.3) [45.5 ± 12.8 (77.5)] | AR = 0.25 | 20.6 ± 16.1 (74.8) [20.1 ± 24.3 (90.4)] |
| AR = 0.50 | 40.2 ± 10.1 (58.8) [41.6 ± 9.7 (52.8)] | AR = 0.50 | 15.5 ± 9.0 (66.5) [17.8 ± 15.4 (82.6)] | ||||
| AR = 1.00 | 43.0 ± 11.7 (59.3) [42.9 ± 13.6 (53.8)] | AR = 1.00 | 39.7 ± 10.1 (70.8) [50.6 ± 18.2 (80.4)] | ||||
| AR = 2.00 | 41.1 ± 15.3 (55.4) [40.3 ± 16.3 (55.0)] | AR = 2.00 | 19.6 ± 18.2 (67.9) [21.2 ± 25.0 (91.3)] | ||||
| Ice | Sphere | Section 4.2.2 | AR = 0.25 | 45.6 ± 10.6 (88.3) [46.6 ± 12.8 (75.1)] | AR = 0.25 | 16.2 ± 14.6 (74.4) [18.0 ± 22.9 (88.7)] | |
| AR = 0.50 | 41.6 ± 10.7 (60.3) [42.8 ± 10.2 (52.4)] | AR = 0.50 | 26.7 ± 7.6 (65.9) [31.8 ± 12.4 (79.5)] | ||||
| AR = 1.00 | 44.8 ± 11.2 (62.0) [44.0 ± 14.1 (55.2)] | AR = 1.00 | 58.6 ± 19.4 (98.6) [71.1 ± 25.8 (98.2)] | ||||
| AR = 2.00 | 43.3 ± 14.2 (56.7) [41.3 ± 16.8 (56.3)] | AR = 2.00 | 24.5 ± 11.3 (66.5) [27.9 ± 19.2 (89.8)] | ||||
| Ice | Hexagonal column (All ARs) | Section 4.2.3 | AR = 0.25 | 15.7 ± 14.4 (106.7) [8.3 ± 14.8 (89.1)] | AR = 0.25 | 18.7 ± 3.9 (46.6) [19.3 ± 9.8 (73.7)] | |
| AR = 0.50 | 14.3 ± 10.1 (103.3) [7.8 ± 6.2 (70.7)] | AR = 0.50 | 19.3 ± 7.4 (74.3) [13.8 ± 3.9 (58.0)] | ||||
| AR = 1.00 | 12.0 ± 8.5 (69.1) [7.2 ± 10.5 (76.0)] | AR = 1.00 | 33.5 ± 8.6 (86.7) [29.0 ± 2.7 (83.5)] | ||||
| AR = 2.00 | 14.7 ± 10.2 (82.5) [11.4 ± 13.9 (90.1)] | AR = 2.00 | 15.9 ± 3.4 (37.5) [16.3 ± 9.5 (75.4)] | ||||
| Hexagonal column (AR = 1.0) | AR = 1.00 | 5.6 ± 8.8 (64.9) [13.2 ± 17.7 (70.5)] | AR = 1.00 | 0.0 ± 0.0 (0.0) [8.2 ± 13.2 (53.5)] | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, S.; Kim, J.; McFarquhar, G.M.; Park, S.; Lee, S.S.; Jung, C.H.; Park, S.S.; Cha, J.W.; Lee, K.; Um, J. Theoretical Calculations of Directional Scattering Intensities of Small Nonspherical Ice Crystals: Implications for Forward Scattering Probes. Remote Sens. 2022, 14, 2795. https://doi.org/10.3390/rs14122795
Jang S, Kim J, McFarquhar GM, Park S, Lee SS, Jung CH, Park SS, Cha JW, Lee K, Um J. Theoretical Calculations of Directional Scattering Intensities of Small Nonspherical Ice Crystals: Implications for Forward Scattering Probes. Remote Sensing. 2022; 14(12):2795. https://doi.org/10.3390/rs14122795
Chicago/Turabian StyleJang, Seonghyeon, Jeonggyu Kim, Greg M. McFarquhar, Sungmin Park, Seoung Soo Lee, Chang Hoon Jung, Sang Seo Park, Joo Wan Cha, Kyoungmi Lee, and Junshik Um. 2022. "Theoretical Calculations of Directional Scattering Intensities of Small Nonspherical Ice Crystals: Implications for Forward Scattering Probes" Remote Sensing 14, no. 12: 2795. https://doi.org/10.3390/rs14122795
APA StyleJang, S., Kim, J., McFarquhar, G. M., Park, S., Lee, S. S., Jung, C. H., Park, S. S., Cha, J. W., Lee, K., & Um, J. (2022). Theoretical Calculations of Directional Scattering Intensities of Small Nonspherical Ice Crystals: Implications for Forward Scattering Probes. Remote Sensing, 14(12), 2795. https://doi.org/10.3390/rs14122795







