An Ensemble Model-Based Estimation of Nitrogen Dioxide in a Southeastern Coastal Region of China

Abstract

NO₂ (nitrogen dioxide) is a common pollutant in the atmosphere that can have serious adverse effects on the health of residents. However, the existing satellite and ground observation methods are not enough to effectively monitor the spatiotemporal heterogeneity of near-surface NO₂ concentrations, which limits the development of pollutant remediation work and medical health research. Based on TROPOMI-NO₂ tropospheric column concentration data, supplemented by meteorological data, atmospheric condition reanalysis data and other geographic parameters, combined with classic machine learning models and deep learning networks, we constructed an ensemble model that achieved a daily average near-surface NO₂ of 0.03° exposure. In this article, a meteorological hysteretic effects term and a spatiotemporal term were designed, which considerably improved the performance of the model. Overall, our ensemble model performed better, with a 10-fold CV R² of 0.89, an RMSE of 5.62 µg/m³, and an MAE of 4.04 µg/m³. The model also had good temporal and spatial generalization capability, with a temporal prediction R² and a spatial prediction R² of 0.71 and 0.81, respectively, which can be applied to a wider range of time and space. Finally, we used an ensemble model to estimate the spatiotemporal distribution of NO₂ in a coastal region of southeastern China from May 2018 to December 2020. Compared with satellite observations, the model output results showed richer details of the spatiotemporal heterogeneity of NO₂ concentrations. Due to the advantages of using multi-source data, this model framework has the potential to output products with a higher spatial resolution and can provide a reference for downscaling work on other pollutants.

1. Introduction

Nitrogen dioxide (NO₂) is a common trace gas that plays an important role in the atmosphere’s chemical environment [1,2]. As a component of nitrogen oxides (NO_X), NO₂ has a strong correlation with nitrogen oxides, which can indirectly reflect the total distribution of atmospheric nitrogen oxides [3]. As a precursor of ozone (O₃), NO₂ is of great significance to the formation of changes in acid rain and photochemical smog [4,5]. NO₂ is also a harmful air pollutant in the atmosphere. A large number of medical studies have shown that when the concentration of NO₂ reaches a high level, it will cause respiratory diseases such as coughing and lung infections [6,7], and increase the risk of cancer and cardiovascular disease in humans, seriously endangering public health [8,9]. In order to effectively understand the long-term impact of NO₂ exposure on the region and effectively control atmospheric NO₂ and its related pollutants, it is urgent to monitor atmospheric NO₂ concentrations with a high spatial resolution in long-term sequences.

At the end of 2012, China established an air pollutant monitoring network covering major cities across the country [10], which provided basic support for monitoring air pollutants. However, due to the sparse distribution of the stations and the inherent defects of point source monitoring, it is difficult for ground sites to achieve full coverage of regional NO₂ exposure. In order to solve the shortcomings of long-term observations on the ground, satellites are widely used to monitor the spatial and temporal distribution of atmospheric NO₂ concentrations by virtue of their advantages such as coverage of a large area and a long access period [11,12]. Currently, the mainstream NO₂ monitoring satellites in the world include MetOp-A(B) [13] with the Global Ozone Monitoring Experiment (GOME-2), Aura [14] with the Ozone Monitoring Instrument (OMI), and the tropospheric monitoring instrument (TROPOMI) Sentinel-5p [15]. These are able to acquire light backscattered spectra and use inversion algorithms to estimate NO₂ column concentrations. Among these, TROPOMI, as the latest and best NO₂ monitoring sensor, has provided a stable global perspective of the spatial distribution of atmospheric NO₂ concentrations since 2018, with a resolution of about 7 km.

However, NO₂ in cities mainly comes from mobile source emissions and industrial combustion [16], and the variation gradient within a day is large [17]. The complex multi-source emission characteristics make the NO₂ in cities have obvious spatial and temporal variability. The fixed transit time of satellites and their spatial resolution of less than 7 km are likely to homogenize these spatiotemporal heterogeneities, and the homogenized features are often of great significance to the scientific prevention and control of NO₂ and health research.

Using data from site and satellite observations, a number of high-temporal- and spatial-resolution NO₂ exposure assessment models have been developed and have continued to evolve over the decades. The existing high-spatial-resolution NO₂ estimation models are mainly divided into statistical models and physical models. Physical models improve the spatial resolution of target pollutants through high-precision models of the physical area, such as the Community Multiscale Air Quality (CMAQ). However, these are limited by the amount of computation and precursor data [18,19]. Statistical models are exposure assessment methods that simulate the statistical relationship between pollutants and impact factors. Earlier statistical models, such as geostatistical models [20,21] and land use regression models [22,23], improved spatial accuracy at the expense of reduced temporal resolution. For the development of models, machine-learning- and deep-learning-based methods have been applied in statistical models for NO₂ estimation, which are able to improve the resolution in both time and space [24,25]. Recent studies have shown that these methods and their variants (e.g., ensemble models) capture the nonlinear variation characteristics of pollutants well [26] and are significantly better than traditional statistical models in terms of modeling accuracy, as they can achieve a certain degree of accuracy in capturing the spatiotemporal heterogeneity of the target gas. These models have become more and more popular in modeling studies of various atmospheric pollutants, including NO₂, at a high temporal and spatial resolution. For example, You et al. [27], Dou et al. [28], and Liu [29] realized a fine-scale evaluation of NO₂ in China based on machine learning algorithms. However, research on high-precision modeling of NO₂ at medium and small regional scales in China has not been fully discussed, and there is still room for improvements in the accuracy of the model. How to make full use of multi-source data, including satellite, station, and physical model outputs; strengthen the ability of explanatory variables to characterize changes in NO₂ concentrations; and further improve the models’ estimation accuracy require further consideration.

In order to improve the model performance and obtain high-precision, daily average NO₂ near-surface concentration distribution data with a high-spatial-resolution, we designed a meteorological hysteretic effects term and a spatiotemporal term. At the same time, by combining multi-source explanatory variables such as the tropospheric NO₂ column concentration observed by Sentinel-5p, atmospheric conditions, and human activities, an ensemble “Classic Machine Learning + Deep Neural Network” model was constructed. On this basis, the NO₂ concentration of a coastal region of southeastern China was generated with a high spatial resolution, and the accuracy and error of three classic machine learning algorithms and the ensemble model were compared and analyzed. Finally, based on temporal, spatial, and completely random-set partitioning strategies, the inferring power of the ensemble model in time and space was comprehensively evaluated.

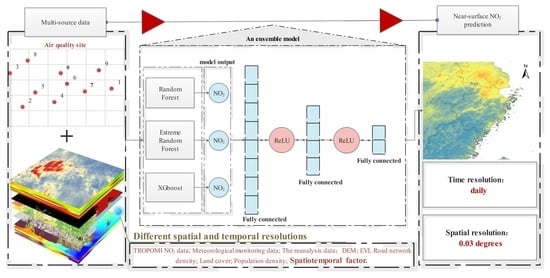
2. Materials and Methods

2.1. Data and Pretreatment

2.1.1. Ground-Level NO₂ Observations

This study obtained the hourly NO₂ observation data from May 2018 to December 2020 from the China Environmental Monitoring Center (CEMC). All sites are based on the GB3095-2012 standard, and the near-ground NO₂ concentration is measured by the chemiluminescence method [30]. The study area is the coastal area (116–124°E, 25–33°N) with the main cities of the Yangtze River Delta as the core. There are 258 monitoring stations within the range, most of which are located in urban areas, and a few are located in suburban areas (Figure 1). In order to build a high-precision NO₂ exposure assessment model, we averaged the hourly NO₂ observation records to the day, eliminated daily observation data of less than 18 h, and finally obtained 225,197 valid observation records.

2.1.2. TROPOMI NO₂ Data

The TROPOspheric Monitoring Instrument (TROPOMI) can monitor the data of air pollutants such as NO₂, O₃, SO₂, and HCHO. The time when the satellite passes through the study area (Beijing time) is about 13:00–14:00, and the spatial resolution is 7 km × 3.5 km (30 April 2018 to 6 August 2019) and 5.5 km × 3.5 km (7 August 2019 to now), making it the best atmospheric observation spectrometer at present. Under the processing framework of the retrieval–assimilation–modeling system, the TROPOMI NO₂ Level 2 product combines the DOAS algorithm and the TM5 chemical transport model, and converts the measured Level-1B radiance and irradiance spectra into NO₂ vertical column concentrations, in units of molec/cm² [24]. For this article, the TROPOMI NO₂ Level 2 product from NASA (https://disc.gsfc.nasa.gov/, accessed on 7 July 2021) was obtained and the tropospheric NO₂ column concentration was taken from it as a modeling factor. To weaken cloud cover, snow landscapes, and other dubious retrievals, we kept the pixels in the file that had a quality assurance value (QA) greater than 0.75. Data missing more than 30% were also removed, as too many missings would increase uncertainty.

2.1.3. Meteorological Data

To include the influence of near-surface meteorological conditions on the potential chemical and physical processes of NO₂ in the atmosphere, we obtained the daily average air pressure, air temperature, relative humidity, land surface temperature, 24 h cumulative rainfall, and wind speed from China’s National Meteorological Data Center (http://data.cma.cn/, accessed on 23 July 2021).

2.1.4. The Reanalysis Data

We also obtained ERA5 reanalysis data for 2018–2020 from the European Centre Medium-Range Weather Forecasts (ECMWF), which combined past observations with models to simulate hour-by-hour atmospheric, ocean wave, and land surface quantities systematically. In order to assist in the establishment of an exposure assessment model between satellite-observed NO₂ and ground-level NO₂, we selected 22 indicators from the ERA5 data, including radiation, heat, atmospheric conditions, and wind fields, which may affect changes in NO₂ concentration (Table S1). According to the physical meaning of the different indicators, the daily data of each indicator are generated by summing or averaging, with a resolution of 0.25° × 0.25°.

2.1.5. Geographical Variable Data

Human activities and the distribution of emission sources are also important factors affecting regional NO₂ changes. Transportation activities and industrial production activities are the main reasons for the uneven distribution of NO₂ in space, and geographical features are closely related to these activities and also affect the spatial distribution of near-ground NO₂ concentrations to a certain extent [26,31,32]. Therefore, we selected five parameters of the geographic environment, including elevation data (DEM), vegetation index data (NDVI/EVI), road network data (L), gridded population data (POP), and land cover data (LAND), to characterize these effects.

Among these, the 300 m land cover data come from the Climate Change Initiative (CCI) project of the European Space Agency (ESA, http://maps.elie.ucl.ac.be/CCI/viewer/index.php, accessed on 4 March 2021). This study reclassified the 22 types of land in the original data from 2018 to 2020 into six types: forest land, grassland, agricultural land, urban land, water bodies, and other land, and calculated the area within a grid range of 0.03° and the proportion of each. The road network data were downloaded from OpenStreetMap (OSM, http://download.geofabrik.de/asia/china.html#, accessed on 19 March 2021), and we calculated the road network length and road network density within a 0.03° grid range year by year.

In addition, we also processed the MODIS vegetation index data (MOD13A2), the 90 m DEM data of SRTM, and the grid population data of Worldpop. Detailed data descriptions and sources can be seen in the modeling variable pre-selection table (Table S1). All variables may affect the NO₂ concentration but may not be necessary for high-precision NO₂ exposure assessment modeling.

2.1.6. Data Integration

In order to unify the explanatory variables with different scales from multiple sources, we constructed a 0.03° × 0.03° (about 3 km) grid mesh, and integrated all data on the basis of this standard. For data with a spatial resolution lower than 0.03°, the inverse distance weighting method (IDW) was used to interpolate them into the mesh; for the data with a spatial resolution higher than 0.03°, we used resampling technology to upscale it into the standard mesh. By matching the geographic locations of the NO₂ ground observation sites, all the data finally formed a dataset for modeling and validation.

2.1.7. Feature Selection

In both traditional statistical models and machine learning models, too many explanatory variables are an important factor causing model instability [33,34]. Although machine learning is better at learning the nonlinear relationship between variables and weakens the effect of collinearity between similar variables to a certain extent, it is still necessary to reduce similar and unnecessary predictors. By considering the Pearson correlation coefficient between the variables (Figure S1a,b), we initially screened the explanatory variables with low correlations with near-ground NO₂ concentrations and deleted explanatory variables with similar physical meanings and a high correlation between each other (|r| > 0.95) on the premise of ensuring the completeness of the predictor system.

Finally, the NO₂ column concentration (NO2_5p), air pressure (AP), land surface temperature (LST), relative humidity (HD), rainfall (RF), boundary layer height (BLH), surface latent heat flux (SLHF), lower surface solar radiation (SSRD), top net solar radiation (TSR), 10 m wind speed (U10/V10), total column ozone (TCO3), road network density (ROAD_E), elevation (DEM), population (POP), vegetation index (EVI), the proportion of grassland (GLA_P), the proportion of forest land (tree_p), the proportion of agricultural land (AGR_P), and the proportion of urban land (CITY_P) were used as the basic predictors. By combining these with the meteorological hysteretic effects term and the spatiotemporal term proposed in Section 2.2, we improved the underlying predictors and formed the final set of predictors for the model.

2.2. Methodology

2.2.1. Hysteretic Effects Term

Meteorological conditions often have a continuous impact on atmospheric pollutants. Over time, a change in the mechanism of influence or the accumulated effects of the influence may increase the magnitude of the influence, usually called the hysteretic effects. Examples include the chemical accumulation process of temperature-induced changes in atmospheric pollutant concentrations [35] and the interaction mechanism between the short-term wet deposition of trace gases by rainfall and the hydrolysis of pollutants such as formaldehyde polymers in a humid atmospheric environment [36]. These physicochemical processes create a certain hysteresis effect.

Therefore, in this study, we bundled the meteorological predictors observed at the site with the records of the previous 2 days and used them as the meteorological hysteretic effects to construct a NO₂ exposure assessment model, which is conducive to solving the problem that the single-day variables cannot fully characterize the characteristics of the change in NO₂ concentration due to the hysteretic impact. The details are shown in Equation (1):

$$V_{ti}=\left(v_{ti},v_{ti-1},v_{ti-2}\right)$$

(1)

where $V_{ti}$ is the meteorological hysteretic effects term of day $ti$, and $v_{ti},v_{ti-1}$ and $v_{ti-2}$ are the meteorological factors of day $ti$ and the previous two days, respectively.

2.2.2. Spatiotemporal Term

The spatiotemporal distribution of NO₂ concentrations is highly spatially heterogeneous, as is the case for other air pollutants, such as formaldehyde and PM2.5. Spatially, the NO₂ concentration varies with location and exhibits different statistical relationships with covariates. Incorporating spatial information into the model can effectively capture the spatial variation in the target gas pollutants. Methods such as geographic weighted regression [37] and spatiotemporal geographic weighted regression [38,39] use spatial coordinates to capture spatial heterogeneity. However, spatial coordinates are absolute coordinates of the world as a whole. In applying machine learning methods directly to a small- and medium-scale regions, it may not be able to explain spatial nonstationarity and spatial autocorrelation well. Therefore, for this study, we calculated the Vincenty relative ellipsoid distance from the sample location to the lower left corner (116°E, 25°N) and the upper right corner (124°E, 33°N) of the study area in the WGS84 coordinate system [40] as the spatiotemporal terms, which are reflected in Equation (2). Studies have shown that machine learning models built with field distance as a spatial factor have a good ability to capture spatially heterogeneous features [41,42]. In terms of time, the NO₂ concentration showed a strong cyclical trend, basically showing the characteristics of being high in spring and winter, and low in summer and autumn (Figure S2). Therefore, we constructed a time factor of months and introduced this rule into the model to improve the performance of the NO₂ exposure assessment model. See Equation (3) for details.

$$S_{\left(x,y\right)=}(Vincenty\left(p_{\left(x,y\right) }, L_{\left(x,y\right)}\right),Vincenty\left(p_{\left(x,y\right) }, R_{\left(x,y\right)}\right))$$

(2)

$$T_i=\cos \left(\frac{t_i\pi }{11}+\frac{9\pi }{22}+1\right)$$

(3)

where $S_{\left(x,y\right) }$ is the spatial term at the grid’s center point, $p_{\left(x,y\right) }$ is the geographic coordinates of the center of a grid point, $L_{\left(x,y\right)}$ is the geographic coordinates of the lower left corner of the study area, $R_{\left(x,y\right)}$ is the geographic coordinates of the upper right corner of the study area, $Vincenty()$ represents an iterative function of the ellipsoid distance, $T_i$ represents the temporal heterogeneity factor for month $i$, and $t_i$ represents month i.

2.2.3. Ensemble Model

Our study adopted a “Classic Machine Learning + Deep Neural Network“ ensemble model to evaluate the near-ground NO₂ concentrations. First, we constructed a statistical relationship between the explanatory variables and the NO₂ concentrations based on three machine learning models: Random Forest (RF), Extreme Random Forest (EXT), and XGboost (XGB). These three models are all based on regression trees, which can learn the nonlinear relationships among variables very well. However, due to the differences in their principles, the deviation and variance in the predicted results will also be quite different. Both RF and EXT are ensemble learning models based on the bagging strategy: they randomly select prediction samples to increase the generalization of the model [43]. On the other hand, XGB is a boosting ensemble learning method and its base learners are related to each other, which can maximize the model’s accuracy, although this will reduce the generalizability to a certain extent [44]. Considering the prediction performance and generalization ability of the model, the key hyperparameters of the three algorithms were optimized with grid search. For RF and EXT, the number of trees (n_estimators) and the tree depth (max_depth) were set to 150 and 25, respectively; for XGB, the number of trees (n_estimators) and the tree depth (max_depth) were set to 500 and 13, respectively. In order to prevent the model overfitting, we also set the gamma coefficient to 1.

Finally, in order to integrate and optimize the prediction results of these machine learning methods, we inputted their prediction results into a deep learning network composed of 3 fully connected layers and 2 ReLU layers, and realized the near-ground NO₂ concentration exposure assessment. All models were implemented by the pytorch and scikit-learn packages, and the detailed structure is shown in Figure 2.

2.2.4. Model Validation

In the 10-fold cross-validation technique (10-fold CV), the dataset is randomly divided into 10 data subsets and 1 data subset is selected in turn for model validation, with the remaining 9 used for model establishment. The final evaluation of the 10-fold CV results is the average of the 10 time validations, which can more realistically evaluate the model’s performance. To evaluate the fitting performance and generalization performance of the ensemble model, we used the 10-fold cross-validation technique to calculate the R² (goodness of fit), MAE (mean absolute error), and RMSE (root-mean-square error). The details are shown in Equations (4)–(7).

$$R^2=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\overline{y}\right)}^2}$$

(4)

$$\mathrm{MAE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|\left(y_i-\widehat{y_i}\right)\right|$$

(5)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(6)

$$\mathrm{CV}\left(p\right)=\frac{1}{10}{\displaystyle \sum }_{j=1}^{10}C{V}_j\left(p\right),p\in \left(R^2,\mathrm{MAE},\mathrm{RMSE}\right)$$

(7)

where $y_i \mathrm{and} \widehat{y_i}$ are the true value and the model’s predicted value for the ith sample, respectively, $\overline{y}$ is the average value of whole sample, and $C{V}_j\left(p\right)$ is the jth cross-validation result of the $p$ statistic.

3. Results

3.1. Model Development and Validation

3.1.1. Analysis of the Impact of Enhanced Variables on the Model

In order to explore the influence of the spatiotemporal term and the hysteretic effects term on the model, we designed four variable combination schemes and used the CV verification method to analyze the performance of different independent variable schemes in the RF, EXT, and XGB models, which are shown in

Table 1. Evaluation of the performance of three machine learning models with different variable combinations.

Scheme Name	Predictors (x)	Predictand (y)	RF (R2)	EXT (R2)	XGB (R2)
Plan 1	Basic predictors	NO2 concentration monitored by the station	0.77	0.78	0.82
Plan 2	Basic predictors + meteorological lag factors		0.80	0.81	0.86
Plan 3	Basic predictors + spatiotemporal heterogeneity factor		0.81	0.82	0.88
Plan 4	Basic predictors + spatiotemporal heterogeneity factor + meteorological lag factors		0.82	0.84	0.88

. The results show that the CV R² of the three machine learning models were significantly improved when the two model enhancement factors were added separately (Plan2 and Plan3). In particular, when the spatiotemporal term was added, the R² of the RF, EXT, and XGB models reached 0.81, 0.82, and 0.88, meaning that the performance of the three models was improved by 4%, 4%, and 6%, respectively. When the meteorological hysteretic effects term and the spatiotemporal term were added at the same time, the performance of each machine learning model still increased slightly with an increase in the explanatory variables, and the R² range was 0.82–0.88. Under the same scheme, the performances of the three models were ranked in descending order as XGB, EXT, and RF.

Figure S3a–d show the relative importance of the independent variables for the four schemes. When no model enhancement variables were introduced (Figure S3a), TROPOMI NO₂ was the most important factor (RF: 35%, EXT: 25%, XGB: 25%), followed by air pressure (AP) and boundary layer height (BLH), which were two or three times less important than TROPOMI NO₂ concentrations. When the meteorological hysteretic effect term was introduced into the model (Figure S3b,d), its relative importance in all models was 2–14%. The relative importance of air pressure and land surface temperature two days ago was higher than that of the current day, which indicates that the meteorological hysteretic effects term is better than the simple meteorological factor. When the spatiotemporal term was introduced into the model (Figure S3c,d), the temporal heterogeneity factor became one of the most important factors (7–20%), second only to TROPOMI NO₂. Overall, although there were some differences in the relative importance of the variables in different models, TROPOMI NO₂, boundary layer height, the meteorological hysteretic effects term, and the spatiotemporal term had important effects in all models.

3.1.2. Model Evaluation

We finally constructed a near-ground NO₂ concentration exposure assessment model based on the variable system of Plan 4. Figure 3 shows the CV results of the six models. The RMSE values of the multiple linear, SVM, RF, EXT, XGB, and ensemble models were 11.88, 7.56, 7.22, 6.76, 5.71, and 5.62 µg/m³, and the corresponding MAE values were 9.20, 5.43, 5.26, 4.91, 4.11, and 4.04 µg/m³, respectively. The 10-fold cross-validation R² of the ensemble model was 0.89, which was significantly better than the multiple linear model (CV R²: 0.51) and the SVM model (CV R²: 0.80). The RF, EXT, and ensemble models overestimated the near-ground NO₂ concentration, and the SVM, multiple linear, and XGB models underestimated the near-surface NO₂ concentration. Overall, the ensemble model corrected the predictions of the different machine learning models through the deep learning network and outperformed the individual machine learning models.

Figure 4 shows the local R² distribution information. Spatially, the local R² of the annual statistical scale and the full-time statistical scale have similar regional distribution characteristics. The local R² is high in the areas with a large population and densely distributed monitoring stations, while the local R² in the areas with a small population and sparsely distributed stations is low. In the case of sparse sites, it is difficult for the model to fully explore the statistical relationship between the NO₂ concentration and the explanatory variables. Across the entire study period, the range of local R² is 0.13–0.94, and 92% of the sites have a local R² of >0.7. This result is consistent with the performance results of local RMSE (Figure S4) and MAE (Figure S5), which means that the model has a relatively stable fitting performance.

We also captured the model prediction results for different site locations and plotted the trend of changes in the daily average NO₂ concentration from May 2018 to December 2020 (Figure S6). In the time series, the predicted results are basically consistent with the actual observed results (Figure S2), and there is no obvious deviation, indicating that the model shows high stability for the time series.

Based on the ensemble model framework, three validation sets were designed in this study, namely all samples in the last 3 months of 2020, 30% randomly selected samples from all sites, and 30% randomly selected samples. These validation sets did not participate in model training, and their validation results represent the temporal, spatial, and comprehensive predictive capabilities of the model, respectively, as detailed in Figure 5. The ensemble model had the strongest comprehensive prediction ability (Figure 5a), with an R² of 0.86 between the predicted value and the true value, which means that the model was able to predict 86% of the near-ground NO₂ concentrations. The performance of the model for temporal (Figure 5b) and spatial (Figure 5c) variations was slightly weaker than the comprehensive prediction ability, but it still showed a relatively good spatiotemporal prediction ability and applicability. The temporal and spatial R² values of the model reached 0.71 and 0.81, respectively, and the corresponding RMSE and MAE were 10.24 µg/m³, 7.79 µg/m³, 7.39 µg/m³, and 5.50 µg/m³. Compared with the XGBoost model (Figure 5d–f), the comprehensive prediction R², temporal R², and spatial R² of the ensemble model were improved by 1%, 2%, and 1%, respectively, and the corresponding RMSE was reduced by 0.23 µg/m³, 0.19 µg/m³, and 0.23 µg/m³.

3.2. Analysis of the Fine-Scale Spatiotemporal Variation in NO₂

To analyze the ability of the ensemble model of capturing the spatially heterogeneous features, we interpolated the satellite-observed tropospheric NO₂ vertical column concentrations to a spatial resolution of 0.03° and compared it with the ensemble model’s output of the spatial distribution of the near-surface NO₂ concentration (Figures S7 and S8). The spatial distribution law of the model output and the interpolation results of satellite observations were basically consistent, which proves the correctness of the model output results from a new perspective. In detail, the interpolation results of the satellite observations were relatively smooth. Although the spatial resolution after interpolation was consistent with the model output, the degree of step difference between adjacent pixels was not obvious. Especially in Ningbo, Fuzhou, Wenzhou Province, and other areas with a small area of high NO₂ concentrations, as well as the median NO₂ concentration between mountainous areas, satellite observations cannot easily capture the spatial heterogeneity. The smoothing effect is outstanding. In contrast, the NO₂ concentration results of the model showed obvious step differences, whether in urban areas with higher NO₂ concentrations, such as Shanghai, or in mountainous areas with lower NO₂ concentrations, such as southern Zhejiang Province; these features were directly smoothed in the satellite observations. Therefore, the results of the ensemble model reflect the spatial heterogeneity of the near-ground NO₂ concentration.

Figure 6 shows the seasonal distribution of NO₂ concentrations over the studied area. In Figure S9, the temporal variation in the characteristics of the NO₂ concentration across different seasons is obvious, while the spatial distribution characteristics are similar. The average concentration of NO₂ near the ground, from largest to smallest, is: winter (22.51 µg/m³), autumn (18.89 µg/m³), spring (17.76 µg/m³), and summer (11.91 µg/m³), which is consistent with Pan et al.’s study on the Chinese region [45]. Spatially, the near-surface NO₂ concentrations are high in the north and low in the south, and have a decreasing trend from the coast to the inland areas. The high-value areas are mainly distributed in the north of Zhejiang Province, Anhui Province, Jiangsu Province, and Shanghai. It is worth noting that the average NO₂ concentration level across the four seasons is not high, which is because there are a large number of suburban and rural areas in our research region, and the NO₂ concentration in these areas is at a low level. In fact, NO₂ concentrations in urban areas are still at relatively high levels. Coal-fired heating and natural seasonal conditions of unfavorable diffusion are important factors leading to this phenomenon [45].

3.3. Analysis of Near-Surface NO₂ Concentrations in Major Cities

As a typical area with a high near-surface NO₂ concentration in the study area, the Yangtze River Delta Plain has a large population base and complex human activities, and is also one of the most important economic areas in China. In accordance with the national ambient air quality standard GB 3095-2012, we calculated the NO₂ air quality of major cities in the Yangtze River Delta Plain with a daily average NO₂ concentration of >80 µg/m³. If any grid in the city did not meet the national regulations, it was considered to have exceeded the standard. The details are shown in Figure 7.

Between 28 April 2018 and 31 December 2020, Hefei was the city most seriously polluted by NO₂, with 95 days of air NO₂ exceeding the standard. In addition, Suzhou, Wuxi, Hangzhou, Shanghai, and Nanjing had more than 60 days exceeding the standard, and the corresponding maximum NO₂ concentration was also relatively high, indicating that the air quality of these cities was relatively poor. It is worth noting that when NO₂ air pollution occurs, the near-surface NO₂ concentration in Zhenjiang and Changzhou can reach very high levels (greater than 135 µg/m³), although the number of days when this occurs is not particularly great, indicating that the two cities need to be alert to the occurrence of sudden NO₂ air pollution incidents. Among the many cities in the Yangtze River Delta Plain, only Ningbo City did not have the phenomenon of excessive NO₂ concentrations in the air.

All in all, there is still much room for improvement in the air quality of major cities in the Yangtze River Delta Plain. Most of these places have relatively developed economies, a large population, and low terrain. Anthropogenic emissions may be the main reason for the formation of these high-value areas. In recent years, a series of effective measures for environmental governance have reduced the average concentration of NO₂ in the entire region, but the effect has not been significant. It is still necessary to implement targeted prevention and control measures for cities with more serious pollution.

4. Discussion

Focusing on the scientific issue of assessing near-surface NO₂ concentrations, we designed a model enhancement factor considering the influencing mechanism of multi-source explanatory variables on the near-surface NO₂ concentration and the spatial heterogeneity in NO₂ concentration itself. With an ensemble model composed of a deep neural network and machine learning methods, a high-precision ground NO₂ concentration exposure assessment model was developed.

Compared with previous studies, our model exhibits certain advantages. The ensemble model in this study has a better ability to evaluate the NO₂ concentrations, and its R² in the 10-fold cross-validation results is 0.89, which is better than the performance of most models, such as the annual-scale stepwise regression model (CV R²: 0.78) constructed by Xu et al. [46], the seasonal-scale land use regression model (CV R²: 0.70) constructed by Zhang et al. [23], the annual-scale land use regression model (CV R²: 0.67) constructed by Andrew Larkin et al. [47], the monthly scale random forest model in China constructed by You et al. [27] (CV R²: 0.85), the daily-scale random forest and extreme random forest models constructed by Qin et al. [43] (CV R²: 0.70 and 0.72), the XGBoost daily-scale model (CV R²: 0.83) constructed by Liu [29], and the random forest spatiotemporal kriging (RF-STK) model (CV R²: 0.62) constructed by Zhan et al. [48]. At the same time, the model in this article outputs daily-scale results with a spatial resolution of 0.03° (about 3 km), which can better meet the needs of research such as popular medicine and environmental protection. As far as we know, there are not many daily-scale NO₂ exposure assessment models with a spatial resolution better than 0.03° in China. Only the random forest model constructed by Pan et al. [45] and the ensemble model (Machine Learning + GAM) constructed by Huang et al. [26] and Di et al. [49] reached a spatial resolution of 1 km, but the performance of these models (CV R²: 0.67–0.82) was slightly lower than that of the model in this study. The prediction performance of our model was also good: The spatial prediction R² and the temporal prediction R² were 0.81 and 0.71 respectively, which is slightly weaker than the model with the best temporal prediction ability of the abovementioned studies (Di et al. [49], spatial prediction R²: 0.84, temporal prediction R²: 0.73).

Multi-source predictors and their effective utilization are the keys to improving model performance. As in most studies [29,43], the TROPOMI tropospheric NO₂ column concentration was the most important predictor in this model because it has a consistent trend with near-surface NO₂ concentrations (Figure S2). Compared with OMI-NO₂ (the NO₂ observed by the Ozone Monitoring Instrument), the NO₂ exposure assessment models constructed with TROPOMI-NO₂ had better accuracy, which was demonstrated in the study of Liu et al. [29]. We also designed a meteorological hysteretic effects term and a spatiotemporal term. When used alone, they significantly improved the model’s performance (accuracy improvement: 4–6%) and played an important role in the explanatory variable system (Figure S1), which is consistent with previous studies in China [42,45]. However, when the meteorological hysteretic effects term and the spatiotemporal term were used at the same time, the performance of the model was not improved significantly, which may be because the accuracy of the model itself had reached a high level, and there were systematic errors in the explanatory variables themselves. In addition, the atmospheric condition variables and other geographic factors in the hourly climate analysis data also play a role to varying degrees. Although the relative importance of these variables is not high enough to significantly improve the model’s performance, they increase the spatial heterogeneity of the model. For example, DEM, city proportion, road network density, and population are highly consistent with the predicted spatial distribution of NO₂ concentrations.

The systematic and comprehensive multi-source explanatory variable system also increases the interpretability and applicability of the model. It contains large-scale data sources at fine spatial scales, giving the model the potential to produce higher-spatial-resolution NO₂ products (better than 1 km) and apply them to larger areas. In future studies, the model is also expected to be applicable to other high-level exposure assessment models for atmospheric pollutants that have both site and satellite observations.

However, there are still some limitations of our study. First, although the model proposed in this article has a good temporal prediction ability (R²: 0.71), this is only a short-term prediction, and the stationarity of the long-term prediction of the model needs to be further explored and proved. Second, the performance of the model and the potential for application of the model at higher time scales are limited due to the coarse resolution of the geographic data and atmospheric condition data. On the one hand, the spatial resolution of the analytical data (ERA5) used by the model is 0.25°, and a single pixel record is not enough to perfectly describe the atmospheric conditions at the site location, which increases the uncertainty of the model. On the other hand, at a fine spatiotemporal scale (hourly scales, 100 m level resolution), the information provided by TROPOMI NO₂ and the meteorological data will not be sufficient to reflect the short-term changes in NO₂ concentration caused by transportation, daily life, and industrial emissions. Variations in human activity at a fine enough spatial and temporal resolution are needed to provide relevant information. Currently, such data are difficult to obtain and are not publicly available, which means that it is difficult for the model to improve in terms of temporal resolution. Third, the meteorological hysteretic effects term proposed in this article only considers the meteorological factors over 3 days. This assumption is too simple and may limit the further improvement of the model’s performance. The time span involved in the hysteretic effects may be more than 3 days and is not fixed. In future research, developing a dynamic hysteretic effects term will help to improve the model.

5. Conclusions

In this article, we combined the XGB, RF, EXT, and deep neural network models, and used multi-source data to develop a high-precision ensemble model, which was successfully applied to the central and southern coastal areas of China, generating a near-ground daily average NO₂ concentration distribution of 0.03°. Compared with other studies, the ensemble model had better estimation accuracy, with 10-fold CV R², RMSE, and MAE values of 0.89, 5.62 µg/m³, and 4.04 µg/m³, respectively.

The model has good generalization in space and time, and the short-term daily average NO₂ prediction effects were stable and reliable, which shows that the model can be applied to larger areas and longer time series. Compared with satellite observations and site observations, the ensemble model output provides rich and accurate details of the spatiotemporal heterogeneity in NO₂, which will be helpful for air pollutant traceability and urban health research in the future.