Dominant Factors in the Temporal and Spatial Distribution of Precipitation Change in the Beijing–Tianjin–Hebei Urban Agglomeration
Abstract
:1. Introduction
2. Materials and Methods
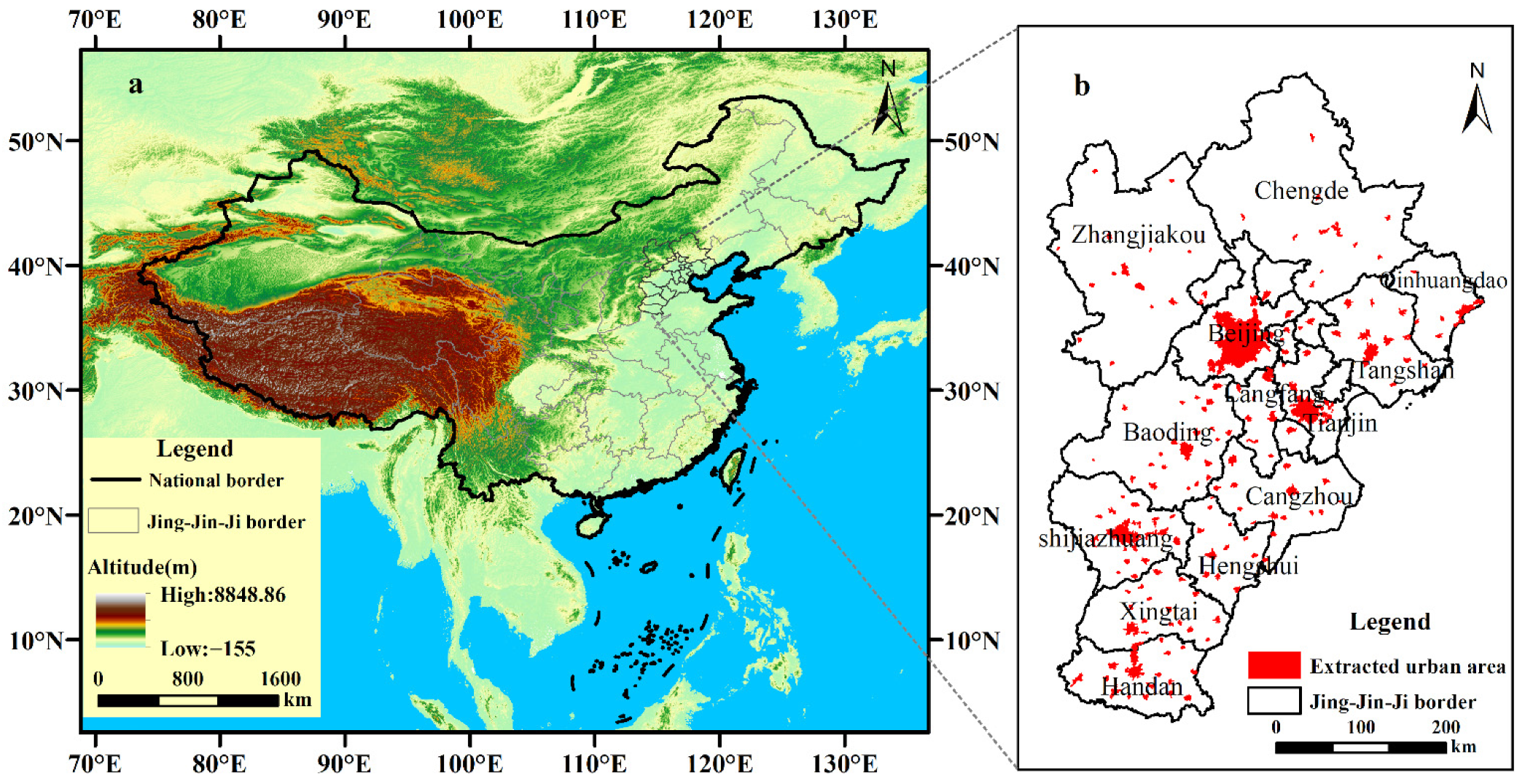
2.1. Study Area
2.2. Data Sources
2.2.1. Selection of Variables
2.2.2. Data Sources for Different Variables
2.3. Methodology
2.3.1. Partial Least Squares Method and Stepwise Regression Analysis
2.3.2. Optimal Subset Regression
2.3.3. Hierarchical Regression Analysis
3. Results and Analysis
3.1. Temporal and Spatial Patterns of Precipitation
3.1.1. Spatial Distribution Characteristics of Precipitation Changes in Different Seasons in the BTHUA
3.1.2. Spatial Distribution of Urban Precipitation Changes in Inner Urban Areas of Different Cities in the BTHUA
3.2. Significant Influencing Factors on Precipitation
3.2.1. Significant Influencing Factors on Precipitation in the Whole Factor Layers
3.2.2. Significant Influencing Factors on Precipitation in Each Factor Layer
3.3. Optimal Regression Model
3.4. Relative Importance of Precipitation Influencing Factors
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Pang, X.; Xia, J.; Shao, Q.; Yu, E.; Zhao, T.; She, D.; Sun, J.; Yu, J.; Pan, X.; et al. Regional patterns of extreme precipitation and urban signatures in metropolitan areas. J. Geophys. Res.-Atmos. 2019, 124, 641–663. [Google Scholar] [CrossRef]
- Carvalho, D.; Martins, H.; Marta-Almeida, M.; Rocha, A.; Borrego, C. Urban resilience to future urban heatwaves under a climate change scenario: A case study for Porto urban area (Portugal). Urban Clim. 2017, 19, 1–27. [Google Scholar] [CrossRef]
- Macintyre, H.L.; Heaviside, C.; Taylor, J.; Picetti, R.; Symonds, P.; Cai, X.M.; Vardoulakis, S. Assessing urban population vulnerability and environmental risks across an urban area during heatwaves—Implications for health protection. Sci. Total Environ. 2018, 610, 678–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mendez-Lazaro, P.A.; Perez-Cardona, C.M.; Rodriguez, E.; Martinez, O.; Taboas, M.; Bocanegra, A.; Mendez-Tejeda, R. Climate change, heat, and mortality in the tropical urban area of San Juan, Puerto Rico. Int. J. Biometeorol. 2018, 62, 699–707. [Google Scholar] [CrossRef] [PubMed]
- Oleson, K.W.; Anderson, G.B.; Jones, B.; McGinnis, S.A.; Sanderson, B. Avoided climate impacts of urban and rural heat and cold waves over the US using large climate model ensembles for RCP8.5 and RCP4.5. Clim. Chang. 2018, 146, 377–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polrolniczak, M.; Tomczyk, A.M.; Kolendowicz, L. Thermal conditions in the city of Poznan (Poland) during selected heat waves. Atmosphere 2018, 9, 15. [Google Scholar] [CrossRef] [Green Version]
- Seino, N.; Aoyagi, T.; Tsuguti, H. Numerical simulation of urban impact on precipitation in Tokyo: How does urban temperature rise affect precipitation? Urban Clim. 2018, 23, 8–35. [Google Scholar] [CrossRef]
- Zhao, L.; Oppenheimer, M.; Zhu, Q.; Baldwin, J.W.; Ebi, K.L.; Bou-Zeid, E.; Guan, K.Y.; Liu, X. Interactions between urban heat islands and heat waves. Environ. Res. Lett. 2018, 13, 11. [Google Scholar] [CrossRef]
- Suzuki, K.; Zupanski, M.; Zupanski, D. A case study involving single observation experiments performed over snowy Siberia using a coupled atmosphere-land modelling system. Atmos. Sci. Lett. 2017, 18, 106–111. [Google Scholar] [CrossRef]
- Knist, S.; Goergen, K.; Buonomo, E.; Christensen, O.B.; Colette, A.; Cardoso, R.M.; Fealy, R.; Fernandez, J.; Garcia-Diez, M.; Jacob, D.; et al. Land-atmosphere coupling in EURO-CORDEX evaluation experiments. J. Geophys. Res.-Atmos. 2017, 122, 79–103. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Luo, Y.; Zhang, D.-L.; Wu, M. Urbanization enhanced summertime extreme hourly precipitation over the Yangtze river delta. J. Clim. 2020, 33, 5809–5826. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Fowler, H.J.; Argueso, D.; Blenkinsop, S.; Evans, J.P.; Lenderink, G.; Yan, X.; Guerreiro, S.B.; Lewis, E.; Li, X.-F. Strong intensification of hourly rainfall extremes by urbanization. Geophys. Res. Lett. 2020, 47, e2020GL088758. [Google Scholar] [CrossRef]
- Lin, L.; Gao, T.; Luo, M.; Ge, E.; Yang, Y.; Liu, Z.; Zhao, Y.; Ning, G. Contribution of urbanization to the changes in extreme climate events in urban agglomerations across China. Sci. Total Environ. 2020, 744, 140264. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Smith, J.; Niyogi, D. Urban impacts on extreme monsoon rainfall and flooding in complex terrain. Geophys. Res. Lett. 2019, 46, 5918–5927. [Google Scholar] [CrossRef]
- Zhao, N.; Jiao, Y.; Ma, T.; Zhao, M.; Fan, Z.; Yin, X.; Liu, Y.; Yue, T. Estimating the effect of urbanization on extreme climate events in the Beijing-Tianjin-Hebei region, China. Sci. Total Environ. 2019, 688, 1005–1015. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.B.; Du, Y.D.; Mao, C.Y.; Zhang, L. Urbanization effect on precipitation over the Pearl River Delta based on CMORPH data. Adv. Clim. Chang. Res. 2015, 6, 16–22. [Google Scholar] [CrossRef]
- Han, J.Y.; Baik, J.J.; Lee, H. Urban impacts on precipitation. Asia-Pac. J. Atmos. Sci. 2014, 50, 17–30. [Google Scholar] [CrossRef]
- Hanson, S.; Nicholls, R.; Ranger, N.; Hallegatte, S.; Corfee-Morlot, J.; Herweijer, C.; Chateau, J. A global ranking of port cities with high exposure to climate extremes. Clim. Chang. 2011, 104, 89–111. [Google Scholar] [CrossRef] [Green Version]
- Kebede, A.S.; Nicholls, R.J. Exposure and vulnerability to climate extremes: Population and asset exposure to coastal flooding in Dar es Salaam, Tanzania. Reg. Environ. Chang. 2012, 12, 81–94. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Ambrizzi, T.; Young, A.; Barreto, N.J.C.; Ramos, A.M. Trends in extreme rainfall and hydrogeometeorological disasters in the Metropolitan Area of Sao Paulo: A review. Ann. N. Y. Acad. Sci. 2020, 1472, 5–20. [Google Scholar] [CrossRef]
- Sterzel, T.; Ludeke, M.K.B.; Walther, C.; Kok, M.T.; Sietz, D.; Lucas, P.L. Typology of coastal urban vulnerability under rapid urbanization. PLoS ONE 2020, 15, e0220936. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, X.W.; Wang, D.S.; Ziegler, A.D.; Liu, X.P.; Zeng, H.; Xu, Z.B.; Zeng, Z.Z. Influence of urbanization on hourly extreme precipitation over China. Environ. Res. Lett. 2022, 17, 12. [Google Scholar] [CrossRef]
- Seino, N.; Oda, R.; Sugawara, H.; Aoyagi, T. Observations and simulations of the mesoscale environment in TOMACS urban heavy rain events. J. Meteorol. Soc. Jpn. 2018, 96A, 221–245. [Google Scholar] [CrossRef] [Green Version]
- Hua, P.; Yang, W.Y.; Qi, X.C.; Jiang, S.S.; Xie, J.Q.; Gu, X.Y.; Li, H.H.; Zhang, J.; Krebs, P. Evaluating the effect of urban flooding reduction strategies in response to design rainfall and low impact development. J. Clean. Prod. 2020, 242, 118515. [Google Scholar] [CrossRef]
- Zhou, Q.Q. A review of sustainable urban drainage systems considering the climate change and urbanization impacts. Water 2014, 6, 976–992. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhao, X.; Wu, D.H.; Tang, R.Y.; Du, X.Z.; Wang, H.Y.; Zhao, J.C.; Xu, P.P.; Peng, Y.F. Impact of urbanization and climate on vegetation coverage in the Beijing-Tianjin-Hebei region of China. Remote Sens. 2019, 11, 2452. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.Q.; Leng, G.Y.; Su, J.H.; Ren, Y. Comparison of urbanization and climate change impacts on urban flood volumes: Importance of urban planning and drainage adaptation. Sci. Total Environ. 2019, 658, 24–33. [Google Scholar] [CrossRef]
- de Lima, G.N.; Lombardo, M.A.; Magana, V. Urban water supply and the changes in the precipitation patterns in the metropolitan area of Sao Paulo—Brazil. Appl. Geogr. 2018, 94, 223–229. [Google Scholar] [CrossRef] [Green Version]
- Matchett, E.L.; Fleskes, J.P. Projected impacts of climate, urbanization, water management, and wetland restoration on waterbird habitat in California’s central valley. PLoS ONE 2017, 12, e0169780. [Google Scholar] [CrossRef]
- Shukla, S.; Gedam, S. Evaluating hydrological responses to urbanization in a tropical river basin: A water resources management perspective. Nat. Resour. Res. 2019, 28, 327–347. [Google Scholar] [CrossRef]
- Alamdari, N.; Hogue, T.S. Assessing the effects of climate change on urban watersheds: A review and call for future research. Environ. Rev. 2022, 30, 61–71. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, L.; Xiao, Y.C.; Chang, C.C.; Zhi, X.S.; Shen, Z.Y. New framework for assessing urban stormwater management measures in the context of climate change. Sci. Total Environ. 2022, 813, 13. [Google Scholar] [CrossRef] [PubMed]
- Jin, K.; Wang, F.; Li, P.F. Responses of vegetation cover to environmental change in large cities of China. Sustainability 2018, 10, 270. [Google Scholar] [CrossRef] [Green Version]
- Cao, Q.; Liu, Y.P.; Georgescu, M.; Wu, J.G. Impacts of landscape changes on local and regional climate: A systematic review. Landsc. Ecol. 2020, 35, 1269–1290. [Google Scholar] [CrossRef]
- Cao, Q.; Yu, D.Y.; Georgescu, M.; Wu, J.G.; Wang, W. Impacts of future urban expansion on summer climate and heat-related human health in eastern China. Environ. Int. 2018, 112, 134–146. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Sun, P.; Singh, V.P.; Shi, P.; Song, C. Impact of urbanization on hourly precipitation in Beijing, China: Spatiotemporal patterns and causes. Glob. Planet. Chang. 2019, 172, 307–324. [Google Scholar] [CrossRef]
- Mondal, S.K.; Wang, Y.J.; Zhai, J.Q.; Su, B.D.; Jiang, S.; Huang, J.L.; Jing, C.; Lin, Q.G.; Zhou, J.; Gao, M.N.; et al. Projected urban exposure to extreme precipitation over South Asia. Sci. Total Environ. 2022, 822, 15. [Google Scholar] [CrossRef]
- Deng, Y.; Cao, G.; Jiang, W.; Wu, J.; Li, Z.; Wang, X. Spatiotemporal changes in heavy precipitation events in the Beijing-Tianjin-Hebei region revealed by hourly meteorological station observations. Theor. Appl. Climatol. 2020, 141, 483–494. [Google Scholar] [CrossRef]
- Kusaka, H.; Nishi, A.; Mizunari, M.; Yokoyama, H. Urban impacts on the spatiotemporal pattern of short-duration convective precipitation in a coastal city adjacent to a mountain range. Q. J. R. Meteorol. Soc. 2019, 145, 2237–2254. [Google Scholar] [CrossRef]
- Zhang, W.; Villarini, G.; Vecchi, G.A.; Smith, J.A. Urbanization exacerbated the rainfall and flooding caused by hurricane Harvey in Houston. Nature 2018, 563, 7731. [Google Scholar] [CrossRef]
- Beshir, A.A.; Song, J. Urbanization and its impact on flood hazard: The case of Addis Ababa, Ethiopia. Nat. Hazards 2021, 109, 1167–1190. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, Y.P.; Cai, X.T.; Tang, J.Y.; Yang, L. Role of underlying surface, rainstorm and antecedent wetness condition on flood responses in small and medium sized watersheds in the Yangtze River Delta region, China. Catena 2021, 206, 11. [Google Scholar] [CrossRef]
- Oliveros, J.M.; Vallar, E.A.; Galvez, M.C.D. Investigating the effect of urbanization on weather using the Weather Research and Forecasting (WRF) model: A case of metro Manila, Philippines. Environments 2019, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Patel, P.; Ghosh, S.; Kaginalkar, A.; Islam, S.; Karmakar, S. Performance evaluation of WRF for extreme flood forecasts in a coastal urban environment. Atmos. Res. 2019, 223, 39–48. [Google Scholar] [CrossRef]
- Gu, Y.F.; Li, D. A modeling study of the sensitivity of urban heat islands to precipitation at climate scales. Urban Clim. 2018, 24, 982–993. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Jin, M.L.S.; Leach, M. A study of the Oklahoma City urban heat island effect using a WRF/single-layer urban canopy model, a joint urban 2003 field campaign, and MODIS satellite observations. Climate 2017, 5, 20. [Google Scholar] [CrossRef] [Green Version]
- Song, X.M.; Zhang, J.Y.; Zhang, C.H.; Zou, X.J. A comprehensive analysis of the changes in precipitation patterns over Beijing during 1960–2012. Adv. Meteorol. 2019, 2019, 6364040. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, D.-L.; Luo, Y.; Ma, R. On the extreme rainfall event of 7 may 2017 over the coastal city of Guangzhou. Part I: Impacts of urbanization and orography. Mon. Weather Rev. 2020, 148, 955–979. [Google Scholar] [CrossRef]
- Lin, Y.Z.; Liu, A.P.; Ma, E.J.; Li, X.; Shi, Q.L. Impacts of future urban expansion on regional climate in the Northeast Megalopolis, USA. Adv. Meteorol. 2013, 10, 362925. [Google Scholar] [CrossRef]
- Wang, J.; Feng, J.M.; Wu, Q.Z.; Yan, Z.W. Impact of anthropogenic aerosols on summer precipitation in the Beijing-Tianjin-Hebei urban agglomeration in China: Regional climate modeling using WRF-Chem. Adv. Atmos. Sci. 2016, 33, 753–766. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, S.Y.; Wang, Y.Y.; Wei, F.L.; Huang, J.; Shen, J.S.; Li, S.C. The relationship between urban form and heat island intensity along the urban development gradients. Sci. Total Environ. 2020, 708, 135011. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Wei, F.L.; Wang, Y.Y.; Huang, J.; Jiang, H.; Sun, F.Y.; Li, S.C. The context-dependent effect of urban form on air pollution: A panel data analysis. Remote Sens. 2020, 12, 1793. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Y.Y.; Huang, J.; Wei, F.L.; Wu, S.Y.; Shen, J.S.; Sun, F.Y.; Li, S.C. Seasonal and diurnal variations in the relationships between urban form and the urban heat island effect. Energies 2020, 13, 5909. [Google Scholar] [CrossRef]
- Zhong, S.; Qian, Y.; Zhao, C.; Leung, R.; Yang, X.Q. A case study of urbanization impact on summer precipitation in the Greater Beijing Metropolitan Area: Urban heat island versus aerosol effects. J. Geophys. Res.-Atmos. 2015, 120, 10903–10914. [Google Scholar] [CrossRef]
- Wei, F.L.; Liang, Z.; Wang, Y.Y.; Huang, Z.B.; Wang, H.; Sun, F.Y.; Li, S.C. Exploring the driving factors of the spatiotemporal variation of precipitation in the Jing-Jin-Ji Urban agglomeration from 2000 to 2015. Sustainability 2020, 12, 7426. [Google Scholar] [CrossRef]
- Xie, Y.H.; Weng, Q.H. Spatiotemporally enhancing time-series DMSP/OLS nighttime light imagery for assessing large-scale urban dynamics. ISPRS J. Photogramm. Remote Sens. 2017, 128, 1–15. [Google Scholar] [CrossRef]
- Zhang, Q.; Pandey, B.; Seto, K.C. A Robust method to generate a consistent time series from DMSP/OLS nighttime light data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5821–5831. [Google Scholar] [CrossRef]
- Luo, M.; Lau, N.C. Urban expansion and drying climate in an urban agglomeration of East China. Geophys. Res. Lett. 2019, 46, 6868–6877. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, Y. Impact of urbanization in different regions of Eastern China on precipitation and its uncertainty. J. Trop. Meteorol. 2014, 30, 601–611. [Google Scholar]
- Keshavarzian, E.; Jin, R.Z.; Dong, K.J.; Kwok, K.C.S.; Zhang, Y.; Zhao, M. Effect of pollutant source location on air pollutant dispersion around a high-rise building. Appl. Math. Model. 2020, 81, 582–602. [Google Scholar] [CrossRef]
- Wang, J.; Feng, J.; Yan, Z.; Hu, Y.; Jia, G. Nested high-resolution modeling of the impact of urbanization on regional climate in three vast urban agglomerations in China. J. Geophys. Res. Atmos. 2011, 117, 21103. [Google Scholar] [CrossRef] [Green Version]
- Grabowski, W.W. Can the impact of aerosols on deep convection be isolated from meteorological effects in atmospheric observations? J. Atmos. Sci. 2018, 75, 3347–3363. [Google Scholar] [CrossRef]
- Kawecki, S.; Henebry, G.; Steiner, A. Effects of urban plume aerosols on a mesoscale convective system. J. Atmos. Sci. 2016, 73, 4641–4660. [Google Scholar] [CrossRef]
- Carrasco, C.; Palme, M.; Angel Galvez, M.; Inostroza, L.; Padilla, U.; Fonseca, A. Urban heat island of Valparaíso, Chile—A comparison between 2007 and 2016. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 072036. [Google Scholar] [CrossRef] [Green Version]
- Krall, J.M.; Uthoff, V.A.; Harley, J.B. A step-up procedure for selecting variables associated with survival. Biometrics 1975, 31, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Anthony, Y.C.K. All subsets regression in a proportional hazards model. Biometrika 1984, 71, 587–592. [Google Scholar] [CrossRef]
- Hamada, C.A.; Hamada, M.S. All-subsets regression under effect heredity restrictions for experimental designs with complex aliasing. Qual. Reliab. Eng. Int. 2010, 26, 75–81. [Google Scholar] [CrossRef]
- Liebminger, A.; Papesch, W.; Haberhauer, G.; Varmuza, K. Multivariate models for the concentration of oxygen-18 in precipitation based on meteorological and geographical features. Chemom. Intell. Lab. Syst. 2007, 89, 1–8. [Google Scholar] [CrossRef]
- Liu, S.P.; Lu, J.C.; Kolpin, D.W.; Meeker, W.Q. Analysis of environmental data with censored observations. Environ. Sci. Technol. 1997, 31, 3358–3362. [Google Scholar] [CrossRef] [Green Version]
- Morrice, J.A.; Danz, N.P.; Regal, R.R.; Kelly, J.R.; Niemi, G.J.; Reavie, E.D.; Hollenhorst, T.; Axler, R.P.; Trebitz, A.S.; Cotter, A.M.; et al. Human influences on water quality in Great Lakes coastal wetlands. Environ. Manag. 2008, 41, 347–357. [Google Scholar] [CrossRef]
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Mac Nally, R. Regression and model-building in conservation biology, biogeography and ecology: The distinction between—and reconciliation of—‘predictive’ and ‘explanatory’ models. Biodivers. Conserv. 2000, 9, 655–671. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; AghaKouchak, A.; Sen Roy, S.; Xuan, Y.; Wang, G.; He, R.; Wang, X.; Liu, C. Rapid urbanization and changes in spatiotemporal characteristics of precipitation in Beijing metropolitan area. J. Geophys. Res.-Atmos. 2014, 119, 11250–11271. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Zhang, J.; Kong, F.; Wang, G.; He, R.; Zhu, K. Spatio-temporal variation characteristics of precipitation extremes in Beijing. Adv. Water Sci. 2017, 28, 161–173. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zou, X.; Zhang, C.; AghaKouchak, A.; Kong, F. Changes in precipitation extremes in the Beijing metropolitan area during 1960–2012. Atmos. Res. 2019, 222, 134–153. [Google Scholar] [CrossRef]
- Wang, J.; Feng, J.M.; Yan, Z.W. Impact of extensive urbanization on summertime rainfall in the Beijing region and the role of local precipitation recycling. J. Geophys. Res.-Atmos. 2018, 123, 3323–3340. [Google Scholar] [CrossRef]
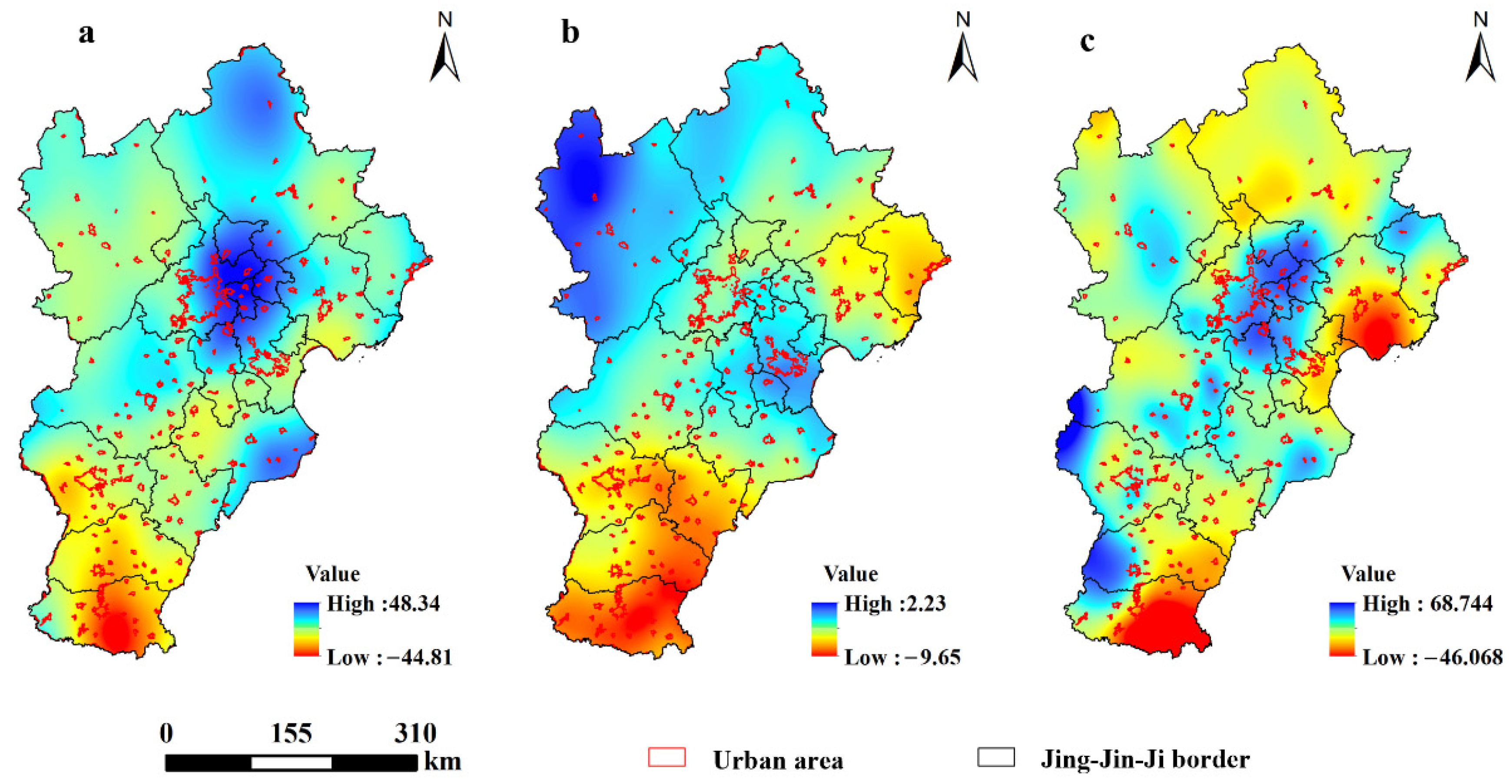
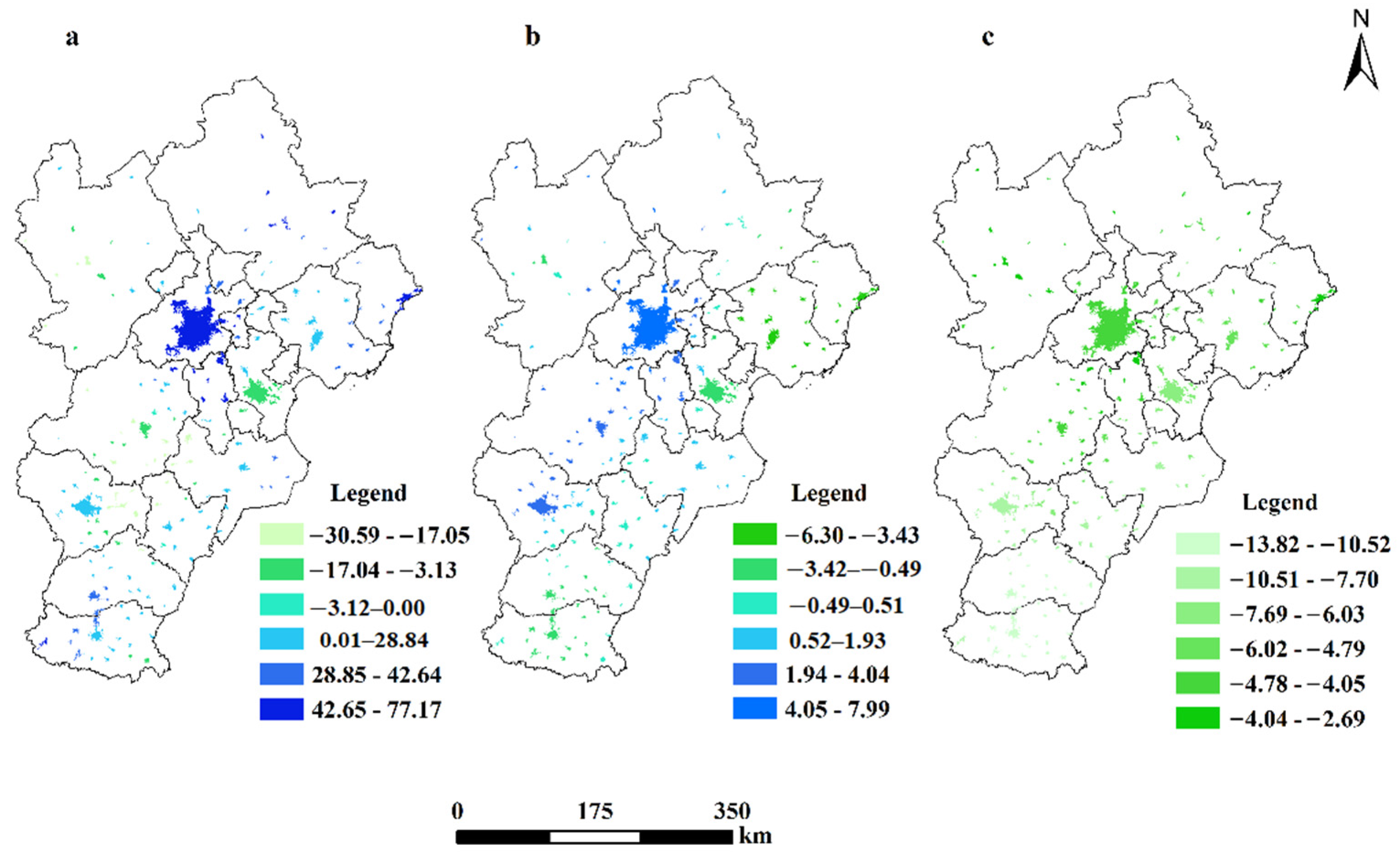

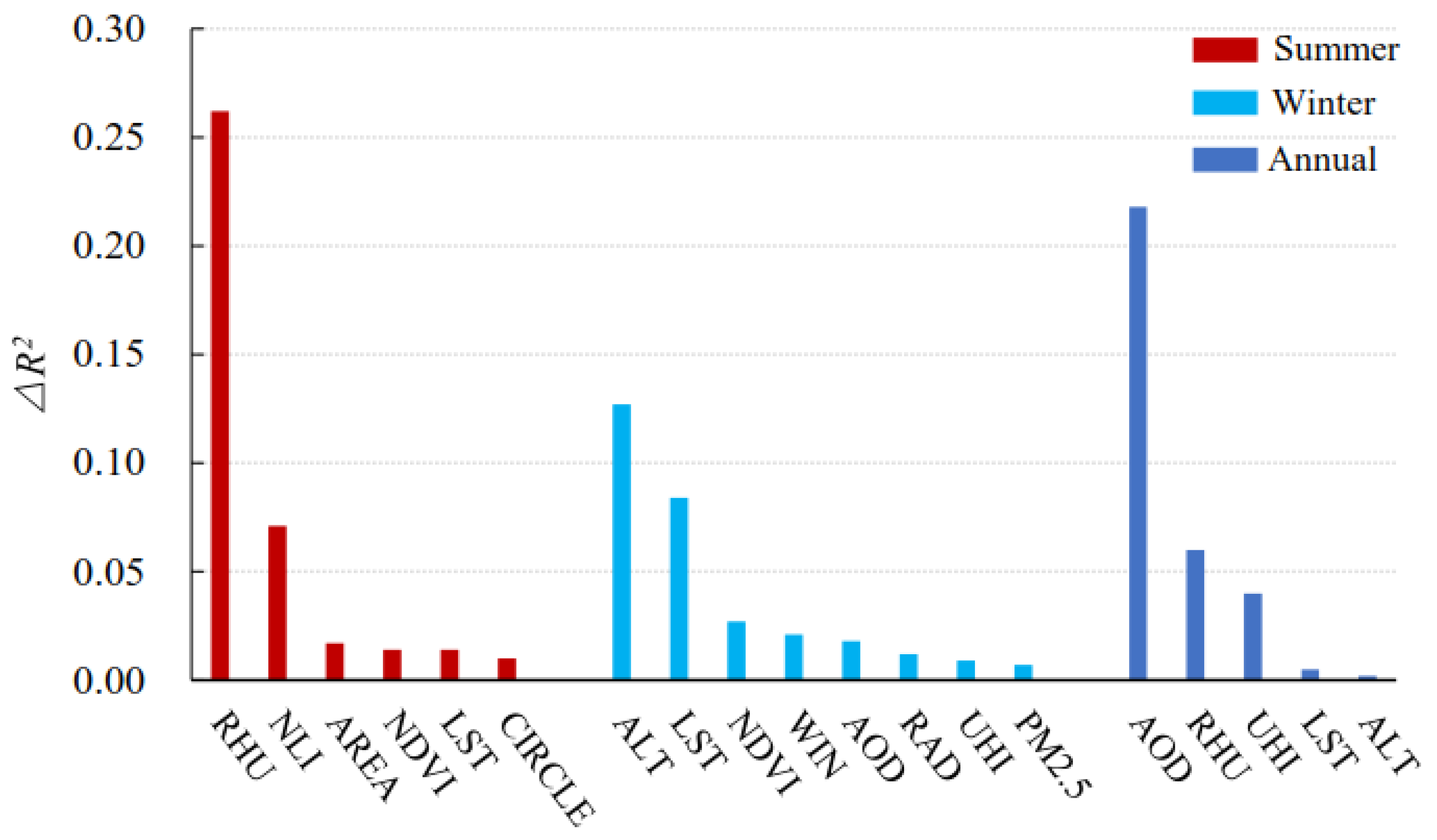
| Category of Variable | Variable | Meaning of Variable | Data Sources |
|---|---|---|---|
| Urban form factor | FRAC | , = perimeter (m) of patch ij, area (m2) of patch ij. FRAC can help quantify the degree of complexity of the planar shapes. | Calculated from the 30 m land use data (https://www.resdc.cn/data.aspx?DATAID=283) (accessed on 1 September 2020) |
| CIRCLE | area (m2) of grid ij. area (m2) of smallest circumscribing circle around grid ij. CIRCLE is used to distinguish patches that are linear (narrow) or elongated | Calculated from the 30 m land use data (https://www.resdc.cn/data.aspx?DATAID=283) (accessed on 1 September 2020) | |
| CONTIG | = contiguity value of pixel p in zone ij, = area of zone ij is represented by the number of grids, s = sum of the values in a 3-by-3 grid template. CONTIG assesses the spatial connectedness or contiguity of cells within a grid cell patch (equals 0 for a one-pixel patch and increases to a limit of 1 as patch contiguity or connectedness increases) | Calculated from the 30 m land use data (https://www.resdc.cn/data.aspx?DATAID=283) (accessed on 1 September 2020) | |
| Urbanization development level | POP | Represents the degree of population density | http://sedac.ciesin.columbia.edu/data/set/gpw-v4-population-density-rev10 (accessed on 1 September 2020) |
| NLI | Denotes the light generated from electricity (areas of high economic prosperity and population are generally well-illuminated) | Defense Meteorological Satellite Program-Operational Linescan System (DMSP-OLS) | |
| AREA | Indicates the area of urban expansion | Based on the 30 m land use data (https://www.resdc.cn/data.aspx?DATAID=283) (accessed on 20 September 2020) | |
| Natural/meteorological conditions | RHU | Average relative humidity of an urban administrative unit | http://data.cma.cn/data/detail/dataCode/A.0012.0001.html (accessed on 20 September 2020) |
| WIN | Average wind speed of an urban administrative unit (m/s) | http://data.cma.cn/data/detail/dataCode/A.0012.0001.html (accessed on 20 September 2020) | |
| RAD | Average radiation of an urban administrative unit | http://data.cma.cn/data/cdcdetail/dataCode/RADI_MUL_CHN_DAY.html (accessed on 20 September 2020) | |
| ALT | Average altitude of urban areas obtained from DEM (digital elevation model) data with a resolution of 30 m | ||
| Surface properties | NDVI | Normalized transform of the NIR (near-infrared radiation) to red reflectance ratio (commonly designed to standardize vegetation indices values to between −1 and +1) | https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod13a3_v006 (accessed on 1 September 2020) |
| TREE | Percentage of urban forest coverage | https://modis.gsfc.nasa.gov/data/dataprod/mod44.php (accessed on 1 September 2020) | |
| Air quality | AOD | Aerosol optical depth, the key physical quantity that characterizes the degree of atmospheric turbidity | https://sedac.ciesin.columbia.edu/data/set/sdei-global-annual-gwr-pm2–5-modis-misr-seawifs-aod-v4-gl-03 (accessed on 1 September 2020) |
| PM2.5 | Particulate matter with a diameter of less than 2.5 microns can enter the lungs (expressed as fine particulate matter, in terms of the annual average concentration of micrograms per cubic meter) | https://nasasearch.nasa.gov/search?query=PM2.5&affiliate=nasa&utf8=%E2%9C%93 (accessed on 20 September 2020) | |
| Urban thermal environment | UHI | Average surface temperature of the inner city area minus the average surface temperature of the suburbs 10 km from the buffer zone | Calculated from LST data (http://www.gscloud.cn/sources/accessdata/336?pid=333) (accessed on 20 September 2020) |
| LST | Average surface temperature of the inner city area | http://www.gscloud.cn/sources/accessdata/336?pid=333 (accessed on 20 September 2020) |
| Category of Variable | Variable | Summer | Winter | Annual | |||
|---|---|---|---|---|---|---|---|
| R2 | Adj R2 | R2 | Adj R2 | R2 | Adj R2 | ||
| Urban form factor | FRAC | 0.01 ** (+) | 0.01 | 0.002 (+/) | / | 0.006 (−) | 0.05 |
| CIRCLE | 0.01 ** (+/) | 0.003 (+/) | 0.001 (−/) | ||||
| CONTIG | 0.000 (+/) | 0.000 (+/) | 0.004 (−/) | ||||
| Urbanization development level | POP | 0.000 (+/) | 0.103 | 0.004 (−) | 0.046 | 0.000 (−) | 0.075 |
| NLI | 0.072 *** (+) | 0.017 ** (+) | 0.032 *** (−) | ||||
| AREA | 0.007 * (+) | 0.000 (−/) | 0.036 *** (−) | ||||
| Natural/meteorological conditions | RHU | 0.314 *** (+) | 0.345 | 0.003 (−/) | 0.159 | 0.060 *** (+) | 0.107 |
| WIN | 0.003 (+) | 0.021 *** (−) | 0.000 (−/) | ||||
| RAD | 0.012 *** (−) | 0.011 ** (+/) | 0.000 (+) | ||||
| ALT | 0.000 (+) | 0.135 *** (+) | 0.025 *** (−) | ||||
| Surface properties | NDVI | 0.093 *** (+) | 0.132 | 0.111 *** (−) | 0.109 | 0.001 (−/) | 0.006 |
| TREE | 0.000 (−) | 0.019 ** (−/) | 0.008 (+) | ||||
| Air quality | AOD | 0.002 (−/) | / | 0.128 *** (−) | 0.148 | 0.014 ** (−) | 0.012 |
| PM2.5 | 0.005 (−/) | 0.093 *** (−) | 0.003 (−/) | ||||
| Urban thermal environment | UHI | 0.041 *** (+) | 0.166 | 0.011 ** (−) | 0.228 | 0.051 *** (−) | 0.062 |
| LST | 0.140 *** (−) | 0.226 *** (−) | 0.008 * (+) | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, F.; Liang, Z.; Ma, W.; Shen, J.; Wang, Y.; Liu, D.; Li, S. Dominant Factors in the Temporal and Spatial Distribution of Precipitation Change in the Beijing–Tianjin–Hebei Urban Agglomeration. Remote Sens. 2022, 14, 2880. https://doi.org/10.3390/rs14122880
Wei F, Liang Z, Ma W, Shen J, Wang Y, Liu D, Li S. Dominant Factors in the Temporal and Spatial Distribution of Precipitation Change in the Beijing–Tianjin–Hebei Urban Agglomeration. Remote Sensing. 2022; 14(12):2880. https://doi.org/10.3390/rs14122880
Chicago/Turabian StyleWei, Feili, Ze Liang, Weijing Ma, Jiashu Shen, Yueyao Wang, Dahai Liu, and Shuangcheng Li. 2022. "Dominant Factors in the Temporal and Spatial Distribution of Precipitation Change in the Beijing–Tianjin–Hebei Urban Agglomeration" Remote Sensing 14, no. 12: 2880. https://doi.org/10.3390/rs14122880
APA StyleWei, F., Liang, Z., Ma, W., Shen, J., Wang, Y., Liu, D., & Li, S. (2022). Dominant Factors in the Temporal and Spatial Distribution of Precipitation Change in the Beijing–Tianjin–Hebei Urban Agglomeration. Remote Sensing, 14(12), 2880. https://doi.org/10.3390/rs14122880








