Retrieval of Soil Moisture Content Based on Multisatellite Dual-Frequency Combination Multipath Errors
Abstract
:1. Introduction
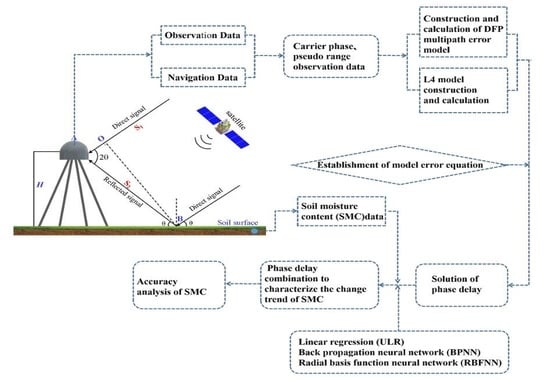
2. Materials and Methods
2.1. GNSS-IR SMC Retrieval Principle
2.1.1. GNSS Multipath Error Principle
2.1.2. Calculation of Multipath Error of Linear Combination of Observations
2.1.3. Error Calculation of Dual-Frequency Pseudorange Multipath
2.1.4. Multipath Error Calculation of Dual-Frequency Carrier Phase Linear Combination
2.2. Establishment of Model Error Equation
2.3. Solving the Phase Delay
2.4. Data Sources
3. Experiment and Results
3.1. Experimental Technical Scheme
3.2. SMC Retrieval
3.2.1. Choice of Elevation Angle
3.2.2. Choice of Azimuth
3.2.3. Selection of Effective Satellites
3.3. GNSS-IR SMC Retrieval Results
- (1)
- Cycle slip detection and repair were conducted on the observed carrier phase value;
- (2)
- We assumed that the amplitude attenuation factor and phase delay did not change in a short time;
- (3)
- To avoid the large difference between the delay phase and the acquisition time of soil moisture, considering the necessary observation number, taking the acquisition time of soil moisture as a reference, we took the multipath error of five epochs before and after as the observation value. That is, we ignored the change in the delay phase with satellite elevation angle in the short term. We regarded the multipath error selected in each period as the repeated observation of the same parameter. According to Equations (15) and (16), the dual-frequency pseudorange multipath error MP could be calculated; According to Equation (19), the dual-frequency carrier-phase combination multipath error L4 could be calculated. We performed high-order fitting (we used 10-degree polynomial fitting) of L4 to remove the influence of ionospheric delay and obtain L4_IF. According to Equation (2), the initial value of the delay phase and the initial value of AAF () are determined. According to Equation (5), we constructed the error equation of the corresponding method, and performed the Lomb–Scargle periodogram (LSP) and least square adjustment method. We solved each period to obtain a delay phase representing the change trend in soil moisture.
4. Discussion
5. Conclusions
- (1)
- The delay phases obtained by the multipath error solution and the soil moisture are strongly correlated. For the P041 station, the R values of the L4_IF and DFP methods are 0.97 and 0.91, respectively. For the MFLE station, the R values of the L4_IF and DFP methods are 0.93 and 0.86, respectively. Because the observation error of the L4 linear combination is low and the change in the ionospheric delay in the short term is small, we used the high-order fitting to further weaken the influence of the ionospheric delay. The L4_IF method has higher R and soil moisture estimation accuracy than the DFP method. When the BPNN model, RBFNN model and ULR model are used to predict soil moisture, the results show that the prediction results of the BPNN model are better than the RBFNN model and ULR model, and the RBFNN model is slightly better than the ULR model. The results show that BPNN can improve the inversion accuracy of GNSS-IR soil moisture.
- (2)
- Since the calculation of the phase delay only requires a small amount of multipath error compared to the soil moisture retrieval based on the SNR, the proposed method does not require the diagnostic signal frequency, and only a tiny number of epoch multipath errors needs to be used to calculate the delay phase. So, achieving high-time-resolution GNSS-IR SMC retrieval is easier. Therefore, this method can be used to easily obtain high-time-resolution and accurate soil moisture estimations.
- (3)
- Given the changes in soil moisture, the reflectivity of the surface changes, which in turn will lead to changes in the amplification, attenuation factor , and phase delay. A further new finding is that the phase delay and the amplification attenuation factor based on the L4_IF method show the same change trend, and the Pearson correlation coefficient between them is 1. Conversely, the phase delay based on the MP2 method and the amplification attenuation factor show the opposite trend, and the Pearson correlation coefficient between them is −1. These results show that the phase delay is closely related to the amplification attenuation factor . In other words, the amplification and attenuation factor can also be used for soil moisture estimation, which can obtain the same result as the phase delay. For the sake of brevity, this article does not list the research results of the amplification and attenuation factor .
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Ray, R.L.; Jacobs, J.M. Relationships among remotely sensed soil moisture, precipitation and landslide events. Nat. Hazards. 2007, 43, 211–222. [Google Scholar] [CrossRef]
- Wanders, N.; Karssenberg, D.; de Roo, A.; de Jong, S.M.; Bierkens, M.F.P. The suitability of remotely sensed soil moisture for improving operational flood forecasting. Hydrol. Earth Syst. Sci. 2014, 18, 2343–2357. [Google Scholar] [CrossRef] [Green Version]
- Schaufler, G.; Kitzler, B.; Schindlbacher, A.; Skiba, U.; Sutton, M.A.; Zechmeister-Boltenstern, S. Greenhouse gas emissions from European soils under different land use: Effects of soil moisture and temperature. Eur. J. Soil Sci. 2010, 61, 683–696. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, Q.; Zhang, X. New Progress and Application Prospects of Global Navigation Satellite System Reflectometry (GNSS + R). Acta Geod. Cartogr. Sin. 2017, 46, 1389–1398. [Google Scholar] [CrossRef]
- Wan, W.; Chen, X.; Peng, X.; Huang, B.; Ming, X.; Hong, L.; Min, Z.; Pang, X.; Ting, Y.; Chang, Y.; et al. Overview and outlook of GNSS remote sensing technology and applications. J. Remote Sens. 2016, 20, 858–874. (In Chinese) [Google Scholar] [CrossRef]
- Ge, L.; Han, S.; Rizos, C. Multipath Mitigation of Continuous GPS Measurements Using an Adaptive Filter. GPS Solut. 2000, 4, 19–30. [Google Scholar] [CrossRef]
- Li, Y.; Chang, X.; Yu, K.; Wang, S.; Li, J. Estimation of snow depth using pseudorange and carrier phase observations of GNSS single-frequency signal. GPS Solut. 2019, 23, 118. [Google Scholar] [CrossRef]
- Ozeki, M.; Heki, K. GPS snow depth meter with geometry-free linear combinations of carrier phases. J. Geod. 2012, 86, 209–219. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A. Use of GPS receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35, 851–854. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Braun, J.J.; Small, E.E.; Zavorotny, V.; Gutmann, E.; Bilich, A. GPS multipath and its relation to near-surface soil moisture content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 91–99. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Wang, L.; Zhang, J.; Peng, J.; Liu, Q. Evaluation of GNSS-IR for Retrieving Soil Moisture and Vegetation Growth Characteristics in Wheat Farmland. J. Surv. Eng. 2021, 147, 04021009. [Google Scholar] [CrossRef]
- Liang, Y.; Ren, C.; Wang, H.; Huang, Y.; Zheng, Z. Research on soil moisture inversion method based on GA-BP neural network model. Int. J. Remote Sens. 2019, 40, 2087–2103. [Google Scholar] [CrossRef]
- Han, M.; Zhu, Y.; Yang, D.; Hong, X.; Song, S. A Semi-Empirical SNR Model for Soil Moisture Retrieval Using GNSS SNR Data. Remote Sens. 2018, 10, 280. [Google Scholar] [CrossRef] [Green Version]
- Jin, L.; Yang, L.; Han, M.; Hong, X.; Sun, B.; Liang, Y. Soil moisture inversion method based on GNSS-IR dual frequency data fusion. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 1248. [Google Scholar] [CrossRef]
- Ran, Q.; Zhang, B.; Yao, Y.; Li, J. Editing arcs to improve the capacity of GNSS-IR for soil moisture retrieval in undulating terrains. GPS Solut. 2022, 26, 1–11. [Google Scholar] [CrossRef]
- Han, M.; Zhu, Y.; Yang, D.; Chang, Q.; Hong, X.; Song, S. Soil moisture monitoring using GNSS interference signal: Proposing a signal reconstruction method. Remote Sens. Lett. 2020, 11, 373–382. [Google Scholar] [CrossRef]
- Li, Y.; Yu, K.; Jin, T.; Chang, X.; Zhang, Q.; Xu, C.; Li, J. Soil moisture estimation using amplitude attenuation factor of low-cost GNSS receiver based SNR observations. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7654–7657. [Google Scholar] [CrossRef]
- Roussel, N.; Frappart, F.; Ramillien, G.; Darrozes, J.; Baup, F.; Lestarquit, L.; Ha, M.C. Detection of soil moisture variations using GPS and GLONASS SNR data for elevation angles ranging from 2° to 70°. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4781–4794. [Google Scholar] [CrossRef]
- Yu, K.; Ban, W.; Zhang, X.; Yu, X. Snow Depth Estimation Based on Multipath Phase Combination of GPS Triple-Frequency Signals. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5100–5109. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, S.; Zhang, C.; Zhang, J.; Cai, H. Soil moisture estimation based on triple-frequency multipath error. Int. J. Remote Sens. 2021, 42, 5953–5968. [Google Scholar] [CrossRef]
- Shen, F.; Sui, M.; Zhu, Y.; Cao, X.; Ge, Y.; Wei, H. Using BDS MEO and IGSO Satellite SNR Observations to Measure Soil Moisture Fluctuations Based on the Satellite Repeat Period. Remote Sens. 2021, 13, 3967. [Google Scholar] [CrossRef]
- Bilich, A.; Larson, K.M. Mapping the GPS multipath environment using the signal-to-noise ratio (SNR). Radio Sci. 2007, 42, 1–16. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, F.; Zhang, X. Triple-frequency multi-GNSS reflectometry snow depth retrieval by using clustering and normalization algorithm to compensate terrain variation. GPS Solut. 2020, 24, 52. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, R.; Yu, B.; Pang, J.; Liao, M.; Liu, G. A GPS-IR Method for Retrieving NDVI from Integrated Dual-Frequency Observations. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, N.; Xue, T.; Gao, F.; Xu, G. Sea Level Estimation Based on GNSS Dual-Frequency Carrier Phase Linear Combinations and SNR. Remote Sens. 2018, 10, 470. [Google Scholar] [CrossRef] [Green Version]
- Katzberg, S.J.; Torres, O.; Grant, M.S.; Masters, D. Utilizing calibrated GPS reflected signals to estimate soil reflectivity and dielectric constant: Results from SMEX02. Remote Sens. Environ. 2006, 100, 17–28. [Google Scholar] [CrossRef] [Green Version]
- Yu, K.; Li, Y.; Chang, X. Snow Depth Estimation Based on Combination of Pseudorange and Carrier Phase of GNSS Dual-Frequency Signals. IEEE Trans. Geosci. Remote Sens 2019, 57, 1817–1828. [Google Scholar] [CrossRef]
- Chew, C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2015, 20, 525–537. [Google Scholar] [CrossRef]


















| Project | Parameter |
|---|---|
| Type of receiver | POLARX5 |
| Sampling interval | 15 s |
| Type of antenna | TRM59800.80 |
| Antenna height | 1.90 m |
| Observation Period Number | GPS Satellite Number (PRN) | Azimuth (/°) | Height Angle (/°) | GPS Time (hh:mm:ss) |
|---|---|---|---|---|
| 1 | PRN16 | 170.75–171.16 | 6.08–7.05 | 01:28:45–01:31:15 |
| 2 | PRN03 | 44.55–44.68 | 14.72–15.69 | 03:28:45–03:31:15 |
| 3 | PRN26 | 239.89–240.82 | 24.45–25.25 | 05:58:45–06:01:15 |
| 4 | PRN20 | 50.47–51.46 | 12.70–12.94 | 07:58:45–08:01:15 |
| 5 | PRN24 | 221.92–222.65 | 13.37–14.22 | 09:58:45–10:01:15 |
| 6 | PRN04 | 67.64–68.26 | 7.66–8.46 | 11:28:45–11:31:15 |
| 7 | PRN15 | 156.52–157.09 | 14.87–15.82 | 12:28:45–12:31:15 |
| 8 | PRN05 | 57.21–57.69 | 11.33–12.21 | 14:28:45–14:31:15 |
| 9 | PRN16 | 275.01–275.94 | 6.19–6.73 | 15:28:45–15:31:15 |
| 10 | PRN31 | 184.73–184.91 | 8.41–9.47 | 17:58:45–18:01:15 |
| 11 | PRN25 | 73.92–75.11 | 22.27–22.47 | 19:58:45–20:01:15 |
| 12 | PRN16 | 170.75–171.17 | 6.09–7.05 | 20:58:45–21:01:15 |
| Station ID | Method | Correlation Coefficient (R) | STD (cm3 cm−3) | MAE (cm3 cm−3) | RMSE (cm3 cm−3) |
|---|---|---|---|---|---|
| P041 | L4_IF | 0.97 | 0.040 | 0.037 | 0.014 |
| DFP | 0.91 | 0.040 | 0.038 | 0.026 | |
| MFLE | L4_IF | 0.93 | 0.047 | 0.043 | 0.029 |
| DFP | 0.86 | 0.047 | 0.049 | 0.042 |
| Station ID | Method | Model | STD (cm3 cm−3) | MAE (cm3 cm−3) |
|---|---|---|---|---|
| P041 | L4_IF | ULR | 0.040 | 0.037 |
| BPNN | 0.039 | 0.034 | ||
| RBFNN | 0.039 | 0.035 | ||
| DFP | ULR | 0.040 | 0.038 | |
| BPNN | 0.033 | 0.033 | ||
| RBFNN | 0.039 | 0.038 | ||
| MFLE | L4_IF | ULR | 0.047 | 0.043 |
| BPNN | 0.039 | 0.037 | ||
| RBFNN | 0.045 | 0.042 | ||
| DFP | ULR | 0.047 | 0.049 | |
| BPNN | 0.042 | 0.046 | ||
| RBFNN | 0.047 | 0.049 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, S.; Wang, Y.; Tu, J.; Li, P.; Xu, J.; Li, N.; Wang, M.; Huang, D.; Song, J. Retrieval of Soil Moisture Content Based on Multisatellite Dual-Frequency Combination Multipath Errors. Remote Sens. 2022, 14, 3193. https://doi.org/10.3390/rs14133193
Nie S, Wang Y, Tu J, Li P, Xu J, Li N, Wang M, Huang D, Song J. Retrieval of Soil Moisture Content Based on Multisatellite Dual-Frequency Combination Multipath Errors. Remote Sensing. 2022; 14(13):3193. https://doi.org/10.3390/rs14133193
Chicago/Turabian StyleNie, Shihai, Yanxia Wang, Jinsheng Tu, Peng Li, Jianhui Xu, Nan Li, Mengke Wang, Danni Huang, and Jia Song. 2022. "Retrieval of Soil Moisture Content Based on Multisatellite Dual-Frequency Combination Multipath Errors" Remote Sensing 14, no. 13: 3193. https://doi.org/10.3390/rs14133193
APA StyleNie, S., Wang, Y., Tu, J., Li, P., Xu, J., Li, N., Wang, M., Huang, D., & Song, J. (2022). Retrieval of Soil Moisture Content Based on Multisatellite Dual-Frequency Combination Multipath Errors. Remote Sensing, 14(13), 3193. https://doi.org/10.3390/rs14133193