Experimental Proof of Concept for the Hurricane Imaging Radiometer (HIRAD) Measurement of a Hurricane Ocean Surface Wind Speed Field
Abstract
1. Introduction
2. Materials and Methods
2.1. HIRAD Instrument Overview
2.1.1. Design Heritage
2.1.2. Instrument Architecture
2.2. Other Sensors
2.3. HIRAD Data
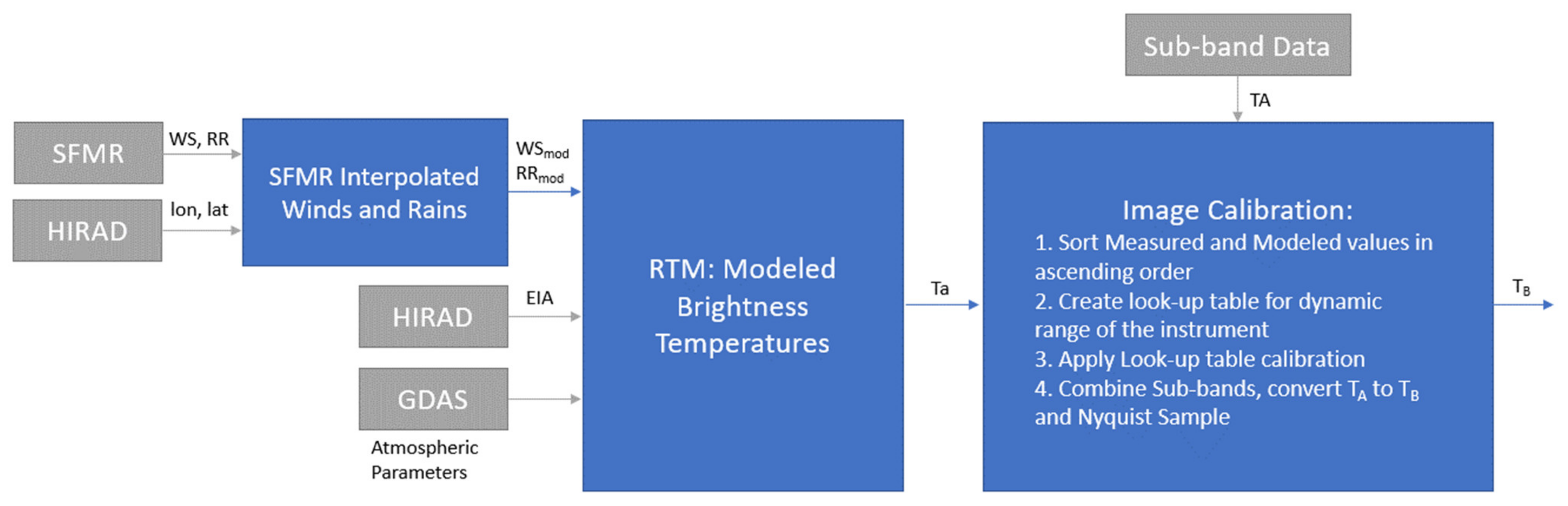
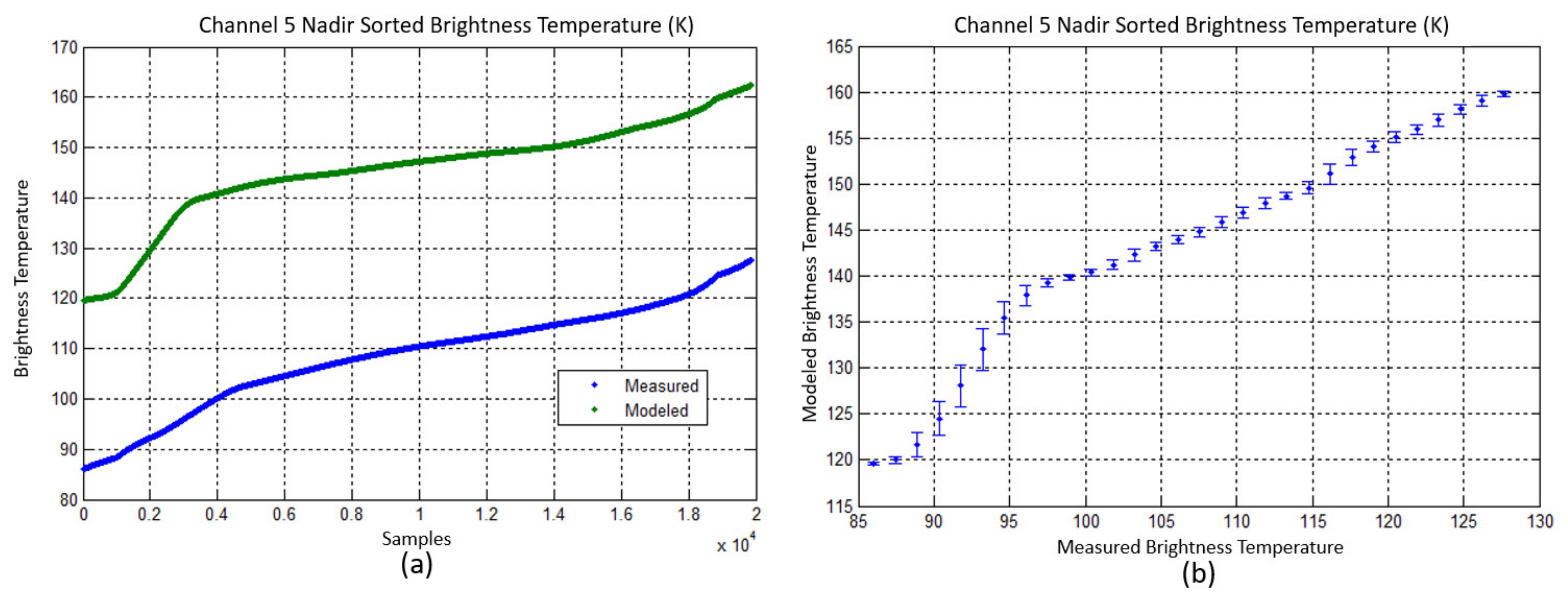
2.4. TA Image Calibration
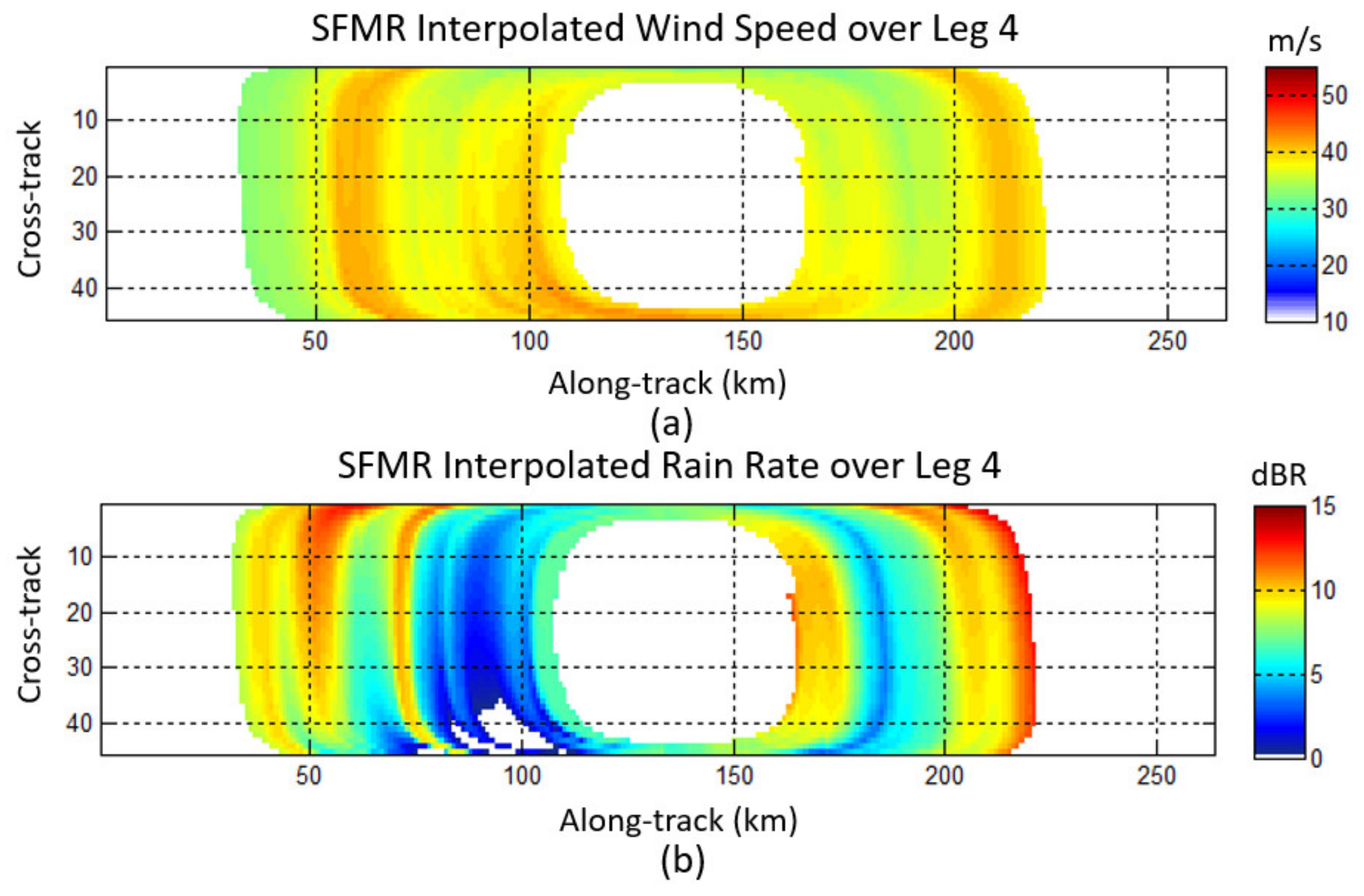
2.4.1. Hurricane WS and RR 2D Model
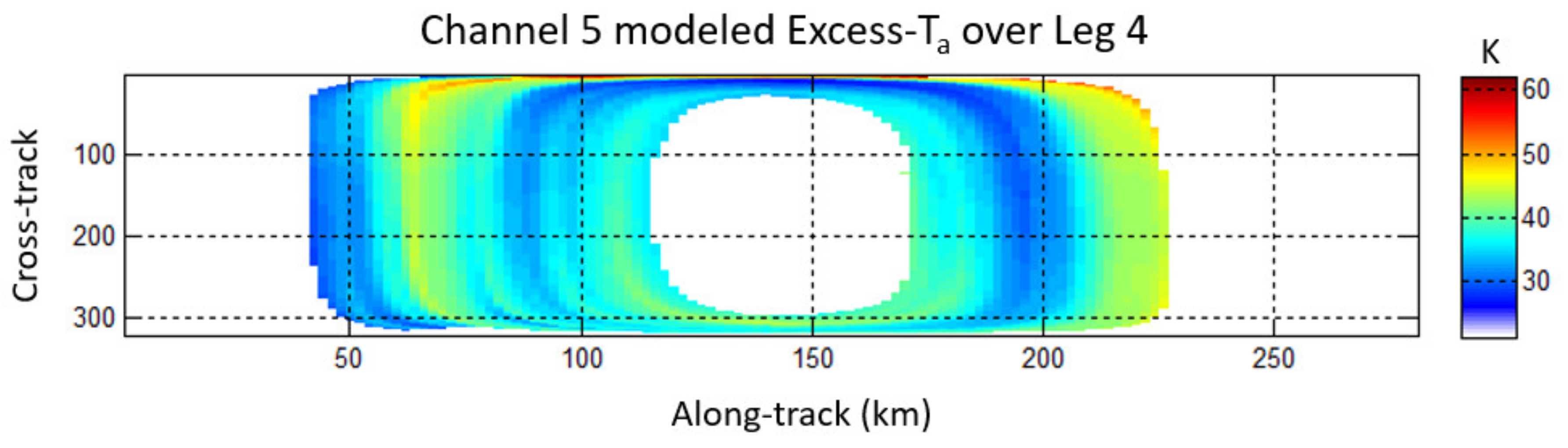
2.4.2. HIRAD RTM
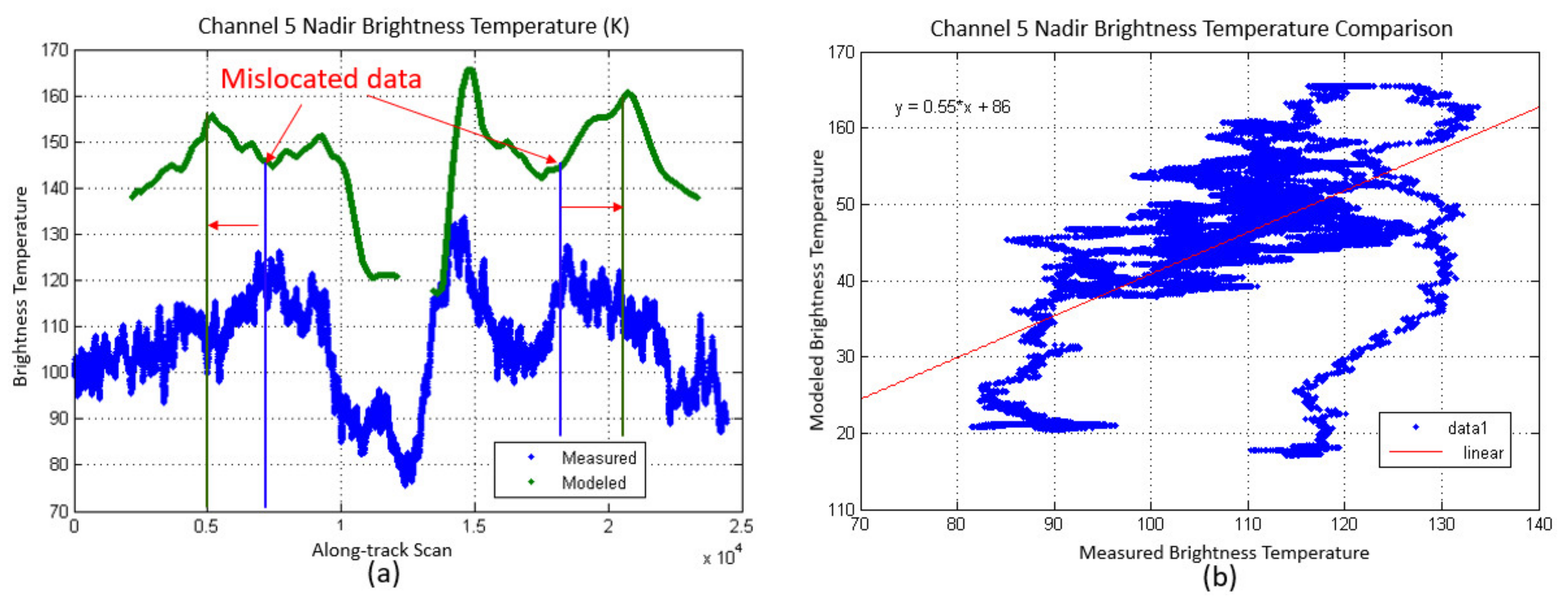
2.4.3. HIRAD Image Calibration
2.5. Geophysical Retrieval Algorithm
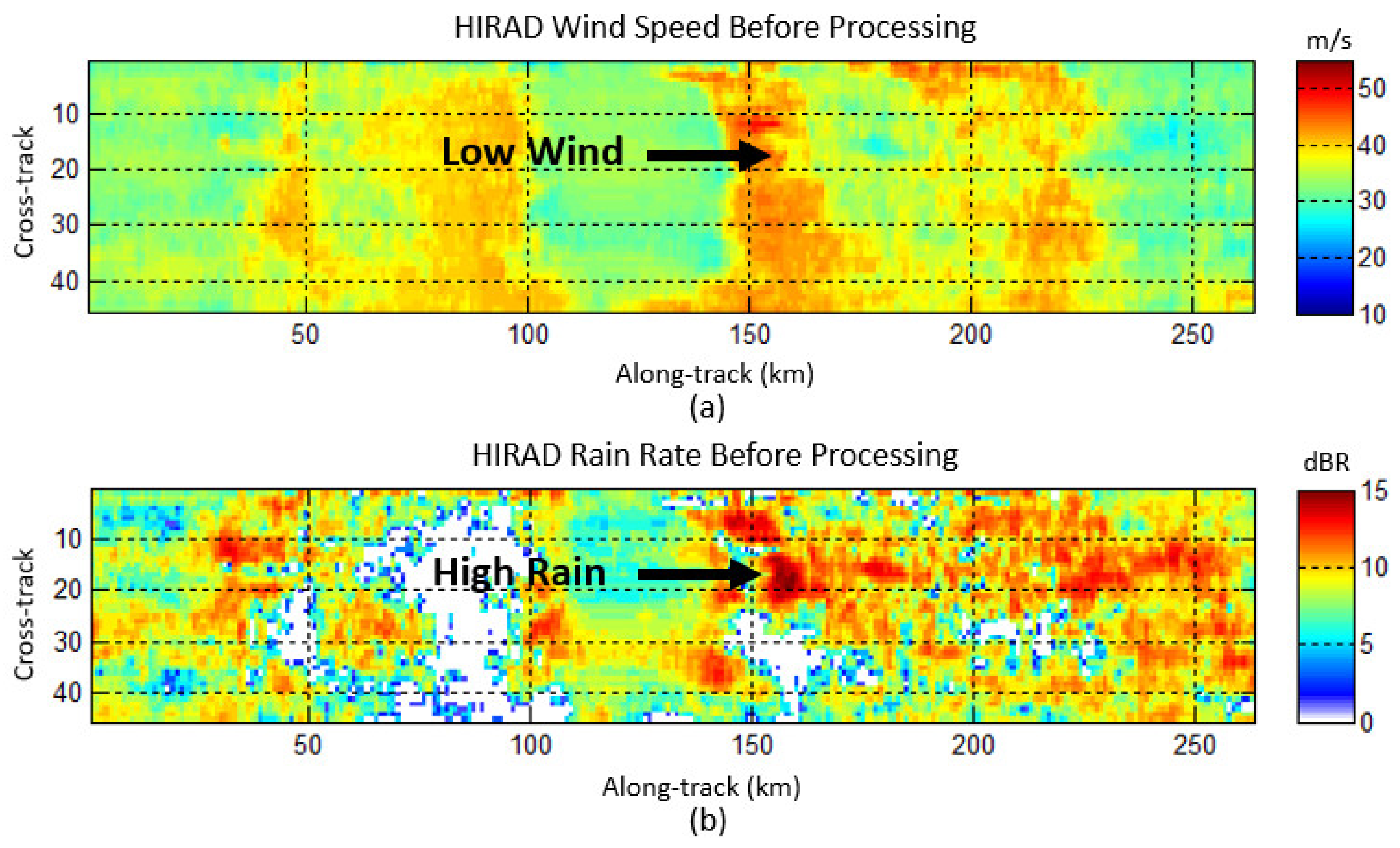
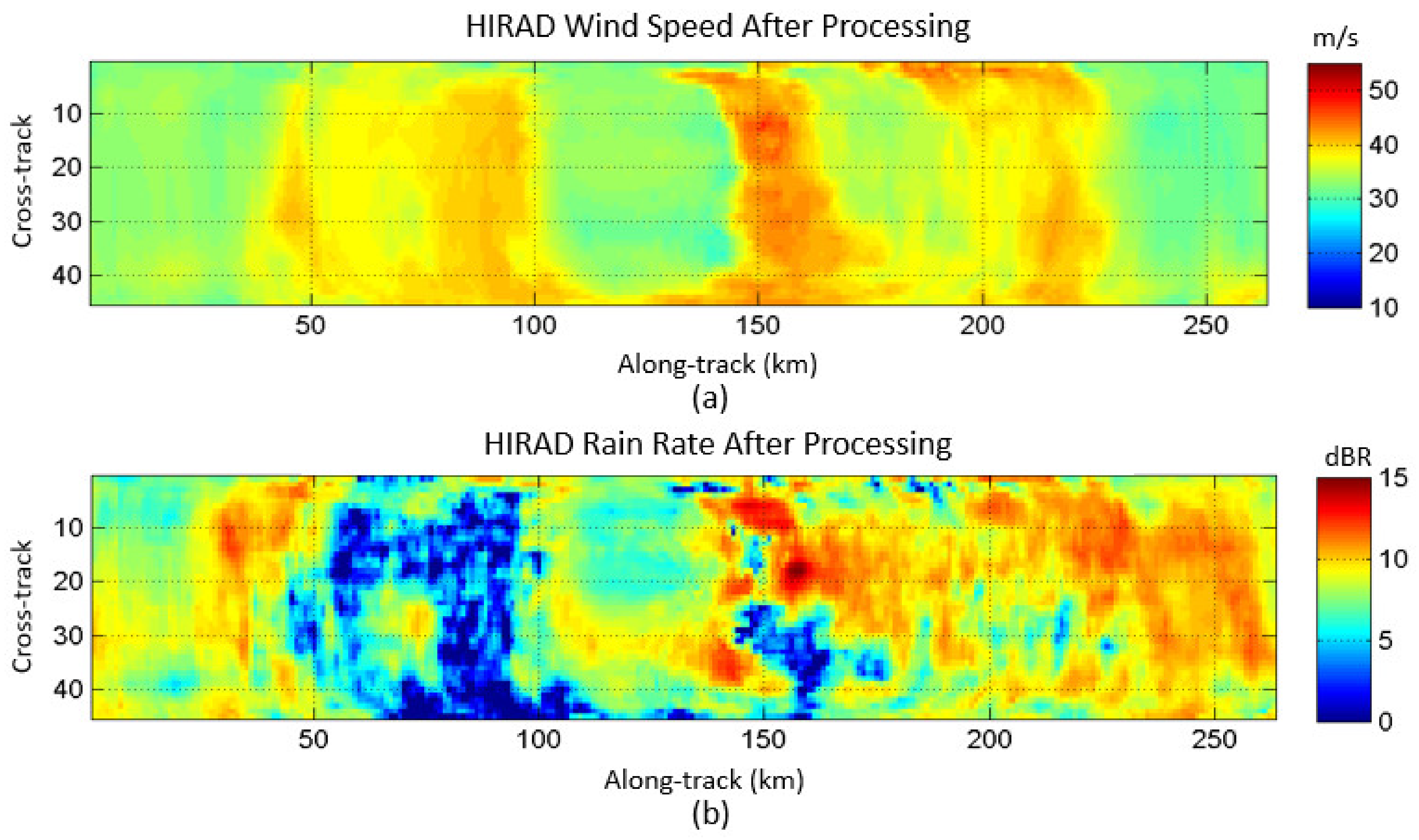
WS Retrievals in Heavy Rain
3. Results
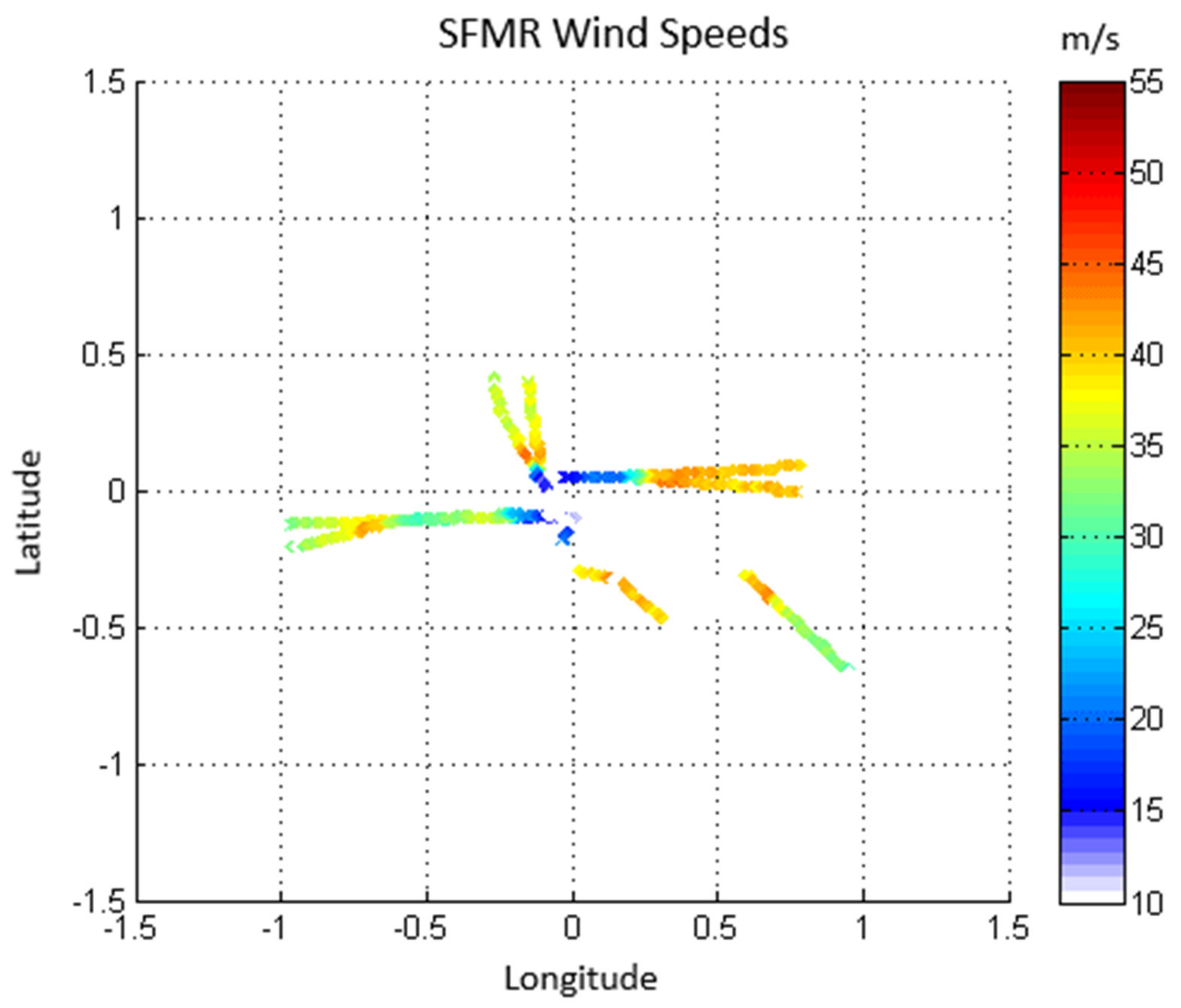
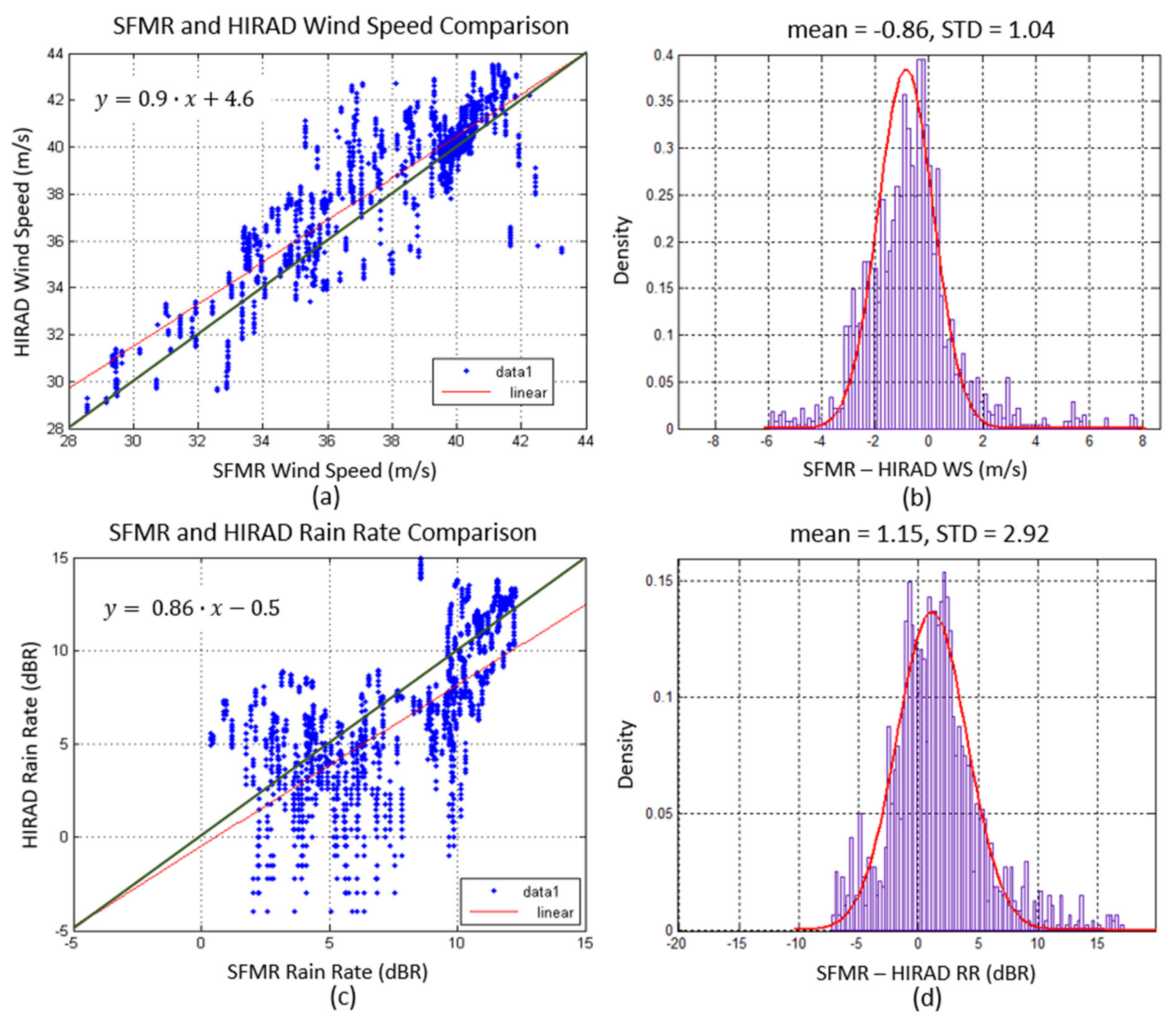
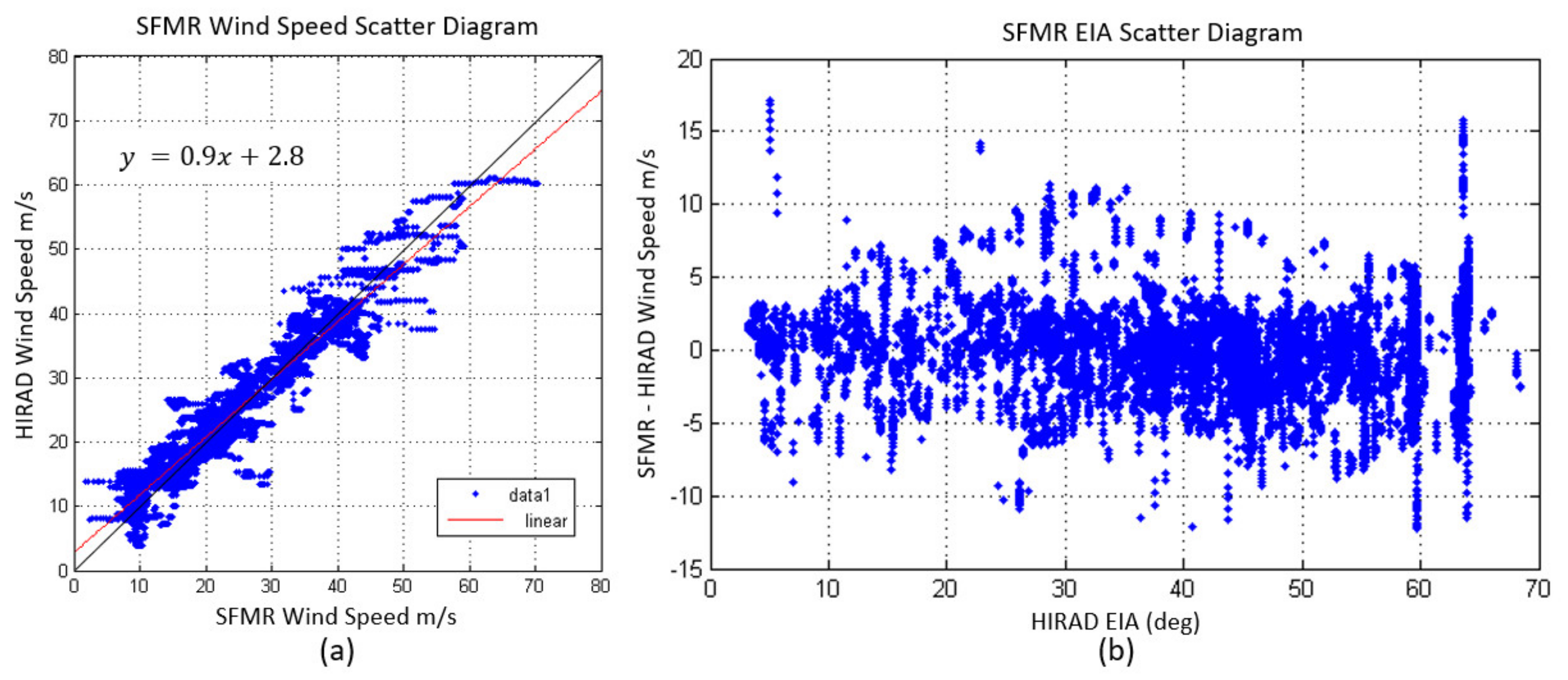
3.1. HIRAD Validation Using SFMR
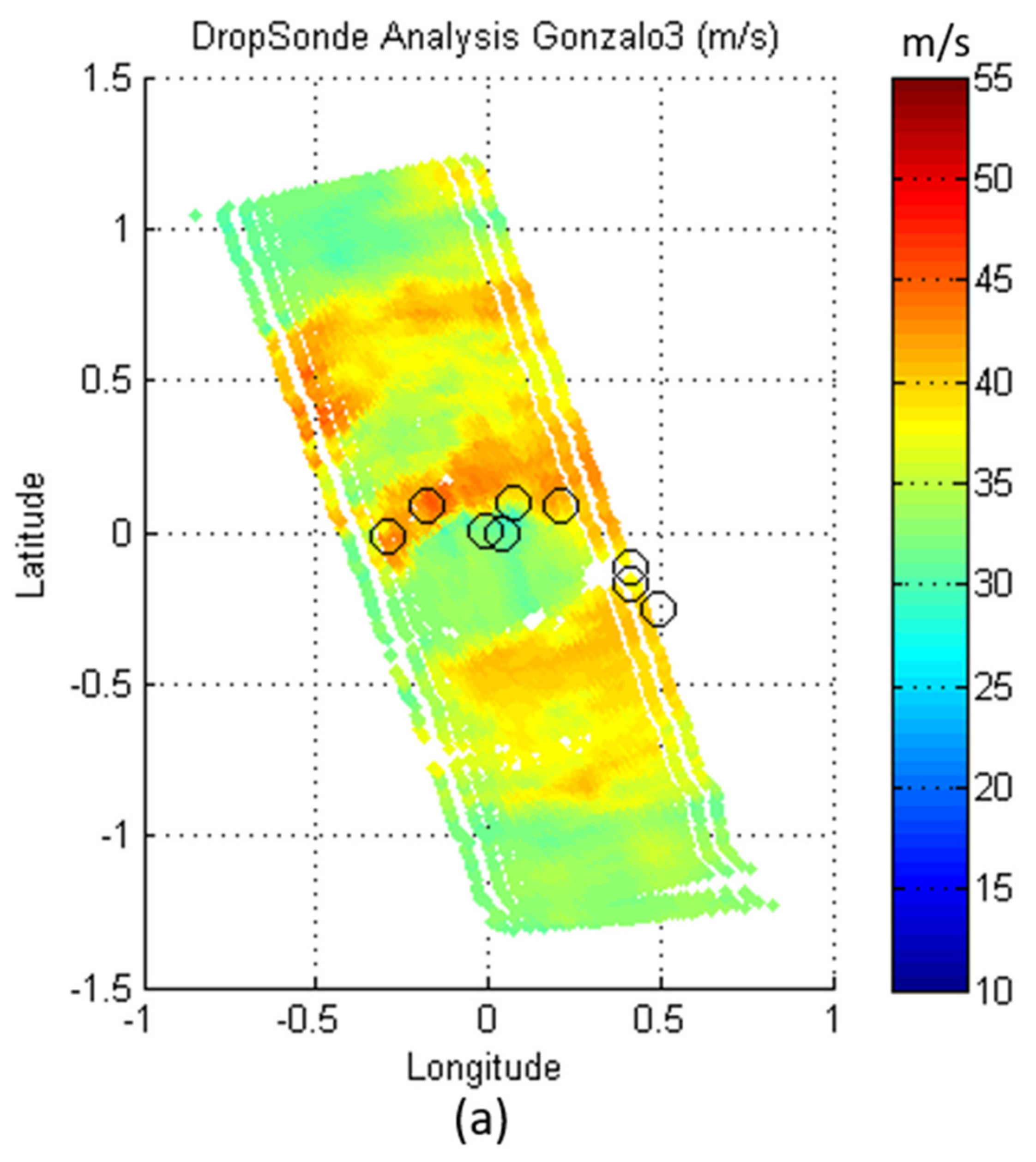
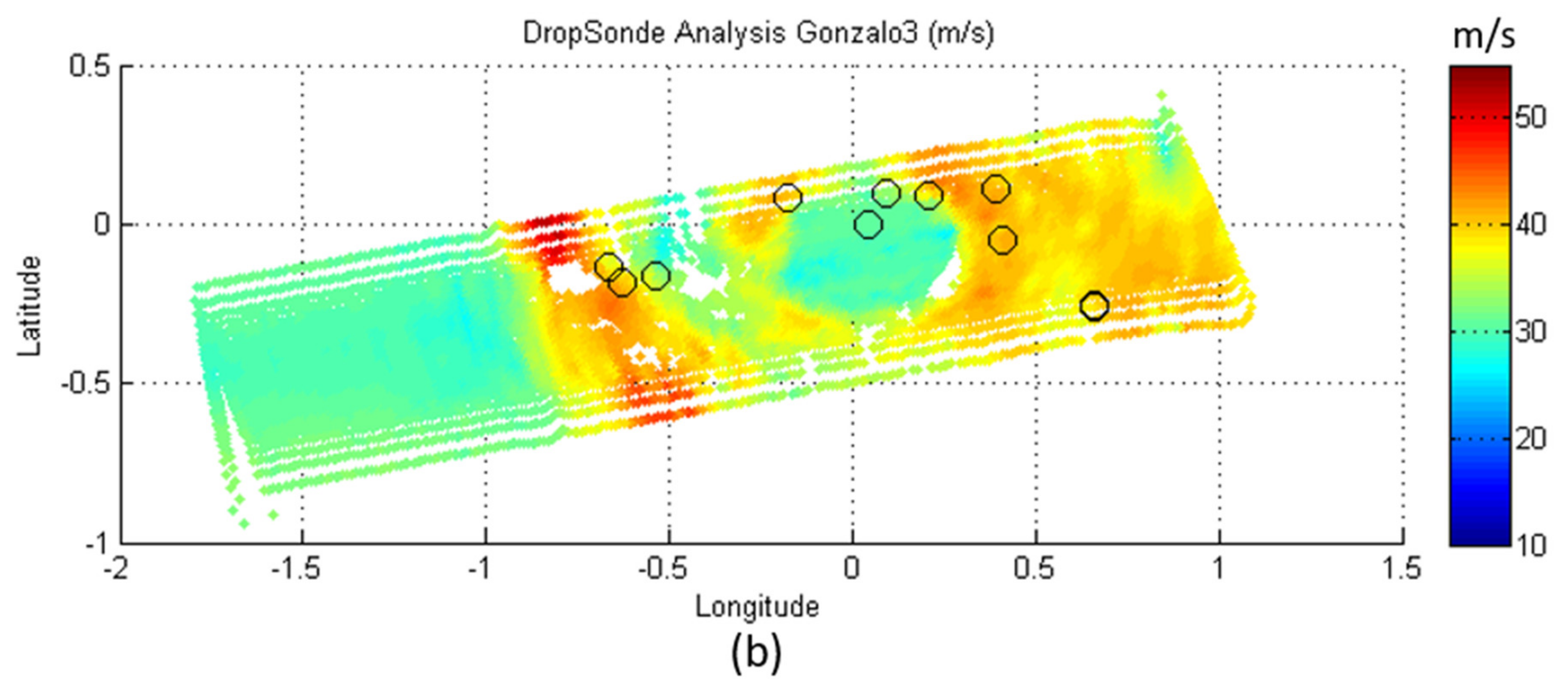
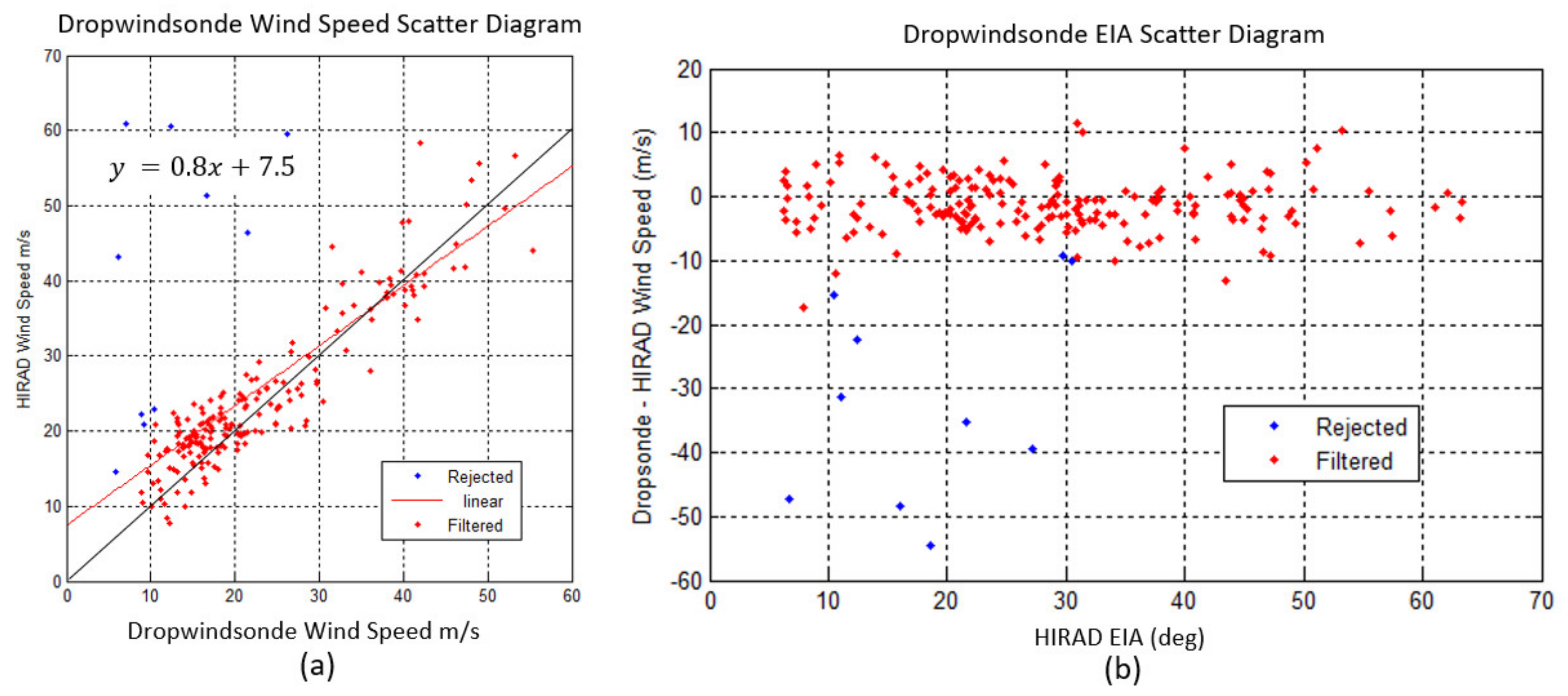
3.2. Wind Speed Validation Using GPS Dropwindsondes
3.3. Rain Rate Validation Using LFR and HIWRAP Rain Rates
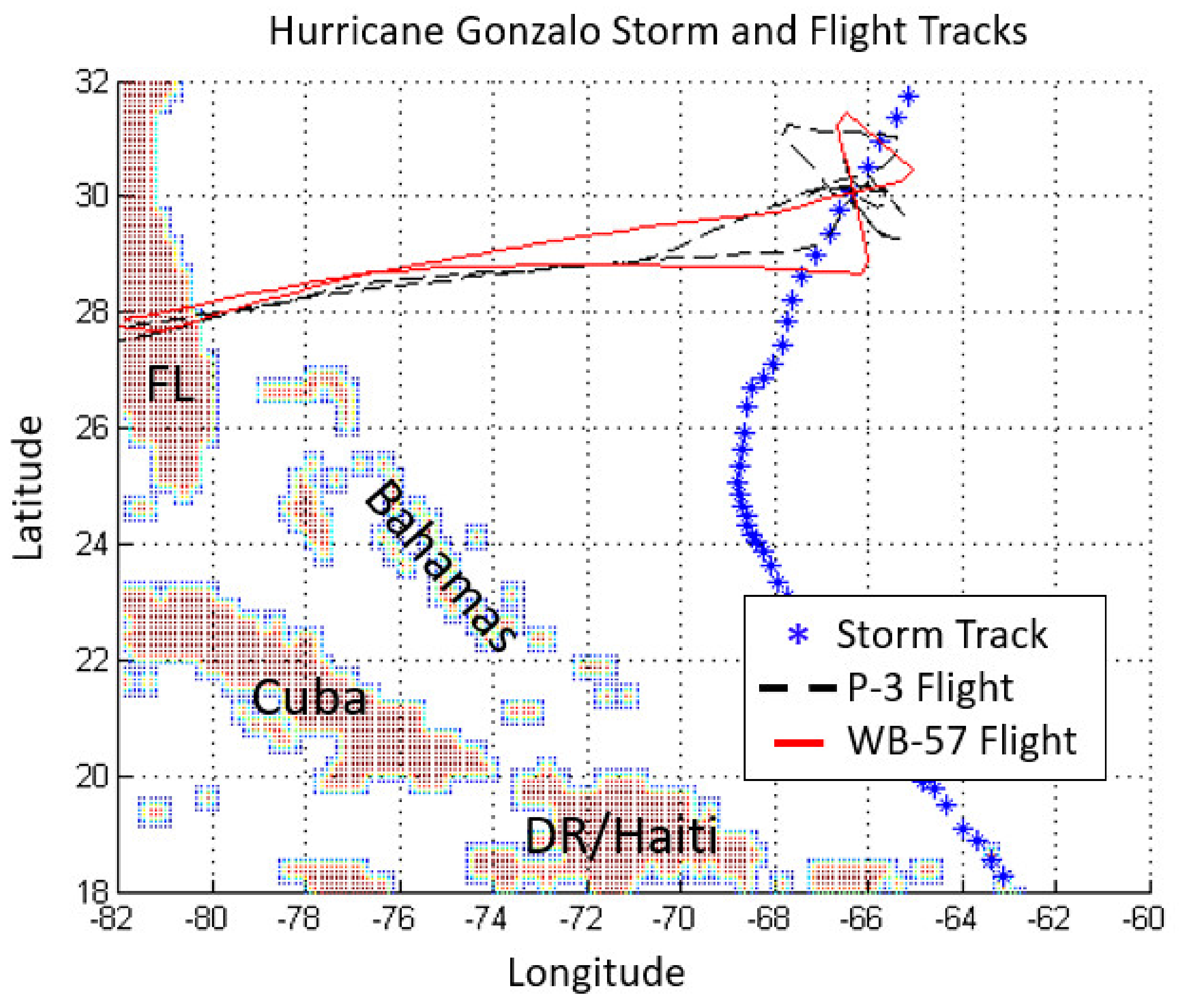
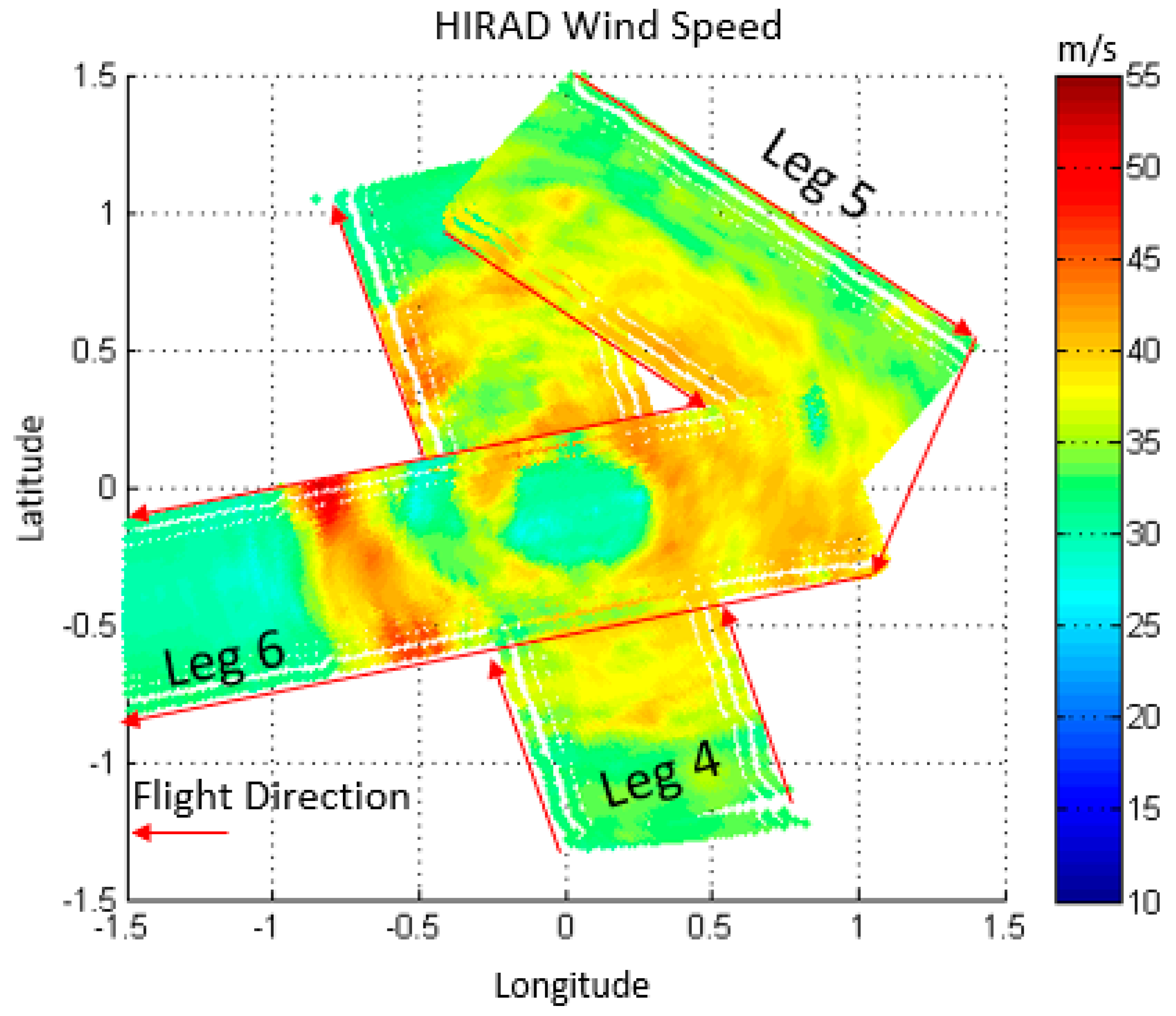
3.4. Hurricane Validation Using Mulitple Hurricane Flights
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. SFMR Polar Interpolation
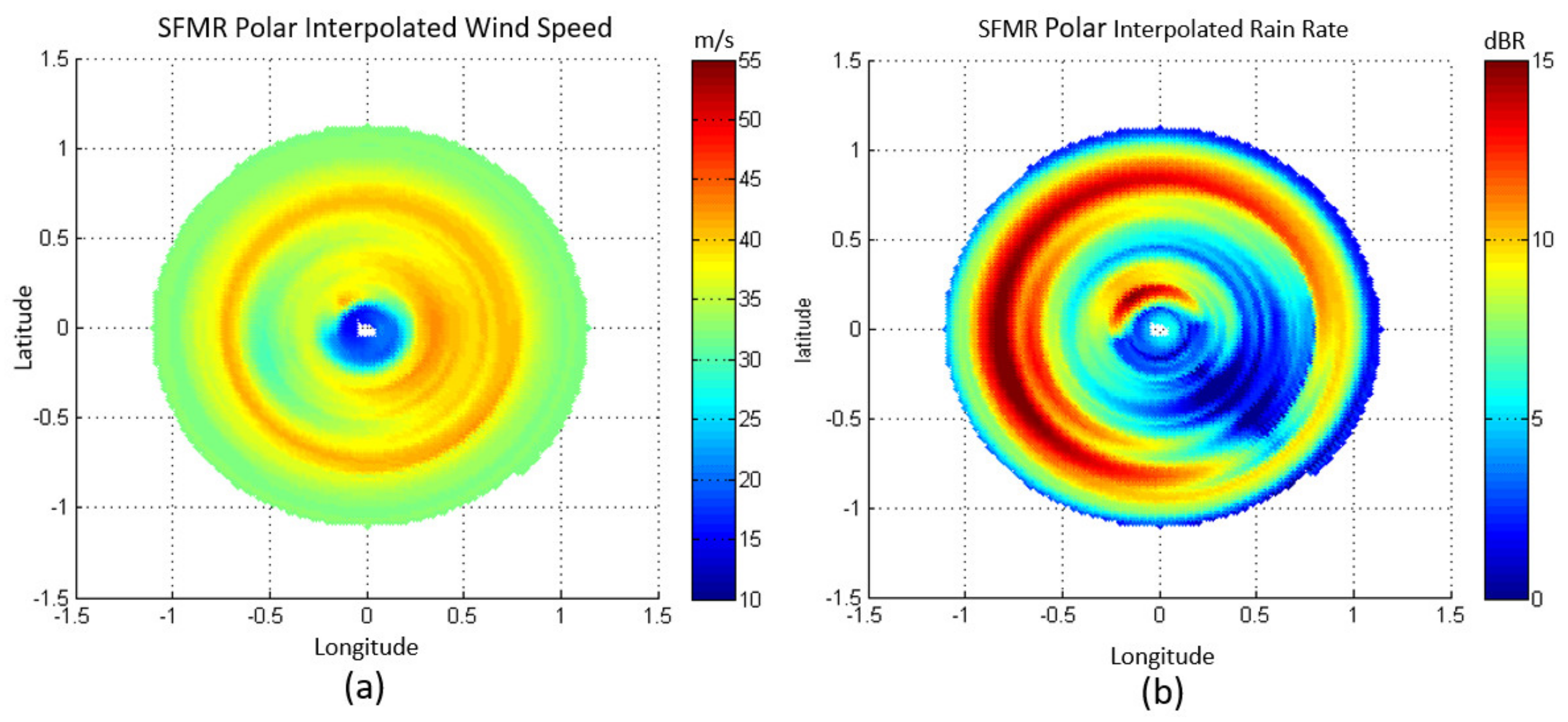
Appendix A.2. LFR Measurement and Calibration
References
- Jones, W.L.; Black, P.G.; Delnore, V.E.; Swift, C.T. Airborne Remote Sensing Measurements of Hurricane Alle. Science 1981, 24, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Uhlhorn, E.W.; Black, P.G.; Franklin, J.L.; Goodberlet, M.; Carswell, J.; Goldstein, A.S. Hurricane surface wind measurements from an operational stepped frequency microwave radiometer. Mon. Weather. Rev. 2007, 135, 3070–3085. [Google Scholar] [CrossRef]
- Tanner, A.B.; Swift, C.T. Calibration of a synthetic aperture radiometer. IEEE Trans. Geosci. Remote Sens. 1993, 31, 257–267. [Google Scholar] [CrossRef]
- Didlake, A.C., Jr.; Heymsfield, G.M.; Reasor, P.D.; Guimond, S.R. Concentric Eyewall Asymmetries in Hurricane Gonzalo (2014) Observed by Airborne Radar. Mon. Weather. Rev. 2017, 145, 729–749. Available online: https://journals.ametsoc.org/view/journals/mwre/145/3/mwr-d-16-0175.1.xml (accessed on 30 May 2022). [CrossRef]
- Brown, D.P. National Hurricane Center Tropical Cyclone Report: Hurricane Gonzalo (AL082014); National Hurricane Center: Miami, FL, USA, 2015.
- Black, G.P.; Swift, C.L. Airborne stepped frequency microwave radiometer measurements of rainfall rate and surface wind speed in hurricanes. Am. Meteorol. Soc. 1984, 433, 438. [Google Scholar]
- Uhlhorn, W.E.; Black, P.G. Verification of remotely sensed sea surface winds in hurricanes. J. Atmos. Ocean. Technol. 2003, 20, 99–116. [Google Scholar] [CrossRef]
- Jiang, H.; Black, P.; Zipser, E.; Marks, F.; Uhlhorn, E. Validation of Rain-Rate Estimation in Hurricanes from the Stepped Frequency Microwave Radiometer: Algorithm Correction and Error Analysis. J. Atmos. Sci. 2006, 63, 252–267. [Google Scholar] [CrossRef]
- Le Vine, D.M.; Griffis, A.J.; Swift, C.T.; Jackson, T.J. ESTAR: A Synthetic Aperture Microwave Radiometer for Remote Sensing Applications. Proc. IEEE 1994, 82, 1787–1801. [Google Scholar] [CrossRef]
- Ruff, C.; Principe, C. X-band Lightweight Rainfall Radiometer first flight. In Proceedings of the 2003 IEEE International Geoscience Remote Sensing Symposium, Toulouse, France, 21–25 July 2003. [Google Scholar]
- Ruf, C.S. Numerical annealing of low redundancy linear arrays. IEEE Trans. Antennas Propag. 1993, 41, 85–90. [Google Scholar] [CrossRef]
- Ruf, C.; Roberts, J.B.; Biswas, S.; James, M.; Miller, T. Calibration and image reconstruction for The Hurricane Imaging Radiometer (HIRAD). In Proceedings of the IEEE IGARSS 2012, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Cecil, D.J.; Sayak, B. Hurricane and Severe Storm Sentinel (HS3) Hurricane Imaging Radiometer (HIRAD). Available online: https://hs3.nsstc.nasa.gov/pub/hs3/HIRAD/ (accessed on 17 October 2014). [CrossRef]
- Alasgah, A.; Jacob, M.; Jones, W.L. Removal of Artifacts from Hurricane Imaging Radiometer Tb Images. In Proceedings of the IEEE 2017 Southeast Conference, Concord, NC, USA, 3 March–2 April 2017. [Google Scholar] [CrossRef]
- Biswas, S.; Cecil, D. Recent improvements in Hurricane Imaging Radiometer’s brightness temperature image reconstruction. Results Phys. 2017, V7, 4349–4351. [Google Scholar] [CrossRef]
- Alasgah, A.; Jacob, M.; Jones, L.; Schneider, L. Validation of the Hurricane Imaging Radiometer Forward Radiative Transfer Model for a Convective Rain Event. Remote Sens. 2019, 11, 2650. [Google Scholar] [CrossRef]
- El-Nimri, S.; Jones, W.; Uhlhorn, E.; Ruf, C.; Black, P. An Improved C-Band Ocean Surface Emissivity Model at Hurricane-Force Wind Speeds Over a Wide Range of Earth Incidence Angles. Geosci. Remote Sens. Lett. IEEE 2010, 7, 641–645. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization: Theory and Practice, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. Available online: http://www.jstor.org/stable/24869236 (accessed on 1 June 2022). [CrossRef]
- Amarin, R.A.; Jones, W.L.; El-Nimri, S.F.; Johnson, J.W.; Ruf, C.S.; Miller, T.L.; Uhlhorn, E. Hurricane Wind Speed Measurements in Rainy Conditions Using the Airborne Hurricane Imaging Radiometer (HIRAD). IEEE Trans. Geosci. Remote Sens. 2012, 50, 180–192. [Google Scholar] [CrossRef]
- Morris, M.; Ruf, C. A Coupled-Pixel Model (CPM) Atmospheric Retrieval Algorithm for High Resolution Imagers. J. Atmos. Ocean. Technol. 2015, 32, 150804114856003. [Google Scholar] [CrossRef]
- Franklin, J.L.; Black, M.L.; Valde, K. GPS drop-windsonde wind profiles in hurricanes and their operational implications. Weather Forecast. 2003, 18, 32–44. [Google Scholar] [CrossRef]
- Sellwood, K.; Aksoy, A.; Dunion, J.P.; Cecil, D.J. An Observing System Experiment (OSE) Study of the Hurricane Imaging Radiometer (HIRAD) instrument. In Proceedings of the 33rd Conference on Hurricanes and Tropical Meteorology, AMS, Ponte Vedra, FL, USA, 17–18 April 2018. [Google Scholar]
- Coto, J.; Jones, W.L.; Heymsfield, G.M. Validation of the High-Altitude Wind and Rain Airborne Profiler during the Tampa Bay Rain Experiment. Climate 2021, 9, 89. [Google Scholar] [CrossRef]
- Rao, U.N.; Sarkar, A.; Mohan, M. Theoretical Z-R relationship for precipitating systems using Mie scattering approach. Indian J. Radio Space Phys. 2005, 34, 191–196. [Google Scholar]





| Instrument | Aircraft | Description | Relevant Product |
|---|---|---|---|
| SFMR | P-3 | 6 channel (4.74, 5.31, 5.57, 6.02, 6.69, 7.09 GHz) nadir pointing C-band MW radiometer, measuring ocean brightness temperatures | Wind speed m/s Path Average Rain Rate mm/h (provided) |
| LFR | P-3 | 5.37 GHz Horizontally Scanning Radar measuring 2D images of rain reflectivity | Rain Rate mm/h (calculated) |
| GPS Dropwindsonde | P-3 | Dispensed and parachuted instrument measuring vertical profiles of atmospheric winds | GPS-derived wind speeds m/s (provided) |
| HIRAD | WB-57 | 4 channel (4.0, 5.0, 6.0, 6.6 GHz) push-broom radiometer, measuring a 60 km swath of ocean brightness temperatures | 2D wind speeds m/s 2D rain rates mm/h (calculated) |
| HIWRAP | WB-57 | Conically scanning, Ku-band (13.9 GHz) radar with an H-pol 30° inner beam and V-pol 40° outer beam | Rain Flag Detection 3D Rain Rates (mm/h) (calculated) |
| HIRAD Leg | Dropsondes | Mean Difference m/s | Standard Error m/s | RMS Error m/s |
|---|---|---|---|---|
| MSFC Leg 4 | 6 | −15.6 | 7.9 | 17.2 |
| MSFC Leg 6 | 9 | −8.4 | 3.7 | 9.1 |
| MSFC Combined | 13 | −11.3 | 6.1 | 12.7 |
| New Cal Leg 4 | 6 | −0.0 | 2.9 | 2.6 |
| New Cal Leg 6 | 9 | −0.1 | 4.3 | 4.1 |
| New Combined | 13 | −0.3 | 3.8 | 3.7 |
| HIRAD Leg | Mean Difference | Standard Error | RMS Error |
|---|---|---|---|
| Leg 4 | −2.3 | 5.3 | 5.8 |
| Leg 5 | 0.4 | 3.1 | 3.8 |
| Leg 6 | −5.6 | 4.0 | 7.6 |
| All rains | −2.0 | 5.2 | 5.6 |
| All rains > 10 mm/h | 0.2 | 2.3 | 4.9 |
| Hurricane | Date | Samples Sonde | ME Sonde | SE Sonde | RMSE Sonde | Samples SFMR | ME SFMR | SE SFMR | RMSE SFMR |
|---|---|---|---|---|---|---|---|---|---|
| Ingrid | 15 September 2013 | 5 | −0.7 | 2.5 | 2.3 | 1.5 k | 0.0 | 3.0 | 3.0 |
| Gonzalo | 17 October 2014 | 13 | −0.3 | 3.9 | 3.8 | 2.0 k | 0.7 | 1.7 | 1.8 |
| Marty | 28 August 2015 | 50 | 0.3 | 3.7 | 3.7 | 1.5 k | −1.5 | 4.4 | 4.7 |
| Patricia | 21 October 2015 | 46 | −1.2 | 3.0 | 3.2 | 1.6 k | −1.0 | 3.1 | 3.3 |
| Patricia | 22 October 2015 | 45 | −4.1 | 4.0 | 5.6 | 2.6 k | 0.0 | 3.2 | 3.2 |
| Patricia | 23 October 2015 | 49 | −2.5 | 5.2 | 5.9 | 2.5 k | 0.0 | 3.4 | 3.4 |
| Total | - | 208 | −1.7 | 3.2 | 4.7 | 11.7 k | −0.2 | 3.3 | 3.3 |
| Wind Speed | Samples of Sonde | ME Sonde | SE Sonde | RMS Sonde | Samples of SFMR | ME SFMR | SE SFMR | RMS SFMR |
|---|---|---|---|---|---|---|---|---|
| <20 | 106 | −2.8 | 2.5 | 4.2 | 4.4 k | −1.4 | 2.9 | 3.3 |
| 20–30 | 52 | −0.3 | 3.3 | 5.0 | 3.5 k | 0.1 | 3.1 | 3.1 |
| 30–40 | 21 | −1.6 | 3.3 | 4.8 | 2.2 k | 0.0 | 2.5 | 2.5 |
| 40–50 | 17 | −0.2 | 4.4 | 5.7 | 1.3 k | 1.8 | 3.5 | 3.9 |
| 50+ | 3 | 3.4 | 5.3 | 7 | 0.2 k | 3.6 | 4.7 | 6.0 |
| EIA | Samples of Sonde | ME Sonde | SE Sonde | RMS Sonde | Samples of SFMR | ME SFMR | SE SFMR | RMS SFMR |
|---|---|---|---|---|---|---|---|---|
| <20 | 54 | −1.4 | 3.1 | 4.2 | 1.6 k | 0.4 | 2.1 | 3.0 |
| 20–35 | 88 | −2.2 | 3.4 | 5.3 | 2.3 k | 0.6 | 2.5 | 3.6 |
| 35–50 | 44 | −1.5 | 3.0 | 4.2 | 4.2 k | −0.8 | 2.2 | 3.0 |
| 50–65 | 13 | −0.3 | 2.9 | 3.5 | 4.5 k | −0.2 | 2.6 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coto, J.; Jones, W.L.; Cecil, D.J.; Biswas, S. Experimental Proof of Concept for the Hurricane Imaging Radiometer (HIRAD) Measurement of a Hurricane Ocean Surface Wind Speed Field. Remote Sens. 2022, 14, 3634. https://doi.org/10.3390/rs14153634
Coto J, Jones WL, Cecil DJ, Biswas S. Experimental Proof of Concept for the Hurricane Imaging Radiometer (HIRAD) Measurement of a Hurricane Ocean Surface Wind Speed Field. Remote Sensing. 2022; 14(15):3634. https://doi.org/10.3390/rs14153634
Chicago/Turabian StyleCoto, Jonathan, W. Linwood Jones, Daniel J. Cecil, and Sayak Biswas. 2022. "Experimental Proof of Concept for the Hurricane Imaging Radiometer (HIRAD) Measurement of a Hurricane Ocean Surface Wind Speed Field" Remote Sensing 14, no. 15: 3634. https://doi.org/10.3390/rs14153634
APA StyleCoto, J., Jones, W. L., Cecil, D. J., & Biswas, S. (2022). Experimental Proof of Concept for the Hurricane Imaging Radiometer (HIRAD) Measurement of a Hurricane Ocean Surface Wind Speed Field. Remote Sensing, 14(15), 3634. https://doi.org/10.3390/rs14153634







