LCNS Positioning of a Lunar Surface Rover Using a DEM-Based Altitude Constraint
Abstract
:1. Introduction
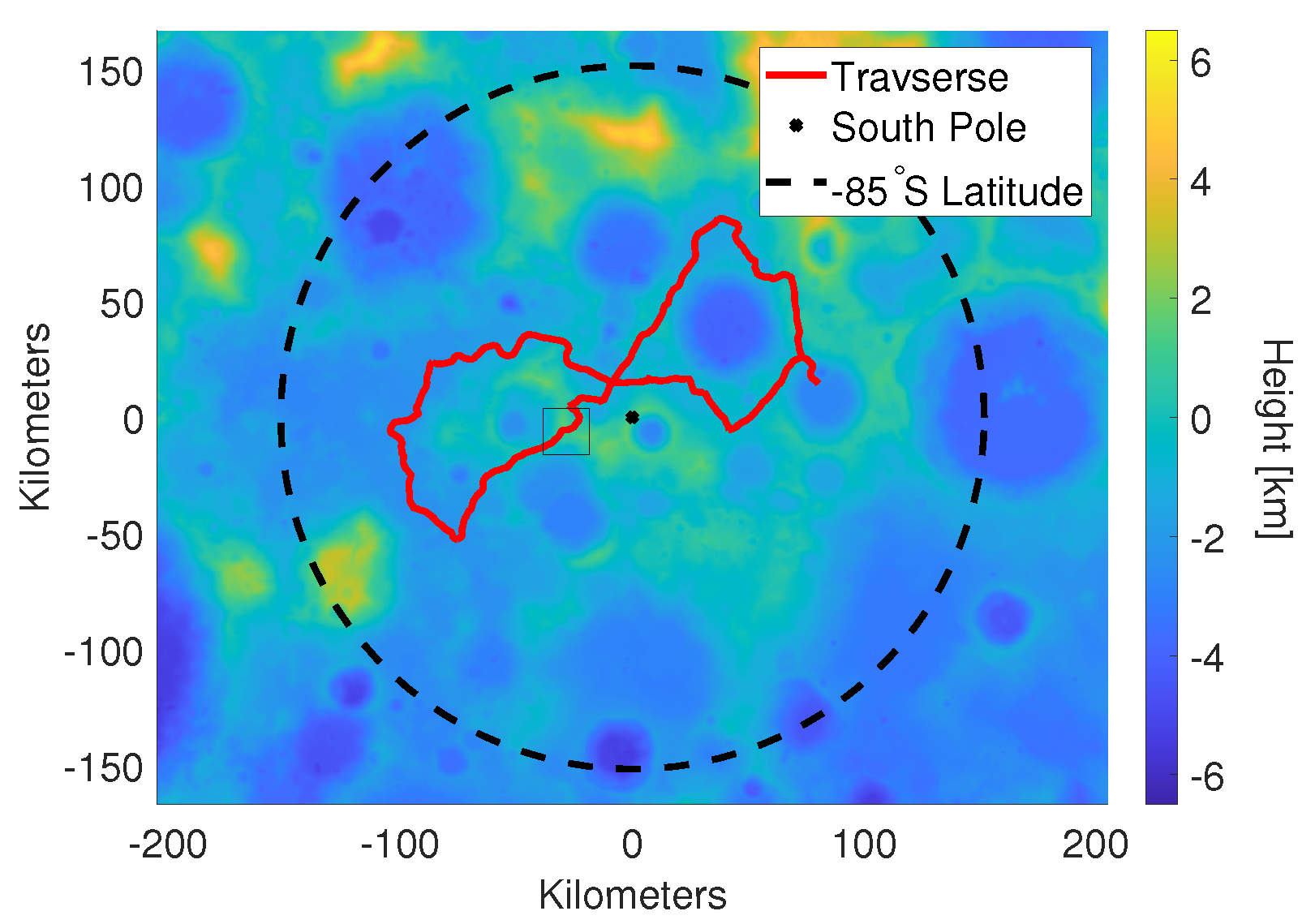
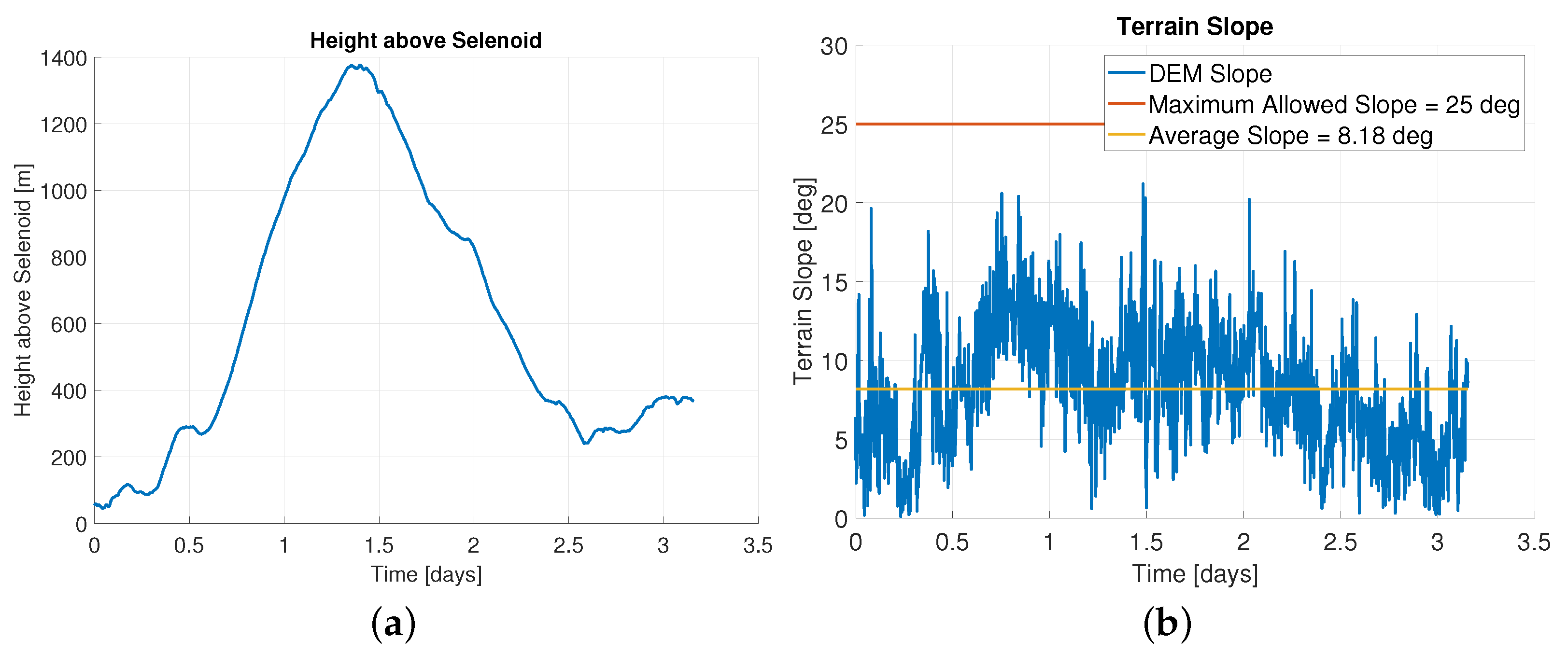
2. Lunar Surface Rover Mission Profile
- Loading the 2D traverse [22] provided in a replaced[id=fm]geographic information systemGeographic Information System (GIS) shapefile;
- Time tagging the points along the traverse such that the horizontal velocity equals 0.36 km/h;
- Interpolating the horizontal traverse at the requested time-step (1 s);
- Interpolating the DEM to get the rover position in polar stereograhic reference frame (including the height). As the velocity is horizontally constrained, the actual velocity in three dimensions will be slightly larger than 0.36 km/h;
- Converting the polar stereographic coordinates to a selenodetic reference frame.
3. Moonlight and LCNS
- Phase 1–Use of High-Sensitivity Space Receivers (2022–2025): Based on the reception of Earth GNSS signals with high-sensitivity receivers, on-board dynamic filters and high-gain antennas. This phase should provide initial services for Earth-Moon transfers and lunar orbit operations.
- Phase 2–Lunar Communication and Navigation Services (LCNS) (2025–2035): Enhancing the Phase 1 with the transmission of additional ranging signals from both the Moon orbit and surface. This phase should allow a major reduction of the geometric DOP (dilution of precision) and improve the service availability, which, in turn, would translate into enhanced lunar orbit navigation and initial landing/surface PNT (position, navigation and timing) services (e.g., on the Moon’s South Pole).
- Phase 3–Full Lunar PNT System (2035-onwards): This phase should provide PNT services on the whole Moon surface and enhance the positioning availability and accuracy in the Moon orbit and on the lunar South Pole. This could be obtained by complementing Phase 2 with additional lunar orbiting satellites and Moon surface beacons. This phase could also allow for the provision of integrity services for safety critical applications, leading to increased autonomy.
3.1. LCNS Constellation
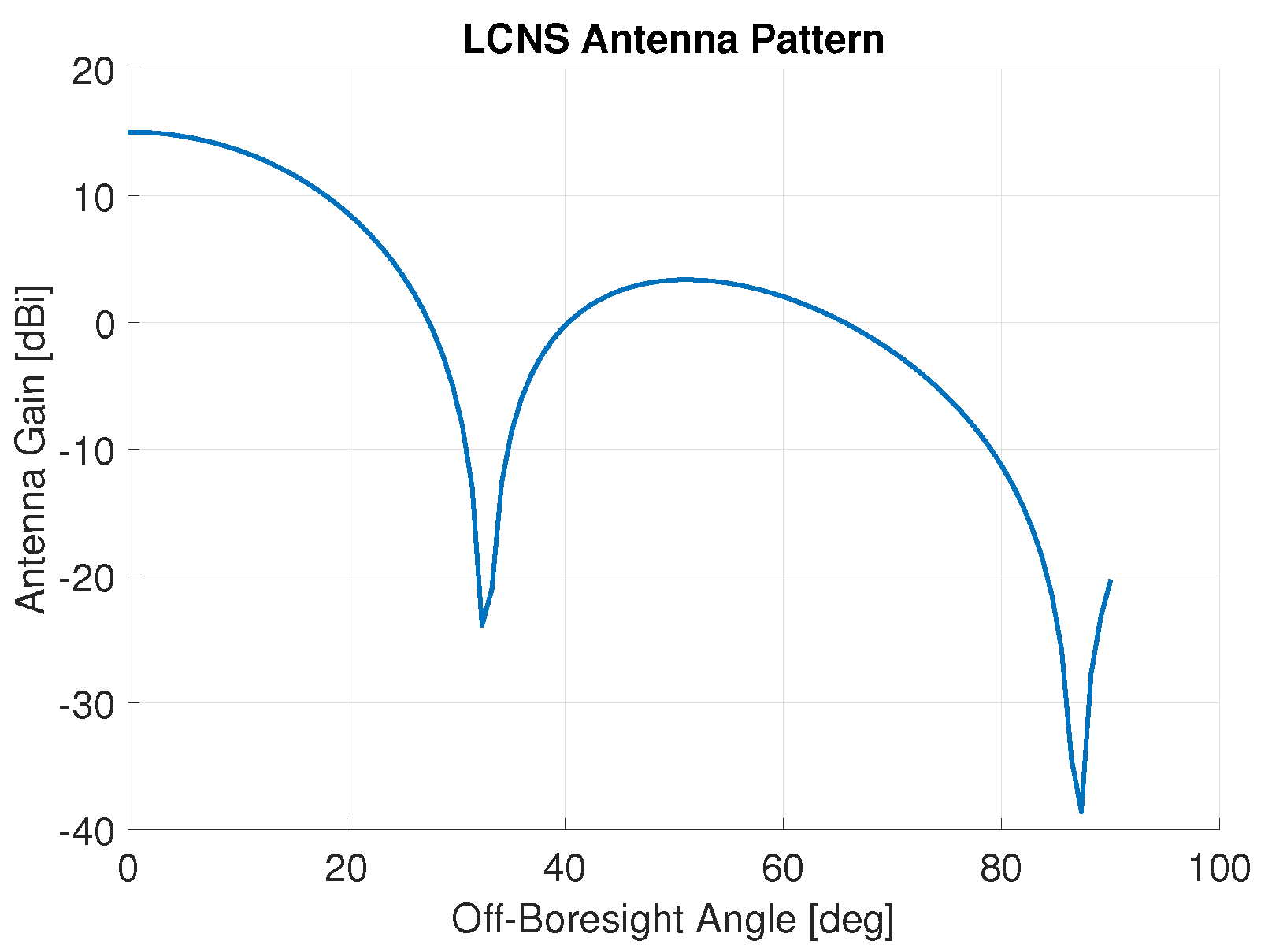
3.2. LCNS Payload
3.3. Rover LCNS Receiver
| Navigation Grade | Tactical Grade | |
|---|---|---|
| Weight | 9.0 kg | 748 g |
| Example | iMAR iNAV-RQH-1001 [38] | Northtrop Grumman LN-200S [37] |
| Velocity Random Walk | 8 μg/ | 35 g/ |
| Velocity Process Noise () | 7.8 m/s/ | 3.4 m/s/ |
| Product | Microchip OX-249 [39] | AXTAL AXIOM6060 [40] | AXTAL AXIOM70SL [41] |
|---|---|---|---|
| Weight | 14 g | 200 g | 20 g |
| Reference frequency | n/a | 100 MHz | 10 MHz |
| Frequency Stability | 100 ppb | 50 ppb | 10 ppb |
| Allan Deviation ( = 1 s) | |||
| Clock Bias Process Noise () | 0.003 m/ | 0.030 m/ | 0.001 m/ |
| Clock Drift Process Noise () | 30 m/s/ | 15 m/s/ | 3 m/s/ |
4. Covariance Analysis
4.1. Extended Kalman Filter
4.2. Prediction Model
4.3. Measurement Model
4.4. Simulation Settings
4.5. Measurement Covariance Modelling
4.5.1. LCNS Covariance Model
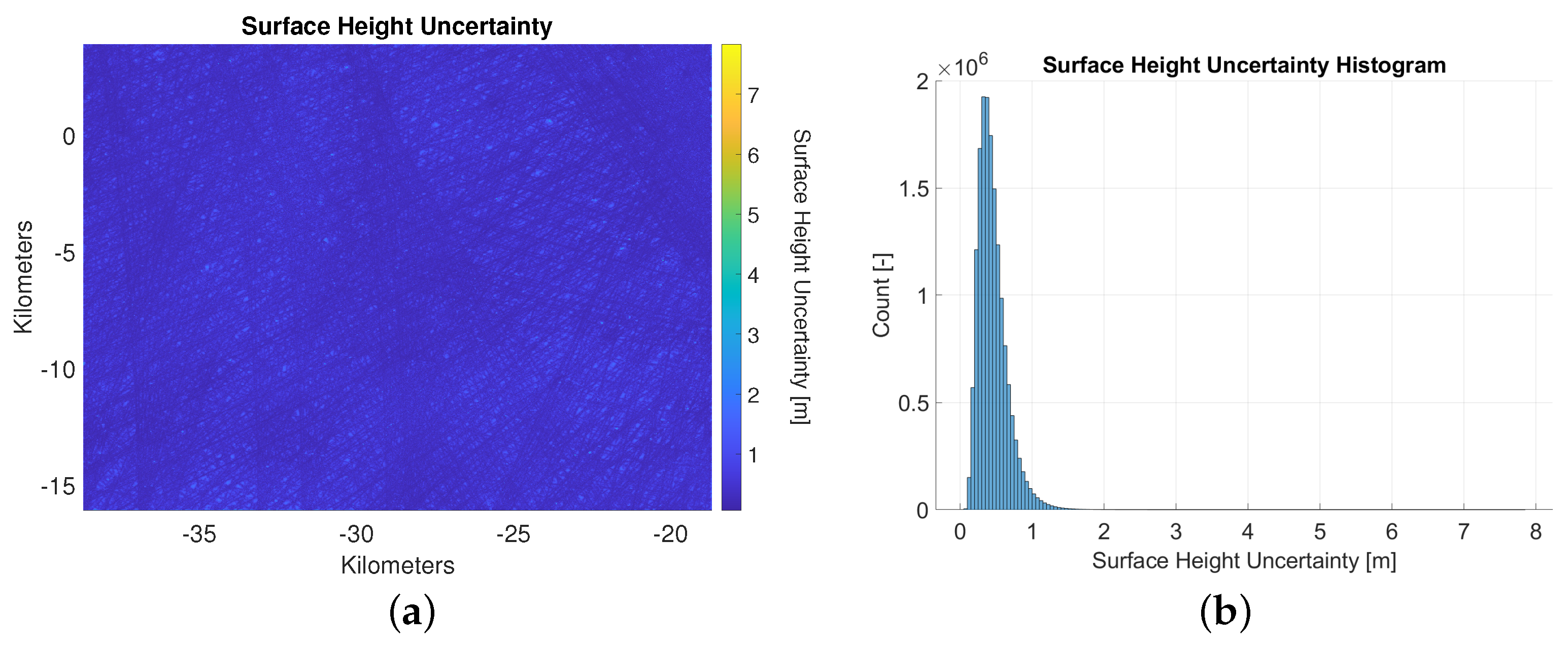
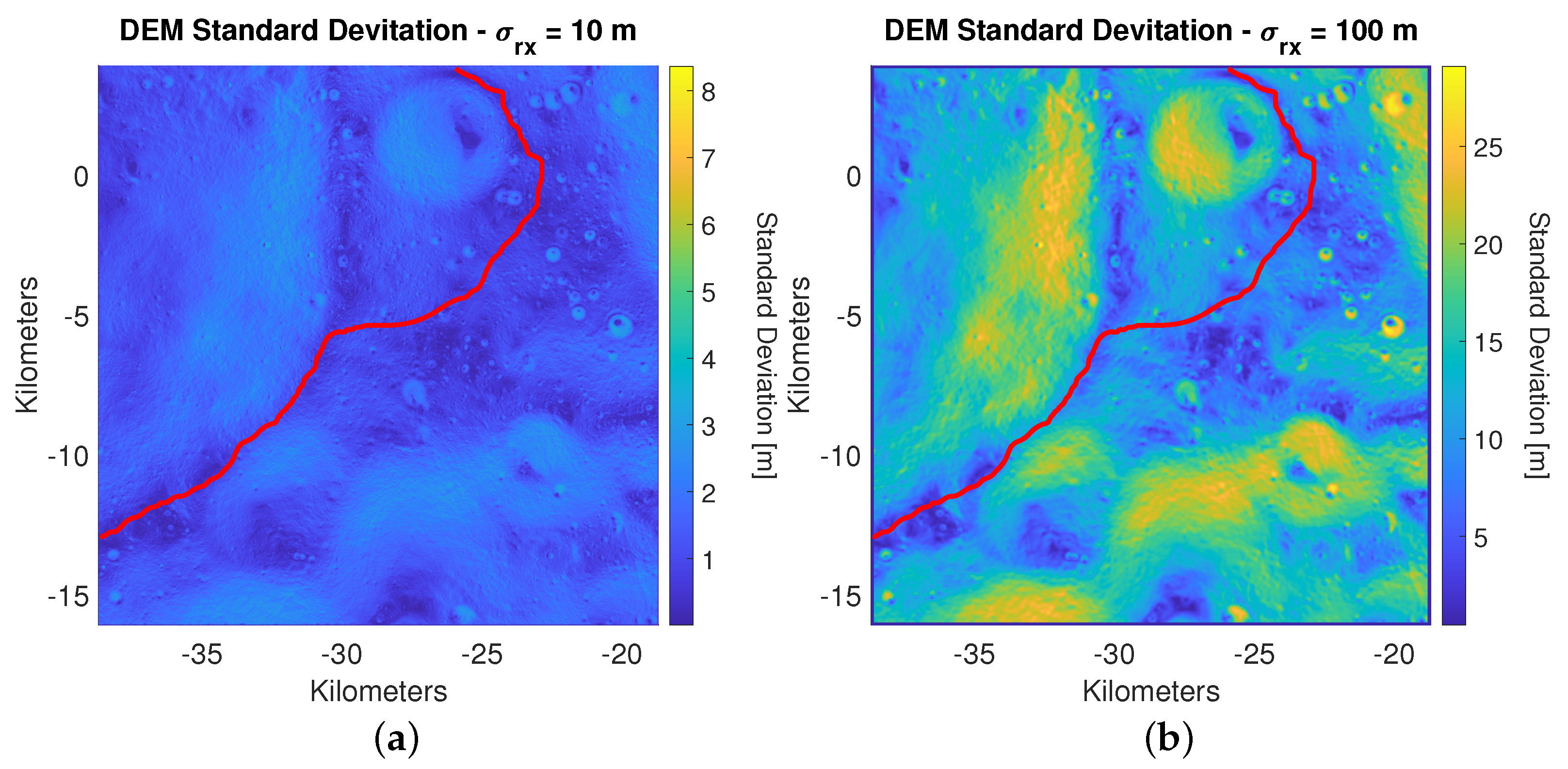
4.5.2. DEM Covariance Model
- The data component, which is related to the orbital errors and interpolation;
- A geologic component, which is related to natural terrain variations (e.g., variation of the terrain within one pixel);
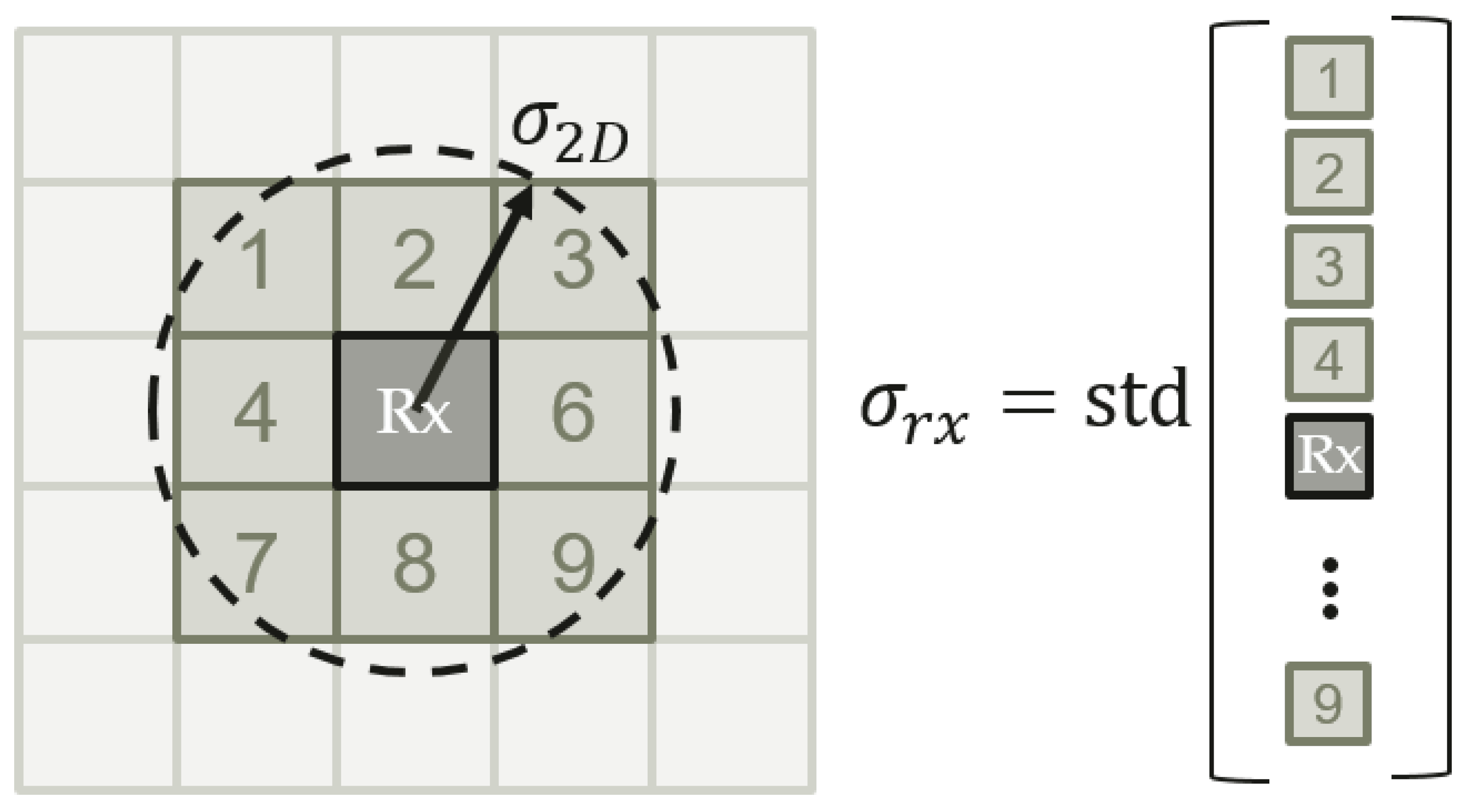
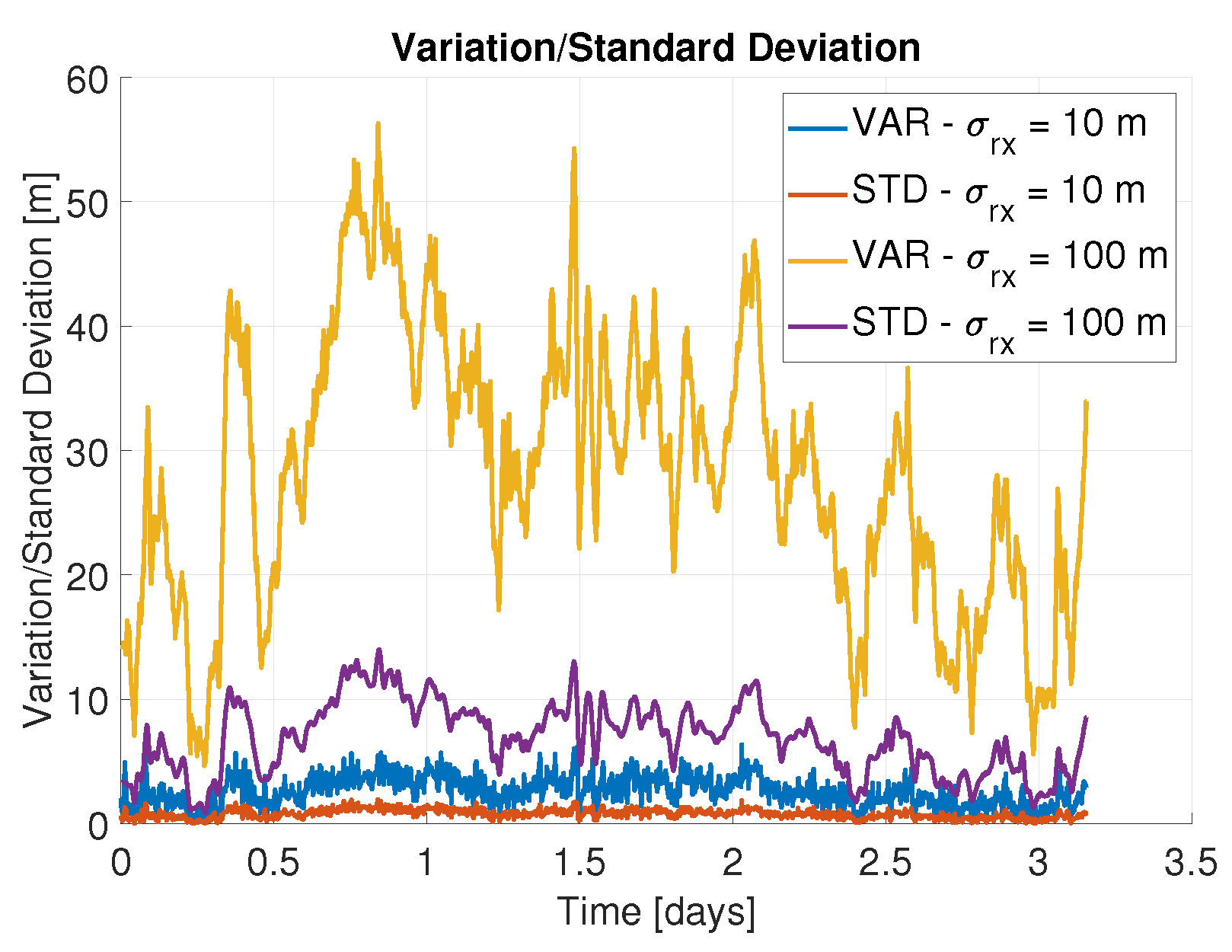
- A component that is related to the horizontal covariance of the receiver of the rover. When the covariance of the rover is larger than 5 m (i.e., the width of a pixel), the rover can also be located in adjacent pixels, which introduces an additional uncertainty component in the height measurement.
5. Results
5.1. Baseline
5.2. Sensitivity Analysis ODTS
5.3. Sensitivity Analysis Process Noise
5.4. Sensitivity Analysis ODTS and Process Noise
6. Conclusions
7. Disclaimer
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AOD | Age of Data |
| BPSK | Binary Phase Shift Keying |
| CDF | Cumulative Density Function |
| CNSA | China National Space Administration |
| DEM | Digital Elevation Model |
| DLL | Delay Locked Loop |
| DOP | Dilution of Precision |
| DSN | Deep Space Network |
| EIRP | Effective Isotropic Radiated Power |
| EKF | Extended Kalman Filter |
| ELFO | Elliptical Lunar Frozen Orbit |
| ESA | European Space Agency |
| FLL | Frequency Locked Loop |
| GIS | Geographic Information System |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| HDOP | Horizontal Dilution of Precision |
| IMU | Inertial Measurement Unit |
| INS | Inertial Navigation System |
| JAXA | Japan Aerospace Exploration Agency |
| LANS | Lunar Augmented Navigation Service |
| LCNS | Lunar Communication and Navigation Services |
| LiASON | Linked Autonomous Interplanetary Satellite Orbit Navigation |
| LIDAR | LIght Detection and Ranging |
| LNA | Low Noise Amplifier |
| LOLA | Lunar Orbiter Laser Altimeter |
| LRO | Lunar Reconnaissance Orbiter |
| MER | Mars Exploration Rovers |
| NASA | National Aeronautics and Space Administration |
| OCXO | Oven Controlled Crystal Oscillator |
| ODTS | Orbit Determination and Time Synchronization |
| PDS | Planetary Data System |
| PLL | Phase Locked Loop |
| PNT | Position Navigation and Timing |
| RAAN | Right Ascension of the Ascending Node |
| RF | Radio Frequency |
| RFFE | Radio Frequency Front-End |
| SDD | Service Definition Document |
| SFCG | Space Frequency Coordination Group |
| SISE | Signal-in-Space Error |
| SPR | Small Pressurized Rover |
| VO | Visual Odometry |
References
- International Space Exploration Coordination Group. The Global Exploration Roadmap. 2018. Available online: https://www.nasa.gov/sites/default/files/atoms/files/ger_2018_small_mobile.pdf (accessed on 13 June 2022).
- Johnson, A.E.; Montgomery, J.F. Overview of terrain relative navigation approaches for precise lunar landing. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–10. [Google Scholar]
- European Space Agency. Moonlight: Connecting Earth with the Moon. 2020. Available online: https://www.esa.int/ESA_Multimedia/Videos/2020/11/Moonlight_connecting_Earth_with_the_Moon/%28lang%29 (accessed on 23 June 2022).
- Lockheed Martin. Communicating with the Moon Is Getting Easier. 2022. Available online: https://www.lockheedmartin.com/en-us/news/features/2021/lunar-communication-and-navigation-network.html (accessed on 21 June 2022).
- GPS World. Ark Edge Space to Study Lunar Positioning, Communications for JAXA 2022. Available online: https://www.gpsworld.com/ark-edge-space-to-study-lunar-positioning-communications-for-jaxa/ (accessed on 21 June 2022).
- GPS World. Russia Plans to Place Positioning Satellites around the Moon 2018. Available online: https://www.gpsworld.com/russia-plans-to-place-positioning-satellites-around-the-moon/ (accessed on 21 June 2022).
- China.org.cn. China Starts Enginereing Development of Lunar Exploration Program’s Fourth Phase. 2022. Available online: http://www.china.org.cn/china/2022-04/25/content_78185065.htm (accessed on 21 June 2022).
- Draft LunaNet Interoperability Specifications. Technical report, NASA. 2022. Available online: https://esc.gsfc.nasa.gov/static-files/Draft%20LunaNet%20Interoperability%20Specification%20Final.pdf (accessed on 21 June 2022).
- Trexler, T.T.; Odden, R.B. Lunar Surface Navigation. IEEE Trans. Aerosp. Electron. Syst. 1966, AES-2, 252–259. [Google Scholar] [CrossRef]
- Yenilmez, L.; Temeltas, H. Autonomous navigation for planetary exploration by a mobile robot. In Proceedings of the International Conference on Recent Advances in Space Technologies, 2003. RAST’03, Istanbul, Turkey, 20–22 November 2003; pp. 397–402. [Google Scholar]
- Li, R.; Squyres, S.W.; Arvidson, R.E.; Archinal, B.A.; Bell, J.; Cheng, Y.; Crumpler, L.; Des Marais, D.J.; Di, K.; Ely, T.A.; et al. Initial results of rover localization and topographic mapping for the 2003 Mars Exploration Rover mission. Photogramm. Eng. Remote Sens. 2005, 71, 1129–1142. [Google Scholar] [CrossRef]
- Li, R.; Di, K.; Howard, A.B.; Matthies, L.; Wang, J.; Agarwal, S. Rock modeling and matching for autonomous long-range Mars rover localization. J. Field Robot. 2007, 24, 187–203. [Google Scholar] [CrossRef]
- Maimone, M.; Johnson, A.; Cheng, Y.; Willson, R.; Matthies, L. Autonomous navigation results from the Mars Exploration Rover (MER) mission. In Experimental Robotics IX; Springer: Berlin/Heidelberg, Germany, 2006; pp. 3–13. [Google Scholar]
- Goldberg, S.B.; Maimone, M.W.; Matthies, L. Stereo vision and rover navigation software for planetary exploration. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; Volume 5, p. 5. [Google Scholar]
- Geromichalos, D.; Azkarate, M.; Tsardoulias, E.; Gerdes, L.; Petrou, L.; Perez Del Pulgar, C. SLAM for autonomous planetary rovers with global localization. J. Field Robot. 2020, 37, 830–847. [Google Scholar] [CrossRef]
- Carle, P.J.; Barfoot, T.D. Global rover localization by matching lidar and orbital 3d maps. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 20; pp. 881–886.
- Matthies, L.; Daftry, S.; Tepsuporn, S.; Cheng, Y.; Atha, D.; Swan, R.M.; Ravichandar, S.; Ono, M. Lunar Rover Localization Using Craters as Landmarks. arXiv 2022, arXiv:2203.10073. [Google Scholar]
- Jun, W.W.; Cheung, K.M.; Lightsey, E.G.; Lee, C. A minimal architecture for real-time lunar surface positioning using joint Doppler and ranging. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1367–1376. [Google Scholar] [CrossRef]
- Parker, T.; Golombek, M.; Powell, M. Geomorphic/geologic mapping, localization, and traverse planning at the Opportunity landing site, Mars. In Proceedings of the 4st Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 1–5 March 2010; p. 2638, No. 1533. [Google Scholar]
- Chelmins, D.T.; Welch, B.W.; Sands, O.S.; Nguyen, B.V. A Kalman Approach to Lunar Surface Navigation Using Radiometric and Inertial Measurements; Technical Report; NASA: Washington, DC, USA, 2009. [Google Scholar]
- Hesar, S.G.; Parker, J.S.; Leonard, J.M.; McGranaghan, R.M.; Born, G.H. Lunar far side surface navigation using linked autonomous interplanetary satellite orbit navigation (LiAISON). Acta Astronaut. 2015, 117, 116–129. [Google Scholar] [CrossRef]
- Allender, E.J.; Orgel, C.; Almeida, N.V.; Cook, J.; Ende, J.J.; Kamps, O.; Mazrouei, S.; Slezak, T.J.; Soini, A.J.; Kring, D.A. Traverses for the ISECG-GER design reference mission for humans on the lunar surface. Adv. Space Res. 2019, 63, 692–727. [Google Scholar] [CrossRef]
- Li, S.; Lucey, P.G.; Milliken, R.E.; Hayne, P.O.; Fisher, E.; Williams, J.P.; Hurley, D.M.; Elphic, R.C. Direct evidence of surface exposed water ice in the lunar polar regions. Proc. Natl. Acad. Sci. USA 2018, 115, 8907–8912. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.E.; Zuber, M.T.; Jackson, G.B.; Cavanaugh, J.F.; Neumann, G.A.; Riris, H.; Sun, X.; Zellar, R.S.; Coltharp, C.; Connelly, J.; et al. The lunar orbiter laser altimeter investigation on the lunar reconnaissance orbiter mission. Space Sci. Rev. 2010, 150, 209–241. [Google Scholar] [CrossRef]
- Tooley, C.R.; Houghton, M.B.; Saylor, R.S.; Peddie, C.; Everett, D.F.; Baker, C.L.; Safdie, K.N. Lunar Reconnaissance Orbiter mission and spacecraft design. Space Sci. Rev. 2010, 150, 23–62. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Head, J.W. Improved LOLA elevation maps for south pole landing sites: Error estimates and their impact on illumination conditions. Planet. Space Sci. 2021, 203, 105119. [Google Scholar] [CrossRef]
- Barker, M.; Mazarico, E.; Neumann, G.; Zuber, M.; Haruyama, J.; Smith, D. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. Available online: http://imbrium.mit.edu/ (accessed on 9 August 2022). [CrossRef]
- Delépaut, A.; Giordano, P.; Ventura-Traveset, J.; Blonski, D.; Schönfeldt, M.; Schoonejans, P.; Aziz, S.; Walker, R. Use of GNSS for lunar missions and plans for lunar in-orbit development. Adv. Space Res. 2020, 66, 2739–2756. [Google Scholar] [CrossRef]
- Grenier, A.; Giordano, P.; Bucci, L.; Cropp, A.; Zoccarato, P.; Swinden, R.; Ventura-Traveset, J. Positioning and Velocity Performance Levels for a Lunar Lander using a Dedicated Lunar Communication and Navigation System. Navig. J. Inst. Navig. 2022, 69, navi.513. [Google Scholar] [CrossRef]
- Barton, G.H.; Sheppard, S.W.; Brand, T.J. Proposed autonomous lunar navigation system. Astrodynamics 1993, 1993, 1717–1736. [Google Scholar]
- Schönfeldt, M.; Grenier, A.; Delépaut, A.; Giordano, P.; Swinden, R.; Ventura-Traveset, J. Across the Lunar Landscape: Towards a Dedicated Lunar PNT System. Inside GNSS. 2020. Available online: https://insidegnss.com/across-the-lunar-landscape-exploration-with-gnss-technology/ (accessed on 9 August 2022).
- Giordano, P.; Grenier, A.; Zoccarato, P.; Bucci, L.; Cropp, A.; Swinden, R.; Gomez Otero, D.; El-Dali, W.; Carey, W.; Duvet, L.; et al. Moonlight navigation service-how to land on peaks of eternal light. In Proceedings of the 72nd International Astronautical Congress (IAC), Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Space Frequency Coordination Group. Communication AND Positioning, Navigation, and Timing Frequency Allocations and Sharing in the Lunar Region. 2021. Available online: https://www.sfcgonline.org/Recommendations/REC%20SFCG%2032-2R3%20(Freqs%20for%20Lunar%20region).pdf (accessed on 14 June 2022).
- Giordano, P.; Melman, F.; Swinden, R.; Zoccarato, P.; Ventura-Traveset, J. The Lunar Pathfinder PNT Experiment and Moonlight Navigation Service: The Future of Lunar Position, Navigation and Timing. In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 23–26 January 2023; pp. 632–642. [Google Scholar]
- Analytical Graphics Inc. Using Communication Constraints to Design Communication Links. 2016. Available online: https://help.agi.com/stk/11.0.1/Content/training/Constraints.htm (accessed on 5 August 2022).
- Das, P.; Ortega, L.; Vilà-Valls, J.; Vincent, F.; Chaumette, E.; Davain, L. Performance limits of GNSS code-based precise positioning: GPS, galileo & meta-signals. Sensors 2020, 20, 2196. [Google Scholar]
- Northtrop Grumman. LN-200S: Inertial Measurement Unit (IMU). 2021. Available online: https://www.northropgrumman.com/wp-content/uploads/LN-200S-Inertial-Measurement-Unit-IMU-datasheet.pdf (accessed on 20 June 2022).
- iMAR. iNAV-RQH-1001. 2014. Available online: https://www.imar-navigation.de/downloads/NAV_RQH_1001_en.pdf (accessed on 21 June 2022).
- Vectron Oscillators. OX-249 Space Qualified Oven Controlled Crystal Osciallator (OCXO). 2021. Available online: https://www.vectron.com/products/ocxo/OX-249.pdf (accessed on 14 June 2022).
- AXTAL GmbH. AXIOM6060: Ultra-Low Phase Noise 100 MHz OCXO for Space Application. 2015. Available online: https://www.axtal.com/cms/docs/doc91629.pdf (accessed on 14 June 2022).
- AXTAL GmbH. AXIOM70SL: Ultra-Low Phase Noise 10 MHz OCXO with HCMOS Output for Space Application (Space COTS version). 2022. Available online: https://www.axtal.com/cms/docs/doc124949.pdf (accessed on 14 June 2022).
- Brown, R.; Whang, P. Introduction to Random Signals and Applied Kalman Filtering; John Wiley & Sons, Inc.: New York, NY, USA, 1992; Volume 152. [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- European Commission. European GNSS (Galileo) Open Service Definition Document. 2021. Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo-OS-SDD_v1.2.pdf (accessed on 14 June 2022).
- Petovello, M.; Cannon, M.; Lachapelle, G. Benefits of using a tactical-grade IMU for high-accuracy positioning. Navigation 2004, 51, 1–12. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C. Understanding GPS/GNSS: Principles and Applications; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Farrell, J. Aided Navigation: GPS with High Rate Sensors; McGraw-Hill, Inc.: New York, NY, USA, 2008. [Google Scholar]
- International Space Exploration Coordination Group. Telerobotics Control of Systems with Time Delay–Gap Assessment Report. 2018. Available online: https://www.globalspaceexploration.org/wordpress/docs/Telerobotic%20Control%20of%20Systems%20with%20Time%20Delay%20Gap%20Assessment%20Report.pdf (accessed on 14 June 2022).
- Lunar Communications Relay and Navigation Systems (LCRNS)–Preliminary Lunar Relay Services Requirements Document (SRD). Technical Report, NASA. 2022. Available online: https://esc.gsfc.nasa.gov/static/2fbc056474937c4e3ecfdba1dc595f06/ee60f0dad022948b2e8ce03e6e86a2f0.pdf (accessed on 24 June 2022).





| Satellite Number | Semi-Major Axis | Eccentricity | Inclination | Argument of Pericenter | RAAN | True Anomaly |
|---|---|---|---|---|---|---|
| 1 | 9750.73 km | 0.6383 | 54.33 | 55.18 | 277.53 | 123.42 |
| 2 | 9750.73 km | 0.6383 | 54.33 | 55.18 | 277.53 | 0 |
| 3 | 9750.73 km | 0.6383 | 61.96 | 121.7 | 59.27 | 180 |
| 4 | 9750.73 km | 0.6383 | 61.96 | 121.7 | 59.27 | 0 |
| Element | Parameter | Value |
|---|---|---|
| Signal Carrier | Carrier Frequency () | 2491.005 MHz |
| Carrier Wavelength () | 12.04 cm | |
| Signal Modulation | Chipping Frequency () | BPSK(5) |
| Chip Length () | 58.61 m |
| Parameter | Value |
|---|---|
| RF Front-end Noise Figure | 1 dB |
| Noise Temperature | 113 K |
| LNA Gain | 30 dB |
| Coherent Integration Time () | 20 ms |
| cutoff | 30 dB-Hz |
| Parameter | State Vector Element | Value |
|---|---|---|
| LCNS ODTS Uncertainty (1-sigma) | Position () | 15 m |
| Velocity () | 0.15 m/s | |
| Clock () | 10 m | |
| Clock drift () | 0.1 m/s | |
| EKF Process Noise (1-sigma) | Position () | 0.01 m/ |
| Velocity () | 0.15 m/s/ | |
| Clock () | 1 m/ | |
| Clock drift () | 10 m/s/ | |
| Intitial EKF Uncertainty (1-sigma) | Position | 100 m |
| Velocity | 10 m/s | |
| Clock | 100 m | |
| Clock drift | 1 m/s |
| Parameter | Value |
|---|---|
| DLL Loop bandwidth () | 0.5 Hz |
| FLL Loop bandwidth () | 10 Hz |
| Coherent integration time () | 20 ms |
| Early-late spacing (d) | 1 chip |
| Parameter | Value |
|---|---|
| Threshold to enable DEM measurement | 150 m |
| Multiplier n for | 3 |
| Scenario | Availability [%] | Longest Continuous Availability [hr] | 68th Percentile [m] | 95th Percentile [m] | 99.7th Percentile [m] |
|---|---|---|---|---|---|
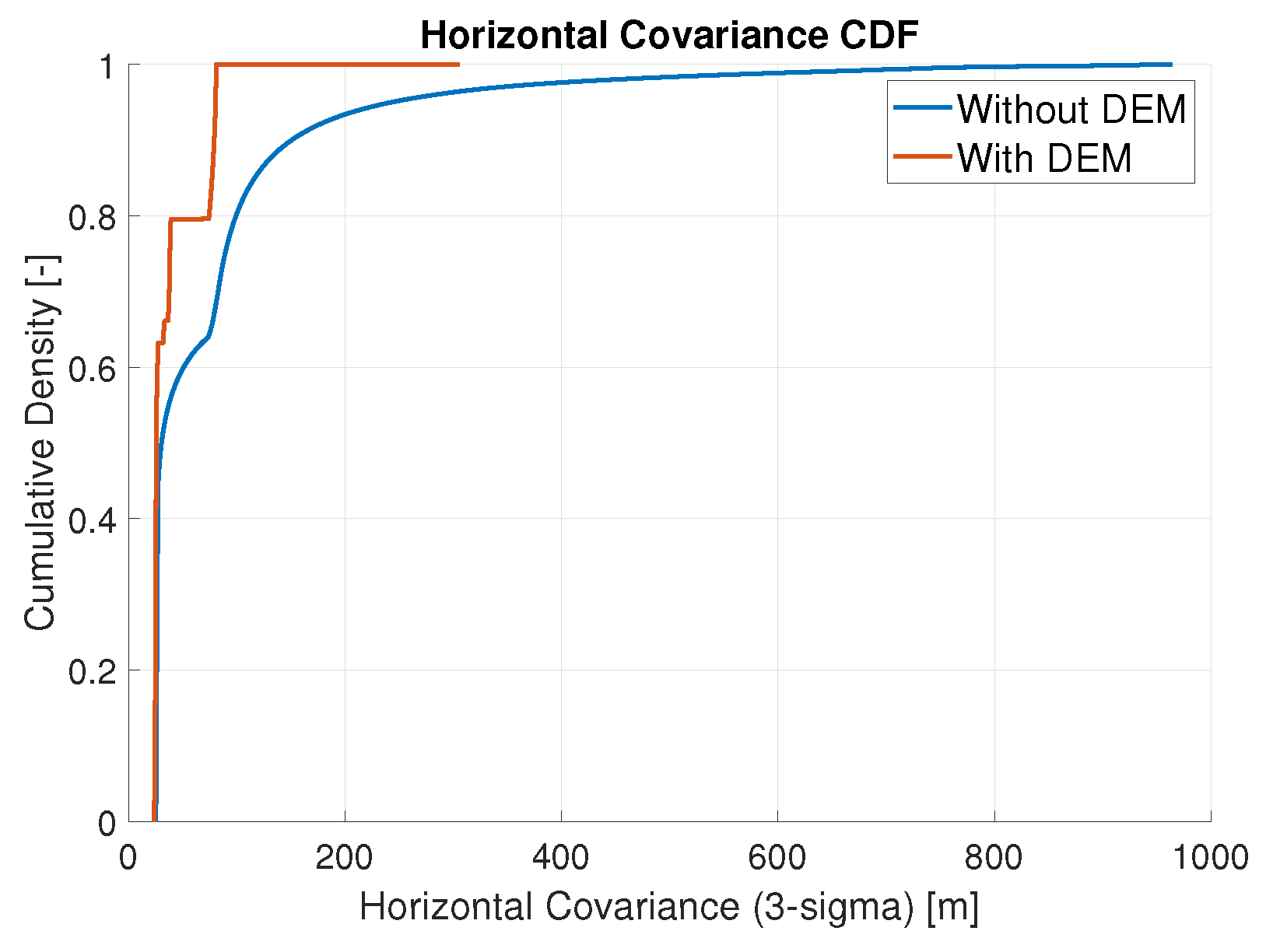
| 1. Without DEM | 52.0 | 5.2 | 80.3 | 242.8 | 810.2 |
| 2. With DEM | 82.2 | 19.9 | 37.2 | 80.3 | 81.0 |
| Scenario | Position [m] | Velocity [m/s] | Clock Bias [m] | Clock Drift [m/s] |
|---|---|---|---|---|
| 1. Baseline (1-sigma 1) | 15 | 0.15 | 10 | 0.1 |
| 2. Improved (3-sigma 1) | 5 | 0.05 | 3.333 | 0.033 |
| Scenario | 68th Percentile [m] | 95th Percentile [m] | 99.7th Percentile [m] |
|---|---|---|---|
| 1. Baseline ODTS | 37.2 | 80.3 | 81.0 |
| 2. Improved ODTS | 23.4 | 50.1 | 50.6 |
| Scenario | [m/] | [m/s/] | [m/] | [m/s/] |
|---|---|---|---|---|
| 1. Baseline | 0.01 | 0.15 | 1 | 10 |
| 2. Improved (Tactical-Grade IMU) | 1 | 10 | ||
| 3. Improved (Navigation-Grade IMU) | 1 | 10 |
| Scenario | 68th Percentile [m] | 95th Percentile [m] | 99.7th Percentile [m] |
|---|---|---|---|
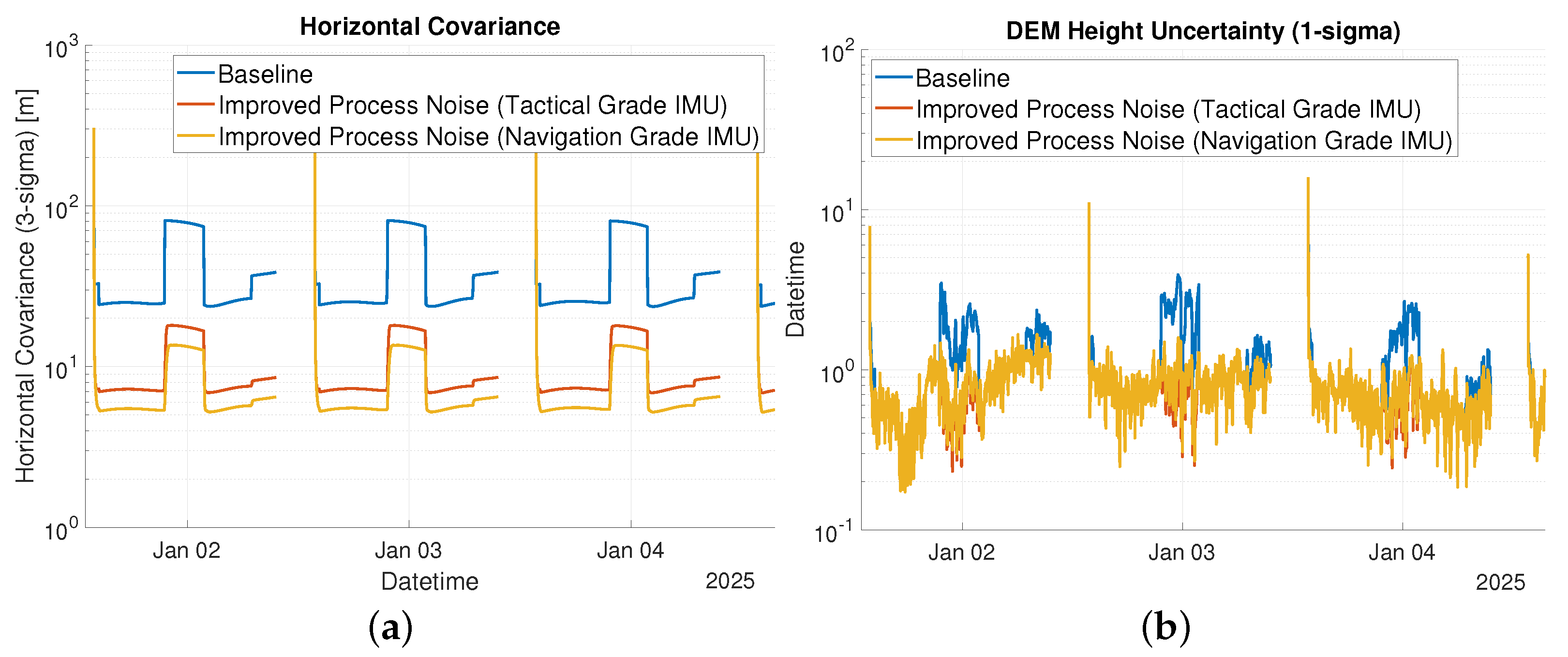
| 1. Baseline | 37.2 | 80.3 | 81.0 |
| 2. Improved (Tactical-Grade IMU) | 8.3 | 17.9 | 18.1 |
| 3. Improved (Navigation-Grade IMU) | 6.3 | 13.5 | 15.3 |
| Scenario | 68th Percentile [m] | 95th Percentile [m] | 99.7th Percentile [m] |
|---|---|---|---|
| 1. Baseline | 37.2 | 80.3 | 81.0 |
| 2. Improved ODTS and Tactical-Grade IMU | 3.9 | 8.4 | 8.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melman, F.T.; Zoccarato, P.; Orgel, C.; Swinden, R.; Giordano, P.; Ventura-Traveset, J. LCNS Positioning of a Lunar Surface Rover Using a DEM-Based Altitude Constraint. Remote Sens. 2022, 14, 3942. https://doi.org/10.3390/rs14163942
Melman FT, Zoccarato P, Orgel C, Swinden R, Giordano P, Ventura-Traveset J. LCNS Positioning of a Lunar Surface Rover Using a DEM-Based Altitude Constraint. Remote Sensing. 2022; 14(16):3942. https://doi.org/10.3390/rs14163942
Chicago/Turabian StyleMelman, Floor Thomas, Paolo Zoccarato, Csilla Orgel, Richard Swinden, Pietro Giordano, and Javier Ventura-Traveset. 2022. "LCNS Positioning of a Lunar Surface Rover Using a DEM-Based Altitude Constraint" Remote Sensing 14, no. 16: 3942. https://doi.org/10.3390/rs14163942
APA StyleMelman, F. T., Zoccarato, P., Orgel, C., Swinden, R., Giordano, P., & Ventura-Traveset, J. (2022). LCNS Positioning of a Lunar Surface Rover Using a DEM-Based Altitude Constraint. Remote Sensing, 14(16), 3942. https://doi.org/10.3390/rs14163942








