Object Tracking in Satellite Videos Based on Improved Kernel Correlation Filter Assisted by Road Information
Abstract
:1. Introduction
1.1. Background
1.2. Object Tracking
1.3. Object Tracking in Satellite Videos
2. Kernel Correlation Filter
3. Proposed Method
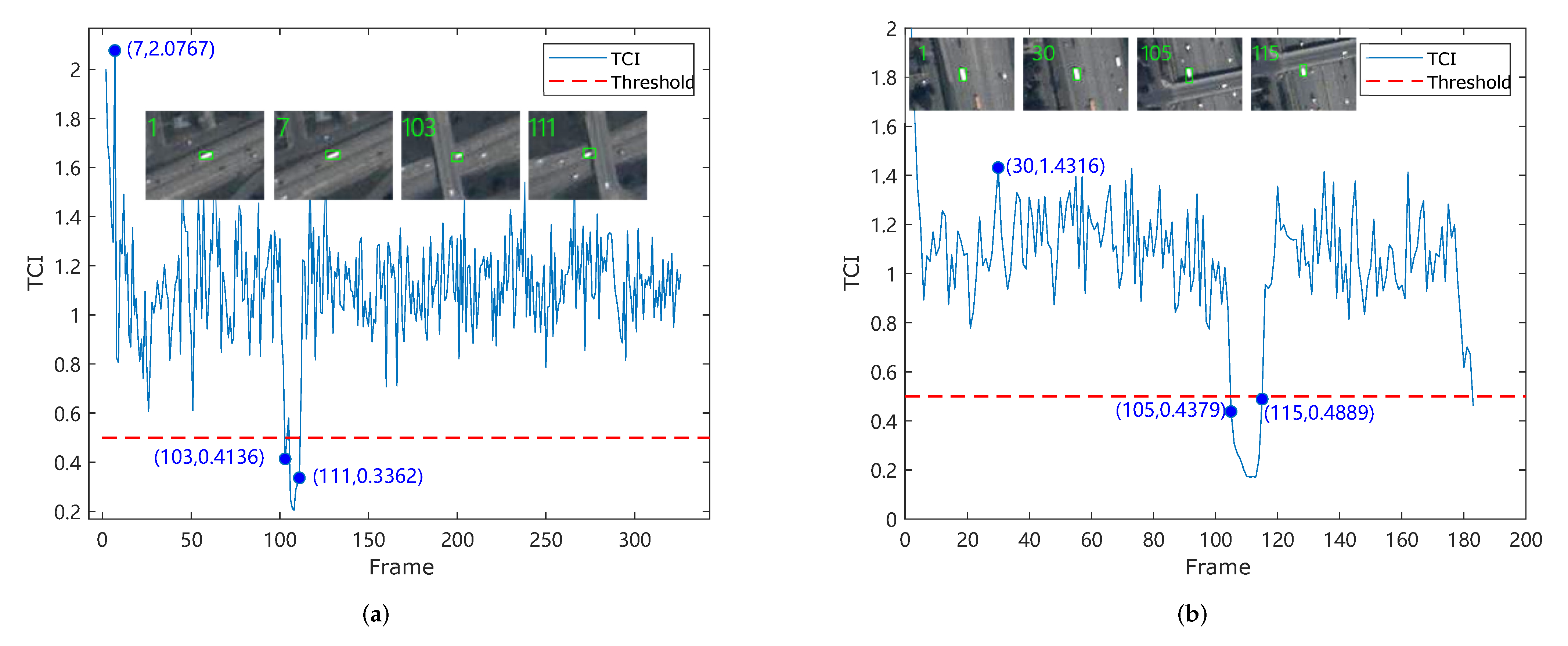
3.1. Tracking Confidence Module
3.2. Motion Estimation
3.3. Object Detection Based on Road Information
4. Experiments
4.1. Datasets and Compared Tracker
4.2. Setting of Parameters
4.3. Evaluation Metrics
5. Results and Analysis
5.1. Threshold of Occlusion
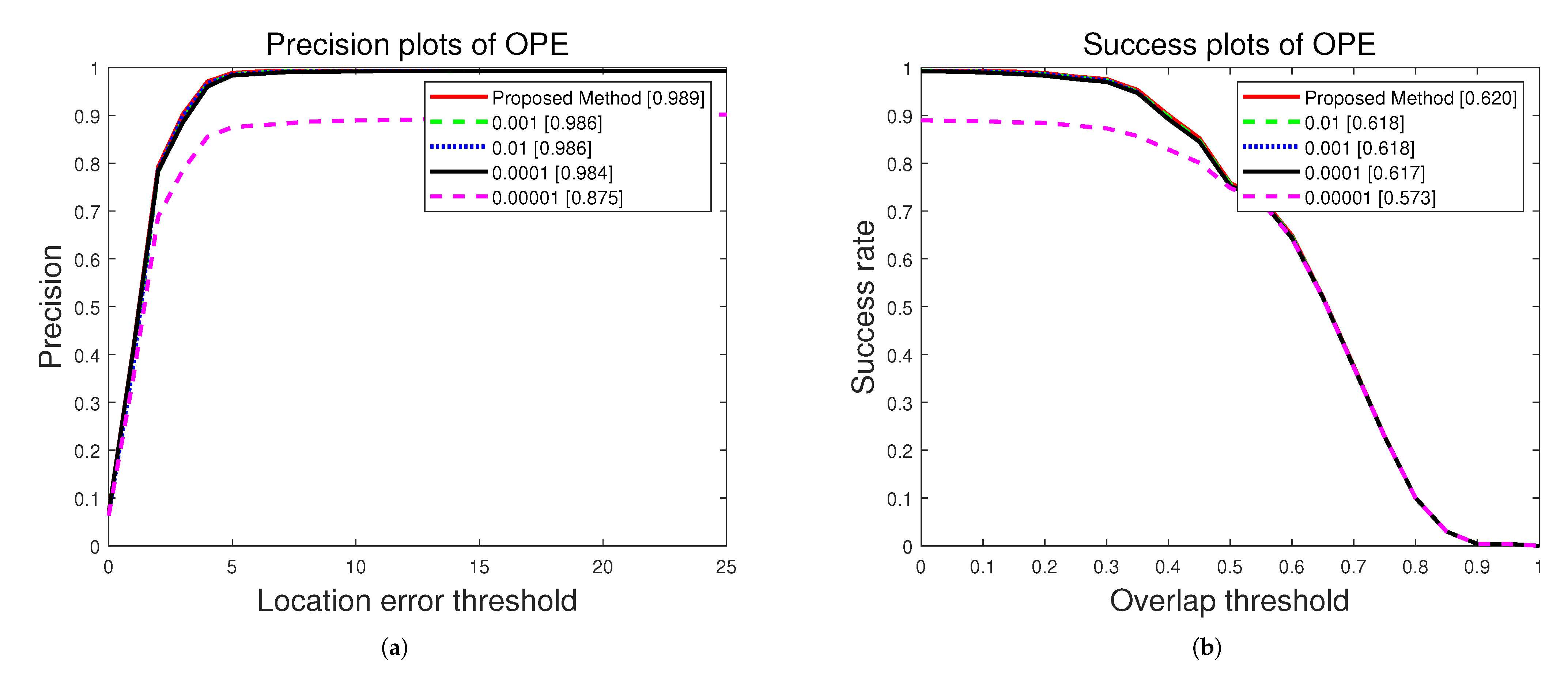
5.2. Noise Covariance Matrix
5.3. Tracking Result Analysis
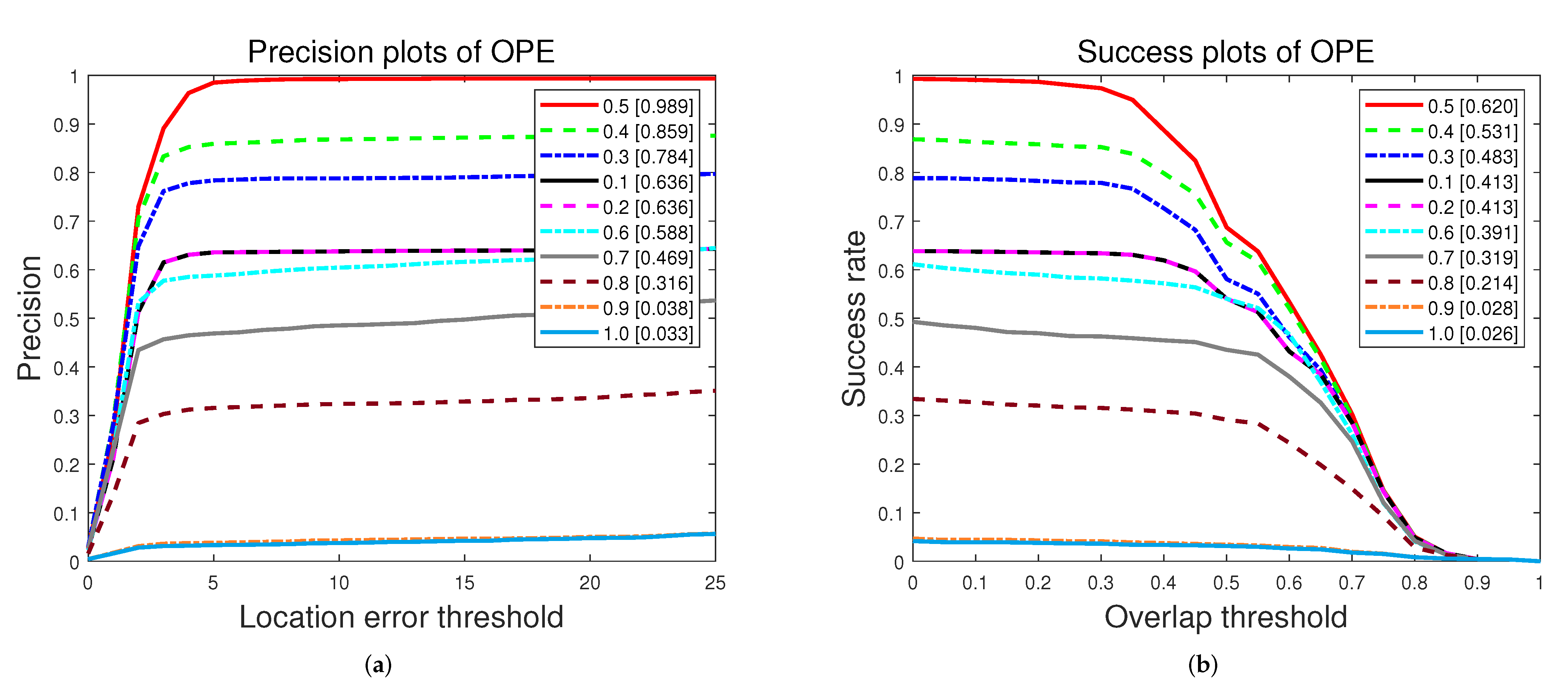
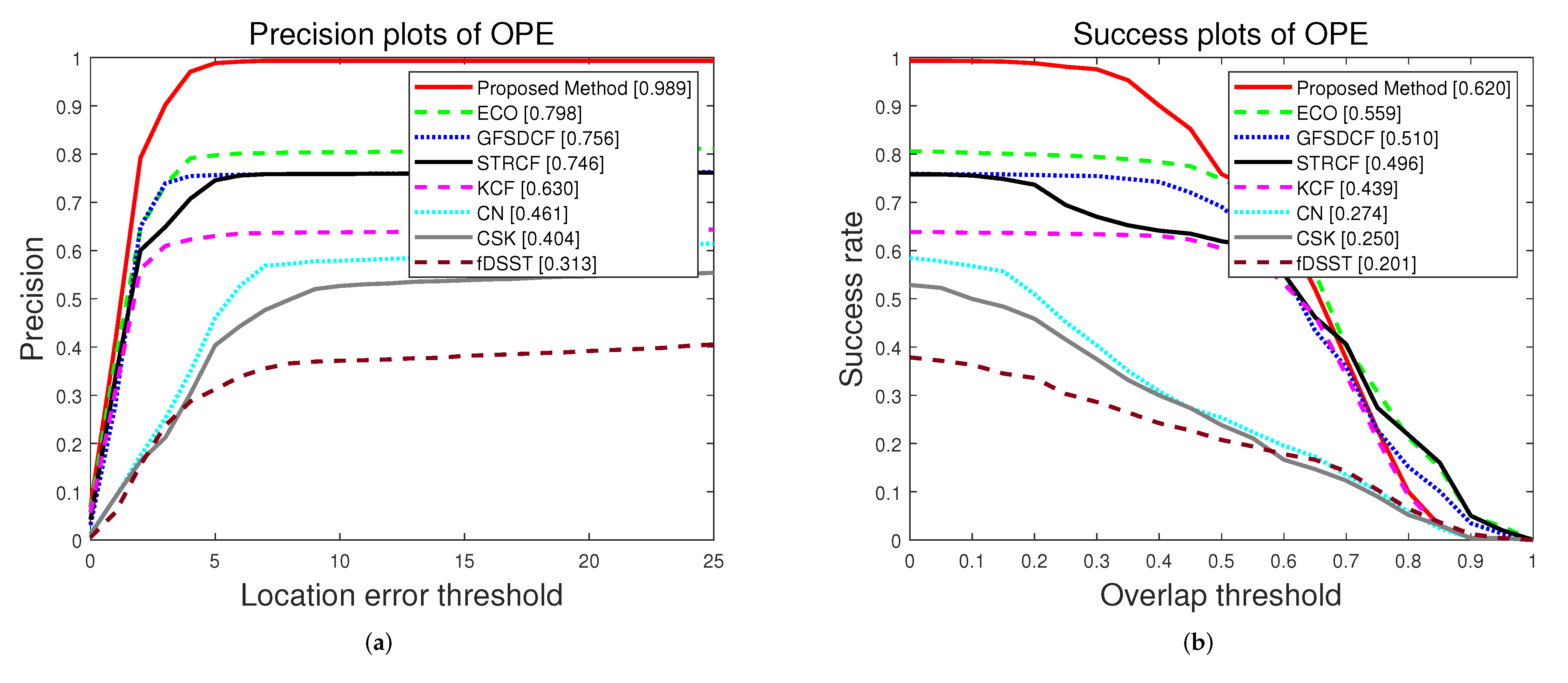
5.3.1. Quantitative Evaluation
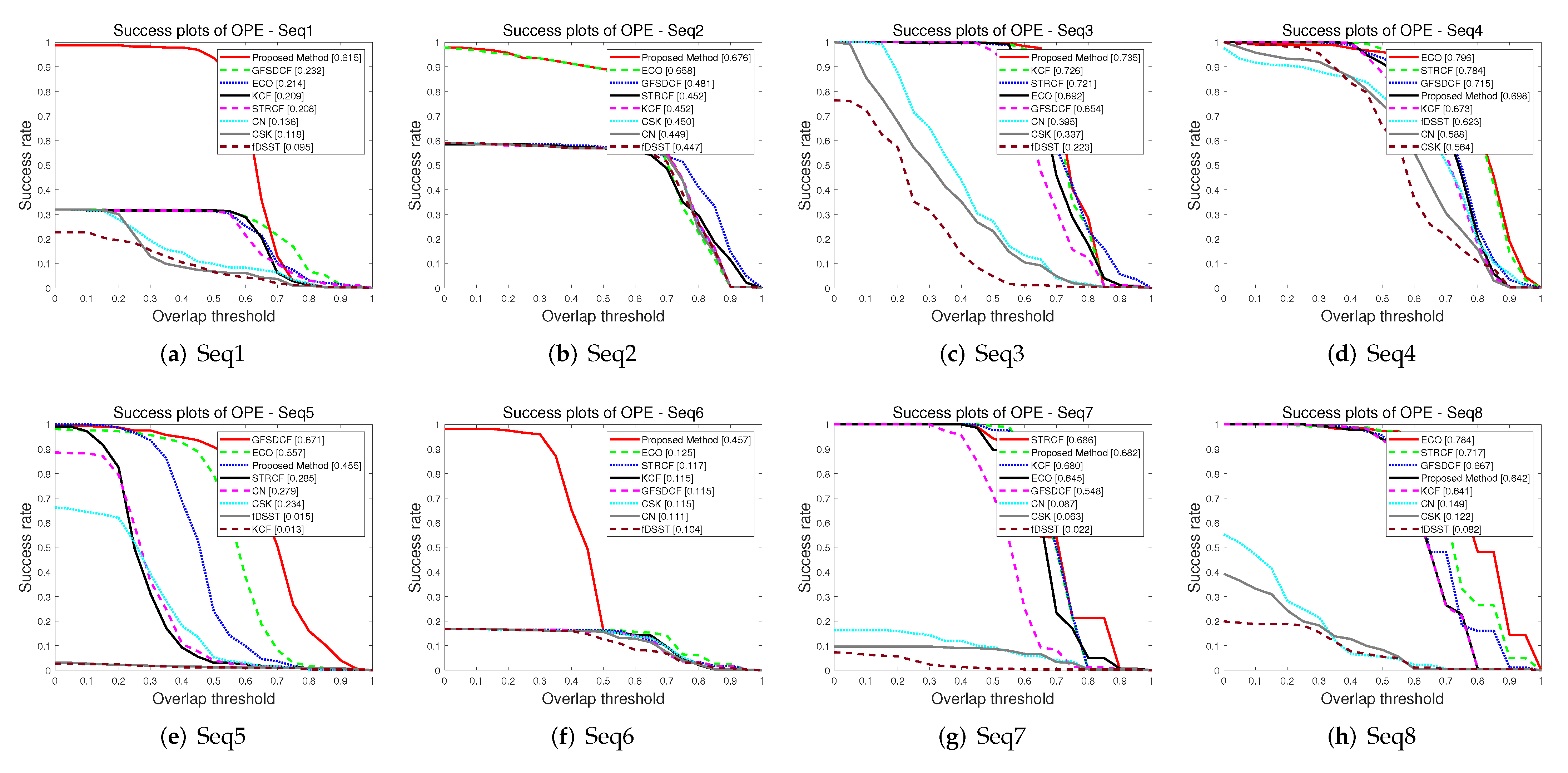
5.3.2. Qualitative Evaluation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual object tracking using adaptive correlation filters. In Proceedings of the Twenty-Third IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2010, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Henriques, J.F.; Rui, C.; Martins, P.; Batista, J. Exploiting the Circulant Structure of Tracking-by-Detection with Kernels. In Proceedings of the 12th European Conference on Computer Vision Part IV, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-Speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Danelljan, M.; Khan, F.S.; Felsberg, M.; Weijer, J. Adaptive Color Attributes for Real-Time Visual Tracking. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Yang, L.; Zhu, J. A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration. In Proceedings of the IEEE European Conference on Computer Vision, Zurich, Switzerland, 6–7 September 2014. [Google Scholar]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Accurate Scale Estimation for Robust Visual Tracking. In Proceedings of the British Machine Vision Conference, Nottingham, UK, 1–5 September 2014. [Google Scholar]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Discriminative Scale Space Tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1561–1575. [Google Scholar] [CrossRef] [PubMed]
- Danelljan, M.; Hger, G.; Khan, F.S.; Felsberg, M. Learning Spatially Regularized Correlation Filters for Visual Tracking. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Li, F.; Tian, C.; Zuo, W.; Zhang, L.; Yang, M.H. Learning Spatial-Temporal Regularized Correlation Filters for Visual Tracking. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Danelljan, M.; Robinson, A.; Khan, F.S.; Felsberg, M. Beyond Correlation Filters: Learning Continuous Convolution Operators for Visual Tracking; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Danelljan, M.; Bhat, G.; Khan, F.S.; Felsberg, M. ECO: Efficient Convolution Operators for Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Xu, T.; Feng, Z.H.; Wu, X.J.; Kittler, J. Joint Group Feature Selection and Discriminative Filter Learning for Robust Visual Object Tracking. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Held, D.; Thrun, S.; Savarese, S. Learning to Track at 100 FPS with Deep Regression Networks. In Proceedings of the European Conference Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Tao, R.; Gavves, E.; Smeulders, A.W. Siamese instance search for tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1420–1429. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H. Fully-convolutional siamese networks for object tracking. In Proceedings of the European Conference on Computer Vision, (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 850–865. [Google Scholar]
- Li, B.; Yan, J.; Wu, W.; Zhu, Z.; Hu, X. High performance visual tracking with siamese region proposal network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognitio, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8971–8980. [Google Scholar]
- Li, B.; Wu, W.; Wang, Q.; Zhang, F.; Xing, J.; Yan, J. Siamrpn++: Evolution of siamese visual tracking with very deep networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4282–4291. [Google Scholar]
- Chen, Z.; Zhong, B.; Li, G.; Zhang, S.; Ji, R. Siamese box adaptive network for visual tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6668–6677. [Google Scholar]
- Du, B.; Sun, Y.; Cai, S.; Wu, C.; Du, Q. Object Tracking in Satellite Videos by Fusing the Kernel Correlation Filter and the Three-Frame-Difference Algorithm. IEEE Geosci. Remote Sens. Lett. 2018, 5, 168–172. [Google Scholar] [CrossRef]
- Shao, J.; Du, B.; Wu, C.; Zhang, L. Tracking Objects From Satellite Videos: A Velocity Feature Based Correlation Filter. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7860–7871. [Google Scholar] [CrossRef]
- Shao, J.; Du, B.; Wu, C.; Zhang, L. Can We Track Targets From Space? A Hybrid Kernel Correlation Filter Tracker for Satellite Video. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8719–8731. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, D.; Chen, Z. Object Tracking on Satellite Videos: A Correlation Filter-Based Tracking Method With Trajectory Correction by Kalman Filter. IEEE J. Select. Top. Appl. Earth Observat. Remote Sens. 2019, 2, 3538–3551. [Google Scholar] [CrossRef]
- Xuan, S.; Li, S.; Han, M.; Wan, X.; Xia, G.S. Object Tracking in Satellite Videos by Improved Correlation Filters With Motion Estimations. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1074–1086. [Google Scholar] [CrossRef]
- Xuan, S.; Li, S.; Zhao, Z.; Zhou, Z.; Gu, Y. Rotation Adaptive Correlation Filter for Moving Object Tracking in Satellite Videos. Neurocomputing 2021, 438, 94–106. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, Y.; Lin, C.; Jia, Y.; Li, Z.; Yang, X. Object Tracking in Satellite Videos Based on Correlation Filter with Multi-Feature Fusion and Motion Trajectory Compensation. Remote Sens. 2022, 14, 777. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, D.; Zheng, Y. Satellite Video Tracking by Multi-Feature Correlation Filters with Motion Estimation. Remote Sens. 2022, 14, 2691. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, Y.; Yin, Z.; Han, T.; Zou, B.; Feng, H. Single Object Tracking in Satellite Videos: A Correlation Filter-Based Dual-Flow Tracker. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2022, 1–13. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, Y.; Han, T.; Zhang, Y.; Zou, B.; Feng, H. RAMC: A Rotation Adaptive Tracker with Motion Constraint for Satellite Video Single-Object Tracking. Remote Sens. 2022, 14, 3108. [Google Scholar] [CrossRef]
- Wang, M.; Yong, L.; Huang, Z. Large Margin Object Tracking with Circulant Feature Maps. In Proceedings of the International Conference on Computer Vision and Pattern Recognition, Venice, Italy, 30 October–1 November 2017. [Google Scholar]
- Zhou, L.; Zhang, C.; Wu, M. D-LinkNet: LinkNet with pretrained encoder and dilated convolution for high resolution satellite imagery road extraction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 182–186. [Google Scholar]
- Yin, Q.; Hu, Q.; Liu, H.; Zhang, F.; Wang, Y.; Lin, Z.; An, W.; Guo, Y. Detecting and Tracking Small and Dense Moving Objects in Satellite Videos: A Benchmark. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Zhao, M.; Li, S.; Xuan, S.; Kou, L.; Gong, S.; Zhou, Z. SatSOT: A Benchmark Dataset for Satellite Video Single Object Tracking. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M.H. Object Tracking Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [PubMed] [Green Version]


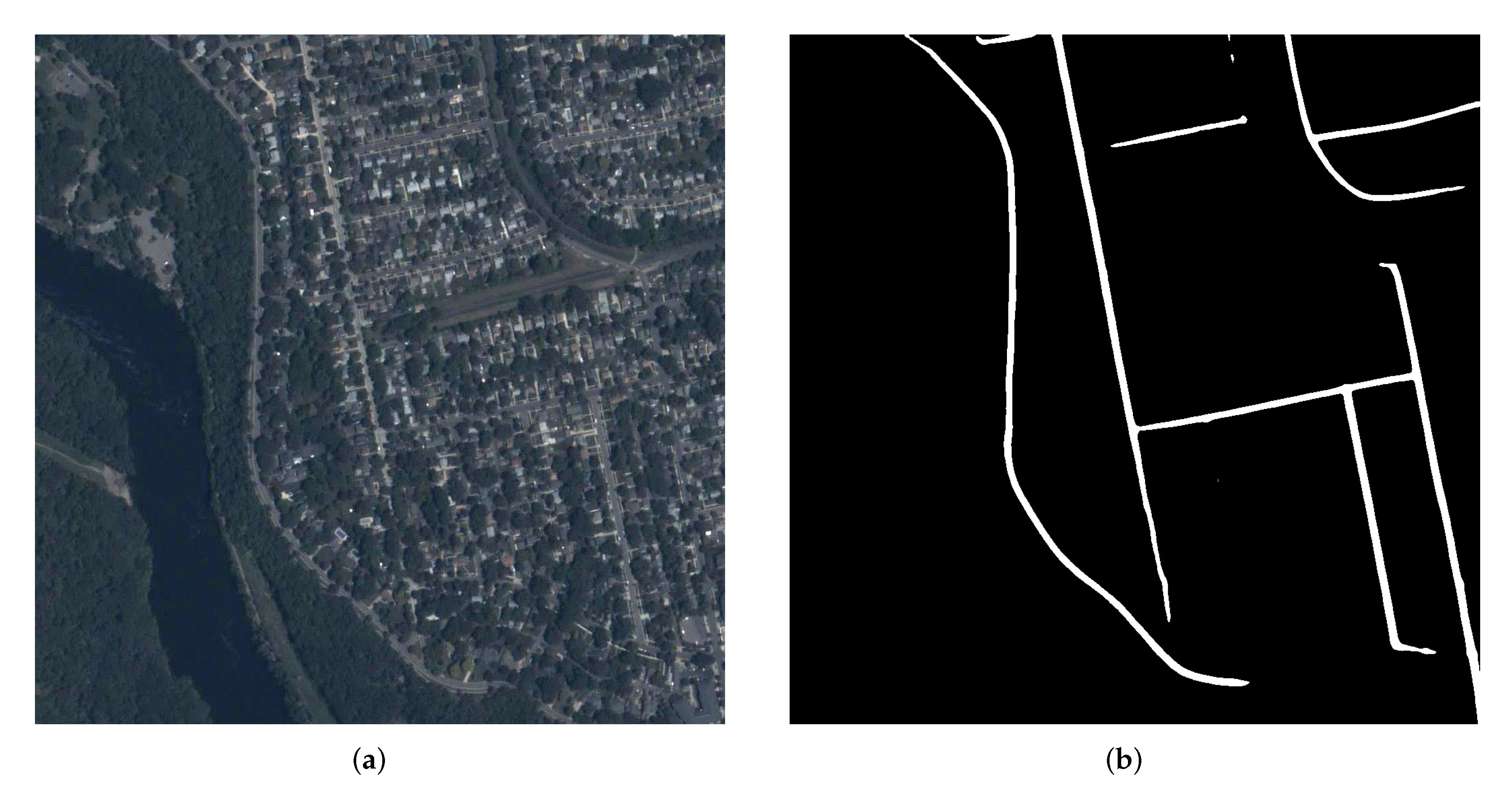




| Sequences | Object Size | Total Number of Frames | Effective Number of Frames | Challenges |
|---|---|---|---|---|
| 1 | 326 | 322 | FOC,TO | |
| 2 | 183 | 179 | FOC,TO | |
| 3 | 250 | 250 | LQ | |
| 4 | 180 | 180 | IV,ROT,DEF | |
| 5 | 326 | 326 | POC,TO | |
| 6 | 326 | 320 | IV,TO,ROT,FOC,DEF | |
| 7 | 300 | 300 | LQ,ROT,TO | |
| 8 | 181 | 181 | TO,ROT |
| Attribute | Definition |
|---|---|
| IV | Illumination Variation: the illumination of the object region changes significantly |
| FOC | Full Occlusion: the object is fully occluded in the video |
| LQ | Low Quality: the image is low quality and the object is difficult to be distinguished |
| ROT | Rotation: the object rotates in the video |
| DEF | Deformation: non-rigid object deformation |
| POC | Partial Occlusion: the object is partially occluded in the video |
| TO | Tiny Object: at least one ground truth bounding box has less than pixels |
| Proposed Method | Q = 0.001 | Q = 0.01 | Q = 0.0001 | Q = 0.00001 | |
|---|---|---|---|---|---|
| Precision Score (%) | 0.989 | 0.986 | 0.986 | 0.984 | 0.875 |
| AUC (%) | 0.620 | 0.618 | 0.618 | 0.617 | 0.573 |
| Success Score (%) | 0.758 | 0.752 | 0.757 | 0.753 | 0.748 |
| Sequences | Evaluation Metrics | Ours | ECO | GFSDCF | STRCF | KCF | CN | CSK | fDSST |
|---|---|---|---|---|---|---|---|---|---|
| Seq1 | Precision score(%) | 98.8 | 31.9 | 31.9 | 31.9 | 31.9 | 26.7 | 27.0 | 20.9 |
| AUC(%) | 61.5 | 21.4 | 23.2 | 20.8 | 20.9 | 13.6 | 11.8 | 9.5 | |
| Success score(%) | 93.6 | 31.3 | 31.6 | 31.3 | 31.6 | 9.8 | 6.7 | 6.4 | |
| FPS | 271 | 11 | 5 | 32 | 389 | 872 | 2669 | 298 | |
| Seq2 | Precision score(%) | 96.7 | 95.1 | 58.5 | 58.5 | 57.9 | 58.5 | 58.5 | 58.5 |
| AUC(%) | 67.6 | 65.8 | 48.1 | 45.2 | 45.2 | 44.9 | 45.0 | 44.7 | |
| Success score(%) | 89.1 | 89.1 | 57.4 | 56.8 | 56.8 | 56.8 | 56.8 | 56.8 | |
| FPS | 212 | 11 | 5 | 33 | 310 | 1022 | 3397 | 335 | |
| Seq3 | Precision score(%) | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 71.2 | 56.8 | 41.6 |
| AUC(%) | 73.5 | 69.2 | 65.4 | 72.1 | 72.6 | 39.5 | 33.7 | 22.3 | |
| Success score(%) | 99.6 | 99.6 | 96.4 | 99.2 | 99.6 | 27.2 | 23.2 | 4.8 | |
| FPS | 478 | 8 | 5 | 33 | 462 | 832 | 2579 | 249 | |
| Seq4 | Precision score(%) | 98.5 | 97.9 | 100.0 | 95.7 | 95.7 | 79.4 | 75.5 | 85.6 |
| AUC(%) | 69.8 | 79.6 | 71.5 | 78.4 | 67.3 | 58.8 | 56.4 | 62.3 | |
| Success score(%) | 91.4 | 96.0 | 93.6 | 97.2 | 87.4 | 74.5 | 65.6 | 77.9 | |
| FPS | 107 | 8 | 5 | 33 | 204 | 756 | 2657 | 241 | |
| Seq5 | Precision score(%) | 98.8 | 96.3 | 97.9 | 93.6 | 1.8 | 54.3 | 46.6 | 1.8 |
| AUC(%) | 45.5 | 55.7 | 67.1 | 28.5 | 1.3 | 27.9 | 23.4 | 1.5 | |
| Success score(%) | 23.9 | 79.4 | 90.8 | 3.1 | 1.2 | 4.0 | 5.2 | 1.2 | |
| FPS | 384 | 9 | 6 | 33 | 605 | 840 | 3112 | 289 | |
| Seq6 | Precision score(%) | 98.2 | 16.9 | 16.9 | 16.9 | 16.9 | 16.9 | 16.9 | 16.9 |
| AUC(%) | 45.7 | 12.5 | 11.5 | 11.7 | 11.5 | 11.1 | 11.5 | 10.4 | |
| Success score(%) | 16.0 | 16.3 | 15.6 | 16.3 | 16.0 | 15.6 | 16.0 | 12.6 | |
| FPS | 261 | 9 | 6 | 35 | 452 | 958 | 3249 | 285 | |
| Seq7 | Precision score(%) | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 16.3 | 9.7 | 6.0 |
| AUC(%) | 68.2 | 64.5 | 54.8 | 68.6 | 68.0 | 8.7 | 6.3 | 2.2 | |
| Success score(%) | 99.3 | 89.7 | 71.7 | 94.3 | 97.7 | 9.3 | 8.7 | 0.7 | |
| FPS | 540 | 13 | 5.3 | 33 | 549 | 716 | 2197 | 234 | |
| Seq8 | Precision score(%) | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 45.3 | 32.0 | 18.8 |
| AUC(%) | 64.2 | 78.4 | 66.7 | 71.7 | 64.1 | 14.9 | 12.2 | 8.2 | |
| Success score(%) | 93.9 | 97.2 | 95.6 | 97.2 | 93.4 | 5.5 | 8.3 | 5.5 | |
| FPS | 541 | 12 | 5 | 33 | 537 | 693 | 2196 | 250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Song, H.; Fan, C. Object Tracking in Satellite Videos Based on Improved Kernel Correlation Filter Assisted by Road Information. Remote Sens. 2022, 14, 4215. https://doi.org/10.3390/rs14174215
Wu D, Song H, Fan C. Object Tracking in Satellite Videos Based on Improved Kernel Correlation Filter Assisted by Road Information. Remote Sensing. 2022; 14(17):4215. https://doi.org/10.3390/rs14174215
Chicago/Turabian StyleWu, Di, Haibo Song, and Caizhi Fan. 2022. "Object Tracking in Satellite Videos Based on Improved Kernel Correlation Filter Assisted by Road Information" Remote Sensing 14, no. 17: 4215. https://doi.org/10.3390/rs14174215
APA StyleWu, D., Song, H., & Fan, C. (2022). Object Tracking in Satellite Videos Based on Improved Kernel Correlation Filter Assisted by Road Information. Remote Sensing, 14(17), 4215. https://doi.org/10.3390/rs14174215







