Adaptive Cloud-to-Cloud (AC2C) Comparison Method for Photogrammetric Point Cloud Error Estimation Considering Theoretical Error Space
Abstract
:1. Introduction
2. Related Work
2.1. Major Error Sources
2.2. Theoretical and Empirical Error Estimation Methods
2.3. Evaluation of the Measurement Errors of SfM-MVS in Practice
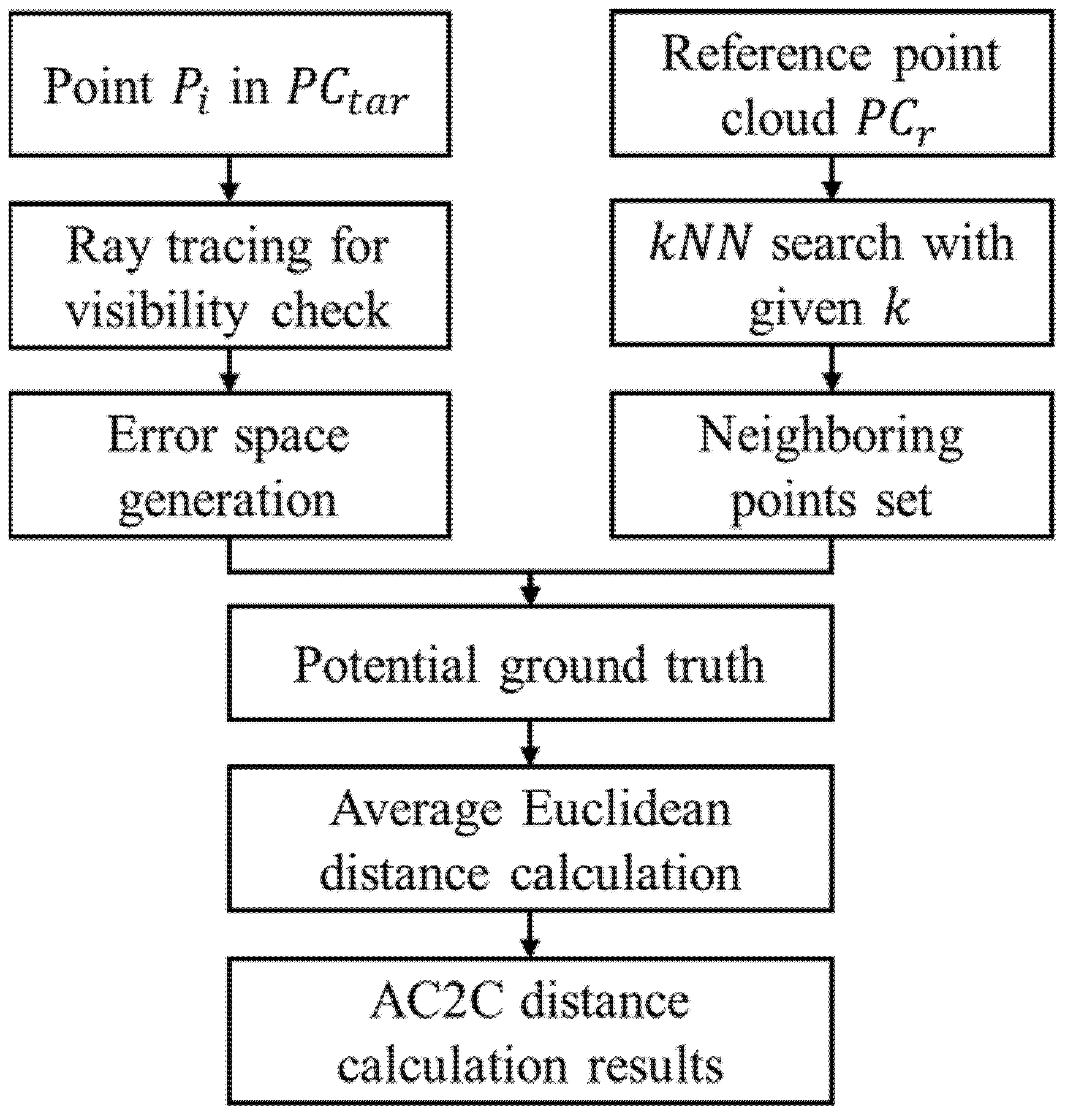
3. Proposed Methodology
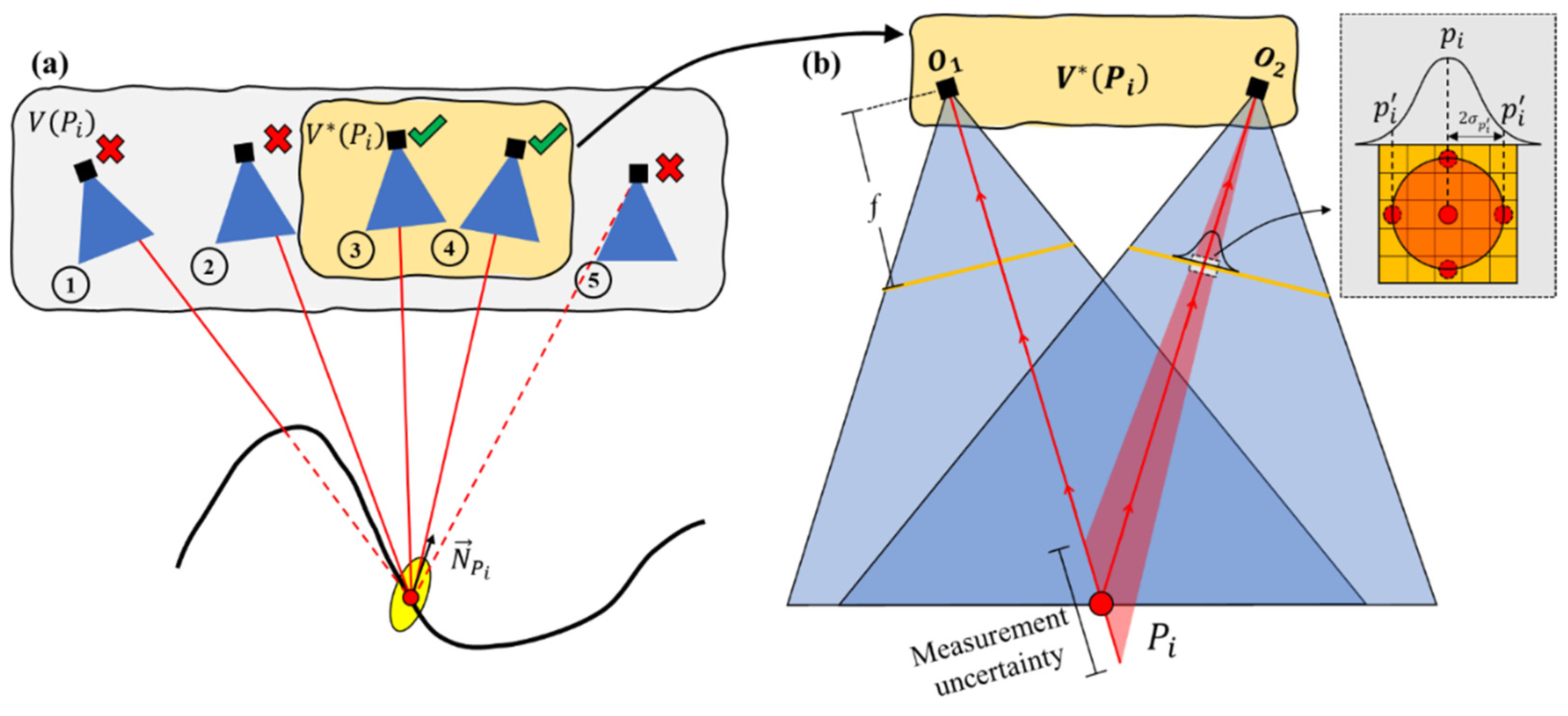
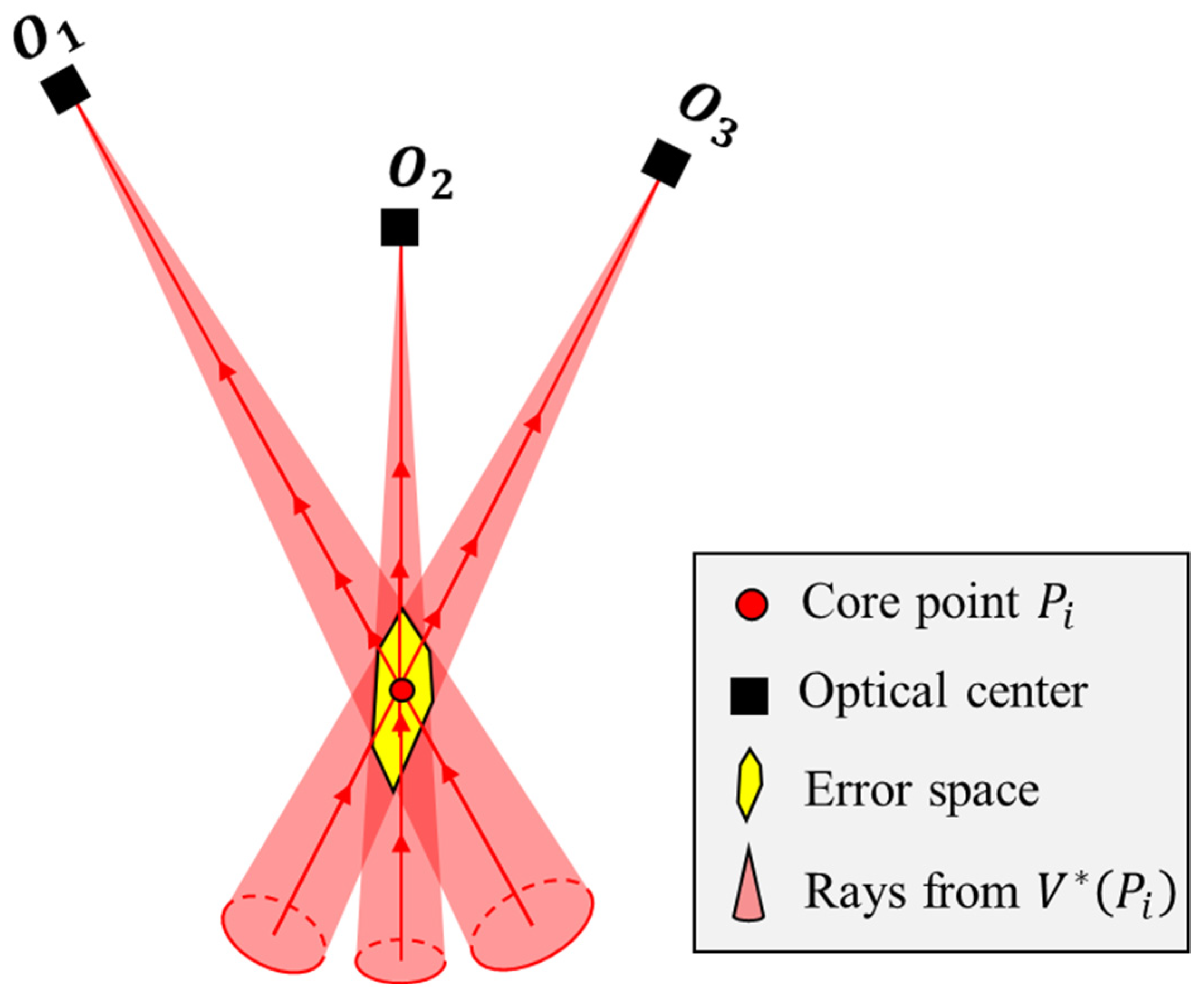
3.1. Step 1: Error Space Estimation
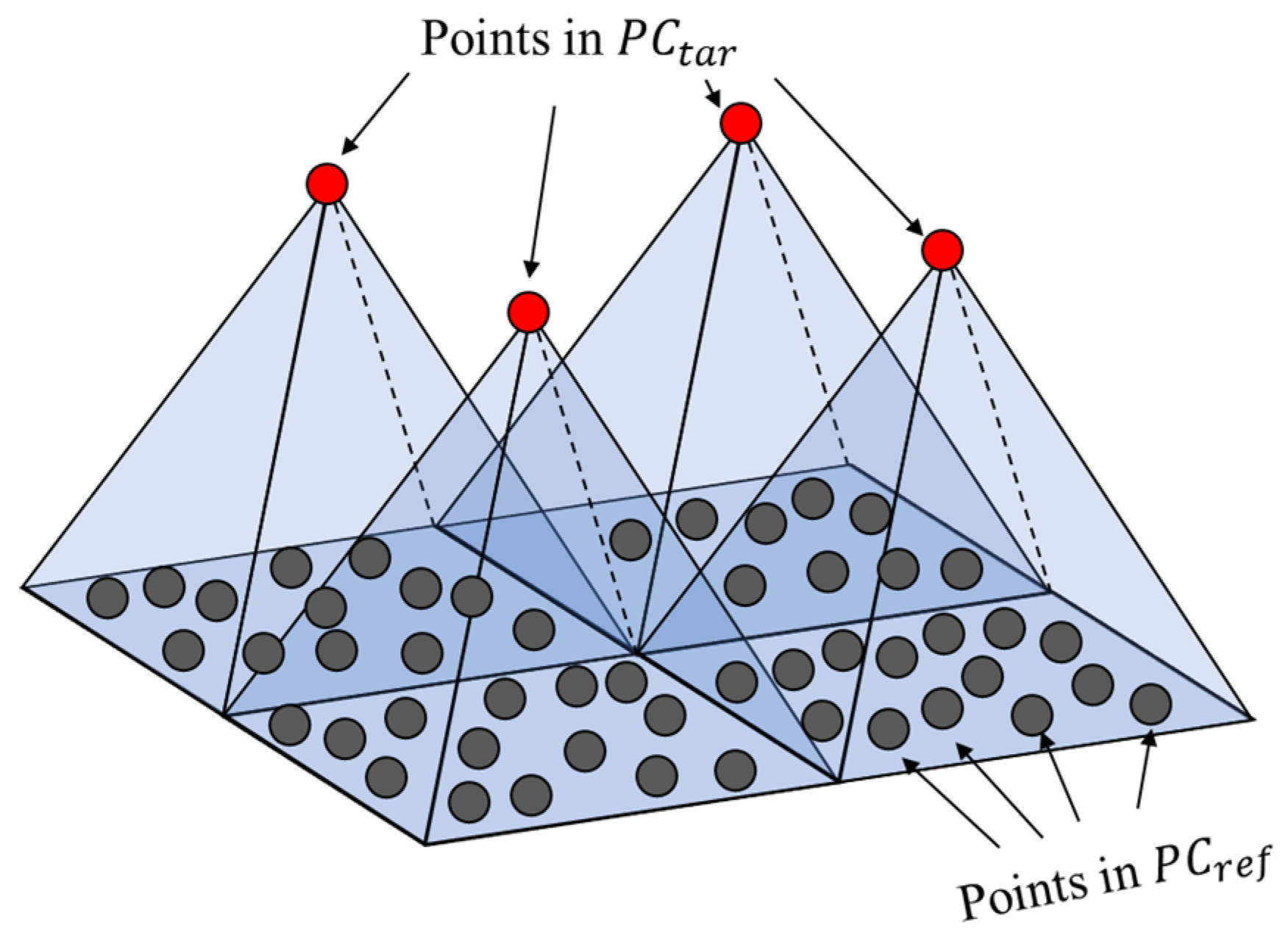
3.2. Step 2: Neighboring Points Search and Filtering
3.3. Step 3: Measurement Error Evaluation
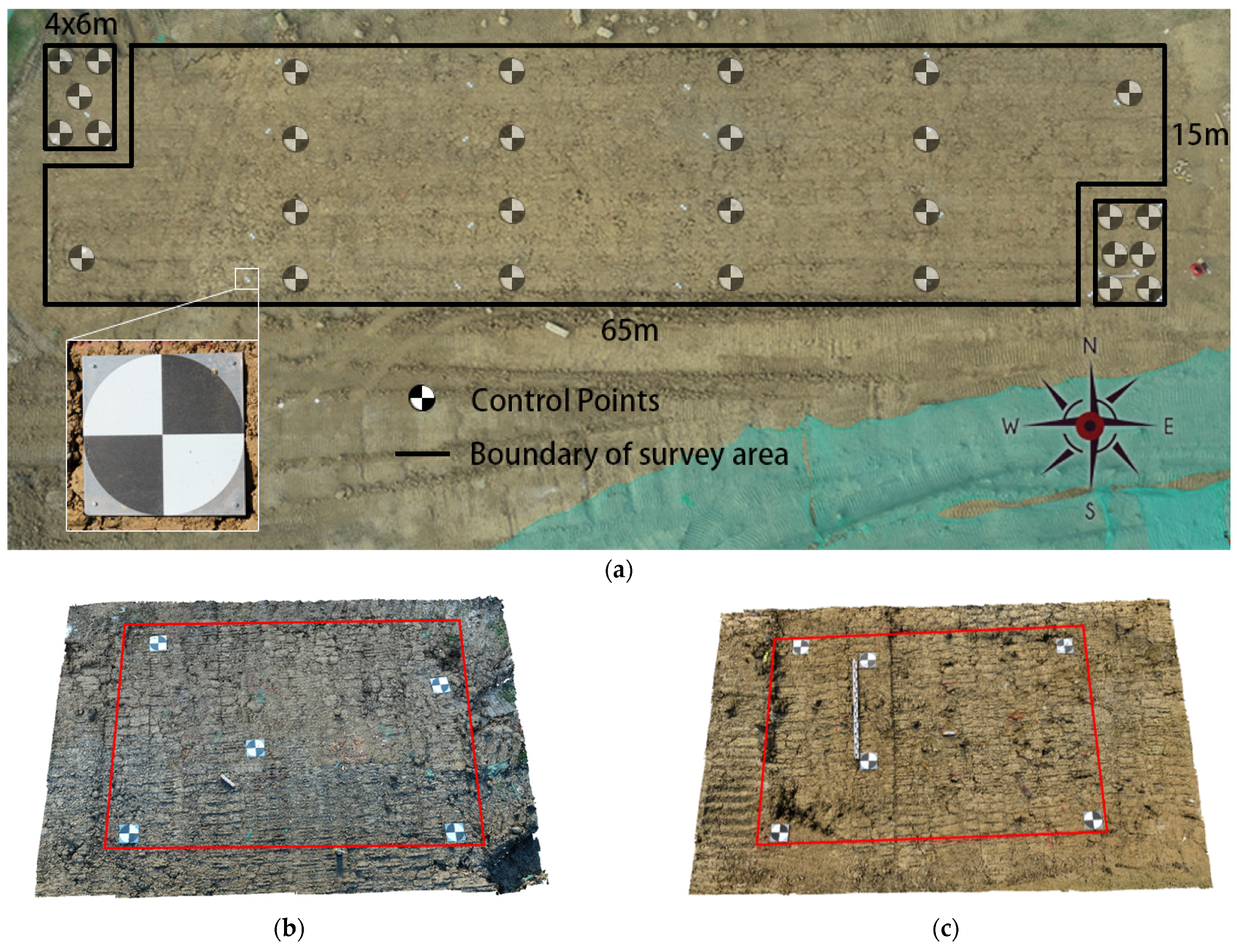
4. Data Collection and Setup
4.1. Data Collection for Reference Point Cloud
4.2. Data Collection for Target Point Cloud
5. Results and Discussion
5.1. Measurement Error of Using Control Points
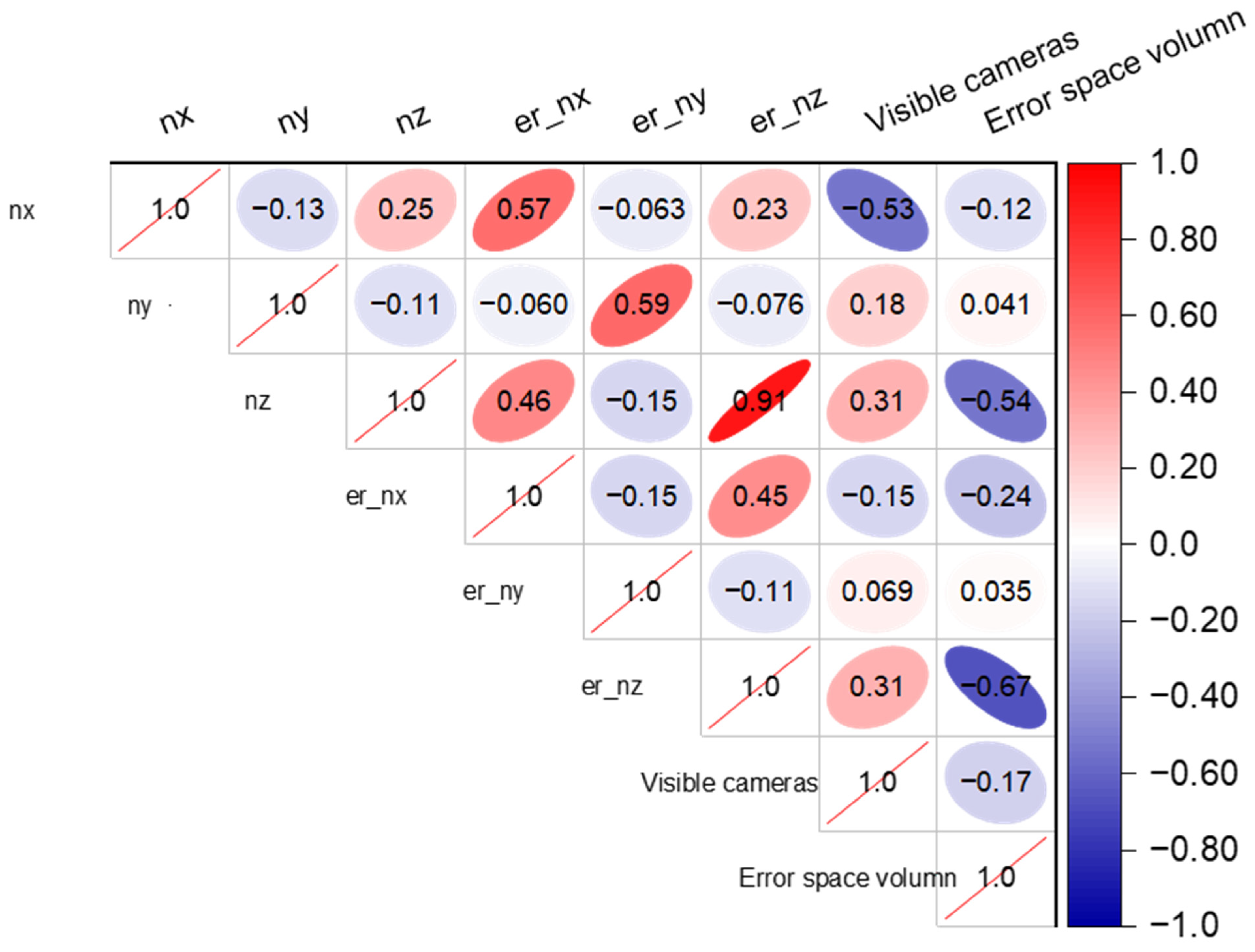
5.2. Visibility Check and Error Space Estimation
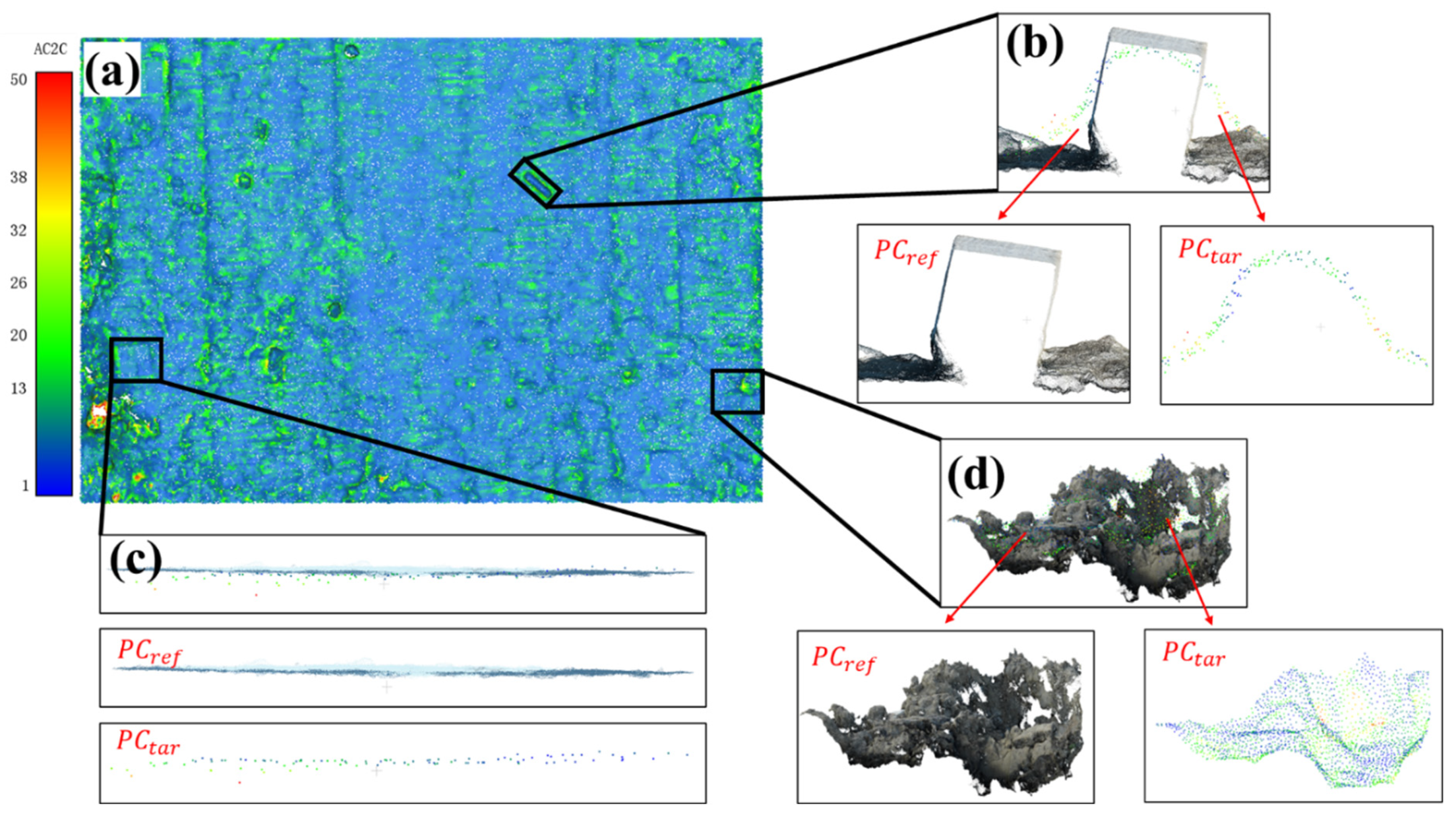
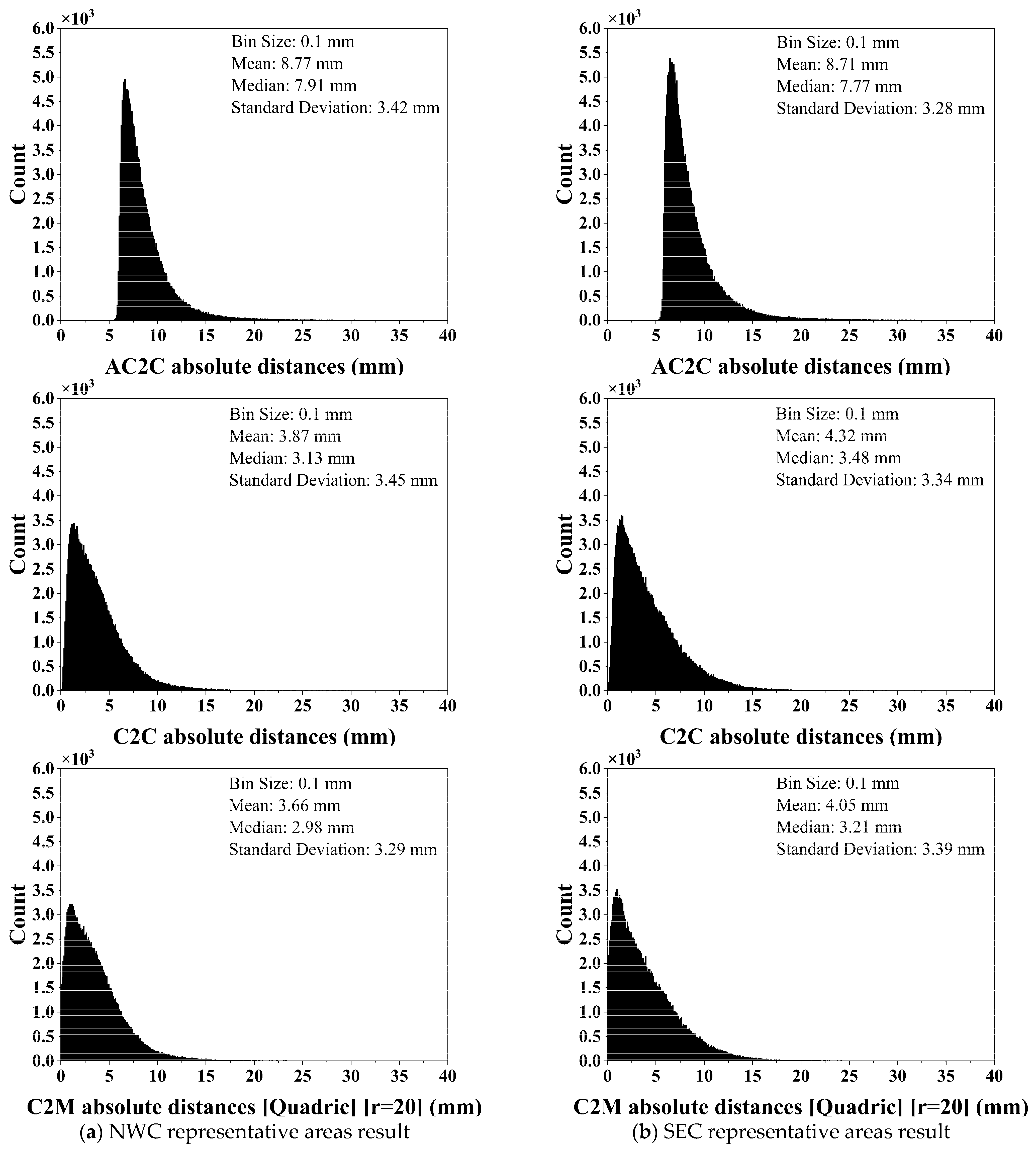
5.3. AC2C Distance Calculation Results
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moon, D.; Chung, S.; Kwon, S.; Seo, J.; Shin, J. Comparison and utilization of point cloud generated from photogrammetry and laser scanning: 3D world model for smart heavy equipment planning. Autom. Constr. 2019, 98, 322–331. [Google Scholar] [CrossRef]
- Saovana, N.; Yabuki, N.; Fukuda, T. Development of an unwanted-feature removal system for Structure from Motion of repetitive infrastructure piers using deep learning. Adv. Eng. Inform. 2020, 46, 101169. [Google Scholar] [CrossRef]
- Balali, V.; Jahangiri, A.; Machiani, S.G. Multi-class US traffic signs 3D recognition and localization via image-based point cloud model using color candidate extraction and texture-based recognition. Adv. Eng. Inform. 2017, 32, 263–274. [Google Scholar] [CrossRef]
- Lane, S.N.; James, T.D.; Crowell, M.D. Application of Digital Photogrammetry to Complex Topography for Geomorphological Research. Photogramm. Rec. 2000, 16, 793–821. [Google Scholar] [CrossRef]
- Chio, S.-H.; Chiang, C.-C. Feasibility Study Using UAV Aerial Photogrammetry for a Boundary Verification Survey of a Digitalized Cadastral Area in an Urban City of Taiwan. Remote Sens. 2020, 12, 1682. [Google Scholar] [CrossRef]
- Grenzdörffer, G.; Engel, A.; Teichert, B. The photogrammetric potential of low-cost UAVs in forestry and agriculture. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 31, 1207–1214. [Google Scholar]
- Lo, Y.; Zhang, C.; Ye, Z.; Cui, C. Monitoring road base course construction progress by photogrammetry-based 3D reconstruction. Int. J. Constr. Manag. 2022, 1–15. [Google Scholar] [CrossRef]
- Shi, Z.; Lin, Y.; Li, H. Extraction of urban power lines and potential hazard analysis from mobile laser scanning point clouds. Int. J. Remote Sens. 2020, 41, 3411–3428. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, X. Above-Ground Biomass Estimation of Plantation with Complex Forest Stand Structure Using Multiple Features from Airborne Laser Scanning Point Cloud Data. Forests 2021, 12, 1713. [Google Scholar] [CrossRef]
- Balsa-Barreiro, J.; Fritsch, D. Generation of visually aesthetic and detailed 3D models of historical cities by using laser scanning and digital photogrammetry. Digit. Appl. Archaeol. Cult. Herit. 2018, 8, 57–64. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef] [Green Version]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The Utility of Image-Based Point Clouds for Forest Inventory: A Comparison with Airborne Laser Scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Green, S.; Bevan, A.; Shapland, M. A comparative assessment of structure from motion methods for archaeological research. J. Archaeol. Sci. 2014, 46, 173–181. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application. J. Geophys. Res.-Earth Surf. 2012, 117, 17. [Google Scholar] [CrossRef]
- Barazzetti, L. Network design in close-range photogrammetry with short baseline images. In Proceedings of the 26th International CIPA Symposium on Digital Workflows for Heritage Conservation, Ottawa, ON, Canada, 28 August–1 September 2017; pp. 17–23. [Google Scholar]
- Luhmann, T.; Fraser, C.; Maas, H.G. Sensor modelling and camera calibration for close-range photogrammetry. Isprs J. Photogramm. Remote Sens. 2016, 115, 37–46. [Google Scholar] [CrossRef]
- Sapirstein, P. Accurate measurement with photogrammetry at large sites. J. Archaeol. Sci. 2016, 66, 137–145. [Google Scholar] [CrossRef]
- Tavani, S.; Pignalosa, A.; Corradetti, A.; Mercuri, M.; Smeraglia, L.; Riccardi, U.; Seers, T.; Pavlis, T.; Billi, A. Photogrammetric 3D Model via Smartphone GNSS Sensor: Workflow, Error Estimate, and Best Practices. Remote Sens. 2020, 12, 3616. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-based surface reconstruction in geomorphometry—Merits, limits and developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Processes Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A. Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef]
- Martinez-Carricondo, P.; Aguera-Vega, F.; Carvajal-Ramirez, F.; Mesas-Carrascosa, F.J.; Garcia-Ferrer, A.; Perez-Porras, F.J. Assessment of UAV-photogrammetric mapping accuracy based on variation of ground control points. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 1–10. [Google Scholar] [CrossRef]
- Tonkin, T.N.; Midgley, N.G. Ground-Control Networks for Image Based Surface Reconstruction: An Investigation of Optimum Survey Designs Using UAV Derived Imagery and Structure-from-Motion Photogrammetry. Remote Sens. 2016, 8, 786. [Google Scholar] [CrossRef]
- Luhmann, T. 3D Imaging—How to Achieve Highest Accuracy. In Proceedings of the Conference on Videometrics, Range Imaging, and Applications XI, Munich, Germany, 25–26 May 2011. [Google Scholar]
- Luhmann, T. Close range photogrammetry for industrial applications. Isprs J. Photogramm. Remote Sens. 2010, 65, 558–569. [Google Scholar] [CrossRef]
- Huang, H.; Ye, Z.; Zhang, C. An Innovative Approach of Evaluating the Accuracy of Point Cloud Generated by Photogrammetry-Based 3D Reconstruction. In Computing in Civil Engineering, Proceedings of the ASCE International Conference on Computing in Civil Engineering, Orlando, FL, USA, 12–14 September 2021; ASCE: Reston, VA, USA, 2021; pp. 926–933. [Google Scholar]
- Gómez-Gutiérrez, Á.; Sanjosé-Blasco, D.; Juan, J.; Lozano-Parra, J.; Berenguer-Sempere, F.; Matías-Bejarano, D. Does HDR pre-processing improve the accuracy of 3D models obtained by means of two conventional SfM-MVS software packages? The case of the Corral del Veleta rock glacier. Remote Sens. 2015, 7, 10269–10294. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In Proceedings of the International Workshop on Vision Algorithms, Corfu, Greece, 21–22 September 1999; pp. 298–372. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from motion photogrammetry in physical geography. Prog. Phys. Geogr. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- Ahmadabadian, A.H.; Robson, S.; Boehm, J.; Shortis, M.; Wenzel, K.; Fritsch, D. A comparison of dense matching algorithms for scaled surface reconstruction using stereo camera rigs. ISPRS J. Photogramm. Remote Sens. 2013, 78, 157–167. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multiview Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Towards Internet-scale multi-view stereo. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1434–1441. [Google Scholar]
- Nesbit, P.R.; Hugenholtz, C.H. Enhancing UAV-SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef]
- James, M.R.; Antoniazza, G.; Robson, S.; Lane, S.N. Mitigating systematic error in topographic models for geomorphic change detection: Accuracy, precision and considerations beyond off-nadir imagery. Earth Surf. Processes Landf. 2020, 45, 2251–2271. [Google Scholar] [CrossRef]
- Felipe-García, B.; Hernández-López, D.; Lerma, J.L. Analysis of the ground sample distance on large photogrammetric surveys. Appl. Geomat. 2012, 4, 231–244. [Google Scholar] [CrossRef]
- Nagendran, S.K.; Tung, W.Y.; Ismail, M.A.M. Accuracy assessment on low altitude UAV-borne photogrammetry outputs influenced by ground control point at different altitude. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 9th IGRSM International Conference and Exhibition on Geospatial & Remote Sensing (IGRSM 2018), Kuala Lumpur, Malaysia, 24–25 April 2018; IOP Publishing: Bristol, UK, 2018; p. 012031. [Google Scholar]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change detection on points cloud data acquired with a ground laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, W19. [Google Scholar]
- Jafari, B.; Khaloo, A.; Lattanzi, D. Deformation Tracking in 3D Point Clouds Via Statistical Sampling of Direct Cloud-to-Cloud Distances. J. Nondestruct. Eval. 2017, 36, 10. [Google Scholar] [CrossRef]
- Carrea, D.; Abellan, A.; Derron, M.H.; Jaboyedoff, M. Automatic Rockfalls Volume Estimation Based on Terrestrial Laser Scanning Data. In Proceedings of the 12th International IAEG Congress, Torino, Italy, 15–19 September 2014; pp. 425–428. [Google Scholar]
- Cignoni, P.; Rocchini, C.; Scopigno, R. Metro: Measuring error on simplified surfaces. Comput. Graph. Forum 1998, 17, 167–174. [Google Scholar] [CrossRef]
- Charbonnier, P.; Chavant, P.; Foucher, P.; Muzet, V.; Prybyla, D.; Perrin, T.; Grussenmeyer, P.; Guillemin, S. Accuracy assessment of a canal-tunnel 3d model by comparing photogrammetry and laserscanning recording techniques. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W2, 171–176. [Google Scholar] [CrossRef]
- Favalli, M.; Fornaciai, A.; Isola, I.; Tarquini, S.; Nannipieri, L. Multiview 3D reconstruction in geosciences. Comput. Geosci. 2012, 44, 168–176. [Google Scholar] [CrossRef]
- DiFrancesco, P.M.; Bonneau, D.; Hutchinson, D.J. The Implications of M3C2 Projection Diameter on 3D Semi-Automated Rockfall Extraction from Sequential Terrestrial Laser Scanning Point Clouds. Remote Sens. 2020, 12, 1885. [Google Scholar] [CrossRef]
- Walsh, G. Leica scanstation P-series—Details that matter. In Leica ScanStation—White Paper; Leica Geosystems AG: St. Gallen, Switzerland, 2015. [Google Scholar]
- Huang, H.; Zhang, C.; Hammad, A. Effective Scanning Range Estimation for Using TLS in Construction Projects. J. Constr. Eng. Manage. 2021, 147, 13. [Google Scholar] [CrossRef]
- Pearson, K.; Galton, F., VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]


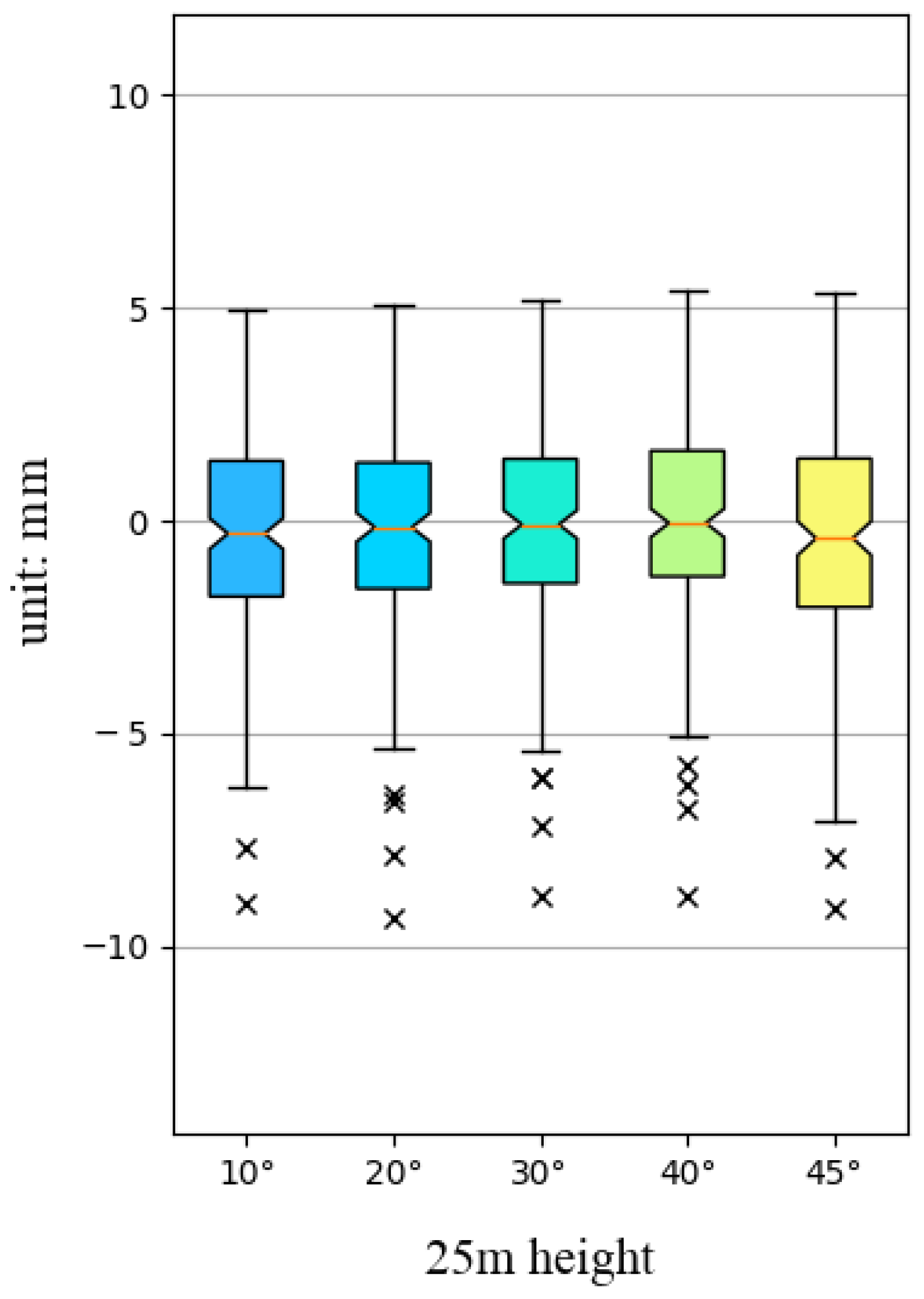


| Fore-and-aft Overlap (%) | Side Overlap (%) | Height (m) | |
|---|---|---|---|
| 90 | 90 | 25 | 10, 20, 30, 40, 45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Ye, Z.; Zhang, C.; Yue, Y.; Cui, C.; Hammad, A. Adaptive Cloud-to-Cloud (AC2C) Comparison Method for Photogrammetric Point Cloud Error Estimation Considering Theoretical Error Space. Remote Sens. 2022, 14, 4289. https://doi.org/10.3390/rs14174289
Huang H, Ye Z, Zhang C, Yue Y, Cui C, Hammad A. Adaptive Cloud-to-Cloud (AC2C) Comparison Method for Photogrammetric Point Cloud Error Estimation Considering Theoretical Error Space. Remote Sensing. 2022; 14(17):4289. https://doi.org/10.3390/rs14174289
Chicago/Turabian StyleHuang, Hong, Zehao Ye, Cheng Zhang, Yong Yue, Chunyi Cui, and Amin Hammad. 2022. "Adaptive Cloud-to-Cloud (AC2C) Comparison Method for Photogrammetric Point Cloud Error Estimation Considering Theoretical Error Space" Remote Sensing 14, no. 17: 4289. https://doi.org/10.3390/rs14174289
APA StyleHuang, H., Ye, Z., Zhang, C., Yue, Y., Cui, C., & Hammad, A. (2022). Adaptive Cloud-to-Cloud (AC2C) Comparison Method for Photogrammetric Point Cloud Error Estimation Considering Theoretical Error Space. Remote Sensing, 14(17), 4289. https://doi.org/10.3390/rs14174289









