An Adaptive and Accurate Method for Rotational Angular Velocity Estimation of Rotor Targets via Fourier Coefficient Interpolation
Abstract
:1. Introduction
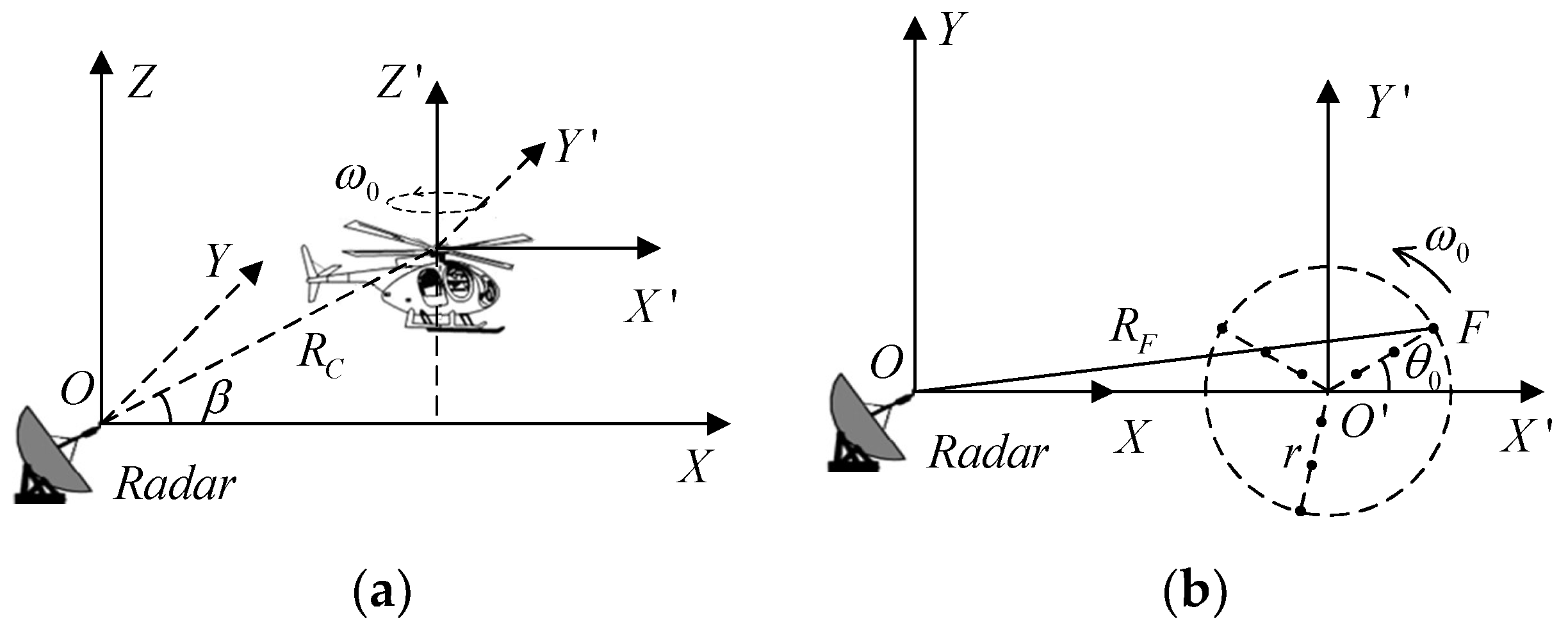
2. Signal Model
3. Proposed Method
3.1. Instantaneous Doppler Frequency Estimation through Time-Frequency Analysis
3.2. Rotational Angular Velocity Estimation via Fourier Coefficient Interpolation
3.3. Initialization of the Frequency Index Residue, Based on a Normalized Fourier Spectrum
3.4. The Cramér–Rao Lower Bound of the Rotational Angular Velocity Estimation
4. Experimental Results
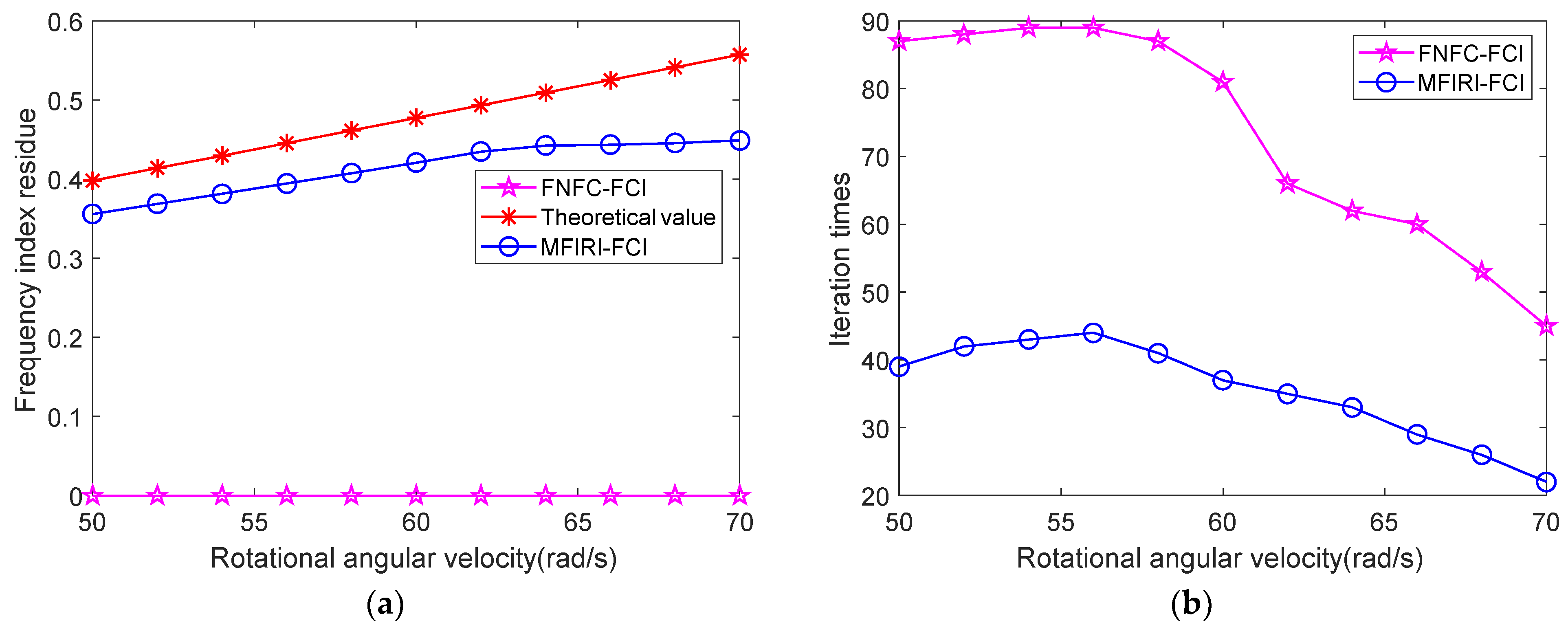
4.1. Effectiveness Validation of Parameter Initialization
4.2. Comparative Analysis of the Estimation Error of Rotational Angular Velocity
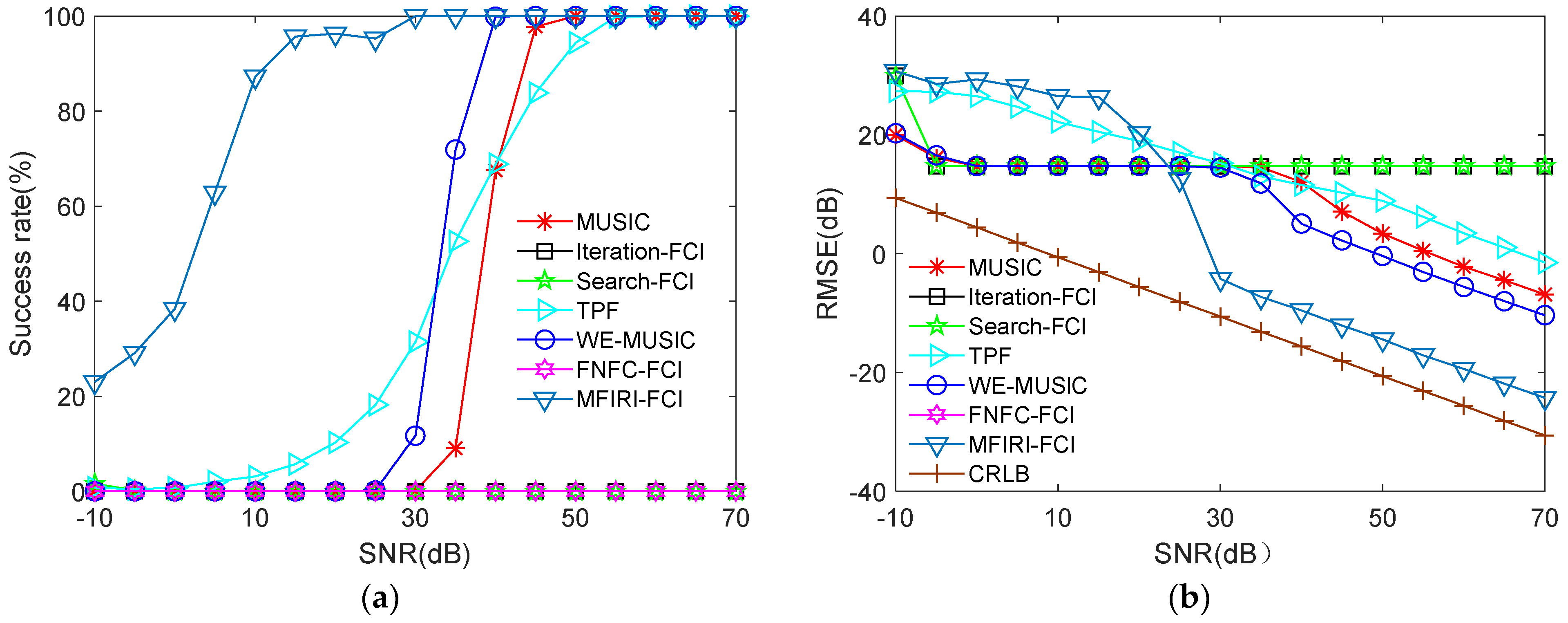
4.2.1. Comparative Analysis of Signal-to-Noise Ratio Threshold
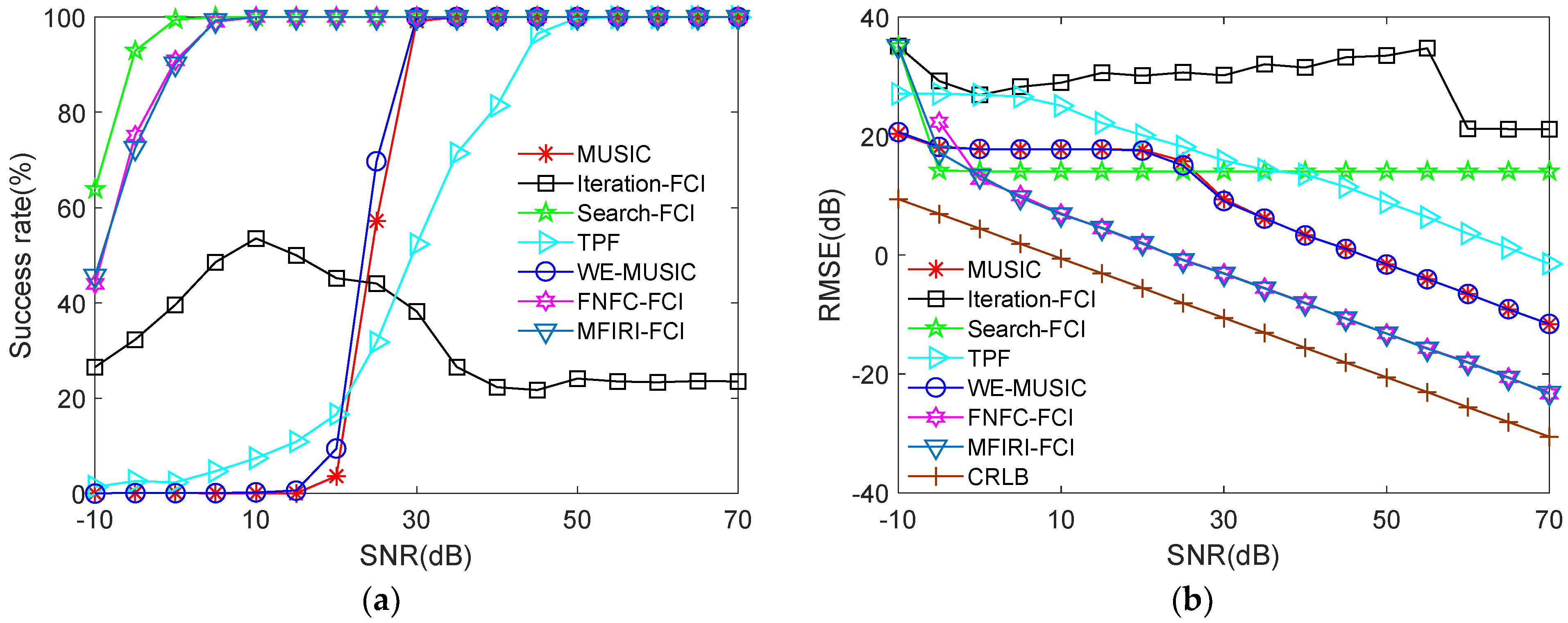
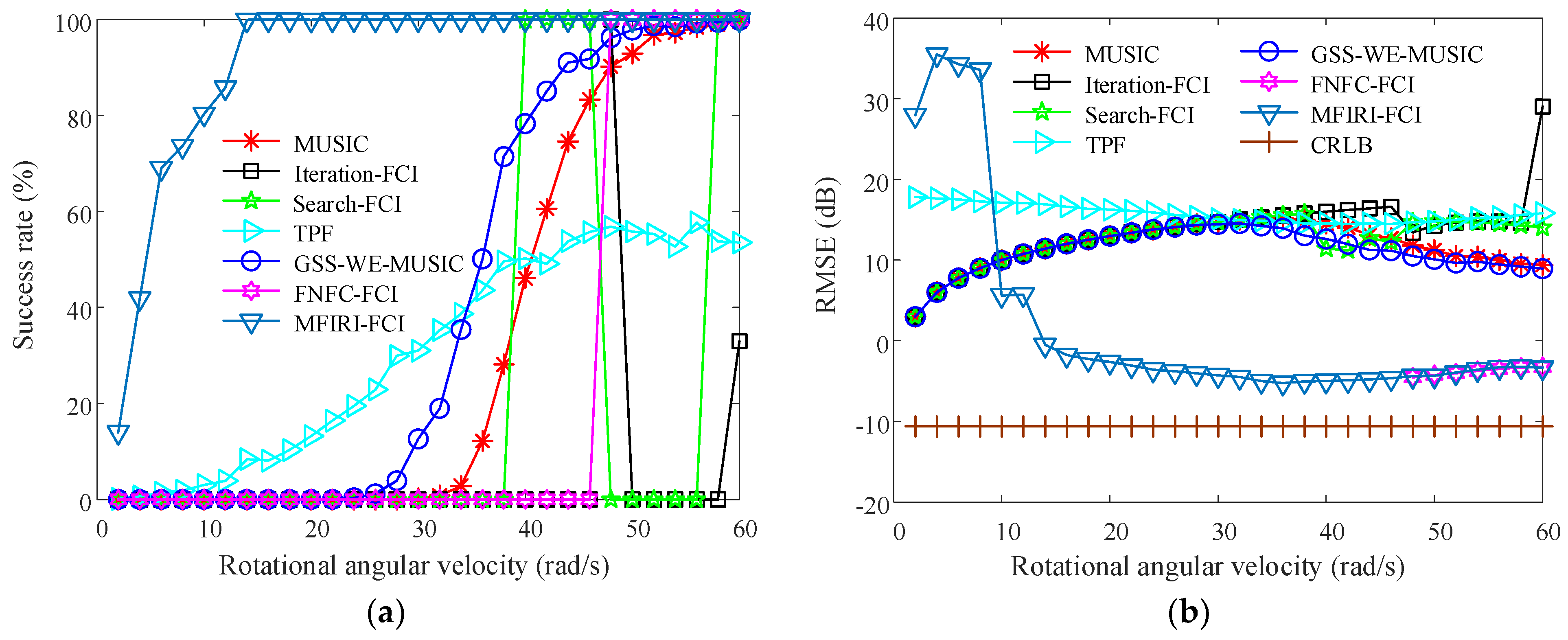
4.2.2. Comparative Analysis of the Rotational Angular Velocity Threshold
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, W.T.; Zhu, Y.; Tang, Z.Y.; Chen, Y.C.; Zhu, Z.B.; Sun, Y.J.; Zhou, C. Efficient rotational angular velocity estimation of rotor target via modified short-time fractional Fourier transform. Remote Sens. 2021, 13, 1970. [Google Scholar] [CrossRef]
- Li, G.; Varshney, P.K. Micro-Doppler parameter estimation via parametric sparse representation and pruned orthogonal matching pursuit. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4937–4948. [Google Scholar] [CrossRef]
- Wang, K.; Wen, H.; Tai, W.S.; Li, G.Q. Estimation of damping factor and signal frequency for damped sinusoidal signal by three points interpolated DFT. IEEE Signal Process. Lett. 2019, 16, 1927–1930. [Google Scholar] [CrossRef]
- Rao, V.; Gaddipati, P.; Rao, P. Signal-driven window-length adaptation for sinusoid detection in polyphonic music. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 342–348. [Google Scholar] [CrossRef]
- Follum, J.; Pierre, J.W.; Martin, R. Simultaneous estimation of electromechanical modes and forced oscillations. IEEE Trans-Actions Power Syst. 2017, 32, 3958–3967. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. An adaptive filtering approach to spectral estimation and SAR imaging. IEEE Trans. Signal Process. 1996, 44, 1469–1484. [Google Scholar] [CrossRef]
- Yardibi, T.; Li, J.; Stoica, P.; Xue, M.; Baggeroer, A.B. Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 425–443. [Google Scholar] [CrossRef]
- Xie, Y.Q.; Li, Y.S.; Gu, Y.T.; Cao, J.W.; Chen, B.D. Fixed-point minimum error entropy with fiducial points. IEEE Trans. Signal Process. 2020, 68, 3824–3833. [Google Scholar] [CrossRef]
- Naha, A.; Samanta, A.K.; Routray, A.; Deb, A.K. Determining autocorrelation matrix size and sampling frequency for MUSIC algorithm. IEEE Signal Process. Lett. 2015, 22, 1016–1020. [Google Scholar] [CrossRef]
- Shahapurkar, N.; Ramalingam, C.S. Threshold performance of MUSIC when using the forward-backward data matrix. IEEE Signal Process. Lett. 2006, 13, 80–83. [Google Scholar] [CrossRef]
- Liao, K.F.; Yu, Z.R.; Xie, N.B.; Jiang, J.Z. Joint estimation of azimuth and distance for far-field multi targets based on graph signal processing. Remote Sens. 2022, 14, 1110. [Google Scholar] [CrossRef]
- Wang, W.T.; Liu, S.X.; Shen, X.Z.; Zheng, W.J. 3D imaging algorithm of directional borehole radar based on root-MUSIC. Remote Sens. 2021, 13, 2957. [Google Scholar] [CrossRef]
- Liu, Z.X.; Quan, Y.H.; Wu, Y.J.; Xing, M.D. Super-resolution range and velocity estimation for SFA-OFDM radar. Remote Sens. 2022, 14, 278. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Y.X.; Xiong, Z.H. An approximate maximum likelihood estimator for instantaneous frequency estimation of multicomponent nonstationary signals. IEEE Trans. Instrum. Meas. 2022, 71, 6501509. [Google Scholar] [CrossRef]
- Bresler, Y.; Macovski, A. Exact maximum likelihood parameter estimation of superimposed exponential signals in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1081–1089. [Google Scholar] [CrossRef]
- Chan, F.K.W.; So, H.C.; Lau, W.H.; Chan, C.F. Efficient approach for sinusoidal frequency estimation of gapped data. IEEE Signal Process. Lett. 2010, 17, 611–614. [Google Scholar] [CrossRef]
- So, H.C.; Chan, K.W.; Chan, Y.T.; Ho, K.C. Linear prediction approach for efficient frequency estimation of multiple real sinusoids: Algorithms and analyses. IEEE Trans. Signal Process. 2005, 53, 2290–2305. [Google Scholar] [CrossRef]
- Aboutanios, E.; Mulgrew, B. Iterative frequency estimation by interpolation on Fourier coefficients. IEEE Trans. Signal Process. 2005, 53, 1237–1242. [Google Scholar] [CrossRef]
- Candan, Ç. A method for fine resolution frequency estimation from three DFT samples. IEEE Signal Process. Lett. 2011, 18, 351–354. [Google Scholar] [CrossRef]
- Candan, Ç. Analysis and further improvement of fine resolution frequency estimation method from three DFT samples. IEEE Signal Process. Lett. 2013, 20, 913–916. [Google Scholar] [CrossRef]
- Chen, S.W.; Li, D.H.; Wei, X.P. Accurate frequency estimation of real sinusoid signal. Proceeding of the 2nd International Conference on Signal Processing Systems, Dalian, China, 5–7 July 2010. [Google Scholar]
- Djukanović, S. An accurate method for frequency estimation of a real sinusoid. IEEE Signal Process. Lett. 2016, 23, 915–918. [Google Scholar] [CrossRef]
- Ye, S.L.; Sun, J.D.; Aboutanios, E. On the estimation of the parameter of a real sinusoid in noise. IEEE Signal Process. Lett. 2017, 24, 638–642. [Google Scholar] [CrossRef]
- Ye, S.L.; Aboutanios, E. Rapid accurate frequency estimation of multiple resolved exponentials in noise. Signal Process. 2017, 132, 29–39. [Google Scholar] [CrossRef]
- Chen, X.M. On near-field and far-field correlations in reverberation chambers. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 74–76. [Google Scholar] [CrossRef]
- Fu, H.; Kam, P.Y. MAP/ML estimation of the frequency and phase of a single sinusoid in noise. IEEE Trans. Signal Process. 2007, 55, 834–845. [Google Scholar] [CrossRef]
- Aboutanios, E. A modified dichotomous search frequency estimator. IEEE Signal Process. Lett. 2004, 11, 186–188. [Google Scholar] [CrossRef]
- Zakharov, Y.V.; Tozer, T.C. Frequency estimator with dichotomous search of periodogram peak. Electron. Lett. 1999, 35, 1608–1609. [Google Scholar] [CrossRef]


| Transmitted Signal Parameters | Carrier Frequency | Bandwidth | Pulse Repetition Frequency | Observation Time | Pulse Samples |
|---|---|---|---|---|---|
| Value | 1 GHz | 2 MHz | 5 kHz | 50 ms | 250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhang, J.; Wu, H.; Meng, J. An Adaptive and Accurate Method for Rotational Angular Velocity Estimation of Rotor Targets via Fourier Coefficient Interpolation. Remote Sens. 2022, 14, 4342. https://doi.org/10.3390/rs14174342
Wang W, Zhang J, Wu H, Meng J. An Adaptive and Accurate Method for Rotational Angular Velocity Estimation of Rotor Targets via Fourier Coefficient Interpolation. Remote Sensing. 2022; 14(17):4342. https://doi.org/10.3390/rs14174342
Chicago/Turabian StyleWang, Wantian, Jiahao Zhang, Hao Wu, and Jin Meng. 2022. "An Adaptive and Accurate Method for Rotational Angular Velocity Estimation of Rotor Targets via Fourier Coefficient Interpolation" Remote Sensing 14, no. 17: 4342. https://doi.org/10.3390/rs14174342
APA StyleWang, W., Zhang, J., Wu, H., & Meng, J. (2022). An Adaptive and Accurate Method for Rotational Angular Velocity Estimation of Rotor Targets via Fourier Coefficient Interpolation. Remote Sensing, 14(17), 4342. https://doi.org/10.3390/rs14174342






