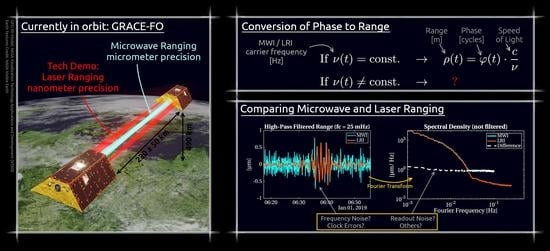
Comparing GRACE-FO KBR and LRI Ranging Data with Focus on Carrier Frequency Variations
Abstract
:1. Introduction
2. Phase Observable
3. LRI Ranging Phase
3.1. Formula 1: Phase-Frequency Ratio
3.2. Formula 2: Integral of Differentiated Phase
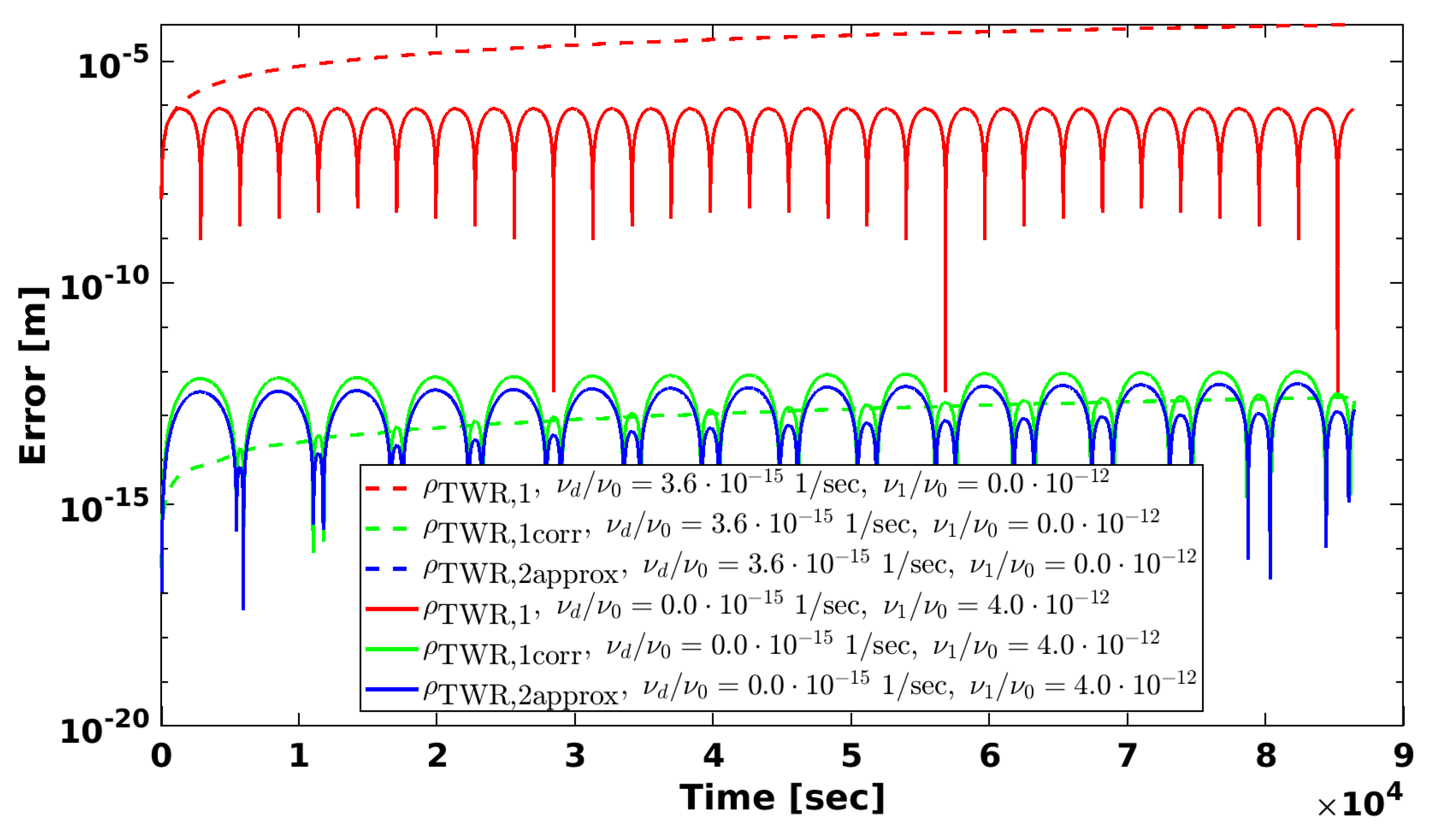
3.3. Accuracy of Approximations
3.4. Model Errors: Scale Factor and Light Propagation Time
4. KBR Dual-One Way Ranging (DOWR)
5. Range Differences between LRI and KBR
6. Instrument Noises and Corrections
6.1. Ionospheric Correction
6.2. Tilt-to-Length Coupling
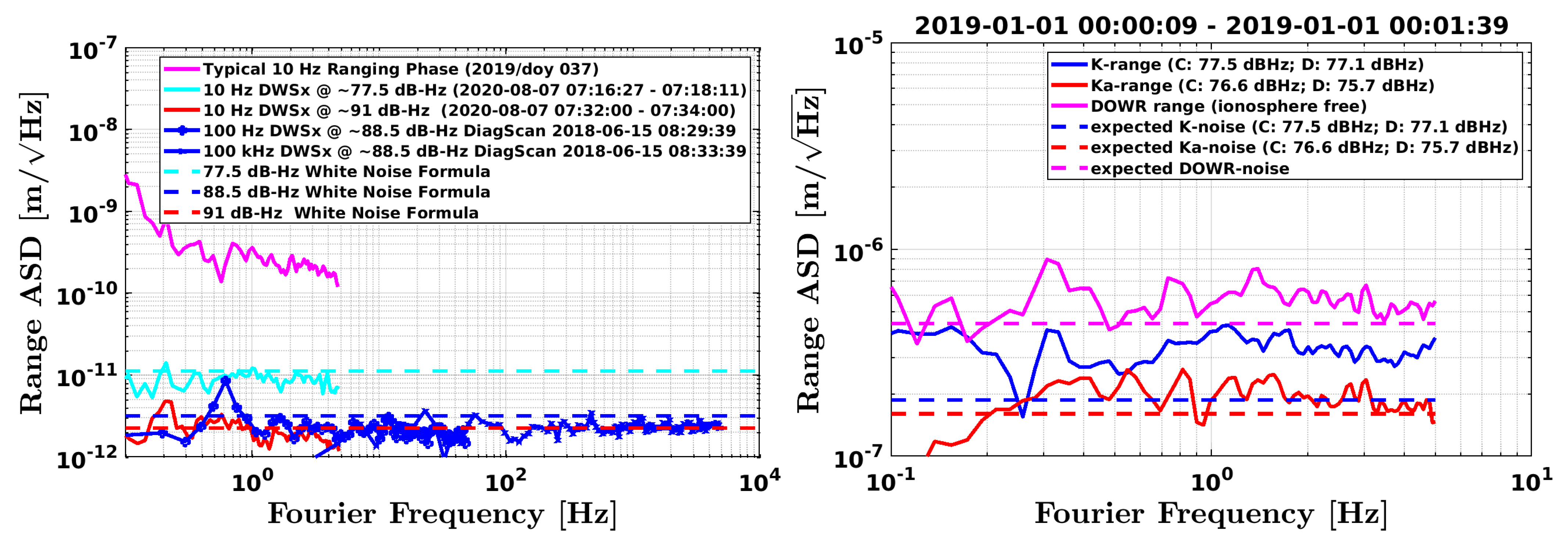
6.3. Phase Readout Noise
6.4. Timetag Errors
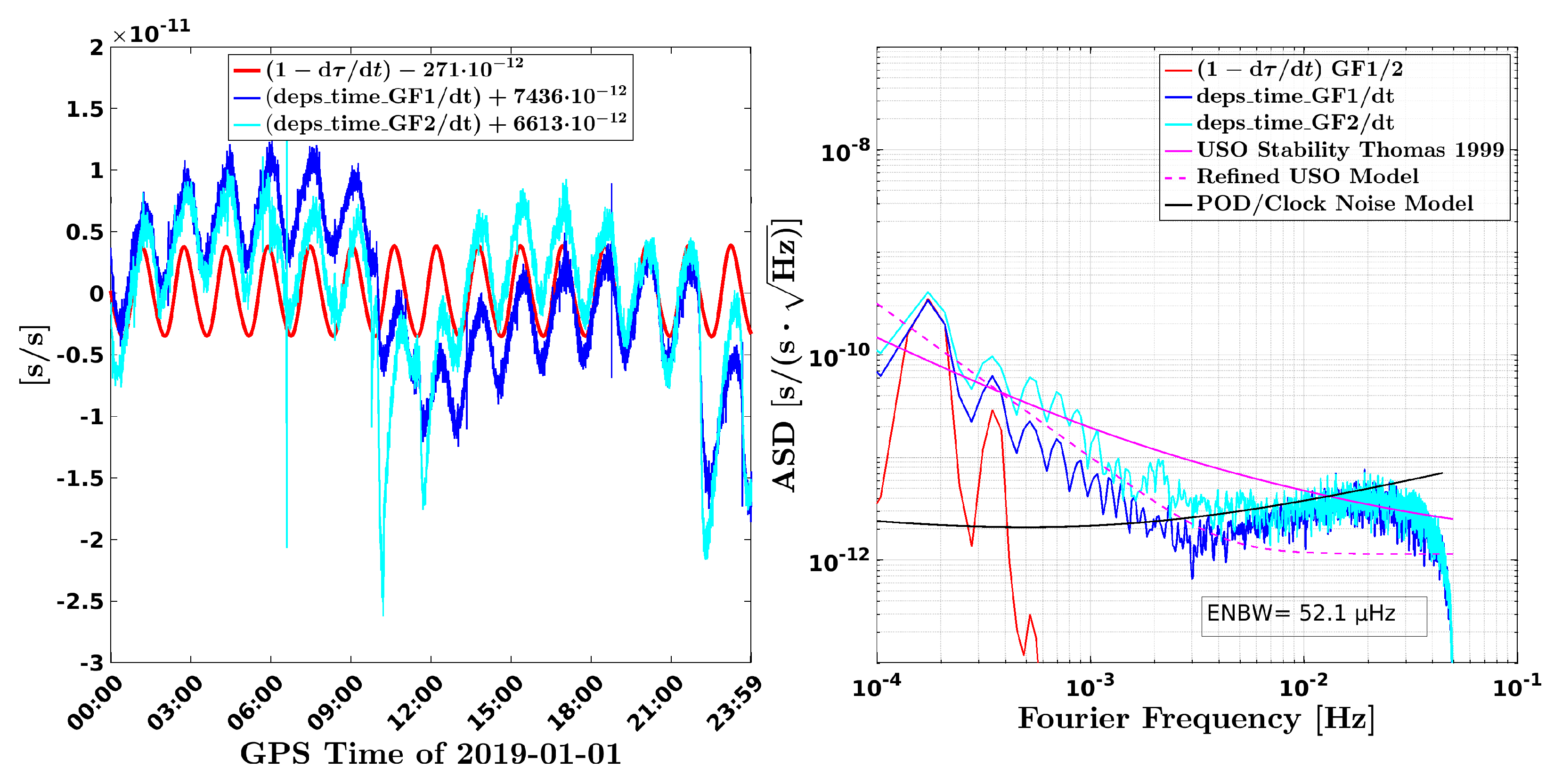
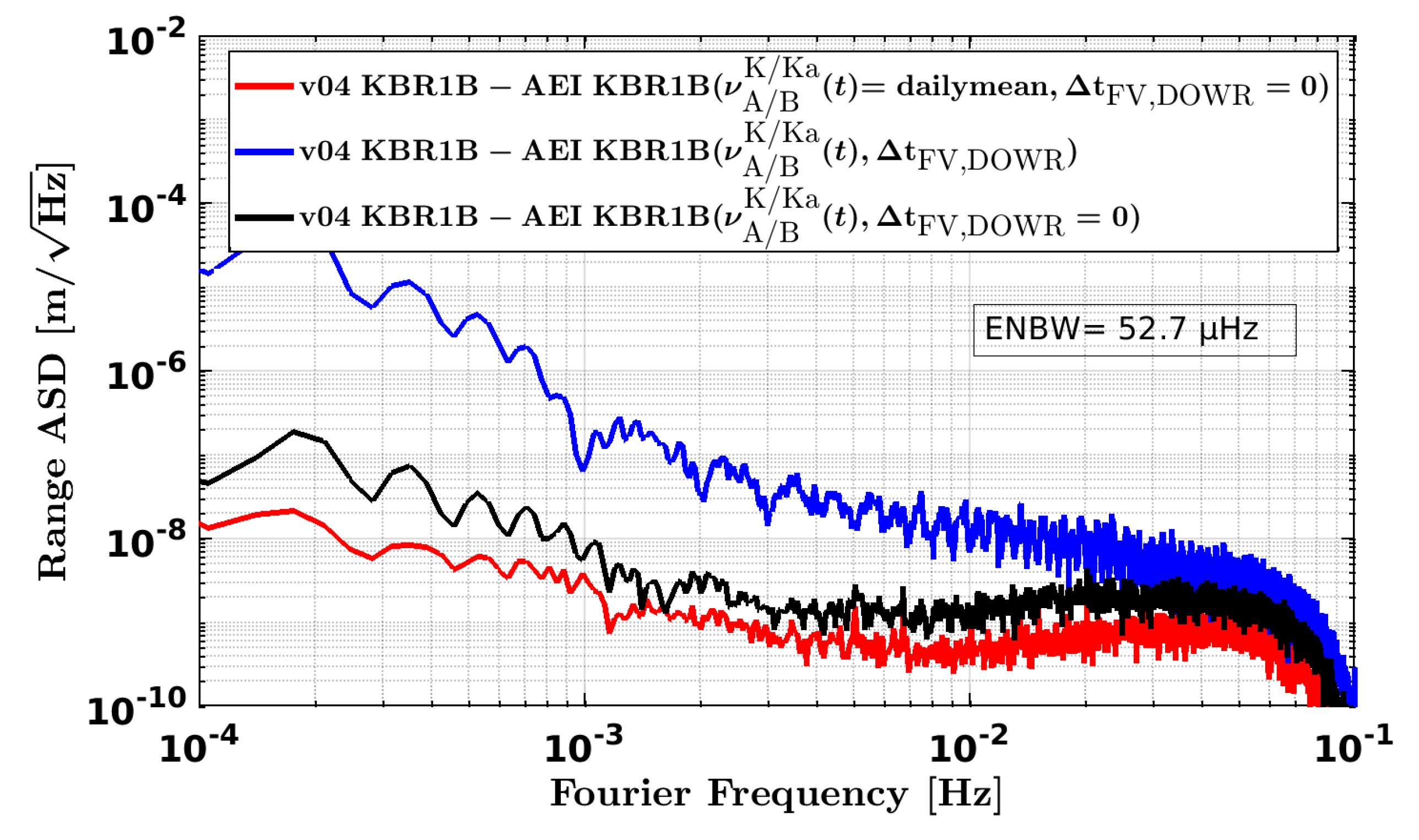
6.5. Carrier Frequency Variations
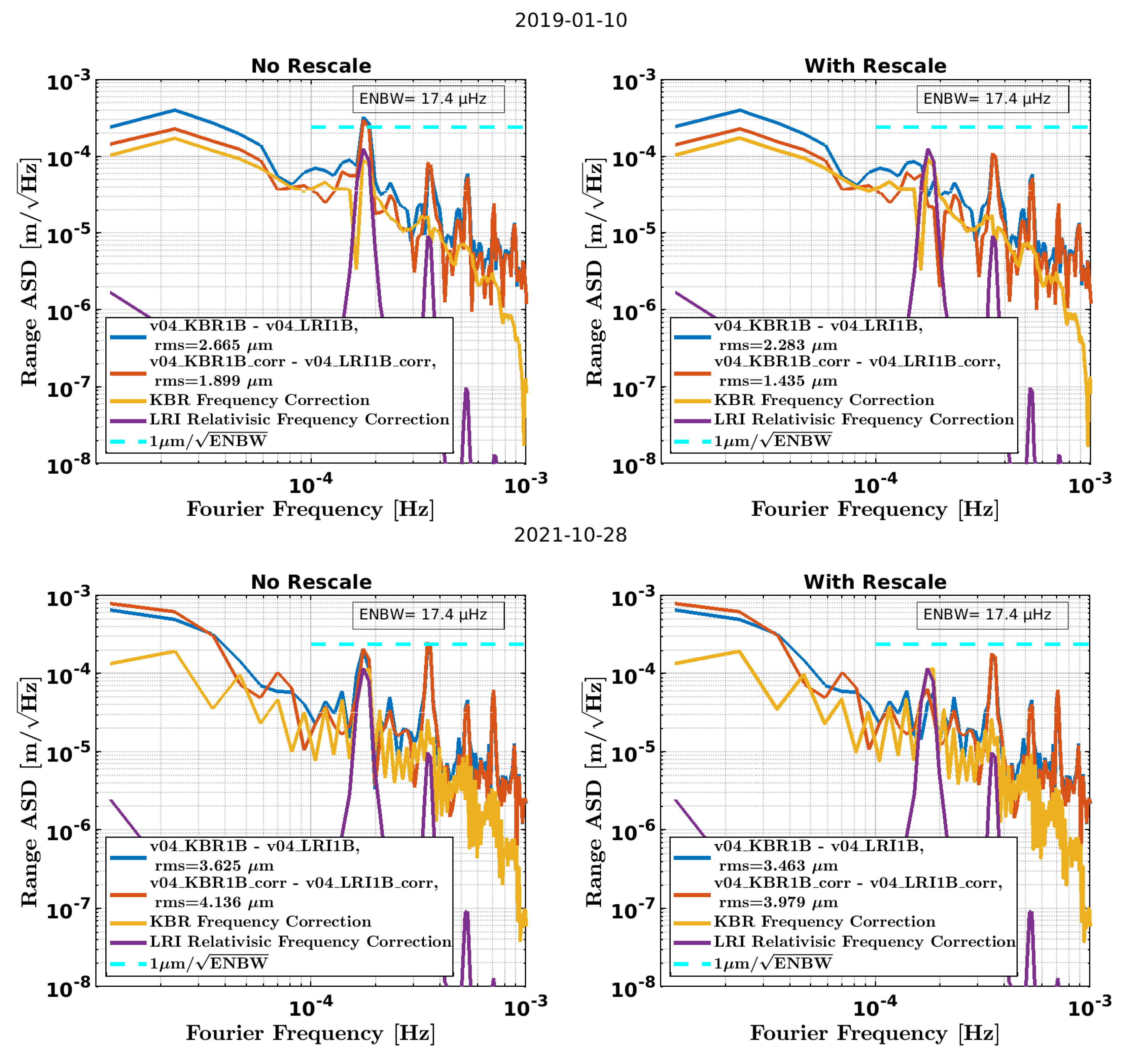
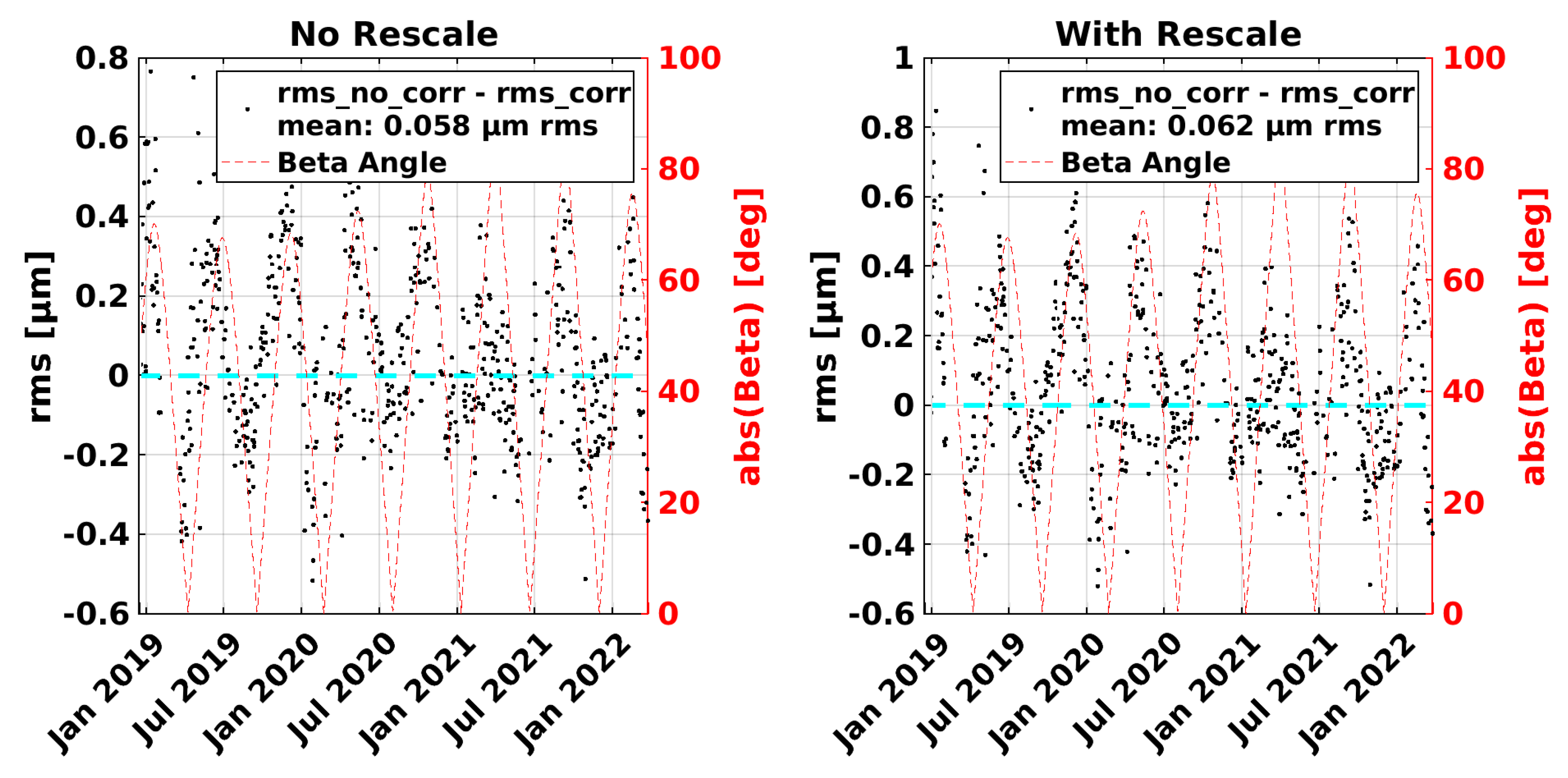
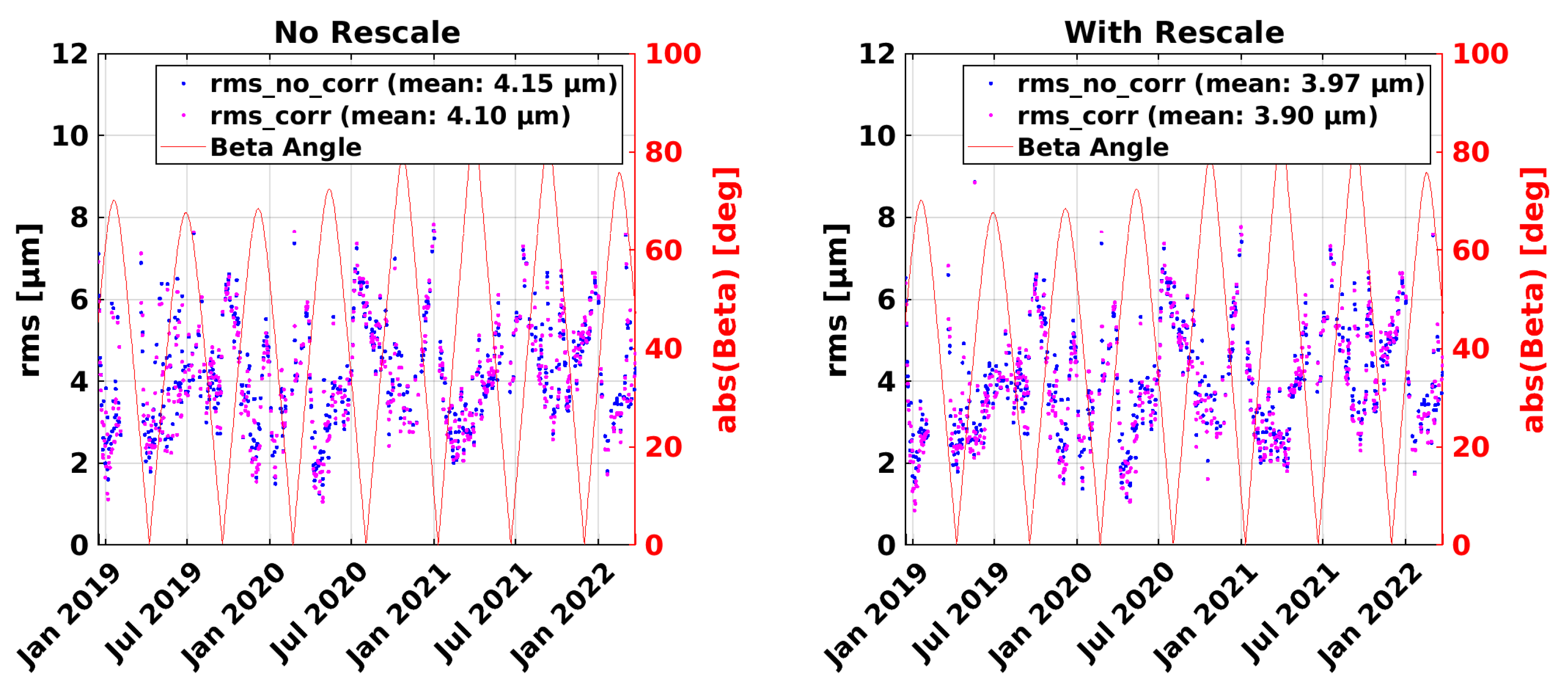
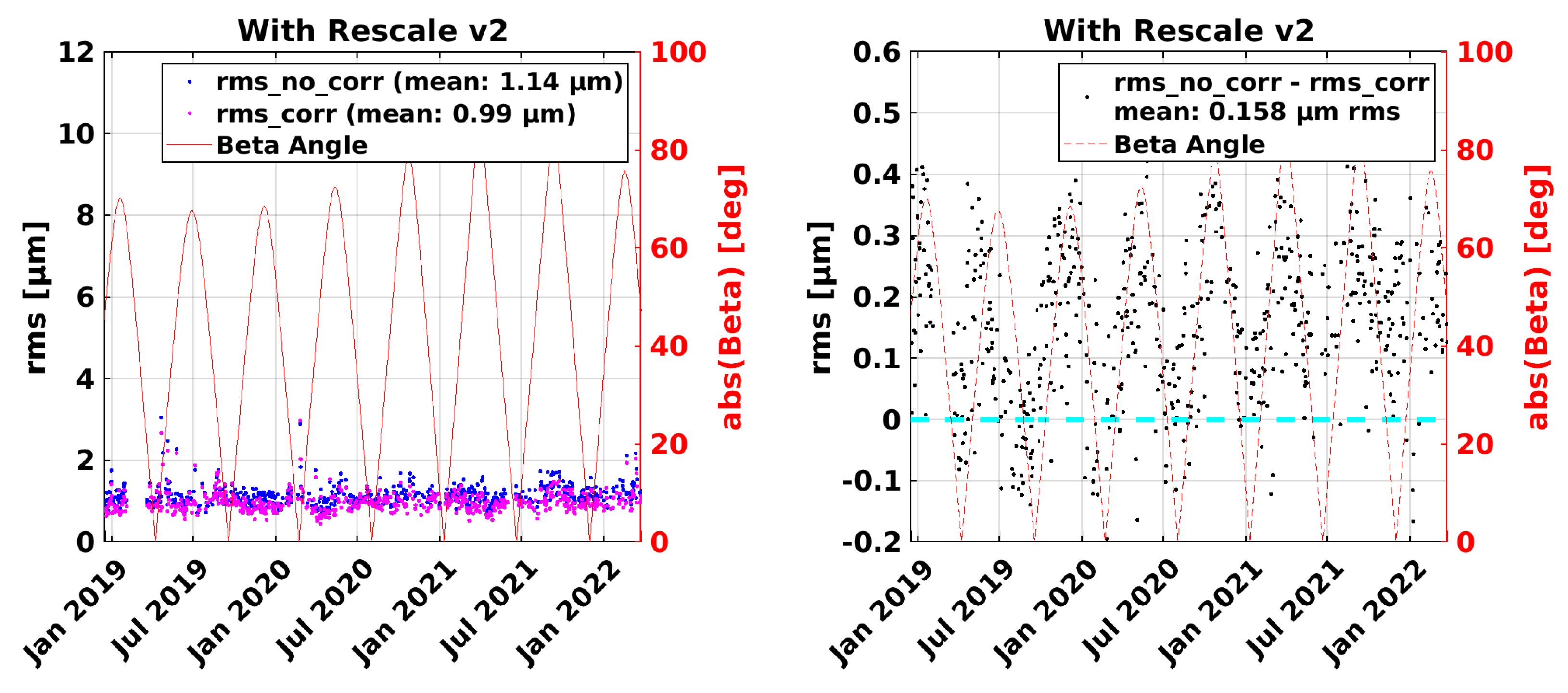
7. Impact of Frequency Variations on KBR-LRI Residuals
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Commonly Used Symbols
| Symbol | Comment | Symbol | Comment |
| virtual oscillator time | unknown constant in phase | ||
| time drift due to frequency variations | eps_time in CLK1B | ||
| speed of light | LRI phase from transponder S/C | ||
| LRI phase from reference S/C | two way ranging phase | ||
| propagation time from transponder to reference S/C | propagation time for round trip | ||
| instantaneous range from LRI | biased range of two-way ranging (LRI) | ||
| light time correction range | quantities at GPS time | ||
| scale factor error (when converting phase to range) | scale factor error (from frequency noise of the cavity) | ||
| dual-one way phase combination of K-/Ka-Band | inter-satellites biased distance from KBR | ||
| instantaneous range from MWI | range correction due to frequency variation | ||
| phase of microwave (GHz) or optical (THz) radiation | proper time |
Appendix A
| Name | Formula/Value | Comment |
|---|---|---|
| 282 THz | LRI optical frequency (1064.5 nm) | |
| proper time 1/rev variation (cf. Figure 1) | ||
| assumption, 87 kHz/day | ||
| satellite separation DC | ||
| 1/rev range variation | ||
| linear range drift | ||
| orbit frequency, 1/rev |
References
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the global mass change data record: GRACE Follow-On instrument and science data performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Landerer, F.W.; Swenson, S. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Han, S.C.; Shum, C.K.; Bevis, M.; Ji, C.; Kuo, C.Y. Crustal dilatation observed by GRACE after the 2004 Sumatra-Andaman earthquake. Science 2006, 313, 658–662. [Google Scholar] [CrossRef] [PubMed]
- Ciracì, E.; Velicogna, I.; Swenson, S. Continuity of the mass loss of the world’s glaciers and ice caps from the GRACE and GRACE Follow-On missions. Geophys. Res. Lett. 2020, 47, e2019GL086926. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Wilson, C.; Cazenave, A.; Seo, K.W.; Kim, J.S. Global ocean mass change from GRACE and GRACE Follow-On and altimeter and Argo measurements. Geophys. Res. Lett. 2020, 47, e2020GL090656. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Zhang, Z.; Ni, S. Long-term groundwater variations in Northwest India from satellite gravity measurements. Glob. Planet. Chang. 2014, 116, 130–138. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; Available online: https://www.ipcc.ch/report/ar6/wg1 (accessed on 19 August 2022). [CrossRef]
- Stocker, T.; Intergovernmental Panel on Climate Change. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; Available online: https://www.ipcc.ch/report/ar5/wg1/ (accessed on 19 August 2022).
- Thomas, J. An Analysis of Gravity-Field Estimation Based on Intersatellite Dual-1-Way Biased Ranging (No. JPL-98-15); Technical Report; Jet Propulsion Laboratory (JPL): Pasadena, CA, USA, 1999; Available online: ftp://isdcftp.gfz-potsdam.de/grace/DOCUMENTS/ANCILLARY/ (accessed on 24 August 2022).
- Kim, J. Simulation Study of a Low-Low Satellite-to-Satellite Tracking Mission. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2000. [Google Scholar]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Ghobadi-Far, K.; Han, S.C.; McCullough, C.M.; Wiese, D.N.; Yuan, D.N.; Landerer, F.W.; Sauber, J.; Watkins, M.M. GRACE Follow-On laser ranging interferometer measurements uniquely distinguish short-wavelength gravitational perturbations. Geophys. Res. Lett. 2020, 47, e2020GL089445. [Google Scholar] [CrossRef]
- Nicklaus, K.; Cesare, S.; Massotti, L.; Bonino, L.; Mottini, S.; Pisani, M.; Silvestrin, P. Laser metrology concept consolidation for NGGM. CEAS Space J. 2020, 12, 313–330. [Google Scholar] [CrossRef]
- Wiese, D.; Boening, C.; Zlotnicki, V.; Luthcke, S.; Loomis, B.; Rodell, M.; Sauber, J.; Bearden, D.; Chrone, J.; Horner, S.; et al. The NASA Mass Change Designated Observable Study: Overview, Progress, and Future Plans. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6121–6124. [Google Scholar] [CrossRef]
- Flechtner, F. Realization of a Satellite Mission “GRACE-I” for Parallel Observation of Changing Global Water Resources and Biodiversity; Technical Report, Copernicus Meetings; 2020; Available online: https://ui.adsabs.harvard.edu/abs/2020AGUFMG020...07F/abstract (accessed on 24 August 2022).
- Wen, H.; Gerhard, K.; William, B.; Meegyeong, P.; Carly, S.; Felix, L. Gravity Recovery and Climate Experiment (GRACE) Follow-On (GRACE-FO) Level-1 Data Product User Handbook; JPL D-56935. 2019. Available online: https://podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo/docs/GRACE-FO_L1_Handbook.pdf (accessed on 24 August 2022).
- Sheard, B.; Heinzel, G.; Danzmann, K.; Shaddock, D.; Klipstein, W.; Folkner, W. Intersatellite laser ranging instrument for the GRACE follow-on mission. J. Geod. 2012, 86, 1083–1095. [Google Scholar] [CrossRef]
- Abich, K.; Abramovici, A.; Amparan, B.; Baatzsch, A.; Okihiro, B.B.; Barr, D.C.; Bize, M.P.; Bogan, C.; Braxmaier, C.; Burke, M.J.; et al. In-Orbit Performance of the GRACE Follow-on Laser Ranging Interferometer. Phys. Rev. Lett. 2019, 123, 031101. [Google Scholar] [CrossRef] [PubMed]
- Schütze, D.; Stede, G.; Müller, V.; Gerberding, O.; Bandikova, T.; Sheard, B.S.; Heinzel, G.; Danzmann, K. Laser beam steering for GRACE Follow-On intersatellite interferometry. Opt. Express 2014, 22, 24117–24132. [Google Scholar] [CrossRef] [PubMed]
- Müller, V. Design Considerations for Future Geodesy Missions and for Space Laser Interferometry. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität, Hannover, Germany, 2017. [Google Scholar] [CrossRef]
- Kim, J.; Tapley, B. Error analysis of a low-low satellite-to-satellite tracking mission. J. Guid. Control Dyn. 2002, 25, 1100–1106. [Google Scholar] [CrossRef]
- Kim, J.; Tapley, B. Simulation of dual one-way ranging measurements. J. Spacecr. Rocket. 2003, 40, 419–425. [Google Scholar] [CrossRef]
- Ko, U.D. Analysis of the Characteristics of the GRACE Dual One-Way Ranging System. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2008. Available online: http://hdl.handle.net/2152/17977 (accessed on 21 August 2022).
- Kim, J.; Lee, S.W. Flight performance analysis of GRACE K-band ranging instrument with simulation data. Acta Astronaut. 2009, 65, 1571–1581. [Google Scholar] [CrossRef]
- Goswami, S.; Devaraju, B.; Weigelt, M.; Mayer-Gürr, T. Analysis of GRACE range-rate residuals with focus on KBR instrument system noise. Adv. Space Res. 2018, 62, 304–316. [Google Scholar] [CrossRef] [Green Version]
- Ko, U.D.; Tapley, B.D.; Ries, J.C.; Bettadpur, S.V. High-frequency noise in the gravity recovery and climate experiment intersatellite ranging system. J. Spacecr. Rocket. 2012, 49, 1163–1173. [Google Scholar] [CrossRef]
- Kim, J.; Tapley, B. Optimal frequency configuration for dual one-way ranging systems. J. Spacecr. Rocket. 2005, 42, 749–751. [Google Scholar] [CrossRef]
- Bandikova, T.; Flury, J.; Ko, U.D. Characteristics and accuracies of the GRACE inter-satellite pointing. Adv. Space Res. 2012, 50, 123–135. [Google Scholar] [CrossRef]
- Ko, U.D.; Tapley, B. Computing the USO frequency instability of GRACE satellites. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Abich, K.; Bogan, C.; Braxmaier, C.; Danzmann, K.; Dehne, M.; Gohlke, M.; Görth, A.; Heinzel, G.; Herding, M.; Mahrdt, C.; et al. GRACE-follow on laser ranging interferometer: German contribution. J. Phys. Conf. Ser. 2015, 610, 012010. [Google Scholar] [CrossRef]
- Schuetze, D.; Team, L. Measuring Earth: Current status of the GRACE Follow-On Laser Ranging Interferometer. In Proceedings of the 11th Eduardo Amaldi Conference On Gravitational Waves (AMALDI 11), Gwangju, Korea, 21–26 June 2015; Lee, H., Oh, J., Eds.; 2016; Volume 716. [Google Scholar] [CrossRef]
- Schuetze, D.; Mueller, V.; Stede, G.; Sheard, B.S.; Heinzel, G.; Danzmann, K.; Sutton, A.J.; Shaddock, D.A. Retroreflector for GRACE follow-on: Vertex vs. point of minimal coupling. Opt. Express 2014, 22, 9324–9333. [Google Scholar] [CrossRef] [PubMed]
- Bachman, B.; de Vine, G.; Dickson, J.; Dubovitsky, S.; Liu, J.; Klipstein, W.; McKenzie, K.; Spero, R.; Sutton, A.; Ware, B.; et al. Flight phasemeter on the Laser Ranging Interferometer on the GRACE Follow-On mission. In Proceedings of the 11th International LISA Symposium, Hamilton Island, Australia, 7–12 May 2017; Volume 840. [Google Scholar] [CrossRef]
- Wuchenich, D.M.R.; Mahrdt, C.; Sheard, B.S.; Francis, S.P.; Spero, R.E.; Miller, J.; Mow-Lowry, C.M.; Ward, R.L.; Klipstein, W.M.; Heinzel, G.; et al. Laser link acquisition demonstration for the GRACE Follow-On mission. Opt. Express 2014, 22, 11351–11366. [Google Scholar] [CrossRef]
- Koch, A.; Sanjuan, J.; Gohlke, M.; Mahrdt, C.; Brause, N.; Braxmaier, C.; Heinzel, G. Line of sight calibration for the laser ranging interferometer on-board the GRACE Follow-On mission: On-ground experimental validation. Opt. Express 2018, 26, 25892–25908. [Google Scholar] [CrossRef]
- Mahrdt, C. Laser Link Acquisition for the GRACE Follow-On Laser Ranging Interferometer. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität, Hannover, Germany, 2014. [Google Scholar] [CrossRef]
- Wegener, H.; Müller, V.; Heinzel, G.; Misfeldt, M. Tilt-to-Length Coupling in the GRACE Follow-On Laser Ranging Interferometer. J. Spacecr. Rocket. 2020, 57, 1362–1372. [Google Scholar] [CrossRef]
- Goswami, S.; Francis, S.P.; Bandikova, T.; Spero, R.E. Analysis of GRACE Follow-On Laser Ranging Interferometer Derived Inter-Satellite Pointing Angles. IEEE Sens. J. 2021, 21, 19209–19221. [Google Scholar] [CrossRef]
- Misfeldt, M.; Müller, V.; Müller, L.; Wegener, H.; Heinzel, G. Scale Factor Determination for the GRACE-Follow On Laser Ranging Interferometer including Thermal Correction. arXiv 2022, arXiv:2207.11470. [Google Scholar]
- Misfeldt, M.; Müller, V.; Müller, L.; Wegener, H.; Heinzel, G. Thermal Influence on the LRI Scale Factor. In Proceedings of the 23rd EGU General Assembly, Online, 19–30 April 2021; p. EGU21-1242. [Google Scholar] [CrossRef]
- Burt, E.; Prestage, J.; Tjoelker, R.; Enzer, D.; Kuang, D.; Murphy, D.; Robison, D.; Seubert, J.; Wang, R.; Ely, T. Demonstration of a trapped-ion atomic clock in space. Nature 2021, 595, 43–47. [Google Scholar] [CrossRef]
- Heinzel, G.; Rüdiger, A.; Schilling, R. Spectrum and Spectral Density Estimation by the Discrete Fourier Transform (DFT), Including a Comprehensive List of Window Functions and Some New At-Top Windows; Technical Report; Albert-Einstein-Institute: Hannover, Germany, 2002; Available online: http://hdl.handle.net/11858/00-001M-0000-0013-557A-5 (accessed on 24 August 2022).
- Shiozawa, T. Classical Relativistic Electrodynamics: Theory of Light Emission and Application to Free Electron Lasers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Yan, Y.; Müller, V.; Heinzel, G.; Zhong, M. Revisiting the light time correction in gravimetric missions like GRACE and GRACE follow-on. J. Geod. 2021, 95, 1–19. [Google Scholar] [CrossRef]
- Case, K.; Gerhard, K.; Wu, S.C. Gravity Recovery and Climate Experiment (GRACE) Level-1B Data Product User Handbook. JPL D-22027. 2010. Available online: https://opendap.jpl.nasa.gov/opendap/allData/grace/docs/Handbook_1B_v1.3.pdf (accessed on 19 August 2022).
- Rees, E.R.; Wade, A.R.; Sutton, A.J.; Spero, R.E.; Shaddock, D.A.; Mckenzie, K. Absolute frequency readout derived from ULE cavity for next generation geodesy missions. Opt. Express 2021, 29, 26014–26027. [Google Scholar] [CrossRef]
- Ying, H.; Wen, S. Release Notes of GRACE-FO Level1B Data; Technical Report; PODAAC: Pasadena, CA, USA, 2019. Available online: https://podaac.jpl.nasa.gov/gravity/gracefo-documentation (accessed on 19 August 2022).
- Müller, L.; Müller, V.; Misfeldt, M.; Wegener, H.; Heinzel, G. An Alternative Derivation of the GRACE Follow-On LRI1B Product: Current Status. Technical Report, Copernicus Meetings. In Proceedings of the GRACE/GRACE-FO Science Team Meeting 2020, Online, 27–29 October 2020. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.; Sanz, J.; Orús, R. Second-order ionospheric term in GPS: Implementation and impact on geodetic estimates. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Wegener, H. Analysis of Tilt-to-Length Coupling in the GRACE Follow-On Laser Ranging Interferometer. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität, Hannover, Germany, 2022. [Google Scholar] [CrossRef]
- Spero, R. Point-mass sensitivity of gravimetric satellites. Adv. Space Res. 2021, 67, 1656–1664. [Google Scholar] [CrossRef]



| Name | Value/Formula | Comment |
|---|---|---|
| 4.832000 MHz | exact | |
| 4.832099 MHz | exact | |
| 4.832000 MHz | ||
| 4.832099 MHz | ||
| exact | ||
| exact | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, V.; Hauk, M.; Misfeldt, M.; Müller, L.; Wegener, H.; Yan, Y.; Heinzel, G. Comparing GRACE-FO KBR and LRI Ranging Data with Focus on Carrier Frequency Variations. Remote Sens. 2022, 14, 4335. https://doi.org/10.3390/rs14174335
Müller V, Hauk M, Misfeldt M, Müller L, Wegener H, Yan Y, Heinzel G. Comparing GRACE-FO KBR and LRI Ranging Data with Focus on Carrier Frequency Variations. Remote Sensing. 2022; 14(17):4335. https://doi.org/10.3390/rs14174335
Chicago/Turabian StyleMüller, Vitali, Markus Hauk, Malte Misfeldt, Laura Müller, Henry Wegener, Yihao Yan, and Gerhard Heinzel. 2022. "Comparing GRACE-FO KBR and LRI Ranging Data with Focus on Carrier Frequency Variations" Remote Sensing 14, no. 17: 4335. https://doi.org/10.3390/rs14174335
APA StyleMüller, V., Hauk, M., Misfeldt, M., Müller, L., Wegener, H., Yan, Y., & Heinzel, G. (2022). Comparing GRACE-FO KBR and LRI Ranging Data with Focus on Carrier Frequency Variations. Remote Sensing, 14(17), 4335. https://doi.org/10.3390/rs14174335