Prediction of Strawberry Dry Biomass from UAV Multispectral Imagery Using Multiple Machine Learning Methods

Abstract

Biomass is a key biophysical parameter for precision agriculture and plant breeding. Fast, accurate and non-destructive monitoring of biomass enables various applications related to crop growth. In this paper, strawberry dry biomass weight was modeled using 4 canopy geometric parameters (area, average height, volume, standard deviation of height) and 25 spectral variables (5 band original reflectance values and 20 vegetation indices (VIs)) extracted from the Unmanned Aerial Vehicle (UAV) multispectral imagery. Six regression techniques—multiple linear regression (MLR), random forest (RF), support vector machine (SVM), multivariate adaptive regression splines (MARS), eXtreme Gradient Boosting (XGBoost) and artificial neural network (ANN)—were employed and evaluated for biomass prediction. The ANN had the highest accuracy in a five-fold cross-validation, with R² of 0.89~0.93, RMSE of 7.16~8.98 g and MAE of 5.06~6.29 g. As for the other five models, the addition of VIs increased the R² from 0.77~0.80 to 0.83~0.86, and reduced the RMSE from 8.89~9.58 to 7.35~8.09 g and the MAE from 6.30~6.70 to 5.25~5.47 g, respectively. Red-edge-related VIs, including the normalized difference red-edge index (NDRE), simple ratio vegetation index red-edge (SR_RedEdge), modified simple ratio red-edge (MSR_RedEdge) and chlorophyll index red and red-edge (CI_red&RE), were the most influential VIs for biomass modeling. In conclusion, the combination of canopy geometric parameters and VIs obtained from the UAV imagery was effective for strawberry dry biomass estimation using machine learning models.

1. Introduction

Biomass is a crucial biophysical parameter for precision agriculture and plant breeding. It is the result of photosynthesis [1,2] and other physiological processes involved in the uptake and use of sunlight, water, and mineral nutrients [3]. Biomass measurements allow farmers to assess crop growth status and soil fertility [4] and thus implement efficient management measures, such as the amount and timing of fertilizer, pesticide, and water supply to ensure crop health [5,6]. It is also a key trait measured by plant breeders [7,8]. Thus, rapid, accurate and non-destructive measurements of plant biomass are of great value in various aspects of precision agriculture.

Traditional destructive measurements are time-consuming and labor-intensive [9,10] and cannot assess the biomass of the same plant throughout its growth cycle [11,12]. To solve this problem, studies on the estimation of plant biomass from image-derived parameters are emerging continuously. Satellite-based data have proven effective in predicting and mapping forest and energy crop biomass [13,14,15,16]. Ahmad et al. [17] investigated the application of high-resolution (≤5 m) optical satellite imagery such as QuickBird, WordView-3 and IKONOS for forest above-ground biomass (AGB) estimation. This work demonstrated that using satellite-derived independent variables including tree canopy, image texture, tree shadow fraction, canopy height and vegetation indices (VIs) can yield prediction accuracies (R²) higher than 0.8 in regional-scale studies. Naik et al. [18] compared multi-source multispectral remote sensing data acquired by Sentinel-2 (10 m, 12 bands), RapidEye (5 m, 5 bands) and Dove (3 m, 4 bands) satellites in the prediction task of forest AGB, showing that red-edge and short-wave infrared (SWIR) channel-dependent variables significantly improved the model performance.

Many attempts have also been made to establish the relationship between satellite VIs and the biomass of various crops, such as rice, wheat, and soybeans [19,20,21]. Geng et al. [22] calculated nine VIs from MODIS satellite reflectance data and adopted four machine learning methods, including random forest (RF), support vector machine (SVM), artificial neural network (ANN) and eXtreme Gradient Boosting (XGBoost), to estimate corn biomass, with R² values between 0.72 and 0.78. Dong et al. [23] extracted multiple red-edge, near-infrared (NIR) and SWIR-based VIs from Landsat 8 and Sentinel-2 satellite data. Statistical approaches (linear and non-linear regressions) were used to obtain the leaf area index (LAI) of six crops (canola, soybean, wheat, corn, oat, and beans). The computed LAI, climate and soil datasets were assimilated to reparametrize a simple crop growth model to estimate the dry biomass of the above crops. The R² of dry biomass estimation reached 0.8, which is higher than when using only empirical methods between biomass and VIs. The limitation of the satellite VI-based statistical/machine learning methods is that satellite VIs are often affected by the plant growth state and external environmental conditions (e.g., cloud cover), which makes it non-universal for different crops and regions [13,24]. In addition, for precision agriculture at the single plant level, satellite imagery does not have sufficient spatial resolution.

Over the past decade, Unmanned Aerial Vehicles (UAVs) (drones) have emerged as one of the most popular tools for field-based phenotyping and precision agriculture [25,26,27]. They provide a flexible and easy-to-operate approach to collect high spatial (centimeter level) and temporal imagery for high-throughput crop phenotyping [28]. Various types of sensors, including spectral sensors (e.g., RGB, multispectral and hyperspectral cameras) and depth sensors (LiDAR), have been mounted on drones to collect data for crop biomass estimation [10,29]. Correspondingly, image processing technologies have also improved greatly. Photogrammetry software using the Structure in Motion (SfM) method, such as Pix4D and Agisoft Metashape, enables the fast and efficient preprocessing of remote sensing data and generates 3D point clouds and high-quality orthoimages, which provide detailed structural properties of crops [30,31,32].

In recent years, numerous studies have been conducted to monitor crop biomass based on variables (usually crop height, canopy area, textual features, VIs, etc.) obtained from UAV imagery. For example, Fu et al. [33] evaluated the influence of two types of features on the winter wheat biomass predictive performance of partial least squares regression (PLSR) and least squares support vector machine (LSSVM) models. One type of feature was the multiscale texture obtained from UAV-based RGB imagery, and the other comprised various spectral features including the two-band normalized difference vegetation index (NDVI) and continuum removal of red-edge spectra (SpeCR) obtained from ground-based hyperspectral data. The results showed that the combination of SpeCR and multiscale textures achieved the highest estimation accuracy, with R² = 0.87 and RMSE = 119.76 g/m². Johansen et al. [34] adopted the RF machine learning approach to predict the biomass of tomato plants based on shape features (plant area, border length, width, etc.), entropy texture and VIs derived from UAV multispectral imagery. The highest explained variances were approximately 87.95%.

Wang et al. [35] estimated the AGB of winter wheat using forty-four VIs extracted from UAV multispectral images. Three methods, including MLR, RF and PLSR, were adopted, and the performance of the RF models was more stable, with R² ranging from 0.83 to 0.93 in the validation dataset. Some influential VIs include the Modified Chlorophyll Absorption Ratio Index—Improved (MCARI2), Leaf Chlorophyll Index (LCI) and Chlorophyll Vegetation Index (CVI), etc. Che et al. [36] established regression models between the biomass of cultivated red algae Pyropia and four VIs derived from UAV multispectral images. The quadratic model of the difference vegetation index (DVI) showed more accuracy, with R² of 0.925. Although the VI approach for predicting above-ground biomass suffers from the saturation problem since VIs tend to lose sensitivity as the crop canopy becomes more dense, it remains a popular method for estimating crop biomass. Several studies also demonstrated that multispectral and hyperspectral data with more wavebands have great potential to overcome the saturation problem [37,38].

For cultivated strawberry (Fragaria × ananassa), there are few studies predicting the dry biomass from image-derived parameters. Guan et al. [39] applied the SfM and Object-Based Image Analysis (OBIA) method on very-high-resolution imagery (0.5 mm for raw images) acquired by a tractor-mounted imaging system to extract canopy-related variables such as area, volume, and average height. Multilinear regression was adopted to model the strawberry canopy dry biomass and leaf area, with accuracy (R²) of 0.79 and 0.84, respectively. Abd-Elrahman et al. [40] continued Guan et al. (2020)’s study and proposed a raster-based geospatial analysis method for automatic canopy delineation, size metric extraction and dry biomass prediction using ArcMap software. However, biomass estimation for strawberry using lower-resolution UAV images has not yet been demonstrated. The overall goal of the present study is to apply various machine learning techniques to model strawberry canopy dry biomass from UAV multispectral imagery. The main objectives of this study were to: (1) compare the predictive performance of six regression methods (MLR, RF, SVM, XGBoost, MARS, ANN) in the estimation of strawberry canopy biomass and examine the stability of these models; (2) compare the influence of strawberry canopy structural parameters (canopy area, average height, volume and standard deviation of height) and VIs on models’ performance; and (3) determine the optimal number of features and significant spectral variables (VIs) for strawberry canopy biomass prediction.

2. Materials and Methods

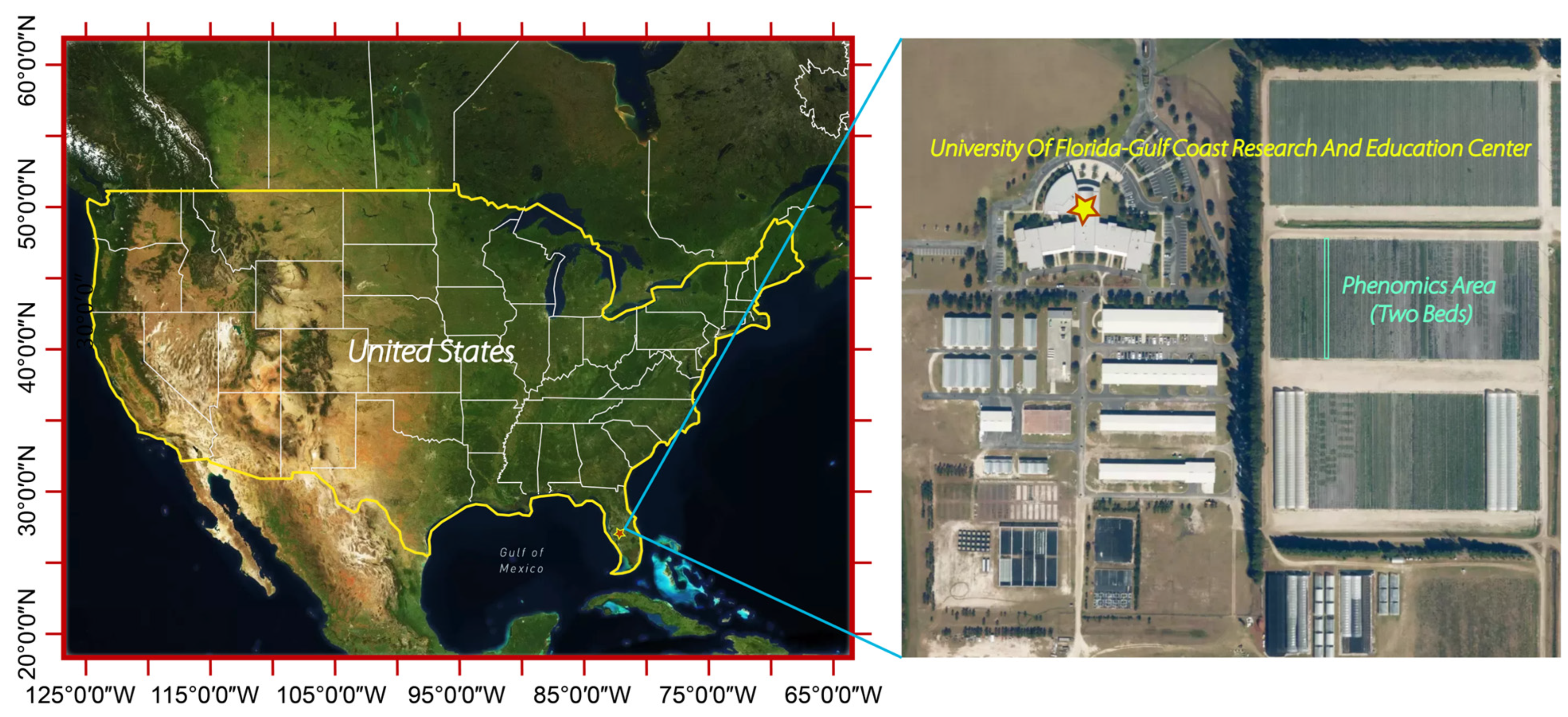
2.1. Study Site and Plant Materials

The study area (27°45′40″N, 82°13′40″W) was situated at the University of Florida’s Gulf Coast Research and Education Center (GCREC), located in Wimauma, Florida, USA (Figure 1). We conducted UAV surveys and in-situ biomass measurements during the winter growing season from 19 November 2020 to 3 March 2021. Two 100-m-long beds cultivated with seventeen strawberry genotypes (

Table 1. Statistics of dry biomass of 17 genotypes measured throughout the 2020–2021 growing season using destructive methods.

Code	Genotype	Dry Biomass
		Mean	Max	Min	Std
A	15.25–6	20.45	37	2.70	10.32
B	15.74–11	16.40	38	1.60	9.72
C	16.30–128	17.46	32	3.30	9.27
D	Brilliance	24.15	42	1.80	12.49
E	13.42–5	16.97	42	1.80	10.29
F	16.33–8	31.80	66	6.40	15.52
G	17.14–155	28.82	61	6.40	14.16
H	17.17–127	27.04	59	5.30	13.88
I	Beauty	19.64	43	2.70	11.73
J	Elyana	36.98	80	9.50	17.22
K	Festival	43.20	109	6.90	26.70
L	18.19–294	30.12	68	3.60	17.17
M	Florida127	47.25	123	6.70	31.48
N	Fronteras	35.70	89	6.80	20.32
O	Radiance	28.21	72	2.10	18.22
P	Treasure	41.90	80	3.90	23.72
Q	Winterstar	27.26	60	1.50	18.17

) were established. Each bed contained sixteen plots, and each plot was planted with seventeen plants, each corresponding to one of the genotypes tested in this experiment. The genotypes represented the range of canopy structures in the UF strawberry breeding germplasm, as well as varieties with unique canopy structures and sizes from other breeding programs. A code using capital letters (A–Q) was marked on the bed surface near each strawberry plant to indicate its genotype. Approximately every week, two plots were randomly selected, and thirty-four plants were removed to the laboratory for dry biomass measurements. The UAV multispectral imagery was acquired within a few hours prior to plant removal. The plants were placed in a drying oven at 65 °C for 5 days to obtain the dry biomass weight. There was a total of 532 strawberry plant samples in the 2020–2021 season. The detailed information of genotypes and plots is shown in Table 1.

2.2. UAV Image Acquisition and Ground Control Points (GCP)

Image acquisition was conducted using a MicaSense RedEdge-M multispectral camera and a downwelling light sensor (DLS) mounted on a Da-Jiang Innovations (DJI) Inspire 2 drone (Figure 2a). The drone operated autonomously, with field flight parameters pre-set using the Litchi flight planning software to cover the whole strawberry experiment area. The UAV flew at an altitude of 15 m above the ground, with a speed of 2 m/s, capturing images with more than 70% overlap and approximately 1-cm raw spatial resolution. The MicaSense multispectral camera contained five spectral bands: blue (475 nm, 20 nm bandwidth), green (560 nm, 20 nm bandwidth), red (668 nm, 10 nm bandwidth), near-infrared (840 nm, 40 nm bandwidth) and red-edge (717 nm, 10 nm bandwidth). The images were captured weekly from 19 November 2020 to 3 March 2021, for a total of 16 collections. The images were captured between 11:00 am and 1:00 pm in as clear and cloudless weather conditions as possible. Before and after each flight, the MicaSense camera was placed above a MicaSense calibrated reflectance panel (Figure 2b) to take white reference images to be used in subsequent image radiometric calibration.

Prior to the UAV flight, we established two sets of centimeter-level ground control points (GCPs) in the field to provide accurate image georeferencing and photo alignment during image preprocessing. Two types of control points were established: (1) 8 GCPs (M1–M8) were placed evenly around the field—for each GCP, we used a survey total station to obtain the positional information of these GCPs (Figure 2c); the other GCPs (N1–N16) were distributed evenly on the plastic strawberry beds as redundant points in case other points were destroyed (Figure 2d). This set of GCPs was surveyed using static GNSS observations.

2.3. Ground-Based Image Collection

In addition to UAVs, this study also used a ground-based platform introduced by Abd-Elrahman et al. [41,42] to obtain high spatial resolution (0.5 mm raw images) to evaluate the quality of UAV images (Figure 3). Two Nikon D300 cameras were used to capture RGB and NIR images, respectively. The imaging system was toweled by a tractor in the strawberry field. More detailed information about this platform is presented in Guan et al. [39] and Abd-Elrahman et al. [40]. Three sets of ground-based images were collected on 8 December 2020, 27 January 2021 and 3 March 2021, which roughly reflected the characteristics of strawberry plants in the early, middle, and mature stages. Orthomosaic images (1 mm per pixel) and DSM products (2 mm per pixel) were generated through the SfM analysis in the Agisoft Metashape software. We extracted four strawberry canopy geometric parameters (canopy area, average height, volume, stand deviation of height) from ground-based images and UAV images, and then compared the differences in the two types of image data, as discussed in Section 3.1.

2.4. Experimental Workflow

Figure 4 illustrates the workflow adopted in this study, which includes (1) UAV multispectral data preprocessing using the Agisoft Metashape software; (2) strawberry plant canopy delineation and structural metric extraction; (3) calculation of vegetation indices; (4) development and validation of the regression models.

2.4.1. UAV Image Preprocessing Using Agisoft Metashape Software

The multispectral images captured by the MicaSense camera were preprocessed using the Agisoft Metashape Photogrammetry software. Radiometric calibration is crucial to the quality of the surface reflectance image produced by the Agisoft software, which is affected by sensor settings, properties, and scene illumination. A white reference image of the calibrated reflectance panel (CRP), along with panel reflectance values provided by the manufacturer, were imported into the Agisoft software, and the UAV images were converted form raw digital number (DN) to radiance and then from radiance to reflectance for each of the five bands. DLS calibration was only used for the images acquired on 25 November 2020 and 13 January 2021, as both dates were cloudy. Using the Structure from Motion (SfM) algorithm, the Agisoft Metashape combined the images taken from multiple angles and generated dense 3D point clouds of scene objects (strawberry canopies, soils, and beds). A digital surface model (DSM) was created from the SfM-based point cloud, and a georeferenced orthomosaic image was generated for each band. The spatial resolution of both DSM and orthomosaic images had 1-cm pixel size.

2.4.2. Canopy Delineation and Structural Parameter Extraction

A geospatial analysis workflow developed by Abd-Elrahman et al. [40] was used for strawberry canopy delineation. This method was implemented on the ESRI’s ArcMap v10.7 and used the marker-controlled watershed algorithm to extract individual plant boundaries. A vector layer containing a point located at the center of each plant canopy, a vegetation mask obtained from the NDVI using the shadow ratio threshold segmentation method and a DSM produced by the SfM algorithm were imported into the model to iteratively generate boundaries for each strawberry plant in the UAV orthomosaic images. As for the canopy size metric extraction, a vegetation-free digital terrain model (DTM) using the local polynomial interpolation technique was created using the elevations of unvegetated areas. Then, the strawberry canopy height model was computed as the difference between the DSM and DTM to extract the canopy area, volume, average height, and standard deviation of height for each strawberry plant canopy (Figure 4).

Figure 4. A workflow diagram showing the methodology adopted in this study, including data preprocessing, feature extraction and biomass predictive modeling.

Figure 4. A workflow diagram showing the methodology adopted in this study, including data preprocessing, feature extraction and biomass predictive modeling.

2.4.3. Selection of Vegetation Indices

In addition to the surface reflectance values of the five spectral bands, we selected 20 VIs that are commonly used to estimate canopy biophysical parameters, as shown in

Table 2. Vegetation indices (VIs) selected for the biomass estimation. ρ_Red, ρ_Green, ρ_Blue, ρ_NIR and ρ_RedEdge are the reflectance values of the red, green, blue, near-infrared, and red-edge bands.

VIs	Equation	Reference
Normalized Difference Vegetation Index (NDVI)	$\frac{{\rho }_{NIR}-{\rho }_{Red}}{{\rho }_{NIR}+{\rho }_{Red}}$	[43]
Renormalized Difference Vegetation Index (RDVI)	$\frac{{\rho }_{NIR}-{\rho }_{Red}}{\sqrt{{\rho }_{NIR}+{\rho }_{Red}}}$	[44]
Blue Normalized Difference Vegetation Index (BNDVI)	$\frac{{\rho }_{NIR}-{\rho }_{Blue}}{{\rho }_{NIR}+{\rho }_{Blue}}$	[45]
Green Normalized Difference Vegetation Index (GNDVI)	$\frac{{\rho }_{NIR}-{\rho }_{Green}}{{\rho }_{NIR}+{\rho }_{Green}}$	[46]
NIR–Green Difference Vegetation Index (GDVI)	${\rho }_{NIR}-{\rho }_{Green}$	[47]
Green–Red Vegetation Index (GRVI)	$\frac{{\rho }_{Green}-{\rho }_{\mathrm{Re}d}}{{\rho }_{Green}+{\rho }_{\mathrm{Re}d}}$	[48]
Green Leaf Index (GLI)	$\frac{2{\rho }_{Green}-{\rho }_{\mathrm{Re}d}-{\rho }_{Blue}}{2{\rho }_{Green}+{\rho }_{\mathrm{Re}d}+{\rho }_{Blue}}$	[49]
Modified Triangular Vegetation Index 1 (MTVI-1)	$1.2[1.2({\rho }_{NIR}-{\rho }_{Green})-2.5({\rho }_{\mathrm{Re}d}-{\rho }_{Green})]$	[50]
Modified Triangular Vegetation Index 2 (MTVI-2)	$\frac{1.8({\rho }_{NIR}-{\rho }_{Green})-3.75({\rho }_{\mathrm{Re}d}-{\rho }_{Green})}{\sqrt{{(2{\rho }_{NIR}+1)}^2-(6{\rho }_{NIR}-5\sqrt{{\rho }_{\mathrm{Re}d}})-0.5}}$	[50]
Pan Normalized Difference Vegetation Index (PNDVI)	$\frac{{\rho }_{NIR}-({\rho }_{Red}+{\rho }_{Green}+{\rho }_{Blue})}{{\rho }_{NIR}+({\rho }_{Red}+{\rho }_{Green}+{\rho }_{Blue})}$	[51]
Enhanced Vegetation Index (EVI)	$\frac{2.5({\rho }_{NIR}-{\rho }_{Red})}{({\rho }_{NIR}+6{\rho }_{Red}-7.5{\rho }_{Blue}+1)}$	[52]
Wide Dynamic Range Vegetation Index (WDRVI)	$\frac{0.2{\rho }_{NIR}-{\rho }_{Red}}{0.2{\rho }_{NIR}+{\rho }_{Red}}$	[53]
Simple Ratio Index (SR)	$\frac{{\rho }_{NIR}}{{\rho }_{Red}}$	[54]
Red-Edge Simple Ratio Index (SRRedEdge)	$\frac{{\rho }_{NIR}}{{\rho }_{RedEdge}}$	[55]
Modified Simple Ratio (MSR)	$\frac{{\rho }_{NIR}/{\rho }_{Red}-1}{\sqrt{{\rho }_{NIR}/{\rho }_{Red}+1}}$	[56]
Modified Simple Ratio Red-Edge (MSRRedEdge)	$\frac{{\rho }_{NIR}/{\rho }_{RedEdge}-1}{\sqrt{{\rho }_{NIR}/{\rho }_{RedEdge}+1}}$	[56]
Chlorophyll Index Red and Red-Edge (CIred&RE)	$\frac{{\rho }_{\mathrm{Re}dEdge}}{{\rho }_{\mathrm{Re}d}}-1$	[57]
Chlorophyll Index Green (CIgreen)	$\frac{{\rho }_{NIR}}{{\rho }_{Green}}-1$	[57]
Normalized Difference Red-Edge Index (NDRE)	$\frac{{\rho }_{NIR}-{\rho }_{\mathrm{Re}dEdge}}{{\rho }_{NIR}+{\rho }_{RedEdge}}$	[58]
Normalized Difference Red-Edge/Red Index (NDRE-R)	$\frac{{\rho }_{\mathrm{Re}dEdge}-{\rho }_{\mathrm{Re}d}}{{\rho }_{\mathrm{Re}dEdge}+{\rho }_{Red}}$	[45]

. The sum and mean values of all pixels within each plant canopy were calculated for the 20 VIs and 5 individual band values to represent the spectral variables. Therefore, we generated a total of 29 dependent variables (25 spectral features and 4 canopy structural variables) for the biomass modeling.

2.4.4. Biomass Modeling

All modeling was implemented in R Studio 1.4 software using the R programming language (R version 4.0.2). The following six regression techniques were employed in this study.

(1)

Multiple linear regression (MLR) is a statistical method that uses several independent variables to predict the outcome of one dependent variable. The regression equation is designed to establish a linear relationship between the response variable with each independent variable and uses the least squares method to calculate the model parameters by minimizing the sum of squared errors [59].

(2)

Random forest (RF) is a supervised machine learning algorithm that uses an ensemble learning (bagging) strategy to solve classification and regression problems. Bagging, also referred to as bootstrap aggregation, is a sampling technique that generates a fixed number of subset training samples from the original dataset. The idea of random forest is to build multiple decision trees by selecting a random number of samples and features (bagging) during the training process and output the average prediction of all regression trees.

(3)

Support vector machine (SVM) is also a popular machine learning algorithm, widely used in pattern recognition, classification and prediction. There are two types of SVM, support vector classification (SVC) [60] for classification and support vector regression (SVR) [61]. The objective of SVM is to construct a hyperplane in a high-dimensional space that distinctly classifies the data points for classification or contains the largest number of points for regression tasks. The most important feature of SVM is a kernel function that maps the data from the original finite-dimensional space into a higher-dimensional space. In this work, we used SVR and selected the radial basis function (RBF) as the kernel.

(4)

Multivariate adaptive regression spline (MARS) is a non-parametric algorithm for nonlinear problems, introduced by Friedman [62]. It constructs a flexible prediction model by applying piecewise linear regressions. This means that various regression slopes are determined for each predictor’s interval. It consists of two steps: forward selection and backward deletion. MARS begins with a model with only an intercept term and iteratively adds basis functions in pairs to the model until a threshold of the residual error or number of terms is reached. Typically, the obtained model in this process (forward selection) has too many knots with high complexity, which leads to overfitting. Then, the knots that do not contribute significantly to the model performance are removed, which is also known as “pruning” (backward selection).

(5)

The eXtreme Gradient Boosting (XGBoost) algorithm is a scalable end-to-end tree boosting method introduced by Chen and Guestrin [63]. It uses a gradient boosting framework and performs a second-order Taylor expansion to optimize the objective function. A regularization term was also added to the objective function to control the model complexity and prevent model overfitting. Different from the RF model, which trains each tree independently, XGBoost grows each tree on the residuals of the previous tree. In addition, another advantage of XGBoost is its scalability in all scenarios, so it can solve the problems of sparse data.

(6)

Artificial neural networks (ANN) have become a hot research topic in the field of artificial intelligence. They simulate the working mechanism of neurons in the human brain and consist of one input layer, one output layer and one or more hidden layers. Each layer includes neurons, and each neuron has an activation function for introducing nonlinearity into relationships. A connection between two neurons represents the weighted value of the signal passing through that connection. ANN contains two phases: forward propagation and backward propagation. Forward propagation is the process of sequentially computing and storing intermediate variables (including outputs) from the input layer to the output layer. Backpropagation is a method of updating the weights in the model and requires an optimization function and a loss function.

The MLR is a traditional regression method that has been used by Guan et al. [39] for strawberry canopy dry biomass prediction based on the ground-based imagery. It served as a benchmark for comparison with other regression methods in this study. The other five methods, especially RF, are advanced machine learning techniques that have been shown to be effective in dealing with multicollinearity and overfitting problems and the estimation of plant biophysical parameters in many previous studies [11,34,64]. Multiple Vis were imported into the above six regression models, and the corresponding optimal model hyperparameters were determined according to the validation accuracy by using an exhaustive method within limits. Model parameter limits for each method are summarized in

Table 3. Maximum, minimum values of six model parameters.

Method	RF			SVM
Parameters	Best_Mtry		Best_Ntree	Cost	Sigma
Min value	1		100	1	0
Max value	20		600	10	1
Method	MARS			ANN
Parameters	nprune		degree	hidden layer 1	hidden layer 2
Min value	10		1	1	1
Max value	100		5	10	10
Method	XGBoost
Parameters	eta	max_depth	min_child_weight	subsample	colsample_bytree	optimal_trees
Min value	0	1	1	0.5	0.5	0
Max value	0.3	10	10	1	1	100

. The optimal values of these parameters are summarized in Tables S1–S6 in the supplementary file.

2.4.5. Model Validation

Due to the small training samples in our experiment, the five-fold cross-validation (CV) method was used to evaluate the performance of the above six regression models in strawberry biomass prediction. It was implemented by randomly splitting the dataset into five subsets. One of the subsets was reserved for validation and the other data were used for model training. The coefficient of determination (R²), root mean square error (RMSE) and mean absolute error (MAE) were calculated to quantify model performance as follows:

$$\begin{array}{l}{R}^2=1-\frac{{\displaystyle {\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}{{\displaystyle {\sum }_{i=1}^n{(y_i-{\overline{y}}_i)}^2}}\\ RMSE=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}{n}}\\ MAE=\frac{{\displaystyle \sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|}}{n}\end{array}$$

(1)

where $y_i$, ${\widehat{y}}_i$ represent the measured and predicted biomass values, $\overline{y}$ is the average measured value and n is the sample number.

3. Results

3.1. Comparison of Ground-Based and UAV Imagery

Figure 5 illustrates the orthomosaic imagery and DSM product generated from the ground-based and UAV images. Four strawberry canopy geometric parameters were calculated from both ground-based and UAV DSM products, including the canopy area, average height, standard deviation of canopy height and volume. The correlation between the ground-based and UAV image-derived canopy metrics is shown in Figure 6. Compared with the UAV image (1 cm), the ground-based DSM product with higher spatial resolution (2 mm) reveals more detail on the height gradient and texture of the strawberry canopy. However, there is little difference in the canopy metrics computed from these two types of DSM products. The R² achieved 0.97, 0.96, 0.97 and 0.97 for the canopy area, average height, standard deviation of canopy height and volume, respectively. The result indicates that a resolution of 1 cm is sufficient to obtain geometric information on individual strawberry canopies.

3.2. Modeling and Validation of Biomass

3.2.1. Variable Importance Evaluation

The image-based features in this study were of two types: (1) plant geometric properties, quantified as four structural traits—canopy area, volume, average height, and standard deviation of height; (2) two sets of spectral variables, including the original 5 band reflectance values and 20 vegetation indices (VIs), which potentially reflect the morphological (such as leaf density) and biochemical (e.g., water content, pigments) characteristics of strawberry plants [65]. When extracting the spectral information of strawberry plants, the mean and sum values of the VIs and spectral bands for all pixels within an individual plant canopy were calculated and used. We firstly used the Boruta R package to evaluate the relative importance of each feature to biomass estimation. All twenty-nine variables were confirmed to have an impact on the biomass modeling. The relative importance of each feature was assessed using the mean decrease accuracy (%IncMSE), which refers to the average increase in squared residuals after permuting the corresponding variable. A higher %IncMSE value indicates higher variable importance.

As shown in Figure 7a,b, the geometric features showed the most predictive power for predicting dry biomass. Among all VIs, the mean MSR_RedEdge, SR_RedEdge, NDRE and CI_red&RE were most influential in the biomass estimation. Strikingly, the sum values of all pixels within each plant of the three VIs (MSR_RedEdge, NDRE and CI_red&RE) were the top ranked features for dry biomass prediction, even more important than the canopy area and volume, as shown in Figure 7c,d. The reason for this difference may be due to the fact that the VIs’ sum (VI mean × area) contains both structural and spectral information. To further observe the relationship between biomass and image-derived features, the distribution characteristics of six variables (the three geometric traits and the three VIs above) in different biomass intervals were computed and are shown in Figure 8. As expected, canopy area, average height and volume of height increased with the increase in the biomass. The mean SR_RedEdge, MSR_RedEdge and NDRE decreased with the increase in biomass.

Next, we examined the model performance of the six regression methods, MLR, RF, SVR, MARS, XGBoost and ANN, by incorporating different numbers of VIs into the modeling (Figure 9). The validation accuracy of MLR, RF and SVR showed stabilized performance values after incorporating only a few VIs. The performance of MARS, XGBoost and ANN became fluctuant after VIs with low relative importance were imported into the model. Overall, the continued increase in the number of input VIs did not appear to remarkably improve the model performance. To avoid the overfitting and model instability caused by a large number of variables, we chose six VI parameters (MSR_RedEdge, SR_RedEdge, BNDVI, NDRE-R, NDRE and CI_green) according to the relative importance and combined four geometric variables to evaluate the performance of the six regression models.

3.2.2. Performance of Prediction Methods in Strawberry Dry Biomass Prediction

Table 4. Average five-fold CV results for the dry biomass models.

Model	R2			RMSE (g)			MAE (g)
	Geometric	Geometric and VImean	Geometric and VIsum	Geometric	Geometric and VImean	Geometric and VIsum	Geometric	Geometric and VImean	Geometric and VIsum
MLR	0.78	0.80	0.85	9.37	8.85	7.54	6.66	6.40	5.33
RF	0.80	0.81	0.85	8.89	8.72	7.73	6.30	5.95	5.37
SVM	0.78	0.80	0.85	9.58	8.92	7.67	6.58	6.09	5.26
XGBoost	0.77	0.82	0.83	9.41	8.67	8.09	6.70	5.85	5.47
MARS	0.79	0.81	0.86	9.27	8.80	7.35	6.53	6.14	5.25
ANN	0.89	0.90	0.93	8.98	8.61	7.16	6.29	5.93	5.06

shows the average five-fold CV results of six regression methods for strawberry dry biomass prediction. To assess the impact of VIs on biomass modeling, two types of feature combinations were used: (1) only geometric parameters (canopy area, average height, standard deviation of canopy height and volume); (2) geometric parameters and the six VIs input. Two methods of VI calculation (mean and sum) were also compared. The model performance was ranked as follows: (1) ANN > RF > MARS > SVM > MLR > XGBoost when only geometric variables were imported; (2) ANN > XGBoost > RF > MARS > SVM > MLR with both geometric variables and VI means as input; (3) ANN > <MARS > SVM > MLR > RF > XGBoost when both geometric variables and VI sums were used. The above ranking results are based on the R² metric. Overall, the results indicate that the ANN significantly outperformed other models, with R² of 0.89~0.93, RMSE of 7.16~8.98 g and MAE of 5.06~6.29 g. The RF seems more stable with different types of input variables than the other four machine learning methods. Compared with the VI mean calculation method, the use of the VI sum is more effective in improving the performance of the model. Figure 10 provides examples of the predicted dry biomass values compared to the field-based measurements using geometric variables and six VI sums as input.

4. Discussion

Our study used widely available technologies represented by the MicaSense multispectral camera mounted on a small UAV to predict strawberry canopy dry biomass weight. The five different bands of the MicaSense images were used to extract 4 geometric parameters and 20 vegetation indices. We firstly assessed the quality of the UAV DSM (1 cm spatial resolution) against higher-resolution (2 mm) DSM derived from ground-based imagery. The canopy geometric variables derived from the two datasets exhibited a high degree of consistency, with R² above 0.96, which suggested that the one-centimeter UAV dataset is sufficient for strawberry biomass estimation.

Previous studies have demonstrated that spectral variables are the most used and effective remote sensing indicators for estimating plant biophysical properties (e.g., canopy nitrogen content, biomass and yield) [66,67,68]. The red-edge spectral region, located in the red-NIR transition zone, where the position of reflectivity changes drastically, was often referred to as a good indicator of leaf chlorophyll content [69]. Meanwhile, the red-edge band can alleviate the saturation problem of high biomass values to a certain extent [37,38]. In our study, the relative importance of four geometric parameters (area, volume, stand deviation of height and average height) and twenty-five spectral variables (5 spectral bands and 20 VIs) to the biomass modeling was evaluated and ranked. As expected, the geometric parameters reflecting the structural characteristics of the strawberry canopy were the top four variables. The R² between dry biomass and canopy volume reached 0.703. As for the mean VIs of all pixels within each strawberry plant canopy, the MSR_RedEdge, NDRE and CI_red&RE appeared to be most influential on the biomass predictive model performance, with R² in the range of [0.5, 0.6] between the three VIs and dry biomass. These results highlight the red-edge-related VIs as good biomass predictors. This is probably because these VIs may be sensitive to the canopy gap fraction and senescence change, and thus can effectively reflect the differences in canopy density or leaf weight properties among strawberry plants [70].

Unlike grasses and grain crops such as wheat, strawberries are dicots and have a more complex plant structure. Thus, two types of VI calculations (mean and sum) were performed for each plant, as described in Section 2.4.3. There was a certain degree of multi-collinearity between the 25 VIs (Figure S1 in the supplementary file). Machine learning techniques have been proven to effectively tackle the multi-collinearity problem and make full use of strongly collinear VIs in previous studies [71,72,73]. In this study, six regression techniques (MLR, RF, SVR, XGBoost, MARS and ANN) were adopted and examined for the biomass prediction. However, the increase in the number of VIs input did not result in a sustained improvement in model performance. The validation accuracy of MARS, XGBoost and ANN fluctuated after importing VIs of relatively low importance into the model, which may have been caused by overfitting. Therefore, we selected six VI variables combined with four geometric parameters to evaluate the above models.

The results show that ANN outperformed other models, with R² of 0.89~0.93, RMSE of 7.16~8.98 g and MAE of 5.06~6.29 g. The performance of the other five models did not exhibit significant differences. For the VI calculation method, the sum of VI improved the model performance over the mean VI values. This result may be due to the nonlinear relationship between VIs and biomass unexplained by the VI mean. The addition of VIs increased the R² from 0.77~0.80 to 0.83~0.86, and reduced the RMSE from 8.89~9.58 to 7.35~8.09 g and the MAE from 6.30~6.70 to 5.25~5.47 g, respectively. Overall, the combination of canopy structure and spectral information led to a noticeable increase in accuracy compared to using only geometric parameters.

5. Conclusions

In this study, six different regression methods were adopted to predict strawberry canopy dry biomass using UAV MicaSense multispectral images. These models were established using the canopy structural indicators extracted from DEM imagery and various vegetation indices (VIs) derived from the reflectance values of the five MicaSense bands. The results indicated the red-edge-related VIs (such as MSR_RedEdge, NDRE, SR_RedEdge and CI_red&RE) to be most influential on model performance, apart from the structural parameters. The ANN model gave greater predictive ability than the other machine learning methods. This experiment demonstrated the potential application of UAV-captured canopy structural indicators, VIs and machine learning to estimate strawberry canopy biomass.