Spatiotemporal Variation of Actual Evapotranspiration and Its Relationship with Precipitation in Northern China under Global Warming
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. Singular Value Decomposition Analysis
2.3.2. Pearson Correlation Analysis
3. Results
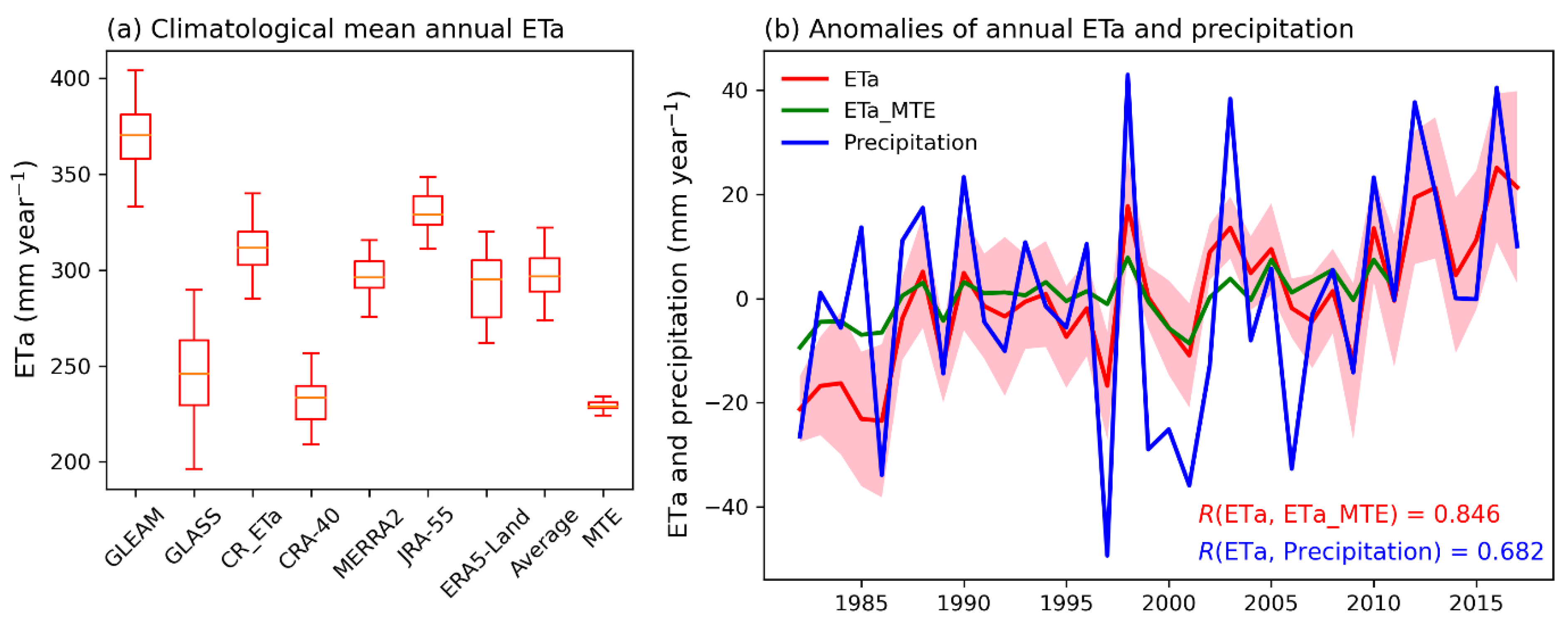
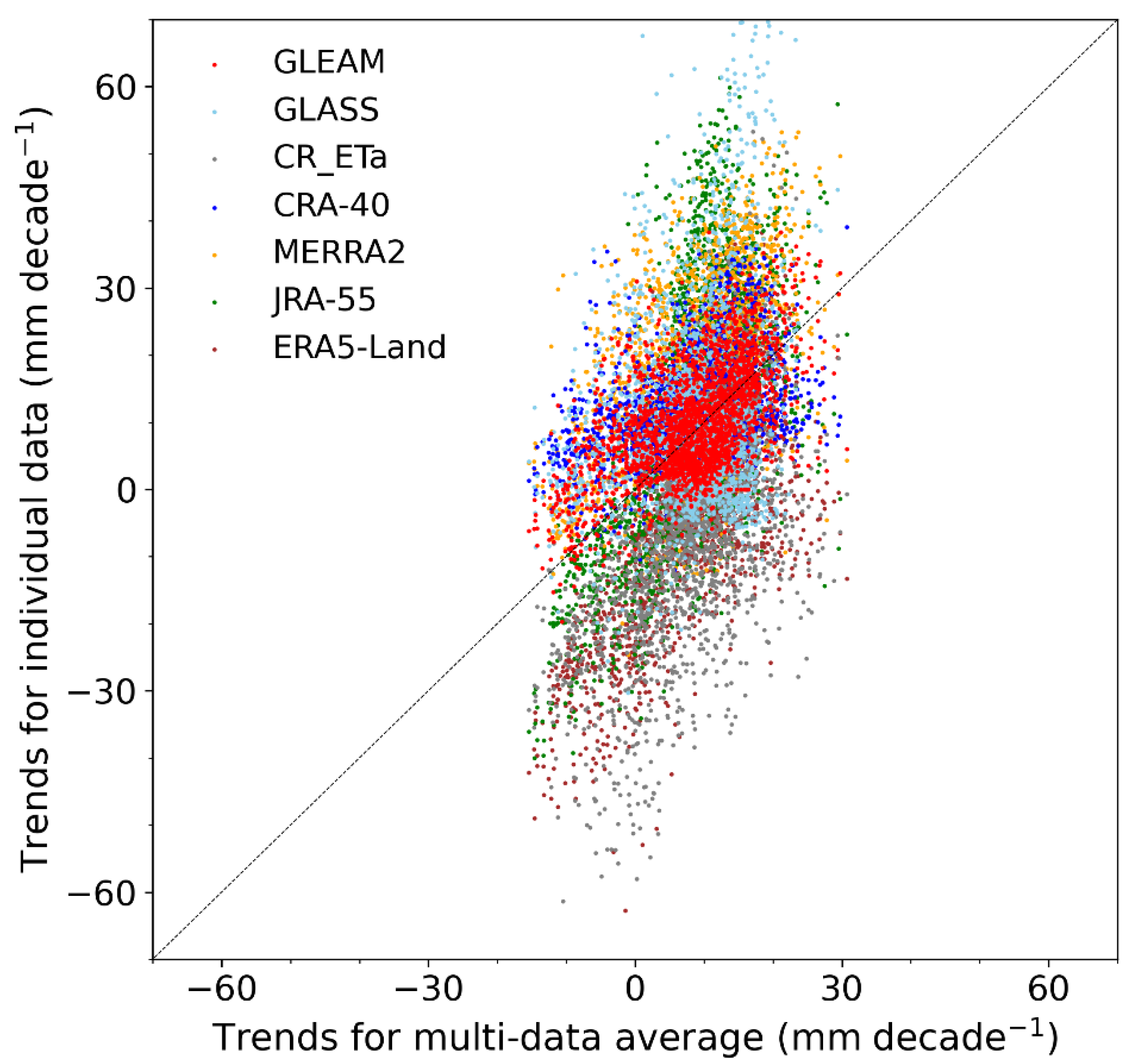
3.1. Spatiotemporal Variations of ETa
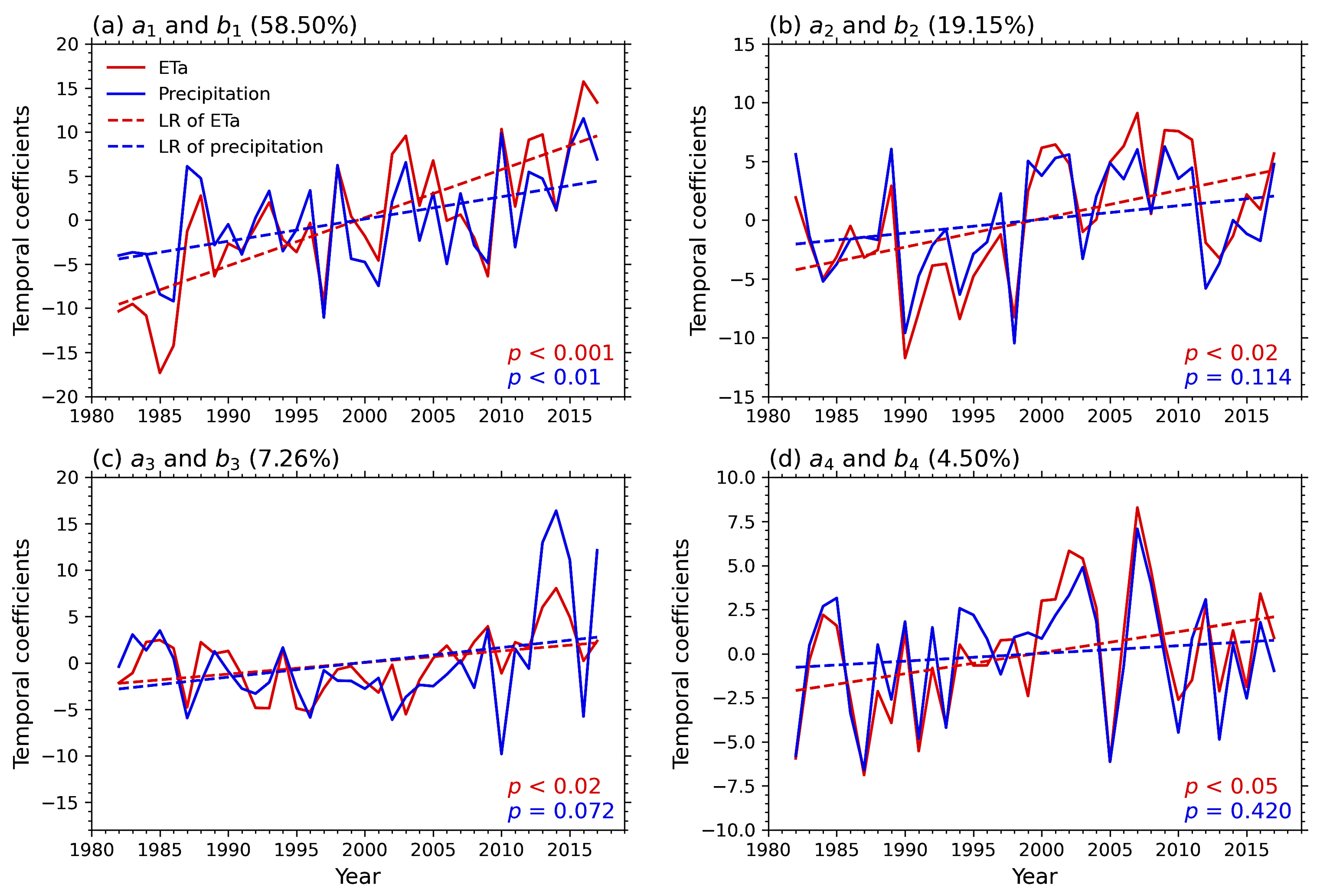
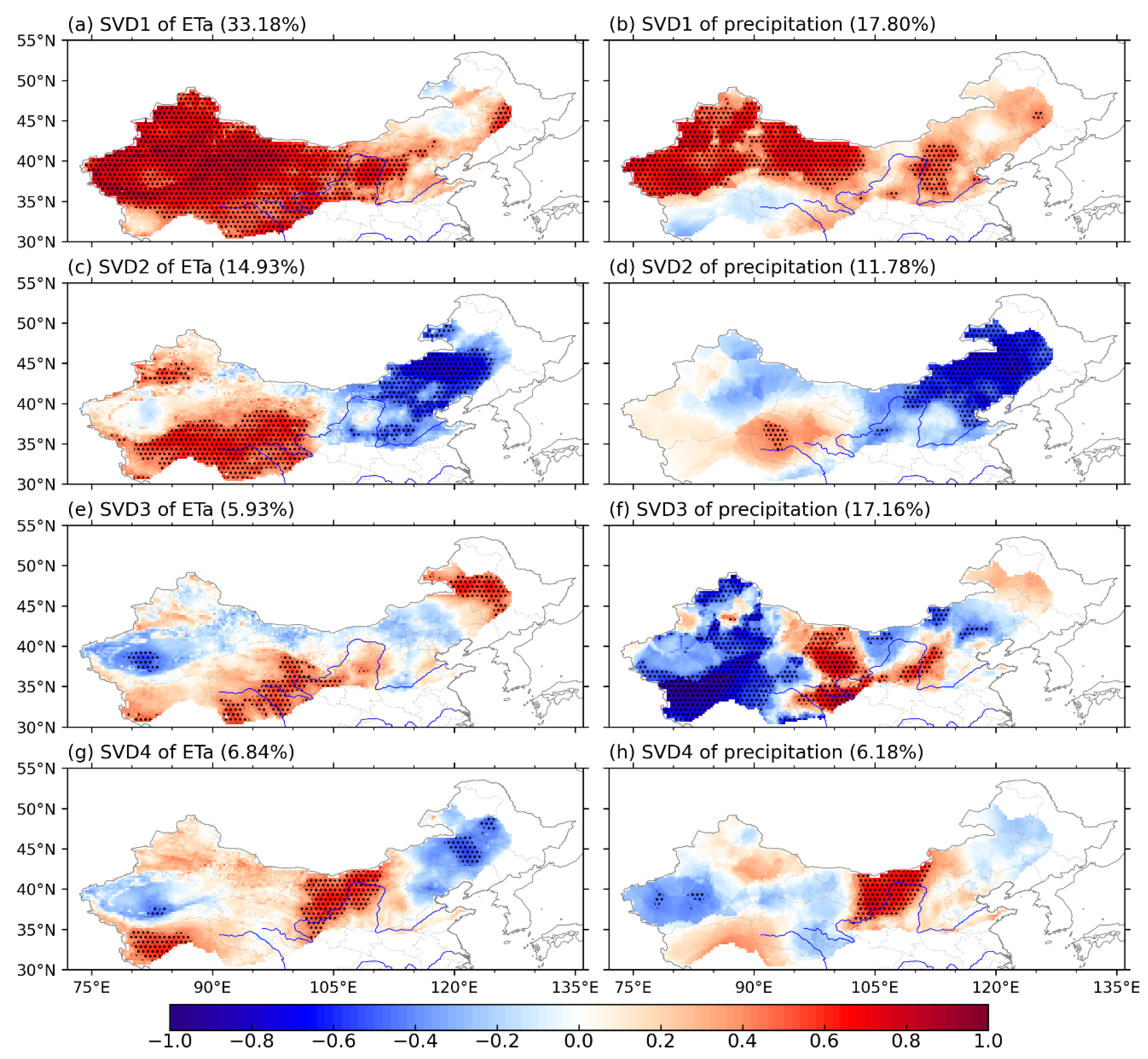
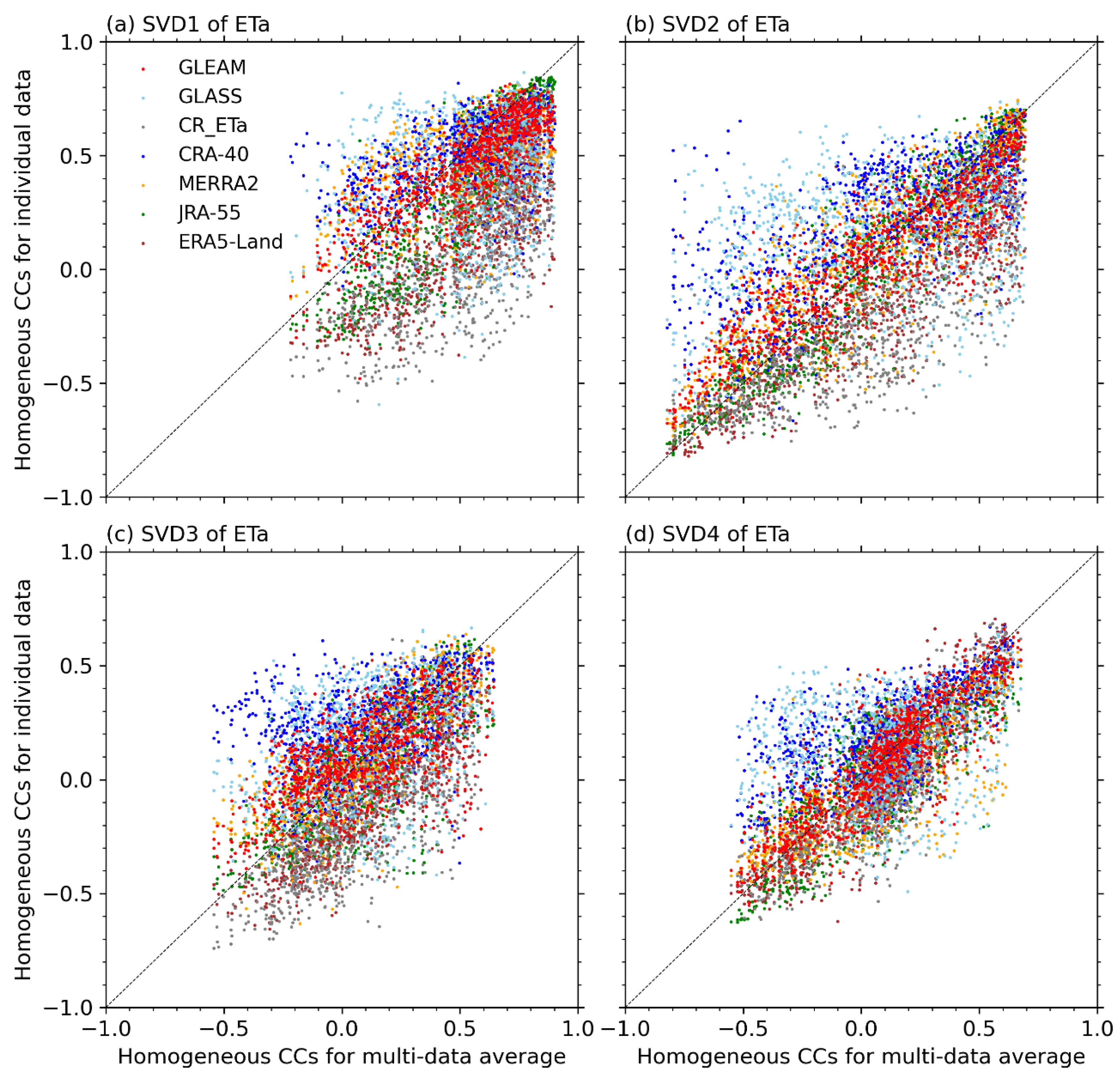
3.2. Relationship between ETa and Precipitation
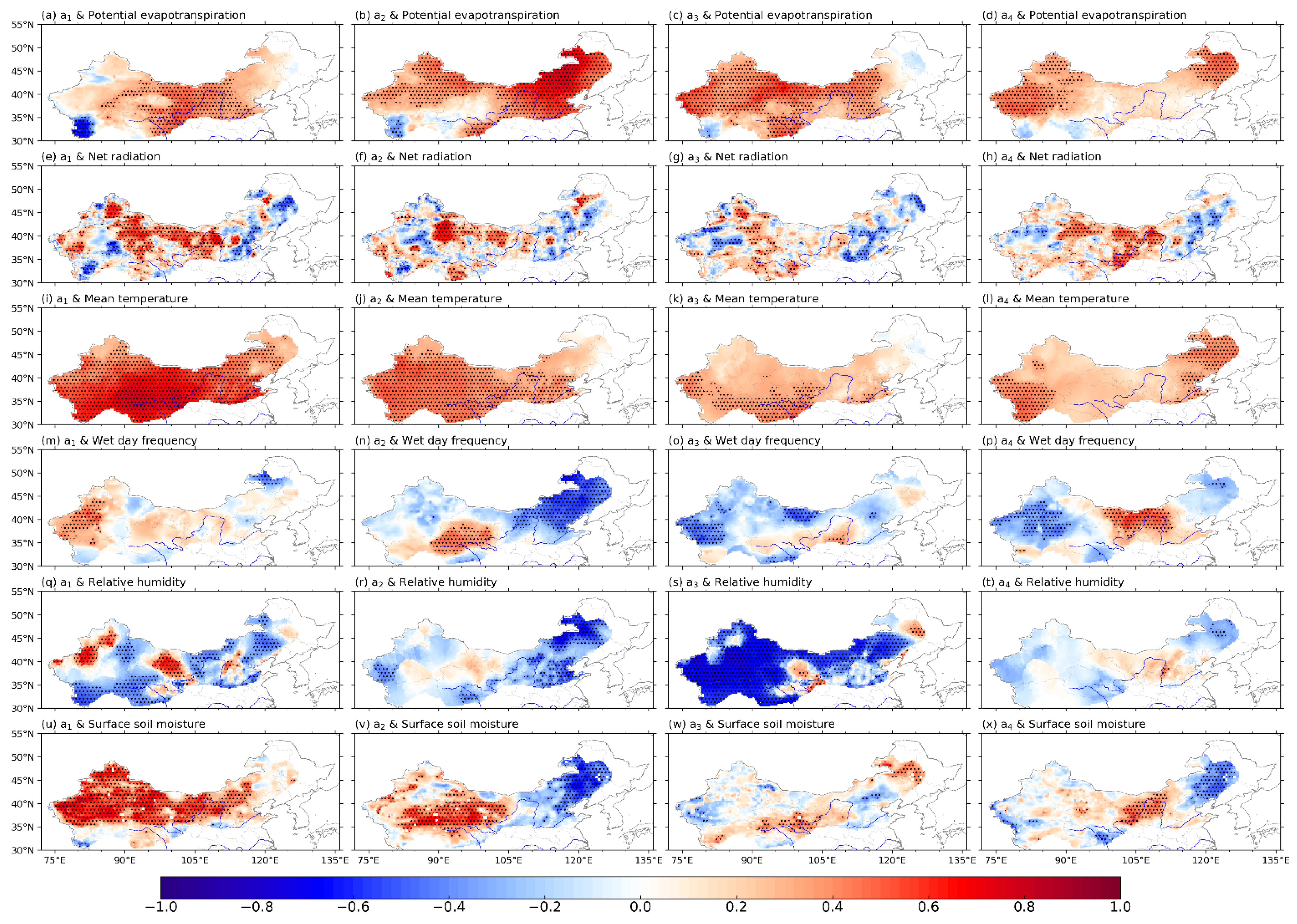
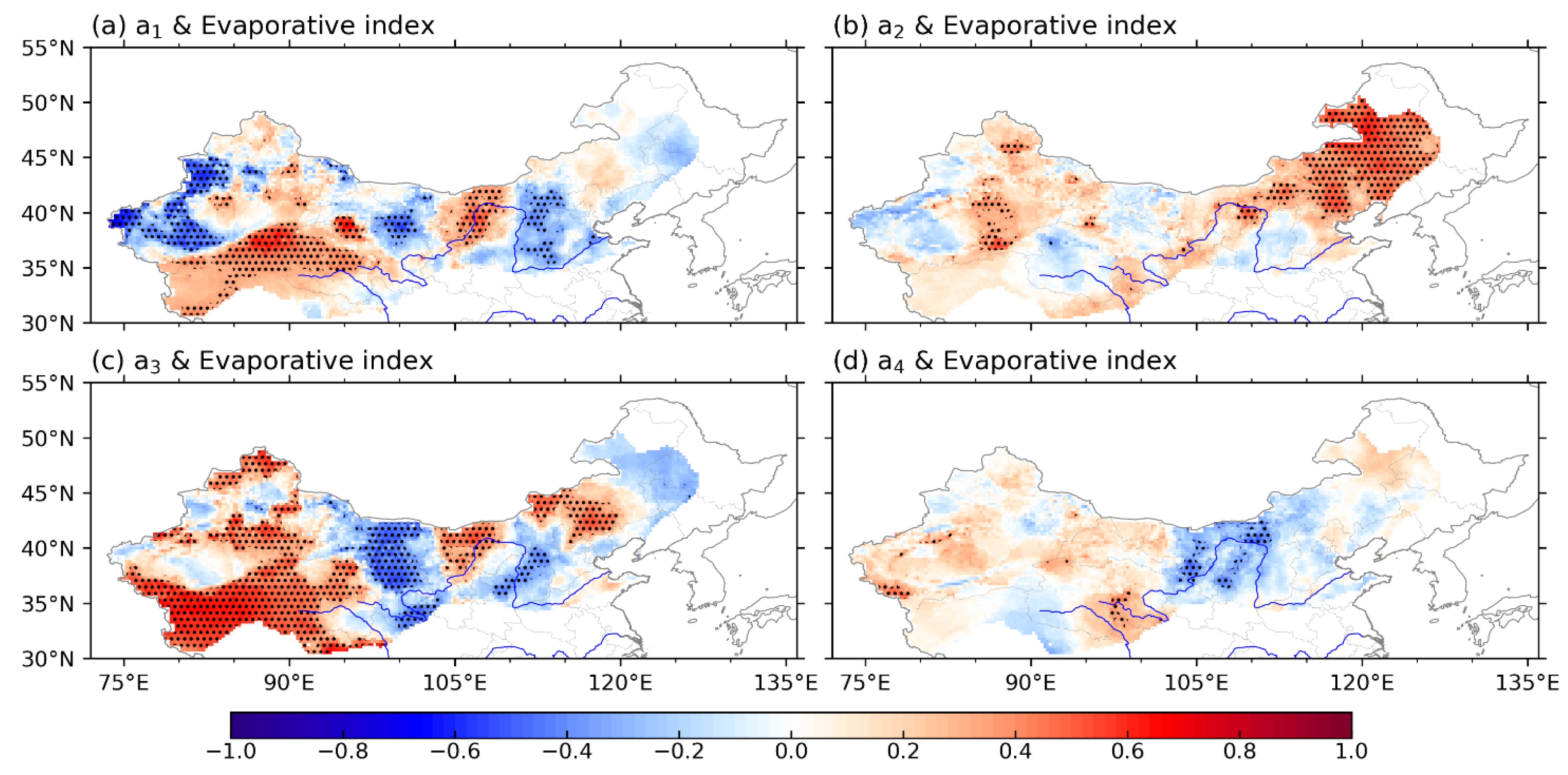
3.3. Factors Regulating the Relationship between ETa and Precipitation
4. Discussion
4.1. Uncertainty of ETa Data
4.2. Impact of Human Activities on ETa
4.3. Impact of Precipitation Intensity on ETa
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- An, L.; Wang, J.; Huang, J.; Pokhrel, Y.; Hugonnet, R.; Wada, Y.; Cáceres, D.; Müller Schmied, H.; Song, C.; Berthier, E.; et al. Divergent Causes of Terrestrial Water Storage Decline Between Drylands and Humid Regions Globally. Geophys. Res. Lett. 2021, 48, e2021GL095035. [Google Scholar] [CrossRef]
- Feng, S.; Fu, Q. Expansion of global drylands under a warming climate. Atmos. Chem. Phys. 2013, 13, 10081–10094. [Google Scholar] [CrossRef]
- Lian, X.; Piao, S.; Chen, A.; Huntingford, C.; Fu, B.; Li, L.Z.X.; Huang, J.; Sheffield, J.; Berg, A.M.; Keenan, T.F.; et al. Multifaceted characteristics of dryland aridity changes in a warming world. Nat. Rev. Earth Environ. 2021, 2, 232–250. [Google Scholar] [CrossRef]
- Feng, T.; Su, T.; Ji, F.; Zhi, R.; Han, Z. Temporal Characteristics of Actual Evapotranspiration Over China under Global Warming. J. Geophys. Res. Atmos. 2018, 123, 5845–5858. [Google Scholar] [CrossRef]
- Li, X.; Gemmer, M.; Zhai, J.; Liu, X.; Su, B.; Wang, Y. Spatio-temporal variation of actual evapotranspiration in the Haihe River Basin of the past 50 years. Quat. Int. 2013, 304, 133–141. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z. Quantitative estimation of the impact of climate change on actual evapotranspiration in the Yellow River Basin, China. J. Hydrol. 2010, 395, 226–234. [Google Scholar] [CrossRef]
- Matin, M.A.; Bourque, C.P.A. Assessing spatiotemporal variation in actual evapotranspiration for semi-arid watersheds in northwest China: Evaluation of two complementary-based methods. J. Hydrol. 2013, 486, 455–465. [Google Scholar] [CrossRef]
- Ma, N.; Szilagyi, J.; Zhang, Y. Calibration-Free Complementary Relationship Estimates Terrestrial Evapotranspiration Globally. Water Resour. Res. 2021, 57, e2021WR029691. [Google Scholar] [CrossRef]
- Ma, N.; Szilagyi, J.; Zhang, Y.; Liu, W. Complementary-Relationship-Based Modeling of Terrestrial Evapotranspiration Across China During 1982-2012: Validations and Spatiotemporal Analyses. J. Geophys. Res. Atmos. 2019, 124, 4326–4351. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Yang, Y.; Hao, X.; Zhang, H. Evaluation of evapotranspiration models over semi-arid and semi-humid areas of China. Hydrol. Process. 2016, 30, 4292–4313. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Hao, X. Environmental and biological controls on monthly and annual evapotranspiration in China’s Loess Plateau. Theor. Appl. Climatol. 2018, 137, 1675–1692. [Google Scholar] [CrossRef]
- Su, T.; Xie, D.; Feng, T.; Huang, B.; Qian, Z.; Feng, G.; Wu, Y. Quantifying the contribution of terrestrial water storage to actual evapotranspiration trends by the extended Budyko model in Northwest China. Atmos. Res. 2022, 273, 106147. [Google Scholar] [CrossRef]
- Huang, J.; Ji, M.; Xie, Y.; Wang, S.; He, Y.; Ran, J. Global semi-arid climate change over last 60 years. Clim. Dyn. 2015, 46, 1131–1150. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, 54. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, Z.; Hao, X.; Yue, P. Conversion features of evapotranspiration responding to climate warming in transitional climate regions in northern China. Clim. Dyn. 2018, 52, 3891–3903. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, C.; Liu, M.; Zeng, Y.; Tian, C. Change in pan evaporation over the past 50 years in the arid region of China. Hydrol. Process. 2009, 24, 225–231. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Peng, S.; Xing, W.; Yang, T.; Luo, Y.; Yong, B.; Xu, J. Reference evapotranspiration change and the causes across the Yellow River Basin during 1957-2008 and their spatial and seasonal differences. Water Resour. Res. 2012, 48, W05530. [Google Scholar] [CrossRef]
- Zuo, H.; Chen, B.; Wang, S.; Guo, Y.; Zuo, B.; Wu, L.; Gao, X. Observational study on complementary relationship between pan evaporation and actual evapotranspiration and its variation with pan type. Agric. For. Meteorol. 2016, 222, 1–9. [Google Scholar] [CrossRef]
- Su, T.; Feng, T.; Feng, G. Evaporation variability under climate warming in five reanalyses and its association with pan evaporation over China. J. Geophys. Res. Atmos. 2015, 120, 8080–8098. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Y.; Shafeeque, M.; Zhou, M.; Li, H. Modelling interannual variations in catchment evapotranspiration considering vegetation and climate seasonality using the Budyko framework. Hydrol. Process. 2021, 35, e14118. [Google Scholar] [CrossRef]
- Douville, H.; Ribes, A.; Decharme, B.; Alkama, R.; Sheffield, J. Anthropogenic influence on multidecadal changes in reconstructed global evapotranspiration. Nat. Clim. Chang. 2013, 3, 59–62. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Bierkens, M.F.P. Asia’s water balance. Nat. Geosci. 2012, 5, 841–842. [Google Scholar] [CrossRef]
- Greve, P.; Orlowsky, B.; Mueller, B.; Sheffield, J.; Reichstein, M.; Seneviratne, S.I. Global assessment of trends in wetting and drying over land. Nat. Geosci. 2014, 7, 716–721. [Google Scholar] [CrossRef]
- Wang, L.; Yuan, X.; Xie, Z.; Wu, P.; Li, Y. Increasing flash droughts over China during the recent global warming hiatus. Sci. Rep. 2016, 6, 30571. [Google Scholar] [CrossRef]
- Wu, C.; Hu, B.X.; Huang, G.; Zhang, H. Effects of climate and terrestrial storage on temporal variability of actual evapotranspiration. J. Hydrol. 2017, 549, 388–403. [Google Scholar] [CrossRef]
- Lu, C.; Huang, G.; Wang, G.; Zhang, J.; Wang, X.; Song, T. Long-Term Projection of Water Cycle Changes over China Using RegCM. Remote Sens. 2021, 13, 3832. [Google Scholar] [CrossRef]
- Yao, J.; Chen, Y.; Guan, X.; Zhao, Y.; Chen, J.; Mao, W. Recent climate and hydrological changes in a mountain–basin system in Xinjiang, China. Earth-Sci. Rev. 2022, 226, 103957. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Adamowski, J.F.; Alizadeh, M.R.; Yin, Z.; Wen, X.; Zhu, M. The role of climate change and vegetation greening on the variation of terrestrial evapotranspiration in northwest China’s Qilian Mountains. Sci. Total Environ. 2021, 759, 143532. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, S.; Yue, P.; Wang, S. Variation characteristics of non-rainfall water and its contribution to crop water requirements in China’s summer monsoon transition zone. J. Hydrol. 2019, 578, 124039. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. 2011, 116, G00J07. [Google Scholar] [CrossRef]
- Liu, W.; Wang, L.; Zhou, J.; Li, Y.; Sun, F.; Fu, G.; Li, X.; Sang, Y.-F. A worldwide evaluation of basin-scale evapotranspiration estimates against the water balance method. J. Hydrol. 2016, 538, 82–95. [Google Scholar] [CrossRef]
- Bhattarai, N.; Wagle, P. Recent Advances in Remote Sensing of Evapotranspiration. Remote Sens. 2021, 13, 4260. [Google Scholar] [CrossRef]
- Wang, G.; Pan, J.; Shen, C.; Li, S.; Lu, J.; Lou, D.; Hagan, D. Evaluation of Evapotranspiration Estimates in the Yellow River Basin against the Water Balance Method. Water 2018, 10, 1884. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, B.; Su, B.; Zhai, J.; Gemmer, M. Trends of Calculated and Simulated Actual Evaporation in the Yangtze River Basin. J. Clim. 2011, 24, 4494–4507. [Google Scholar] [CrossRef]
- Li, X.; He, Y.; Zeng, Z.; Lian, X.; Wang, X.; Du, M.; Jia, G.; Li, Y.; Ma, Y.; Tang, Y.; et al. Spatiotemporal pattern of terrestrial evapotranspiration in China during the past thirty years. Agric. For. Meteorol. 2018, 259, 131–140. [Google Scholar] [CrossRef]
- Ochege, F.U.; Shi, H.; Li, C.; Ma, X.; Igboeli, E.E.; Luo, G. Assessing Satellite, Land Surface Model and Reanalysis Evapotranspiration Products in the Absence of In-Situ in Central Asia. Remote Sens. 2021, 13, 5148. [Google Scholar] [CrossRef]
- Liang, S.; Cheng, J.; Jia, K.; Jiang, B.; Zhou, J. The global land surface satellite (glass) product suite. Bull. Am. Meteorol. Soc. 2021, 102, E323–E337. [Google Scholar] [CrossRef]
- Martens, B.; Gonzalez Miralles, D.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Zhao, D.; Zhang, L.; Zhou, T.; Liu, J. Contributions of Local and Remote Atmospheric Moisture Fluxes to East China Precipitation Estimated from CRA-40 Reanalysis. J. Meteorol. Res. 2021, 35, 32–45. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suarez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.; Giorgi, F.; Chen, D. Changes of effective temperature and cold/hot days in late decades over China based on a high resolution gridded observation dataset. Int. J. Climatol. 2017, 37, 788–800. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Pinzon, J.; Tucker, C. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- Weare, B.C. Composite Singular Value Decomposition Analysis of Moisture Variations Associated with the Madden-Julian Oscillation. J. Clim. 2003, 16, 3779–3792. [Google Scholar] [CrossRef]
- Chen, J.; Tan, H.; Ji, Y.; Tang, Q.; Yan, L.; Chen, Q.; Tan, D. Evapotranspiration Components Dynamic of Highland Barley Using PML ET Product in Tibet. Remote Sensing 2021, 13. [Google Scholar] [CrossRef]
- Ma, N.; Wang, N.; Zhao, L.; Zhang, Z.; Dong, C.; Shen, S. Observation of mega-dune evaporation after various rain events in the hinterland of Badain Jaran Desert, China. Chin. Sci. Bull. 2014, 59, 162–170. [Google Scholar] [CrossRef]
- Berg, A.; Findell, K.; Lintner, B.; Giannini, A.; Seneviratne, S.I.; van den Hurk, B.; Lorenz, R.; Pitman, A.; Hagemann, S.; Meier, A.; et al. Land–atmosphere feedbacks amplify aridity increase over land under global warming. Nat. Clim. Chang. 2016, 6, 869–874. [Google Scholar] [CrossRef]
- Ren, Y.; Yu, H.; Liu, C.; He, Y.; Huang, J.; Zhang, L.; Hu, H.; Zhang, Q.; Chen, S.; Liu, X.; et al. Attribution of Dry and Wet Climatic Changes over Central Asia. J. Clim. 2022, 35, 1399–1421. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, J.; Liu, R.; Ding, L. Influences of Climate Change and Human Activities on NDVI Changes in China. Remote Sens. 2021, 13, 4326. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, K.; Liu, X.; Liu, C. Water storage in reservoirs built from 1997 to 2014 significantly altered the calculated evapotranspiration trends over China. J. Geophys. Res. Atmos. 2016, 121, 10097–10112. [Google Scholar] [CrossRef]
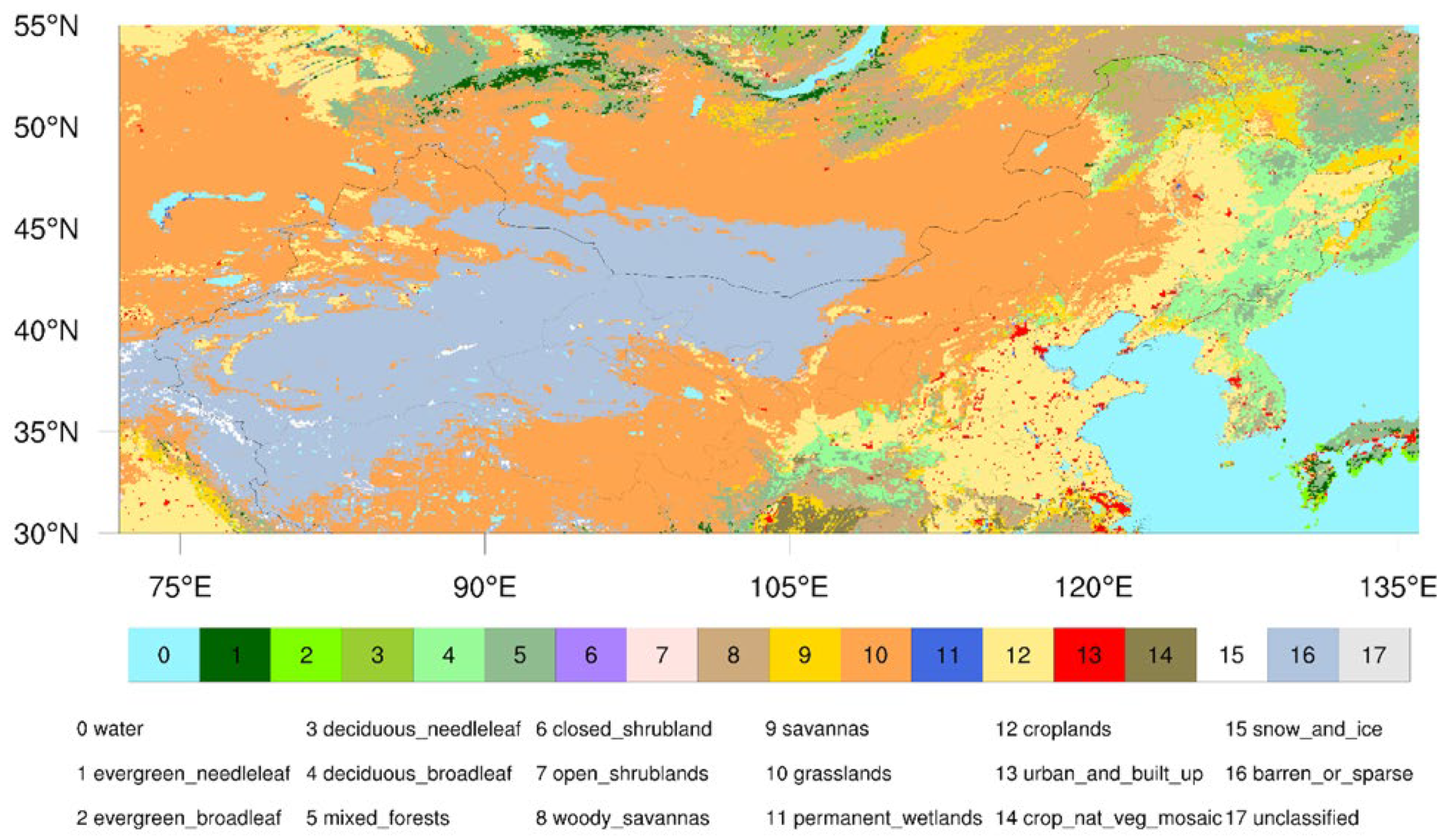


| Product Name | Horizontal Resolution | Datasets | Temporal Coverage | Category | References |
|---|---|---|---|---|---|
| GLEAM v3.3a | 0.25° × 0.25° | ETa, SSM | 1980–2020 | Remote sensing model | Martens et al. [39] |
| GLASS | 0.05° × 0.05° | ETa | 1981–2018 | Bayesian model average | Liang et al. [38] |
| CR_ETa | 0.1° × 0.1° | ETa | 1982–2017 | CR model | Ma et al. [9] |
| CRA-40 | T574 (34 km) | ETa | 1979–2018 | Reanalysis | Zhao et al. [40] |
| MERRA2 | 2/3° × 1/2° | ETa | 1980–present | Reanalysis | Gelaro et al. [41] |
| JRA-55 | 1.25° × 1.25° | ETa | 1958–present | Reanalysis | Kobayashi et al. [42] |
| ERA5-Land | 0.1° × 0.1° | ETa | 1950–present | Reanalysis | Muñoz Sabater et al. [43] |
| FLUXNET-MTE | 0.5° × 0.5° | ETa | 1982–2011 | Upscaling of EC measurements | Jung et al. [31] |
| CN05.1 | 0.25° × 0.25° | PRE, TMP, RHM | 1961–present | Observation data | Wu et al. [44] |
| CRU TS v4.06 | 0.5° × 0.5° | PET, WET | 1901–2019 | ADW interpolation | Harris et al. [45] |
| GIMMS 3gv1 | 1/12° × 1/12° | NDVI | 1982–2015 | Remote sensing | Pinzon and Tucker [46] |
| k | SCF (%) | Variance (%) (ETa) | Variance (%) (Precipitation) | Correlation Coefficient (ak, bk) |
|---|---|---|---|---|
| 1 | 58.50 | 33.18 | 17.80 | 0.86 |
| 2 | 19.15 | 14.93 | 11.78 | 0.90 |
| 3 | 7.26 | 5.93 | 17.16 | 0.73 |
| 4 | 4.50 | 6.84 | 6.18 | 0.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, T.; Sun, S.; Wang, S.; Xie, D.; Li, S.; Huang, B.; Ma, Q.; Qian, Z.; Feng, G.; Feng, T. Spatiotemporal Variation of Actual Evapotranspiration and Its Relationship with Precipitation in Northern China under Global Warming. Remote Sens. 2022, 14, 4554. https://doi.org/10.3390/rs14184554
Su T, Sun S, Wang S, Xie D, Li S, Huang B, Ma Q, Qian Z, Feng G, Feng T. Spatiotemporal Variation of Actual Evapotranspiration and Its Relationship with Precipitation in Northern China under Global Warming. Remote Sensing. 2022; 14(18):4554. https://doi.org/10.3390/rs14184554
Chicago/Turabian StyleSu, Tao, Siyuan Sun, Shuting Wang, Dexiao Xie, Shuping Li, Bicheng Huang, Qianrong Ma, Zhonghua Qian, Guolin Feng, and Taichen Feng. 2022. "Spatiotemporal Variation of Actual Evapotranspiration and Its Relationship with Precipitation in Northern China under Global Warming" Remote Sensing 14, no. 18: 4554. https://doi.org/10.3390/rs14184554
APA StyleSu, T., Sun, S., Wang, S., Xie, D., Li, S., Huang, B., Ma, Q., Qian, Z., Feng, G., & Feng, T. (2022). Spatiotemporal Variation of Actual Evapotranspiration and Its Relationship with Precipitation in Northern China under Global Warming. Remote Sensing, 14(18), 4554. https://doi.org/10.3390/rs14184554








