Pulse Radar Imaging Method in an Anechoic Chamber Based on an Amplitude Modulation Design
Abstract
:1. Introduction
- The proposed amplitude modulation method solves the coupling problem between the transmitted signal and echo.
- The imaging method based on an amplitude modulation design can eliminate the false targets caused by the amplitude-modulated signal and accurately realize the target imaging.
2. Amplitude Modulation Design
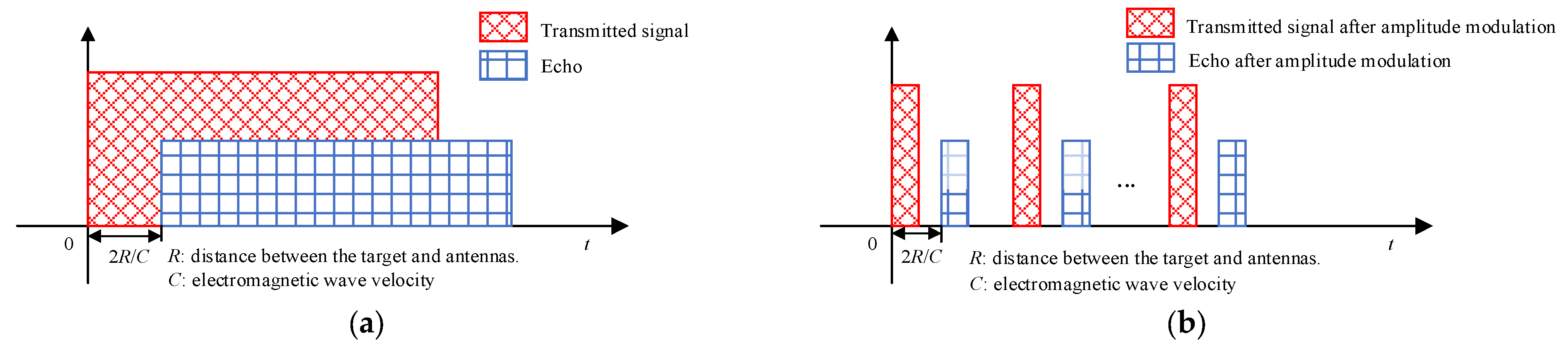
2.1. Signal Coupling and Amplitude Modulation
2.2. Properties of Amplitude Modulation Functions
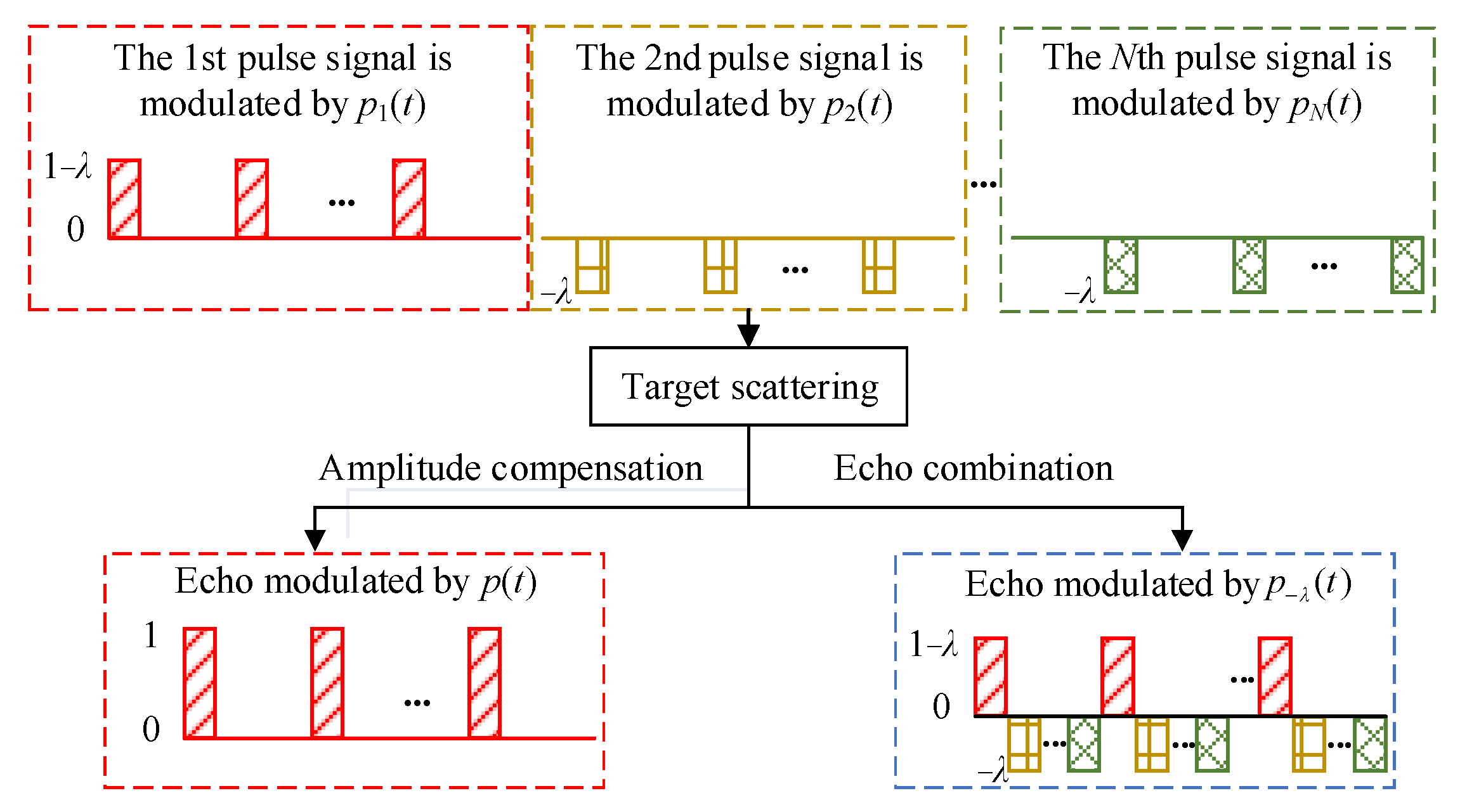
2.3. Amplitude Modulation Design of Pulse Signal
3. Target Imaging Method
3.1. Range Profile Acquisition Based on Amplitude Modulation Design
3.2. ISAR Imaging Based on Amplitude Modulation Design
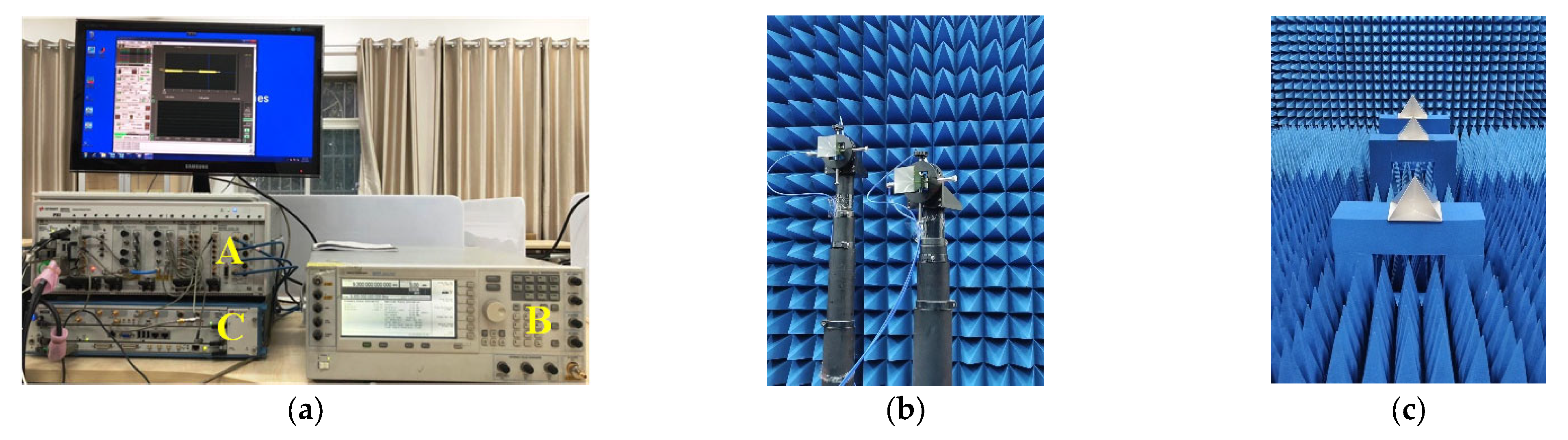
3.3. Imaging Process in Anechoic Chamber
4. Simulation and Experiment
4.1. Numerical Simulation
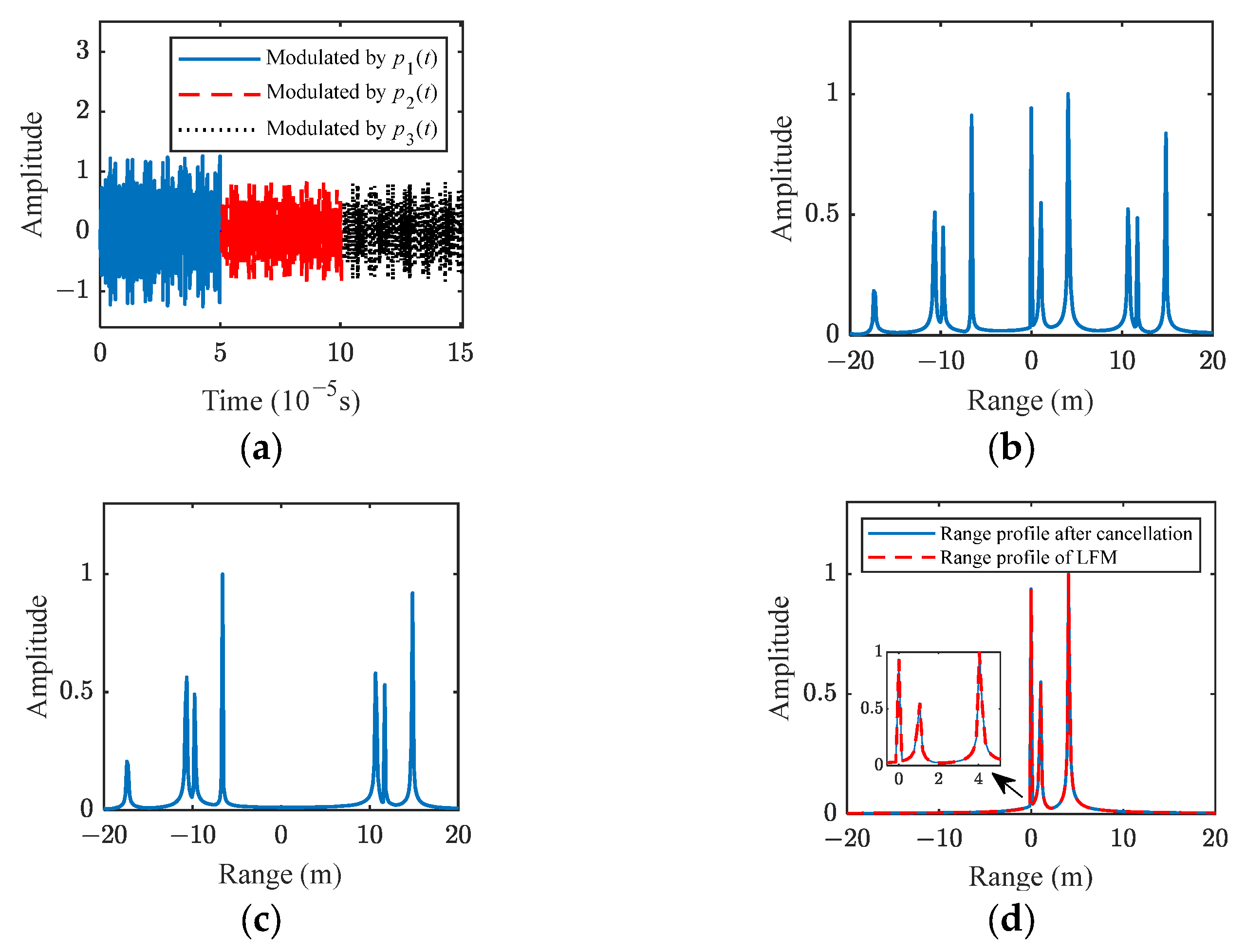
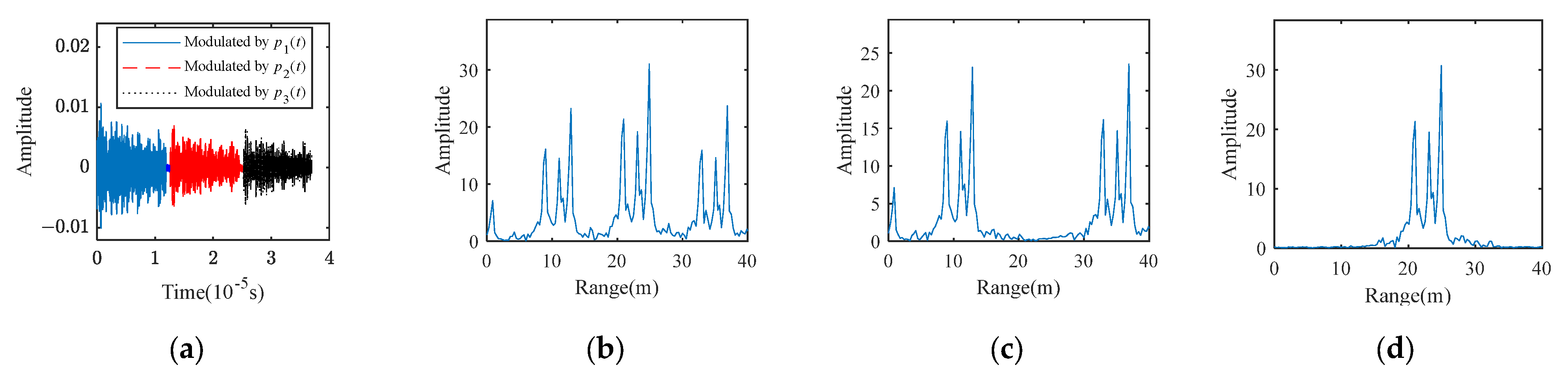
4.1.1. Range Profile Simulation
4.1.2. ISAR Imaging Simulation
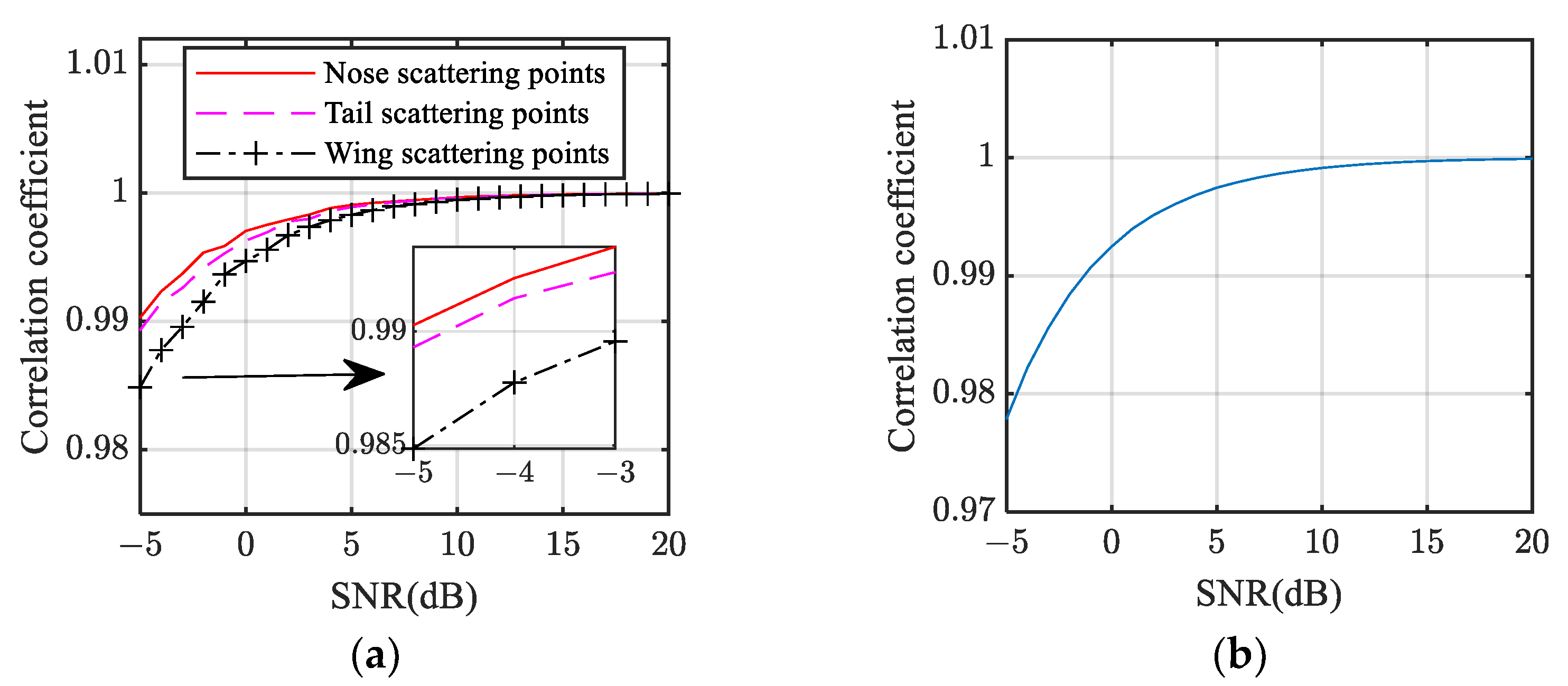
4.2. Influence of SNR on Correlation Coefficient
4.3. Anechoic Chamber Experimental Results
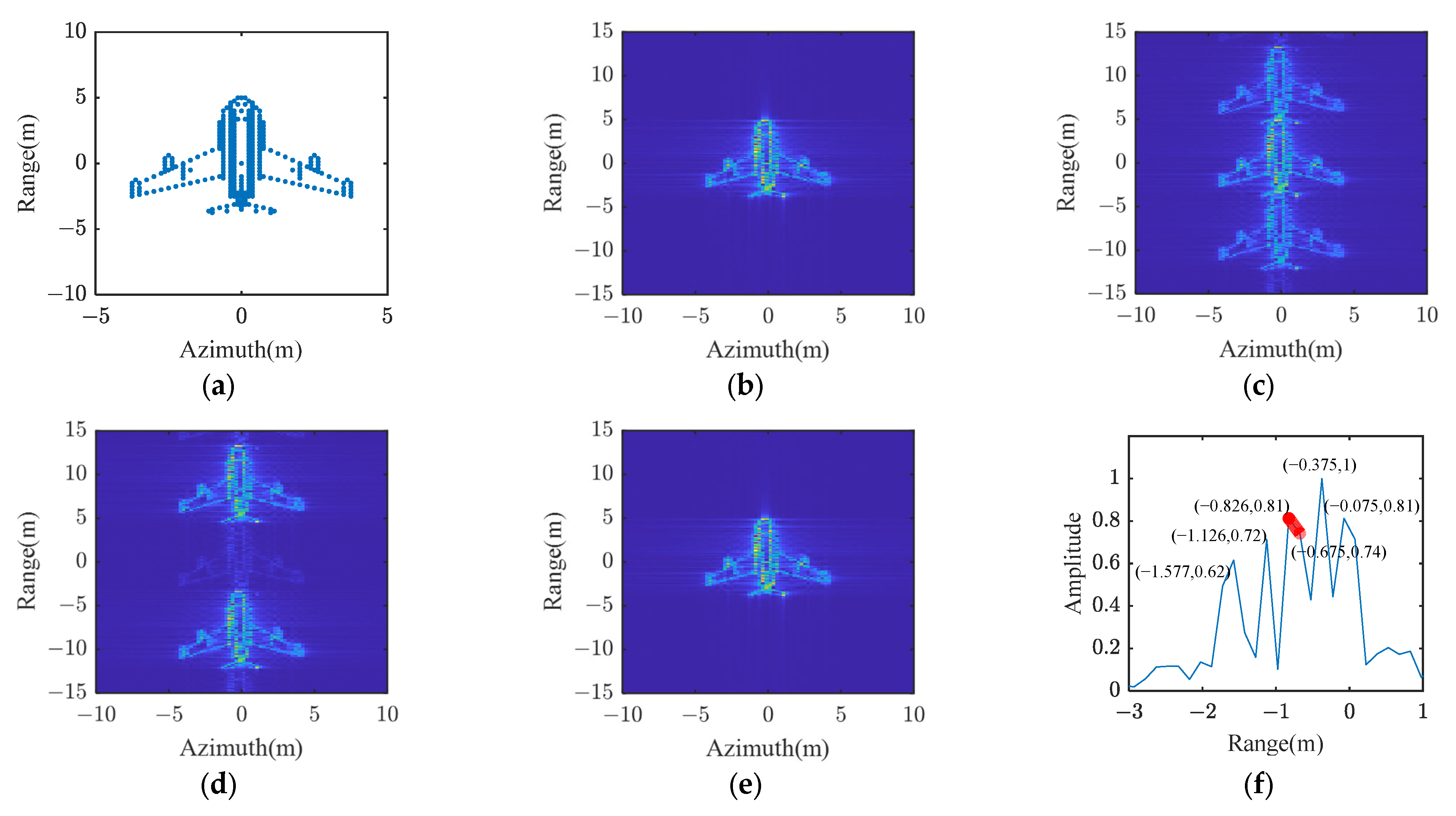
4.3.1. Experiment Results of Range Profile
4.3.2. Experiment Results of ISAR Imaging
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, F.; Huang, D.; Guo, X.; Feng, C. Unambiguous ISAR Imaging Method for Complex Maneuvering Group Targets. Remote Sens. 2022, 14, 2554. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, L.; Liu, H. Integrated Kalman filter of accurate ranging and tracking with wideband radar. IEEE Trans. Geosci. Remote Sens. 2022, 58, 8395–8411. [Google Scholar] [CrossRef]
- Yang, S.; Li, S.; Jia, X.; Liu, Y. An Efficient Translational Motion Compensation Approach for ISAR Imaging of Rapidly Spinning Targets. Remote Sens. 2022, 14, 2208. [Google Scholar] [CrossRef]
- Li, H.; Liao, G.; Xu, J.; Lan, L. An Efficient Maritime Target Joint Detection and Imaging Method with Airborne ISAR System. Remote Sens. 2022, 14, 193. [Google Scholar] [CrossRef]
- Yang, Z.; Li, D.; Tan, X.; Liu, H.; Liu, Y.; Liao, G. ISAR Imaging for Maneuvering Targets with Complex Motion Based on Generalized Radon-Fourier Transform and Gradient-Based Descent under Low SNR. Remote Sens. 2021, 13, 2198. [Google Scholar] [CrossRef]
- Fan, W.; Kyösti, P.; Hentilä, L.; Pedersen, G.F. Experimental Evaluation of MIMO Terminals with User Influence in OTA Setups. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3030–3033. [Google Scholar] [CrossRef]
- Hashim, M.; Stavrou, S. Dynamic impact characterization of vegetation movements on radiowave propagation in controlled environment. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 316–318. [Google Scholar] [CrossRef]
- Tice, T.E. An overview of radar cross section measurement techniques. In Proceedings of the Instrumentation and Measurement Technology Conference, Washington, DC, USA, 25–27 April 1989; pp. 344–346. [Google Scholar]
- Liu, X.; Liu, J.; Zhao, F.; Ai, X.; Wang, G. A novel strategy for pulse radar HRRP reconstruction based on randomly interrupted transmitting and receiving in radio frequency simulation. IEEE Trans. Antennas Propag. 2018, 66, 2569–2580. [Google Scholar] [CrossRef]
- Huang, H.; Pan, M.; Lu, Z. Hardware-in-the-loop simulation technology of wide-band radar targets based on scattering center model. Chin. J. Aeronaut. 2015, 28, 1476–1484. [Google Scholar] [CrossRef]
- Lee, J.; Kim, H.; Myung, N. Analysis of structural anechoic chamber design for improvement of anechoic chamber performance. In Proceedings of the 2015 Asia-Pacific Microwave Conference (APMC), Nanjing, China, 6–9 December 2015; pp. 1–3. [Google Scholar]
- Chen, X.; Kildal, P.; Carlsson, J.; Yang, J. MRC diversity and MIMO capacity evaluations of multi-port antennas using reverberation chamber and anechoic chamber. IEEE Trans. Antennas Propag. 2013, 61, 917–926. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Xue, Z.; Ren, W.; Li, W. S-band time domain near field planar measurement for RCS inside an anechoic chamber. In Proceedings of the 2015 7th Asia-Pacific Conference on Environmental Electromagnetics (CEEM), Hangzhou, China, 4 January 2016; pp. 108–111. [Google Scholar]
- Kudyan, H.M. Sensitivity of frequency-swept shielding effectiveness measurements to reflecting surfaces and EMI noise in the test area. In Proceedings of the 2003 IEEE Symposium on Electromagnetic Compatibility, Boston, MA, USA, 14 October 2003; pp. 526–531. [Google Scholar]
- Lu, L.; Gao, M. A Truncated Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction. Remote Sens. 2022, 14, 97. [Google Scholar] [CrossRef]
- Wang, F.; Li, N.; Pang, C.; Li, C.; Li, Y.; Wang, X. Complementary Sequences and Receiving Filters Design for Suppressing Interrupted Sampling Repeater Jamming. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Wu, W.; Zou, J.; Chen, J.; Xu, S.; Chen, Z. False-target recognition against interrupted-sampling repeater jamming based on integration decomposition. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2979–2991. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Q.; Chen, X. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer. IET Radar Sonar Navig. 2018, 12, 56–63. [Google Scholar] [CrossRef]
- Tan, X.; Yang, Z.; Li, D.; Liu, H.; Liao, G.; Wu, Y.; Liu, Y. An efficient range-Doppler domain ISAR imaging approach for rapidly spinning targets. IEEE Trans. Geosci. Remote Sen. 2019, 58, 2670–2681. [Google Scholar] [CrossRef]
- Qian, J.; Huang, S.; Wang, L.; Bi, G.; Yang, X. Super-resolution ISAR imaging for maneuvering target based on deep-learning-assisted time–frequency analysis. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Gupta, N.; Bhargava, N.; Verma, B.; Khan, M.I.; Kumar, S. A New Approach for CBIR Using Coefficient of Correlation. In Proceedings of the 2009 International Conference on Advances in Computing, Control, and Telecommunication Technologies, Bangalore, India, 28–29 December 2009; pp. 380–384. [Google Scholar]
- Naji, M.A.; Aghagolzadeh, A. Multi-focus image fusion in DCT domain based on correlation coefficient. In Proceedings of the 2015 2nd International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 21 March 2016; pp. 632–639. [Google Scholar]
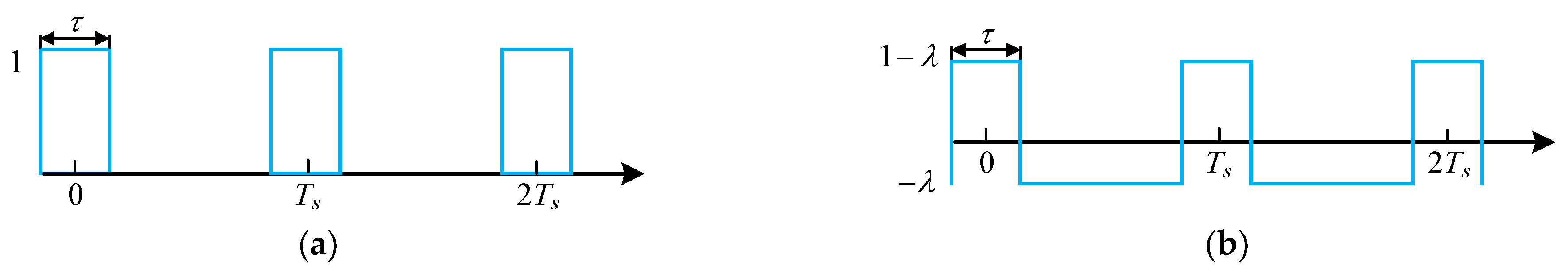



| Parameter | Value |
|---|---|
| Pulse width | 50 μs |
| Bandwidth | 1 GHz |
| Wavelength | 0.0375 m |
| Distances of scattering centers | [0 m, 1 m, 4.1 m] |
| Scattering coefficients | [0.7, 0.5, 0.9] |
| Duty ratio D | 0.4 |
| Parameter | Value |
|---|---|
| Initial frequency | 8 GHz |
| Terminal frequency | 12 GHz |
| Bandwidth | 4 GHz |
| Number of sub-pulses | 200 |
| Pitch angle | 0° |
| Azimuth angle | −180~180° |
| Azimuth interval | 0.2° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, A.; Liu, X.; Zhao, F.; Xiao, S. Pulse Radar Imaging Method in an Anechoic Chamber Based on an Amplitude Modulation Design. Remote Sens. 2022, 14, 4560. https://doi.org/10.3390/rs14184560
Xie A, Liu X, Zhao F, Xiao S. Pulse Radar Imaging Method in an Anechoic Chamber Based on an Amplitude Modulation Design. Remote Sensing. 2022; 14(18):4560. https://doi.org/10.3390/rs14184560
Chicago/Turabian StyleXie, Ailun, Xiaobin Liu, Feng Zhao, and Shunping Xiao. 2022. "Pulse Radar Imaging Method in an Anechoic Chamber Based on an Amplitude Modulation Design" Remote Sensing 14, no. 18: 4560. https://doi.org/10.3390/rs14184560
APA StyleXie, A., Liu, X., Zhao, F., & Xiao, S. (2022). Pulse Radar Imaging Method in an Anechoic Chamber Based on an Amplitude Modulation Design. Remote Sensing, 14(18), 4560. https://doi.org/10.3390/rs14184560





