Proportional Similarity-Based Openmax Classifier for Open Set Recognition in SAR Images
Abstract
:1. Introduction
- A thorough examination of the Openmax classifier and a detailed discussion on the tail-fitting procedure in different OSR scenarios.
- An analysis of the Openmax limitations and source of errors to effectively avoid the situations where either a known or an unknown target is always misclassified.
- Proposing the proportional similarity-based approach, which makes use of the similarity between the test image and different training classes in proportion to the similarity between the training classes, to increase the robustness and the accuracy.
2. Materials and Methods
2.1. The Openmax Approach
| Algorithm 1 Model Calibration |
| Input: AV, …, AV, Output: (Weibull, MAV), …, (Weibull, MAV) 1: for j = 1, 2, …, N do 2: MAV mean(AV) 3: ED = sort(EuclideanDistance (AVMAV)) 4: Weibull= FitHigh (ED |
| Algorithm 2 Openmax scores calculation |
| Input: (Weibull, MAV), …, (Weibull, MAV), AV of the test image, Output: Openmax scores 1: = argsort(AV, “descending”) 2: for i = 1, …, do 3: 4: = EuclideanDistance() 5: = Weibull 6: 7: ()/ 8: ) 9: 10: modAV (N + 1) = unk 11: for j = 1, 2, …, N + 1 do 12: 13: |
2.2. The Proposed Approach
- Feature extraction:In the Openmax classifier, the raw outputs of the last FC layer are directly used for the scores calculations. However, in the new method, a supplementary activation function is used to map the AV into another domain that is more suitable for the OSR problem. It should be noted that the supplementary activation function will be only used during the inference and not in the training. In fact, only the Softmax activation function is applied to AV in the training phase.
- Tail-fitting procedure:The distance values and their distributions can contain useful information for the OSR solution. The most critical hyper-parameter of Openmax is by which it analyzes only the tail of distance values. However, a more accurate OSR solution can be designed by exploiting full information of distance values.
- Activation vector modification:
- (a)
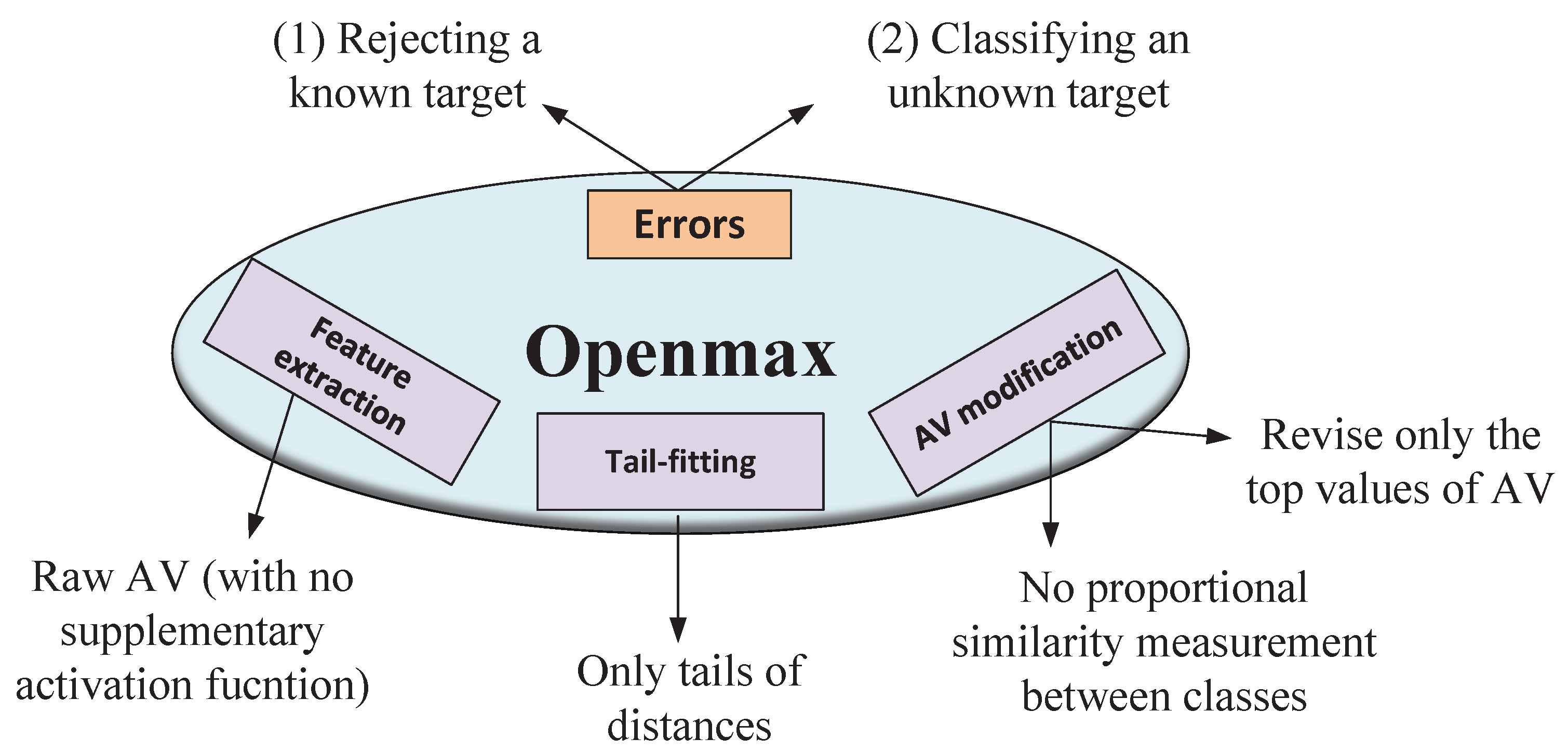
- The choice of :It is worth mentioning that is another hyper-parameter in the original Openmax, and similar to , it has to be carefully chosen beforehand. By modifying only the top values of AV, i.e., subtracting different portions from those elements, Openmax generates an extra class dedicated to the unknown inputs. In fact, Openmax takes to reduce the number of changeable neurons in AV, especially in the case of CNNs that generate some negative scores in their AV. Therefore, the aim of is to discard some of the negative values of AV, in other words, to exclude smallest values of AV, in order to avoid the new element from having a possibly large negative value. This large negative value forces the classifier not to reject the unknown input image and ends up with the second error shown in Figure 1. Note that by discarding some of the negative values of AV using , the original Openmax lets the new element have the largest value in the case of an unknown input image. However, choosing in the original Openmax implies a priori knowledge. We will introduce our PS-based classifier that obviates this limitation and has an improved performance toward unknown images.
- (b)
- Class-independent subtraction:According to the CNN model and the input test image, it is also quite probable that the new element of AV ends up being a very large positive value and the first error shown in Figure 1, i.e., rejecting a known image, happens. This problem is likely to happen in CNNs that do not generate negative scores in their AV. Therefore, even by reducing the number of changeable neurons in AV, i.e., , it is still probable that the new element becomes the greatest one, and this forces the classifier to reject the known image. Note that in the original Openmax classifier, the subtraction in each element of AV is performed independently from the others, and the relationship between different classes is not studied. By exploiting this aspect, the PS-based classifier provides an improved accuracy toward the input images of the known classes.
| Algorithm 3 PS-Openmax scores calculation |
| Input: (MAV, …, MAV), AV of the test image Output: PS-Openmax scores 1: for i = 1, …, N do 2: = EuclideanDistance 3: 4: 5: AVAV-min(AV) 6: AV=[1+M-CDAV 7: 8: 9: for j = 1, 2, …, N + 1 do 10: 11: |
2.3. Experimental Setup and Materials
2.3.1. CNN Structure
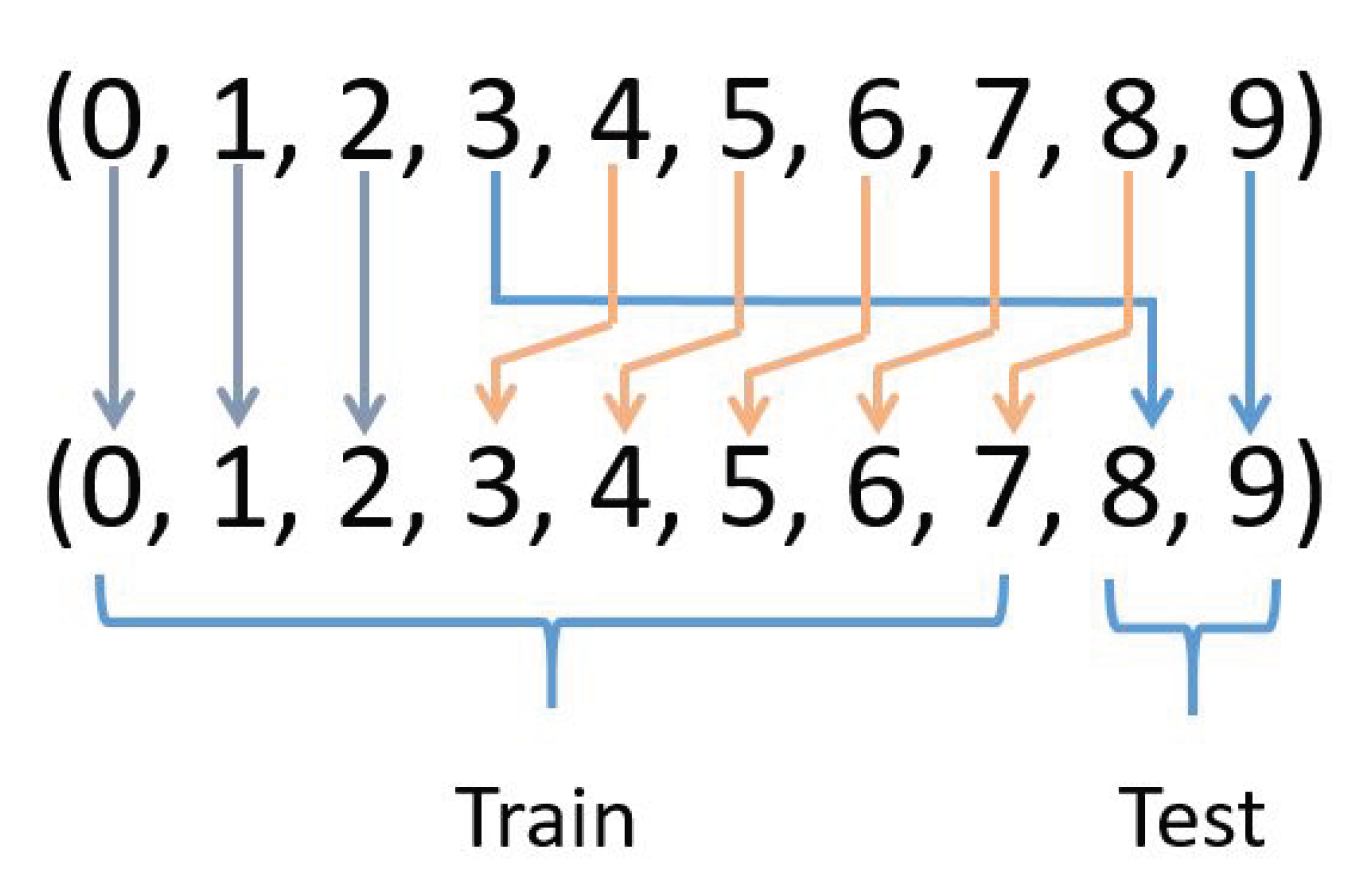
2.3.2. Dataset Description
2.3.3. Performance Indexes
3. Results
3.1. Openmax Pre-Processing
3.2. Openmax Preliminary Test
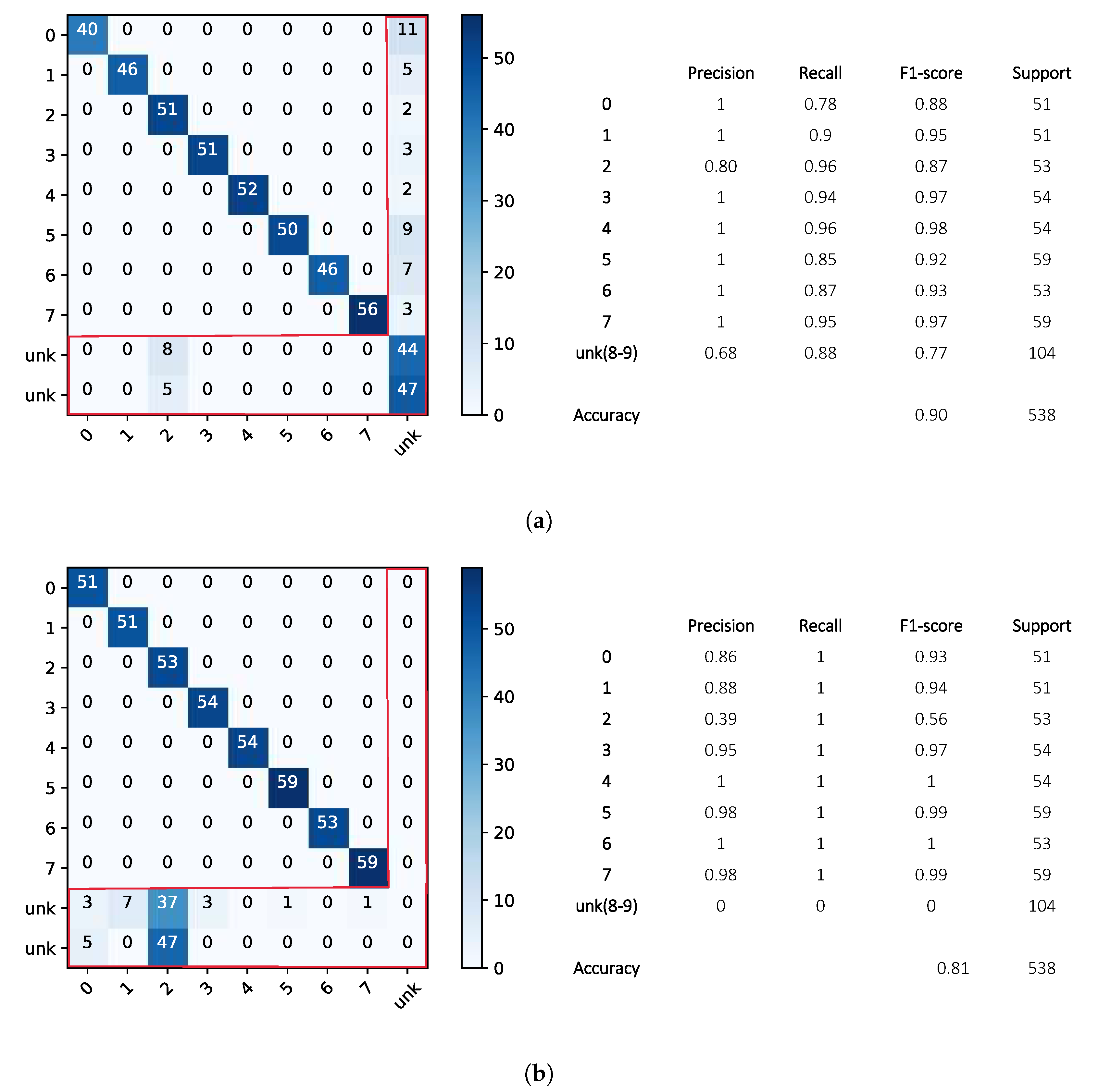
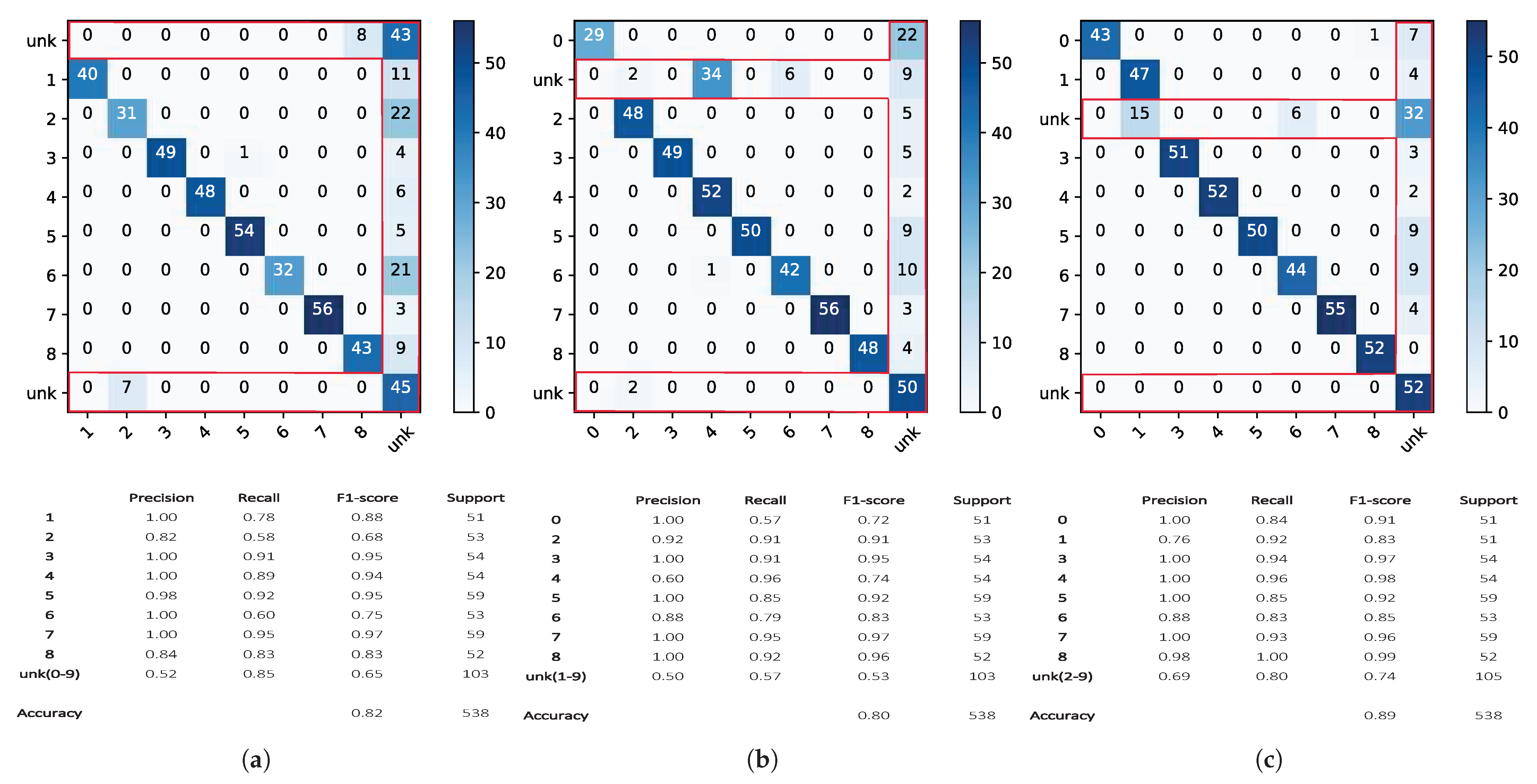
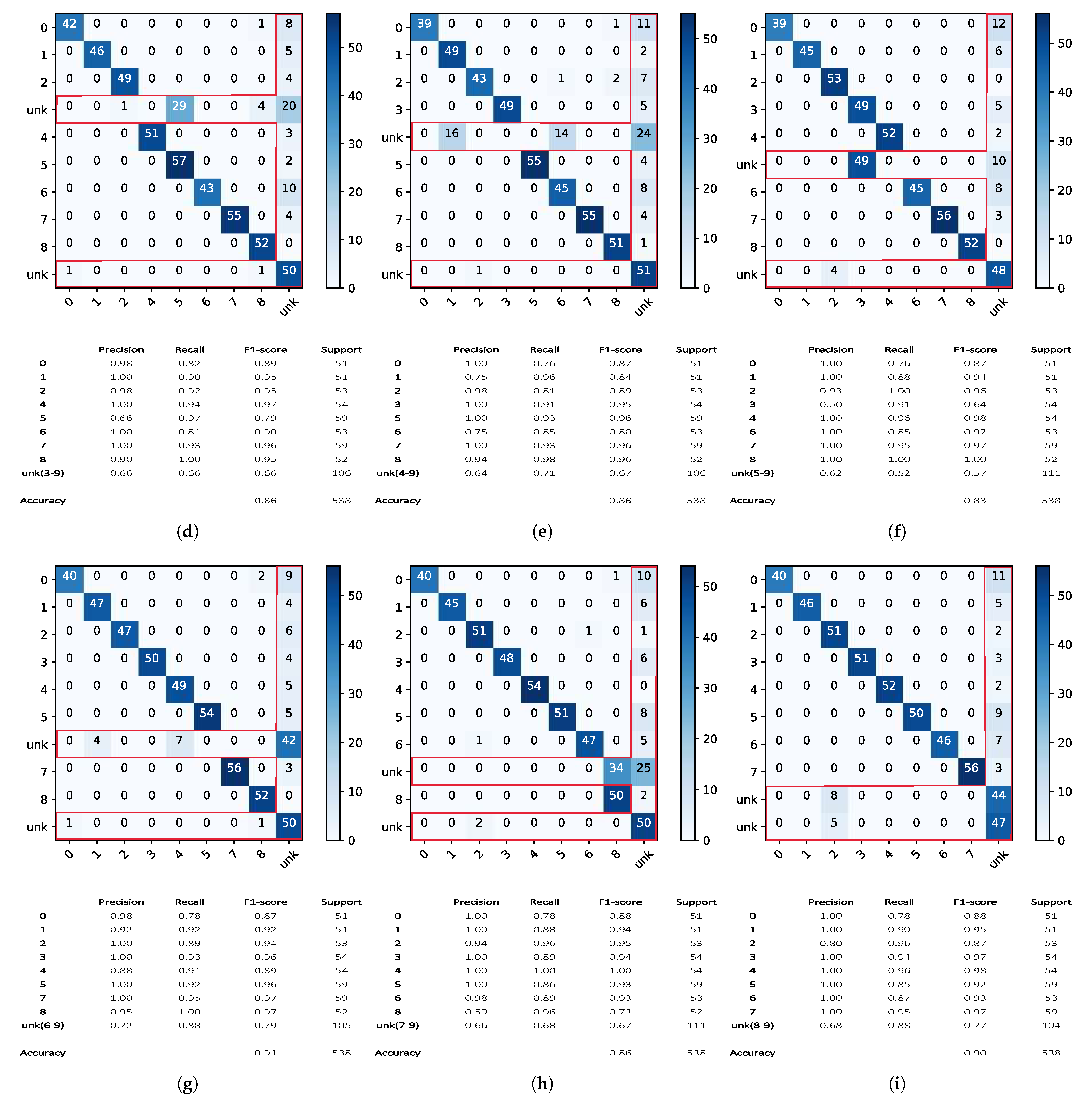
3.3. Classification Results: Openmax vs. Softmax
3.4. Statistical Analysis: The Effects of the Tail Size and of the CDF Type on Openmax
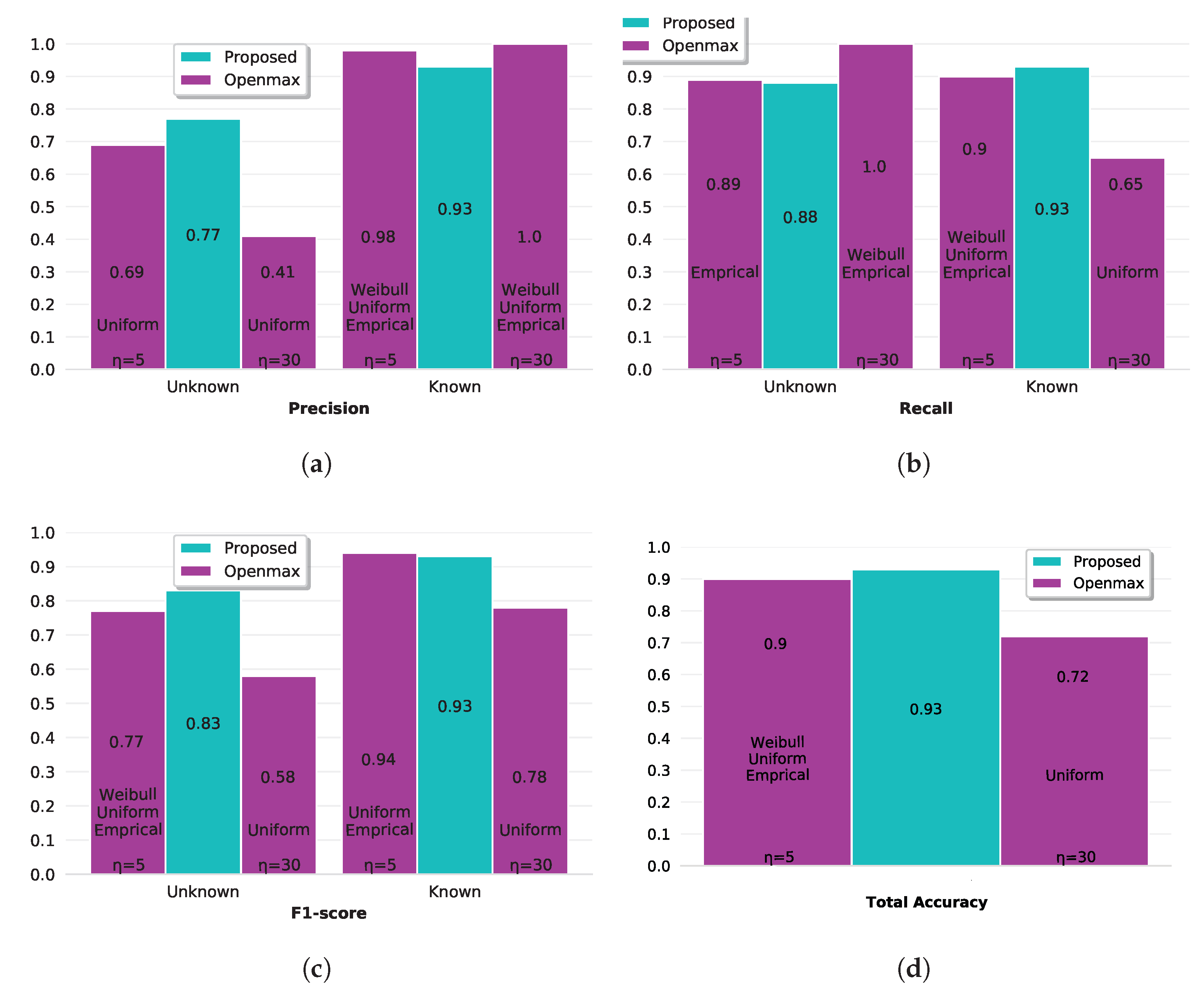
3.5. The Proposed Approach
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huizing, A.; Heiligers, M.; Dekker, B.; de Wit, J.; Cifola, L.; Harmanny, R. Deep Learning for Classification of Mini-UAVs Using Micro-Doppler Spectrograms in Cognitive Radar. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 46–56. [Google Scholar] [CrossRef]
- Martorella, M.; Giusti, E.; Capria, A.; Berizzi, F.; Bates, B. Automatic Target Recognition by Means of Polarimetric ISAR Images and Neural Networks. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3786–3794. [Google Scholar] [CrossRef]
- Martorella, M.; Giusti, E.; Demi, L.; Zhou, Z.; Cacciamano, A.; Berizzi, F.; Bates, B. Target Recognition by Means of Polarimetric ISAR Images. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 225–239. [Google Scholar] [CrossRef]
- Wagner, S.A. SAR ATR by a combination of convolutional neural network and support vector machines. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2861–2872. [Google Scholar] [CrossRef]
- Ding, J.; Chen, B.; Liu, H.; Huang, M. Convolutional Neural Network With Data Augmentation for SAR Target Recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [Google Scholar] [CrossRef]
- Feng, S.; Ji, K.; Zhang, L.; Ma, X.; Kuang, G. SAR target classification based on integration of ASC parts model and deep learning algorithm. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 10213–10225. [Google Scholar] [CrossRef]
- Yang, M.; Bai, X.; Wang, L.; Zhou, F. Mixed loss graph attention network for few-shot SAR target classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Liu, H.; Sun, Y. Attribute-guided multi-scale prototypical network for few-shot SAR target classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 12224–12245. [Google Scholar] [CrossRef]
- Li, Y.; Du, L.; Wei, D. Multiscale CNN based on component analysis for SAR ATR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Lang, P.; Fu, X.; Feng, C.; Dong, J.; Qin, R.; Martorella, M. LW-CMDANet: A Novel Attention Network for SAR Automatic Target Recognition. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 6615–6630. [Google Scholar] [CrossRef]
- Li, C.; Du, L.; Li, Y.; Song, J. A novel SAR target recognition method combining electromagnetic scattering information and GCN. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zeng, Z.; Sun, J.; Han, Z.; Hong, W. SAR Automatic Target Recognition Method based on Multi-Stream Complex-Valued Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Zhang, M.; An, J.; Yu, D.H.; Yang, L.D.; Wu, L.; Lu, X.Q. onvolutional neural network with attention mechanism for SAR automatic target recognition. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar]
- Choi, J.H.; Lee, M.J.; Jeong, N.H.; Lee, G.; Kim, K.T. Fusion of Target and Shadow Regions for Improved SAR ATR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Boult, T.E.; Cruz, S.; Dhamija, A.R.; Gunther, M.; Henrydoss, J.; Scheirer, W.J. Learning and the Unknown: Surveying Steps Toward Open World Recognition. Proc. AAAI 2019, 33, 9801–9807. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. A baseline for detecting misclassified and out-of-distribution examples in neural networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 1–12. [Google Scholar] [CrossRef]
- Guisti, E.; Ghio, S.; Oveis, A.H.; Martorell, M. Transfer Learning-Based Fully-Polarimetric Radar Image Classification with a Rejection Option. In Proceedings of the 18th European Radar Conference (EuRAD), London, UK, 5–7 April 2022; pp. 357–360. [Google Scholar]
- Bendale, A.; Boult, T.E. Towards open set deep networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1563–1572. [Google Scholar] [CrossRef]
- Ge, Z.Y.; Demyanov, S.; Chen, Z.; Garnavi, R. Generative openmax for multi-class open set classification. arXiv 2017, arXiv:1707.07418. [Google Scholar]
- Geng, C.; Huang, S.-J.; Chen, S. Recent advances in open set recognition: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3614–3631. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, G.; Huang, M. Out-of-domain detection for natural language understanding in dialog systems. IEEE ACM Trans. Audio Speech Lang. Process. 2020, 28, 119–1209. [Google Scholar] [CrossRef]
- Lee, K.; Lee, K.; Lee, H.; Shin, J. A simple unified framework for detecting out-of-distribution samples and adversarial attacks. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31, pp. 7167–7177. [Google Scholar]
- Inkawhich, N.A.; Davis, E.K.; Inkawhich, M.J.; Majumder, U.K.; Chen, Y. Training sar-atr models for reliable operation in open-world environments. IEEE J. Select. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 3954–3966. [Google Scholar] [CrossRef]
- Guisti, E.; Ghio, S.; Oveis, A.H.; Martorella, M. Open Set Recognition in Synthetic Aperture Radar Using the Openmax Classifier. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022. [Google Scholar]
- Oveis, A.H.; Guisti, E.; Ghio, S.; Martorella, M. Extended Openmax Approach for the Classification of Radar Images with a Rejection Option. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- The Air Force Moving and Stationary Target Recognition Database. Available online: www.sdms.afrl.af.mil/index.php?collection=mstar (accessed on 5 April 2014).
- Scheirer, W.J.; Rocha, A.; Micheals, R.J.; Boult, T.E. Meta-recognition: The theory and practice of recognition score analysis. IEEE Trans. Pattern Anal. 2011, 33, 1689–1695. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Y.; Song, J.; Li, Y. Open set HRRP recognition based on convolutional neural network. J. Eng. 2019, 21, 7701–7704. [Google Scholar] [CrossRef]
- Lewis, B.; Scarnati, T.; Sudkamp, E.; Nehrbass, J.; Rosencrantz, S.; Zelnio, E. A SAR dataset for ATR development: The Synthetic and Measured Paired Labeled Experiment (SAMPLE). In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery, Baltimore, MD, USA, 18 April 2019; pp. 39–54. [Google Scholar]
- Chen, S.; Wang, H. SAR target recognition based on deep learning. In Proceedings of the 2014 International Conference on Data Science and Advanced Analytics (DSAA), Shanghai, China, 30 October–1 November 2014; pp. 541–547. [Google Scholar]
- Du, K.; Deng, Y.; Wang, R.; Zhao, T.; Li, N. SAR ATR based on displacement- and rotation-insensitive CNN. Remote Sens. Lett. 2016, 7, 895–904. [Google Scholar] [CrossRef]
- Wang, L.; Bai, X.; Zhou, F. SAR ATR of ground vehicles based on ESENet. Remote Sens. 2019, 11, 1316. [Google Scholar] [CrossRef]
- Mossing, J.C.; Ross, T.D. Evaluation of sar atr algorithm performance sensitivity to mstar extended operating conditions. Proc. SPIE Int. Soc. Opt. Eng. 1998, 13, 554–565. [Google Scholar]
- Scheirer, W.J.; Rocha, A.d.; Sapkota, A.; Boult, T.E. Toward open set recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1757–1772. [Google Scholar] [CrossRef]
- Oveis, A.H.; Guisti, E.; Ghio, S.; Martorella, M. A Survey on the Applications of Convolutional Neural Networks for Synthetic Aperture Radar: Recent Advances. IEEE Aerosp. Electron. Syst. Mag. 2021, 37, 18–42. [Google Scholar] [CrossRef]
- Giannakopoulos, T.; Pikrakis, A. Introduction to Audio Analysis: A MATLAB® Approach; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Oveis, A.H.; Giusti, E.; Ghio, S.; Martorella, M. CNN for Radial Velocity and Range Components Estimation of Ground Moving Targets in SAR. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: New York, NY, USA, 2001. [Google Scholar]
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]




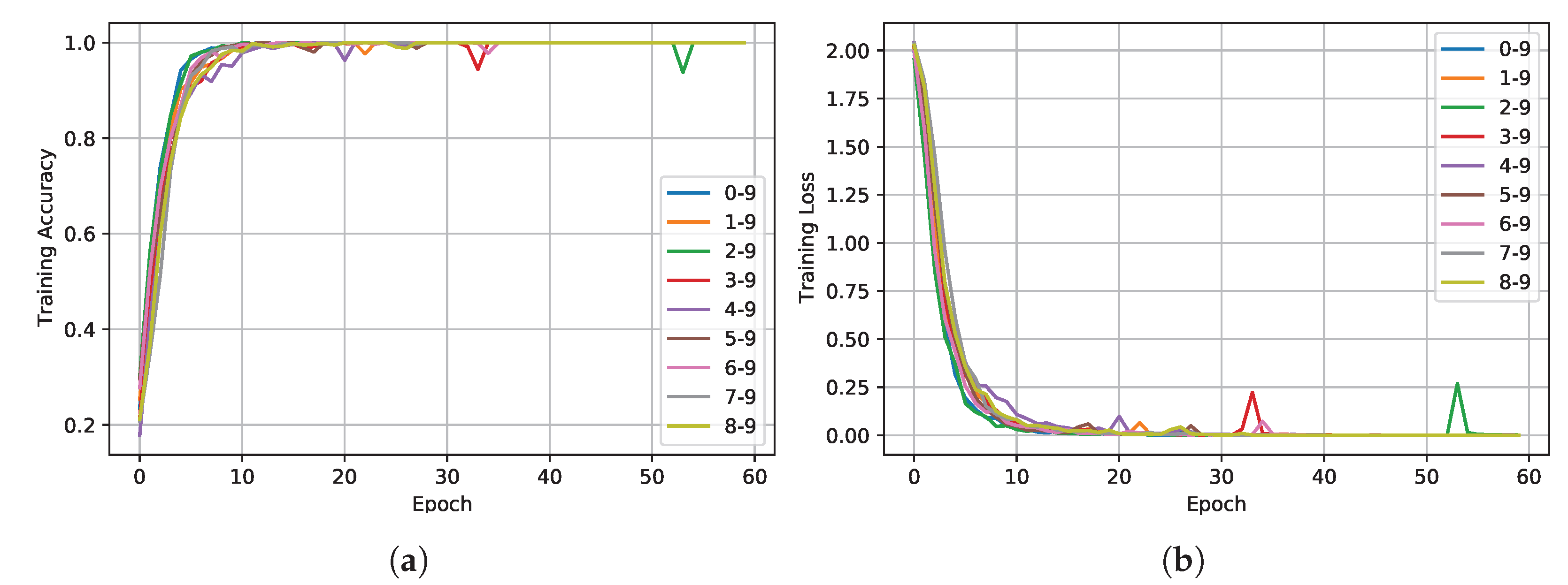
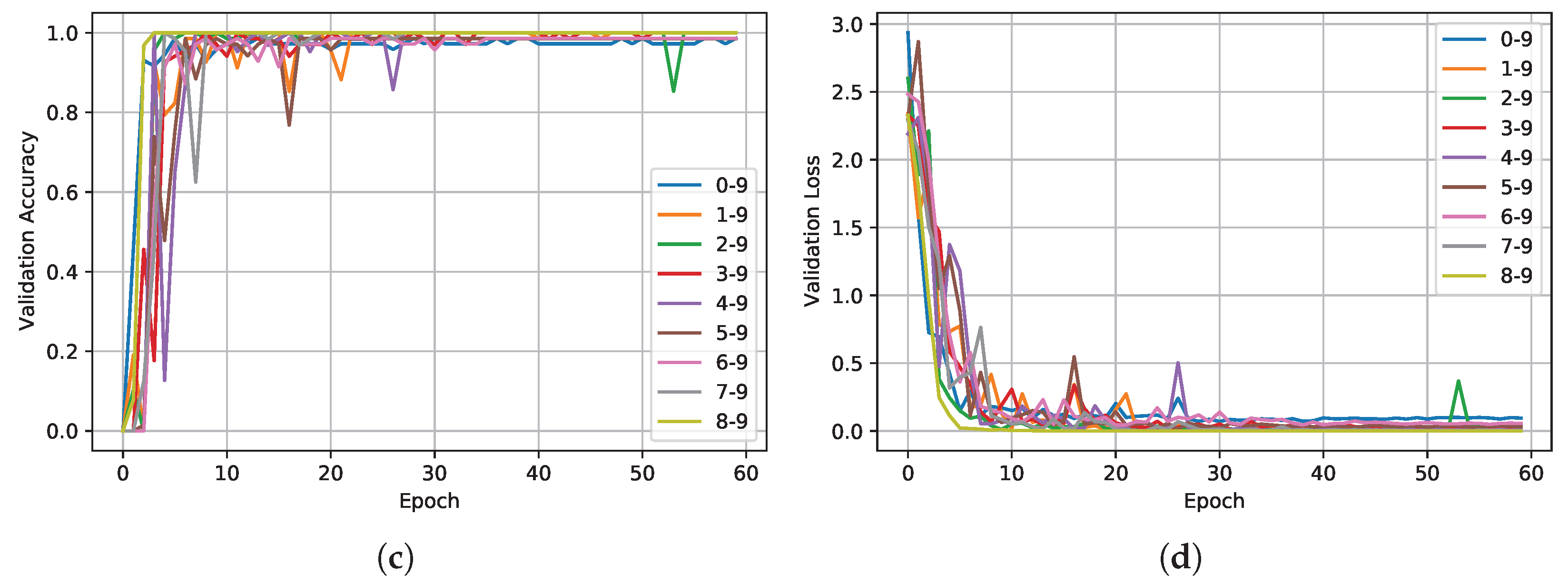
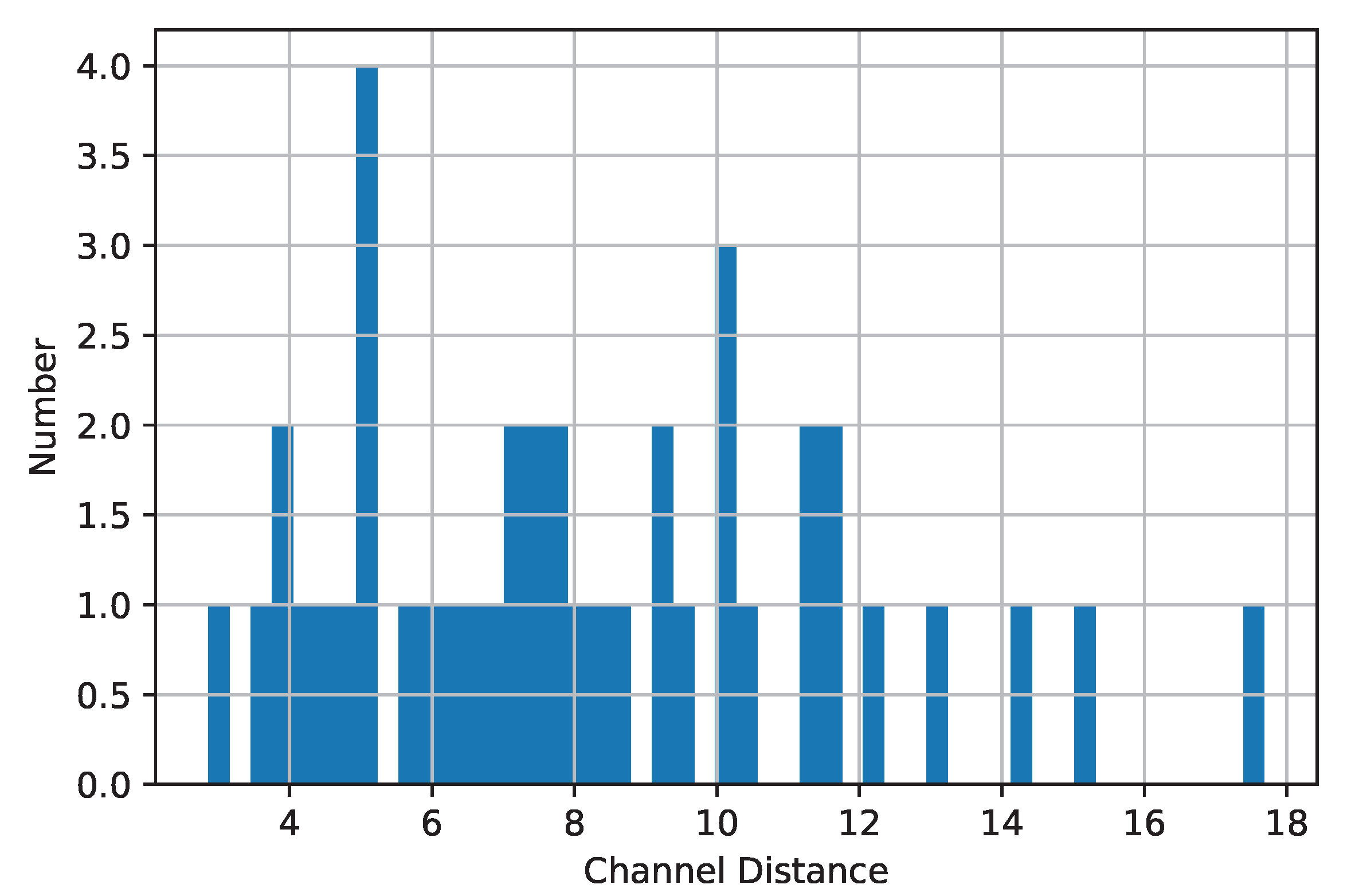
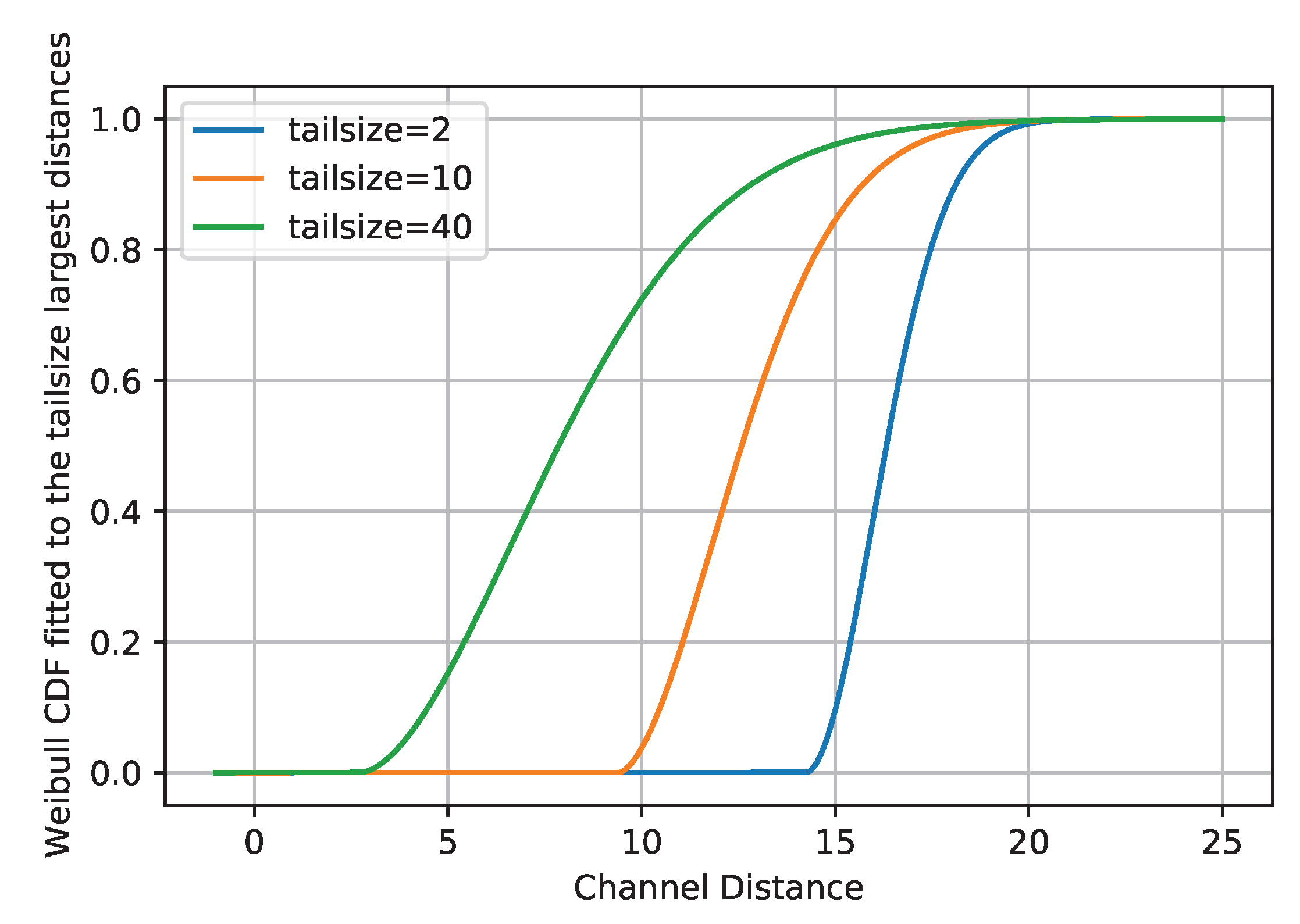

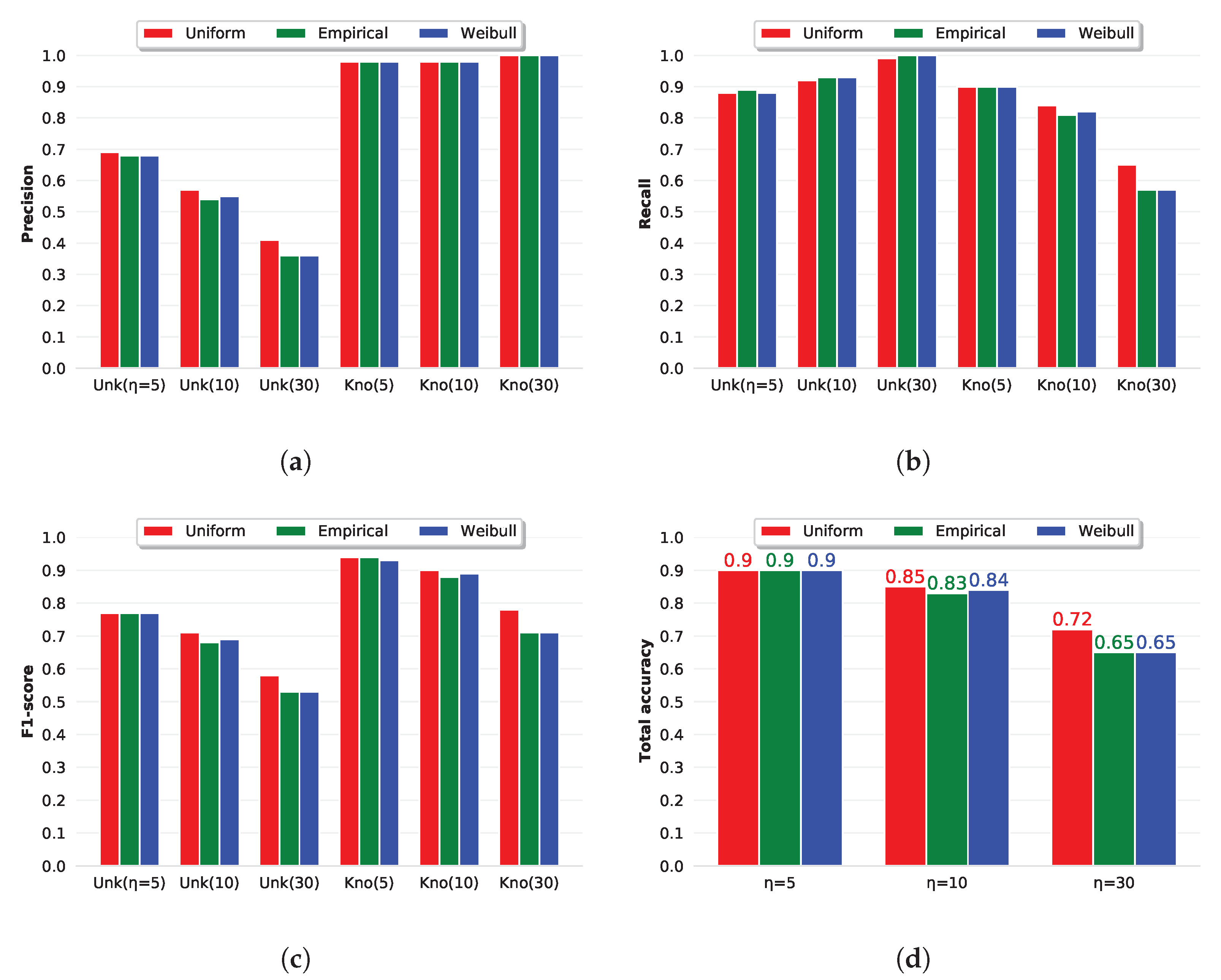
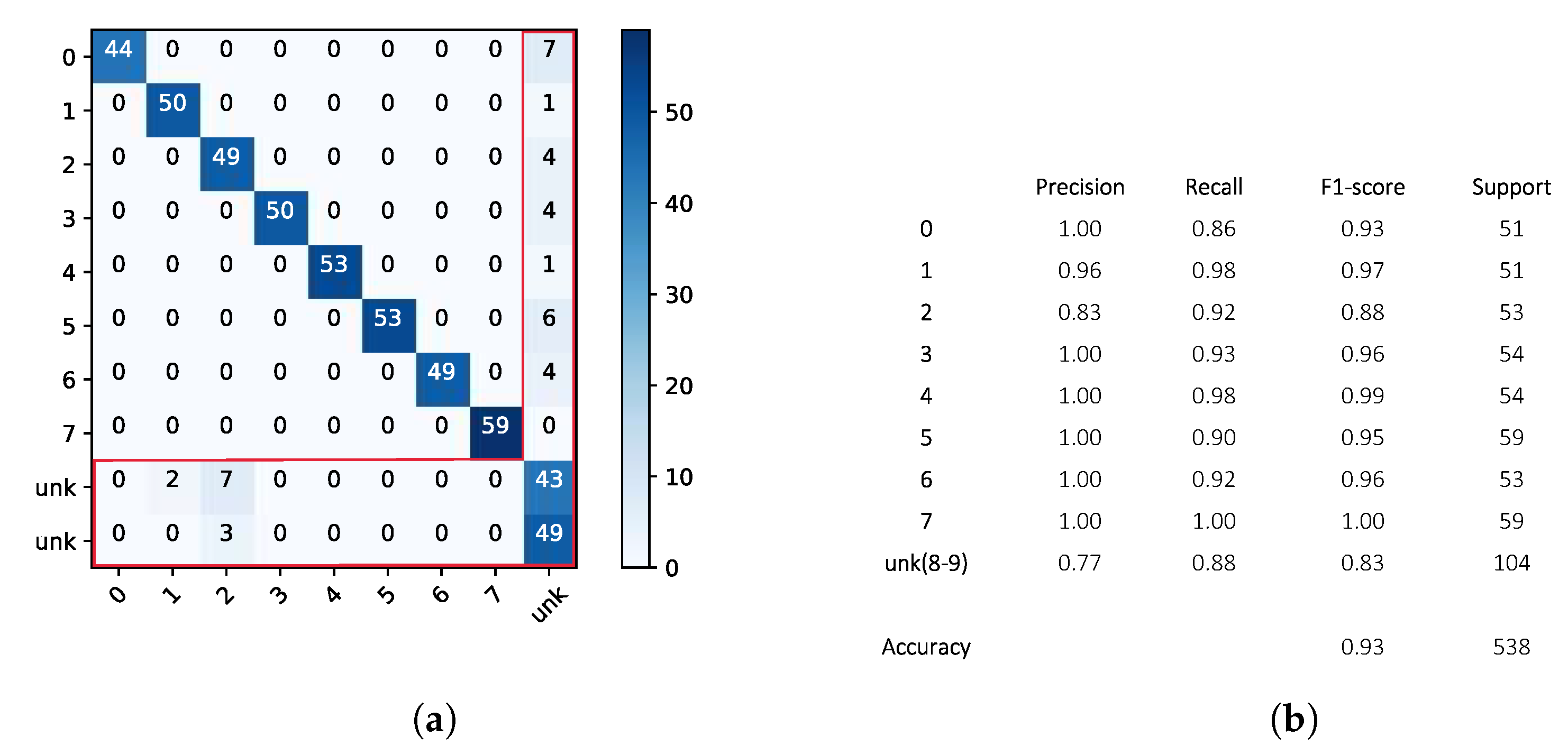
| Layer | Name | Output Size | Act. Func. | Param. |
|---|---|---|---|---|
| 0 | Input | 64 × 64 × 1 | - | 0 |
| 1 | Conv1 | 64 × 64 × 16 | ReLU | 160 |
| 2 | MaxPooling1 | 32 × 32 × 16 | - | 0 |
| 3 | Conv2 | 32 × 32 × 16 | ReLU | 2320 |
| 4 | MaxPooling2 | 16 × 16 × 16 | - | 0 |
| 5 | Conv3 | 16 × 16 × 64 | ReLU | 25,664 |
| 6 | Flattening | 16,384 | - | 0 |
| 7 | FC1 | 50 | - | 819,250 |
| 8 | FC2 | 8 | - | 408 |
| 9 | Classifier | 8 | Softmax | 0 |
| Label | Name | Serial Number | N Train | N Test | |
|---|---|---|---|---|---|
| known | 0 | BTR 70 | C71 | 41 | 51 |
| 1 | M1 | 0AP00N | 78 | 51 | |
| 2 | M2 | MV02GX | 75 | 53 | |
| 3 | M35 | T839 | 75 | 54 | |
| 4 | M60 | 3336 | 122 | 54 | |
| 5 | M548 | C245HAB | 69 | 59 | |
| 6 | T72 | 812 | 55 | 53 | |
| 7 | ZSU23-4 | D08 | 115 | 59 | |
| unknown | 8 | 2S1 | B01 | 0 | 52 |
| 9 | BMP2 | 9563 | 0 | 52 | |
| total | - | - | - | 630 | 538 |
| Class | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 25.8774 | 0.592523 | 14.0206 | 9.63976 | −19.1118 | 0.505812 | 1.15104 | −13.4153 |
| 1 | −9.37342 | 16.4302 | 2.61673 | −1.71236 | 5.15303 | −2.03516 | 4.97492 | −0.208769 |
| 2 | 3.53298 | 4.8171 | 16.9942 | −0.0574321 | −5.61154 | −1.5206 | 6.13859 | −8.09596 |
| 3 | −3.97235 | 0.510664 | −5.95034 | 24.1043 | −6.40276 | 11.6505 | 4.77716 | −2.15785 |
| 4 | −13.0375 | 9.81838 | −1.27891 | 0.350657 | 18.859 | −6.83463 | 6.97438 | 0.575225 |
| 5 | −5.16936 | 0.803306 | −4.19961 | 18.1028 | −12.6156 | 29.3176 | 4.1984 | 1.5873 |
| 6 | −4.98337 | 5.71393 | 4.89013 | 1.9776 | 3.75332 | −3.92143 | 15.4734 | −7.05234 |
| 7 | −9.56859 | 5.69773 | −2.10884 | 1.12619 | −0.957903 | 2.00531 | −4.04335 | 19.9382 |
| Channel | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|---|
| Channel Distance () | 5.53 | 45.82 | 24.63 | 41.77 | 55.79 | 48.64 | 39.15 | 51.35 | |
| w = Weibull CDF (on ) | 0 | 1 | 0.99 | 1 | 1 | 1 | 1 | 1 | |
| Softmax | 0.99 | ||||||||
| 1 | 0.5 | 0.875 | 0.75 | 0.125 | 0.375 | 0.625 | 0.25 | ||
| AV | 22.38 | 1.09 | 13.92 | 8.01 | −17.27 | −2.07 | 1.99 | −11.23 | |
| modAV (@ line 8 Algorithm 2) | 22.38 | 0.55 | 1.74 | 2 | −15.11 | −1.3 | 0.75 | −8.43 | |
| AV-modAV | 0 | 0.54 | 12.18 | 6.01 | −2.15 | −0.77 | 1.24 | −2.8 | |
| modAV (@ line 10 Algorithm 2) | 22.38 | 0.55 | 1.74 | 2 | −15.11 | −1.3 | 0.75 | −8.43 | 14.24 |
| Openmax | 0.99 |
| Channel | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|---|
| Channel Distance () | 19.15 | 44.92 | 20.26 | 45.42 | 53.99 | 51.04 | 34.5 | 55.67 | |
| w = Weibull CDF (on ) | 0.99 | 1 | 0.99 | 1 | 1 | 1 | 1 | 1 | |
| Softmax | |||||||||
| 0.875 | 0.375 | 1 | 0.625 | 0.25 | 0.5 | 0.75 | 0.125 | ||
| AV | 16.17 | −0.93 | 20.95 | 2.72 | −12.94 | 0.59 | 11.76 | −18.31 | |
| modAV (@ line 8 Algorithm 2) | 2.12 | −0.58 | 0.01 | 1.0 | −9.71 | 0.3 | 2.94 | −16.02 | |
| AV-modAV | 14.05 | −0.35 | 20.94 | 1.7 | −3.23 | 0.29 | 8.82 | −2.2 | |
| modAV (@ line 10 Algorithm 2) | 2.12 | −0.58 | 0.01 | 1.0 | −9.71 | 0.3 | 2.94 | −16.02 | 39.94364 |
| Openmax | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giusti, E.; Ghio, S.; Oveis, A.H.; Martorella, M. Proportional Similarity-Based Openmax Classifier for Open Set Recognition in SAR Images. Remote Sens. 2022, 14, 4665. https://doi.org/10.3390/rs14184665
Giusti E, Ghio S, Oveis AH, Martorella M. Proportional Similarity-Based Openmax Classifier for Open Set Recognition in SAR Images. Remote Sensing. 2022; 14(18):4665. https://doi.org/10.3390/rs14184665
Chicago/Turabian StyleGiusti, Elisa, Selenia Ghio, Amir Hosein Oveis, and Marco Martorella. 2022. "Proportional Similarity-Based Openmax Classifier for Open Set Recognition in SAR Images" Remote Sensing 14, no. 18: 4665. https://doi.org/10.3390/rs14184665
APA StyleGiusti, E., Ghio, S., Oveis, A. H., & Martorella, M. (2022). Proportional Similarity-Based Openmax Classifier for Open Set Recognition in SAR Images. Remote Sensing, 14(18), 4665. https://doi.org/10.3390/rs14184665