Unbiasing the Estimation of Chlorophyll from Hyperspectral Images: A Benchmark Dataset, Validation Procedure and Baseline Results
Abstract
:1. Introduction
1.1. Contribution
- We introduce a publicly available set of (i) chlorophyll content measurements with some complementary information, including the soil moisture, weather parameters collected during the measurements or the relative water content, being the amount of water in a leaf at the time of sampling relative to the maximal water a leaf can hold and (ii) the corresponding high-resolution hyperspectral imagery (2.2 cm GSD). The dataset encompasses the orthophotomaps with the marked plots where the chlorophyll sampling has been completed, as well as the extracted images of separate plots. We performed the on-the-ground chlorophyll measurements, which resulted in four ground-truth parameters (Section 3.1):
- The SPAD index [22];
- The maximum quantum yield of the PSII photochemistry (Fv/Fm) [24];
- The performance index for energy conservation from photons absorbed by PSII to the final PSI electron acceptors (PI) [26];
- Relative water content (RWC) measurements for the sampled canopy, for capturing additional derivative information on the nutrition of the plants.
- We introduce a procedure for the unbiased validation of machine learning algorithms for estimating the chlorophyll-related parameters from HSI, and we ensure the full reproducibility of the experiments over our dataset (Section 3.2).
- We deliver the baseline results obtained for the introduced dataset (for four ground-truth parameters) using 15 machine learning techniques which can constitute the reference for any future studies emerging from our work (Section 4). Additionally, we show that the performance of a selected model can be further improved through regularization.
1.2. Structure of the Paper
2. Related Literature
3. Materials and Methods
3.1. Chlorophyll Estimation Dataset (CHESS)
3.2. Unbiased Validation of Chlorophyll Estimation
4. Experimental Results
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGB | Above-ground biomass |
| ALOS | Advanced Land Observing Satellite |
| CHESS | CHlorophyll EStimation DataSet |
| CHRIS | Compact High Resolution Imaging Spectrometer |
| CWT | Continuous wavelet transform |
| DNN | Deep neural network |
| EFFIS | The European Forest Fire Information System |
| EVI | Enhanced vegetation index |
| FvFm | The maximum quantum yield of the PSII photochemistry |
| GBDT | Gradient boosting decision tree |
| GBVI | Green brown vegetation index |
| GSD | Ground sample distance |
| GPR | Gaussian process regression |
| HSI | Hyperspectral image |
| k-NN | k-nearest neighbor |
| LAI | Leaf area index |
| LSWI | Land surface water index |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MLR | Multiple linear regression |
| MSE | Mean squared error |
| MSI | Multispectral image |
| NBSI | Non-binary snow index |
| NDVI | Normalized difference vegetation index |
| NIR | Near-infrared spectra |
| NIRv | Near-infrared reflectance of vegetation |
| PALSAR | Phased Array L-band Synthetic Aperture Radar |
| PCA | Principal component analysis |
| PI | The index for energy conservation from photons absorbed by PSII to PSI electron acceptors |
| Coefficient of determination | |
| RDP | Ratio of the performance to deviation |
| RF | Random forest |
| RFE | Recursive-feature-elimination |
| RMSE | Root mean squared error |
| RRMSE | Relative root mean squared error |
| RWC | Relative water content measurements for the sampled canopy |
| SAVI | Soil-adjusted vegetation index |
| SAR | Synthetic-aperture radar |
| SOC | Soil organic carbon |
| SPAD | The actual level of chlorophyll utilizing the soil-plant analysis development |
| SVD | Singular value decomposition |
| SVM | Support vector machine |
| VHGPR | Variational heteroscedastic GPR |
| VIS-NIR | Visible–near-infrared spectra |
| VH | Vertical transmitted and horizontal received |
| VV | Vertical transmitted and vertical received polarization |
| XGB | Extreme gradient boosting |
References
- Shen, Q.; Lin, J.; Yang, J.; Zhao, W.; Wu, J. Exploring the Potential of Spatially Downscaled Solar-Induced Chlorophyll Fluorescence to Monitor Drought Effects on Gross Primary Production in Winter Wheat. IEEE J-STARS 2022, 15, 2012–2022. [Google Scholar] [CrossRef]
- Long, Y.; Ma, M. Recognition of Drought Stress State of Tomato Seedling Based on Chlorophyll Fluorescence Imaging. IEEE Access 2022, 10, 48633–48642. [Google Scholar] [CrossRef]
- Oláh, V.; Hepp, A.; Irfan, M.; Mészáros, I. Chlorophyll Fluorescence Imaging-Based Duckweed Phenotyping to Assess Acute Phytotoxic Effects. Plants 2021, 10, 2763. [Google Scholar] [CrossRef] [PubMed]
- Lazzeri, G.; Frodella, W.; Rossi, G.; Moretti, S. Multitemporal Mapping of Post-Fire Land Cover Using Multiplatform PRISMA Hyperspectral and Sentinel-UAV Multispectral Data: Insights from Case Studies in Portugal and Italy. Sensors 2021, 21. [Google Scholar] [CrossRef] [PubMed]
- Pyo, J.; Duan, H.; Baek, S.; Kim, M.S.; Jeon, T.; Kwon, Y.S.; Lee, H.; Cho, K.H. A Convolutional Neural Network Regression for Quantifying Cyanobacteria Using Hyperspectral Imagery. Remote Sens. Environ. 2019, 233, 111350. [Google Scholar] [CrossRef]
- Hill, P.R.; Kumar, A.; Temimi, M.; Bull, D.R. HABNet: Machine Learning, Remote Sensing-Based Detection of Harmful Algal Blooms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3229–3239. [Google Scholar] [CrossRef]
- Torres Palenzuela, J.M.; Vilas, L.G.; Bellas Aláez, F.M.; Pazos, Y. Potential Application of the New Sentinel Satellites for Monitoring of Harmful Algal Blooms in the Galician Aquaculture. Thalass. Int. J. Mar. Sci. 2020, 36, 85–93. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Cwiek, M.; Zak, L.; Lakota, T.; Tulczyjew, L.; Kawulok, M. Towards On-Board Hyperspectral Satellite Image Segmentation: Understanding Robustness of Deep Learning through Simulating Acquisition Conditions. Remote Sens. 2021, 13, 1532. [Google Scholar] [CrossRef]
- Liu, N.; Liu, G.; Sun, H. Real-Time Detection on SPAD Value of Potato Plant Using an In-Field Spectral Imaging Sensor System. Sensors 2020, 20, 3430. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated Narrow-Band Vegetation Indices for Prediction of Crop Chlorophyll Content for Application to Precision Agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Hai-ling, J.; Li-fu, Z.; Hang, Y.; Xiao-ping, C.; Shu-dong, W.; Xue-ke, L.; Kai, L. Comparison of Accuracy and Stability of Estimating Winter Wheat Chlorophyll Content Based on Spectral Indices. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2985–2988. [Google Scholar] [CrossRef]
- Raya-Sereno, M.D.; Alonso-Ayuso, M.; Pancorbo, J.L.; Gabriel, J.L.; Camino, C.; Zarco-Tejada, P.J.; Quemada, M. Residual Effect and N Fertilizer Rate Detection by High-Resolution VNIR-SWIR Hyperspectral Imagery and Solar-Induced Chlorophyll Fluorescence in Wheat. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Q.; Shang, J.; Liu, C.; Zhuang, T.; Ding, J.; Xian, Y.; Zhao, L.; Wang, W.; Zhou, G.; et al. UAV- and Machine Learning-Based Retrieval of Wheat SPAD Values at the Overwintering Stage for Variety Screening. Remote Sens. 2021, 13, 5166. [Google Scholar] [CrossRef]
- Yuan, Z.; Ye, Y.; Wei, L.; Yang, X.; Huang, C. Study on the Optimization of Hyperspectral Characteristic Bands Combined with Monitoring and Visualization of Pepper Leaf SPAD Value. Sensors 2021, 22, 183. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Tang, S.; Yang, C. Deep Learning for Chlorophyll-a Concentration Retrieval: A Case Study for the Pearl River Estuary. Remote Sens. 2021, 13, 3717. [Google Scholar] [CrossRef]
- Tulczyjew, L.; Kawulok, M.; Longépé, N.; Le Saux, B.; Nalepa, J. A Multibranch Convolutional Neural Network for Hyperspectral Unmixing. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Kapoor, S.; Narayanan, A. Leakage and the Reproducibility Crisis in ML-based Science. arXiv 2022, arXiv:2207.07048. [Google Scholar] [CrossRef]
- Inoue, Y.; Guérif, M.; Baret, F.; Skidmore, A.; Gitelson, A.; Schlerf, M.; Darvishzadeh, R.; Olioso, A. Simple and Robust Methods for Remote Sensing of Canopy Chlorophyll Content: A Comparative Analysis of Hyperspectral Data for Different Types of Vegetation. Plant Cell Environ. 2016, 39, 2609–2623. [Google Scholar] [CrossRef] [Green Version]
- Mayranti, F.P.; Saputro, A.H.; Handayani, W. Chlorophyll A and B Content Measurement System of Velvet Apple Leaf in Hyperspectral Imaging. In Proceedings of the ICICOS, Semarang, Indonesia, 29–30 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Tomaszewski, M.; Gasz, R.; Smykała, K. Monitoring Vegetation Changes Using Satellite Imaging—NDVI and RVI4S1 Indicators. In Proceedings of the Control, Computer Engineering and Neuroscience, Opole, Poland, 21 September 2021; Paszkiel, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 268–278. [Google Scholar] [CrossRef]
- Bannari, A.; Khurshid, K.S.; Staenz, K.; Schwarz, J.W. A Comparison of Hyperspectral Chlorophyll Indices for Wheat Crop Chlorophyll Content Estimation Using Laboratory Reflectance Measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3063–3074. [Google Scholar] [CrossRef]
- El-Hendawy, S.; Dewir, Y.H.; Elsayed, S.; Schmidhalter, U.; Al-Gaadi, K.; Tola, E.; Refay, Y.; Tahir, M.U.; Hassan, W.M. Combining Hyperspectral Reflectance Indices and Multivariate Analysis to Estimate Different Units of Chlorophyll Content of Spring Wheat under Salinity Conditions. Plants 2022, 11, 456. [Google Scholar] [CrossRef] [PubMed]
- Middleton, E.M.; Julitta, T.; Campbell, P.E.; Huemmrich, K.F.; Schickling, A.; Rossini, M.; Cogliati, S.; Landis, D.R.; Alonso, L. Novel Leaf-Level Measurements of Chlorophyll Fluorescence for Photosynthetic Efficiency. In Proceedings of the IGARSS, Milan, Italy, 26–31 July 2015; pp. 3878–3881. [Google Scholar] [CrossRef]
- Jia, M.; Zhou, C.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W.; Yao, X. Inversion of Chlorophyll Fluorescence Parameters on Vegetation Indices at Leaf Scale. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4359–4362. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Validating Hyperspectral Image Segmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1264–1268. [Google Scholar] [CrossRef] [Green Version]
- Singh, H.; Kumar, D.; Soni, V. Performance of Chlorophyll a Fluorescence Parameters in Lemna Minor under Heavy Metal Stress Induced by Various Concentration of Copper. Sci. Rep. 2022, 12, 10620. [Google Scholar] [CrossRef] [PubMed]
- Yue, J.; Zhou, C.; Guo, W.; Feng, H.; Xu, K. Estimation of Winter-Wheat Above-Ground Biomass Using the Wavelet Analysis of Unmanned Aerial Vehicle-Based Digital Images and Hyperspectral Crop Canopy iImages. Int. J. Remote Sens. 2021, 42, 1602–1622. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Deep Neural Network Algorithm for Estimating Maize Biomass Based on Simulated Sentinel 2A Vegetation Indices and Leaf Area Index. Crop J. 2020, 8, 87–97. [Google Scholar] [CrossRef]
- Lu, B.; He, Y. Evaluating Empirical Regression, Machine Learning, and Radiative Transfer Modelling for Estimating Vegetation Chlorophyll Content Using Bi-Seasonal Hyperspectral Images. Remote Sens. 2019, 11, 1979. [Google Scholar] [CrossRef] [Green Version]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Brewer, K.; Clulow, A.; Sibanda, M.; Gokool, S.; Naiken, V.; Mabhaudhi, T. Predicting the Chlorophyll Content of Maize over Phenotyping as a Proxy for Crop Health in Smallholder Farming Systems. Remote Sens. 2022, 14, 518. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent Advances of Hyperspectral Imaging Technology and Applications in Agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Liu, J.; Liu, H.; Zhang, X.; Zhang, Y.; Wang, P.; Tang, H.; Kong, F. Regional Soil Organic Carbon Prediction Model Based on a Discrete Wavelet Analysis of Hyperspectral Satellite Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Chen, Y.; Linderman, M.; Mouazen, A.M.; Liu, Y.; Guo, L.; Yu, L.; Liu, Y.; Cheng, H.; et al. Comparing Laboratory and Airborne Hyperspectral Data for the Estimation and Mapping of Topsoil Organic Carbon: Feature Selection Coupled with Random Forest. Soil Tillage Res. 2020, 199, 104589. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, C.; Zhang, X.; Cheng, X.; Feng, G.; Wang, Y.; Gao, Q. Estimating the Maize Biomass by Crop Height and Narrowband Vegetation Indices Derived from UAV-based Hyperspectral Images. Ecol. Indic. 2021, 129, 107985. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling Maize Above-Ground Biomass Based on Machine Learning Approaches Using UAV Remote-Sensing Data. Plant Methods 2019, 15, 1746–4811. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D Convolutional Neural Networks for Crop Classification with Multi-Temporal Remote Sensing Images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef] [Green Version]
- Cui, Z.; Kerekes, J.P. Potential of Red Edge Spectral Bands in Future Landsat Satellites on Agroecosystem Canopy Green Leaf Area Index Retrieval. Remote Sens. 2018, 10, 1458. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Zhou, G. Estimation of Vegetation Water Content using Hyperspectral Vegetation Indices: A Comparison of Crop Water Indicators in Response to Water Stress Treatments for Summer Maize. BMC Ecol. 2019, 19, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Mansaray, L.R.; Zhang, K.; Kanu, A.S. Dry Biomass Estimation of Paddy Rice With Sentinel-1A Satellite Data Using Machine Learning Regression Algorithms. Comput. Electron. Agric. 2020, 176, 105674. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating Leaf Area Index and Aboveground Biomass of Grazing Pastures Using Sentinel-1, Sentinel-2 and Landsat Images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Liu, J.; Xiao, Z.; Xiao, L. Deep CNN-based Hyperspectral Image Classification Using Discriminative Multiple Spatial-spectral Feature Fusion. Remote Sens. Lett. 2020, 11, 827–836. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P. Advantage of Hyperspectral EO-1 Hyperion over Multispectral IKOMOS, Geoeye-1, Worldview-2, Landsat ETM+, and MODIS Vegetation Indices in Crop Biomass Estimation. ISPRS J. Photogramm. Remote Sens. 2015, 108, 205–218. [Google Scholar] [CrossRef] [Green Version]
- Ribalta Lorenzo, P.; Tulczyjew, L.; Marcinkiewicz, M.; Nalepa, J. Hyperspectral Band Selection Using Attention-Based Convolutional Neural Networks. IEEE Access 2020, 8, 42384–42403. [Google Scholar] [CrossRef]
- Zheng, Q.; Ye, H.; Huang, W.; Dong, Y.; Jiang, H.; Wang, C.; Li, D.; Wang, L.; Chen, S. Integrating Spectral Information and Meteorological Data to Monitor Wheat Yellow Rust at a Regional Scale: A Case Study. Remote Sens. 2021, 13, 278. [Google Scholar] [CrossRef]
- Rao, K.; Williams, A.P.; Flefil, J.F.; Konings, A.G. SAR-enhanced Mapping of Live Fuel Moisture Content. Remote Sens. Environ. 2020, 245, 111797. [Google Scholar] [CrossRef]
- Estévez, J.; Vicent, J.; Rivera-Caicedo, J.P.; Morcillo-Pallarés, P.; Vuolo, F.; Sabater, N.; Camps-Valls, G.; Moreno, J.; Verrelst, J. Gaussian Processes Retrieval of LAI from Sentinel-2 Top-of-atmosphere Radiance Data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 289–304. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, Y.; Atkinson, P.M.; Yao, H. Predicting Soil Organic Carbon Content in Spain by Combining Landsat TM and ALOS PALSAR Images. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102182. [Google Scholar] [CrossRef]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Marais Sicre, C.; Le Dantec, V.; Demarez, V. Estimating Maize Biomass and Yield over Large Areas Using High Spatial and Temporal Resolution Sentinel-2 like Remote Sensing Data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Kalaji, H.M.; Račková, L.; Paganová, V.; Swoczyna, T.; Rusinowski, S.; Sitko, K. Can Chlorophyll-a Fluorescence Parameters Be Used as Bio-indicators to Distinguish Between Drought and Salinity Stress in Tilia Cordata Mill? Environ. Exp. Bot. 2018, 152, 149–157. [Google Scholar] [CrossRef]
- Li, C.; Chen, P.; Ma, C.; Feng, H.; Wei, F.; Wang, Y.; Shi, J.; Cui, Y. Estimation of potato chlorophyll content using composite hyperspectral index parameters collected by an unmanned aerial vehicle. Int. J. Remote Sens. 2020, 41, 8176–8197. [Google Scholar] [CrossRef]
- Liu, N.; Xing, Z.; Zhao, R.; Qiao, L.; Li, M.; Liu, G.; Sun, H. Analysis of Chlorophyll Concentration in Potato Crop by Coupling Continuous Wavelet Transform and Spectral Variable Optimization. Remote Sens. 2020, 12, 2826. [Google Scholar] [CrossRef]
- Yang, H.; Hu, Y.; Zheng, Z.; Qiao, Y.; Zhang, K.; Guo, T.; Chen, J. Estimation of Potato Chlorophyll Content from UAV Multispectral Images with Stacking Ensemble Algorithm. Agronomy 2022, 12, 2318. [Google Scholar] [CrossRef]
- Ruszczak, B.; Boguszewska-Mańkowska, D. Deep potato—The Hyperspectral Imagery of Potato Cultivation with Reference Agronomic Measurements Dataset: Towards Potato Physiological Features Modeling. Data Brief 2022, 42, 108087. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Nalepa, J.; Myller, M.; Tulczyjew, L.; Kawulok, M. Deep Ensembles for Hyperspectral Image Data Classification and Unmixing. Remote Sens. 2021, 13, 4133. [Google Scholar] [CrossRef]
- Lin, C.Y.; Lin, C. Using Ridge Regression Method to Reduce Estimation Uncertainty in Chlorophyll Models Based on Worldview Multispectral Data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1777–1780. [Google Scholar] [CrossRef]
- Ziaja, M.; Bosowski, P.; Myller, M.; Gajoch, G.; Gumiela, M.; Protich, J.; Borda, K.; Jayaraman, D.; Dividino, R.; Nalepa, J. Benchmarking Deep Learning for On-Board Space Applications. Remote Sens. 2021, 13, 3981. [Google Scholar] [CrossRef]
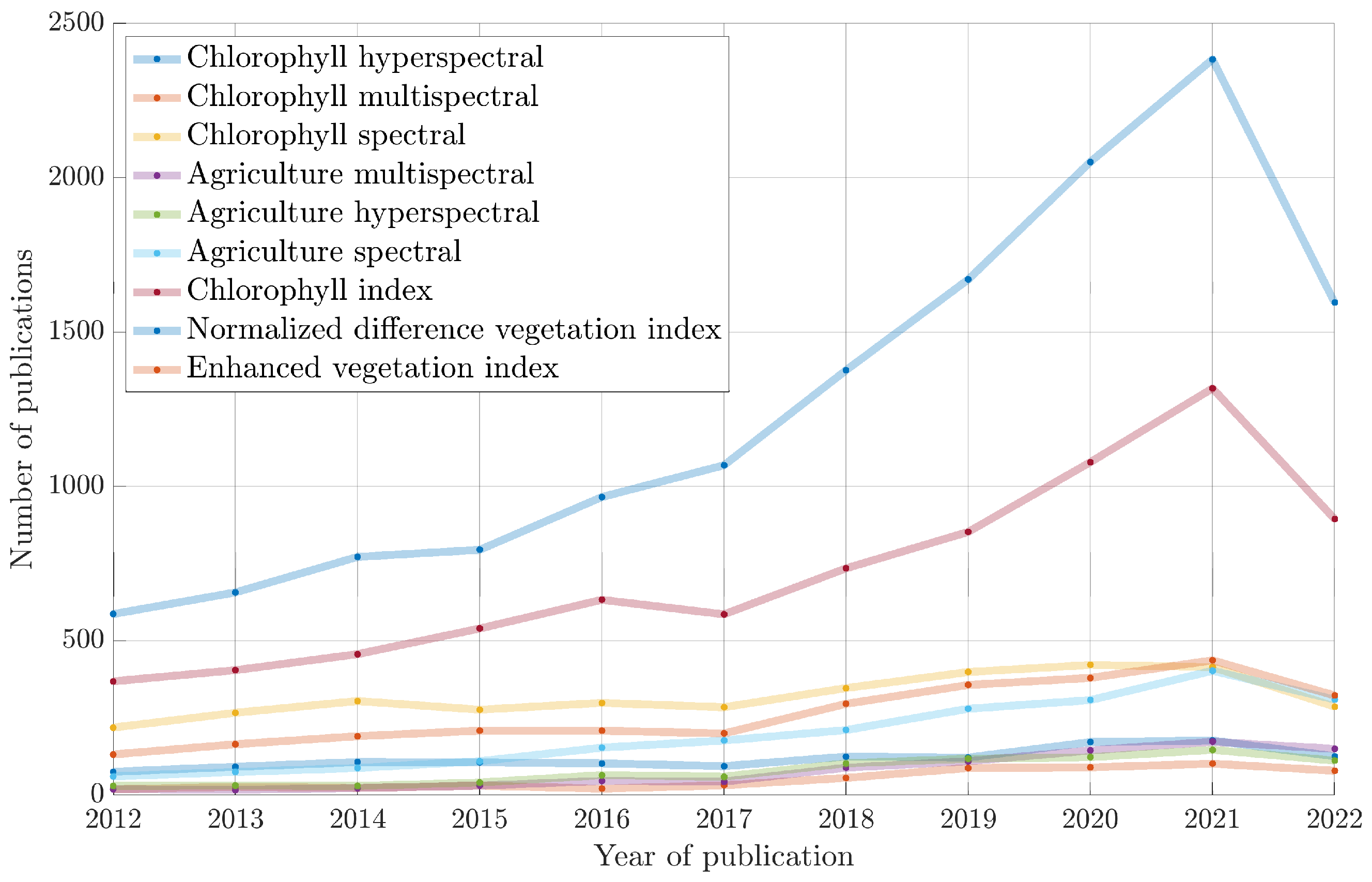




| Ref. | Year | Goal | Feature Extraction | Algorithm |
|---|---|---|---|---|
| [31] | 2022 | prediction of chlorophyll content in maize | selected bands; vegetation indices | random forest |
| [35] | 2021 | monitoring of above-ground biomass of maize | vegetation indices | stepwise regression; random forest; extreme gradient boosting |
| [45] | 2021 | monitoring of wheat yellow rust | vegetation indices; meteorological features | linear discriminant analysis; support vector machine; artificial neural network |
| [46] | 2020 | mapping of live fuel moisture content | NDVI; NDWI; NIRv | recurrent neural network |
| [28] | 2020 | estimation of biomass | vegetation indices | deep neural network |
| [27] | 2020 | monitoring of crop growth | high-frequency IWD information; continuous wavelet transform (CWT) | multiple linear stepwise regression |
| [40] | 2020 | dry biomass estimation of paddy rice | VH; VV | random forest; support vector machine; k-nearest neighbor; gradient boosting decision tree |
| [47] | 2020 | LAI detection | LAI | Gaussian process regression (GPR); variational heteroscedastic GPR |
| [33] | 2020 | estimation of soil organic carbon | principal component analysis; NDI; RI; DI | discrete wavelet transform at different scales; random forest; support vector machine; back-propagation neural network |
| [48] | 2020 | estimation of soil organic carbon | vegetation indices: NDVI, SAVI, NBSI, NDWI, NDBI, FI | random forest |
| [36] | 2019 | monitoring of above-ground biomass of maize | recursive-feature elimination | multiple linear regression; support vector machine; artificial neural network; random forest |
| [41] | 2019 | pasture conditions, seasonal dynamics of LAI and AGB | NDVI; EVI; LSWI | multiple linear regression; support vector machine; random forest |
| [38] | 2018 | canopy green leaf area | GBVI; NDVI; CI | empirical vegetation index regression (NDVIa-b and CIa-b); physically-based inversion, support vector regression |
| [49] | 2016 | maize biomass estimation, the seasonal variation | specific leaf area | simple algorithm for yield estimates |
| [43] | 2015 | detection of favorable wavelengths | singular value decomposition | stepwise regression |
| Ref. | Date Source | Type | Wavelength | Amount of Data | Measure | Value |
|---|---|---|---|---|---|---|
| [31] | DJI S1000 UAV; MicaSense Altum; Downwelling Light Sensor 2 (DLS-2) | MSI | 465, 532, 630 nm, 680–730 nm, 1200–1600 nm | 3576 | RMSE RRMSE | results reported for the seasons |
| [35] | DJI S1000 UAV; Cubert UHD 185 | HSI | 454–950 nm | 1809 | RMSE RRMSE | 0.85 0.27 0.84% |
| [45] | Sentinel-2; National Meteorological Information Center | MSI | 490, 560, 665, 842, 705 nm | 58 | accuracy | 84.20% |
| [46] | Sentinel-1; Landsat-8 | SAR MSI | C-band; 450–510 nm, 530–590 nm, 640–670 nm, 850–880 nm, 1570–1650 nm, 2110–2290 nm | not specified | RMSE bias | 0.63 25.00% 1.90% |
| [28] | Sentinel-2 | MSI | 443–2190 nm | 209 | RMSE RRMSE | 0.87 1.84 24.76% |
| [27] | DJI S1000 UAV; Cubert UHD 185; Sony DSC QX100 | HSI | 454–882 nm | 144 | RMSE MAE | 0.85 0.79 1.01 |
| [40] | Sentinel-1A | SAR | C-band | 175 | RMSE | 0.72 362.40 |
| [47] | Sentinel-2 | MSI | 400–2400 nm | 114 | RMSE RMSE | 0.78 (GPR) 0.70 (GPR) 0.80 (VHGPR) 0.63 (VHGPR) |
| [33] | Gaofen-5 | HSI | 433–1342 nm, 1460–1763 nm, 1990–2445 nm | 14 | RMSE | 0.83 2.89 |
| [48] | ALOS PALSAR; Landsat TM | SAR MSI | L-band; 530–590 nm, 640–670 nm, 850–880 nm, 1570–1650 nm, 2110–2290 nm | not specified | RMSE RDP | 0.59 9.27 1.98 |
| [36] | DJI S1000 UAV; 1.2 megapixel Parrot Sequoia camera | MSI | 550–790 nm | 120 185 | RMSE MAE | 0.94 0.50 0.36 |
| [41] | Sentinel-1A; Landsat-8; Sentinel-2 | SAR MSI | C-band; 452–512 nm, 636–673 nm, 851–879 nm, 1566–1651 nm | not specified | RMSE | 0.78 119.40 |
| [38] | HyMap; CHRIS/PROBA | HSI MSI | 677–707 nm | 118 | 0.79 | |
| [49] | Formosat-2; SPOT4-Take5; Landsat-8; Deimos-1 | MSI | specific to the sensor | 195 | RRMSE | 0.96 4.6% |
| [43] | Landsat ETM+; KONOS; GeoEye-1; WorldView-2; Hyperion | HSI MSI | 772, 539, 758, 914, 1130, 1320 nm | 9, 23, 23, 24, 10 | RMSE | 0.12–0.97 1.15–2.47 |
| Parameter | SPAD | FvFm | PI | RWC |
|---|---|---|---|---|
| SPAD | 1.000 (1.000) | 0.668 (0.000) | 0.675 (0.000) | 0.109 (0.363) |
| FvFm | 0.574 (0.000) | 1.000 (1.000) | 0.743 (0.000) | 0.352 (0.002) |
| PI | 0.674 (0.000) | 0.877 (0.000) | 1.000 (1.000) | (0.434) |
| RWC | 0.697 (0.550) | 0.253 (0.161) | (0.692) | 1.000 (1.000) |
| Algorithm | Hyperparameters |
|---|---|
| Ada Boost | Maximum number of estimators: 50, learning rate: 1, linear loss. |
| Decision Tree | Loss function: squared error, maximum depth of the tree: not set, minimum number of samples required to split an internal node: 2, minimum number of samples required to be at a leaf node: 1, allowing all features to be considered for the best split with unlimited number of leaf nodes. |
| Extra Trees | Maximum number of estimators: , loss function: squared error, maximum depth of the tree: not set, minimum number of samples required to split an internal node: 2, minimum number of samples required to be at a leaf node: 1, allowing all features to be considered for the best split with samples’ bootstrapping while building trees, unlimited number of leaf nodes. |
| Extreme Gradient Boosting | Learning rate: 0.3, maximum depth of an individual estimator: 6, minimum sum of instance weight: 1, maximum delta step: 0, regularization terms: 1 and : 0. |
| Gradient Boosting | Learning rate: 0.1, maximum number of estimators: , maximum depth of an individual estimator: 3, loss function: squared error, percentage of samples required to split an internal node: 10%. |
| Kernel Ridge | : 1, the degree of the linear polynomial kernel: 3, zero coefficient for polynomial and sigmoid kernels: 1. |
| Lasso | : 1, maximum number of iterations: , tolerance stopping criteria: . |
| Light Gradient Boosting Machine | Maximum tree leaves for base learners: 31 without any limit for the tree depth for base learners, boosting learning rate: , number of boosted trees to fit: , number of samples for constructing bins: , no minimum loss reduction required to make a further partition on a leaf node, minimum sum of instance weight in a leaf: , minimum samples in a child: 20. |
| Linear Support Vector Machine | Regularization parameterC: 1, L1 loss, maximum number of iterations: , the tolerance stopping criteria: . |
| Nu Support Vector Machine | Kernel: Radial Basis Function, upper bound on the fraction of training errors and a lower bound of the fraction of support vectors: 0.5, regularization parameterC: 1, : 1 / , where is the number of features, and is the variance of the training set. |
| Random Forest | Maximum number of estimators: , function measuring the quality of split: squared error, minimum number of samples required to split an internal node: 2, minimum number of samples required to be at a leaf: 1, allowing all features to be considered for the best split with unlimited number of leaf nodes, no maximum number of samples for bootstrapping. |
| Ridge | : 1, tolerance stopping criteria: . |
| Stochastic Gradient Descent | Loss function: squared error with L2 regularization, , L1 ratio: 0.15, maximum number of passes over the training data: , the stopping criterion for loss: , data shuffling after each epoch, the initial learning rate: , the exponent for inverse scaling learning rate: 0.25, 10% of training data is the validation set for early stopping with 5 iterations with no improvement termination. |
| Support Vector Machine | Kernel: Radial Basis Function, : 1 / , where denotes the number of features, and is the variance of the training set, tolerance for stopping criterion: , regularization parameter C: 1, : , where specifies the epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance from the actual value. |
| Param. | Model | ↑ | MAPE ↓ | MSE ↓ | MAE ↓ |
|---|---|---|---|---|---|
| Linear Regression | 0.818 | 0.072 | 9.583 | 1.569 | |
| SPAD | Extreme Gradient Boosting | 0.719 | 0.092 | 14.808 | 2.784 |
| AdaBoost | 0.698 | 0.080 | 15.935 | 1.814 | |
| Linear Regression | 0.718 | 0.037 | 0.001 | 0.021 | |
| FvFm | Gradient Boosting | 0.608 | 0.037 | 0.001 | 0.017 |
| AdaBoost | 0.600 | 0.037 | 0.001 | 0.016 | |
| Linear Regression | 0.667 | 0.532 | 0.169 | 0.280 | |
| PI | Extra Trees | 0.379 | 1.251 | 0.315 | 0.368 |
| Random Forest | 0.213 | 1.594 | 0.400 | 0.470 | |
| Ridge | 0.817 | 0.014 | 2.249 | 1.207 | |
| RWC | Extreme Gradient Boosting | 0.793 | 0.014 | 2.541 | 1.021 |
| Support Vector Machine | 0.745 | 0.017 | 3.127 | 1.541 |
| Param. | ↑ | MAPE ↓ | MSE ↓ | MAE ↓ | |
|---|---|---|---|---|---|
| SPAD | 0.827 | 0.072 | 9.095 | 1.625 | |
| FvFm | 0.727 | 0.036 | 0.001 | 0.021 | |
| PI | 0.667 | 0.532 | 0.169 | 0.280 | |
| RWC | 0.859 | 0.013 | 1.731 | 0.941 |
| Parameter | Model | ↑ | MAPE ↓ | MSE ↓ | MAE ↓ |
|---|---|---|---|---|---|
| SPAD | AdaBoost | 0.698 | 0.080 | 15.935 | 1.814 |
| Decision Tree | 0.178 | 0.132 | 43.324 | 2.640 | |
| ExtraTrees | 0.649 | 0.099 | 18.494 | 2.307 | |
| Extreme Gradient Boosting | 0.719 | 0.092 | 14.808 | 2.784 | |
| Gradient Boosting | 0.639 | 0.095 | 19.025 | 2.059 | |
| Kernel Ridge | 0.132 | 0.179 | 45.768 | 4.787 | |
| Lasso | −0.091 | 0.213 | 57.509 | 6.045 | |
| Light Gradient Boosting Machine | 0.180 | 0.178 | 43.255 | 5.016 | |
| Linear Regression | 0.818 | 0.072 | 9.583 | 1.569 | |
| Linear Support Vector Machine | 0.216 | 0.131 | 41.321 | 3.242 | |
| Nu Support Vector Machine | −0.142 | 0.219 | 60.211 | 6.065 | |
| Random Forest | 0.587 | 0.123 | 21.760 | 3.029 | |
| Ridge | 0.037 | 0.202 | 50.789 | 6.153 | |
| Ridge with L2 | 0.827 | 0.072 | 9.095 | 1.625 | |
| Stochastic Gradient Descent | 0.119 | 0.187 | 46.465 | 5.794 | |
| Support Vector Machine | −0.289 | 0.231 | 67.984 | 6.831 | |
| FvFm | AdaBoost | 0.600 | 0.037 | 0.001 | 0.016 |
| Decision Tree | −0.005 | 0.055 | 0.003 | 0.020 | |
| ExtraTrees | 0.136 | 0.049 | 0.003 | 0.016 | |
| Extreme Gradient Boosting | 0.407 | 0.044 | 0.002 | 0.019 | |
| Gradient Boosting | 0.608 | 0.037 | 0.001 | 0.017 | |
| Kernel Ridge | −1.609 | 0.100 | 0.009 | 0.054 | |
| Lasso | −0.002 | 0.061 | 0.003 | 0.028 | |
| Light Gradient Boosting Machine | −0.002 | 0.061 | 0.003 | 0.028 | |
| Linear Regression | 0.718 | 0.037 | 0.001 | 0.021 | |
| Linear Support Vector Machine | 0.363 | 0.048 | 0.002 | 0.022 | |
| Nu Support Vector Machine | 0.316 | 0.047 | 0.002 | 0.022 | |
| Random Forest | 0.510 | 0.043 | 0.002 | 0.019 | |
| Ridge | 0.272 | 0.051 | 0.003 | 0.025 | |
| Ridge with L2 | 0.727 | 0.036 | 0.001 | 0.021 | |
| Stochastic Gradient Descent | −4.424 | 0.155 | 0.019 | 0.102 | |
| Support Vector Machine | −0.112 | 0.070 | 0.004 | 0.034 | |
| PI | AdaBoost | −0.067 | 1.825 | 0.542 | 0.262 |
| Decision Tree | −0.150 | 0.955 | 0.584 | 0.350 | |
| Extra Tree | 0.379 | 1.251 | 0.315 | 0.368 | |
| Extreme Gradient Boosting | 0.168 | 1.407 | 0.423 | 0.388 | |
| Gradient Boosting | 0.114 | 1.508 | 0.450 | 0.296 | |
| Kernel Ridge | −0.147 | 1.834 | 0.583 | 0.588 | |
| Lasso | −0.020 | 1.941 | 0.518 | 0.502 | |
| Light Gradient Boosting Machine | −0.010 | 1.623 | 0.513 | 0.456 | |
| Linear Regression | 0.667 | 0.532 | 0.169 | 0.280 | |
| Linear Support Vector Machine | −0.133 | 1.334 | 0.576 | 0.465 | |
| Nu Support Vector Machine | −0.010 | 1.529 | 0.513 | 0.634 | |
| Random Forest | 0.213 | 1.594 | 0.400 | 0.470 | |
| Ridge | −0.036 | 1.993 | 0.526 | 0.442 | |
| Ridge with L2 | 0.667 | 0.532 | 0.169 | 0.280 | |
| Stochastic Gradient Descent | −0.108 | 1.550 | 0.563 | 0.601 | |
| Support Vector Machine | 0.019 | 1.818 | 0.499 | 0.506 | |
| RWC | AdaBoost | 0.657 | 0.018 | 4.213 | 1.233 |
| Decision Tree | 0.432 | 0.025 | 6.977 | 1.900 | |
| Extra Tree | 0.704 | 0.018 | 3.641 | 1.090 | |
| Extreme Gradient Boosting | 0.793 | 0.014 | 2.541 | 1.021 | |
| Gradient Boosting | 0.646 | 0.020 | 4.350 | 1.250 | |
| Kernel Ridge | −4.435 | 0.074 | 66.776 | 4.045 | |
| Lasso | 0.000 | 0.036 | 12.288 | 3.549 | |
| Light Gradient Boosting Machine | 0.000 | 0.036 | 12.288 | 3.549 | |
| Linear Regression | 0.720 | 0.018 | 3.440 | 1.385 | |
| Linear Support Vector Machine | −14.497 | 0.125 | 190.396 | 7.235 | |
| Nu Support Vector Machine | 0.695 | 0.019 | 3.745 | 1.610 | |
| Random Forest | 0.709 | 0.018 | 3.581 | 1.499 | |
| Ridge | 0.817 | 0.014 | 2.249 | 1.207 | |
| Ridge with L2 | 0.859 | 0.013 | 1.731 | 0.941 | |
| Stochastic Gradient Descent | −1.491 | 0.051 | 30.598 | 3.334 | |
| Support Vector Machine | 0.745 | 0.017 | 3.127 | 1.541 |
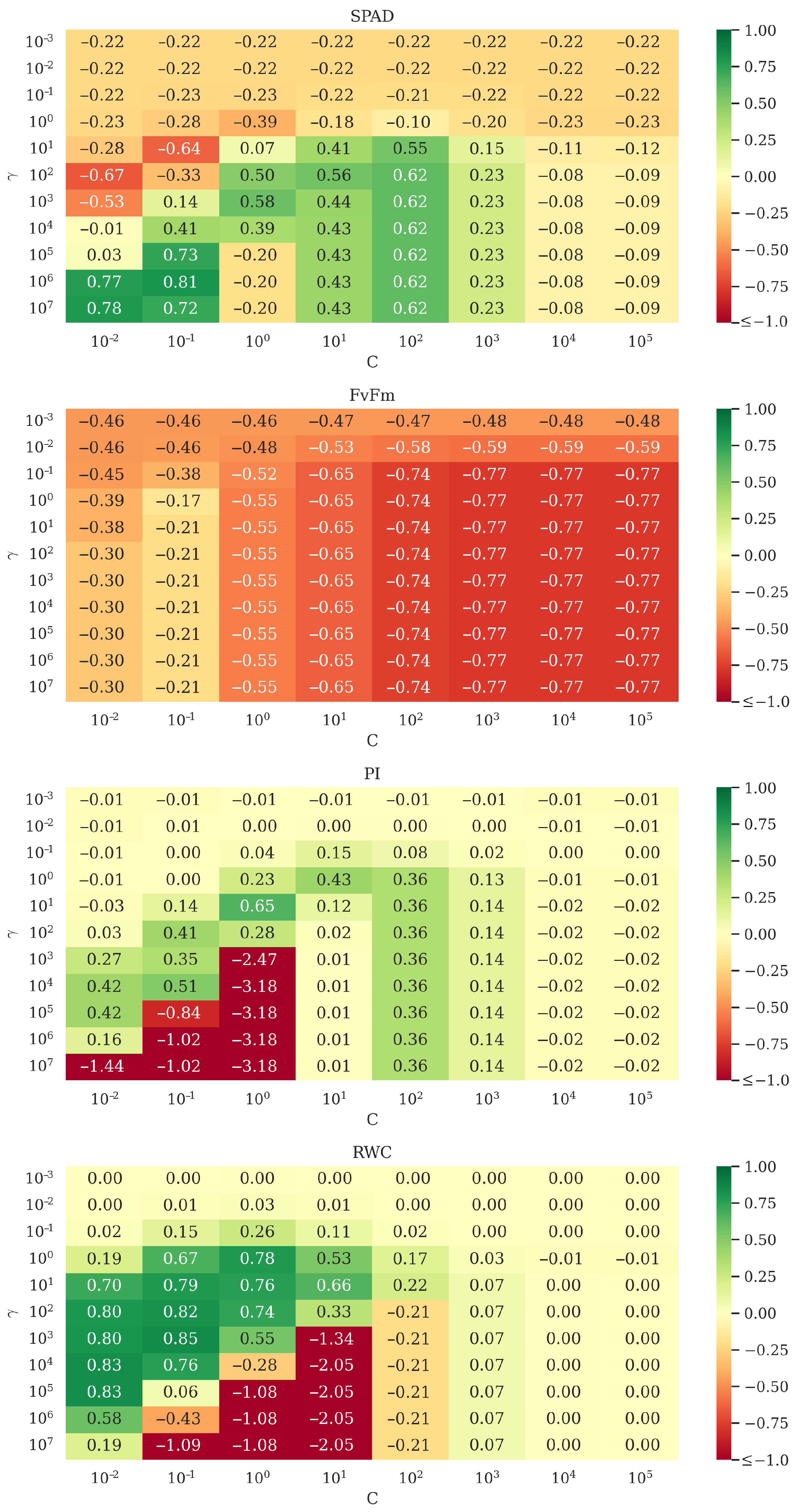
| Param. | C | ↑ | MAPE ↓ | MSE ↓ | MAE ↓ | |
|---|---|---|---|---|---|---|
| SPAD | 0.808 | 0.073 | 10.136 | 2.401 | ||
| FvFm | −0.169 | 0.076 | 0.004 | 0.052 | ||
| PI | 0.652 | 1.157 | 0.177 | 0.372 | ||
| RWC | 0.845 | 0.016 | 1.904 | 1.006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruszczak, B.; Wijata, A.M.; Nalepa, J. Unbiasing the Estimation of Chlorophyll from Hyperspectral Images: A Benchmark Dataset, Validation Procedure and Baseline Results. Remote Sens. 2022, 14, 5526. https://doi.org/10.3390/rs14215526
Ruszczak B, Wijata AM, Nalepa J. Unbiasing the Estimation of Chlorophyll from Hyperspectral Images: A Benchmark Dataset, Validation Procedure and Baseline Results. Remote Sensing. 2022; 14(21):5526. https://doi.org/10.3390/rs14215526
Chicago/Turabian StyleRuszczak, Bogdan, Agata M. Wijata, and Jakub Nalepa. 2022. "Unbiasing the Estimation of Chlorophyll from Hyperspectral Images: A Benchmark Dataset, Validation Procedure and Baseline Results" Remote Sensing 14, no. 21: 5526. https://doi.org/10.3390/rs14215526
APA StyleRuszczak, B., Wijata, A. M., & Nalepa, J. (2022). Unbiasing the Estimation of Chlorophyll from Hyperspectral Images: A Benchmark Dataset, Validation Procedure and Baseline Results. Remote Sensing, 14(21), 5526. https://doi.org/10.3390/rs14215526







