1. Introduction
Campi Flegrei is a nested caldera related to two main eruptive events, the Campanian Ignimbrite eruption (about 39 ka) and the Neapolitan Yellow tuff eruption (about 15 ka) (e.g., [
1,
2]). It is located within a densely populated volcanic region to the west of Naples (about 3 million inhabitants) and is one of the most hazardous area in the world. The last 15 ka were accompanied by several tens of eruptions (at least 60) and resurgence of the caldera center; the caldera-wide uplift has been largest in the coastal town of Pozzuoli (Pozzuoli area, P in
Figure 1). The last eruption (Monte Nuovo, MN in
Figure 1) occurred in 1538 AD, after about 3 ka of quiescence, more than 1 ka of subsidence from the Roman times, and a period of increasing seismicity and uplift from about 1400 to 1536; the eruption was followed by deflation.
Campi Flegrei caldera is renowned for its continual slow vertical movements (bradyseism) and is in intermittent unrest since the 1950s. At least three major unrest episodes occurred between 1950–1952, 1969–1972, and 1982–1984, followed by long-lasting subsidence overlapped by a few short uplift phases. Since 2005, the Campi Flegrei area is mostly rising at an accelerating rate [
4] and the uplift has raised again Pozzuoli to about its 1984 level (e.g.,
Figure 2). The Solfatara fumarolic area (SF in
Figure 1) is currently experiencing an escalation in fluid release at the surface (e.g., [
7]), as a result of massive magma degassing in the deep portion of the plumbing system (e.g., [
8]). There is no general consensus about the nature—magmatic, hydrothermal or hybrid—of Campi Flegrei unrests; in all cases, they appear to belong to an evolving sequence of long-term disturbance in the magmatic system (e.g., [
9]).
Understanding the processes that take place at Campi Flegrei is of major importance not only for the scientific knowledge of an intriguing volcanic area, but also for assessing future unrest hazard. A comprehensive view of its dynamics should take into account deformation, seismicity, gravity data, changes of geochemical indicators, crustal structures and the (at least simplified) source of each observable; obviously, inferences from different data should be consistent with each other, and possible spatial and temporal correlation between different geophysical and geochemical/petrological data would help to clarify sources of deformation, seismicity and geochemical changes.
Without demanding completeness, we mention that the physical processes that take place at Campi Flegrei are probably the result of interactions between the superficial hydrothermal system, magmatic-related source(s) at intermediate depths and deep magmatic source(s)—between the deep source and the magmatic-related intermediate one (e.g., [
10,
11]), between the magmatic-related intermediate source and the hydrothermal system (e.g., [
6,
12]), between an ∼8-km-deep source and the hydrothermal system (e.g., [
13,
14]), between an even deeper source, the ∼8-km-deep one, and the hydrothermal system (e.g., [
8,
14]). All aspects have been abundantly studied and the literature on Campi Flegrei is immense, mainly as regards the dynamics after 1980; thus, only what is needed to contextualize the deformation data analyses in this work and our results is outlined here.
As for the major 1982–1984 unrest, deformation data from leveling and geodetic precise-traversing surveys (electronic distance and angular measurements) are satisfied by inflation of a horizontal sill (PTE in
Figure 1), centered offshore Pozzuoli at about 3–4 km depth [
5,
10]. Although it is obviously a simplification, 1980–2013 geodetic data—including continuous Global Positioning System (GPS) data and Synthetic Aperture Radar (SAR) images—indicate that the deformation history during the whole period is mostly satisfied by two simple paired deformation sources for both inflation and deflation phases [
5,
15]. Large-scale deformation can be explained almost completely by inflation/deflation of the PTE, whose location is consistent with the 3–4 km deep coda-wave high-attenuation patch detected under Pozzuoli [
16]. The PTE can be fed by magma and/or magmatic fluids from the partially molten zone detected beneath the caldera at depth larger than 7.5 km (e.g., [
17,
18]). Almost all the residual deformation is confined to the area of the Solfatara fumarolic field—not covered by leveling surveys before 1983—and can be explained by a local source (PS in
Figure 1). The PS can be thought in terms of hydrothermally driven poroelastic deformation [
19] near the injection point of hot magmatic fluids into the hydrothermal system.
As for the major 1983–1984 unrest, seismic analyses have enlightened [
6]: (i) The seismicity related to the paired deformation sources in [
5]; (ii) The seismic evidence of repeated daily fluid injections modeled by [
12] (RFI in
Figure 1); (iii) The connection of the 3–4 km deep high-attenuation reservoir under Pozzuoli with the fumaroles at Mofete and Monte Nuovo (M and MN in
Figure 1, PMC indicates where the spatial 1983–1984 seismic pattern turns from E-W to NW-SE); (iv) The release of fluids which reached Solfatara from the the 3–4 km deep reservoir; (v) The stress release that halted the seismic unrest. Until now, there is no evidence of deformation anomalies in the areas where the repeated fluid injections and the opening of the Pozzuoli-Monte Nuovo pathway were envisaged; furthermore—and much more important—there is no deformation evidence of the deep source activity.
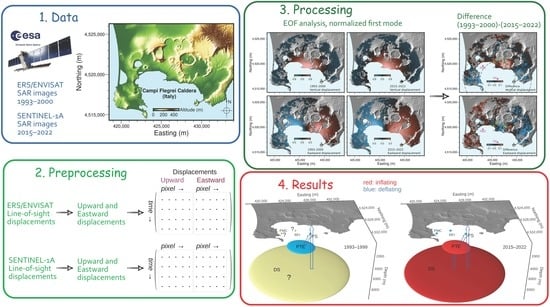
In this work, we show that long-lasting (years) faint deformation signatures of various complex processes—related to the dynamics of the different portions of the plumbing system, from the hydrothermal system to the deeper source—can be revealed by proper analyses of deformation data. Of most importance is the detection of the arrival of fresh, mafic hot magma from the mantle, inflating the deeper source. We use ground displacement time series obtained from ERS-ENVISAT ([
20]) and Sentinel-1A ([
21]) SAR images, spanning 1993–2000 and 2015–2022, respectively. We apply the empirical orthogonal function analysis to SAR data inside the circular region bounded by the black dashed circle in
Figure 1. Our analyses: confirm that most of the deformation is related to the activity of a sill-like source at 3–4 km depth; confirm the deformation anomaly (excess of subsidence) at Solfatara during 1993–2000; indicate that the Solfatara area is uplifting at a lower rate than the surroundings since 2015; identify persistent deformation features close to RFI and PMC; and, most importantly, give evidence of deep inflation at least since 2015.
2. Materials and Methods
2.1. SAR Data and Analysis
We use ground displacement time series obtained from ERS-ENVISAT ([
20]) and Sentinel-1A ([
21]) SAR images. We refer displacements to the median value inside a circular area, 500 m in radius, centered on LR (
Figure 1).
As for ERS-ENVISAT data, we use a subset of the line-of-sight (LOS) displacement time series in [
5], obtained through the Small BAseline Subset Differential Synthetic Aperture Radar Interferometry (SBAS DInSAR) technique ([
22]). The time series include 138 ascending-orbit images from 1993.03 to 2010.73 and 155 descending-orbit images from 1992.44 to 2010.71 (
Figure 3a). The angle between the LOS direction and the vertical (i.e., the incidence angle) in the study area is about 23
for the ascending orbit and 21
for the descending orbit. The temporal interferometric coherence of the time series is larger than 0.55 for the ascending orbit and 0.5 for the descending orbit. To decrease the amount of data and noise, we spatially filter and decimate each map of the LOS time series by computing a median value for every non-empty block in a regular (150 m × 150 m) grid.
Figure 3b,d show the mean LOS displacement rate during 1993–1999, i.e., before the onset of the 2000 mini-uplift (see
Figure 2a).
As for Sentinel-1A data, we use Level-1 Single Look Complex (SLC) Sentinel-1A interferometric wide swath imagery [
23], provided by the European Space Agency (ESA) and downloaded from the Alaska Satellite Facility [
24]. SLC products consist of focused SAR data, that are geo-referenced using orbit and attitude data from the satellite and provided in slant-range geometry. The time series include 193 ascending-orbit images from 2014.84 to 2022.22 and 192 descending-orbit images from 2015.26 to 2022.19 (
Figure 3a). The incidence angle in the study area is about 35.6
for the ascending orbit and 35
for the descending orbit. We created times series of ascending-orbit and descending-orbit images using SBAS within GMTSAR InSAR processing system, version 11 July 2022 ([
25]), through the Sentinel TOPS-mode processing and interferometry procedure. Main steps to make LOS time series are: image alignment and registration, enhanced spectral diversity, elevation antenna pattern correction, interferogram processing, and SBAS, after selecting image couples having temporal baseline shorter than 90 days and spatial baseline smaller than 50 m. We also mask out low coherence areas (e.g., wet and densely vegetated areas) and discard image couples whose mean interferometric correlation is smaller than 0.35 out of the masked areas. At last, we spatially filter and decimate each map of the LOS time series by computing a median value for every non-empty block in a regular (150 m × 150 m) grid. The resulting gridded time series are validated against continuous GPS data [
4] acquired at several stations located in the Neapolitan Volcanic Area. As digital elevation model (DEM) we use TINITALY/01 (10 m-cell size grid [
3]).
Figure 3c,e show the mean LOS displacement rate during 2015–2022. We have also carried out some tests including correction for radar phase delays due to atmospheric propagation [
26]; however, differences with uncorrected time series are so small that we do not further consider the displacement time series obtained including the atmospheric correction.
LOS displacements from ascending and descending orbits are combined as follows to obtain vertical and eastward displacements. First, we select ascending- and descending-orbit SAR acquisitions whose lag is shorter than 1 week (ERS-ENVISAT) or 1 day (Sentinel-1A) and generate a set of LOS–displacement map couples (times given in
Figure 4a). Then, we combine gridded ascending and descending LOS displacements for each map couple, neglecting the small northward LOS components.
Figure 4b–e show the mean upward and eastward displacement rates.
Figure 5 compares Sentinel-1A vertical and eastward displacements with GPS displacements for the stations located inside the circular region bounded by the black dashed circle in
Figure 1.
2.2. EOF Analysis
We apply the empirical orthogonal function (EOF) analysis to the SAR displacement time series inside the circular region bounded by the black dashed circle in
Figure 1. EOF analysis decomposes a space-time field into spatial patterns and associated temporal evolutions, and is commonly used to detect spatial and temporal changes in climatic modes ([
27]). This technique is also known as principal component analysis (PCA) and was applied to Campi Flegrei for denoising SAR data in [
28].
For a time series of displacement maps each of pixels, data can be arranged in a matrix (spatial organization) or matrix (temporal organization). In this work we organize data spatially—putting together vertical and eastward displacements in a single data matrix—because we search for uncorrelated spatial patterns of vertical and eastward displacements which share the same temporal evolutions.
We separately subtract the mean value to the upward and eastward displacement in each corresponding row of the original data matrix so as to have zero mean “relative” (with respect to the mean) upward and eastward displacement vectors at each time, and obtain a new data matrix . Data could be also normalized by dividing each column of by its standard deviation; doing so, pixels are considered equally important, and as a result, the spatial patterns will try to describe the overall variation of the deformation field. If data are not normalized, spatial patterns will try to optimize the variation of the deformation field in the regions of highest standard deviation; spatial patterns from non-normalized data are usually of simpler physical interpretation and we decide to avoid normalization.
We factorize into three matrices by singular value decomposition using svd() function in Octave programming tool, thus , where and are orthonormal, i.e., and , contains the singular values and is diagonal, i.e., all entries whose column number is different from the row number are zero, and is the identity matrix; superscript T denotes transpose. Squared singular values are also the eigenvalues of the covariance matrix .
Since data are spatially organized, , and are , and matrices, respectively. Columns of give uncorrelated spatial patterns, and columns of give related temporal evolutions; each column of and represents a mode. The displacement at pixel j and time related to mode m is given by ; thus, if then the displacement at pixel j follows the same temporal evolution as the mode, while if then the displacement at pixel j follows an opposite temporal evolution.
EOFs, i.e., the columns of , are given in descending order of the singular values, which means in descending order of importance. Generally speaking, the mathematical properties of the EOFs imply that each component may not have individual—dynamical, kinematic, statistical—meaning independent of other EOF modes; however, careful inspection of spatial patterns, temporal evolutions and singular values may allow to discern possible mode contamination. We separately apply the EOF analysis to the displacement ERS-ENVISAT time series from 1993 to end 2000 and to the Sentinel-1A ones from 2015 to 2022, focusing on the first mode.
2.3. Modeling
As outlined in
Section 1, different processes may cause deformation at Campi Flegrei. Accurate realistic modeling of those processes and induced deformation is practically impossible because of the complexities of the processes and the medium; however, seismic tomography (e.g., [
17]) shows that a layered model is a first-order effective approximation of the real rock heterogeneities beneath Campi Flegrei. Rock heterogeneity affects superficial deformation even for layered media; the presence of soft superficial layers above a source causes it to appear shallower (“focusing effect”, e.g., [
10,
29]) and amplifies horizontal-to-vertical displacement ratio [
30]. Thus, we decided to use simple models of the deformation sources and the medium, and look for deformation evidences of previously suggested processes acting at Campi Flegrei.
Tested sources are embedded in an elastic homogeneous isotropic flat half-space; Poisson ratio is 0.25. As for the deformation sources, since most of the deformation is due to a quasi-circular horizontal sill—the PTE in [
5]—and, to a minor extent, to a source which is approximately equivalent to a pressurized vertical oblate spheroid—the PS in [
5]—we only consider pressurized circular horizontal sills and vertical (prolate or oblate) spheroids as effective—i.e., giving deformation patterns similar to the real ones—deformation sources. Deformation from circular horizontal sills is computed as in [
31] by using the Matlab code available in dMODELS collection [
32]. As for prolate or oblate spheroids, we use the approach in [
33]. We schematize the PTE and the deep reservoir (DS) as circular horizontal sills, the PS as oblate spheroid and the RFI and PMC as vertical spheroids. To account—at least approximately—for the effects of rock layering on the horizontal-to-vertical displacement ratio, we multiply horizontal displacements by 1.5 or 1.3 if the deformation source is deeper or shallower than 3 km, respectively [
30].
2.4. Differences between Subsidence and Uplift Spatial Patterns
To see if the deformation sources during subsidence (1993–2000) are the same as during uplift (2015–2022) and reveal possible differences, we compare the deformation spatial pattern obtained from ERS/ENVISAT data with that from Sentinel-1A data. Comparison is carried out as follows.
We prepare two separate
data matrices, each consisting of upward and eastward relative displacements (i.e., pixel-wise mean is null at each time,
Section 2.2) inside the circular region bounded by the dashed black circle in
Figure 1, from ERS/ENVISAT and Sentinel-1A data, respectively.
We apply the EOF analysis to each data matrix.
We retain only EOFs related to the first mode, which captures the main deformation during both investigated periods (
Figure 6c,d) and is the sole mode clearly related to long-lasting (years) processes (
Figure 6a,b). Positive EOF elements indicate downward or westward relative displacement during 1993–2000 and upward or eastward relative displacement during 2015–2022, because related temporal evolutions represent subsidence and uplift, respectively (
Figure 6a,b); the opposite holds for negative values.
From the first mode EOFs we generate four datasets: (i) 1993–2000 vertical relative displacements (), (ii) 1993–2000 eastward relative displacements (), (iii) 2015–2022 vertical relative displacements (), (iv) 2015–2022 eastward relative displacements (), where v stands for “vertical”, e stands for “eastward”, is the number of pixels common to the gridded ERS/ENVISAT and Sentinel-1A time series, subscript 1 is for 1993–2000, and subscript 2 is for 2015–2022.
We compute vertical () and eastward () displacements from the PTE (), DS (), PS (), RFI () and PMC () on the pixels common to the gridded ERS/ENVISAT and Sentinel-1A time series, for unit source volume change (i.e., potency).
We assume that the first mode EOF coefficient for pixel
j (
) is approximately given by a linear combination of the effects of the PTE, DS, PS, RFI and PMC:
where
and
are multiplication factors for the
k-th source;
,
,
and
make
, consistently with the pixel-wise zero-mean displacements in the data matrices.
To compare the 1993–2000 and 2015–2022 deformation patterns, we normalize EOFs by computing
,
,
, and
, where
and
are the range of variability (difference between the maximum and minimum values) of
and
,
, respectively:
From Equation (
2) we obtain:
Subtracting the normalized EOF related to 2015–2022 from the normalized EOF related to 1993–2000 (left sides of Equation (
3)) cancels out or at least reduces the effects of deformation sources which contributed similarly to the normalized EOFs during the two time periods, and enhances the effects of deformation sources that contributed differently (in intensity and/or polarity). Because of the EOF normalization, left sides of Equation (
3) are not affected by the largely different amplitudes of the subsidence and uplift (
Figure 2). The left and right sides of Equation (
3) act as “observations” and “computations”, respectively; thus, their differences act as “model residuals”.
For simplicity, we fix the geographic position of the PTE, PS, RFI and PMC centers relying on previous works [
5,
6]. We carry out a least squares minimization of the model residuals by choosing the other sources parameters (i.e., the depth of the PTE, PS, RFI and PMC, the 3D position of the DS center, the PTE and DS radius, and the PS, RFI and PMC aspect ratios) through trial and error; namely, for each tested source parameter set we compute
and
and perform a linear optimization of
,
, and
.
is the difference between the normalized vertical displacements caused to pixel
j by source
k during 1993–2000 and 2015–2022; analogously,
is the difference between the normalized eastward displacements caused to pixel
j by source
k during 1993–2000 and 2015–2022.
2.5. Source Volume Changes during Subsidence and Uplift Periods
We start from Equation (
2) to see whether the same five sources satisfy each of the 1993–2000 and 2015–2022 deformation patterns as approximated by the first EOFs and estimate source volume changes. First, we compute
and
for unit potency using the source parameters obtained after analyzing the difference between the subsidence and uplift spatial patterns (
Section 2.4). Second, parameters
,
,
,
,
and
are optimized by least squares minimization. Third, we compute the range of variability (difference of the maximum and minimum values) of the pixel-wise mean displacement rate during the subsidence and uplift periods (
and
, respectively). Quantities
give estimates of the volume change rates for the
k-th source.
4. Discussion
Ground deformation is a powerful source of information for studying the activity of magmatic sources and hydrothermal systems, even when difficult to detect otherwise. As this work also demonstrates, Campi Flegrei is an excellent example to illustrate the potential of deformation data. However, it is well known that the “true values” of the deformation at a given area cannot be actually measured, and that each geodetic technique has its own detection threshold. Generally speaking, accuracy of data from permanent GNSS stations and geodetic leveling surveys are better than from SAR imagery (e.g., [
35]). GNSS systems provide 3-dimensional displacements while SAR measures ground deformation in the LOS direction; however, GNSS measurements are affected by spatial aliasing and possible very local environmental noise—e.g., soil compaction—which can result in differences among time series recorded at different stations that are merely related to artifacts. GNSS data drawbacks are partially overcome by SAR measurements, considering their wide areal coverage—GNSS stations are absent in many potentially interesting locations—and geometric resolution. The opportunity of jointly consider each pixel value and that of the neighboring pixels—e.g., averaging over small areas—allows to provide a more reliable identification even of local deformation. Geodetic leveling measurements were (and are) occasionally carried out along leveling lines and observe 1-dimensional—namely, vertical—deformation only; past and present frequency of the surveys allows comparisons with other kind of geodetic data, but only for enough slow or long-lasting processes (e.g., the 1982–1984 unrest).
Differently from previous studies, which have mainly focused on interpreting the unrests and/or particular—even long—time periods related to uplift and/or subsidence, we compare the Campi Flegrei deformation fields during different periods with each other to discern similarities or differences in the deformation pattern and changes over time. We aim to highlight possible anomalies in particular areas and their time history, which could be diagnostic of local and/or large-scale unrevealed processes. For this purpose, we apply the EOF analysis to ground displacement data obtained from ERS-ENVISAT and Sentinel-1A SAR images to investigate the 1993–2000 subsidence—including the 2000 mini-uplift—and part (2015–2022) of the present unrest (
Figure 2), and decompose the space-time fields into uncorrelated spatial patterns and associated time patterns.
After identifying the main differences in the deformation field between the two periods (
Figure 7), we test if they can be linked to known or still unknown processes. Although reality is probably much more complex and we have considered very simple models for the deformation sources (sills and spheroids) and the medium (isotropic homogeneous elastic half–space, with an approximate correction for the rock layering effects), the agreement between computations and observations is very good and our results confirm or evidence some important features of the Campi Flegrei caldera system.
More specifically, we substantiate the persistence of an offshore deformation source (PTE) at 3–4 km depth ([
5,
10,
15,
34]) intruded by degassing magma and/or magmatic fluids. Further, persistent deformation features are caused by a paired local hydrothermal deformation source (PS) located beneath Solfatara ([
5,
15]), where a similar rate of local subsidence with respect to the surrounding area is observed during both subsidence and uplift of the caldera at least as regards the caldera dynamics accounted for by the first mode. This demonstrates that the related deformation anomaly is not a mere local distortion of the large-scale deformation field. Confirmation of the existence of the PTE and PS comes also from seismic data (e.g., [
16] for the 1982–1984 unrest); moreover, the two paired large-scale and local deformation sources are compatible with many previous studies (e.g., [
11,
12]). If the PS contribution to the overall deformation field is not taken into account and deformation data are inverted to derive the features of a single source, the inferred source of the 1993–2000 inflation would be ENE–WSW oriented instead of NW to SE, as our PTE is. Moreover, depending on the time-varying activity of the PS and thus of its contribution to the overall deformation field, features of the large-scale source would seem to change over time. The peculiar behavior of the PS may be related to degassing from fluid pockets (e.g., [
6]) and a conduit-like path—recognized by seismic and audio-magneto-telluric measurements—which is a permeable zone allowing fluid discharge from the hottest and deepest portions of the system, behaving as a valve and allowing the temporary depressurization of the source region (e.g., [
36]).
During 2015–2022, deformation anomalies are clearly detected at RFI, where repeated fluid injections occurred at least in September–October 1983 [
6,
12], and PMC, where the spatial 1983–1984 seismic pattern (connecting the 3–4 km deep reservoir to the fumaroles at Mofete/Monte Nuovo) turns from E-W to NW-SE [
6]. Those anomalies are probably more linked to a peculiar response of fluid-rich fractured rock to the uplift-generated stress, resulting in a local “uplift deficiency”, than to real deflation.
Figure 12 summarizes the behavior of the PTE, DS, PS, RFI and PMC during 1993–1999 and 2015–2022.
Differences between the normalized EOFs and the computed cumulated contributions of the tested sources (PTE, DS, PS, RFI and PMC) are probably ascribable in large part to the simple assumptions of the modeling, which is based on circular sills and oblate spheroids embedded in a homogeneous isotropic elastic half-space, with some correction to the computed horizontal-to-vertical displacement ratio so to roughly account at least for rock layering. However, those differences are very similar for the 1993–2000 subsidence and 2015–2022 uplift (
Figure 10c,d and
Figure 11c,d), thus suggesting persistent local distortion of the deformation field.
The most intriguing result is certainly the evidence of the inflation of a deep (>7 km) reservoir (DS) since 2015. Until now, some indication of the activity of the deep source—identified by seismic data [
17]—had been obtained from the geochemical composition of the fumaroles, but no direct evidence of its dynamics has been provided. Two opposite-polarity sources, about 3000 m and 8000 m deep, respectively, were obtained by [
28] from SAR images related to 1993–1999 (subsidence) and 2007–2013 (uplift), after inverting the sole vertical displacements for two Mogi pressure sources embedded in a homogeneous half-space. However, as pointed out e.g., by [
37], fitting a Mogi pressure source to uplift data only may yield estimates of the source parameters that are not reliable. Reliability of the source parameters is also affected by the use of a homogeneous half-space without any correction for the presence of layered rock heterogeneity, particularly important at Campi Flegrei [
30]. We demonstrate that inflation of the deep source is necessary to justify the differences between the 1993–2000 and 2015–2022 deformation fields, and is currently contributing to about 20% of the caldera deformation (
Figure 11g,h). As shown in [
34], the contribution of a deformation source at about 8 km depth is also necessary to satisfy vertical displacement data during the period (1400–1536) of increasing seismicity and uplift which preceded the Monte Nuovo eruption.
The activity of the deep source is worrying also given the current elevation of Pozzuoli, which can be considered the point of maximum elevation of the caldera and has returned to the levels of 1984. It becomes even more troubling when considering suggestions by [
9] to distinguish between pre-eruptive and non-eruptive unrests: according to [
9], successive unrests have promoted the accumulation of stress in the crust, the continuation of the current uplift could lead to a notable increase in seismicity, and there is a greater potential for eruption than during previous unrests.
5. Conclusions
We analyze ground displacement from ERS-ENVISAT and Sentinel-1A SAR images to investigate the 1993–2000 subsidence—including the 2000 uplift—and part (2015–2022) of the present unrest at Campi Flegrei caldera, Italy. Space-time fields are decomposed into uncorrelated spatial patterns and associated temporal evolutions by applying the empirical orthogonal function analysis to the displacement time series. We find that the first EOF is able to capture most of the long-lasting deformation history, while the other modes do not seem to bring clear information, as also suggested by the singular values.
Our main results:
Confirm that most of the deformation is related to the activity of a 3–4 km deep sill-like source (the PTE), which is inflated by magma and/or magmatic fluids during periods of unrest and deflates during periods of subsidence;
Evidence ongoing deformation linked to local fluid migration in the Solfatara area (the PS);
Identify persistent deformation features where peculiar fluid migration processes occurred during the 1982–1984 unrest (the RFI and PMC);
Evidence inflation of the ∼8 km deep reservoir (the DS) at least since 2015.
The last result is particular important and worrisome. Whatever is really happening, the deep source should be carefully monitored from now on, because magma of the next eruption will come from there.
Future work will be devoted to analyze EOF modes other than the first, link the persistent distortions of the deformation field to geological features of the caldera and/or non-modeled source complexity and, mainly, analyze deformation in a larger area, so to improve on detection of the deep source activity and investigate possible interconnected processes in the Neapolitan volcanic area.