Abstract
Accurate accounting of spatiotemporal variability of precipitation is essential for understanding the changing climate. Among the available precipitation estimates, the Global Precipitation Measurement (GPM) is an international satellite network providing advanced global precipitation estimates. The integrated multi-satellite retrievals for GPM (IMERG) algorithm combines information from the GPM satellite constellation to estimate precipitation and yields a better performance in detecting precipitation events and spatial resolution. Here, we used twenty years (2001–2020) of IMERG Final data over the entire Nepal to analyze the spatial and temporal distribution of precipitation. This study evaluates the dynamic characteristics of the precipitation amounts, intensities, frequencies, and other relevant data across Nepal, using four IMERG datasets: (i) microwave only, (ii) infrared only, (iii) multi satellites gauge uncalibrated, and (iv) multi satellites gauge calibrated. A total of 28 precipitation indices was computed: threshold-based counts, consecutive days, precipitation amounts and extremes, precipitation intensity, percentile-based extremities, proportion-based indices, and additional seasonal indices. Results show that all four IMERG datasets are promising in capturing spatial details. The frequency of wet days corresponds with ground-based precipitation. Still, most indices, including consecutive wet days, annual and monsoon precipitation, and days when precipitation equaled or exceeded 20 and 50 mm, were substantially underestimated. In addition, the microwave-only dataset highly underestimated the precipitation amount. Notably, a substantial proportion of false alarms is a problem for all four IMERG datasets. Moreover, our results demonstrate that the IMERG uncalibrated dataset tends to overestimate precipitation during heavy precipitation events. These advantages and shortcomings of IMERG datasets over the rugged terrain of Nepal can provide useful feedback for sensor and algorithm developers to overcome limitations and improve retrieval algorithms. The study findings are helpful to the broader data users and practitioners for effective water decision applications.
1. Introduction
Precipitation is the most crucial parameter for any hydrological/water modeling and water resources planning and management [1,2]. Precipitation is a vertical flux that modulates local/regional/global climate, atmospheric circulation, water/energy cycles, and runoff propagation [3,4]. To understand the complex hydrologic processes, several water models are employed, including hydrometeorological, hydrodynamic, and climate models. These models range from spatially lumped to fully distributed or/and conceptual to physically-based [5]. However, uncertainty in modeling exists as the accuracy of precipitation variability impacts the accuracy of the runoff volume estimates, peak flows, and the nature of hydrographs [6,7]. In addition, climate change and climate variability under a warming climate indicated a rise in the moisture-holding capacity of the atmosphere by ∼7% per degree of warming, indicating a higher chance of heavier precipitation [8,9,10]. Such extreme precipitation events would increase the risk of flash floods and landslides, threatening socioeconomic infrastructures [11,12,13,14]. Therefore, accurate accounting of the spatiotemporal precipitation variability is the starting point for filling the “real holes” in understanding the precipitation’s nexus with coherent and recurrent climatic [15,16,17].
Various methods of precipitation measurements are prevalent, including ground-based precipitation (GP) stations, weather radars, and satellite-based precipitation estimates (SPEs). GP observation is the most traditional and accurate method of precipitation measurement [18]. However, it is a challenging task to capture the spatiotemporal dynamics for larger regions, especially the estimation of the extreme across remote locations, which becomes worse with instrumental and measurement error [19,20] and decreasing number of GP stations across the world with the lack of a budget for effective operation, maintenance [21,22,23]. Complementary to GP observations, space-borne sensors and satellite-based retrieval algorithms provide great spatiotemporal details with global coverage, establishing them as a robust complement for water system modeling globally, especially in data-scarce regions [24,25]. Reanalysis products such as ERA-Interim Reanalysis of European Centre for Medium-Range Weather Forecasts (ECMWF), Japanese 55-year Reanalysis (JRA-55), National Centers for Environmental Prediction/National Center for Atmospheric Research Reanalysis-1 (NCEP/NCAR-1), and High Asia Refined analysis (HAR) [26] are based on in-situ data, numerical models or/and SPEs.
Precipitation estimates using multiple SPEs provide greater confidence in accuracy and consistency in precipitation magnitude and detection [27]. Multi SPEs based datasets include Multi-Source Weighted-Ensemble Precipitation (MSWEP) [28], Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA) [29], the Precipitation Estimation from Remotely Sensed Imagery Using Artificial Neural Networks (PERSIANN) [30], IR-based PERSIANN [31], PERSIANN-Cloud Classification System (CCS) [32], Climate Prediction Center morphing technique (CMORPH) [33], Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) [34], NRL-Blend satellite rainfall estimates [35,36] from the Naval Research Laboratory (NRL), GsMap [37,38], and AIMERG: IMERG calibrated using APHRODITE [39], and many others. In particular, TMPA has been accepted to capture intense tropical cyclone rainfall and correlate with GP observations [40,41]. Along with extreme precipitation events, TMPA has been successful on various terrain, including most low-latitude areas and large-medium scales, and has been applied for hydrological modeling, soil moisture prediction, fire detection, and agriculture [42,43]. However, the performance of the TMPA is prejudiced by several factors, such as spatial–temporal scales, regions, and seasons [44]. As an illustration, the underperformance of the TMPA has been reported in rugged and high-elevation areas [45,46,47]. Gao et al. [46] compared the individual performance of several SPEs, including TMPA, against GP observations in the Tibetan Plateau and explored that these products tended to overestimate light rainfall and underestimate moderate and heavy rainfall. Moreover, the performance was better in humid regions than in arid regions [48]. A similar overestimation in seasonal performance was reported in Saudi Arabia and Bangladesh [49,50]. As a progressive step, IMERG was launched in February 2014 [29].
The IMERG product has been evaluated and applied in the majority of fields due to high spatial (0.1° × 0.1°, compared to 0.25° × 0.25° of TMPA) and temporal (30 min) resolution, global coverage, open access, and relative short latency by combining the passive MW sensors from low Earth orbit satellites and geosynchronous Earth orbit IR sensors [51,52]. Several previous studies have evaluated the performance of new-era IMERG products on global aspects by considering the effect of topography, landscape, and seasonal characteristics. Studies have reported good performance agreement with the gauge and ground-based radar data [16,43,53,54,55]. Moreover, a few studies in the Asian region demonstrate a wide range of diversity in climate patterns and fluctuating topography [53,56,57]. In a nutshell, notable findings of these studies are (i) IMERG attained substantial improvement in capturing spatiotemporal precipitation variability and very light to light rainfall events along with low bias and improved correlation coefficient with GP stations across the climatic and geographic conditions, and (ii) IMERG demonstrates better improvement and yields better results of false alarm ratio (FAR), probability of detection (POD), and critical success index (CSI).
IMERG provides three products: IMERG early run (ER), IMERG late run (LR), and IMERG final run (FR). Various comparative assessments of these products have been conducted, e.g., central Himalayan country Nepal [58], a temperate broad-leaved forest climate in Austria [59], the subtropical monsoon climate in Pearl River Basin of China [60], the tropical desert climate in Saudi Arabia [56], southwest Pacific region [61], and the temperate monsoon climate in Huaihe River Basin of China [62]. Talchabhadel et al. [58] evaluated the performance of IMERG’s three runs (ER, LR, and FR) over Nepal with reference to 231 GP stations, and they reported IMERG FR to be slightly better than the other two. Tapiador et al. [63] compared all IMERG products over Spain at multiple temporal scales using a high-resolution gridded precipitation product derived from ~2300 rain gauges. Huang et al. [64] conducted a comparative study of the IMERG ER and IMERG FR over the extreme precipitation of typhoons in China. They demonstrated a good correlation on spatiotemporal between IMERG data and GP observations. Likewise, Li et al. [65] concluded that IMERG captures precipitation during hurricane (tropical cyclone) events and storm cores reasonably well. In addition, the above comparative studies have reported that FR is generally verified to have high accuracy and reasonable practicability on a monthly scale in comparison to ER and LR based on the study conducted in China [53,66], East Asia [67], Austria (temperate climate) [68], Saudi Arabia [69], Pakistan [70], and Italy [71]. However, few studies have contradicted this superiority of FR as studies have reported either no significant improvement of FR run or even outperformance by ER, at least in some aspect (i.e., POD, correlation, extreme events) [72,73].
Challenges exist for precipitation retrieval algorithms to detect very light/heavy precipitation events, precipitation over rugged topography, and differentiate rain from snow. So, evaluation results are regional and climate specific; it is always recommended to carry out such evaluation tasks over distinct geographical regions [74]. In the process, few past studies using ER data have been conducted; for instance, Derin et al. [75] noticed the better performance of IMERG-V05B to capture the light and heavy precipitation amount compared to IMERG-V06B for the evaluated regions, though they have used ten stations. Sunilkumar et al. [74] found a good agreement between IMERG and APH_V18 (as a reference) over the Nepal Himalayas. However, Sharma et al. [47] explored the ability of IMERG FR of V06 to capture the drought event frequency in the Nepal Himalayas. In addition, most evaluations of SPEs on the topography of Nepal are based on previous-generation satellite products, i.e., the TRMM era. Managing water resources is the utmost and most challenging task in the climatic change-prone and topographic variant region [57,76,77].
The above-mentioned counterintuitive behavior of IMERG at geography and lack of comprehensive evaluation motivates us to compare the four datasets: (i) MW only, (ii) IR only, (iii) multi satellites but gauge uncalibrated, and (iv) multi satellites gauge calibrated. We have computed 28 precipitation indices, including threshold-based counts, consecutive days, precipitation amounts and extremes, precipitation intensity, percentile-based extremities, and proportion-based indices. These precipitation indices help understand the dynamic characteristics of precipitation amount, intensity, wet days, and other relevant information. The study findings are the first ones, per our knowledge, to serve as feedback to the end-users and algorithm developers in understanding the performance of each product with potential improvement, if needed.
2. Study Area, Data, and Methodology
2.1. Study Area
Nepal is a landlocked country located in the central part of the Himalayan region, bounded by China in the North and India in the remaining direction (Figure 1). An abrupt change in elevation gradient (e.g., less than 100 to over 8000 m masl, including Mount Sagarmatha: the world’s highest peak of 8848.86 masl) is observed in the relatively smaller proportion of extent in latitude [78,79]. A typical north-to-south (N-S) cross-section consists of the high Himalayas in the North, a series of mountains and hills, including river valleys, and low-elevated hills and flat lands in the south [78,79]. A number of microclimates [80] and climate classes [81] exist across the country ranging from tropical to polar, because of diverse topography, altitudinal contrasts, orographic effects, and climatic systems.
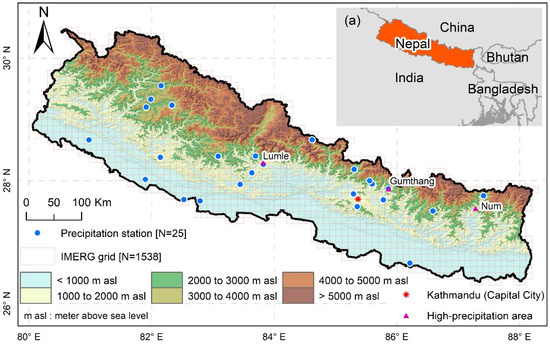
Figure 1.
Map of Nepal superimposed with the network of selected ground-based precipitation stations [N = 25] and IMERG grids [N = 1538]. The background is the elevation. Three high-precipitation areas are shown in a triangle, i.e., Lumle, Gumthang, and Num. (a) The inset at the top right shows the neighboring countries of Nepal.
The summer monsoon (southeast to northwest) is the main large-scale wind circulation modulating the spatial feature of rainfall (Shrestha, 2000). However, due to topographical features, orographic effects, sharp altitudinal variation along short latitudinal distances, and local wind circulation, the spatial characteristics of precipitation vary a lot. In addition, the western disturbance (northwest to southeast) dominates during the winter season [80]. As a result, westerly derived precipitation is greater in the high northwest mountains in the form of rain and snow [82]. The influence of two large systems (summer monsoon and westerly-derived winter precipitation) is not evenly distributed across the country. Generally, about 80% of the country’s precipitation occurs during the summer monsoon [80,82]. In particular, July and August contribute to almost half of annual precipitation [83]. Based on precipitation and other meteorological characteristics throughout the country, there are four broad seasons: (1) pre-monsoon (March–May), (2) monsoon (June–September), (3) post-monsoon (October–November), and (4) winter (December–February). The monsoon is the most important season for agriculture, and the post-monsoon is the harvesting season of main crops. Although low temperatures limit plant/crop growth during winter, cultivations are equally feasible in mid-hills and lowlands [83].
2.2. Data
2.2.1. IMERG Datasets
IMERG (0.1° × 0.1° lat/lon) merges, inter-calibrates, and interpolates MW precipitation estimates from GPM constellation, MW-calibrated IR, SPEs, Global Precipitation Climatology Centre (GPCC) monthly gauge analyses [16]. IMERG provides three sets of precipitation estimates: the IMERG-ER, IMERG-LR, and IMERG-FR. In this study, we analyze IMERG-FR (from now on IMERG). These products have four precipitation estimates based on different data sources and methodologies: IMERG_Cal, IMERG_Uncal, IMERG_HQ, and IMERG_IR (Table 1). In addition, the latest Version 06B of IMERG extends the time range of data back to June 2000 by integrating the precipitation estimates collected during the TRMM era. Please follow the IMERG technical documentation (https://gpm.nasa.gov/sites/default/files/document_files/IMERG_doc.pdf, accessed on 15 March 2022) for detailed information. We used daily aggregated IMERG data (i.e., the cumulative sum of 48 values of half-hour precipitation) for all 4 IMERG datasets. The GP stations are mostly equipped with 24 h accumulated precipitation, recorded by a gauge reader using the US Standard (8” diameter) manual rain gauge [84]. Therefore, we used daily aggregated IMERG data, which allowed us to directly compare with GP station data. A total of 1538 grids (0.1° × 0.1° lat/lon) covered the selected study area (Figure 1).

Table 1.
Description of types of IMERG datasets.
2.2.2. Ground-Based Precipitation Data
Twenty-year (2001 to 2020), quality-controlled, and homogenous gauged precipitation data were collected from the Department of Hydrology and Meteorology (DHM), Government of Nepal. A total of 40 sparsely distributed representative precipitation stations were selected, falling under different climate classes and altitudinal locations, though only 25 stations with less than 10% data gaps were used during the study period (Figure 1).
2.3. Methodology
2.3.1. Ground-Based Data Preparation
Table 2 provides information on the data gaps percentage. Since the computation of precipitation indices would be affected due to the data gaps, though small, we first attempted to fill these gaps using the best available reanalysis or/and interpolated products. We estimated precipitation values using a point-to-pixel [47] approach for the data gap days. Asian Precipitation—Highly-Resolved Observational Data Integration Toward Evaluation (APHRODITE) (available for 2001–2015), with 0.25° spatial resolution, was used for the data from 2001 to 2015, and NOAA Climate Prediction Center (CPC) with 0.5° spatial resolution was used for the remaining period from 2016 to 2020. Quality-controlled gauge data are used to generate interpolation-based gridded data for both products, i.e., APHRODITE [85] and CPC [86]. A refined APHRODITE algorithm (under the APHRODITE-2 project from June 2016 to March 2019) was used for the precipitation data from 1998 to 2015. If the data gaps were substantially large, these data fillings using low-resolution products (i.e., 0.25° and 0.5°) would have a greater influence. Here, the objective of this paper is to analyze the spatial details of several precipitation indices based on four IMERG datasets rather than GP stations. However, to have better confidence in the applicability of IMERG datasets, we attempt to compare them with GP stations at key locations. Therefore, though the data-filling process would bring some uncertainty, the effects are not considered in this study.

Table 2.
List of selected ground-based precipitation stations. The mean and standard deviation (SD) of annual precipitation is computed from precipitation data from 2001 to 2020.
Nevertheless, we compared precipitation data of two gridded products (i.e., APHRODITE and CPC) during non-data gaps. We observed that these products have fewer biases and apply to filling data gaps. It is to be noted that they, however, might not exactly replicate the ground conditions during the data gap days on a day-to-day basis. Importantly, these gridded datasets generally conserve spatial characteristics on a seasonal and annual scale. Figure 1 shows the spatial distribution of the network of selected precipitation stations. The mean annual precipitation (MAP) from 2001 to 2020 ranges from 658.8 mm at Larke Samdo (St. No. 806) to Bhadaure Deurali (St. No. 813), representing a more-or-less country’s precipitation variability [79,80]. The arithmetic average of 25 selected MAPs is 1799.5 mm, equal to a country-averaged MAP [79,80] (Table 2). Based on normal climatic values, we can infer that the selected 25 stations represent key locations of the country and provide indicative information of country-averaged precipitation.
2.3.2. Precipitation Indices
Table A1 in Appendix A shows the list of precipitation indices used in this study. These precipitation indices were adapted from the joint CCl/WCRP/JCOMM Expert TeamExpert Team on Climate Change Detection and Indices (ETCDDI) (https://www.wcrp-climate.org/etccdi-members, accessed on 15 March 2022) and CCI Expert Team on Sector-Specific Climate Indices (ET-SCI) (https://climpact-sci.org/about/project/, accessed on 15 March 2022). Daily IMERG precipitation estimates were used to compute these indices at IMERG grid locations, and daily GP precipitation values were used to compute the same at GP locations.
Annual Total Precipitation (PRCPTOT), Wet Days (R1), and Daily Intensity (SDII)
We assigned a daily precipitation threshold of 1 mm to define a wet and dry day. R1 was computed by counting the number of wet days in a year. PRCPTOT was computed by adding all the daily precipitation values during those wet days. SDII is a simple ratio between PRCPTOT and R1, which informs the average daily precipitation value during wet days over a year.
Percentile-Based Precipitation Indices (95th and 99th Percentile)
Similar to the PRCPTOT, these percentile-based precipitation indices (r95p and r99p) were computed by summing the daily precipitation value exceeding a threshold. However, instead of summing all wet days’ precipitation, r95p accounts only for those precipitation values equal to or greater than the 95th percentile threshold. Furthermore, for r99p, the threshold is the 99th percentile. The percentage contribution of these extreme events (r95p and r99p) to the total annual precipitation (PRCPTOT) defines r95pTOT and r99pTOT.
Frequency-Related Precipitation Extremes (R10, R20, R50, and R100)
Similar to R1, these frequency-based precipitation indices (R10, R20, R50, and R100) were computed by counting the days when the daily precipitation value exceeds a certain threshold. However, instead of counting all wet days, R10 accounts only for those days when the precipitation value equals or exceeds 10 mm. Furthermore, the threshold for R20, R50, and R100 are 20, 50, and 100 mm, respectively.
Consecutive Dry and Wet Spells (CDD and CWD)
For the calculation of CDD, a time series of the length of consecutive dry days (dry spells) was computed. Then, the maximum dry spell length over a year is taken as the CDD of that year. Similar to the CDD, CWD was computed for consecutive wet days (wet spells).
Maximum 1-Day, Consecutive 3-, 5-, and 7-Day Precipitation Extremes
The maximum value of daily wet days precipitation over a year is taken as the RX1day of that year. For RX3day, a time series of 3 consecutive days of precipitation total was computed using a rolling window of three days. Then, the maximum value of 3 consecutive days precipitation total is taken as the RX3day of that year. Similar to the RX3day, RX5day and RX7day were computed for consecutive 5- and 7-days. The percentage contribution of these extreme events to that year’s total annual precipitation (PRCPTOT) defines RX1dayTOT, RX3dayTOT, RX5dayTOT, and RX7dayTOT.
Seasonal Precipitation and Monsoon Contribution (MonsoonTOT)
Similar to the PRCPTOT, these seasonal precipitations (pre-monsoon, monsoon, post-monsoon, and winter) were computed by summing the wet day precipitation value during its period. We computed MonsoonTOT to provide the percentage contribution of monsoon precipitation to that year’s total annual precipitation (PRCPTOT).
Extra Precipitation Indices (CDDmonsoon and CWDwinter)
We computed some extra seasonal indices to capture the maximum dry spell information during the monsoon season (CDDmonsoon) and the maximum wet spell information during the winter season (CDDwinter). The computation of these extra indices involved the same techniques as for the annual time series, except the computation was limited to only monsoon season for CDDmonsoon, and winter for CWDwinter.
The above-mentioned twenty-eight indices were calculated for each IMERG grid point and GP station. For spatial mapping, values of all grid points are presented with the proper color legends where the same color for 25 GP stations was used.
2.3.3. Trend Analysis
The monotonic trend at these grid locations and precipitation stations was evaluated using a non-parametric rank-based Mann–Kendall (MK) test [87,88] for statistical significance and Theil–Sen (TS) slope estimator [89,90] for trend magnitude. MK, in conjunction with TS, has been widely used in trend detection for hydrometeorological time-series data [80]. In addition, statistical significance was computed at a threshold p-value of 0.1 (i.e., 90% confidence level). Finally, we used the pyMannKendall package [91] following Yue and Wang’s [92] pre-whitening method to limit the serial correlation contaminated in observations [93].
3. Results
This section presents key results from analyzing the spatial distribution of annual average values (2001–2020) of 28 precipitation indices (Figure 2, Figure 3, Figure 4 and Figure 5).

Figure 2.
Spatial distribution of annual average values (2001–2020) of PRCPTOT, R1, SDII, r95p, r95pTOT, r99p, and r99pTOT across Nepal based on four IMERG datasets (Cal, Uncal, HQ, and IR). Refer to Table 1 and Appendix A Table A1 for the details of the indices and types of IMERG datasets. The color code used for the precipitation stations (points) and background (grids) is the same for each precipitation index (i.e., row). The label showing the mean value represents the country-averaged value computed by averaging 1538 grid point values.

Figure 3.
Spatial distribution of annual average values (2001–2020) of R10, R20, R50, R100, CDD, CWD, and RX1day across Nepal based on four IMERG datasets (Cal, Uncal, HQ, and IR). Refer to Table 1 and Appendix A Table A1 for the details of the indices and types of IMERG datasets. The color code used for the precipitation stations (points) and background (grids) is the same for each precipitation index (i.e., row). The label showing the mean value represents the country-averaged value computed by averaging 1538 grid point values.
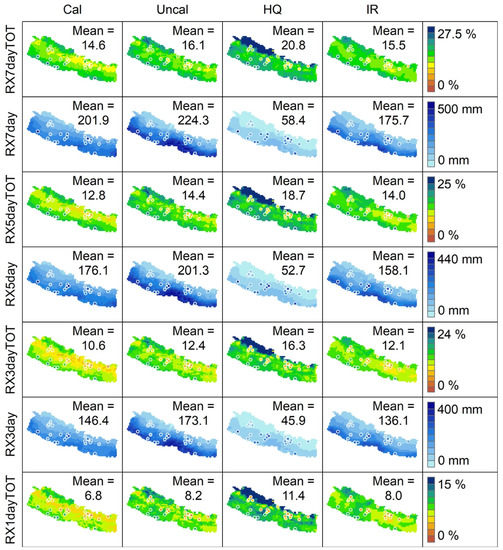
Figure 4.
Spatial distribution of annual average values of RX1dayTOT, RX3day, RX3dayTOT, RX5day, RX5dayTOT, RX7day, and RX7dayTOT across Nepal based on four IMERG datasets (Cal, Uncal, HQ, and IR). Refer to Table 1 and Appendix A Table A1 for the details of the indices and types of IMERG datasets. The color code used for the precipitation stations (points) and background (grids) is the same for each precipitation index (i.e., row). The label showing the mean value represents the country-averaged value computed by averaging 1538 grid point values.
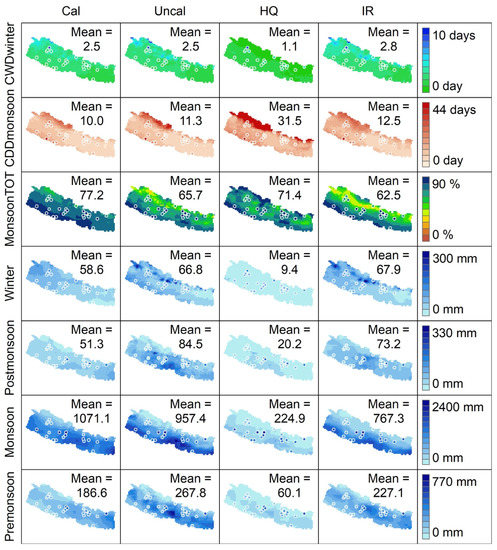
Figure 5.
Spatial distribution of average values (2001–2020) of pre-monsoon, monsoon, post-monsoon, winter, MonsoonTOT, CDDmonsoon, and CWDwinter across Nepal based on four IMERG datasets (Cal, Uncal, HQ, and IR). Refer to Table 1 and Appendix A Table A1 for the details of the indices and types of IMERG datasets. The color code used for the precipitation stations (points) and background (grids) is the same for each precipitation index (i.e., row). The label showing the mean value represents the country-averaged value computed by averaging 1538 grid point values.
3.1. Annual Total Precipitation (PRCPTOT), Wet Days (R1), and Daily Intensity (SDII)
The spatial map of the annual average value of PRCPTOT informs the mean annual precipitation (MAP), an important precipitation characteristic of the region. Several studies [79,80,81,83,94] that used key GP stations (i.e., over hundreds) show high-precipitation pockets around the windward sides of hills in the central (Lumle) and eastern regions (Gumthang and Num) of the country. However, our results show that the IMERG datasets fail to match these previously explored high-precipitation areas. Instead, as seen in Figure 2, the IMERG datasets show higher precipitation locations in the southern belt. In particular, the IMERG_Uncal indicates high PRCPTOT across the entire southern belt (higher concentration around the central region). After gauge-based calibration under the IMERG’s algorithm, the IMERG_Cal indicates a more promising spatial distribution, except for the inability to capture high-precipitation areas. The absolute value of IMERG_HQ highly underestimates the ground reality despite convincing the spatial distribution. Similarly, the spatial distribution of IMERG_IR is similar to IMERG_HQ and IMERG_Uncal versions (Figure 2). As the selected GP stations (N = 25) do not match perfectly with any of the IMERG datasets, we can advocate that all these products fail to capture the dynamics of local-scale precipitation information. Nevertheless, these estimates are successful in decent mimic of the general characteristics of precipitation’s spatial variability. The country-averaged MAP is ~1390 mm for IMERG_Cal and IMERG_Uncal and ~1140 mm for IMERG_IR. Since IMERG_HQ is highly underestimated, the country-averaged MAP is only ~one-fourth of what IMERG_Cal and IMERG_Uncal estimated (Figure 2). It is interesting to note that IMERG datasets well represented the rainy days (daily precipitation >1 mm) for Cal, Uncal, and IR despite the higher biases between IMERG estimates and gauge precipitation (selected 25 stations) in total precipitation. However, IMERG_HQ estimates underestimate the rainy days, and its country-averaged R1 is almost half of other estimates. In addition, SDII explains the simple average precipitation during rainy days, which is expressed as the ratio of PRCPTOT to R1. The country-averaged SDII is about 12 mm per rainy day.
3.2. Percentile-Based Precipitation Indices (95th and 99th Percentile)
As indicated in Figure 2, IMERG_Uncal shows a higher amount of the total precipitation across the southern belt of the country from high-precipitation events featuring > 95th and 99th percentile precipitation, similar to that reported by [79] based on 76 high-quality GP stations. However, in the case of IMERG_Cal, an absolute value is comparatively reduced in the southern belt of the country despite similar spatial distribution to IMERG_Uncal. Country-averaged r95p (r99p) for IMERG_Uncal (IMERG_Cal) is about 777 (310) and 735(268) mm, respectively. Similarly, IMERG_IR estimates a slightly lower value than Cal and Uncal datasets, where IMERG_HQ- highly underestimates. Furthermore, Most GP exhibits a similar pattern to IMERG_Cal, IMERG_Uncal, and IMERG_IR datasets, with few noticeable contrasts in some stations.
Two Indices (r95pTOT and r99pTOT) that depict percentage contributions of heavy precipitation events (r95p and r99p) to the total annual precipitation (PRCPTOT) have shown higher values (higher percentage contributions) in the country’s southern region because of higher precipitation during those events (Figure 2). Alongside, we also evidence a higher percentage contribution around the country’s northwest region, although the absolute values of r95p and r99p are very low (Figure 2). The possible reason for this unusual phenomenon is that these regions are comparatively dry, with low annual precipitation and wet days. Therefore, these few heavy precipitation events almost contribute to over 50% of total annual precipitation.
3.3. Frequency-Related Precipitation Extremes (R10, R20, R50, and R100)
As shown in Figure 3, it has been known that the country’s northern region is characterized by low total precipitation, where daily precipitation amounts do not range in heavy precipitation > 100 mm a day (R100). However, occasional precipitation events exist > 50 mm (R50) and can be treated as heavy to very heavy precipitation events attributed to these dry regions. Regarding the frequency of R50 and R100, IMERG_Uncal exhibits a higher number than other datasets, where IMERG_Cal exceeds the other three for R10 and R20. Since R10 and R20 are common events during the monsoon season over most parts of the country [79] and represent moderate precipitation events over large areas, except high altitude regions (Figure 3). IMERG_Uncal shows a higher absolute value of extreme precipitation frequency across the country’s southern region. The frequency of precipitation extremes (R10, R20, R50, and R100) for IMERG_HQ is too low due to the high underestimation of the precipitation amount. Despite the magnitude difference, similar spatial distribution is observed for all IMERG datasets.
3.4. Consecutive Dry and Wet Spells (CDD and CWD)
It is crucial to explore the Information about consecutive dry and wet spells for agriculture, irrigation, and water resources management [95]. Our study unveils that CDD and CWD (Figure 3) information are almost congruous between IMERG (Cal, Uncal, and IR) datasets and GP at the selected locations. As the IMERG_HQ estimates are very low, dry days are substantially high with very high CDD and very low CWD (Figure 3). The country-averaged CDD and CWD are about two months and half a month, respectively. Some dry regions indicate CDD exceeding three months, meaning an entire winter season. Moreover, some sporadic wet regions show CWD of greater than 30–35 days, indicating a continuous moderate to heavy rainfall for more than a month during the monsoon season. In the subsequent section, we show the spatial distribution of CDD during monsoon and CWD during winter to analyze dry days during the winter and wet days during the monsoon season.
3.5. Maximum 1-Day, Consecutive 3-, 5-, and 7-Day Precipitation Extremes
Index maximum 1-day precipitation (RX1day) informs the maximum daily (extreme event) precipitation of a year at that location. However, such an event is highly localized [80]. The spatial mapping of RX1day reveals that higher extreme values are concentrated across the country’s southern belt, with the highest intensity in the central region (Figure 3 top panel). During the monsoon season, the moisture-bearing monsoonal wind approaches the country; heavier precipitation falls in the southern foothill, the first windward side of low-elevated hills (Churia) across the region [80]. As previously mentioned, IMERG_Uncal shows higher precipitation extremes than IMERG_Cal; the country-averaged RX1day by IMERG_Uncal (IMERG_Cal) is 112 (93) mm. Another index, RX1dayTOT (ratio of RX1day to the PRCPTOT), updates the contribution of max 1-day precipitation to the total precipitation, where higher RX1dayTOT indicates high severity of extremities in a day with respect to total annual precipitation.
The spatial distribution of RX1dayTOT (Figure 4) is similar to that of r95pTOT and r99pTOT (Figure 2), indicating two pockets with high contribution from extreme precipitation: (i) southern lowlands because of the higher absolute value of extreme precipitation events and (ii) northwestern high-altitude region because of lower annual precipitation and a smaller number of wet days. The spatial distribution of maximum consecutive 3-, 5-, and 7-day precipitation (RX3day, RX5day, and RX7day in Figure 4) are similar to the spatial distribution of RX1day (Figure 3 top panel). This similar pattern is evident for RX3dayTOT, RX5dayTOT, and RX7dayTOT, but the absolute value differs (Figure 4). The country-averaged RX3day, RX5day, and RX7day are 173 mm, 201 mm, and 224 mm based on IMERG_Uncal, and 146 mm, 176 mm, and 202 mm based on IMERG_Cal, respectively. Regions with a higher extreme precipitation contribution to PRCPTOT possess a higher chance of waterlogging, inundation, and other geo- and hydrometeorological hazards [96].
3.6. Seasonal Precipitation and Monsoon Contribution (MonsoonTOT)
The knowledge about the spatial distribution of the annual average value of seasonal precipitation (pre-monsoon, monsoon, post-monsoon, and winter) characterizes the region, and its essence is helpful to agricultural zonation and water management. IMERG_Cal reports that the country-averaged monsoon contribution to PRCPTOT is 77% (Figure 5). In addition, most locations across the country have above 80% contribution during the monsoon season. On the other hand, the southeastern region attributes the higher pre-monsoon precipitation, which is mainly attached to thunderstorms. The season after pre-monsoon (i.e., the monsoon season) exhibits similar spatial distribution to the pre-monsoon season (Figure 5). In the post-monsoon season (transition between monsoon and winter), the retreat starts from west to east; the western region has lower precipitation, similar to the pre-monsoon and monsoon seasons. In contrast to these seasons, winter precipitation is higher in northwestern regions. The country-averaged seasonal precipitation based on IMERG_Cal (IMERG_Uncal) is 186 (267), 1071 (957), 51 (84), and 58 (66) mm during pre-monsoon, monsoon, post-monsoon, and winter, respectively. IMERG_IR demonstrates a similar pattern to IMERG_Uncal in the overall scenario though Its magnitude is deficient in monsoon seasons compared to IMERG_Cal and IMERG_Uncal datasets. MERG_IR precipitation is comparatively lower than IMERG_Cal and IMERG_Uncal datasets. The absolute value of IMERG_HQ is undoubtedly very low compared to other datasets.
3.7. Extra Precipitation Indices (CDDmonsoon and CWDwinter)
We evaluated consecutive dry during monsoon and wet spells during winter. IMERG_Cal reports that country-averaged CDDmonsoon and CWDwinter are about ten and two to three days, respectively. Some dry regions (i.e., northwestern region) show CDDmonsoon for almost a month (Figure 5). Even during the monsoon season, these dry regions have dry days for a prolonged period, which limits plant and vegetation growth [97]. At the same time, the same region shows a comparatively higher CWDwinter. Therefore, continuous precipitation for more than a day in winter is attributed to the country’s northwestern region. GP stations show a similar pattern for these indices (CDDmonsoon and CWDwinter) with IMERG datasets, with some exceptional contrasts at some locations.
4. Discussion
Global warming is unequivocal, and the frequency and intensity of extreme precipitation are ever-increasing. Understanding the impacts of extreme precipitation events under a warming climate is crucial. A more thorough analysis of the spatiotemporal distribution of seasonal and annual precipitation dynamics and several precipitation indices is critical for effectively managing water resources and associated socioeconomic development. The country has a high spatial variability from east to west (longitudinal), north to south (latitudinal), and topography (elevation) [79,83]. Ranges of high mountains and low-mid elevated hills, along with dense river networks and sporadic locations of flatland and river valleys, create several microclimatic features and unique precipitation patterns and make highly heterogeneous distribution across the country. [6,78,98,99,100,101,102]. Along with spatial variation, a large seasonal precipitation gradient is seen across the country, resulting in highly temporal variation.
Figure 6 shows the temporal fluctuation of country-averaged extreme precipitation indices based on GP stations and all IMERG grids. Since it is not a one-to-one comparison, we evaluated satellite estimates at the precipitation observation station using the point-to-pixel approach (Figure A1 in Appendix A). Overall, the country-averaged temporal precipitation variation, represented by the 25 selected grid locations of selected GPs, is in correspondence with the one computed using the entire IMERG grids. The temporal variation of most precipitation indices confirms the similar temporal fluctuation between satellite estimates and ground-based stations except for IMERG_HQ. However, IMERG_Cal stands out among MERG datasets for achieving a congruous pattern with GP observation, which agrees with the importance of gauge calibration on multi-satellite estimates [57,59]. Specifically, the frequency of wet days (R1) is well captured by IMERG_Cal, IMERG_Uncal, and IMERG_IR, indicating that precipitation detection is well captured. Figure A2 in Appendix A section shows the performance metrics of precipitation detection based on POD, CSI, false alarm ratio (FAR), and frequency bias index (FBI). For instance, POD ranges from 0.4 to 0.76 (0.32 to 0.77), with an average value of 0.63 (0.6), respectively, for IMERG_Cal (IMERG_Uncal). These obtained ranges of POD and CSI indicate good detection. However, these estimates have sizeable false alarms, indicating substantial false precipitation detections during non-precipitation days depicted by GP but FAR ranges in a similar range for all IMERG datasets. For example, its value ranges from 0.2 to 0.73, with an average of 0.41 for IMERG_Cal. Likewise, other indices, such as IMERG datasets underestimate CWD, PRCPTOT, monsoon, R20, and R50 throughout the study period. Though the frequency of wet days is well represented, the simple daily precipitation intensity index is highly underestimated because of the underestimation of total annual precipitation. IMERG_Uncal shows slightly overestimated extreme precipitation for many years, such as R100, r95p, r99p, RX1day, RX3day, RX5day, and RX7day (i.e., heavy precipitation events), which is in line with previous studies [57,66,103]. Further, Figure 7 shows the spatial distribution of the monotonic trend of precipitation indices at each grid based on IMERG_Cal and ground-based observations (Figures S1–S3 in the supplement section for IMERG_Uncal, IMERG_HQ, and IMERG_IR). Again, we could see a mixed pattern of increasing and decreasing trends, where most locations have a falling trend except for consecutive dry and wet spells.
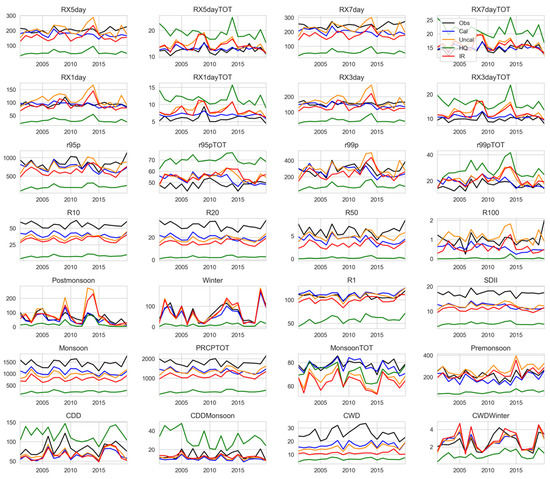
Figure 6.
Temporal variation of the country-averaged value of 28 precipitation indices based on 25 ground-based precipitation stations (obs) and 1538 grid points of 4 IMERG datasets (Cal, Uncal, HQ, and IR) for the period from 2001 to 2020. Refer to Table 1 and Appendix A Table A1 for the details of the indices and types of IMERG datasets. Figure A1 shows a similar plot based on the respective 25 point-to-pixel grid locations of 4 IMERG datasets (Cal, Uncal, HQ, and IR) from 2001 to 2020.

Figure 7.
Spatial distribution of annual trends from 2001 to 2020 of the selected 28 precipitation indices across Nepal based on the IMERG Cal dataset. Refer to Table A1 in Appendix A for the details of the indices. The color code used for the precipitation stations (points) and background (grids) represents the same for each precipitation index.
Upon characterizing the seasonal trend, pre-monsoon has been rising across more than half of the country’s area, concentrated in the western region, which was also reported by [7,79]. Likewise, winter precipitation is rising in the northwestern region [7,78,82,100]. Moreover, the frequency of wet days is increasing at most locations, which is similar to findings reported by previous studies [77,104,105,106]. However, most heavy precipitation-related indices show a sporadic rising tendency across the southern belt of the country [76,79,101,107]. One of the possible reasons for this rising tendency is physiographic controls upon precipitation; topographic barriers induce rain shadows (leeward side) and precipitation hotspots (windward side); for instance, heavier rainfall occurs in the southern part as approaching monsoon winds in Nepal are first intercepted by the foothills of Churia range (southern region). Another explanation could be the behavior of the Indian summer monsoon, which interposes significantly to annual precipitation levels, and its influence decreases from the lower to Higher altitudes of Nepal [79,107,108]. Nevertheless, the harmonious trend is evident compared to GP observations, despite some noticeable contrasts at some locations. Importantly, as most precipitation indices reveal a strong inter-annual variation, it is challenging to compute a monotonic trend based on a short period of data (i.e., 20 years).
Although the new generation of IMERG products is characterized by improved precipitation retrieval algorithms and more advanced satellite sensors, the accuracy of this product remains affected by various sources. Among them, the complex topography and atmospheric processes make it challenging to estimate precipitation. Monsoon and topographic variations may generate considerably. Furthermore, latitude, longitude, and elevation modulate seasonal and annual precipitation. Therefore, the location and topography characterize the climate of that location. However, most of the time, extreme precipitation events are unique and highly local in themselves. Nevertheless, topographic setting, monsoonal circulation, and climatic characteristics of location provide persistent information on the likelihood of severity of extreme precipitation. For instance, it is quite obvious that the foothills of Nepal are hardly hit by a strong monsoonal system every year. However, the severity depends on the location of the monsoon trough. In addition, some past cloud burst events have shown that when westerly and summer monsoon coincides, such episodes provide a favorable synoptic condition for heavy precipitation over a large area, affecting more than one major river basin.
Depending on location and season, the impact of extreme precipitation events on humans, the economy, and nature vary a lot. Across Nepal, there are locations where one-day maximum precipitation towards the windward side of a mountain is almost equivalent to the total annual precipitation of the leeward side of the same mountain. Therefore, heavy precipitation in terms of amounts for one region could be a moderate event for many locations. Therefore, this study computed several indices based on amounts, frequencies, percentiles, and contribution percentages to annual precipitation. Precipitation intensity and duration on a sub-daily scale impact a lot. For instance, low-intensity but longer-duration precipitation can saturate the soil, causing landslides. Intense short-duration precipitation can bring local urban or flash floods. We currently limit this study to daily precipitation. Since IMERG-like products have data on a half-hourly scale, future works could look at several other extreme precipitation indices on a sub-daily scale. However, comparing the performance of SPEs on a sub-daily scale is challenging due to the lack of high-temporal GP station observations.
This study has some limitations. First, a point-to-pixel method implemented for evaluating IMERG against GP may lead to biases due to spatial mismatch between point measurements of rain gauges and area-averaged rainfall of each grid cell [109]. Similarly, most IMERG evaluation pixels encompass only one rain gauge. As a result, they may cover inhomogeneous terrain, resulting in the partial representation of the precipitation pixel value, which fails to provide better results in a complex landscape, such as Nepal. Another notable scarcity of enough rainfall networks for the higher altitude networks makes analysis complex and problematic, though general trends are exhibited. Since this study uses only 25 key GP stations, the appraisal of the performance of IMERG datasets at each grid point has higher uncertainty. However, due to the lack of high-quality GP stations, this study focused on spatial variation of several precipitation indices across the country rather than the performance evaluation at different locations, climates, and topography. With the availability of long-term automatic weather station data, a detailed investigation of the performances of IMERG datasets could be conducted even on a sub-daily scale [110].
5. Conclusions
Precipitation information is crucial in the global, regional, and local water cycle. Though GP stations are considered ground truth, they suffer from low spatial density and sizeable temporal gaps, particularly in remote areas, including high mountains. SPEs, in the form of gridded data, inform spatially seamless precipitation distribution. This study evaluated the spatiotemporal variability of precipitation using several precipitation indices across Nepal. These indices capture information related to seasonal and annual totals, frequency and intensity of extreme precipitation, and the maximum length of dry and wet spells. Normalized indices (percentage contributions) and extra seasonal indices (Monsoon CDD and Winter CWD) provide spatially comparable and temporally local precipitation information. Though these indices are adapted from popular ETCCDI and ET-SCI, they have additional benefits in understanding the spatiotemporal distribution of precipitation. With a minor modification, these indices can be applied to other regions to capture local and regional insights.
Across Nepal, based on 25 GP stations, we observed that IMERG datasets showed good detection efficiency. Nevertheless, there are also sizable false alarms, which is a serious concern. Importantly, the spatial distribution of several precipitation indices shows a convincing variability, which captures seasonal monsoonal variability across the country. Based on the annual average values of PRCPTOT, the country’s southern region showed a high-precipitation pocket, missing three local pockets of high-precipitation regions (>3500 mm in a year), which are depicted by previous studies. Therefore, local high-precipitation areas are still not tracked by the IMERG datasets. In addition, upon looking at heavy to very heavy precipitation event-related indices, most of the indices clearly showed the foothills of the country as the highest extreme precipitation areas, supported by GP station observations. This study finds that seasonal precipitation has location-specific rising and falling trends, but extreme precipitation indices have sporadic pockets, indicating the spatial behavior of extreme precipitation is highly local.
Among four IMERG datasets, IMERG_Cal is best-suited for further hydrological and water resources implications. IMERG_Uncal is equally applicable, but the uncalibrated version generally shows higher precipitation totals during extreme events. Interannual variations of IMERG_cal and IMERG_uncal are congruous to each other. IMERG_IR slightly underestimates most occasions. IMERG_HQ underestimates substantially. As all IMERG products captured wet days accurately, a proper blending of all these products using several statistical and machine learning approaches could be explored to estimate absolute precipitation values for future hydrologic and water resources applications. A take-home message from this study is that although SPEs provide spatial details irrespective of location, the accuracy and uncertainty of these products vary differently from location to location.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14235954/s1, Figure S1: the same as in Figure 7 but for IMERG_Uncal; Figure S2: the same as in Figure 7 but for IMERG_HQ; Figure S3: the same as in Figure 7 but for IMERG_IR.
Author Contributions
Conceptualization, R.T., S.S. and B.A.; methodology, R.T.; software, R.T.; validation, R.T. formal analysis, R.T.; investigation, R.T.; resources, R.T. and S.S.; data curation, R.T. and S.S.; writing—original draft preparation, R.T. and S.S.; writing—review and editing, R.T., S.S. and B.A.; visualization, R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data are openly accessible and available at https://zenodo.org/record/7316023, accessed on 15 March 2022, DOI: 10.5281/zenodo.7316023.
Acknowledgments
We thank the Department of Hydrology and Meteorology, Government of Nepal, for sharing the observed ground-based precipitation observations of the selected stations. We also thank the NASA/Goddard Space Flight Center team, which developed the IMERG datasets and made all datasets publicly available.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Precipitation indices used in this study.
Table A1.
Precipitation indices used in this study.
| SN | Symbol | Name | Definitions | Units |
|---|---|---|---|---|
| 1 | CDD | Consecutive dry days | Maximum number of consecutive days with PRCP < 1 mm | days |
| 2 | CWD | Consecutive wet days | Maximum number of consecutive days with PRCP ≥ 1 mm | days |
| 3 | PRCPTOT | Annual total wet-day precipitation | Annual total precipitation on wet days (PRCP ≥ 1 mm) | mm |
| 4 | R1 | Number of wet days | Annual count of days when PRCP1 ≥ 1 mm | days |
| 5 | R10 | Number of slightly heavy precipitation days | Annual count of days when PRCP1 ≥ 10 mm | days |
| 6 | R20 | Number of heavy precipitation days | Annual count of days when PRCP1 ≥ 20 mm | days |
| 7 | R50 | Number of very heavy precipitation days | Annual count of days when PRCP1 ≥ 50 mm | days |
| 8 | r95p | Total annual precipitation from heavy precipitation days | Annual total precipitation in wet days (PRCP ≥ 95 percentile) | mm |
| 9 | r95pTOT | Contribution from heavy precipitation days | Ratio of r95p with PRCPTOT | % |
| 10 | r99p | Total annual precipitation from very heavy precipitation days | Annual total precipitation in wet days (PRCP ≥ 99 percentile) | mm |
| 11 | r99pTOT | Contribution from very heavy precipitation days | Ratio of r99p with PRCPTOT | % |
| 12 | R100 | Number of extremely heavy precipitation days | Annual count of days when PRCP1 ≥ 100 mm | days |
| 13 | RX1day | Max 1-day precipitation | Yearly maximum 1-day precipitation | mm |
| 14 | RX1dayTOT | Contribution from max 1-day precipitation | Ratio of RX1day with PRCPTOT | % |
| 15 | RX3day | Max consecutive 3-day precipitation | Yearly maximum consecutive 3-day precipitation | mm |
| 16 | RX3dayTOT | Contribution from max 3-day precipitation | Ratio of RX3day with PRCPTOT | % |
| 17 | RX5day | Max consecutive 5-day precipitation | Yearly maximum consecutive 5-day precipitation | mm |
| 18 | RX5dayTOT | Contribution from max 5-day precipitation | Ratio of RX5day with PRCPTOT | % |
| 19 | RX7day | Max consecutive 7-day precipitation | Yearly maximum consecutive 7-day precipitation | mm |
| 20 | RX7dayTOT | Contribution from max 7-day precipitation | Ratio of RX7day with PRCPTOT | % |
| 21 | SDII | Simple daily intensity index | Average precipitation on wet days (PRCPTOT/R1) | mm/day |
| 22 | Pre-monsoon | Pre-monsoon total wet-day precipitation | Annual total precipitation in wet days (PRCP ≥ 1 mm) from March to May | mm |
| 23 | Monsoon | Monsoon total wet-day precipitation | Annual total precipitation in wet days (PRCP ≥ 1 mm) from June to September | mm |
| 24 | Post-monsoon | Post-monsoon total wet-day precipitation | Annual total precipitation in wet days (PRCP ≥ 1 mm) from October to November | mm |
| 25 | Winter | Winter total wet-day precipitation | Annual total precipitation in wet days (PRCP ≥ 1 mm) from December to February | mm |
| 26 | MonsoonTOT | Contribution from monsoon precipitation | Ratio of monsoon with PRCPTOT | % |
| 27 | CDDmonsoon | Consecutive dry days during monsoon | Maximum number of consecutive days with PRCP < 1 mm during monsoon | days |
| 28 | CWDwinter | Consecutive wet days during winter | Maximum number of consecutive days with PRCP ≥ 1 mm during winter | days |
| PRCP : 24 h accumulated precipitation amount | ||||
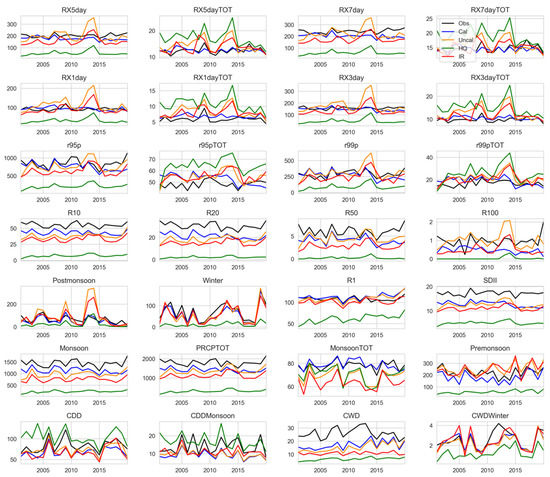
Figure A1.
Temporal variations of the country-averaged values of 28 precipitation indices based on 25 ground-based precipitation stations (obs) and the respective 25 point-to-pixel grid points of 4 IMERG datasets (Cal, Uncal, HQ, and IR) from 2001 to 2020. Refer to Table 1 and supplement Table A1 for the details of the indices and types of IMERG datasets. Figure A1 shows a similar plot based on the respective 25 point-to-pixel grid locations of 4 IMERG datasets (Cal, Uncal, HQ, and IR) from 2001 to 2020.
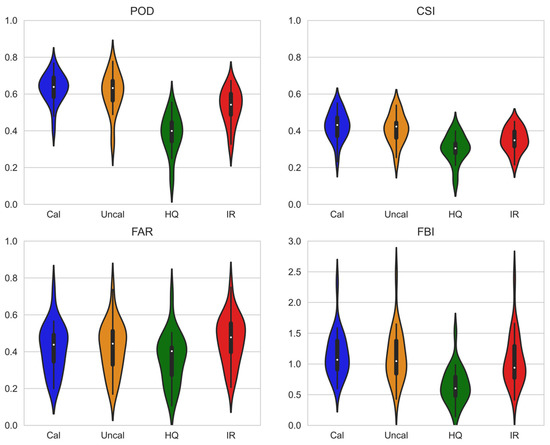
Figure A2.
Violin plots showing the distribution of performances of precipitation detection indices at the selected 25 stations. The probability of detection (POD) = T/(T + M), critical success index (CSI) = T/(T + M + F), false alarm ratio (FAR) = F/(T + F), and frequency bias index (FBI) = (T + F)/(T + M), where the precipitation detection is True (T) when both satellite estimates and ground-based precipitation observations show daily precipitation ≥ 1 mm, and False (F) when satellite estimates detect precipitation during non-wet days based on ground observations. Similarly, precipitation detection is Miss (M) when satellite estimates fail to detect ground observations. The precipitation detection is Null (N) when satellite estimates and ground observations show daily precipitation < 1 mm.
References
- Rouholahnejad, E.; Abbaspour, K.C.; Srinivasan, R.; Bacu, V.; Lehmann, A. Water resources of the Black Sea Basin at high spatial and temporal resolution. Water Resour. Res. 2014, 50, 5866–5885. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Smith, L.; Qian, T.; Dai, A.; Fasullo, J. Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data. J. Hydrometeorol. 2007, 8, 758–769. [Google Scholar] [CrossRef]
- Ruhi, A.; Messager, M.L.; Olden, J.D. Tracking the pulse of the Earth’s fresh waters. Nat. Sustain. 2018, 1, 198–203. [Google Scholar] [CrossRef]
- Herold, N.; Alexander, L.V.; Donat, M.G.; Contractor, S.; Becker, A. How much does it rain over land? Geophys. Res. Lett. 2016, 43, 341–348. [Google Scholar] [CrossRef]
- Shah, S.; Duan, Z.; Song, X.; Li, R.; Mao, H.; Liu, J.; Ma, T.; Wang, M. Evaluating the added value of multi-variable calibration of SWAT with remotely sensed evapotranspiration data for improving hydrological modeling. J. Hydrol. 2021, 603, 127046. [Google Scholar] [CrossRef]
- Duncan, J.M.A.; Biggs, E.M. Assessing the accuracy and applied use of satellite-derived precipitation estimates over Nepal. Appl. Geogr. 2012, 34, 626–638. [Google Scholar] [CrossRef]
- Duncan, J.M.A.; Biggs, E.M.; Dash, J.; Atkinson, P.M. Spatio-temporal trends in precipitation and their implications for water resources management in climate-sensitive Nepal. Appl. Geogr. 2013, 43, 138–146. [Google Scholar] [CrossRef]
- Fujibe, F. Clausius-Clapeyron-like relationship in multidecadal changes of extreme short-term precipitation and temperature in Japan. Atmos. Sci. Lett. 2013, 14, 127–132. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The Changing Character of Precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Yeşilırmak, E.; Atatanır, L. Spatiotemporal variability of precipitation concentration in western Turkey. Nat. Hazards 2016, 81, 687–704. [Google Scholar] [CrossRef]
- Fowler, H.J.; Ali, H. Analysis of extreme rainfall events under the climatic change. In Rainfall Modeling, Measurement and Applications; Elsevier: Amsterdam, The Netherlands, 2022; pp. 307–326. [Google Scholar] [CrossRef]
- Fadhel, S.; Rico-Ramirez, M.A.; Han, D. Sensitivity of peak flow to the change of rainfall temporal pattern due to warmer climate. J. Hydrol. 2018, 560, 546–559. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Aryal, A.; Kawaike, K.; Yamanoi, K.; Nakagawa, H. A comprehensive analysis of projected changes of extreme precipitation indices in West Rapti River basin, Nepal under changing climate. Int. J. Climatol. 2021, 41, joc.6866. [Google Scholar] [CrossRef]
- Cobon, D.H.; Ewai, M.; Inape, K.; Bourke, R.M. Food shortages are associated with droughts, floods, frosts and ENSO in Papua New Guinea. Agric. Syst. 2016, 145, 150–164. [Google Scholar] [CrossRef]
- Xie, W.; Yi, S.; Leng, C.; Xia, D.; Li, M.; Zhong, Z.; Ye, J. The evaluation of IMERG and ERA5-Land daily precipitation over China with considering the influence of gauge data bias. Sci. Rep. 2022, 12, 8085. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.; Tiwari, A.; Song, X.; Talchabahdel, R.; Habiyakare, T.; Adhikari, A. Drought index predictability for historical and future periods across the Southern plain of Nepal Himalaya. Environ. Monit. Assess. 2022, 194, 642. [Google Scholar] [CrossRef]
- Petersen, W.A.; Christian, H.J.; Rutledge, S.A. TRMM observations of the global relationship between ice water content and lightning. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Hartke, S.H.; Wright, D.B. Where Can IMERG Provide a Better Precipitation Estimate than Interpolated Gauge Data? Remote Sens. 2022, 14, 5563. [Google Scholar] [CrossRef]
- Shige, S.; Kida, S.; Ashiwake, H.; Kubota, T.; Aonashi, K. Improvement of TMI Rain Retrievals in Mountainous Areas. J. Appl. Meteorol. Climatol. 2013, 52, 242–254. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Estimating Climatic-Scale Precipitation from Space: A Review. J. Clim. 1989, 2, 1229–1238. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Tang, G.; Kirstetter, P.; Gao, S.; Li, J.L.F.; Wen, Y.; Hong, Y. Evaluation of GPM IMERG and its constellations in extreme events over the conterminous united states. J. Hydrol. 2022, 606, 127357. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Zhang, W.; Furtado, K.; Wu, P.; Zhou, T.; Chadwick, R.; Marzin, C.; Rostron, J.; Sexton, D. Increasing precipitation variability on daily-to-multiyear time scales in a warmer world. Sci. Adv. 2021, 7, 8021–8049. [Google Scholar] [CrossRef]
- Maussion, F.; Scherer, D.; Mölg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation seasonality and variability over the Tibetan Plateau as resolved by the high Asia reanalysis. J. Clim. 2014, 27, 1910–1927. [Google Scholar] [CrossRef]
- Prajapati, R.; Silwal, P.; Duwal, S.; Shrestha, S.; Kafle, A.S.; Talchabhadel, R.; Kumar, S. Detectability of Rainfall Characteristics over a Mountain River Basin in the Himalayan Region from 2000 to 2015 Using Ground- and Satellite-Based Products. Theor. Appl. Climatol. 2021. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Behrangi, A.; Lebsock, M.; Wong, S.; Lambrigtsen, B. On the quantification of oceanic rainfall using spaceborne sensors. J. Geophys. Res. Atmos. 2012, 117, 1–14. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite–Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Turk, J.T.; Mostovoy, G.V.; Anantharaj, V. The NRL-Blend High Resolution Precipitation Product and its Application to Land Surface Hydrology. In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 85–104. [Google Scholar]
- Turk, F.J.; Miller, S.D. Toward improved characterization of remotely sensed precipitation regimes with MODIS/AMSR-E blended data techniques. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1059–1069. [Google Scholar] [CrossRef]
- Kubota, T.; Aonashi, K.; Ushio, T.; Shige, S.; Takayabu, Y.N.; Kachi, M.; Arai, Y.; Tashima, T.; Masaki, T.; Kawamoto, N.; et al. Global Satellite Mapping of Precipitation (GSMaP) Products in the GPM Era. In Satellite Precipitation Measurement; Springer: Cham, Switzerland, 2020; pp. 355–373. [Google Scholar]
- Tashima, T.; Kubota, T.; Mega, T.; Ushio, T.; Oki, R. Precipitation Extremes Monitoring Using the Near-Real-Time GSMaP Product. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5640–5651. [Google Scholar] [CrossRef]
- Ma, Z.; Xu, J.; Zhu, S.; Yang, J.; Tang, G.; Yang, Y.; Shi, Z.; Hong, Y. AIMERG: A new Asian precipitation dataset (0.1°/half-hourly, 2000–2015) by calibrating the GPM-era IMERG at a daily scale using APHRODITE. Earth Syst. Sci. Data 2020, 12, 1525–1544. [Google Scholar] [CrossRef]
- Chen, C.; Yu, Z.; Li, L.; Yang, C. Adaptability evaluation of TRMM satellite rainfall and its application in the Dongjiang River Basin. Procedia Environ. Sci. 2011, 10, 396–402. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.-E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J.; et al. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res. Atmos. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and trmm 3B42V7 rainfall products over Southern Tibetan plateau based on a high-density rain gauge network. J. Geophys. Res. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; He, J.; Ge, F.; Chen, Q.; Tang, S.; Yao, S. Can the GPM IMERG Hourly Products Replicate the Variation in Precipitation During the Wet Season Over the Sichuan Basin, China? Earth Sp. Sci. 2020, 7, e2020EA001090. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, W.; Wang, W. Evaluation of TRMM 3B43 data over the Yangtze River Delta of China. Sci. Rep. 2018, 8, 5290. [Google Scholar] [CrossRef]
- Xia, T.; Wang, Z.J.; Zheng, H. Topography and Data Mining Based Methods for Improving Satellite Precipitation in Mountainous Areas of China. Atmosphere 2015, 6, 983–1005. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef]
- Sharma, S.; Khadka, N.; Hamal, K.; Shrestha, D.; Talchabhadel, R.; Chen, Y. How Accurately Can Satellite Products (TMPA and IMERG) Detect Precipitation Patterns, Extremities, and Drought Across the Nepalese Himalaya? Earth Space Sci. 2020, 7, e2020EA001315. [Google Scholar] [CrossRef]
- Ji, H.; Peng, D.; Gu, Y.; Liang, Y.; Luo, X. Evaluation of multiple satellite precipitation products and their potential utilities in the Yarlung Zangbo River Basin. Sci. Rep. 2022, 12, 13334. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.N.; Uyeda, H. Use of TRMM in determining the climatic characteristics of rainfall over Bangladesh. Remote Sens. Environ. 2007, 108, 264–276. [Google Scholar] [CrossRef]
- Almazroui, M. Calibration of TRMM rainfall climatology over Saudi Arabia during 1998–2009. Atmos. Res. 2011, 99, 400–414. [Google Scholar] [CrossRef]
- Zhou, Y.; Nelson, K.; Mohr, K.I.; Huffman, G.J.; Levy, R.; Grecu, M. A Spatial-Temporal Extreme Precipitation Database from GPM IMERG. J. Geophys. Res. Atmos. 2019, 124, 10344–10363. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Vargas Godoy, M.R.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Pradhan, A.; Indu, J. Assessment of SM2RAIN derived and IMERG based precipitation products for hydrological simulation. J. Hydrol. 2021, 603, 127191. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Hamouda, M.A.; Mohamed, M.M. Spatiotemporal evaluation of the GPM satellite precipitation products over the United Arab Emirates. Atmos. Res. 2019, 219, 200–212. [Google Scholar] [CrossRef]
- Kazamias, A.P.; Sapountzis, M.; Lagouvardos, K. Evaluation of GPM-IMERG rainfall estimates at multiple temporal and spatial scales over Greece. Atmos. Res. 2022, 269, 106014. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Sharma, S.; Khadka, N.; Hamal, K.; Karki, S.; Thapa, B.R. An outlook on the applicability of satellite precipitation products for monitoring extreme precipitation events in Nepal Himalaya. Weather 2022, 77, 174–180. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Multi time-scale evaluation of high-resolution satellite-based precipitation products over northeast of Austria. Atmos. Res. 2018, 206, 46–63. [Google Scholar] [CrossRef]
- Wang, W.; Ding, Y.; Shao, Q.; Xu, J.; Jiao, X.; Luo, Y.; Yu, Z. Bayesian multi-model projection of irrigation requirement and water use efficiency in three typical rice plantation region of China based on CMIP5. Agric. For. Meteorol. 2017, 232, 89–105. [Google Scholar] [CrossRef]
- Wild, A.; Chua, Z.-W.; Kuleshov, Y. Evaluation of Satellite Precipitation Estimates over the South West Pacific Region. Remote Sens. 2021, 13, 3929. [Google Scholar] [CrossRef]
- Su, J.; Lü, H.; Zhu, Y.; Cui, Y.; Wang, X. Evaluating the hydrological utility of latest IMERG products over the Upper Huaihe River Basin, China. Atmos. Res. 2019, 225, 17–29. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Marcos, C.; Sancho, J.M.; Santos, C.; Núñez, J.Á.; Navarro, A.; Kummerow, C.; Adler, R.F. The September 2019 floods in Spain: An example of the utility of satellite data for the analysis of extreme hydrometeorological events. Atmos. Res. 2021, 257, 105588. [Google Scholar] [CrossRef]
- Huang, C.; Hu, J.; Chen, S.; Zhang, A.; Liang, Z.; Tong, X.; Xiao, L.; Min, C.; Zhang, Z. How well can IMERG products capture typhoon extreme precipitation events over southern China? Remote Sens. 2019, 11, 70. [Google Scholar] [CrossRef]
- Li, Z.; Chen, M.; Gao, S.; Hong, Z.; Tang, G.; Wen, Y.; Gourley, J.J.; Hong, Y. Cross-examination of similarity, difference and deficiency of gauge, radar and satellite precipitation measuring uncertainties for extreme events using conventional metrics and multiplicative triple collocation. Remote Sens. 2020, 12, 1258. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of Integrated Multi-satellite Retrievals for Global Precipitation Measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- O, S.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of global precipitation measurement satellite products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Ahmad, I.; Ijaz, M.W.; Farid, H.U.; Yagoub, Y.E.; Zaman, M.; Adnan, M. Performance evaluation of latest integrated multi-satellite retrievals for Global Precipitation Measurement (IMERG) over the northern highlands of Pakistan. Atmos. Res. 2018, 205, 134–146. [Google Scholar] [CrossRef]
- Chiaravalloti, F.; Brocca, L.; Procopio, A.; Massari, C.; Gabriele, S. Assessment of GPM and SM2RAIN-ASCAT rainfall products over complex terrain in southern Italy. Atmos. Res. 2018, 206, 64–74. [Google Scholar] [CrossRef]
- Maghsood, F.F.; Hashemi, H.; Hosseini, S.H.; Berndtsson, R. Ground validation of GPM IMERG precipitation products over Iran. Remote Sens. 2020, 12, 48. [Google Scholar] [CrossRef]
- Shawky, M.; Moussa, A.; Hassan, Q.K.; El-Sheimy, N. Performance assessment of sub-daily and daily precipitation estimates derived from GPM and GSMaP products over an arid environment. Remote Sens. 2019, 11, 2840. [Google Scholar] [CrossRef]
- Sunilkumar, K.; Yatagai, A.; Masuda, M. Preliminary Evaluation of GPM-IMERG Rainfall Estimates Over Three Distinct Climate Zones With APHRODITE. Earth Space Sci. 2019, 6, 1321–1335. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.H.; Chen, H.; Delrieu, G.; Hsu, Y.C.; et al. Evaluation of GPM-era Global Satellite Precipitation Products over Multiple Complex Terrain Regions. Remote Sens. 2019, 11, 2936. [Google Scholar] [CrossRef]
- Lamichhane, D.; Dawadi, B.; Acharya, R.H.; Pudasainee, S.; Shrestha, I.K. Observed Trends and Spatial Distribution in Daily Precipitation Indices of Extremes over the Narayani River Basin, Central Nepal. Appl. Ecol. Environ. Sci. 2020, 8, 106–118. [Google Scholar] [CrossRef]
- Subba, S.; Ma, Y.; Ma, W. Spatial and Temporal Analysis of Precipitation Extremities of Eastern Nepal in the Last Two Decades (1997–2016). J. Geophys. Res. Atmos. 2019, 124, 7523–7539. [Google Scholar] [CrossRef]
- Kansakar, S.R.; Hannah, D.M.; Gerrard, J.; Rees, G. Spatial pattern in the precipitation regime of Nepal. Int. J. Climatol. 2004, 24, 1645–1659. [Google Scholar] [CrossRef]
- Karki, R.; Hasson, S.u.; Schickhoff, U.; Scholten, T.; Böhner, J. Rising Precipitation Extremes across Nepal. Climate 2017, 5, 4. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Karki, R.; Thapa, B.R.; Maharjan, M.; Parajuli, B. Spatio-temporal variability of extreme precipitation in Nepal. Int. J. Climatol. 2018, 38, 4296–4313. [Google Scholar] [CrossRef]
- Karki, R.; Talchabhadel, R.; Aalto, J.; Baidya, S.K. New climatic classification of Nepal. Theor. Appl. Climatol. 2016, 125, 799–808. [Google Scholar] [CrossRef]
- Shrestha, A.B.; Wake, C.P.; Dibb, J.E.; Mayewski, P.A. Precipitation fluctuations in the Nepal Himalaya and its vicinity and relationship with some large scale climatological parameters. Int. J. Climatol. 2000, 20, 317–327. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Karki, R.; Yadav, M.; Maharjan, M.; Aryal, A.; Thapa, B.R. Spatial distribution of soil moisture index across Nepal: A step towards sharing climatic information for agricultural sector. Theor. Appl. Climatol. 2019, 137, 3089–3102. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Karki, R.; Parajuli, B.; Talchabhadel, R. Intercomparison of precipitation measured between automatic and manual precipitation gauge in Nepal. Meas. J. Int. Meas. Confed. 2017, 106, 264–273. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. Aphrodite constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Chen, C.T.; Knutson, T. On the verification and comparison of extreme rainfall indices from climate models. J. Clim. 2008, 21, 1605–1621. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M. Rank correlation. Nature 1938, 142, 402. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis, I, II, III. In Henri Theil’s Contributions to Economics and Econometrics: Econometric Theory and Methodology; Raj, B., Koerts, J., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 386–392, 521–525, 1397–1412. ISBN 978-94-011-2546-8. [Google Scholar]
- Hussain, M.; Mahmud, I. pyMannKendall: A python package for non parametric Mann Kendall family of trend tests. J. Open Source Softw. 2019, 4, 1556. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the Mann-Kendall test. Water Resour. Res. 2002, 38, 4-1–4-7. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann-Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Sharma, S.; Chen, Y.; Zhou, X.; Yang, K.; Li, X.; Niu, X.; Hu, X.; Khadka, N. Evaluation of GPM-Era Satellite Precipitation Products on the Southern Slopes of the Central Himalayas Against Rain Gauge Data. Remote Sens. 2020, 12, 1836. [Google Scholar] [CrossRef]
- Maharjan, M.; Yoneda, M.; Talchabhadel, R.; Thapa, B.R.; Aryal, A. On the Use of Indices on Daily Timescales to Study Change of Extreme Precipitation across Nepal Attributed between 1976–1995 and 1996–2015. Earth Space Sci. 2022. [Google Scholar]
- Islam, H.M.T.; Islam, A.R.M.T.; Abdullah-Al-Mahbub, M.; Shahid, S.; Tasnuva, A.; Kamruzzaman, M.; Hu, Z.; Elbeltagi, A.; Kabir, M.M.; Salam, M.A.; et al. Spatiotemporal changes and modulations of extreme climatic indices in monsoon-dominated climate region linkage with large-scale atmospheric oscillation. Atmos. Res. 2021, 264, 105840. [Google Scholar] [CrossRef]
- Chakraborty, R.; Guha, B.K.; Talukdar, S.; Ratnam, M.V.; Maitra, A. Growth in mid-monsoon dry phases over the Indian region: Prevailing influence of anthropogenic aerosols. Atmos. Chem. Phys. 2019, 19, 12325–12341. [Google Scholar] [CrossRef]
- Lang, T.J.; Barros, A.P. Winter storms in the central Himalayas. J. Meteorol. Soc. Jpn. 2004, 82, 829–844. [Google Scholar] [CrossRef]
- Böhner, J. General climatic controls and topoclimatic variations in Central and High Asia. Boreas 2006, 35, 279–295. [Google Scholar] [CrossRef]
- Ichiyanagi, K.; Yamanaka, M.D.; Muraji, Y.; Vaidya, B.K. Precipitation in Nepal between 1987 and 1996. Int. J. Climatol. 2007, 27, 1753–1762. [Google Scholar] [CrossRef]
- Shrestha, A.B.; Aryal, R. Climate change in Nepal and its impact on Himalayan glaciers. Reg. Environ. Chang. 2011, 11, 65–77. [Google Scholar] [CrossRef]
- Hasson, S.; Lucarini, V.; Pascale, S. Hydrological cycle over South and Southeast Asian river basins as simulated by PCMDI/CMIP3 experiments. Earth Syst. Dyn. 2013, 4, 199–217. [Google Scholar] [CrossRef]
- Tong, K.; Zhao, Y.; Wei, Y.; Hu, B.; Lu, Y. Evaluation and Hydrological Validation of GPM Precipitation Products over the Nanliu River Basin, Beibu Gulf. Water 2018, 10, 1777. [Google Scholar] [CrossRef]
- Bastakoti, R.C.; Bharati, L.; Bhattarai, U.; Wahid, S.M. Agriculture under changing climate conditions and adaptation options in the Koshi Basin. Clim. Dev. 2017, 9, 634–648. [Google Scholar] [CrossRef]
- Myhre, G.; Alterskjær, K.; Stjern, C.W.; Hodnebrog, Ø.; Marelle, L.; Samset, B.H.; Sillmann, J.; Schaller, N.; Fischer, E.; Schulz, M.; et al. Frequency of extreme precipitation increases extensively with event rareness under global warming. Sci. Rep. 2019, 9, 16063. [Google Scholar] [CrossRef] [PubMed]
- Cotterill, D.; Stott, P.; Christidis, N.; Kendon, E. Increase in the frequency of extreme daily precipitation in the United Kingdom in autumn. Weather Clim. Extrem. 2021, 33, 100340. [Google Scholar] [CrossRef]
- Sigdel, M.; Ma, Y. Variability and trends in daily precipitation extremes on the northern and southern slopes of the central Himalaya. Theor. Appl. Climatol. 2016, 130, 571–581. [Google Scholar] [CrossRef]
- Shrestha, M.L. Interannual variation of summer monsoon rainfall over Nepal and its relation to Southern Oscillation Index. Meteorol. Atmos. Phys. 2000, 75, 21–28. [Google Scholar] [CrossRef]
- Freitas, E.d.S.; Coelho, V.H.R.; Xuan, Y.; Melo, D.d.C.D.; Gadelha, A.N.; Santos, E.A.; Galvão, C.d.O.; Ramos Filho, G.M.; Barbosa, L.R.; Huffman, G.J.; et al. The performance of the IMERG satellite-based product in identifying sub-daily rainfall events and their properties. J. Hydrol. 2020, 589, 125128. [Google Scholar] [CrossRef]
- Moazami, S.; Najafi, M.R. A comprehensive evaluation of GPM-IMERG V06 and MRMS with hourly ground-based precipitation observations across Canada. J. Hydrol. 2021, 594, 125929. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).