A Calibrated GPT3 (CGPT3) Model for the Site-Specific Zenith Hydrostatic Delay Estimation in the Chinese Mainland and Its Surrounding Areas
Abstract
:1. Introduction
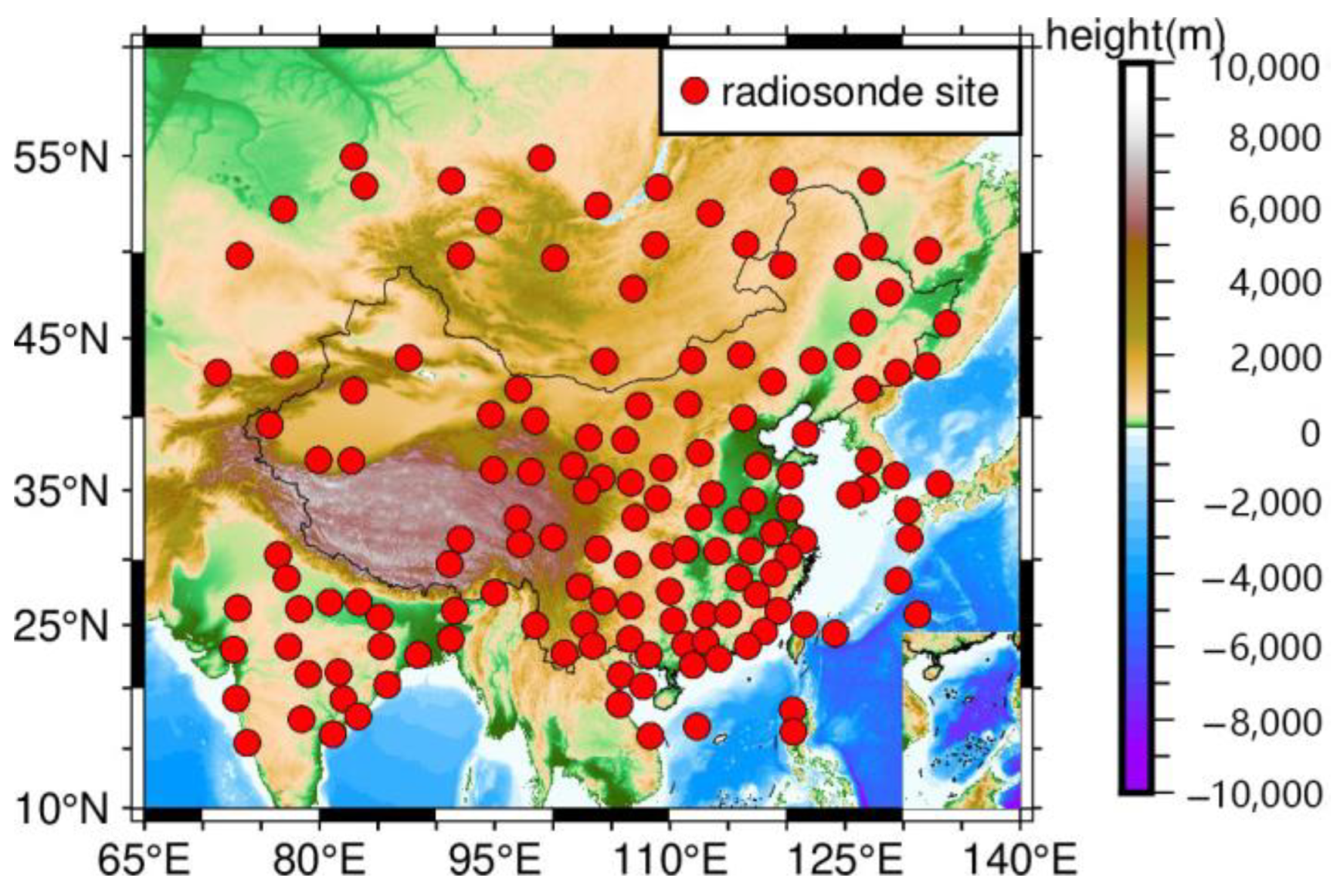
2. Study Area and Data
2.1. Study Area
2.2. Dataset
3. Methods
3.1. Retrieval of ZHD
3.2. GPT3 Model
3.3. GTrop Model
3.4. Performance Validation Metrics
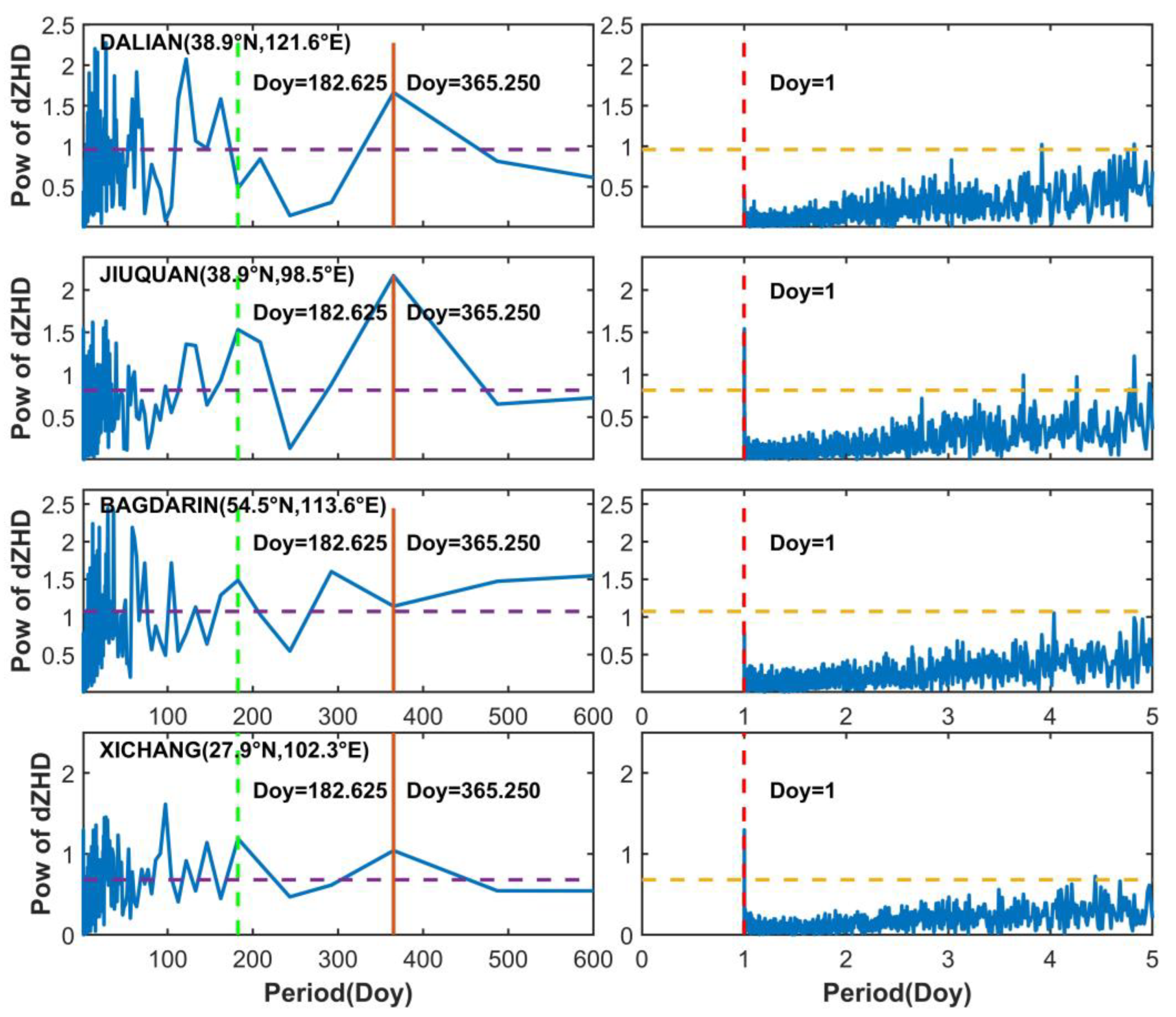
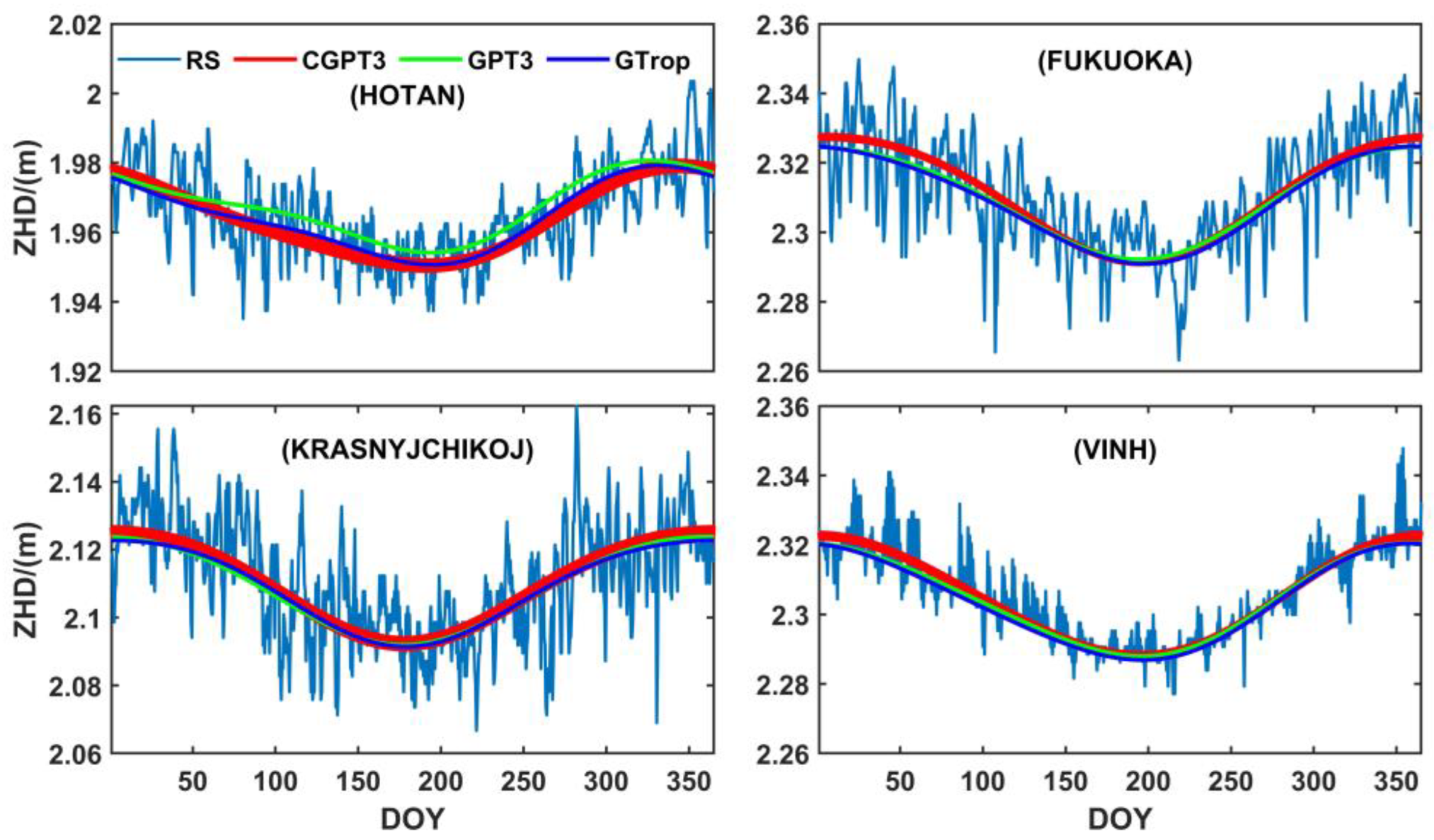
3.5. Variations of GPT3 ZHD Residuals
3.6. Specific Site Calibration Model for GPT3 ZHD
4. Results
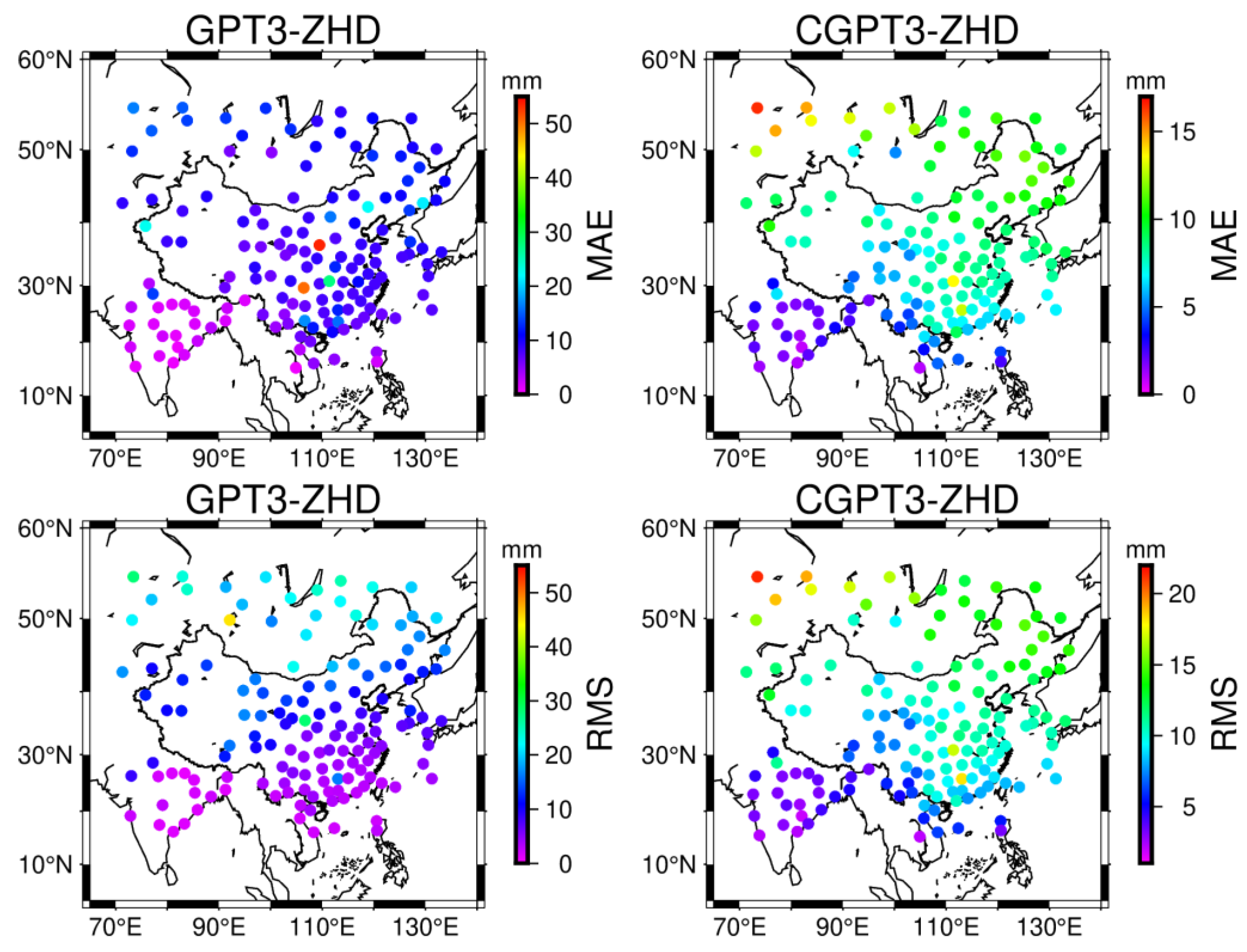
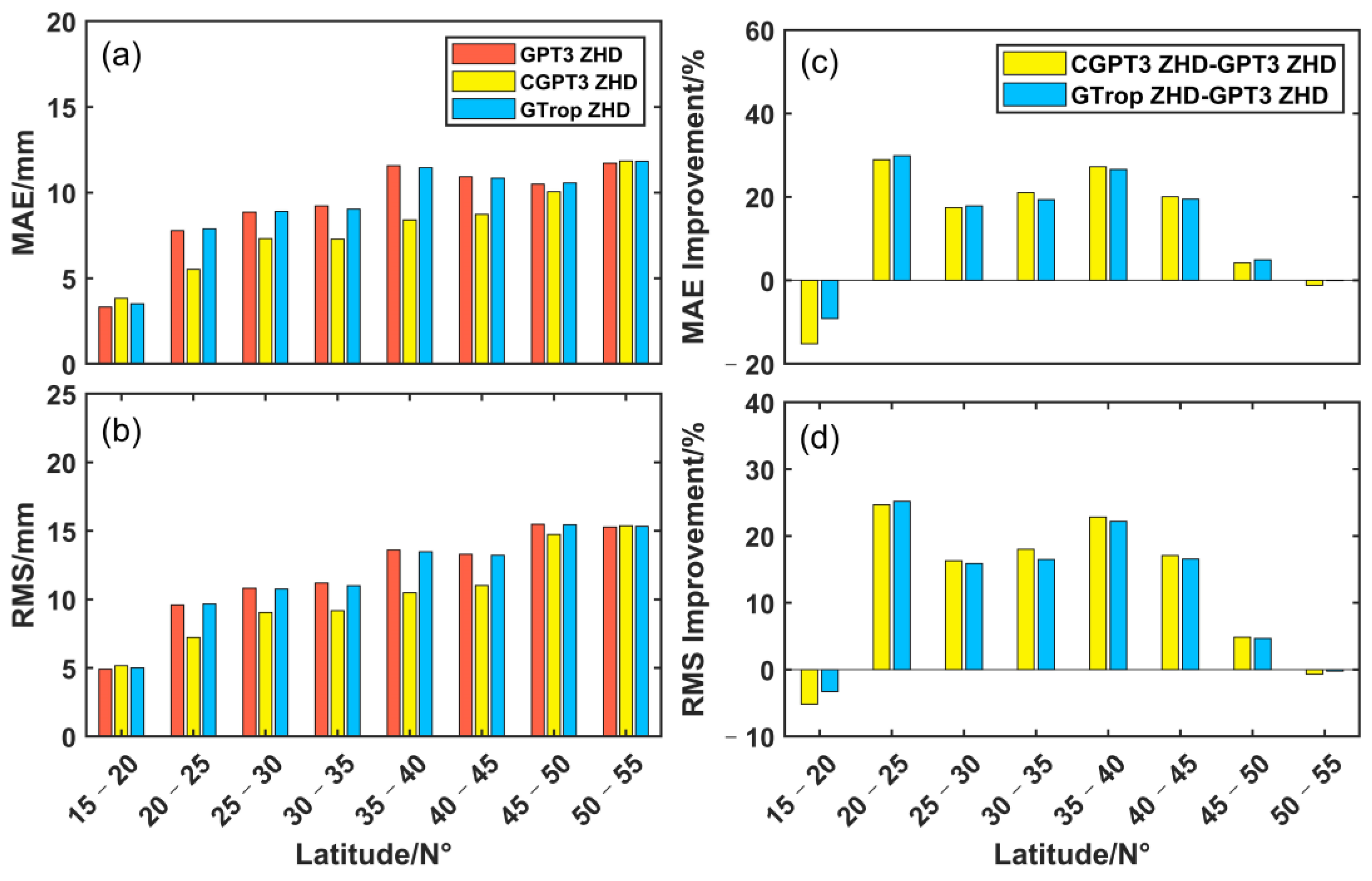
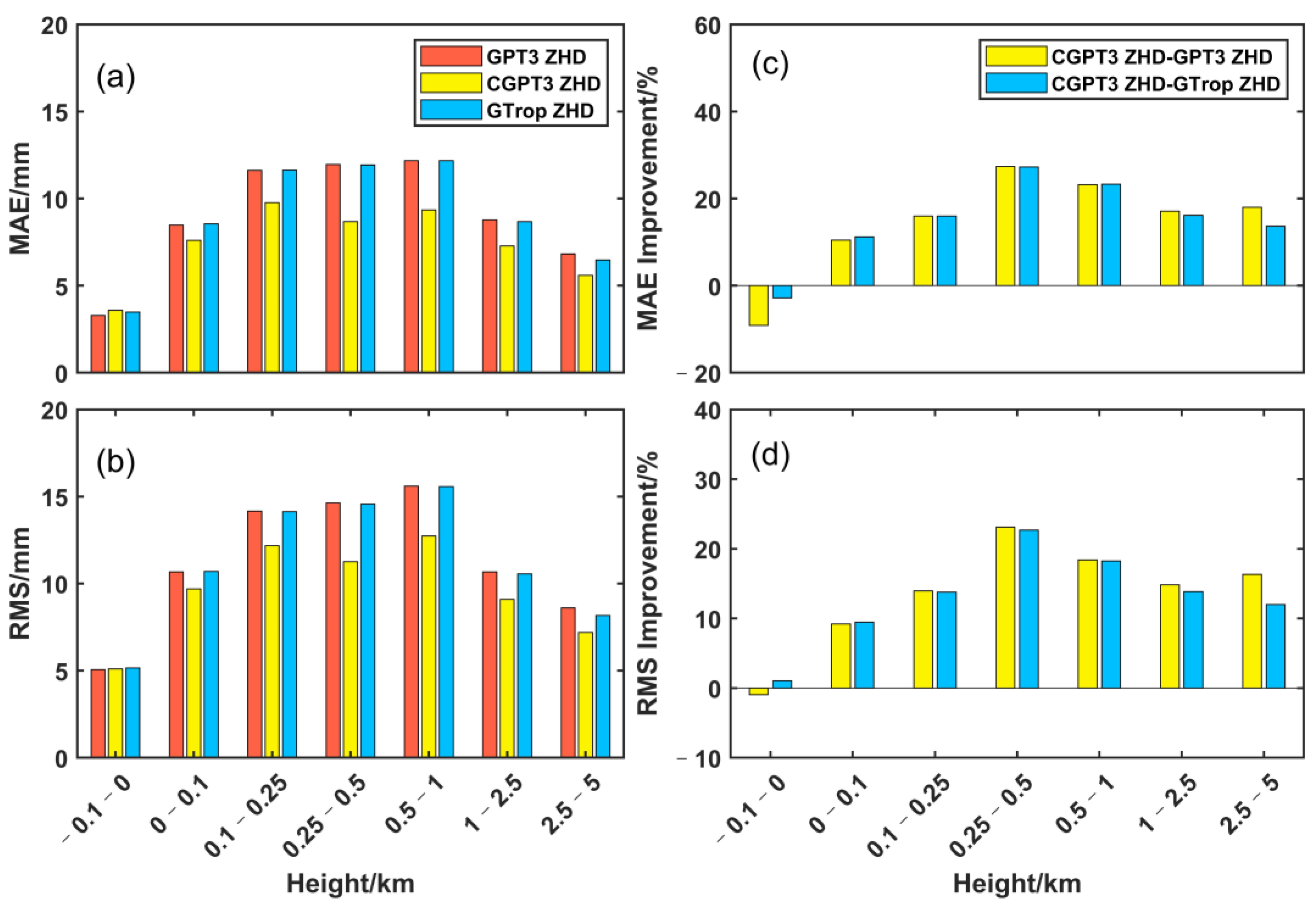
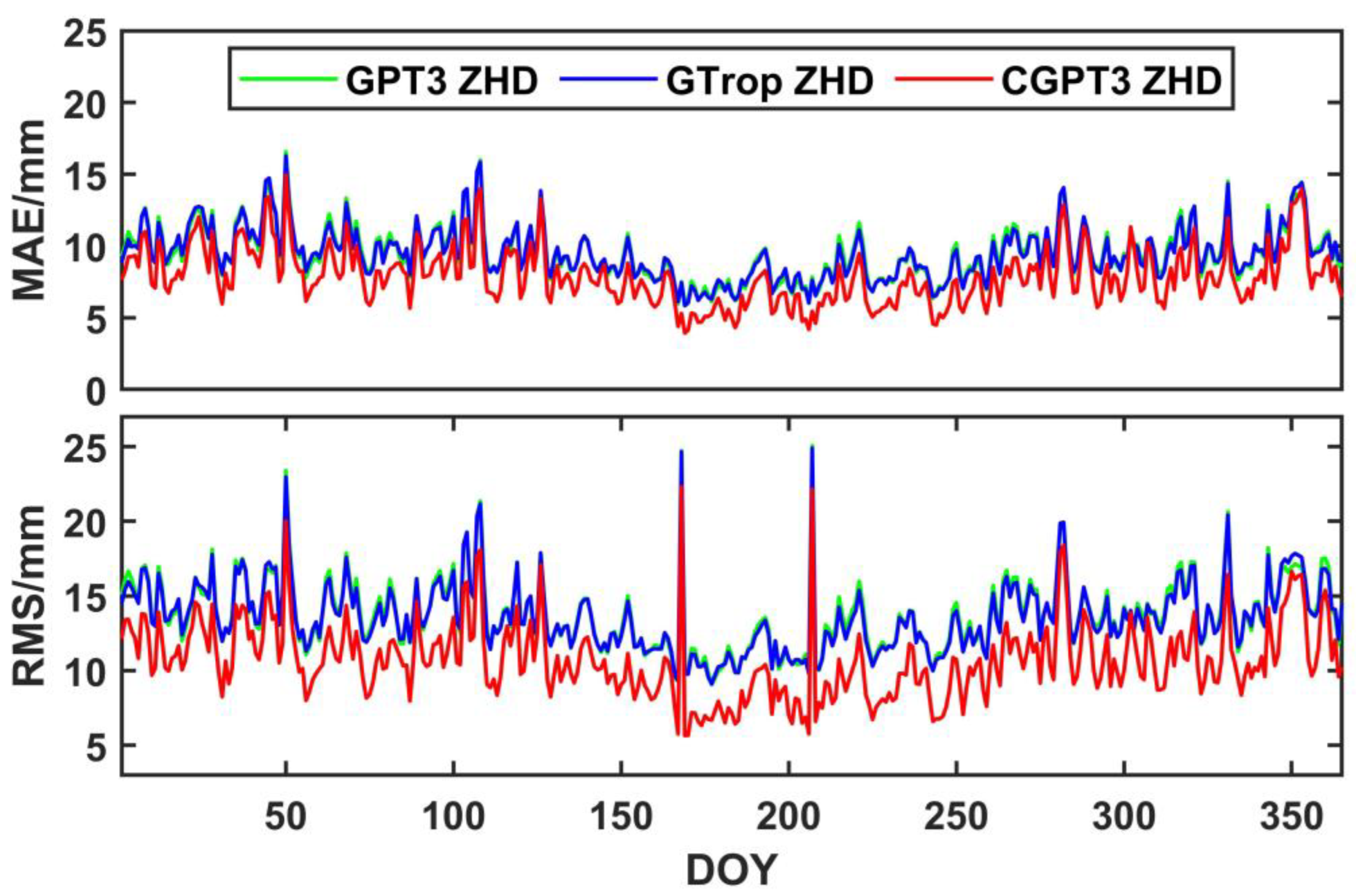
4.1. Validation of Internal Accuracy
4.2. Validation of External Accuracy
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Zus, F.; Heinkelmann, R.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Improving BeiDou Real-Time Precise Point Positioning with Numerical Weather Models. J. Geod. 2017, 91, 1019–1029. [Google Scholar] [CrossRef]
- Rahimi, Z.; Mohd Shafri, H.Z.; Othman, F.; Norman, M. Effect of Tropospheric Models on Derived Precipitable Water Vapor over Southeast Asia. J. Atmos. Sol. Terr. Phys. 2017, 157–158, 55–66. [Google Scholar] [CrossRef]
- Tregoning, P.; Herring, T.A. Impact of a Priori Zenith Hydrostatic Delay Errors on GPS Estimates of Station Heights and Zenith Total Delays. Geophys. Res. Lett. 2006, 33, L23303. [Google Scholar] [CrossRef] [Green Version]
- Arief, S.; Heki, K. GNSS Meteorology for Disastrous Rainfalls in 2017–2019 Summer in SW Japan: A New Approach Utilizing Atmospheric Delay Gradients. Front. Earth Sci. 2020, 8, 182. [Google Scholar] [CrossRef]
- Hordyniec, P.; Bosy, J.; Rohm, W. Assessment of Errors in Precipitable Water Data Derived from Global Navigation Satellite System Observations. J. Atmos. Sol. Terr. Phys. 2015, 129, 69–77. [Google Scholar] [CrossRef]
- Singh, D.; Ghosh, J.; Kashyap, D. Development of a Site-Specific ZHD Model Using Radiosonde Data. Acta Geod. Geophys. Hung. 2012, 47, 90–100. [Google Scholar] [CrossRef]
- Hopfield, H.S. Tropospheric Effect on Electromagnetically Measured Range: Prediction from Surface Weather Data. Radio Sci. 1971, 6, 357–367. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the Theory of Atmospheric Refraction. Bull. Geod. 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Final Contract Report for Nav Canada, Department of Geodesy and Geomatics Engineering Technical Report No. 187; University of New Brunswick: Fredericton, NB, Canada, 1997. [Google Scholar]
- Leandro, R.F.; Langley, R.B.; Santos, M.C. UNB3m_pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques. GPS Solut. 2008, 12, 65–70. [Google Scholar] [CrossRef]
- Krueger, E.; Schueler, T.; Arbesser-Rastburg, B. The Standard Tropospheric Correction Model for the European Satellite Navigation System Galileo. Proc. General Assembly URSI. 2005, 23–29. [Google Scholar]
- Schüler, T. The TropGrid2 Standard Tropospheric Correction Model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [Green Version]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Li, L.; Wu, S.; Zhang, K.; Wang, X.; Li, W.; Shen, Z.; Zhu, D.; He, Q.; Wan, M. A New Zenith Hydrostatic Delay Model for Real-Time Retrievals of GNSS-PWV. Atmos. Meas. Tech. 2021, 14, 6379–6394. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Li, J.; Zhang, C.; Chen, M. Assessment of the Troposphere Products Derived From VMF Data Server With ERA5 and IGS Data Over China. Earth Space Sci. 2021, 8, e2021EA001815. [Google Scholar] [CrossRef]
- Kim, E.-H.; Lee, E.; Lee, S.-W.; Lee, Y.H. Characteristics and Effects of Ground-Based GNSS Zenith Total Delay Observation Errors in the Convective-Scale Model. J. Meteorol. Soc. Jpn. 2019, 97, 1009–1021. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Wang, J.; Wang, A.; Ding, J.; Zhang, Y. SHAtropE—A Regional Gridded ZTD Model for China and the Surrounding Areas. Remote Sens. 2020, 12, 165. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Li, Z.; Blewitt, G. Global Comparisons of ERA5 and the Operational HRES Tropospheric Delay and Water Vapor Products With GPS and MODIS. Earth Space Sci. 2021, 8, e2020EA001417. [Google Scholar] [CrossRef]
- Mao, J.; Wang, Q.; Liang, Y.; Cui, T. A New Simplified Zenith Tropospheric Delay Model for Real-Time GNSS Applications. GPS Solut. 2021, 25, 43. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; He, C.; Cheng, Y.; Li, X. Determination of Zenith Hydrostatic Delay and Its Impact on GNSS-Derived Integrated Water Vapor. Atmos. Meas. Tech. 2017, 10, 2807–2820. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Zhang, B.; Li, J.; Yao, Y.; Liu, L.; Ran, Q.; Xiong, Z. A Regional Model for Predicting Tropospheric Delay and Weighted Mean Temperature in China Based on GRAPES_MESO Forecasting Products. Remote Sens. 2021, 13, 2644. [Google Scholar] [CrossRef]
- Wang, H.S.; Shi, C.; Cao, Y.C. Analysis of Regional Distribution and Change of Tropospheric Delay. AMM 2014, 577, 1189–1192. [Google Scholar] [CrossRef]
- Huang, L.; Wang, X.; Xiong, S.; Li, J.; Liu, L.; Mo, Z.; Fu, B.; He, H. High-Precision GNSS PWV Retrieval Using Dense GNSS Sites and in-Situ Meteorological Observations for the Evaluation of MERRA-2 and ERA5 Reanalysis Products over China. Atmos. Res. 2022, 276, 106247. [Google Scholar] [CrossRef]
- Huang, L.; Zhu, G.; Liu, L.; Chen, H.; Jiang, W. A Global Grid Model for the Correction of the Vertical Zenith Total Delay Based on a Sliding Window Algorithm. GPS Solut. 2021, 25, 98. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z. A Comprehensive Evaluation and Analysis of the Performance of Multiple Tropospheric Models in China Region. IEEE Trans. Geosci. Remote Sens. 2016, 54, 663–678. [Google Scholar] [CrossRef]
- Chen, P.; Ma, Y.; Liu, H.; Zheng, N. A New Global Tropospheric Delay Model Considering the Spatiotemporal Variation Characteristics of ZTD With Altitude Coefficient. Earth Space Sci. 2020, 7, e2019EA000888. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Cao, Y.; Liang, H.; Shi, C.; Huang, J.; Liu, W.; Zhang, Y.; Fan, B. Corrections of Radiosonde-Based Precipitable Water Using Ground-Based GPS and Applications on Historical Radiosonde Data Over China. J. Geophys. Res. Atmos. 2019, 124, 3208–3222. [Google Scholar] [CrossRef]
- Li, T.; Wang, L.; Chen, R.; Fu, W.; Xu, B.; Jiang, P.; Liu, J.; Zhou, H.; Han, Y. Refining the Empirical Global Pressure and Temperature Model with the ERA5 Reanalysis and Radiosonde Data. J. Geod. 2021, 95, 31. [Google Scholar] [CrossRef]
- Miranda, P.M.A.; Mateus, P. Improved GNSS Water Vapor Tomography With Modified Mapping Functions. Geophys. Res. Lett. 2022, 49, e2022GL100140. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787. [Google Scholar] [CrossRef]
- Vedel, H.; Mogensen, K.S.; Huang, X.-Y. Calculation of Zenith Delays from Meteorological Data Comparison of NWP Model, Radiosonde and GPS Delays. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 497–502. [Google Scholar] [CrossRef]
- Xie, W.; Huang, G.; Fu, W.; Shu, B.; Cui, B.; Li, M.; Yue, F. A Quality Control Method Based on Improved IQR for Estimating Multi-GNSS Real-Time Satellite Clock Offset. Measurement 2022, 201, 111695. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A Drought Monitoring Method Based on Precipitable Water Vapor and Precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Yao, Y. A Global Model for Estimating Tropospheric Delay and Weighted Mean Temperature Developed with Atmospheric Reanalysis Data from 1979 to 2017. Remote Sens. 2019, 11, 1893. [Google Scholar] [CrossRef] [Green Version]
- Dilmaghani, S.; Henry, I.C.; Soonthornnonda, P.; Christensen, E.R.; Henry, R.C. Harmonic Analysis of Environmental Time Series with Missing Data or Irregular Sample Spacing. Environ. Sci. Technol. 2007, 41, 7030–7038. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Yao, Y. A New Method for Vertical Stratification of Zenith Tropospheric Delay. Adv. Space Res. 2019, 63, 2857–2866. [Google Scholar] [CrossRef]
- Li, J.; Zhang, B.; Yao, Y.; Liu, L.; Sun, Z.; Yan, X. A Refined Regional Model for Estimating Pressure, Temperature, and Water Vapor Pressure for Geodetic Applications in China. Remote Sens. 2020, 12, 1713. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.-U.; Cho, J.-H.; Park, P.-H. Seasonal Variability of GPS-Derived Zenith Tropospheric Delay (1994–2006) and Climate Implications. J. Geophys. Res. 2007, 112, D09110. [Google Scholar] [CrossRef]
- Du, Z.; Zhao, Q.; Yao, W.; Yao, Y. Improved GPT2w (IGPT2w) Model for Site Specific Zenith Tropospheric Delay Estimation in China. J. Atmos. Sol. Terr. Phys. 2020, 198, 105202. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere Mapping Functions for GPS and Very Long Baseline Interferometry from European Centre for Medium-Range Weather Forecasts Operational Analysis Data: TROPOSPHERE MAPPING FUNCTIONS FROM ECMWF. J. Geophys. Res. 2006, 111, B02406. [Google Scholar] [CrossRef]

| Type 1 | Number |
|---|---|
| A | 102 |
| B | 90 |
| C | 63 |
| A + B | 31 |
| A + C | 18 |
| B + C | 12 |
| A + B + C | 27 |
| NAN | 8 |
| Model | MAE (mm) | RMS (mm) |
|---|---|---|
| GPT3 ZHD | 8.8 [0.6, 53.5] | 11.3 [2.0, 54.5] |
| CGPT3 ZHD | 7.3 [0.8, 16.4] | 9.6 [1.9, 21.4] |
| Model | MAE (mm) | RMS (mm) |
|---|---|---|
| GPT3 ZHD | 9.5 [1.5, 51.5] | 11.9 [3.1, 52.5] |
| GTrop ZHD | 9.5 [1.8, 51.2] | 11.8 [3.1, 52.2] |
| CGPT3 ZHD | 7.9 [1.9, 27.9] | 10.2 [3.1, 32.9] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, F.; Liu, L.; Huang, L.; Zhou, L.; He, H. A Calibrated GPT3 (CGPT3) Model for the Site-Specific Zenith Hydrostatic Delay Estimation in the Chinese Mainland and Its Surrounding Areas. Remote Sens. 2022, 14, 6357. https://doi.org/10.3390/rs14246357
Li J, Li F, Liu L, Huang L, Zhou L, He H. A Calibrated GPT3 (CGPT3) Model for the Site-Specific Zenith Hydrostatic Delay Estimation in the Chinese Mainland and Its Surrounding Areas. Remote Sensing. 2022; 14(24):6357. https://doi.org/10.3390/rs14246357
Chicago/Turabian StyleLi, Junyu, Feijuan Li, Lilong Liu, Liangke Huang, Lv Zhou, and Hongchang He. 2022. "A Calibrated GPT3 (CGPT3) Model for the Site-Specific Zenith Hydrostatic Delay Estimation in the Chinese Mainland and Its Surrounding Areas" Remote Sensing 14, no. 24: 6357. https://doi.org/10.3390/rs14246357
APA StyleLi, J., Li, F., Liu, L., Huang, L., Zhou, L., & He, H. (2022). A Calibrated GPT3 (CGPT3) Model for the Site-Specific Zenith Hydrostatic Delay Estimation in the Chinese Mainland and Its Surrounding Areas. Remote Sensing, 14(24), 6357. https://doi.org/10.3390/rs14246357





