Drought Monitoring and Performance Evaluation Based on Machine Learning Fusion of Multi-Source Remote Sensing Drought Factors
Abstract
:1. Introduction
2. Materials and Methods
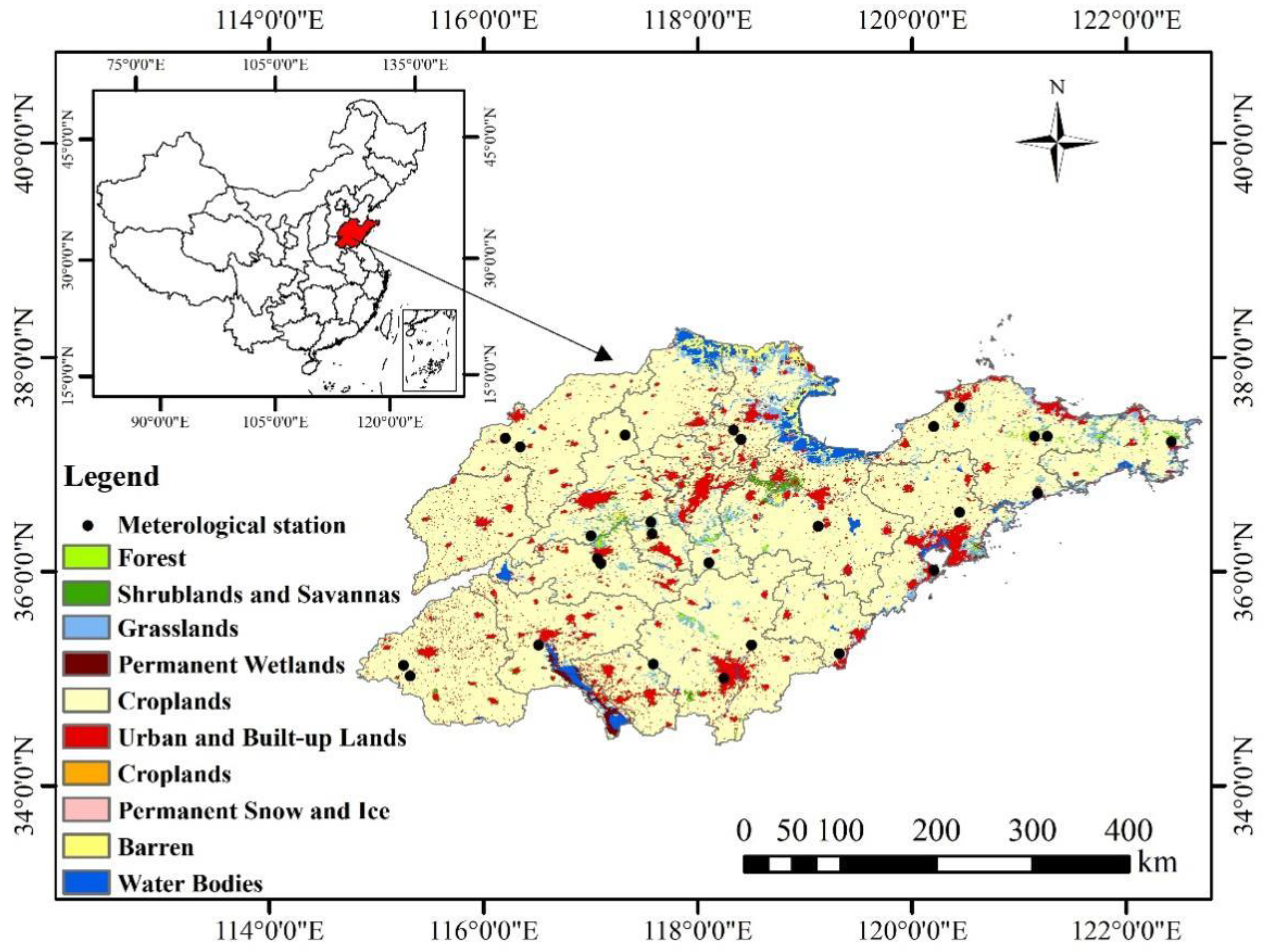
2.1. Study Area
2.2. Data
2.2.1. MODIS Data
2.2.2. GPM Data
2.2.3. GLDAS Data
2.2.4. Observation Data
2.3. Method
2.3.1. Modeling Methodology
2.3.2. Standardized Precipitation Evapotranspiration Index
- (1)
- Calculation of monthly potential evapotranspiration using Thornthwaite method:
- (2)
- Calculate the difference between precipitation and potential evapotranspiration for each month.
- (3)
- To normalize , first, a Log-logistic probability density function is used to build the data series:
- (4)
- Under normal normalization of the cumulative probability density function, the probability of exceeding a certain value is and the probability of weighted moments are .
2.3.3. Establishment of Drought Prediction Indicators
2.4. Machine Learning Approaches
2.4.1. Bias-Corrected Random Forest
- (1)
- Firstly, build the RF model by training dataset Ytrain = RF (Xtrain), where Xtrain and Ytrain represent the independent and dependent variables, respectively.
- (2)
- Calculate the estimated value and residual, rtrain = Ytrain − Ypredict, where rtrain represents the residual and Ypredict represents the estimated value.
- (3)
- Taking the residuals obtained in step (2) to be the dependent variable and training dataset in step (1) to be the independent variable, fit the random forest model, rtrain = rfres (Xtrain, Ytrain). This step is used to estimate the residual of the test dataset.
- (4)
- Calculate the estimated value Ytest from the RF model obtained in step (1) and the test dataset Xtest, Ytest = RF (Xtest).
- (5)
- Calculate the estimated residual using the rfres model in step (3), the estimated value in step 4, and the independent variables in the test dataset, rtest = rfres (Xtest, Ytest).
- (6)
- The estimated residual rtest is added to the estimated value Ytest for deviation correction, Ybias-correction = Ytest + rtest.
2.4.2. XGBoost
- (1)
- To grow a tree, constantly add new trees and continuously split features. Each time a tree is added, a new function is learned f(x) to fit the residual of the last estimation. The optimal model is constructed by minimizing the loss function: .
- (2)
- XGBoost needs to estimate the result of a sample after it has been trained to obtain k trees. Actually, according to the characteristics of this sample, the sample will fall on one corresponding leaf node per tree, and each leaf node corresponds to a score.
2.4.3. Support Vector Machine
2.5. Accuracy Evaluation
3. Results
3.1. Model Accuracy Comparison
3.2. Model Stability Evaluation
3.3. Analyzing the Relative Importance of Drought-Influencing Factors Using the BRF Model
3.4. Simulation of Drought by Spatial Distribution of SPEI-3 in Typical Years
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, S.; Tong, D.M.; Xu, Z.T.; Henchiri, M.; Wilson, K.; Shi, S.Q.; Zhang, J.H. Characterization of Drought Monitoring Events through Modis-and Trmm-Based Dsi and Tvdi over South Asia During 2001–2017. Environ. Sci. Pollut. Res. 2019, 26, 33568–33581. [Google Scholar] [CrossRef] [PubMed]
- Quiring, S.M.; Papakryiakou, T.N. An Evaluation of Agricultural Drought Indices for the Canadian Prairies. Agric. For. Meteorol. 2003, 118, 49–62. [Google Scholar] [CrossRef]
- Wei, W.; Pang, S.F.; Wang, X.F.; Zhou, L.; Xie, B.B.; Zhou, J.J.; Li, C.H. Temperature Vegetation Precipitation Dryness Index (Tvpdi)-Based Dryness-Wetness Monitoring in China. Remote Sens. Environ. 2020, 248, 111957. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Lei, T.J.; Peng, L.L. Drought Evolution, Severity and Trends in Mainland China over 1961–2013. Sci. Total Environ. 2018, 616, 73–89. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Van Der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global Warming and Changes in Drought. Nat. Clim. Change 2014, 4, 17. [Google Scholar] [CrossRef]
- Dai, A.G. Erratum: Drought under Global Warming: A Review. Wiley Interdiscip. Rev.-Clim. Chang. 2012, 3, 617. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; Quiring, S.M.; Pena-Gallardo, M.; Yuan, S.S.; Dominguez-Castro, F. A Review of Environmental Droughts: Increased Risk under Global Warming? Earth-Sci. Rev. 2020, 201, 102953. [Google Scholar] [CrossRef]
- Daryanto, S.; Wang, L.X.; Jacinthe, P.A. Global Synthesis of Drought Effects on Food Legume Production. PLoS ONE 2015, 10, e0127401. [Google Scholar] [CrossRef] [Green Version]
- Daryanto, S.; Wang, L.X.; Jacinthe, P.A. Global Synthesis of Drought Effects on Maize and Wheat Production. PLoS ONE 2016, 11, e0156362. [Google Scholar] [CrossRef] [Green Version]
- Loon, V.; Anne, F. Hydrological Drought Explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; Mcdowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A Global Overview of Drought and Heat-Induced Tree Mortality Reveals Emerging Climate Change Risks for Forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef] [Green Version]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogee, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A.; et al. Europe-Wide Reduction in Primary Productivity Caused by the Heat and Drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.S.; Running, S.W. Drought-Induced Reduction in Global Terrestrial Net Primary Production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [Green Version]
- Aadhar, S.; Mishra, V. High-Resolution near Real-Time Drought Monitoring in South Asia. Sci. Data 2017, 4, 170145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, B.; Wu, J.J.; Lu, A.F.; Cui, X.F.; Zhou, L.; Liu, M.; Zhao, L. Quantitative Assessment and Spatial Characteristic Analysis of Agricultural Drought Risk in China. Nat. Hazards 2013, 66, 155–166. [Google Scholar] [CrossRef]
- Mottaleb, K.A.; Gumma, M.K.; Mishra, A.K.; Mohanty, S. Quantifying Production Losses Due to Drought and Submergence of Rainfed Rice at the Household Level Using Remotely Sensed Modis Data. Agric. Syst. 2015, 137, 227–235. [Google Scholar] [CrossRef]
- Prodhan, F.A.; Zhang, J.H.; Yao, F.M.; Shi, L.M.; Sharma, T.P.P.; Zhang, D.; Cao, D.; Zheng, M.X.; Ahmed, N.; Mohana, H.P. Deep Learning for Monitoring Agricultural Drought in South Asia Using Remote Sensing Data. Remote Sens. 2021, 13, 1715. [Google Scholar] [CrossRef]
- Yang, X.; Li, D. Temporal and Spatial Evolution Characteristics of Strong Drought Events in North and Northeast China. Arid Land Geogr. 2019, 42, 810–821. [Google Scholar]
- Ren, J.; Zhang, T. Evolution Characteristics of Drought and Flood in Shandong Province in Recent 45years Based on Standardized Precipitation Index. Res. Soil Water Conserv. 2021, 28, 149. [Google Scholar]
- Zhang, J.; Mu, Q.Z.; Huang, J.X. Assessing the Remotely Sensed Drought Severity Index for Agricultural Drought Monitoring and Impact Analysis in North China. Ecol. Indic. 2016, 63, 296–309. [Google Scholar] [CrossRef]
- Yan, H.; Wan, Y.; Yan, X.; Xie, Y. A Study of the Temporal and Spatial Features of Dryness & Wetness Last 500-Year Period in China. J. Yunnan Univ. (Nat. Sci.) 2004, 26, 139–143. [Google Scholar]
- Zhang, Y.; Wang, C.; Zhang, J. Analysis of the Spatial and Temporal Characteristics of Drought in the North China Plain Based on Standardized Precipitation Evapotranspiration Index. Acta Ecol. Sin. 2015, 35, 7097–7107. [Google Scholar]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Vicente-Serrano, S.M.; Begueria, S.; Lopez-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Feng, P.Y.; Wang, B.; Liu, D.L.; Yu, Q. Machine Learning-Based Integration of Remotely-Sensed Drought Factors Can Improve the Estimation of Agricultural Drought in South-Eastern Australia. Agric. Syst. 2019, 173, 303–316. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J.; Carbone, G.J. Monitoring Agricultural Drought for Arid and Humid Regions Using Multi-Sensor Remote Sensing Data. Remote Sens. Environ. 2010, 114, 2875–2887. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, J.H.; Zhang, H.R.; Yao, F.M.; Bai, Y.; Zhang, S.; Meng, X.L.; Liu, Q. Evaluating the Performance of Eight Drought Indices for Capturing Soil Moisture Dynamics in Various Vegetation Regions over China. Sci. Total Environ. 2021, 789, 147803. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Liu, Q.Z.; Zhang, S.Y.; Chen, X.G.; Ji, Y.D.; Liu, F.G.; Pulatov, A.; Feng, P.Y. Response of Wheat and Maize Growth-Yields to Meteorological and Agricultural Droughts Based on Standardized Precipitation Evapotranspiration Indexes and Soil Moisture Deficit Indexes. Agric. Water Manag. 2022, 266, 107566. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Jang, E.; Rhee, J. Drought Assessment and Monitoring through Blending of Multi-Sensor Indices Using Machine Learning Approaches for Different Climate Regions. Agric. For. Meteorol. 2016, 216, 157–169. [Google Scholar] [CrossRef]
- Swain, S.; Wardlow, B.D.; Narumalani, S.; Tadesse, T.; Callahan, K. Assessment of Vegetation Response to Drought in Nebraska Using Terra-Modis Land Surface Temperature and Normalized Difference Vegetation Index. Giscience Remote Sens. 2011, 48, 432–455. [Google Scholar] [CrossRef]
- Ali, S.; Henchiri, M.; Yao, F.M.; Zhang, J.H. Analysis of Vegetation Dynamics, Drought in Relation with Climate over South Asia from 1990 to 2011. Environ. Sci. Pollut. Res. 2019, 26, 11470–11481. [Google Scholar] [CrossRef]
- Shi, S.Q.; Yao, F.M.; Zhang, J.H.; Yang, S.S. Evaluation of Temperature Vegetation Dryness Index on Drought Monitoring over Eurasia. IEEE Access 2020, 8, 30050–30059. [Google Scholar] [CrossRef]
- Wu, D.; Qu, J.J.; Hao, X.J. Agricultural Drought Monitoring Using Modis-Based Drought Indices over the USA Corn Belt. Int. J. Remote Sens. 2015, 36, 5403–5425. [Google Scholar] [CrossRef]
- Souza, A.; Neto, A.R.; Rossato, L.; Alvala, R.C.S.; Souza, L.L. Use of Smos L3 Soil Moisture Data: Validation and Drought Assessment for Pernambuco State, Northeast Brazil. Remote Sens. 2018, 10, 1314. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Gao, J.; Zhang, B. Monitoring of Crops Growth Based on Ndvi and Evi. Trans. Chin. Soc. Agric. Mach. 2019, 50, 153–161. [Google Scholar]
- Gu, Y.X.; Brown, J.F.; Verdin, J.P.; Wardlow, B. A Five-Year Analysis of Modis Ndvi and Ndwi for Grassland Drought Assessment over the Central Great Plains of the United States. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Lei, Q.; Zhang, X.; Wang, X.; He, X.; Shang, C. Responses of Vegetation Index to Meteorological Drought in Dongting Lake Basin Based on Modis-Evi and Ci. Resour. Environ. Yangtze Basin 2019, 28, 981–993. [Google Scholar]
- Wang, K.Y.; Li, T.J.; Wei, J.H. Exploring Drought Conditions in the Three River Headwaters Region from 2002 to 2011 Using Multiple Drought Indices. Water 2019, 11, 190. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Liu, R.; Liu, S. Review of Drought Monitoring by Remote Sensing. J. Geo-Inf. Sci. 2012, 14, 232–239. [Google Scholar] [CrossRef]
- Alizadeh, M.R.; Nikoo, M.R. A Fusion-Based Methodology for Meteorological Drought Estimation Using Remote Sensing Data. Remote Sens. Environ. 2018, 211, 229–247. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.X.; Zhang, S.Y.; Zhu, D.H. Drought Forecasting Based on the Remote Sensing Data Using Arima Models. Math. Comput. Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought Modeling—A Review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Wanders, N.; Wood, E.F. Improved Sub-Seasonal Meteorological Forecast Skill Using Weighted Multi-Model Ensemble Simulations. Environ. Res. Lett. 2016, 11, 094007. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought Forecasting Using Artificial Neural Networks and Time Series of Drought Indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Wang, Q.J.; Schepen, A.; Robertson, D.E. Merging Seasonal Rainfall Forecasts from Multiple Statistical Models through Bayesian Model Averaging. J. Clim. 2012, 25, 5524–5537. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Input Selection and Optimisation for Monthly Rainfall Forecasting in Queensland, Australia, Using Artificial Neural Networks. Atmos. Res. 2014, 138, 166–178. [Google Scholar] [CrossRef]
- Hao, Z.C.; Singh, V.P.; Xia, Y.L. Seasonal Drought Prediction: Advances, Challenges, and Future Prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Barua, S.; Ng, A.W.M.; Perera, B.J.C. Artificial Neural Network-Based Drought Forecasting Using a Nonlinear Aggregated Drought Index. J. Hydrol. Eng. 2012, 17, 1408–1413. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches. Atmosphere 2020, 11, 585. [Google Scholar] [CrossRef]
- Khan, N.; Sachindra, D.A.; Shahid, S.; Ahmed, K.; Shiru, M.S.; Nawaz, N. Prediction of Droughts over Pakistan Using Machine Learning Algorithms. Adv. Water Resour. 2020, 139, 103562. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought Forecasting Using Feed-Forward Recursive Neural Network. Ecol. Model. 2006, 198, 127–138. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-Term Spi Drought Forecasting in the Awash River Basin in Ethiopia Using Wavelet Neural Network and Wavelet Support Vector Regression Models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E.; Pote, J.W. An Integrated Svr and Crop Model to Estimate the Impacts of Irrigation on Daily Groundwater Levels. Agric. Syst. 2018, 159, 248–259. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Song, J. Bias Corrections for Random Forest in Regression Using Residual Rotation. J. Korean Stat. Soc. 2015, 44, 321–326. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C.; Assoc Comp, M. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Chen, Y.; Niu, J.Q.; Chen, G.Q.; Wang, J.; Cao, S.L.; Publishing, I.O.P. Precipitation Sequence Analysis of Representative Stations in Shandong Province from 1956 to 2016. In Proceedings of the 6th International Conference on Energy Materials and Environment Engineering (ICEMEE), Zhangjiajie, China, 24–26 April 2020. [Google Scholar]
- Li, H.; Wang, W. Climate Characteristics of Seasonal Drought for Crops Growth in Shandong. J. Arid Land Resour. Environ. 2015, 29, 191–196. [Google Scholar]
- Li, F.; Yang, X. Changes and Driving Force of Grain Production in Shandong Province During 1999–2014. Acta Agric. Zhejiangensis 2016, 28, 535–542. [Google Scholar]
- Han, H.Z.; Bai, J.J.; Yan, J.W.; Yang, H.Y.; Ma, G. A Combined Drought Monitoring Index Based on Multi-Sensor Remote Sensing Data and Machine Learning. Geocarto Int. 2021, 36, 1161–1177. [Google Scholar] [CrossRef]
- Shen, R.P.; Huang, A.Q.; Li, B.L.; Guo, J. Construction of a Drought Monitoring Model Using Deep Learning Based on Multi-Source Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 48–57. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; Garcia-Ortega, E.; Machado, L.A.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global Precipitation Measurement: Methods, Datasets and Applications. Atmos. Res. 2012, 104, 70–97. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, D.H.; Yang, Z.Y.; Hu, Y.; Weng, B.S.; Gong, B.Y. Improvement and Adaptability Evaluation of Standardized Precipitation Evapotranspiration Index. Acta Phys. Sin. 2015, 64, 049202. [Google Scholar] [CrossRef]
- Almeida-Naunay, A.F.; Villeta, M.; Quemada, M.; Tarquis, A.M. Assessment of Drought Indexes on Different Time Scales: A Case in Semiarid Mediterranean Grasslands. Remote Sens. 2022, 14, 565. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, X.; Wang, Y.; Wang, W. Effects of Drought in Multi-Time Scale on Wheat Crop in Eastern Agricultural Region of Qinghai Province. J. Irrig. Drain. 2016, 35, 92–97. [Google Scholar]
- Javed, T.; Zhang, J.H.; Bhattarai, N.; Sha, Z.; Rashid, S.; Yun, B.; Ahmad, S.; Henchiri, M.; Kamran, M. Drought Characterization across Agricultural Regions of China Using Standardized Precipitation and Vegetation Water Supply Indices. J. Clean. Prod. 2021, 313, 127866. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhou, Z.M.; Yao, F.M.; Yang, L.M.; Hao, C. Validating the Modified Perpendicular Drought Index in the North China Region Using in Situ Soil Moisture Measurement. IEEE Geosci. Remote Sens. Lett. 2015, 12, 542–546. [Google Scholar] [CrossRef]
- Wu, L. Classification of Drought Grades Based on Temperature Vegetation Drought Index Using the Modis Data. Res. Soil Water Conserv. 2017, 24, 130–135. [Google Scholar]
- Wang, Y.P.; Wang, S.; Zhao, W.W.; Liu, Y.X. The Increasing Contribution of Potential Evapotranspiration to Severe Droughts in the Yellow River Basin. J. Hydrol. 2022, 605, 127310. [Google Scholar] [CrossRef]
- Seiler, R.A.; Kogan, F.; Sullivan, J. Avhrr-Based Vegetation and Temperature Condition Indices for Drought Detection in Argentina. Adv. Space Res. 1998, 21, 481–484. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of Vegetation Index and Brightness Temperature for Drought Detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Ishwaran, H.; Malley, J.D. Synthetic Learning Machines. Biodata Min. 2014, 7, 28. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.Y.; Lu, Y. Bias-Corrected Random Forests in Regression. J. Appl. Stat. 2012, 39, 151–160. [Google Scholar] [CrossRef]
- Li, H.; Zhu, Y. Xgboost Algorithm Optimization Based on Gradient Distribution Harmonized Strategy. J. Comput. Appl. 2020, 40, 1633–1637. [Google Scholar]
- Chen, J.X.; Zhao, F.; Sun, Y.G.; Yin, Y.L. Improved Xgboost Model Based on Genetic Algorithm. Int. J. Comput. Appl. Technol. 2020, 62, 240–245. [Google Scholar] [CrossRef]
- Corinna, C.; Vladimir, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar]
- Haitao, L.I.; Haiyan, G.U.; Bing, Z.; Lianru, G. Research on Hyperspectral Remote Sensing Image Classification Based on Mnf and Svm. Remote Sens. Inf. 2007, 5, 12–15. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. Isprs J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Shen, R.; Guo, J.; Zhang, J.; Li, L. Construction of a Drought Monitoring Model Using the Random Forest Based Remote Sensing. J. Geo-Inf. Sci. 2017, 19, 125–133. [Google Scholar]
- Were, K.; Bui, D.T.; Dick, O.B.; Singh, B.R. A Comparative Assessment of Support Vector Regression, Artificial Neural Networks, and Random Forests for Predicting and Mapping Soil Organic Carbon Stocks across an Afromontane Landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Xu, Z.; Han, M. Spatio-Temporal Distribution Characteristics of Drought in Shandong Province and It Relationship with Enso. Chin. J. Eco-Agric. 2018, 26, 1236–1248. [Google Scholar]
- Yao, T.; Zhao, Q.; Li, X.Y.; Shen, Z.T.; Ran, P.Y.; Wu, W. Spatiotemporal Variations of Multi-Scale Drought in Shandong Province from 1961 to 2017. Water Supply 2021, 21, 525–541. [Google Scholar] [CrossRef]
- Yang, M.X.; Mou, Y.L.; Meng, Y.R.; Liu, S.; Peng, C.H.; Zhou, X.L. Modeling the Effects of Precipitation and Temperature Patterns on Agricultural Drought in China from 1949 to 2015. Sci. Total Environ. 2020, 711, 135139. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating Soil Moisture-Climate Interactions in a Changing Climate: A Review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Sims, A.P.; Niyogi, D.D.S.; Raman, S. Adopting Drought Indices for Estimating Soil Moisture: A North Carolina Case Study. Geophys. Res. Lett. 2002, 29, 24-1–24-4. [Google Scholar] [CrossRef]









| Data | Temporal Resolution | Spatial Resolution | Time Span | Source |
|---|---|---|---|---|
| Precipitation | 1-month | 0.1° | 2001~2020 | GPM |
| NDVI | 1-month | 1 km | 2002~2020 | MODIS |
| EVI | 1-month | 1 km | 2002~2020 | MODIS |
| LST | 8-day | 1 km | 2002~2020 | MODIS |
| Soil moisture | 1-month | 0.25° | 2002~2020 | GLDAS |
| Evapotranspiration | 1-month | 0.25° | 2002~2020 | GLDAS |
| Potential evapotranspiration | 1-month | 0.25° | 2002~2020 | GLDAS |
| Grade | Drought Condition | SPEI |
|---|---|---|
| I | No drought | −0.5 < SPEI |
| II | Light drought | −1.0 < SPEI ≤ −0.5 |
| III | Moderate drought | −1.5 < SPEI ≤ −1.0 |
| IV | Severe drought | −2.0 < SPEI ≤ −1.5 |
| V | Extreme drought | SPEI ≤ −2.0 |
| Drought Index | Formula | Reference |
|---|---|---|
| PCI | [26] | |
| SMCI | [70] | |
| TCI | [71] | |
| VCI | [71] | |
| Scaled EVI | [71] | |
| Scaled ET | [33] | |
| Scaled PET | [33] |
| Model | Parameters | |
|---|---|---|
| BRF | RF1: criterion = ‘mse’, n_estimators = 800, max_depth = 5, min_samples_leaf = 4, max_features = ‘auto’, random_state = 0, bootstrap = True | RF2: criterion = ‘mse’, n_estimators = 1000, max_depth = 5, min_samples_leaf = 4, max_features = ‘auto’, random_state = 0, bootstrap = True |
| XGBoost | n_estimators = 100, learning_rate = 0.04, max_depth = 5, gamma = 0.5, consample_bytree = 1, consample_bylevel = 1, subsample = 0.52, booster = ‘gbtree’, objective = ‘reg:squarederror’, reg_alpha = 0.7, reg_lambda = 0 | |
| SVM | kernel = ‘rbf’, gamma = 0.85, C = 50, tol = 0.01, cache_size = 5000, degree = 3, coef0 = 2.5 | |
| Impact Factors | Relative Importance (%) |
|---|---|
| One-month timescale precipitation, Pre_1 | 8.61 |
| Three-month timescale precipitation, Pre_3 | 55.17 |
| Land surface temperature, LST | 7.39 |
| Enhanced vegetation index, EVI | 3.54 |
| Normalized difference vegetation index, NDVI | 3.3 |
| Soil moisture, SM | 10.2 |
| Evapotranspiration, ET | 7.3 |
| Potential evapotranspiration, PET | 4.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhang, J.; Bai, Y.; Zhang, S.; Yang, S.; Henchiri, M.; Seka, A.M.; Nanzad, L. Drought Monitoring and Performance Evaluation Based on Machine Learning Fusion of Multi-Source Remote Sensing Drought Factors. Remote Sens. 2022, 14, 6398. https://doi.org/10.3390/rs14246398
Zhao Y, Zhang J, Bai Y, Zhang S, Yang S, Henchiri M, Seka AM, Nanzad L. Drought Monitoring and Performance Evaluation Based on Machine Learning Fusion of Multi-Source Remote Sensing Drought Factors. Remote Sensing. 2022; 14(24):6398. https://doi.org/10.3390/rs14246398
Chicago/Turabian StyleZhao, Yangyang, Jiahua Zhang, Yun Bai, Sha Zhang, Shanshan Yang, Malak Henchiri, Ayalkibet Mekonnen Seka, and Lkhagvadorj Nanzad. 2022. "Drought Monitoring and Performance Evaluation Based on Machine Learning Fusion of Multi-Source Remote Sensing Drought Factors" Remote Sensing 14, no. 24: 6398. https://doi.org/10.3390/rs14246398
APA StyleZhao, Y., Zhang, J., Bai, Y., Zhang, S., Yang, S., Henchiri, M., Seka, A. M., & Nanzad, L. (2022). Drought Monitoring and Performance Evaluation Based on Machine Learning Fusion of Multi-Source Remote Sensing Drought Factors. Remote Sensing, 14(24), 6398. https://doi.org/10.3390/rs14246398








