Flash Flood Water Depth Estimation Using SAR Images, Digital Elevation Models, and Machine Learning Algorithms
Abstract
:1. Introduction
2. Study Area and Dataset
2.1. Study Area
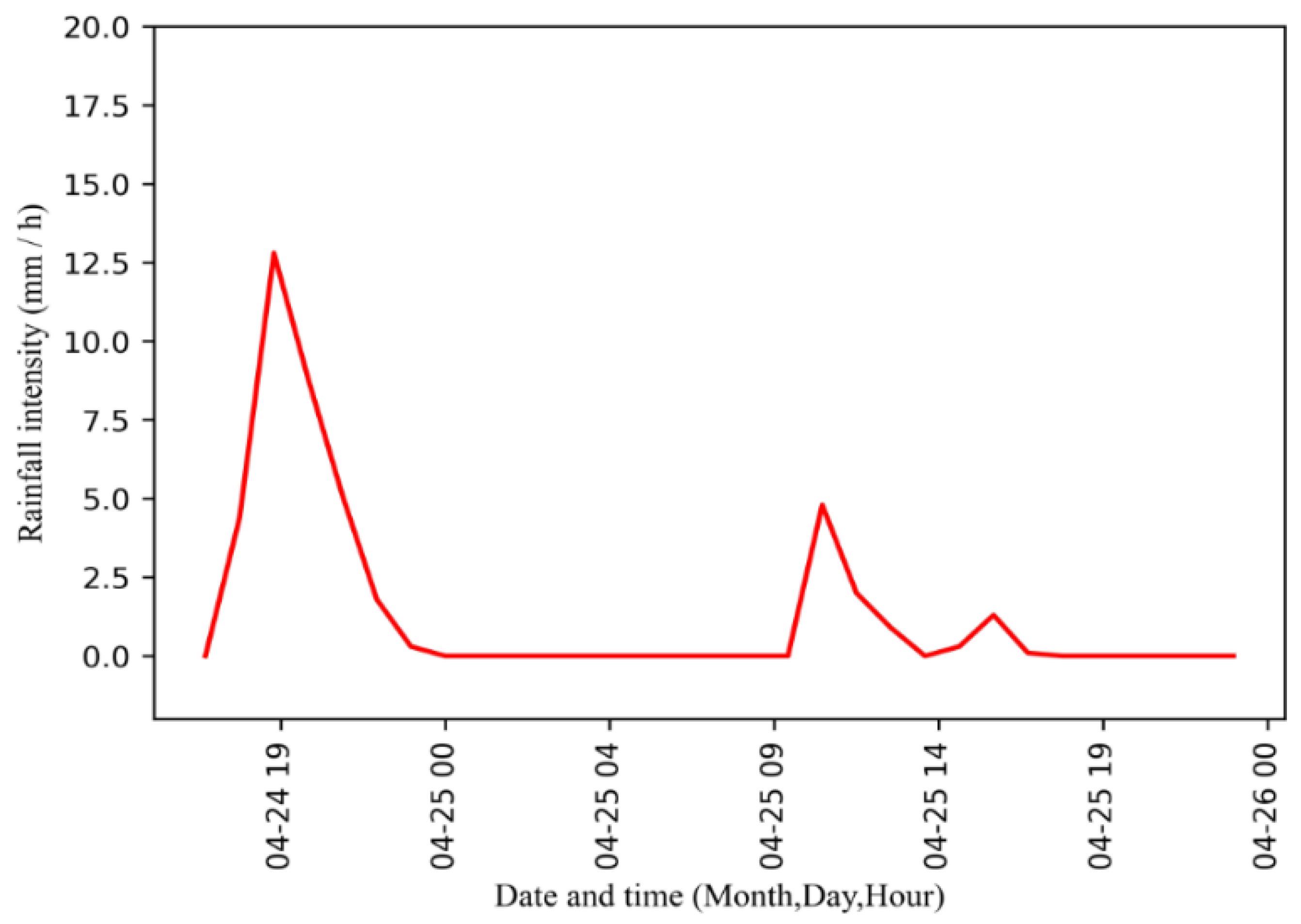
2.2. Rainfall Intensity Data
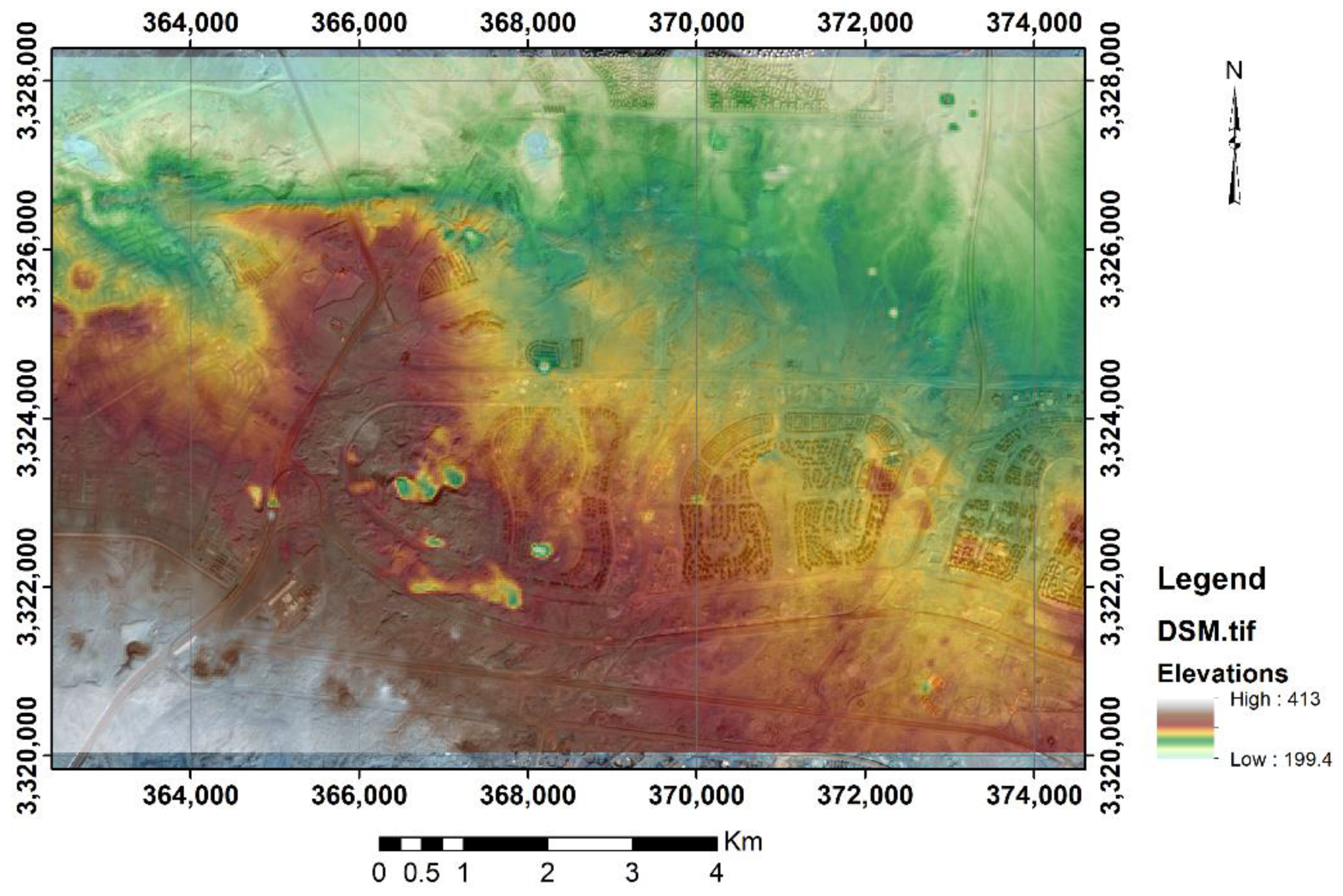
2.3. DSM Data Preparation
2.4. Sentinel-1 Data
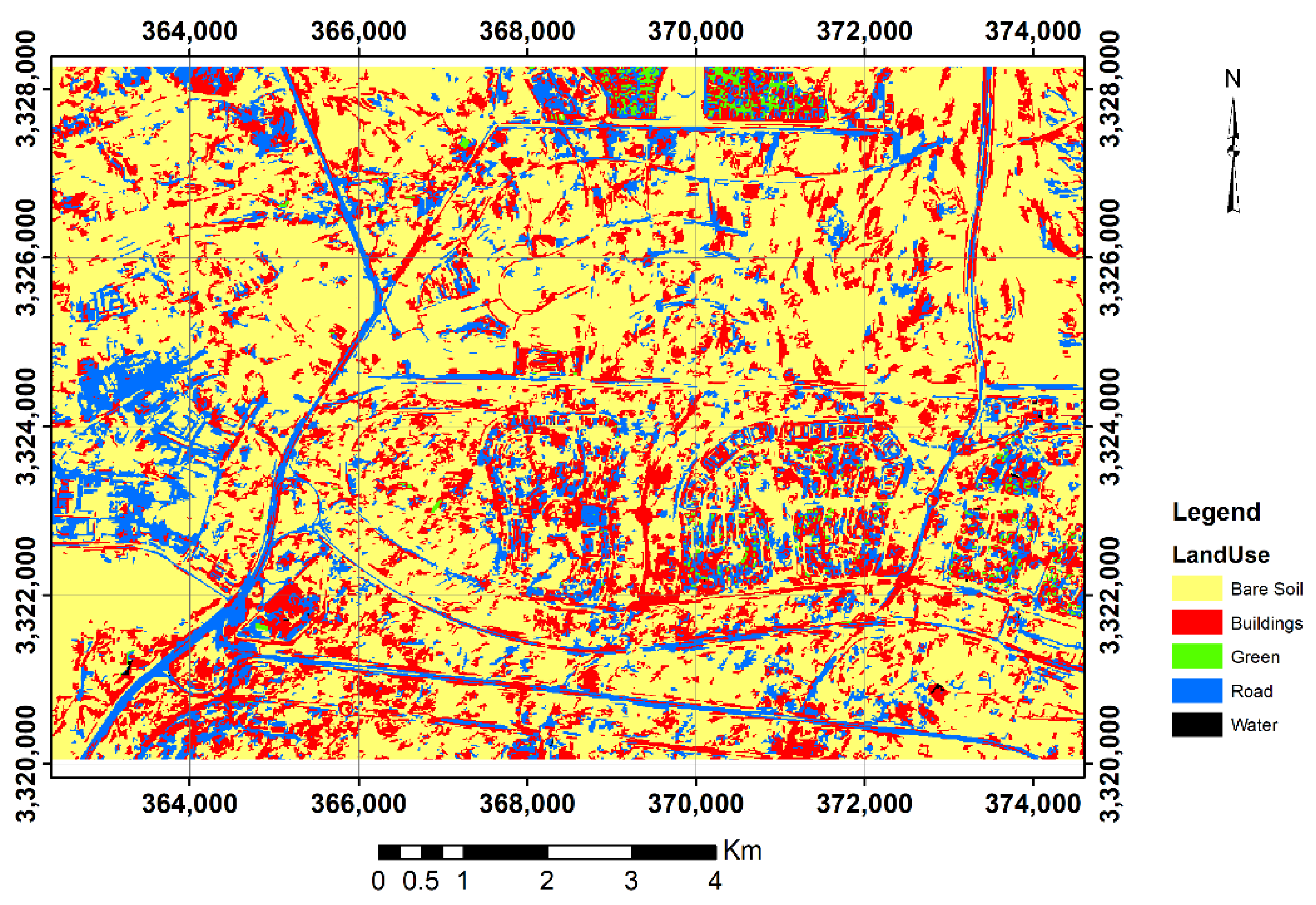
2.5. Land Use
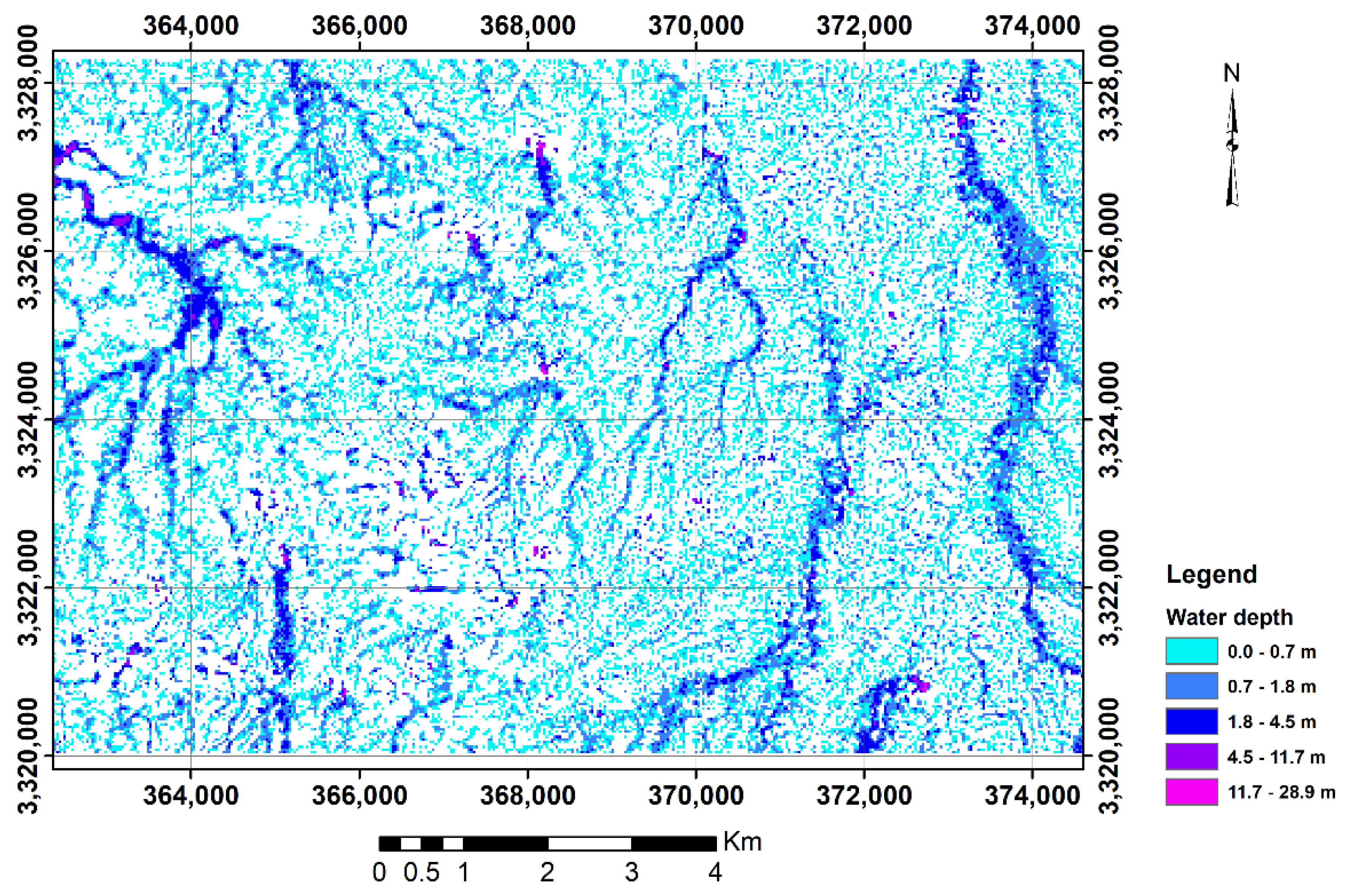
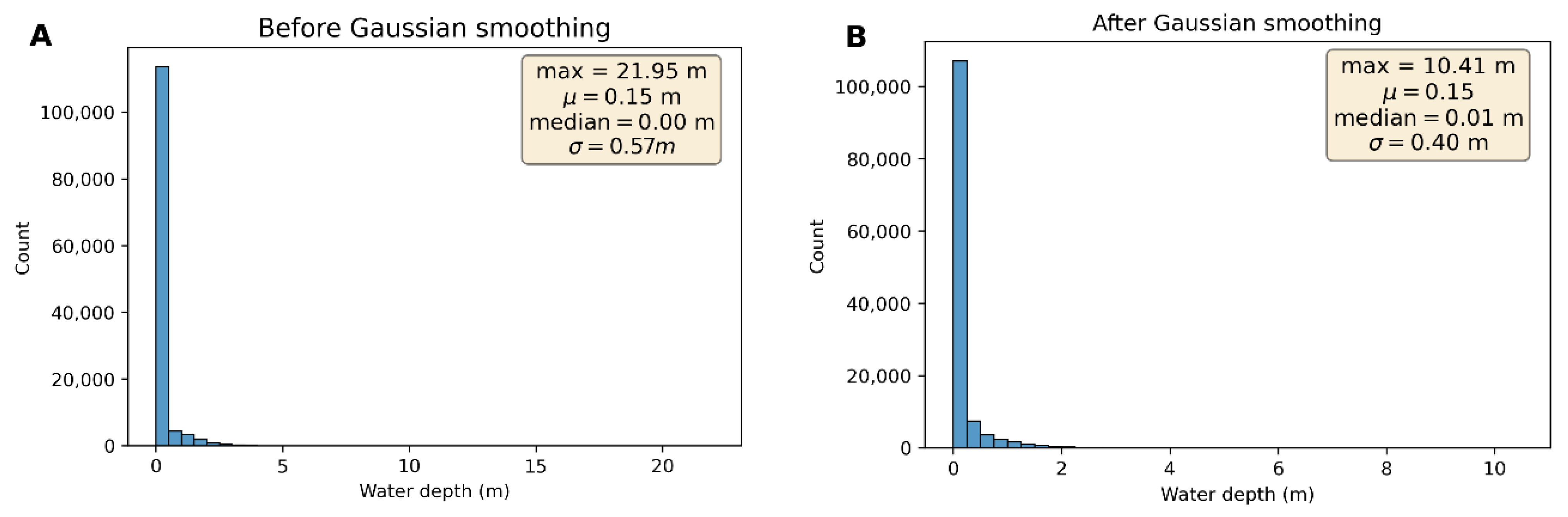
2.6. Water Depth Extraction (Dependent Variable)
3. Methodology and Data Preparation
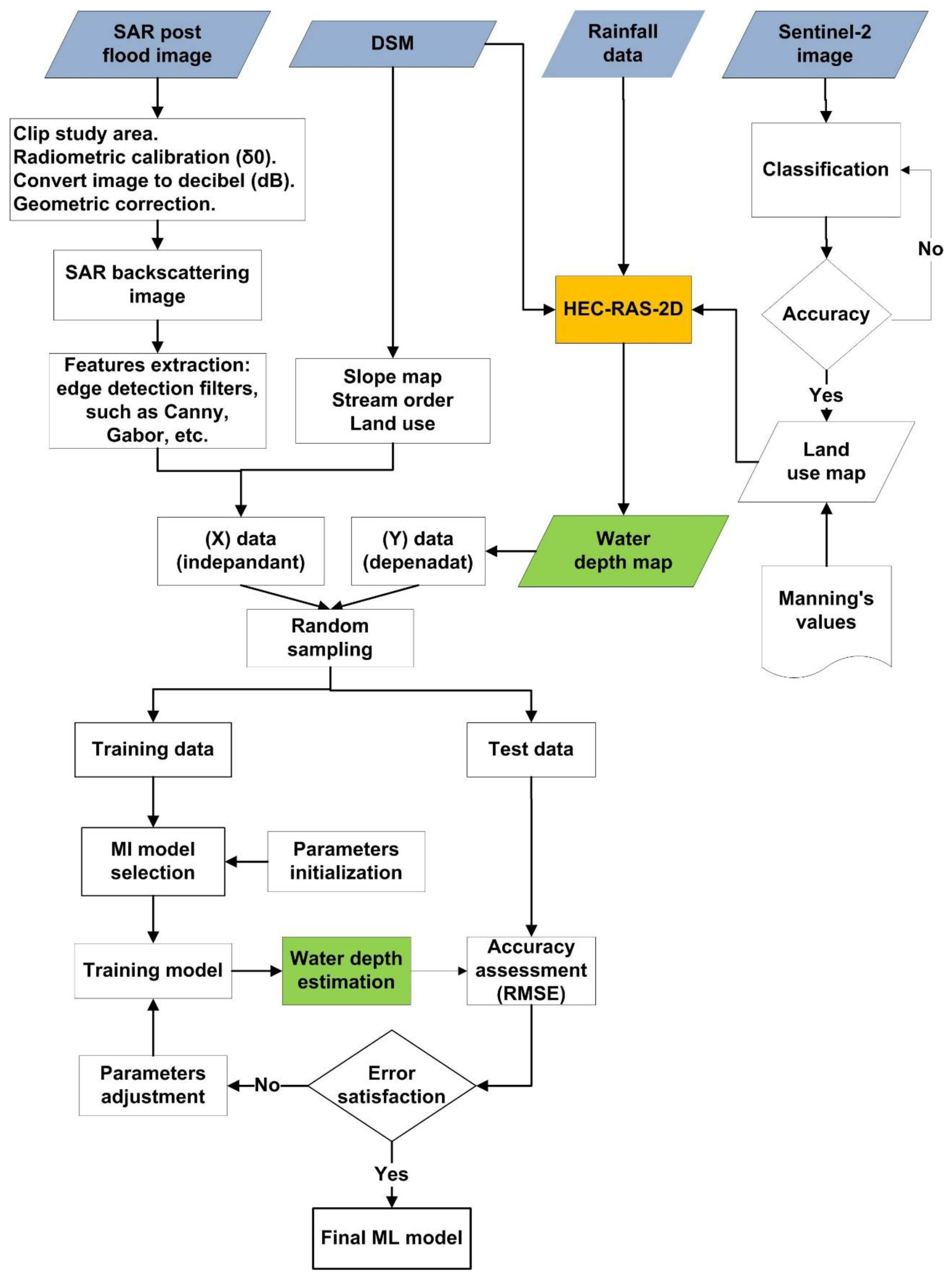
3.1. Research Methodology
3.2. Machine Learning Data Preparation
3.2.1. Dependent Feature Extraction and Preparation (Y)
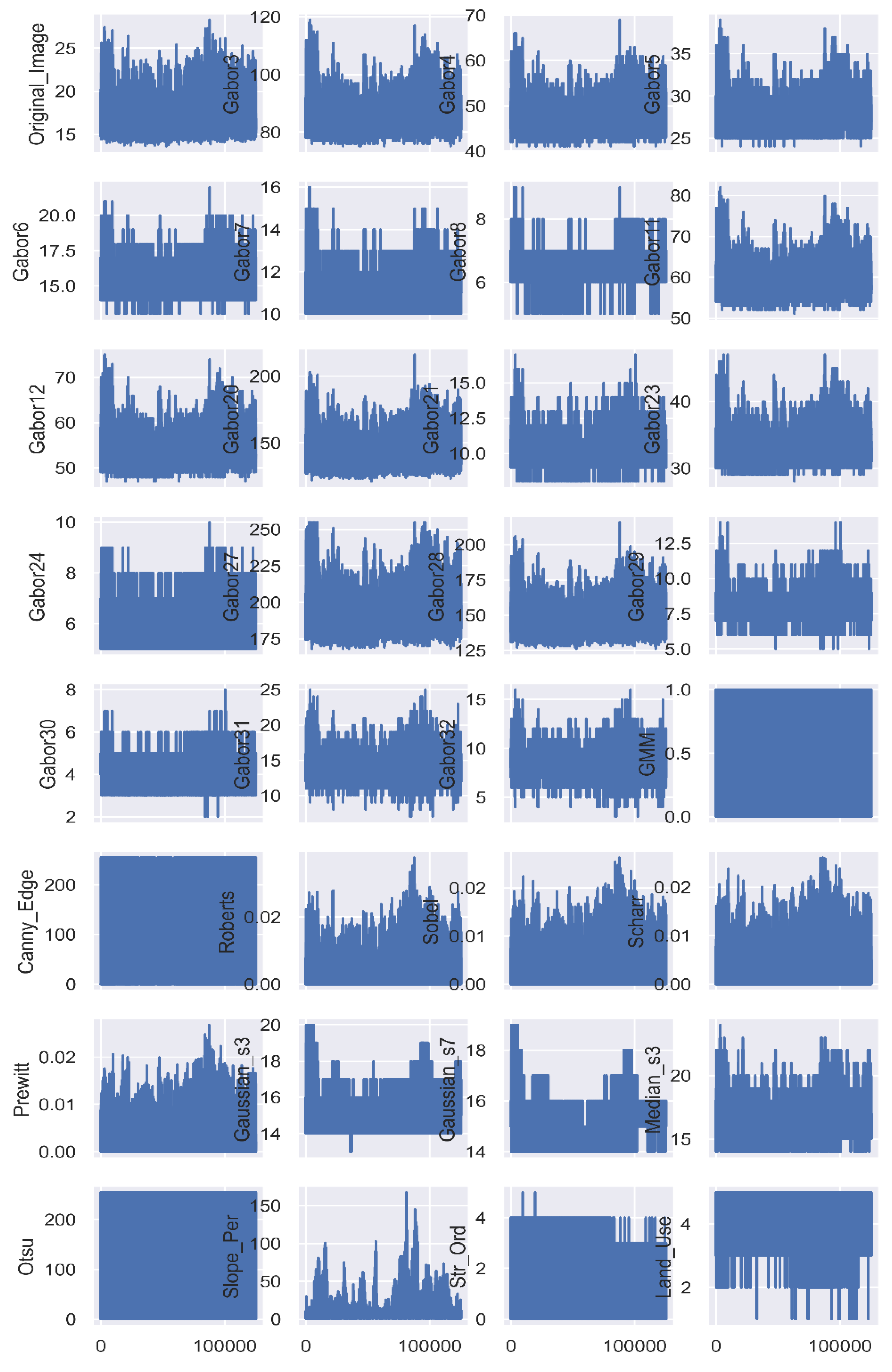
3.2.2. Independent Feature Extraction and Preparation (X)
3.2.3. Independent Feature Extraction Algorithms and Methods
3.3. Quality Assessment
4. Results
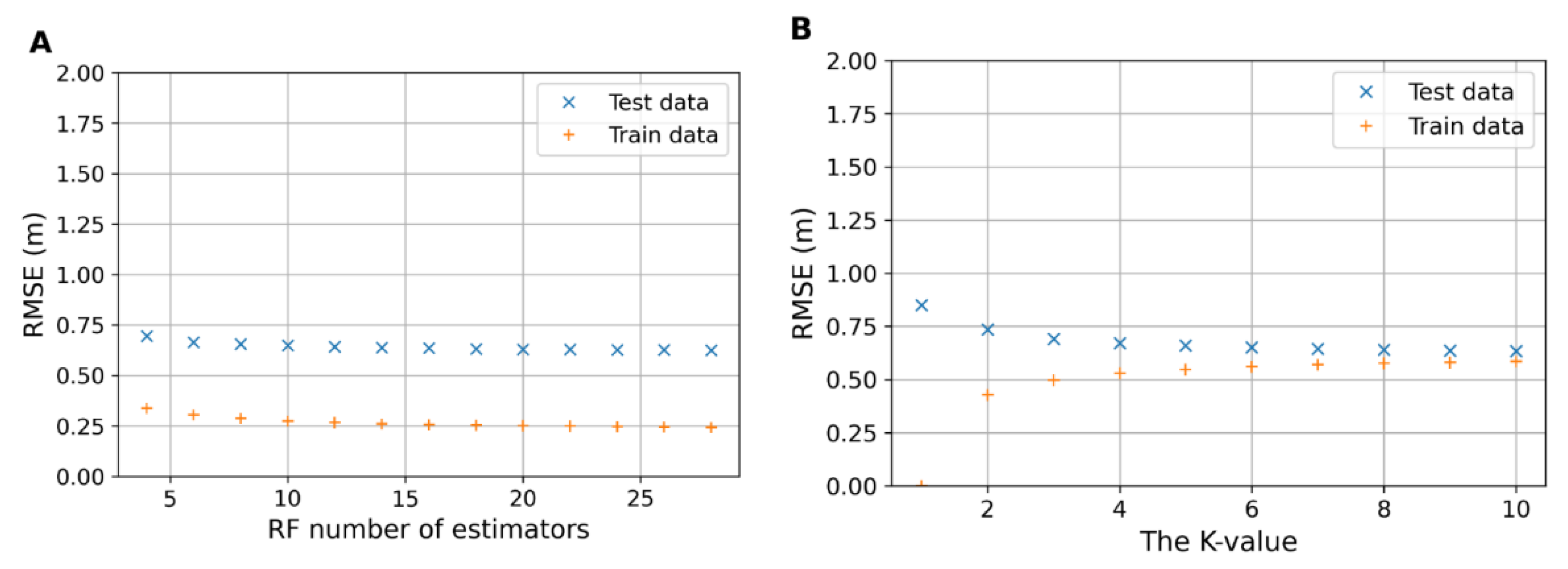
4.1. Machine Learning Hyperparameter Tuning
4.2. Accuracy of Obtained ML Algorithms
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Townsend, P.A.; Walsh, S.J. Modeling floodplain inundation using an integrated GIS with radar and optical remote sensing. Geomorphology 1998, 21, 295–312. [Google Scholar] [CrossRef]
- Vishnu, C.L.; Sajinkumar, K.S.; Oommen, T.; Coffman, R.A.; Thrivikramji, K.P.; Rani, V.R.; Keerthy, S. Satellite-based assessment of the August 2018 flood in parts of Kerala, India. Geomat. Nat. Hazards Risk 2019, 10, 758–767. [Google Scholar] [CrossRef] [Green Version]
- Irwin, K.; Beaulne, D.; Braun, A.; Fotopoulos, G. Fusion of SAR, optical imagery and airborne LiDAR for surface water detection. Remote Sens. 2017, 9, 890. [Google Scholar] [CrossRef] [Green Version]
- Musa, Z.N.; Popescu, I.; Mynett, A. A review of applications of satellite SAR, optical, altimetry and DEM data for surface water modelling, mapping and parameter estimation. Hydrol. Earth Syst. Sci. 2015, 19, 3755–3769. [Google Scholar] [CrossRef] [Green Version]
- Bovenga, F.; Bovenga, F.; Belmonte, A.; Refice, A.; Pasquariello, G.; Nutricato, R.; Nitti, D.O.; Chiaradia, M.T. Performance analysis of satellite missions for multi-temporal SAR interferometry. Sensors 2018, 18, 1359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bioresita, F.; Puissant, A.; Stumpf, A.; Malet, J.P. A method for automatic and rapid mapping of water surfaces from Sentinel-1 imagery. Remote Sens. 2018, 10, 217. [Google Scholar] [CrossRef] [Green Version]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Yalcin, E. Two-dimensional hydrodynamic modelling for urban flood risk assessment using unmanned aerial vehicle imagery: A case study of Kirsehir, Turkey. J. Flood Risk Manag. 2019, 12, e12499. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Barca, P. Is HEC-RAS 2D accurate enough for storm-event hazard assessment? Lessons learnt from a benchmarking study based on rain-on-grid modelling. J. Hydrol. 2021, 603, 126962. [Google Scholar] [CrossRef]
- El Afandi, G.; Morsy, M. Developing an Early Warning System for Flash Flood in Egypt: Case Study Sinai Peninsula. In Advances in Science, Technology and Innovation; Springer: Berlin/Heidelberg, Germany, 2020; pp. 45–60. [Google Scholar]
- Abdeldayem, O.M.; Eldaghar, O.; KMostafa, M.; MHabashy, M.; Hassan, A.A.; Mahmoud, H.; Morsy, K.M.; Abdelrady, A.; Peters, R.W. Mitigation plan and water harvesting of flashflood in arid rural communities using modelling approach: A case study in Afouna village, Egypt. Water 2020, 12, 2565. [Google Scholar] [CrossRef]
- Sadek, M.; Li, X.; Mostafa, E.; Dossou, J.F. Monitoring flash flood hazard using modeling-based techniques and multi-source remotely sensed data: The case study of Ras Ghareb City, Egypt. Arab. J. Geosci. 2021, 14, 2030. [Google Scholar] [CrossRef]
- Elkhrachy, I.; Pham, Q.B.; Costache, R.; Mohajane, M.; Rahman, K.U.; Shahabi, H.; Linh, N.T.T.; Anh, N.T. Sentinel-1 remote sensing data and Hydrologic Engineering Centres River Analysis System two-dimensional integration for flash flood detection and modelling in New Cairo City, Egypt. J. Flood Risk Manag. 2021, 14, e12692. [Google Scholar] [CrossRef]
- El-Haddad, B.A.; Youssef, A.M.; Pourghasemi, H.R.; Pradhan, B.; El-Shater, A.H.; El-Khashab, M.H. Flood susceptibility prediction using four machine learning techniques and comparison of their performance at Wadi Qena Basin, Egypt. Nat. Hazards 2021, 105, 83–114. [Google Scholar] [CrossRef]
- El-Magd, S.A.A.; Pradhan, B.; Alamri, A. Machine learning algorithm for flash flood prediction mapping in Wadi El-Laqeita and surroundings, Central Eastern Desert, Egypt. Arab. J. Geosci. 2021, 14, 323. [Google Scholar] [CrossRef]
- Mudashiru, R.B.; Sabtu, N.; Abustan, I. Quantitative and semi-quantitative methods in flood hazard/susceptibility mapping: A review. Arab. J. Geosci. 2021, 14, 941. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer series in statistics; Springer: New York, NY, USA, 2001; Volume 1, No. 10. [Google Scholar]
- Ghorpade, P.; Gadge, A.; Lende, A.; Chordiya, H.; Gosavi, G.; Mishra, A.; Hooli, B.; Ingle, Y.S.; Shaikh, N. Flood Forecasting Using Machine Learning: A Review. In Proceedings of the 2021 8th International Conference on Smart Computing and Communications: Artificial Intelligence, AI Driven Applications for a Smart World, ICSCC, Kochi, Kerala, India, 1–3 July 2021; Volume 2021, pp. 32–36. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.; Nikolić, M.; Bajat, B. Random forest spatial interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Mao, Z.; Shen, W. Integrating Multiple Datasets and Machine Learning Algorithms for Satellite-Based Bathymetry in Seaports. Remote Sens. 2021, 13, 4328. [Google Scholar] [CrossRef]
- Elkhrachy, I. Vertical accuracy assessment for SRTM and ASTER Digital Elevation Models: A case study of Najran city, Saudi Arabia. Ain Shams Eng. J. 2018, 9, 1807–1817. [Google Scholar] [CrossRef]
- Mesa-Mingorance, J.L.; Ariza-López, F.J. Accuracy assessment of digital elevation models (DEMs): A critical review of practices of the past three decades. Remote Sens. 2020, 12, 2630. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
- Liu, H. Feature Engineering for Machine Learning and Data Analytics; O’Reilly Media, Inc.: Sevastopol, CA, USA, 2018. [Google Scholar]
- Davies, E.R. Machine Vision: Theory, Algorithms, Practicalities; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- McKinney, W.; Team, P.D. Pandas-Powerful python data analysis toolkit. Pandas—Powerful Python Data Anal. Toolkit 2015, 1625. Available online: https://pandas.pydata.org/docs/pandas.pdf (accessed on 15 September 2021).
- Fogel, I.; Sagi, D. Gabor filters as texture discriminator. Biol. Cybern. 1989, 61, 103–113. [Google Scholar] [CrossRef]
- Grigorescu, S.E.; Petkov, N.; Kruizinga, P. Comparison of texture features based on Gabor filters. IEEE Trans. Image Process. 2002, 11, 1160–1167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palm, C.; Lehman, T. Classification of color textures by gabor filtering. Mach. Graph. Vis. 2002, 11, 195–220. [Google Scholar]
- OpenCV, L. Computer Vision with the OpenCV Library; O’Reilly Media, Inc.: Sevastopol, CA, USA, 2008. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: http://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html%5Cnhttp://arxiv.org/abs/1201.0490 (accessed on 15 September 2021).
- Skidmore, A.K. A comparison of techniques for calculating gradient and aspect from a gridded digital elevation model. Int. J. Geogr. Inf. Syst. 1989, 3, 323–334. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Cone, J. Principles of Geographical Information Systems by Peter A; Oxford University Press: Oxford, UK, 1998; Volume 54. [Google Scholar]
- Jenson, S.K. Applications of hydrologic information automatically extracted from digital elevation models. Hydrol. Process. 1991, 5, 31–44. [Google Scholar] [CrossRef]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013, arXiv:1309.0238. [Google Scholar]
- Hall, M.A. Correlation-based Feature Selection for Discrete and Numeric Class Machine Learning. Eff. Br. Mindfulness Interv. Acute Pain ExAn. Exam. Individ. Differ. 2015, 1, 1689–1699. Available online: https://researchcommons.waikato.ac.nz/handle/10289/1024 (accessed on 21 August 2021).
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Cian, F.; Marconcini, M.; Ceccato, P.; Giupponi, C. Flood depth estimation by means of high-resolution SAR images and lidar data. Nat. Hazards Earth Syst. Sci. 2018, 18, 3063–3084. [Google Scholar] [CrossRef] [Green Version]



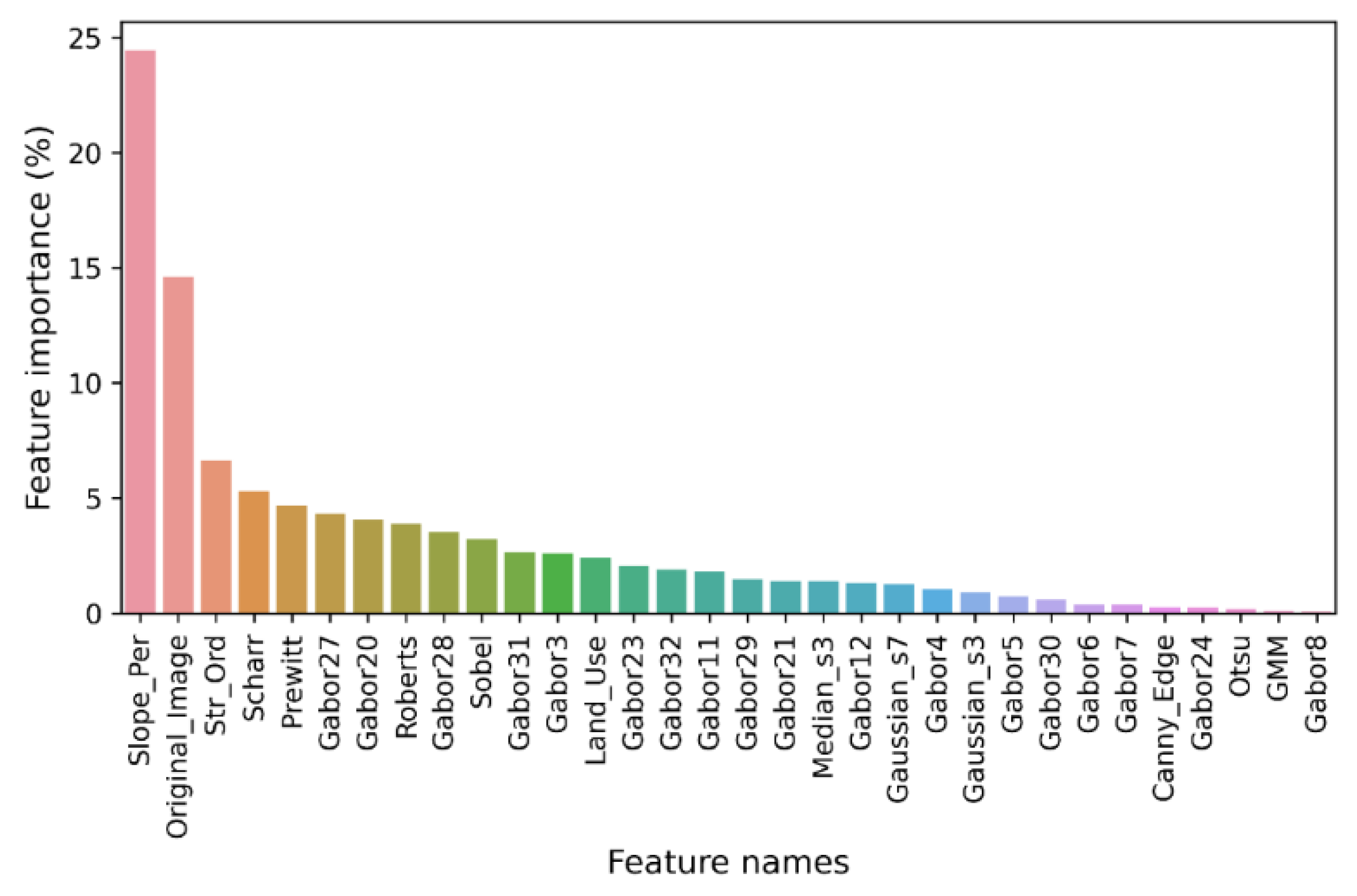
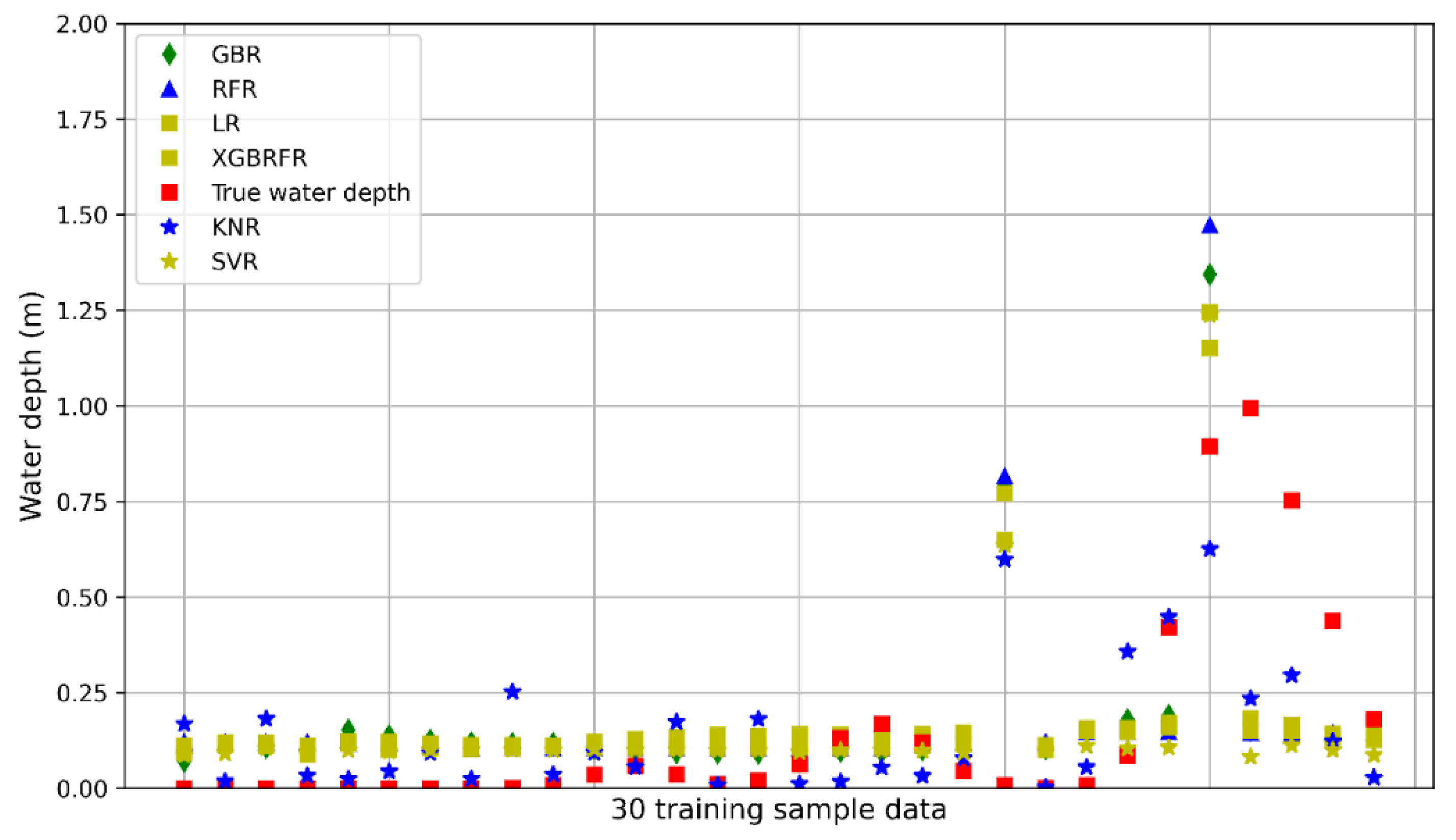
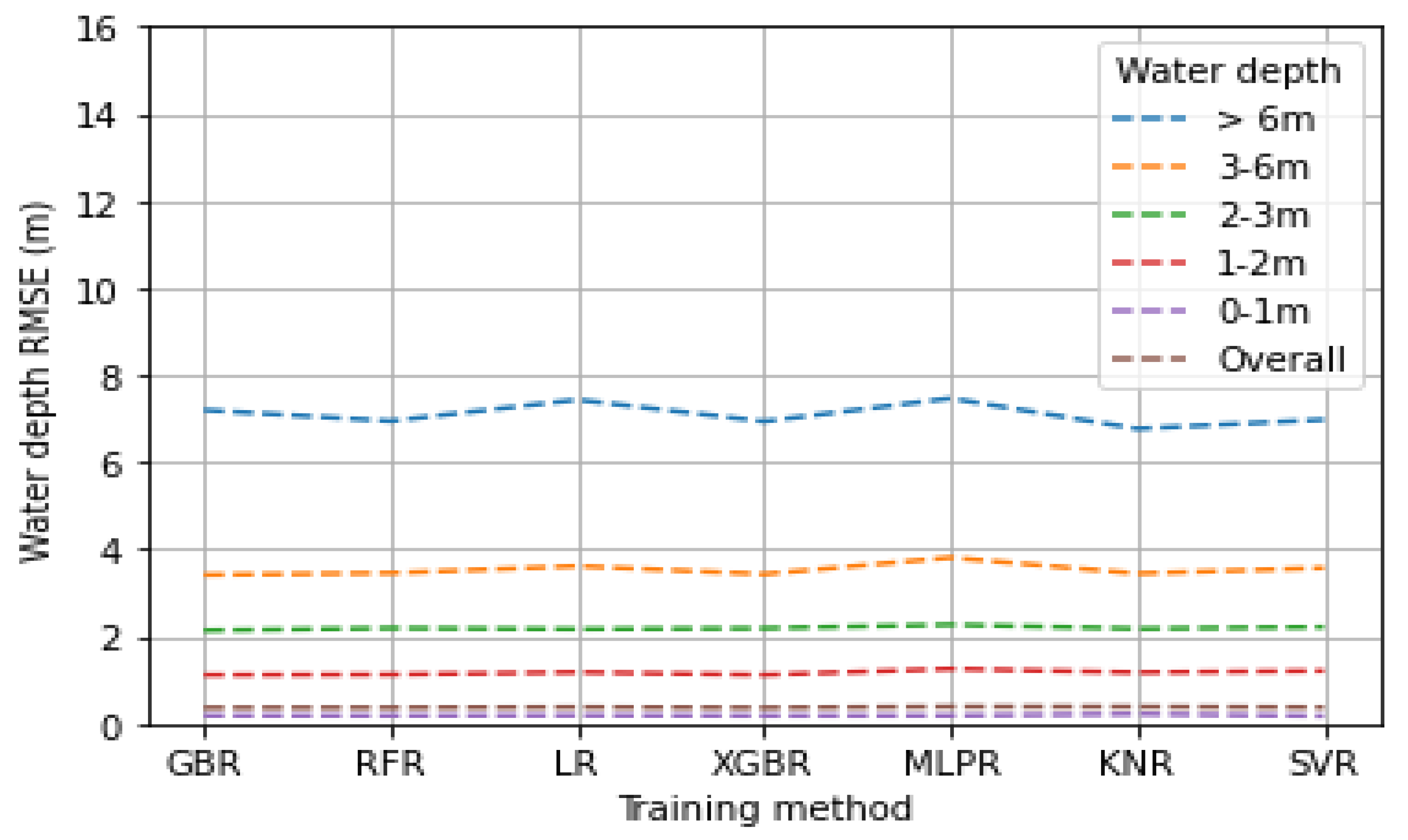
| Bare Soil | Buildings | Green | Roads | Water | Sum | User’s Accuracy | |
|---|---|---|---|---|---|---|---|
| Bare soil | 107 | 0 | 1 | 3 | 2 | 113 | 94.7% |
| Buildings | 2 | 42 | 1 | 2 | 1 | 48 | 87.5% |
| Green | 1 | 1 | 6 | 1 | 1 | 10 | 60.0% |
| Roads | 2 | 1 | 3 | 28 | 2 | 36 | 77.8% |
| Water | 1 | 0 | 1 | 2 | 6 | 10 | 60.0% |
| Sum | 113 | 44 | 12 | 36 | 12 | 217 | |
| Producer’s accuracy | 94.7% | 95.5% | 50.0% | 77.8% | 50.0% | ||
| Total Accuracy | 87.1% | ||||||
| a | 26,714 | ||||||
| b | 32,790 | ||||||
| Kappa | 81.5% |
| ML Data | Based On: | Features | Pixel ID (Sample Number) | ||||
|---|---|---|---|---|---|---|---|
| ID | Filter | 1 | 2 | 125491 | 125492 | ||
| Independent data (X) | SAR image | 1 | Original Image | 19.23 | 18.45 | 16.59 | 15.29 |
| 2 | Gabor3 | 91.00 | 90.00 | 84.00 | 81.00 | ||
| 3 | Gabor4 | 51.00 | 51.00 | 46.00 | 44.00 | ||
| 4 | Gabor5 | 29.00 | 29.00 | 27.00 | 26.00 | ||
| 5 | Gabor6 | 17.00 | 16.00 | 15.00 | 14.00 | ||
| 6 | Gabor7 | 12.00 | 12.00 | 11.00 | 11.00 | ||
| 7 | Gabor8 | 7.00 | 7.00 | 6.00 | 6.00 | ||
| 8 | Gabor11 | 62.00 | 62.00 | 58.00 | 55.00 | ||
| 9 | Gabor12 | 57.00 | 57.00 | 53.00 | 51.00 | ||
| 10 | Gabor19 | 255.00 | 255.00 | 255.00 | 255.00 | ||
| 11 | Gabor20 | 156.00 | 155.00 | 140.00 | 132.00 | ||
| 12 | Gabor21 | 10.00 | 10.00 | 10.00 | 10.00 | ||
| 13 | Gabor23 | 34.00 | 34.00 | 32.00 | 31.00 | ||
| 14 | Gabor24 | 7.00 | 7.00 | 6.00 | 6.00 | ||
| 15 | Gabor27 | 206.00 | 205.00 | 188.00 | 180.00 | ||
| 16 | Gabor28 | 159.00 | 158.00 | 144.00 | 136.00 | ||
| 17 | Gabor29 | 8.00 | 7.00 | 8.00 | 8.00 | ||
| 18 | Gabor30 | 4.00 | 4.00 | 4.00 | 4.00 | ||
| 19 | Gabor31 | 14.00 | 14.00 | 14.00 | 13.00 | ||
| 20 | Gabor32 | 8.00 | 8.00 | 8.00 | 8.00 | ||
| 21 | GMM | 1.00 | 0.00 | 0.00 | 0.00 | ||
| 22 | Canny Edge | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 23 | Roberts | 0.01 | 0.00 | 0.00 | 0.00 | ||
| 24 | Sobel | 0.01 | 0.00 | 0.00 | 0.00 | ||
| 25 | Scharr | 0.01 | 0.00 | 0.00 | 0.00 | ||
| 26 | Prewitt | 0.01 | 0.00 | 0.00 | 0.00 | ||
| 27 | Gaussian s3 | 15.00 | 15.00 | 15.00 | 14.00 | ||
| 28 | Gaussian s7 | 15.00 | 15.00 | 15.00 | 15.00 | ||
| 29 | Median s3 | 18.00 | 18.00 | 16.00 | 15.00 | ||
| 30 | Otsu | 255.00 | 255.00 | 0.00 | 0.00 | ||
| 31 | Slope_Per | 6.25 | 6.09 | 4.48 | 2.98 | ||
| 32 | Str_Ord | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 33 | Land_Use | 3.00 | 3.00 | 3.00 | 3.00 | ||
| 1 | Water_depth | 0.17 | 0.16 | 0.10 | 0.12 | ||
| 31 | Slope_Per | 6.25 | 6.09 | 4.48 | 2.98 | ||
| DSM image | 32 | Str_Ord | 0.00 | 0.00 | 0.00 | 0.00 | |
| Sentinel-2 image | 33 | Land_Use | 3.00 | 3.00 | 3.00 | 3.00 | |
| Dependent data (Y) | HEC-RAS results | 1 | Water_depth | 0.17 | 0.16 | 0.10 | 0.12 |
| Water Depth | Number of Points | Percentages (%) | RMSE (m) ML Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GBR | RFR | LR | XGBR | MLPR | KNR | SVR | |||
| >6 m | 4 | 0.02 | 7.20 | 6.95 | 7.43 | 6.94 | 7.47 | 6.77 | 6.98 |
| 3–6 m | 56 | 0.22 | 3.42 | 3.46 | 3.62 | 3.43 | 3.81 | 3.44 | 3.57 |
| 2–3 m | 157 | 0.63 | 2.14 | 2.19 | 2.17 | 2.19 | 2.27 | 2.18 | 2.22 |
| 1–2 m | 718 | 2.86 | 1.12 | 1.13 | 1.18 | 1.12 | 1.26 | 1.17 | 1.21 |
| 0–1 m | 24,164 | 96.27 | 0.19 | 0.19 | 0.19 | 0.18 | 0.19 | 0.22 | 0.18 |
| Overall | 25,099 | 100 | 0.36 | 0.37 | 0.38 | 0.36 | 0.39 | 0.39 | 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elkhrachy, I. Flash Flood Water Depth Estimation Using SAR Images, Digital Elevation Models, and Machine Learning Algorithms. Remote Sens. 2022, 14, 440. https://doi.org/10.3390/rs14030440
Elkhrachy I. Flash Flood Water Depth Estimation Using SAR Images, Digital Elevation Models, and Machine Learning Algorithms. Remote Sensing. 2022; 14(3):440. https://doi.org/10.3390/rs14030440
Chicago/Turabian StyleElkhrachy, Ismail. 2022. "Flash Flood Water Depth Estimation Using SAR Images, Digital Elevation Models, and Machine Learning Algorithms" Remote Sensing 14, no. 3: 440. https://doi.org/10.3390/rs14030440
APA StyleElkhrachy, I. (2022). Flash Flood Water Depth Estimation Using SAR Images, Digital Elevation Models, and Machine Learning Algorithms. Remote Sensing, 14(3), 440. https://doi.org/10.3390/rs14030440






