Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images
Abstract
:1. Introduction
2. Study Area
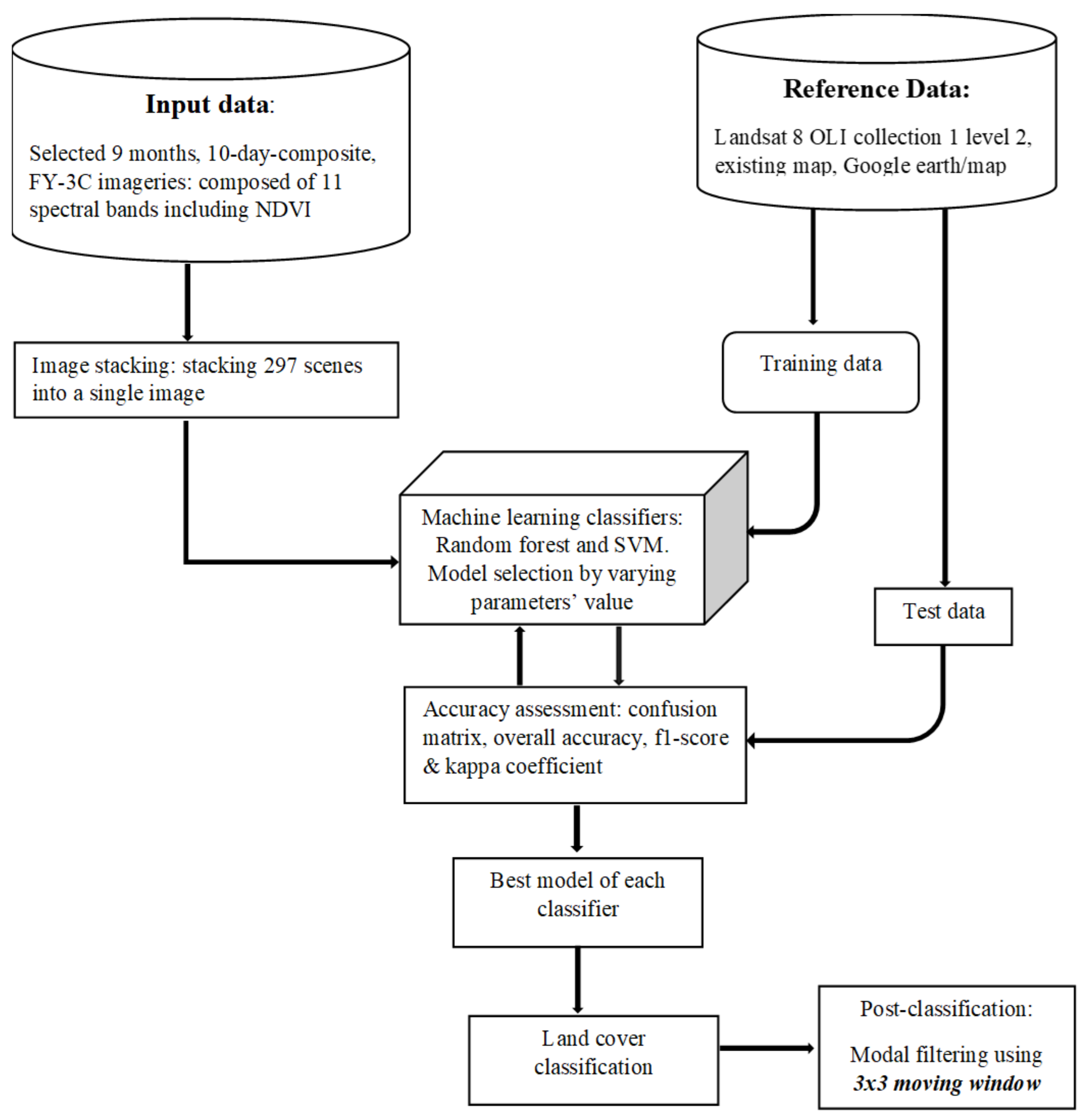
3. Materials and Methods
3.1. Classification Scheme
3.2. Input Data
3.3. Training and Test Data
3.4. Algorithms
3.4.1. Random Forest (RF)
3.4.2. Support Vector Machine (SVM)
3.5. Accuracy Assessment
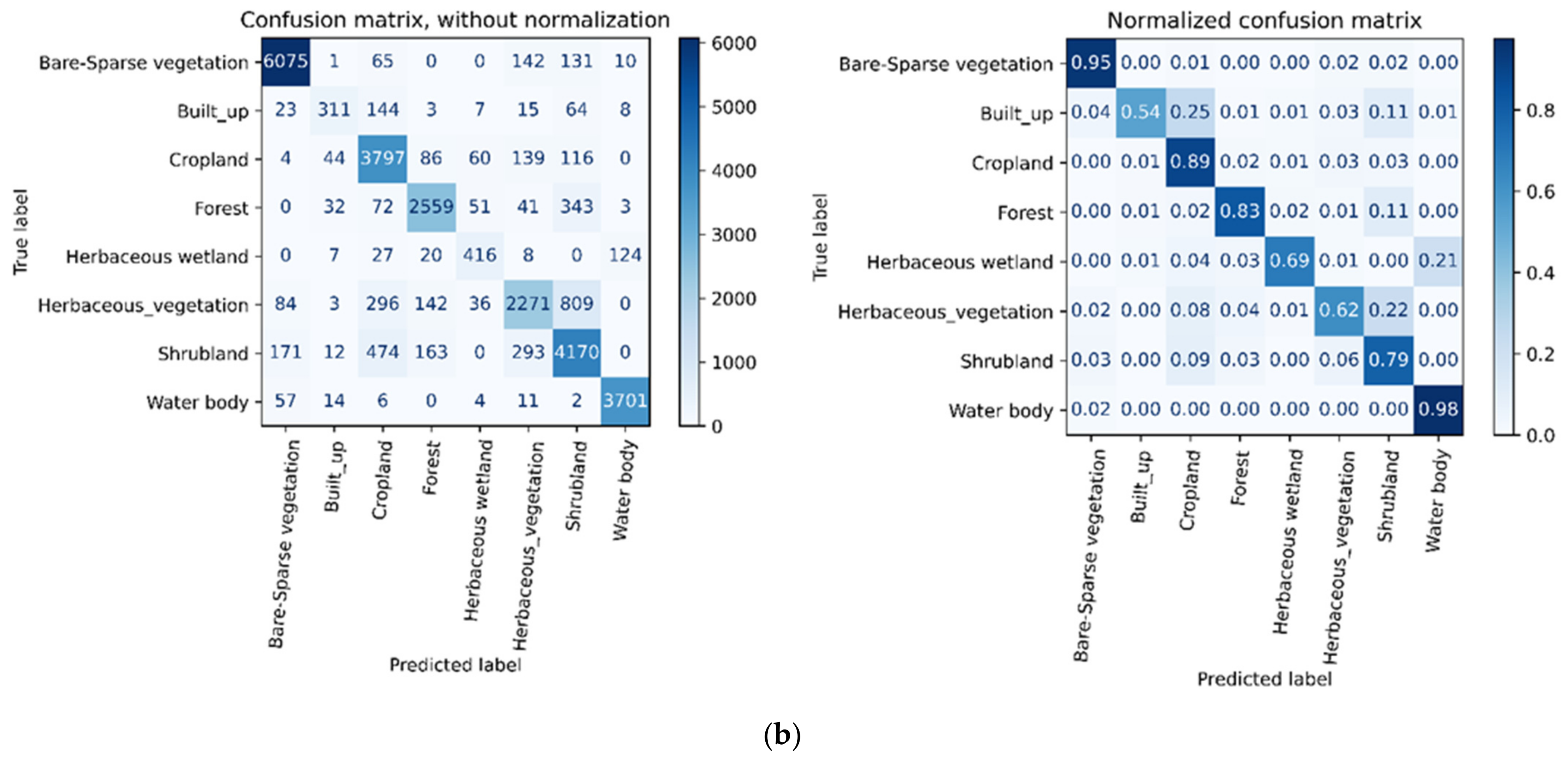
4. Results
5. Discussion
5.1. Effectiveness and Efficiency of the Algorithms
5.2. Impact of Parameter Tuning
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beaubien, J.; Cihlar, J.; Simard, G.; Latifovic, R. Land cover from multiple thematic mapper scenes using a new enhancement-classification methodology. J. Geophys. Res. Atmos. 1999, 104, 27909–27920. [Google Scholar] [CrossRef]
- Latifovic, R.; Olthof, I. Accuracy assessment using sub-pixel fractional error matrices of global land cover products derived from satellite data. Remote Sens. Environ. 2004, 90, 153–165. [Google Scholar] [CrossRef]
- Tchuenté, A.T.K.; Roujean, J.-L.; De Jong, S.M. Comparison and relative quality assessment of the GLC2000, GLOBCOVER, MODIS and ECOCLIMAP land cover datasets at the African continental scale. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 207–219. [Google Scholar] [CrossRef]
- Cihlar, J. Land cover mapping of large areas from satellites: Status and research priorities. Int. J. Remote Sens. 2000, 21, 1093–1114. [Google Scholar] [CrossRef]
- Feng, M.; Li, X. Land cover mapping toward finer scales. Sci. Bull. 2020, 65, 1604–1606. [Google Scholar] [CrossRef]
- Giri, C.P. Remote Sensing of Land Use and Land Cover: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2012; p. 477. [Google Scholar]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Mayaux, P.; Bartholomé, E.; Fritz, S.; Belward, A. A new land-cover map of Africa for the year 2000. J. Biogeogr. 2004, 31, 861–877. [Google Scholar] [CrossRef]
- Tchuenté, A.T.K.; De Jong, S.; Roujean, J.-L.; Favier, C.; Mering, C. Classification of African ecosystems at 1 km resolution using multiannual SPOT/VEGETATION data and a hybrid clustering approach. In Proceedings of the Les Satellites Grand Champ Pour le Suivi de L’environnement, des Ressources Naturelles et des Risques, Clermont-Ferrand, France, 21–22 January 2010. [Google Scholar]
- Loveland, T.R.; Belward, A. The IGBP-DIS global 1 km land cover dataset, DISCover: First results. Int. J. Remote Sens. 1997, 18, 3289–3295. [Google Scholar] [CrossRef]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Arino, O.; Bicheron, P.; Achard, F.; Latham, J.; Witt, R.; Weber, J.-L. The most detailed portrait of Earth. Eur. Space Agency 2008, 136, 25–31. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Galiano, V.R.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. Giscience Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing; Guilford Press: New York, NY, USA, 2011. [Google Scholar]
- Wulder, M.A.; Coops, N.C.; Roy, D.P.; White, J.C.; Hermosilla, T. Land cover 2.0. Int. J. Remote Sens. 2018, 39, 4254–4284. [Google Scholar] [CrossRef] [Green Version]
- Waske, B.; van der Linden, S.; Benediktsson, J.A.; Rabe, A.; Hostert, P.; Sensing, R. Sensitivity of support vector machines to random feature selection in classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2880–2889. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Foody, G.M.; Mathur, A. A relative evaluation of multiclass image classification by support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1335–1343. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.; Warner, T.; Strager, M.; Conley, J.; Sharp, A. Assessing machine-learning algorithms and image-and lidar-derived variables for GEOBIA classification of mining and mine reclamation. Int. J. Remote Sens. 2015, 36, 954–978. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An Assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. Support vector machines for classification in remote sensing. Int. J. Remote Sens. 2005, 26, 1007–1011. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.; Townshend, J. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Gualtieri, J.; Chettri, S. Support vector machines for classification of hyperspectral data. In Proceedings of the IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No. 00CH37120), Honolulu, HI, USA, 24–28 July 2000; pp. 813–815. [Google Scholar]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. A meta-analysis of remote sensing research on supervised pixel-based land-cover image classification processes: General guidelines for practitioners and future research. Remote Sens. Environ. 2016, 177, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Otukei, J.R.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Land-use/cover classification in a heterogeneous coastal landscape using RapidEye imagery: Evaluating the performance of random forest and support vector machines classifiers. Int. J. Remote Sens. 2014, 35, 3440–3458. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Gobakken, T.; Gianelle, D.; Næsset, E. Tree species classification in boreal forests with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2632–2645. [Google Scholar] [CrossRef]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Wang, J.; Wang, L.; Hu, L.; Gong, P. Comparison of classification algorithms and training sample sizes in urban land classification with Landsat thematic mapper imagery. Remote Sens. 2014, 6, 964–983. [Google Scholar] [CrossRef] [Green Version]
- Thanh Noi, P.; Kappas, M. Comparison of random forest, k-nearest neighbor, and support vector machine classifiers for land cover classification using Sentinel-2 imagery. Sensors 2018, 18, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Xie, Z. Object-based vegetation mapping in the Kissimmee River watershed using HyMap data and machine learning techniques. Wetlands 2013, 33, 233–244. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Strager, M.P.; Pal, M. Combining RapidEye satellite imagery and Lidar for mapping of mining and mine reclamation. Photogramm. Eng. Remote Sens. 2014, 80, 179–189. [Google Scholar] [CrossRef]
- Ghosh, A.; Joshi, P.K. A comparison of selected classification algorithms for mapping bamboo patches in lower Gangetic plains using very high resolution WorldView 2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 298–311. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Mutanga, O.; Adam, E.; Ismail, R. Detecting Sirex noctilio grey-attacked and lightning-struck pine trees using airborne hyperspectral data, random forest and support vector machines classifiers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 48–59. [Google Scholar] [CrossRef]
- Shang, X.; Chisholm, L.A. Classification of Australian native forest species using hyperspectral remote sensing and machine-learning classification algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 2481–2489. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Moran, C.J. The AmericaView classification methods accuracy comparison project: A rigorous approach for model selection. Remote Sens. Environ. 2015, 170, 115–120. [Google Scholar] [CrossRef]
- Adugna, T.; Xu, W.; Fan, J. Effect of using different amounts of multi-temporal data on the accuracy: A case of land cover mapping of parts of africa using fengyun-3C data. Remote Sens. 2021, 13, 4461. [Google Scholar] [CrossRef]
- Smets, B.; Buchhorn, M.; Lesiv, M.; Tsendbazar, N.-E. Copernicus Global Land Operations “Vegetation and Energy”; Copernicus Global Land Operations: Geneve, Switzerland, 2017; p. 62. [Google Scholar]
- Tang, Y.; Zhang, J.; Wang, J. FY-3 meteorological satellites and the applications. China J. Space Sci. 2014, 34, 703–709. [Google Scholar]
- Li, N.; Wang, S.; Guan, L.; Liu, M. Assessment of global FY-3C/VIRR sea surface temperature. Remote Sens. 2021, 13, 3249. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, P.; Gu, S.; Hu, X.; Tang, S.; Yang, L.; Xu, N.; Zhen, Z.; Wang, L.; Wu, Q. Capability of fengyun-3D satellite in earth system observation. J. Meteorol. Res. 2019, 33, 1113–1130. [Google Scholar] [CrossRef]
- Xian, D.; Zhang, P.; Gao, L.; Sun, R.; Zhang, H.; Jia, X. Fengyun meteorological satellite products for earth system science applications. Adv. Atmos. Sci. 2021, 38, 1–18. [Google Scholar] [CrossRef]
- Han, X.; Yang, J.; Tang, S.; Han, Y. Vegetation products derived from Fengyun-3D medium resolution spectral imager-II. J. Meteorol. Res. 2020, 34, 775–785. [Google Scholar] [CrossRef]
- Wang, L.; Hu, X.; Chen, L.; He, L. Consistent calibration of VIRR reflective solar channels onboard FY-3A, FY-3B, and FY-3C using a multisite calibration method. Remote Sens. 2018, 10, 1336. [Google Scholar] [CrossRef] [Green Version]
- Jensen, J.R.; Lulla, K. Introductory digital image processing: A remote sensing perspective. Geocarto Int. 1987, 2, 65. [Google Scholar] [CrossRef]
- Colditz, R.R. An evaluation of different training sample allocation schemes for discrete and continuous land cover classification using decision tree-based algorithms. Remote Sens. 2015, 7, 9655–9681. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.C.; Reed, B. A comparison of the IGBP DISCover and University of Maryland 1 km global land cover products. Int. J. Remote Sens. 2000, 21, 1365–1373. [Google Scholar] [CrossRef]
- Yang, X. Parameterizing support vector machines for land cover classification. Photogramm. Eng. Remote Sens. 2011, 77, 27–37. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Tso, B.; Mather, P. Classification Methods for Remotely Sensed Data; CRC Press: Boca Raton, FL, USA, 2009; p. 367. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by random Forest. R News 2002, 2, 18–22. [Google Scholar]
- Kulkarni, V.Y.; Sinha, P.K. Pruning of random forest classifiers: A survey and future directions. In Proceedings of the International Conference on Data Science & Engineering (ICDSE), Cochin, India, 18–20 July 2012; IEEE: Manhattan, NY, USA, 2012. [Google Scholar]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Chapman, M.; Deng, F.; Ji, Z.; Yang, X. Integration of orthoimagery and lidar data for object-based urban thematic mapping using random forests. Int. J. Remote Sens. 2013, 34, 5166–5186. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Qian, Y.; Zhou, W.; Yan, J.; Li, W.; Han, L. Comparing machine learning classifiers for object-based land cover classification using very high-resolution imagery. Remote Sens. 2015, 7, 153–168. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Shi, D.; Yang, X. Support vector machines for land cover mapping from remote sensor imagery. In Monitoring and Modeling of Global Changes: A Geomatics Perspective; Springer: Berlin/Heidelberg, Germany, 2015; pp. 265–279. [Google Scholar]




| Land Cover Class | Class Definition Based on UN LCCS |
|---|---|
| 1. Bare/Sparse vegetation | Barren land or surface covered by plants that should not exceed 10% in every season of the year. |
| 2. Built-up | Area of land covered with buildings and other man-made features. |
| 3. Cropland | Intermittently cultivated land that is harvested and then left fallow (e.g., single and multiple cropping systems). Perennial woody crops are classified as either forest or shrub according to the criteria. |
| 4. Forest | Woody plants cover more than 15% of the land and grow to a height of more than 5 m. Exceptions: even if its height is less than 5 m but larger than 3 m, a woody plant with a characteristic physiognomic trait of a tree can be classified as a tree. |
| 5. Herbaceous wetland | A persistent mixture of water and herbaceous or woody vegetation covers the land. The plants can exist in salt, brackish, or freshwater. |
| 6. Herbaceous vegetation | Plants with no persistent branches or shoots above the surface and no apparent solid structure. Up to 10% of the area may be comprised of trees and plants. |
| 7. Shrubs | Woody perennial plants with persistent and woody stems that are less than 5 m tall and do not have a clear main stem. The shrub’s leaves are either evergreen or deciduous. |
| 8. Water bodies | These include lakes, reservoirs, and rivers. The water could be fresh or brine. |
| Band No. | Name of Bands | Wavelength Range in μm |
|---|---|---|
| Band 1 | FY-3C_VIRR_Day_EV_RefSB | 0.58–0.68 |
| Band 2 | FY-3C_VIRR_Day_EV_RefSB | 0.84–0.89 |
| Band 3 | FY-3C_VIRR_Day_EV_RefSB | 1.55–1.64 |
| Band 4 | FY-3C_VIRR_Day_EV_RefSB | 0.43–0.48 |
| Band 5 | FY-3C_VIRR_Day_EV_RefSB | 0.48–0.53 |
| Band 6 | FY-3C_VIRR_Day_EV_RefSB | 0.53–0.58 |
| Band 7 | FY-3C_VIRR_Day_EV_RefSB | 1.325–1.395 |
| Band 8 | FY-3C_VIRR_Day_EV_Emissive | 3.55–3.93 |
| Band 9 | FY-3C_VIRR_Day_EV_Emissive | 10.3–11.3 |
| Band 10 | FY-3C_VIRR_Day_EV_Emissive | 11.5–12.5 |
| Band 11 | MVC value of NDVI | - |
| Class (Name) | Training Data | Test Data |
|---|---|---|
| Number of Pixels per Class | ||
| Class 1 (Bare/Sparse vegetation) | 20,585 | 6424 |
| Class 2 (Built-up) | 1620 | 575 |
| Class 3 (Cropland) | 15,472 | 4246 |
| Class 4 (Forest) | 11,378 | 3101 |
| Class 5 (Herbaceous wetland) | 1686 | 602 |
| Class 6 (Herbaceous vegetation) | 12,394 | 3641 |
| Class 7 (Shrubs) | 18,956 | 5283 |
| Class 8 (Water bodies) | 9116 | 3795 |
| Total number of pixels | 91,207 | 27,667 |
| Experiment No. | Input Data | Class Name | Bare/Sparse Vegetation | Built-Up | Cropland | Forest | Herbaceous Wetland | Herbaceous Vegetation | Shrub | Water Bodies |
|---|---|---|---|---|---|---|---|---|---|---|
| Class ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| No. of Pixels | 6424 | 575 | 4246 | 3101 | 602 | 3641 | 5283 | 3795 | ||
| 1 | Parameter | Ntree | default (100) | |||||||
| Mtry | default (auto, i.e., is the square root of no. variables) | |||||||||
| Accuracy measures | precision | 0.95 | 0.69 | 0.81 | 0.91 | 0.74 | 0.81 | 0.77 | 0.93 | |
| recall | 0.93 | 0.57 | 0.87 | 0.87 | 0.68 | 0.71 | 0.82 | 0.98 | ||
| f1-score | 0.94 | 0.63 | 0.84 | 0.89 | 0.71 | 0.76 | 0.80 | 0.95 | ||
| OA | 0.86 (0.857) | |||||||||
| k | 0.83 (0.829) | |||||||||
| 2 | Parameter | Ntree | 300 | |||||||
| Mtry | default | |||||||||
| Accuracy measures | precision | 0.95 | 0.63 | 0.81 | 0.91 | 0.73 | 0.81 | 0.77 | 0.93 | |
| recall | 0.92 | 0.57 | 0.87 | 0.86 | 0.71 | 0.71 | 0.82 | 0.98 | ||
| f1-score | 0.93 | 0.60 | 0.84 | 0.88 | 0.72 | 0.76 | 0.80 | 0.95 | ||
| OA | 0.85 (0.854) | |||||||||
| k | 0.83 (0.825) | |||||||||
| 3 | Parameter | Ntree | 500 | |||||||
| Mtry | default | |||||||||
| Accuracy measures | precision | 0.95 | 0.67 | 0.81 | 0.91 | 0.73 | 0.82 | 0.77 | 0.93 | |
| recall | 0.92 | 0.58 | 0.87 | 0.85 | 0.70 | 0.72 | 0.83 | 0.98 | ||
| f1-score | 0.93 | 0.62 | 0.84 | 0.88 | 0.72 | 0.76 | 0.80 | 0.95 | ||
| OA | 0.86 (0.856) | |||||||||
| k | 0.83 (0.828) | |||||||||
| 4 | Parameter | Ntree | 700 | |||||||
| Mtry | default | |||||||||
| Accuracy measures | precision | 0.95 | 0.72 | 0.81 | 0.90 | 0.74 | 0.82 | 0.77 | 0.93 | |
| recall | 0.93 | 0.57 | 0.87 | 0.85 | 0.69 | 0.72 | 0.83 | 0.98 | ||
| f1-score | 0.94 | 0.64 | 0.84 | 0.88 | 0.71 | 0.76 | 0.80 | 0.95 | ||
| OA | 0.86 (0.856) | |||||||||
| k | 0.83 (0.858) | |||||||||
| 5 | Parameter | Ntree | 1000 | |||||||
| Mtry | default | |||||||||
| Accuracy measures | precision | 0.95 | 0.70 | 0.81 | 0.91 | 0.73 | 0.82 | 0.77 | 0.93 | |
| recall | 0.93 | 0.57 | 0.86 | 0.85 | 0.68 | 0.71 | 0.83 | 0.98 | ||
| f1-score | 0.94 | 0.63 | 0.83 | 0.88 | 0.71 | 0.76 | 0.80 | 0.95 | ||
| OA | 0.86 (0.856) | |||||||||
| k | 0.83 (0.827) | |||||||||
| 6 | Parameter | Ntree | default (100) | |||||||
| Mtry | 10 | |||||||||
| Accuracy measures | precision | 0.95 | 0.66 | 0.78 | 0.89 | 0.75 | 0.80 | 0.77 | 0.94 | |
| recall | 0.92 | 0.55 | 0.86 | 0.85 | 0.66 | 0.70 | 0.82 | 0.98 | ||
| f1-score | 0.93 | 0.60 | 0.82 | 0.87 | 0.70 | 0.75 | 0.79 | 0.96 | ||
| OA | 0.85 | |||||||||
| k | 0.82 | |||||||||
| 7 | Parameter | Ntree | default (100) | |||||||
| Mtry | 40 | |||||||||
| Accuracy measures | precision | 0.94 | 0.48 | 0.80 | 0.92 | 0.71 | 0.81 | 0.76 | 0.94 | |
| recall | 0.89 | 0.57 | 0.86 | 0.85 | 0.67 | 0.70 | 0.83 | 0.98 | ||
| f1-score | 0.92 | 0.52 | 0.83 | 0.88 | 0.69 | 0.75 | 0.80 | 0.96 | ||
| OA | 0.85 | |||||||||
| k | 0.82 | |||||||||
| 8 | Parameter | Ntree | default (100) | |||||||
| Mtry | 100 | |||||||||
| Accuracy measures | precision | 0.94 | 0.53 | 0.79 | 0.91 | 0.68 | 0.79 | 0.76 | 0.91 | |
| recall | 0.88 | 0.58 | 0.85 | 0.84 | 0.62 | 0.71 | 0.83 | 0.98 | ||
| f1-score | 0.91 | 0.55 | 0.82 | 0.87 | 0.65 | 0.75 | 0.79 | 0.94 | ||
| OA | 0.84 | |||||||||
| k | 0.81 | |||||||||
| 9 | Parameter | Ntree | default (100) | |||||||
| Mtry | 100 | |||||||||
| Accuracy measures | precision | 0.94 | 0.43 | 0.78 | 0.90 | 0.69 | 0.78 | 0.76 | 0.89 | |
| recall | 0.84 | 0.58 | 0.87 | 0.83 | 0.59 | 0.67 | 0.83 | 0.97 | ||
| f1-score | 0.89 | 0.49 | 0.82 | 0.86 | 0.63 | 0.72 | 0.79 | 0.93 | ||
| OA | 0.83 | |||||||||
| k | 0.79 | |||||||||
| Experiment No. | Input Data | Class Name | Bare/Sparse Vegetation | Built-Up | Cropland | Forest | Herbaceous Wetland | Herbaceous Vegetation | Shrub | Water Bodies |
|---|---|---|---|---|---|---|---|---|---|---|
| Class ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| No. of Pixels | 6424 | 575 | 4246 | 3101 | 602 | 3641 | 5283 | 3795 | ||
| 1 | Parameter | cost | default (1) | |||||||
| gamma | Default (scale (1/(n_features * X.var()) as value of gamma, where X.var is variance) | |||||||||
| Accuracy measures | precision | 0.91 | 0.79 | 0.64 | 0.76 | 0.96 | 0.67 | 0.72 | 0.95 | |
| recall | 0.94 | 0.04 | 0.83 | 0.83 | 0.19 | 0.45 | 0.78 | 0.97 | ||
| f1-score | 0.92 | 0.07 | 0.72 | 0.79 | 0.32 | 0.54 | 0.75 | 0.96 | ||
| OA | 0.78 | |||||||||
| k | 0.74 | |||||||||
| 2 | Parameter | cost | 50 | |||||||
| gamma | default | |||||||||
| Accuracy measures | precision | 0.94 | 0.78 | 0.78 | 0.87 | 0.80 | 0.76 | 0.75 | 0.97 | |
| recall | 0.96 | 0.44 | 0.89 | 0.84 | 0.59 | 0.64 | 0.81 | 0.97 | ||
| f1-score | 0.95 | 0.56 | 0.83 | 0.85 | 0.68 | 0.70 | 0.77 | 0.97 | ||
| OA | 0.85 | |||||||||
| k | 0.81 | |||||||||
| 3 | Parameter | cost | 100 | |||||||
| gamma | default | |||||||||
| Accuracy measures | precision | 0.94 | 0.78 | 0.78 | 0.87 | 0.74 | 0.76 | 0.75 | 0.97 | |
| recall | 0.95 | 0.48 | 0.89 | 0.83 | 0.65 | 0.63 | 0.80 | 0.98 | ||
| f1-score | 0.95 | 0.60 | 0.83 | 0.85 | 0.69 | 0.69 | 0.77 | 0.97 | ||
| OA | 0.85 | |||||||||
| k | 0.81 | |||||||||
| 4 | Parameter | cost | 300 | |||||||
| gamma | default | |||||||||
| Accuracy measures | precision | 0.95 | 0.73 | 0.78 | 0.86 | 0.72 | 0.78 | 0.74 | 0.96 | |
| recall | 0.95 | 0.54 | 0.89 | 0.83 | 0.69 | 0.62 | 0.79 | 0.98 | ||
| f1-score | 0.95 | 0.62 | 0.83 | 0.84 | 0.71 | 0.69 | 0.76 | 0.97 | ||
| OA | 0.84 | |||||||||
| k | 0.81 | |||||||||
| 5 | Parameter | cost | 600 | |||||||
| gamma | default | |||||||||
| Accuracy measures | precision | 0.95 | 0.67 | 0.77 | 0.85 | 0.74 | 0.78 | 0.74 | 0.96 | |
| recall | 0.93 | 0.57 | 0.89 | 0.83 | 0.70 | 0.63 | 0.78 | 0.97 | ||
| f1-score | 0.94 | 0.62 | 0.82 | 0.84 | 0.72 | 0.69 | 0.76 | 0.97 | ||
| OA | 0.84 | |||||||||
| k | 0.8 | |||||||||
| 6 | Parameter | cost | 900 | |||||||
| gamma | default | |||||||||
| Accuracy measures | precision | 0.94 | 0.67 | 0.76 | 0.85 | 0.75 | 0.78 | 0.74 | 0.96 | |
| recall | 0.93 | 0.58 | 0.88 | 0.83 | 0.71 | 0.63 | 0.77 | 0.97 | ||
| f1-score | 0.94 | 0.62 | 0.81 | 0.84 | 0.73 | 0.69 | 0.75 | 0.97 | ||
| OA | 0.83 | |||||||||
| k | 0.8 | |||||||||
| 7 | Parameter | cost | 1500 | |||||||
| gamma | default | |||||||||
| Accuracy measures | precision | 0.94 | 0.64 | 0.74 | 0.84 | 0.78 | 0.78 | 0.73 | 0.96 | |
| recall | 0.91 | 0.61 | 0.88 | 0.83 | 0.70 | 0.62 | 0.77 | 0.97 | ||
| f1-score | 0.93 | 0.62 | 0.80 | 0.83 | 0.74 | 0.69 | 0.75 | 0.97 | ||
| OA | 0.83 | |||||||||
| k | 0.8 | |||||||||
| 8 | Parameter | cost | 300 | |||||||
| gamma | 10−3 | |||||||||
| Accuracy measures | precision | 0.24 | 1.00 | 1.00 | 0.00 | 0.00 | 0.50 | 1.00 | 1.00 | |
| recall | 1.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | ||
| f1-score | 0.38 | 0.04 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.26 | ||
| OA | 0.25 | |||||||||
| k | 0.03 | |||||||||
| 9 | Parameter | cost | 300 | |||||||
| gamma | 10−6 | |||||||||
| Accuracy measures | precision | 0.99 | 1.00 | 1.00 | 0.00 | 0.00 | 0.50 | 0.20 | 1.00 | |
| recall | 0.05 | 0.02 | 0.01 | 0.00 | 0.00 | 0.00 | 1.00 | 0.15 | ||
| f1-score | 0.10 | 0.04 | 0.02 | 0.00 | 0.00 | 0.00 | 0.33 | 0.26 | ||
| OA | 0.22 | |||||||||
| k | 0.04 | |||||||||
| 10 | Parameter | cost | 300 | |||||||
| gamma | 10−8 | |||||||||
| Accuracy measures | precision | 0.94 | 0.61 | 0.78 | 0.88 | 0.77 | 0.80 | 0.78 | 0.80 | |
| recall | 0.85 | 0.71 | 0.83 | 0.82 | 0.71 | 0.72 | 0.78 | 0.99 | ||
| f1-score | 0.89 | 0.65 | 0.80 | 0.84 | 0.74 | 0.75 | 0.78 | 0.88 | ||
| Overall accuracy | 0.82 | |||||||||
| Kappa coefficient | 0.79 | |||||||||
| 11 | Parameter | cost | 300 | |||||||
| gamma | 10−9 | |||||||||
| Accuracy measures | precision | 0.95 | 0.73 | 0.78 | 0.86 | 0.72 | 0.78 | 0.74 | 0.96 | |
| recall | 0.95 | 0.54 | 0.89 | 0.83 | 0.69 | 0.62 | 0.79 | 0.98 | ||
| f1-score | 0.95 | 0.62 | 0.83 | 0.84 | 0.71 | 0.69 | 0.76 | 0.97 | ||
| OA | 0.84 | |||||||||
| k | 0.81 | |||||||||
| 12 | Parameter | cost | 300 | |||||||
| gamma | 10−12 | |||||||||
| Accuracy measures | precision | 0.92 | 0.85 | 0.66 | 0.78 | 0.92 | 0.67 | 0.74 | 0.96 | |
| recall | 0.96 | 0.15 | 0.84 | 0.84 | 0.24 | 0.47 | 0.77 | 0.97 | ||
| f1-score | 0.94 | 0.26 | 0.74 | 0.81 | 0.39 | 0.55 | 0.76 | 0.97 | ||
| OA | 0.80 | |||||||||
| k | 0.76 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adugna, T.; Xu, W.; Fan, J. Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images. Remote Sens. 2022, 14, 574. https://doi.org/10.3390/rs14030574
Adugna T, Xu W, Fan J. Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images. Remote Sensing. 2022; 14(3):574. https://doi.org/10.3390/rs14030574
Chicago/Turabian StyleAdugna, Tesfaye, Wenbo Xu, and Jinlong Fan. 2022. "Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images" Remote Sensing 14, no. 3: 574. https://doi.org/10.3390/rs14030574
APA StyleAdugna, T., Xu, W., & Fan, J. (2022). Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images. Remote Sensing, 14(3), 574. https://doi.org/10.3390/rs14030574








