Performance Analysis of Zero-Difference GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 Point Positioning Using CNES Uncombined Bias Products

Abstract

The modernization of Global Navigation Satellite System (GNSS) including the transmission of signals on multiple frequencies has greatly promoted the development of the popular PPP (Precise Point Positioning) technique. A key issue of multi-frequency PPP is the handling of the observable-specific signal biases in order to allow for carrier-phase ambiguity resolution (AR). As a result, PPP modeling at a user side in the multi-frequency case varies depending on the definition of the applied phase bias products. In this study, we investigate the positioning performance of GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 undifferenced ionosphere-float model in the conventional PPP mode and the single-epoch mode using the uncombined code and phase bias products generated at the French CNES (Centre National D’Etudes Spatiales). A series of widelane ambiguities are configured in our multi-frequency PPP functional model instead of forming the classical Melbourne–Wübbena (MW) combination. The best integer equivariant (BIE) estimator is used for the ambiguity resolution in a conventional cascading scheme according to the wavelength of the combined ambiguities for each constellation. Real data collected at IGS stations with a 30-s sampling interval is applied to evaluate the above models. For the conventional kinematic PPP configuration, a significant accuracy improvement of 63% on the east component of the fixed solution is obtained with respect to the ambiguity-float solution. The PPP convergence is accelerated by 17% after the AR. Regarding the single-epoch positioning, an accuracy of 32 and 31 cm for north and east components can be achieved, respectively, (68th percentile) with the instantaneous widelane-ambiguity resolution, which is improved by 13% and 16% compared to multi-frequency code-based or float solution.

1. Introduction

The Global Navigation Satellite System (GNSS) Precise Point Positioning (PPP) technique is well-known for its flexibility relative to real-time kinematic (RTK) and high-precision capability around the globe. Recent GNSS modernization including the availability of code and phase measurements on multiple frequencies from multiple constellations has boosted the development of PPP model for multi-frequency integrated positioning. In particular, multi-frequency PPP with carrier-phase ambiguity resolution (AR) allowing for more rapid convergence and better precision is of an increasingly great interest within the GNSS community.

The prerequisite precise satellite clock products for PPP are conventionally referenced to the P1/P2 or L1/L2 ionosphere-free combinations in the GPS case. Applying these clock estimates directly to the modelling of the measurements on the third L5 frequency will inevitably result in extra clock bias due to the presence of the observable- and frequency-specific hardware delays. This inter frequency clock bias (IFCB) between the L1/L2 and the L1/L5 clock offset can vary with peak-to-peak amplitudes of 10–40 cm [1]. Many studies therefore have investigated the estimation of IFCB for its compensation in GPS triple-frequency (TF) PPP [2,3]. Ambiguity-resolved GPS TF PPP with the correction of the estimated IFCB is further demonstrated in [4]. In [5] a separated satellite clock parameter is proposed for the L5 frequency to account for the IFCB effect instead of an explicit estimation and GPS TF PPP with ambiguity resolution based on the clock-separated model is also achieved in [6]. For Galileo E1/E5a/E5b PPP, it is found that the magnitude of the time-varying IFCB is negligible and the ambiguity-fixed solutions are also presented in many studies [4,6,7]. In [8], Galileo five-frequency PPP with AR through using pairs of classical ionosphere-free combinations on different frequencies is even showed.

The ambiguity resolution (AR) process for GPS/Galileo multi-frequency PPP in the above studies compute the uncalibrated phase delays (UPDs) [9] or the fractional cycle biases (FCB) first using a network of reference stations. These satellite UPDs are generated in the form of extra-wide lane (EWL), wide lane (WL) and narrow lane (NL) or L1 in the triple-frequency case. Then the integer nature of ambiguity estimates at a PPP user end could be recovered with the correction of these UPDs and ambiguity-fixed solution is then obtained. It is noted that these UPD products in the above studies are dedicated to their TF PPP models and the applicability of their bias products to different TF PPP models is not presented, although it has been demonstrated that the GPS L1/L2 FCB products can be applied to the ionosphere-free or the ionosphere-float dual-frequency PPP models [10,11]. The characteristics of multiple types of EWL UPD for Galileo five-frequency ionosphere-free PPP AR are also studied in [8].

Another form of phase bias representation is the WL Satellite Biases (WSB) and the ‘integer’ phase clocks [12] or ‘decoupled’ clock model [13] in case of the GPS legacy L1/L2 frequencies. Recently these type of products are also available for Galileo E1/E5a measurements enabling millimeter-level ambiguity-resolved kinematic PPP solutions [14,15]. However, as pointed out in [16,17], this bias formulation is limited to the dual-frequency case and difficult to be extended to the triple-frequency case since there are many more possible combinations instead of only two quantities. A new uncombined phase bias representation is proposed in [16] which uses the same adding convention as the existing RTCM (Radio Technical Commission for Maritime Services) standard for the code biases. It also takes into account the inter frequency clock bias [16] and in [18] it is showed that various combined phase ambiguities in the GPS triple-frequency context can conserve their integer property.

Since 15 September 2014, CNES has started broadcasting these uncombined phase bias products on the IGS (International GNSS Service) CLK93 real-time data stream. Currently code and phase biases for GPS L1/L2/L5, Galileo E1/E5a/E5b/E6 and BeiDou-2 B1/B2/B3 signals are issued routinely while only code biases for GLONASS G1/G2 are available. An open source PPP client software PPP-WIZARD (With Integer Furthermore, Zero-Difference Ambiguity Resolution) [19] from CNES also demonstrates the use of their real-time bias products for GPS/Galileo/BeiDou-2 TF PPP with AR in a zero-differenced ambiguity-combined model. More detailed assessment of GPS/Galileo triple-frequency PPP based on the software is presented in [20]. In [21], the bias stream is applied to a between-satellite single-difference PPP model and the performance after AR with the inclusion of Galileo E6 signal is assessed. In [22], an OEUFS (Optimal Estimation using Uncombined Four-frequency Signals) strategy is showed in which GPS L1/L2 and Galileo E1/E5a/E5b/E6 signals allows for instantaneous centimeter-level positioning with ionospheric information from the global ionospheric map (GIM) model. They remarked that this strategy is a generalization of the widelaning technique. CNES now also generates post-processed daily uncombined phase biases for validating their OEUFS strategy. Some other studies have also explored the single-epoch precise positioning ability with fixed widelane ambiguities [8,23].

In order to further evaluate the benefit of the widelane-resolved signals to GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 integrated positioning especially without any external ionospheric information, we applied the CNES post-processed bias products in a zero-difference ambiguity-combined model, where multiple widelane ambiguities are estimated. Our evaluation to this model is twofold: to assess its positioning performance in the conventional filtered setting or PPP; and to validate the single-epoch widelane-resolved solution. This study is organised as follows: first we formulate the GPS/Galileo multi-frequency (GEMF) widelane-based model after applying the CNES uncombined bias products, followed by a single-satellite model analysis; then the positioning solutions with normal PPP filtered and single-epoch settings are presented, respectively. Finally the positioning performance of this model is discussed.

2. Methodology

The CNES uncombined bias formulation can be extended to multi-frequency measurements easily without explicit estimation of the IFCB for the GPS Block IIF satellites [16] and the integer nature of phase ambiguities is also preserved. In this section, we formulate the GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 zero-difference ambiguity-float and ambiguity-fixed positioning models with the use of CNES uncombined bias products and then present a stochastic analysis of Galileo single-satellite multi-frequency model for the ambiguity resolution.

2.1. GPS/Galileo Multi-Frequency Observational Model

Following the CNES new bias representation [19], the triple-frequency code and phase measurements from a GPS satellite (s) observed at a receiver (r) may be modeled as:

$$\begin{array}{cc}\hfill & P_1^{{}^{\prime }}=P_1+\Delta b_{P_1}=\rho +\Delta h+I+T\hfill \\ \hfill & P_2^{{}^{\prime }}=P_2+\Delta b_{P_2}=\rho +\Delta h+{\gamma }_{2}I+T\hfill \\ \hfill & C_5^{{}^{\prime }}=C_5+\Delta b_{C_5}=\rho +\Delta h+{\gamma }_{5}I+T\hfill \\ \hfill & {\lambda }_1{L}_1^{{}^{\prime }}={\lambda }_1(L_1+\Delta b_{L_1})=\rho +\Delta h-I+T+{\lambda }_{1}W+{\lambda }_1{N}_1\hfill \\ \hfill & {\lambda }_2{L}_2^{{}^{\prime }}={\lambda }_2(L_2+\Delta b_{L_2})=\rho +\Delta h-{\gamma }_{2}I+T+{\lambda }_{2}W+{\lambda }_2{N}_2\hfill \\ \hfill & {\lambda }_5{L}_5^{{}^{\prime }}={\lambda }_5(L_5+\Delta b_{L_5})=\rho +\Delta h-{\gamma }_{5}I+T+{\lambda }_{5}W+{\lambda }_5{N}_5\hfill \end{array}$$

(1)

where:

• $P,C$ and L stand for code (in meter) and phase (in cycle) measurements, respectively.
• $\rho$ is the geometric propagation distance of the GPS radio wave between s and r antenna phase center including PCO (Phase Centre Offset) corrections on different frequencies ($f_1,f_2,f_5$).
• $\Delta h=h_r-h^s$ is the clock difference between r and s.
• I is the slant ionospheric delay at $f_1$ for code and is inversely corrected for phase. ${\gamma }_2=f_1^2/f_2^2$, ${\gamma }_5=f_1^2/f_5^2$.
• T is the slant troposeric delay.
• ${\lambda }_i=c/f_i(i=1,2,5)$ is the signal wavelength at frequency $f_i$ with c the speed of light.
• W is the phase wind-up effect (cycle).
• N is the carrier phase ambiguity and has the integer property (cycle) by definition.
• $\Delta b_P=b_{P,r}-b_P^s$ and $\Delta b_L=b_{L,r}-b_L^s$ denote the bias difference between r and s for code and phase, respectively.

After applying precise satellite clock products and also the CNES bias products, the terms $h^s$, $b_P^s$ and $b_L^s$ can be eliminated from the above equations. As a consequence, one receiver clock per observable can be reparameterized at a user end. Alternatively, a common receiver clock offset with additional receiver clock biases may be defined in these equations as:

$$\begin{array}{cc}\hfill & P_1=\rho +d{t}^G+I+T\hfill \\ \hfill & P_2=\rho +d{t}^G+b_{P_2}+{\gamma }_{2}I+T\hfill \\ \hfill & C_5=\rho +d{t}^G+b_{C_5}+{\gamma }_{5}I+T\hfill \\ \hfill & {\lambda }_1{L}_1=\rho +d{t}^G+b_{L_1}-I+T+{\lambda }_{1}W+{\lambda }_1{N}_1\hfill \\ \hfill & {\lambda }_1{L}_2=\rho +d{t}^G+b_{L_2}-{\gamma }_{2}I+T+{\lambda }_{2}W+{\lambda }_2{N}_2\hfill \\ \hfill & {\lambda }_1{L}_5=\rho +d{t}^G+b_{L_5}-{\gamma }_{5}I+T+{\lambda }_{5}W+{\lambda }_5{N}_5\hfill \end{array}$$

(2)

where $d{t}^G$ is the common GPS receiver clock offset and we omit the subscript r of b. It is noted that for simplicity no change is marked in the bias terms but they should be different from those in Equation (1).

Similarly, Galileo E1/E5a/E5b/E6 code and phase measurements are expressed as:

$$\begin{array}{cc}\hfill & C_{E1}=\rho +d{t}^E+I+T\hfill \\ \hfill & C_{E5a}=\rho +d{t}^E+b_{C_{E5a}}+{\gamma }_{E5a}I+T\hfill \\ \hfill & C_{E5b}=\rho +d{t}^E+b_{C_{E5b}}+{\gamma }_{E5b}I+T\hfill \\ \hfill & C_{E6}=\rho +d{t}^E+b_{C_{E6}}+{\gamma }_{E6}I+T\hfill \\ \hfill & {\lambda }_{E1}{L}_{E1}=\rho +d{t}^E+b_{L_{E1}}-I+T+{\lambda }_{E1}W+{\lambda }_{E1}{N}_{E1}\hfill \\ \hfill & {\lambda }_{E5a}{L}_{E5a}=\rho +d{t}^E+b_{L_{E5a}}-{\gamma }_{E5a}I+T+{\lambda }_{E5a}W+{\lambda }_{E5a}{N}_{E5a}\hfill \\ \hfill & {\lambda }_{E5b}{L}_{E5b}=\rho +d{t}^E+b_{L_{E5b}}-{\gamma }_{E5b}I+T+{\lambda }_{E5b}W+{\lambda }_{E5b}{N}_{E5b}\hfill \\ \hfill & {\lambda }_{E6}{L}_{E6}=\rho +d{t}^E+b_{L_{E6}}-{\gamma }_{E6}I+T+{\lambda }_{E6}W+{\lambda }_{E6}{N}_{E6}\hfill \end{array}$$

(3)

where $d{t}^E$ is the Galileo receiver clock offset.

Instead of the usual method of converting the float ambiguity estimates to their widelane combinations or using the Melbourne–Wübbena (MW) combination [24,25] to achieve the ambiguity resolution, an explicit widelane-nested model is presented in [19] for GPS carrier-phase measurements in which the individual ambiguities are configured as follows:

$$\begin{array}{cc}\hfill & {\lambda }_1{N}_1={\lambda }_1{N}_1\hfill \\ \hfill & {\lambda }_2{N}_2={\lambda }_2(N_1+N_{WL})\hfill \\ \hfill & {\lambda }_5{N}_5={\lambda }_5(N_1+N_{WL}+N_{EWL})\hfill \end{array}$$

(4)

where $N_{WL}$ and $N_{EWL}$ are the GPS well-known widelane and extra-widelane ambiguities. Likewise, the Galileo quadruple-frequency phase ambiguities in Equation (3) can also be rearranged as:

$$\begin{array}{ccc}\hfill & {\lambda }_{E1}{N}_{E1}={\lambda }_{E1}{N}_{E1}\hfill & \\ \hfill & {\lambda }_{E5a}{N}_{E5a}={\lambda }_{E5a}(N_{E1}+N_{WL,E1E5a})\hfill \\ \hfill & {\lambda }_{E5b}{N}_{E5b}={\lambda }_{E5b}(N_{E1}+N_{WL,E1E5a}+N_{WL,E5aE5b})\hfill \\ \hfill & {\lambda }_{E6}{N}_{E6}={\lambda }_{E6}(N_{E1}+N_{WL,E1E5a}+N_{WL,E5aE5b}+N_{WL,E5bE6})\hfill \end{array}$$

(5)

where the subscript Galileo frequency pair indicates the used frequencies for forming the widelane observation. These widelane-estimated phase models together with the corresponding code measurements are referred to as GEMF fixed model in this article. These widelane ambiguities with long wavelength (meter level) can be resolved more easily and thus the resolution is usually performed in a cascading manner according to their wavelengths.

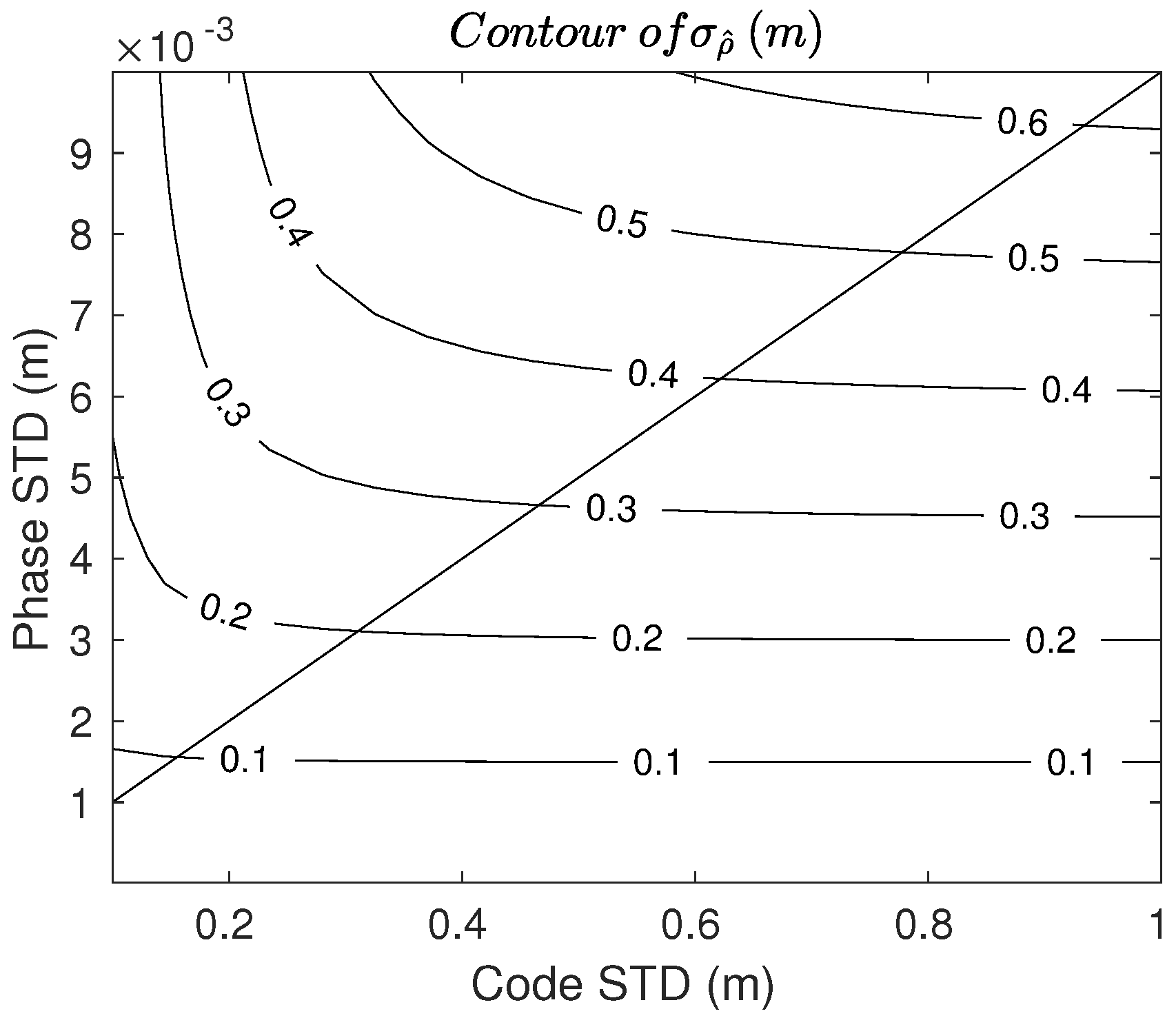
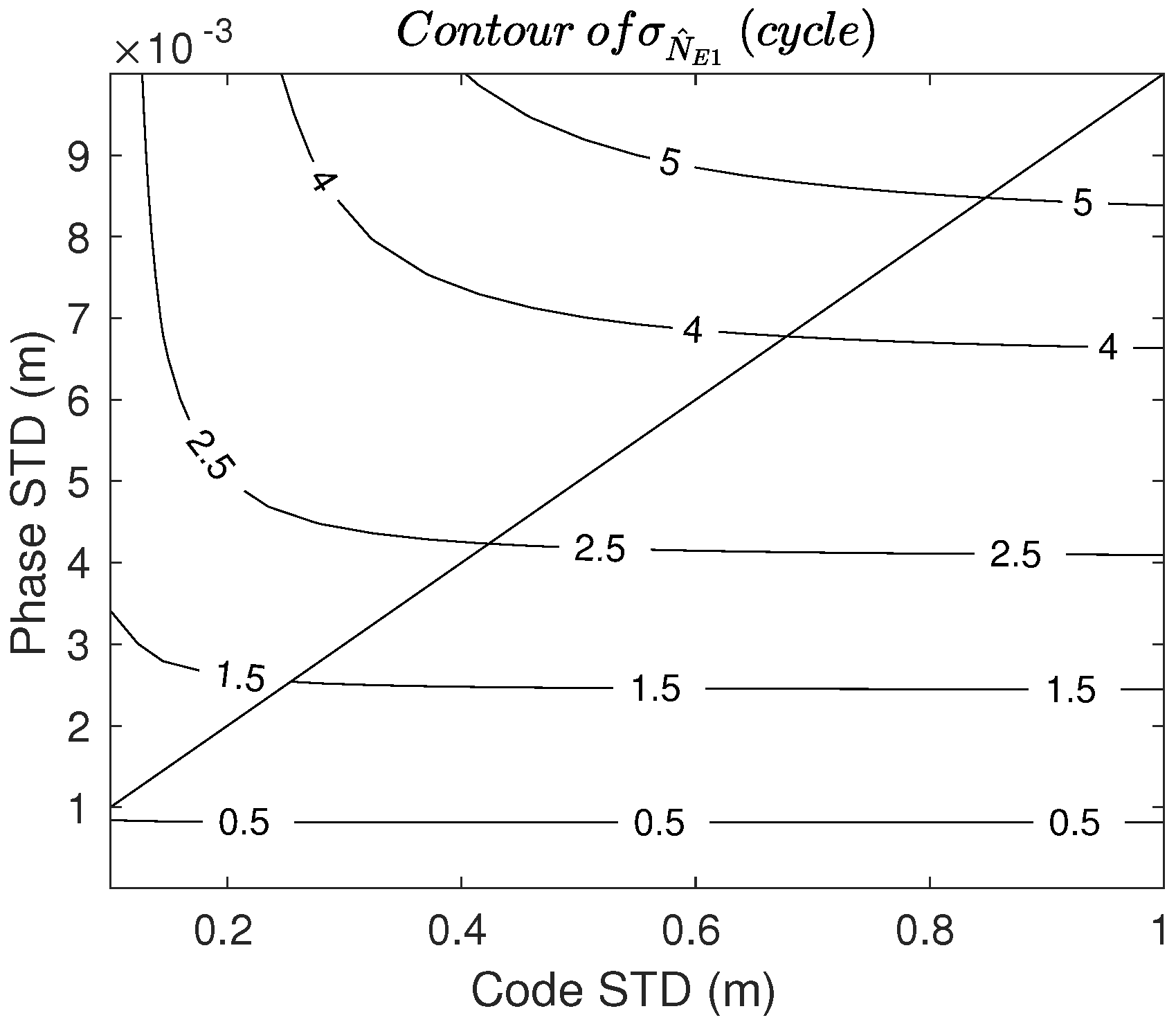
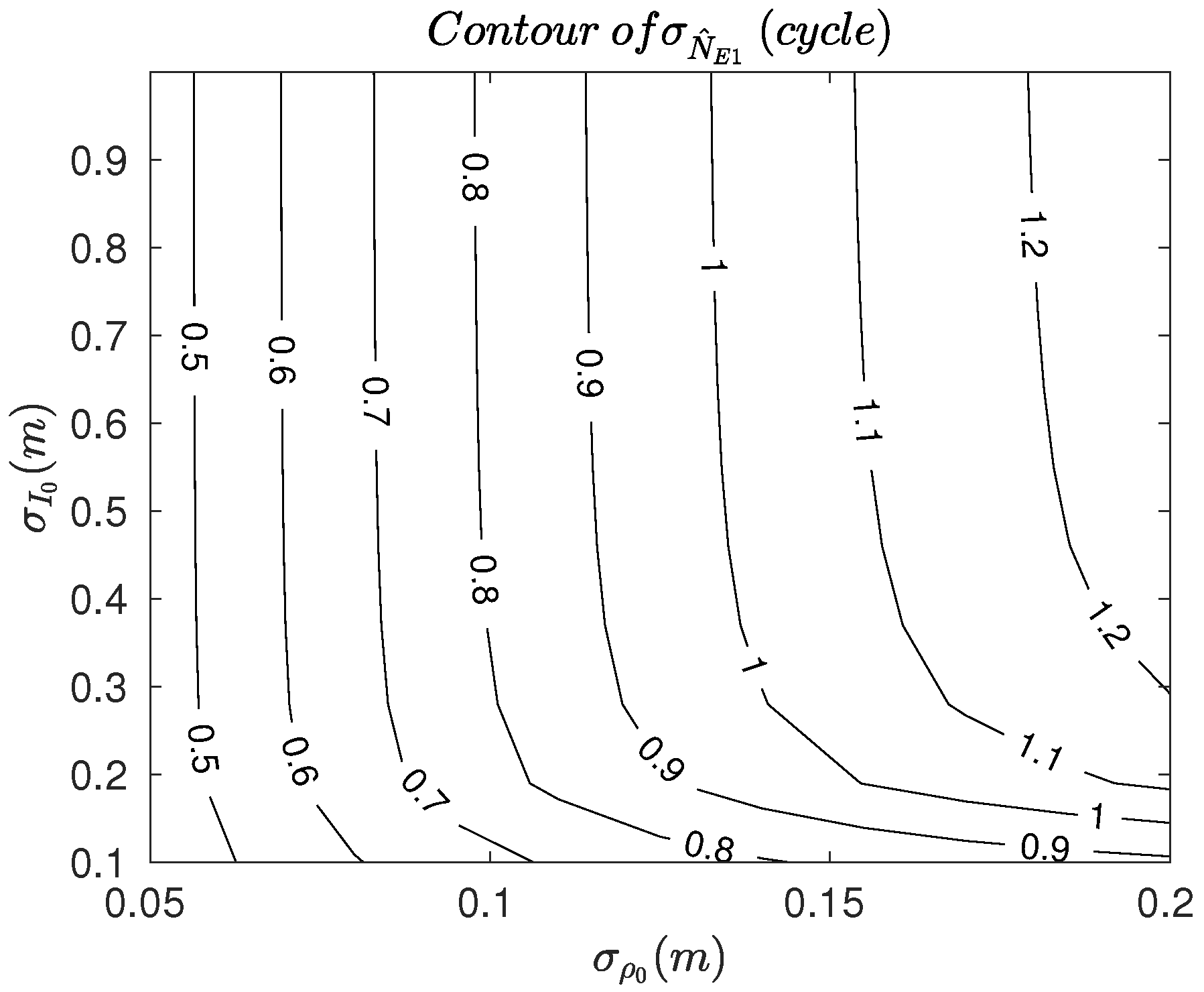
2.2. Stochastic Analysis

As shown in the above multi-frequency model, a series of widelane ambiguities are configured to be estimated and resolved. [22] evaluates the benefit of the Widelane Ambiguity Resolution (WAR) to the range estimates through a Galileo single-satellite quadruple-frequency model. In their analysis, the range precision can reach around 19 cm after WAR with a priori 3 mm and 30 cm for the phase and code standard deviation, respectively. However, the advantage of the WAR on the estimation of the remaining narrow-lane ambiguity is not presented. Further more, with additional constraints provided from other satellite system on the range parameter and external ionospheric information, the effect of the WAR on the resolution of the narrow-lane ambiguity is not clear. To further explore the stochastic characteristics of the estimates with fixed widelanes, we extended their model with the inclusion of pseudo measurements for the range and the ionospheric parameters as below:

$$\begin{array}{cc}\hfill & E\left\{\begin{array}{c}{y}_s\end{array}\right\}=E\left\{\begin{array}{c}\left[\begin{array}{c}\begin{array}{c}{C}_{E1}\hfill \\ C_{E5a}\hfill \\ {\lambda }_{E1}{L}_{E1}\hfill \\ {\lambda }_{E5a}{L}_{E5a}\hfill \\ {\lambda }_{E5b}{L}_{E5b}\hfill \\ {\lambda }_{E6}{L}_{E6}\hfill \\ {\rho }_0\hfill \\ I_0\hfill \end{array}\end{array}\right]\end{array}\right\}=\left[\begin{array}{c}\begin{array}{llllll}1& 1& 0& 0& 0& 0\\ 1& {\gamma }_{E5a}& 0& 0& 0& 0\\ 1& -1& {\lambda }_{E1}& 0& 0& 0\\ 1& -{\gamma }_{E5a}& {\lambda }_{E5a}& {\lambda }_{E5a}& 0& 0\\ 1& -{\gamma }_{E5b}& {\lambda }_{E5b}& {\lambda }_{E5b}& {\lambda }_{E5b}& 0\\ 1& -{\gamma }_{E6}& {\lambda }_{E6}& {\lambda }_{E6}& {\lambda }_{E6}& {\lambda }_{E6}\\ 1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}\rho \hfill \\ I\hfill \\ N_{E1}\hfill \\ N_{WL,E1E5a}\hfill \\ N_{WL,E5aE5b}\hfill \\ N_{WL,E5bE6}\hfill \end{array}\end{array}\right]\hfill \\ & =A_s{\widehat{x}}_s\hfill \\ \hfill & D\left\{y_s\right\}=Q_{y_s}\hfill \end{array}$$

(6)

where E {·} and D {·} are the expectation and dispersion operation. $Q_{y_s}$ is diagonal and consists of the noise of the measurements. Then the covariance matrix of ${\widehat{x}}_s$ will be:

$$\begin{array}{c}\hfill Q_{{\widehat{x}}_s}={\left(A_s^T{Q}_{y_s}^{-1}{A}_s\right)}^{-1}\end{array}$$

(7)

When the float widelane ambiguities in ${\widehat{x}}_s$ are fixed, $Q_{{\widehat{x}}_s}$ will be updated as:

$$\begin{array}{c}\hfill Q_{\check{b}\check{b}}=Q_{\widehat{b}\widehat{b}}-Q_{\widehat{b}\widehat{a}}{Q}_{\widehat{a}\widehat{a}}^{-1}{Q}_{\widehat{b}\widehat{a}}^T\end{array}$$

(8)

where $\widehat{a}$ is the ambiguity states to be fixed; $\widehat{b}$ is the remaining states of ${\widehat{x}}_s$ and $\check{b}$ is the updated states.

Figure 1 shows the possible values of ${\sigma }_{\widehat{\rho }}$ under different ${\sigma }_{code}$ and ${\sigma }_{phase}$ with a loose constraint of 100 m for both ${\sigma }_{{\rho }_0}$ and ${\sigma }_{I_0}$. It can be clearly seen that the range precision after fixing the three widelanes in Equation (6) is substantially dependent on the variation of ${\sigma }_{phase}$ while keeps nearly constant over the specified range of ${\sigma }_{code}$. For the precision of the estimated ${\widehat{N}}_{E1}$, similar pattern is also observed in Figure 2. In particular, at coordinate (0.3, 0.003), ${\sigma }_{{\widehat{N}}_{E1}}$ is still larger than one cycle which indicates the difficulty of resolving the remaining ${\widehat{N}}_{E1}$ instantaneously.

Figure 3 displays that only when the range is sufficiently precise would the resolution of ${\widehat{N}}_{E1}$ be possible. which is mainly due to its short wavelength (≈20 cm); While the contribution of the precision of ionosphere is not significant.

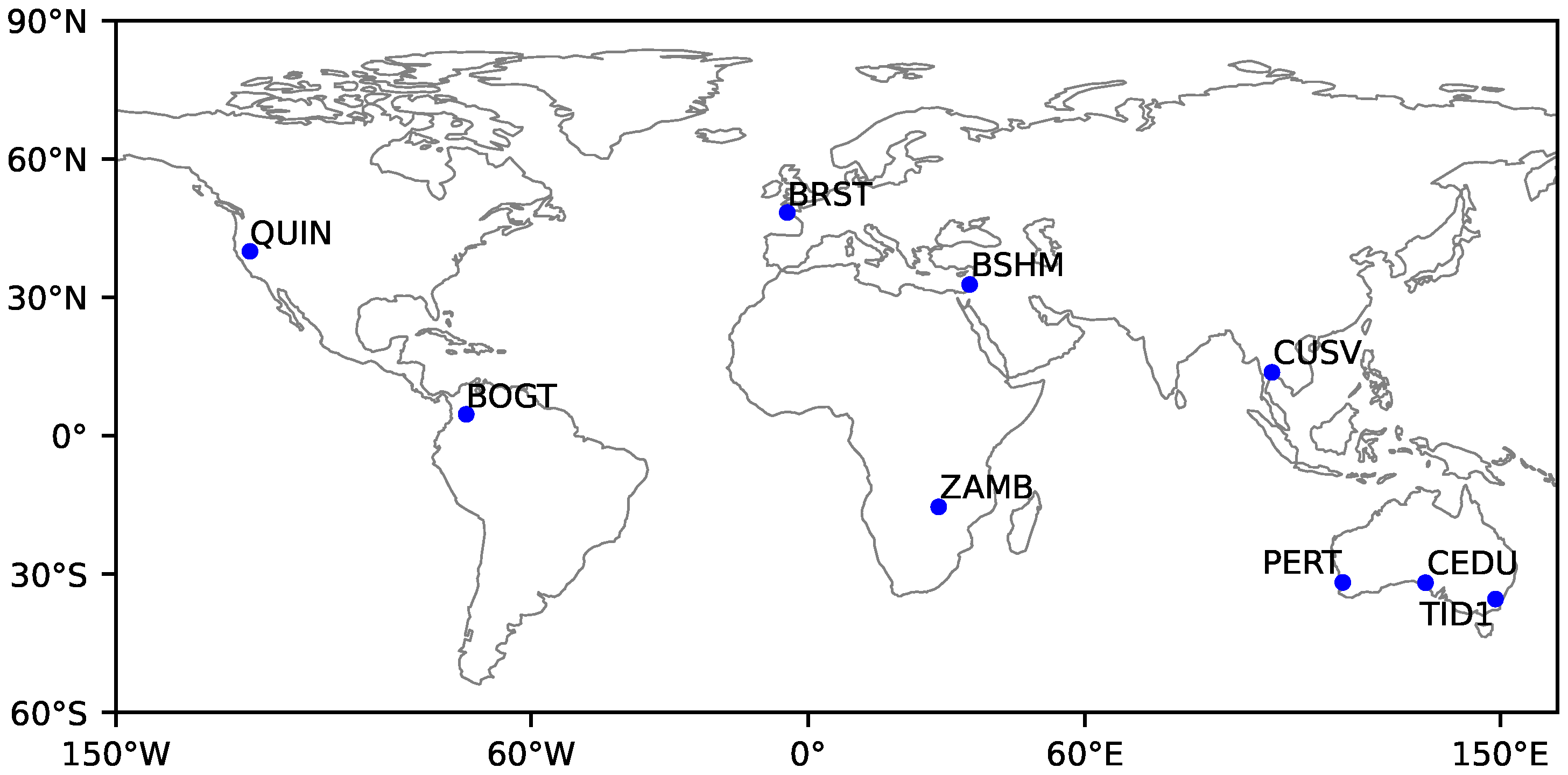
3. Experiments and Results

The GEMF positioning models presented in the above section have been applied to real data collected from 1 to 10 May 2021 with a 30-s sampling interval at nine globally distributed IGS (International GNSS Service) MGEX (Multi-GNSS Experiment) stations. GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 code and carrier-phase observations are routinely collected at these sites as shown in Figure 4.

The POINT (Position Orientation INTegration) software [26] was used for PPP implementation and results evaluation. A common configuration of POINT for all the following tests is listed in

Table 1. Common configuration of POINT for different tests.

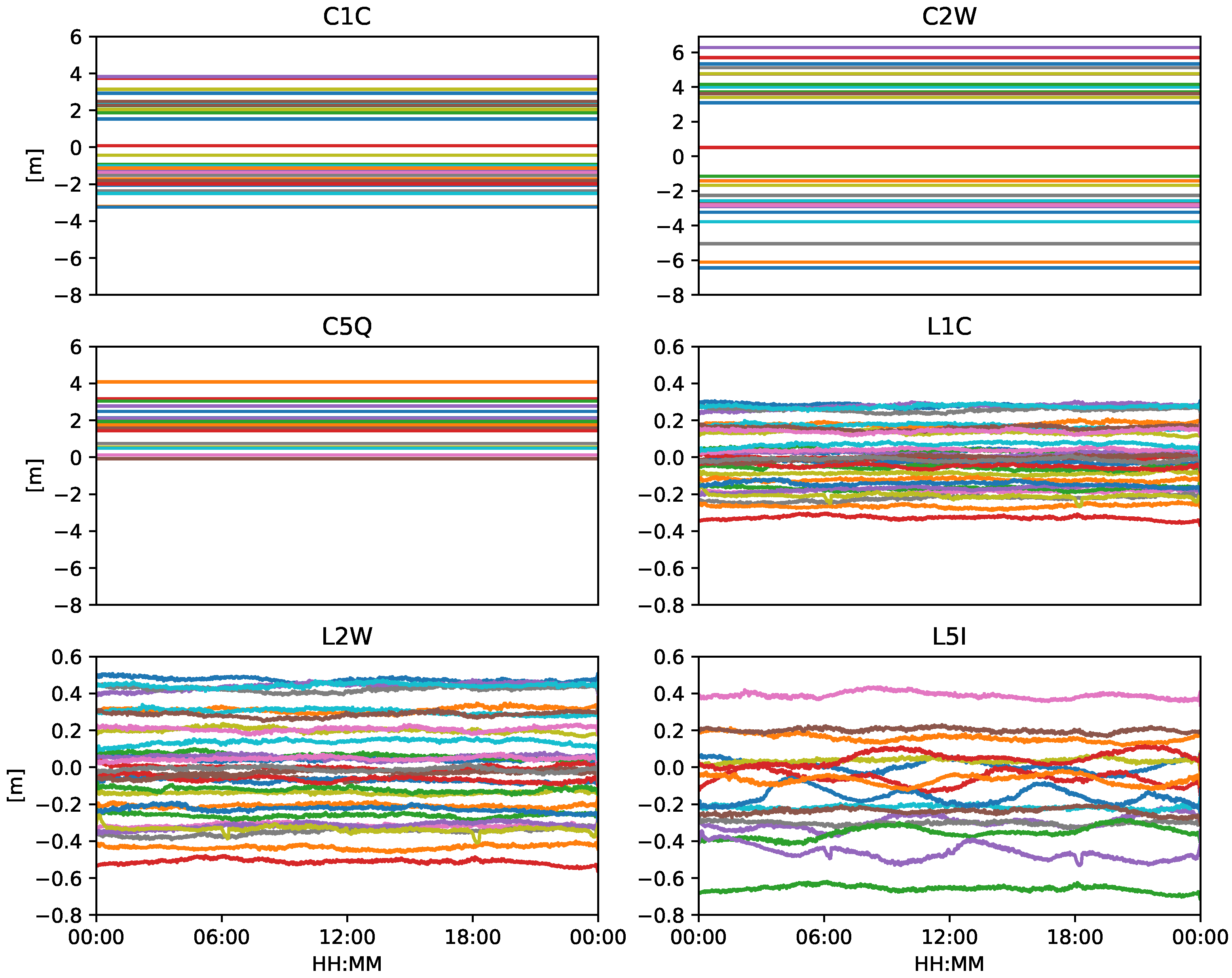
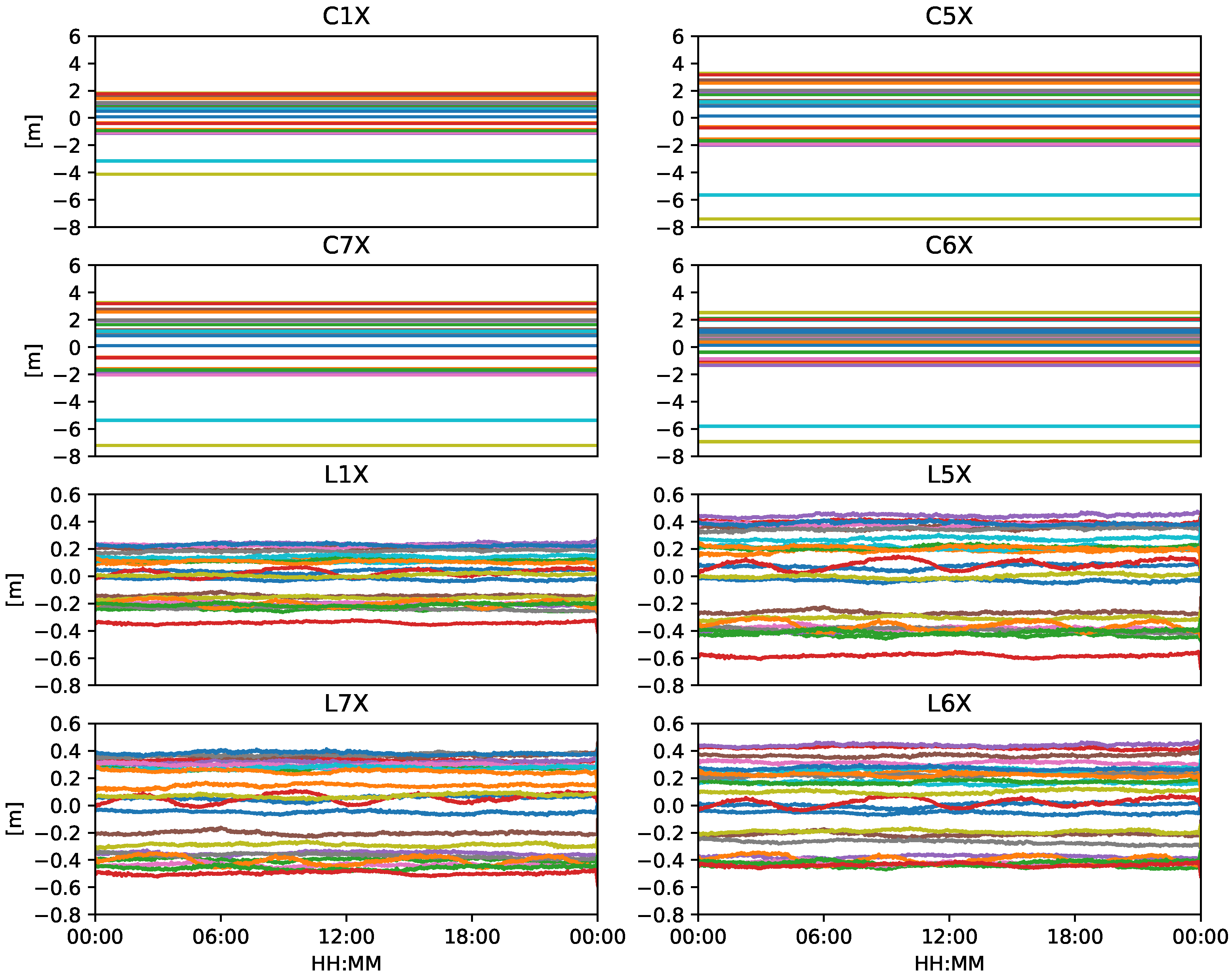
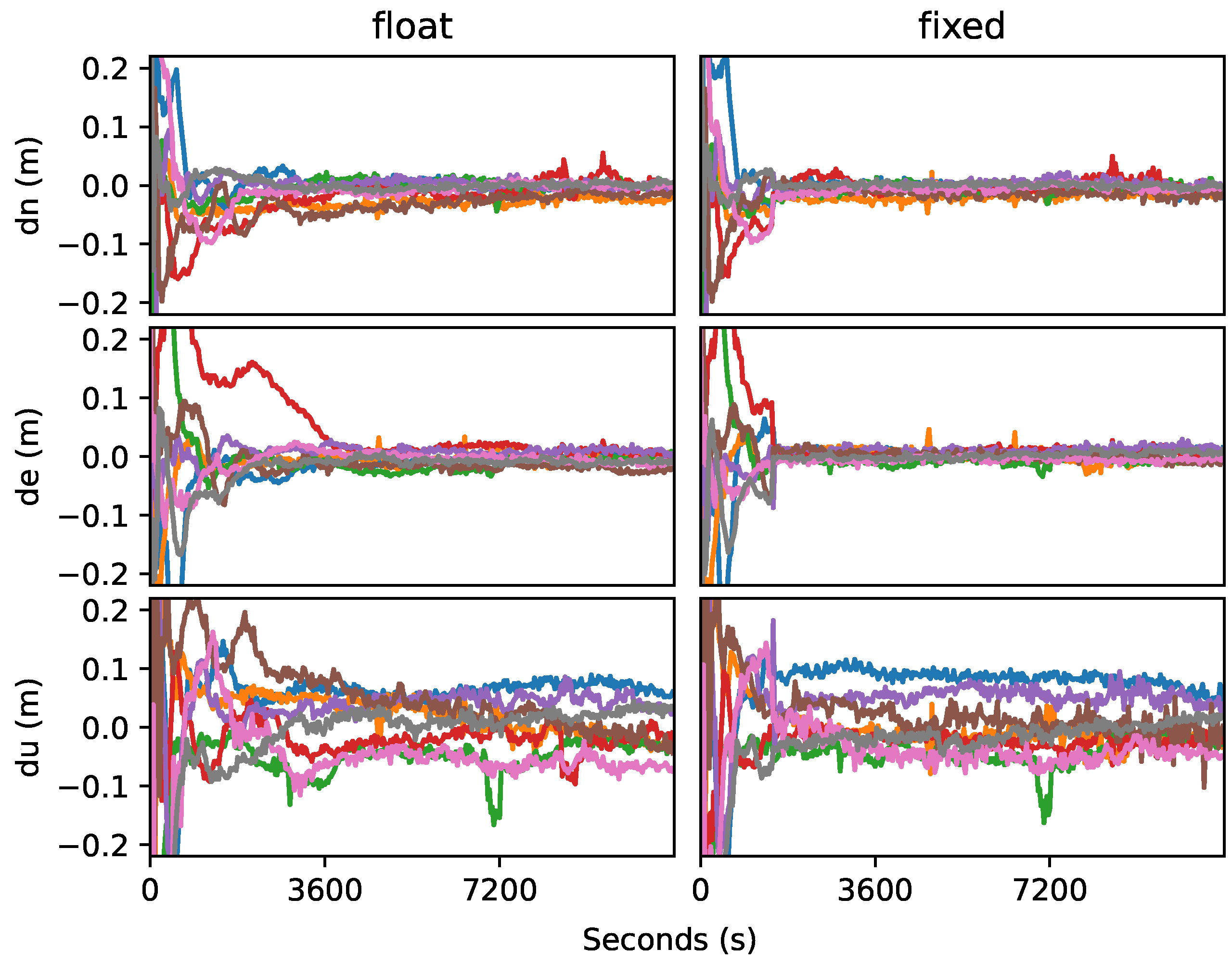
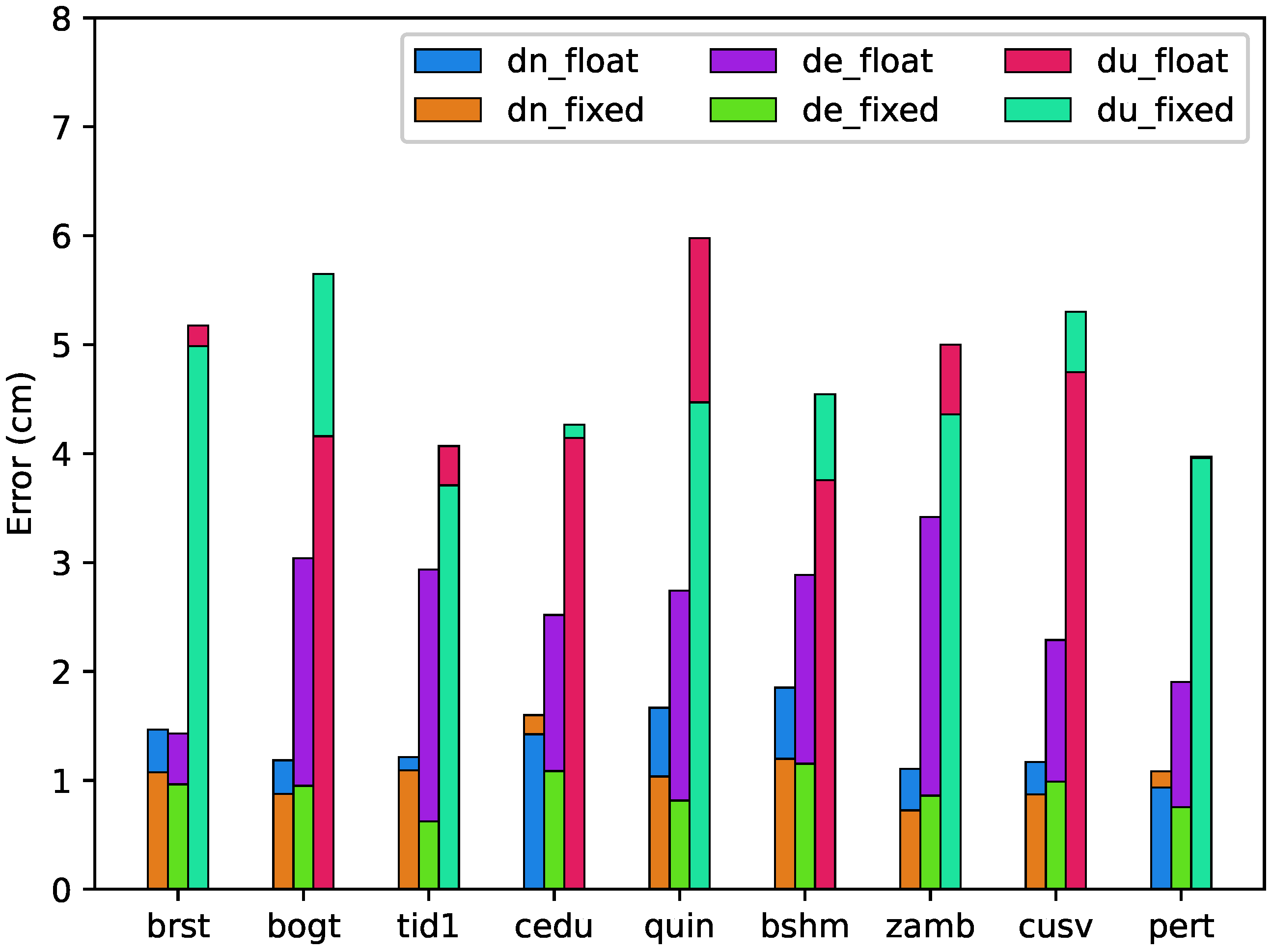
Parameter estimation	Extended Kalman Filter
Orbit and clocks	GFZ rapid products
Biases	CNES post-processed products
Ambiguity resolution	Best integer equivariant (BIE) estimator
Elevation cut-off	7°
Elevation weighting function	$\frac{1.001}{\sqrt{0.002001+si{n}^2\theta }}$ where $\theta$ is the elevation angle (radian)
Antenna PCO/PCV correction	igs14.atx
Site displacement	Pole tides and solid earth tides corrections
	Earth orientation parameters: IERS EOP 14 C04
	(IAU2000A); Solar system body ephemerides:
	NASA NAIF SPICE files
Phase windup	[34]
Phase cycle slip detection	[28]
Troposphere	Saastamoinen model for the hydrostatic delay
	Niell mapping function
	Estimation on the zenith wet delay
	Initial variance: 0.5 m; Model noise: 0.005 mm/s
Ionosphere	Estimation of slant ionospheric delay on L1
	Higher-order terms are ignored
	Initial variance 10 m; Model noise 2 cm/s
Receiver clock offset	Estimated as white noise; Model noise 1000 m/s
Additional receiver clock bias	Initial variance 0 m; Model noise 1 mm/s
Receiver state	Simulated kinematic; Model noise: 100 m/s for X Y Z
Positioning accuracy reference	IGS MGEX coordinate products

. Noted that the additional receiver clock bias refers to the terms $b_{P_2}$, $b_{C_5}$, $b_{L_1}$, $b_{L_2}$ and $b_{L5}$ in Equation (2) for GPS and the same for the terms in Equation (3) of Galileo. Cycle slip detection is still indispensable in our implementation. Because when fixing the undifferenced ambiguities, an ambiguity datum is needed to be selected first. However, when this selection happens on an ambiguity which has unidentified cycle slip, a spike in the positioning error series is observed in our results. For single-epoch processing, the cycle slip detection is not necessary as the ambiguity is reset at each epoch. The classical geometry-free (GF) and MW combinations [27,28] are used for cycle slip detection. However, this method suffers from high ionospheric activity and code measurement noises [29].

The best integer equivariant (BIE) estimator [30,31] is used for ambiguity resolution and may be expressed as

$$\begin{array}{c}\hfill \overline{a}=\sum _{z\in \mathbb{Z}}z{\displaystyle \frac{exp(-\frac{1}{2}||\widehat{a}-z|{|}_{Q_{\widehat{a}\widehat{a}}}^2)}{{\displaystyle \sum _{z\in \mathbb{Z}}}exp(-\frac{1}{2}\left|\right|\widehat{a}-{z\left|\right|}_{Q_{\widehat{a}\widehat{a}}}^2)}}\end{array}$$

(9)

where $\widehat{a}$ is a vector of float ambiguities with its covariance matrix $Q_{\widehat{a}\widehat{a}}$; $z\in \mathbb{Z}$ is an integer candidate; $\left|\right|·{\left|\right|}_{Q_{\widehat{a}\widehat{a}}}^2={(·)}^T{Q}_{\widehat{a}\widehat{a}}^{-1}(·)$. Therefore the output solution $\overline{a}$ is a weighted average of integer candidates, which could mitigate the effect of wrong fixing although $\overline{a}$ is non-integer. The decorrelation and search procedures of the conventional LAMBDA method [32] can still be used for finding integer candidates. The open-source software goGPS [33] is referenced for the implementation of this estimator.

Figure 5 and Figure 6 demonstrate the CNES post-processed code and phase bias products on 1 May 2021. These products are not only relevant to the observable types and frequencies but also to the tracking modes as indicated by the third character in the titles of the subplots (namely the C, W, Q, C, W, I modes in the types C1C, C2W, C5Q, L1C, L2W and L5I for GPS). These tracking modes should be considered when applying the CNES bias products at a user side. It can be seen that the code biases are constant values over the 24-h period and the phase biases are relatively stable on most of the frequencies despite some small variations (a few centimeters) for specific satellites. The GPS L5 phase biases fluctuate more significantly because of the inclusion of the IFCB for the GPS IIF satellites.

3.1. Multiple-Epoch Filtered Positioning

The conventional PPP solution of the above model is first assessed with the filter reset every three hours. The code and phase measurements noise is set to 20 cm and 0.01 cycle at zenith, respectively. The ambiguity resolution process is performed independently at each epoch and the float states and its covariance matrix are delivered to Kalman filter for next measurement update instead of using the fixed states. This process is designed to mitigate the effect of possible wrong fixing and it is also easy to study the difference between the float and fixed solutions.

After resolving the extra-widelane, widelane and the remaining ambiguities sequentially, the ambiguity-fixed positioning solutions are more centered around zero and achieve more rapid convergence especially on the east component as displayed in Figure 7.

Obtaining these more aggregated fixed solutions still requires a certain period of time (roughly half an hour) mainly caused by the slow convergence of $N_1$ and $N_{E1}$ ambiguities. These ambiguities are difficult to be fixed due to short wavelengths and normally have lower fixing rate among all ambiguities.

For each session in Figure 7, the 68th percentile [35] of the absolute positioning errors after half an hour is computed instead of the RMS error to mitigate the impact from possible wrong fixing or outliers. The 68th percentile of positioning errors from all the eight sessions on 1 May 2021 for each station is displayed in Figure 8. It can be seen that the east component achieves substantial improvement for all the stations. The height component degrades at some stations after AR. We found that when using the BIE estimator, it is critical to set proper standard deviations (STD) for code and phase measurements. This is illustrated in Figure 9. It shows that the ambiguity-fixed height solutions are more sensitive to the change of code and phase STD. Therefore improper STD configuration could deteriorate the height accuracy when evaluating as in Figure 8. However proper setting of STD for specific station requires to check its postfit code and phase residuals. Moreover, currently no validation measure for the fixed solution from the BIE estimator is implemented in this study and an effective method could be applied in the future to check the difference between the fixed and the float solution to avoid poor results for user output.

Figure 10 is the distribution of the positioning errors accumulated from all the sessions (after half an hour for each session) over the ten testing days of the selected stations. It clearly shows that significant accuracy improvement on the east component is observed after AR. The fixed north error components are also more precise while for the up direction no apparent improvement is found. As shown in

Table 2. The 68th percentile of GPS L1/L2/L5 + Galileo E1/E5a/E5b/E6 PPP errors at all the testing stations from 1 May 2021 to 10 May 2021 (unit: cm). Float* stands for the float solution based on the frequency-separated model; The Float and Fixed solutions are from the widelane-combined model.

Model	North	East	Up
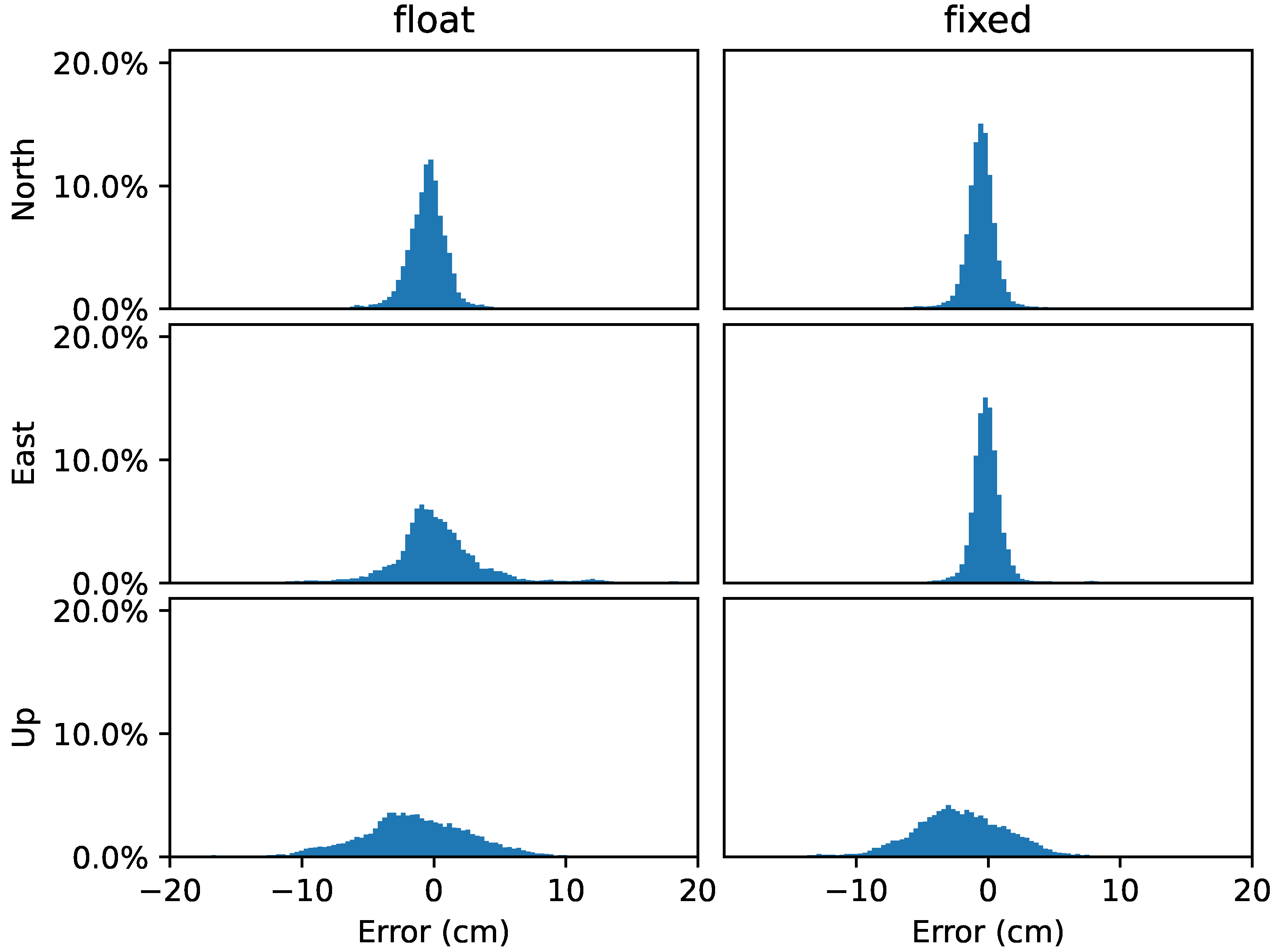
Float*	1.3	2.64	4.34
Float	1.37	2.63	4.48
Fixed	1.16	0.98	4.44

, an improvement of 63% is obtained in the east direction of the fixed solutions. However, the height solution after AR has a marginal improvement. It is noted that our current functional model is based on the widelane combinations and this strategy excludes the measurements if the required frequencies for the widelane combination are not complete or valid in the observation file. It is not uncommon when the receiver misses the measurements on a specific frequency and thus this widelane-nested model will be weakened due to reduced measurements. In order to assess this effect, we also computed the error statistics of the ambiguity-float solutions based on the separated frequencies as listed in Table 2, which outperforms the widelane-nested float solutions in both the north and especially the height components. In this study, all the ’float’ solutions presented refer to the widelane-nested or -combined model.

The convergence time is also evaluated statistically from all the sessions. Here it is defined as the time it takes to converge below 5 cm for at least 10 consecutive epochs in the horizontal plane. Higher peak at around 25 min of the fixed solutions is clearly shown in the histogram of convergence time of Figure 11. From

Table 3. Statistics of convergence time (2D < 5 cm) of GPS L1/L2/L5 + Galileo E1/E5a/E5b/E6 PPP float and fixed solutions for all the testing stations from 1 May 2021 to 10 May 2021 (unit: min).

	Float	Fixed
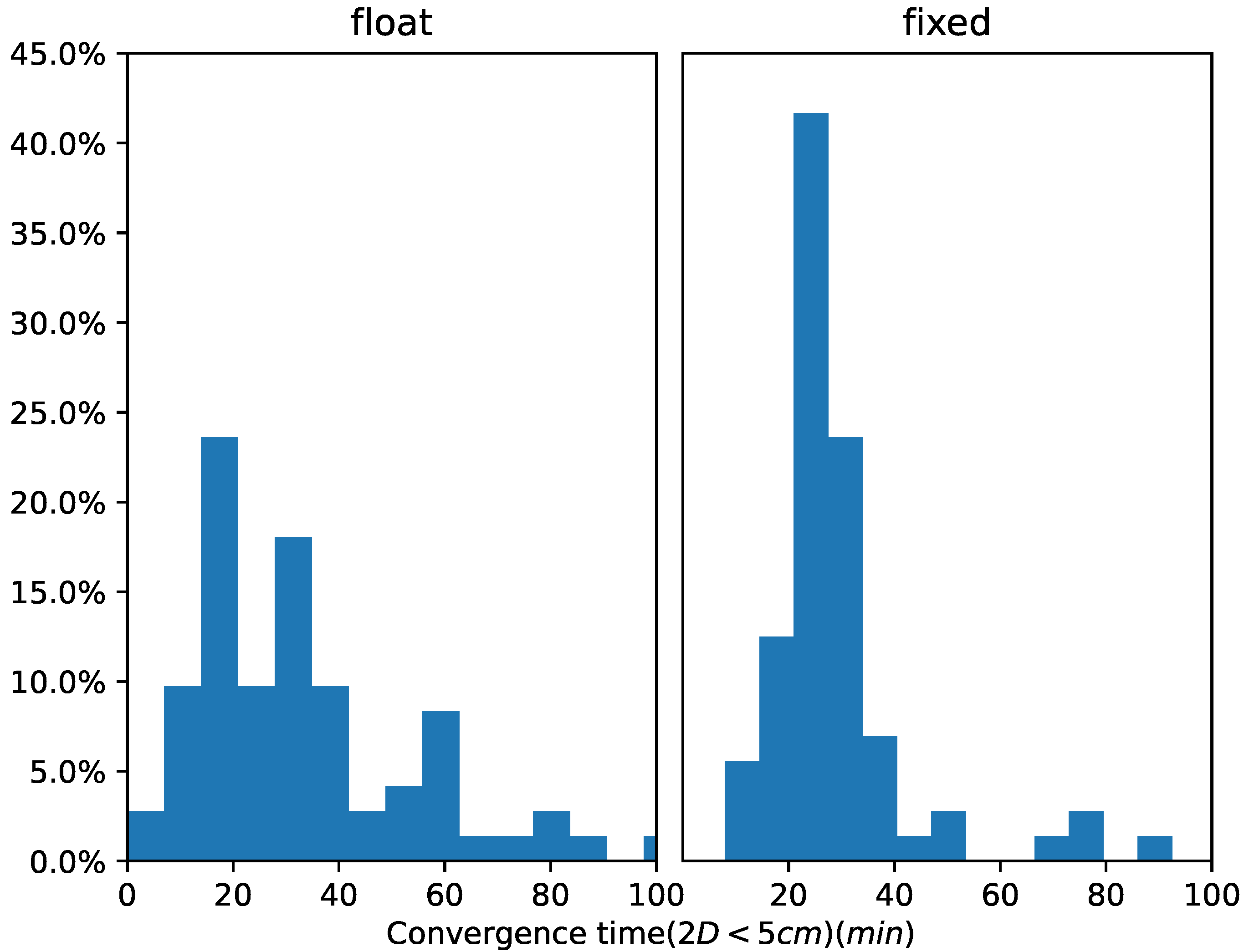
Average	35.1	29.2
Std.	25.3	14.4
68th percentile	37.1	29.6
median	28	25

the averaged convergence time is expedited by 17% after AR.

3.2. Single—Epoch Positioning

In this section, the single-epoch positioning results of the GEMF model is studied. The filter is reset at each epoch for the ten testing days of all stations. Only the widelane ambiguities are fixed in this test since the remaining estimated ambiguity may still have noise level exceeding one cycle as discussed in Section 2.2. As shown in Figure 12, the widelane-fixed solutions have less dispersion than the float or code-only results. This improvement is due to the instantaneously fixed widelane ambiguities. The float solutions are completely determined by the code measurements since the phase ambiguities are reset at each instant.

The 68th percentile of positioning error is still used for results evaluation. Figure 13 shows the percentile error for each station on 1 May 2021. It can be seen that horizontal precision improvement is achieved for all the testing stations while the height solutions from seven of them are negatively impacted by AR. We found that the empirical standard deviations of the phase measurements can significantly affect the height precision of the fixed solutions. Proper configuration of the GPS and Galileo measurements standard deviations could help to achieve a better accuracy in the up direction when using the BIE estimator and this requires further investigation.

As presented in the last section, the distribution of the positioning errors over the ten testing days for all stations is presented in Figure 14, which shows that both of the north and east errors of fixed solutions are more aggregated around zero and have higher peak. From

Table 4. The 68th percentile of GPS L1/L2/L5 + Galileo E1/E5a/E5b/E6 single-epoch positioning errors at all the testing stations from 1 May 2021 to 10 May 2021 (unit: m).

Model	North	East	Up
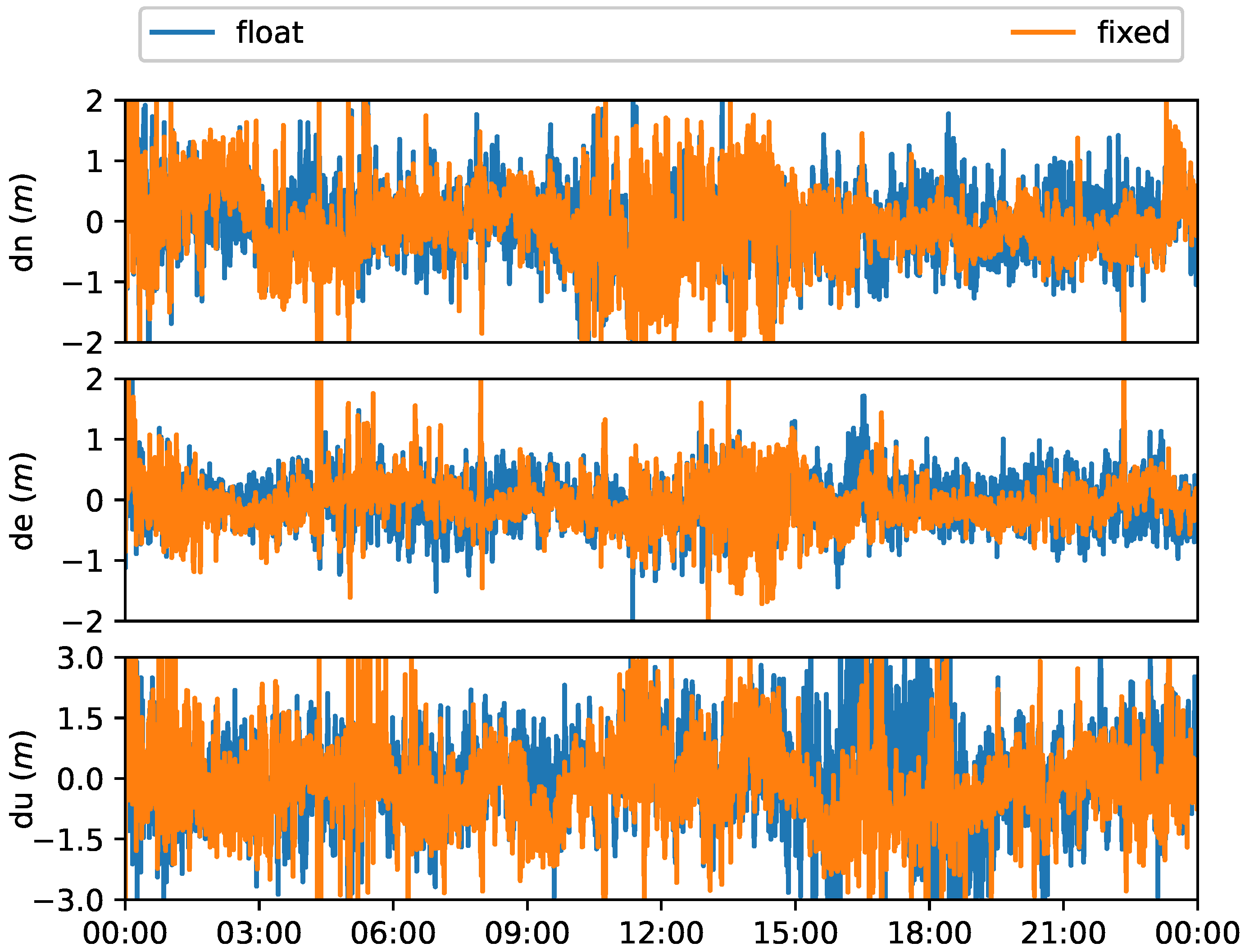
Float	0.37	0.37	1.11
Fixed	0.32	0.31	1.27

, the accuracy of the north and east components after AR can reach 32 cm and 31 cm (68th percentile) improved by 13% and 16% respectively. The height accuracy degrades as found in Figure 13. As discussed in Figure 9, appropriate code and phase standard deviation for specific stations when using the BIE estimator could improve the results further. At the same time, more precise ionospheric information would also benefit the single-epoch solution since there is no convergence process.

4. Discussion

With the use of additional measurements from other constellations, more strengthened geometry would further benefit the multi-frequency PPP solution and it is anticipated that full ambiguity resolution would be more reliable at an instant even without external ionospheric correction. CNES now also issues the uncombined satellite code and phase bias products for the Chinese BeiDou satellite navigation system, the positioning performance of GPS/Galile/BeiDou multi-frequency PPP is to be investigated, especially using this widelane-nested model.

Further investigation would also be required for the validation of the fixed solutions and proper weighting between code and phase observation especially when using the BIE estimator. We recommend that a procedure of hypothesis test about the empirical measurement standard deviation to determine proper measurement weights for the BIE estimator.

As the CNES uncombined bias products also support the ambiguity resolution of linear combinations of phase measurements, the performance of multi-frequency ionosphere-free PPP is also to be studied, especially the single-epoch positioning ability.

5. Conclusions

The GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 point positioning model following CNES new bias representation is implemented in our in-house POINT software and evaluated in this study. By applying CNES uncombined bias products, these multi-frequency code and phase measurements can be modeled in an undifferenced and uncombined form with the estimation of slant ionosphere. In particular, the phase ambiguity parameter can still conserve its integer nature. We resolved the ambiguities in a traditional cascading manner through making a series of widelane combinations. For PPP configuration with 30-s sampling data, ambiguity-fixed solution can achieve an accuracy of 1.16, 0.98 and 4.44 cm in the north, east and up direction, respectively, (68th percentile). A significant improvement of 63% on the east component is obtained with respect to the ambiguity-float solution. The PPP convergence requires 29.2 min on average to be below 5 cm horizontally after AR with an acceleration of 17%. Regarding the instantaneous positioning capability of the multi-frequency model, an accuracy of 32 and 31 cm for north and east components (68th percentile) can be obtained after WAR improved by 13% and 16% respectively relative to the code-only solution. The $N_1$ and $N_{E1}$ AR was deactivated in our single-epoch test as their estimated precisions could still be larger than one cycle and not sufficient for resolution.