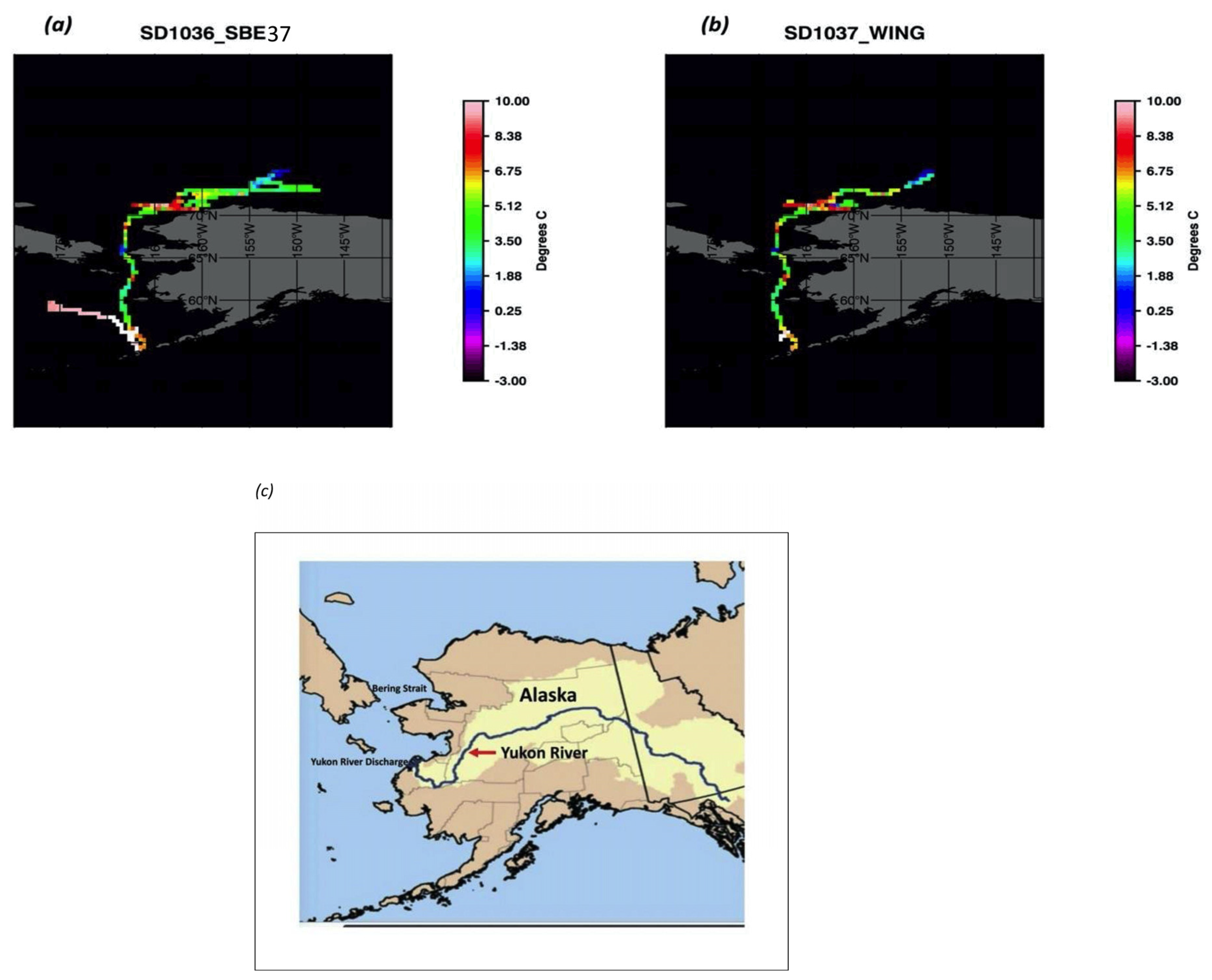
Figure 4 shows images extracted from the different L4 products for the Y–K delta, corresponding to DOY 151. It is notable how the satellite products show substantial differences in the amount of warming near the coast, as well as in the location of these warm features. The coastal variability in SSTs, revealed in
Figure 4, is substantial, and it is hard to say which product is more realistic. Relative to the median temperature given by GMPE (
Figure 4h), the DOISST, MWIR, OSTIA, and, especially, CMC, retrieve coastal SSTs substantially warmer than the average, whereas MUR, DMI, and K10 are substantially underestimating the warming.
It can be seen that the saildrones navigate across the warm water intrusion that exists between the St. Lawrence Island and the Y–K delta. To get the exact position of thermal fronts from satellite imagery is still very challenging, as the resolution of the L4 grid smears the position of the front. The mesoscale feature, associated with the coastal warmer water, is absent in DMI; it is in a different location in K10 but, as the maps indicate, the saildrones were far enough from the shallow coastal waters of the Y–K delta, missing the highly variable area in the L4 products.
3.1. Statistics
The statistics for the differences between the satellite SST retrievals and SBE temperatures, measured from both saildrone deployments (SD1036 and SD1037), are summarized in
Table 2 and
Table 3, respectively. The MUR product showed large negative biases for a substantial period of time (DOY 156–212), likely because, in order to produce a foundation SST, this analysis uses satellite nighttime data only, which is a limiting factor during the Arctic summer, as the sun is often above the horizon and nights are often nonexistent. We opted to include another entry in the tables, corresponding to the statistics from the time, where MUR worked well and nighttime data were available. Both time series are used in different comparisons. In those where the trimmed series is used (Taylor diagrams), we will emphasize that the results are for a shorter duration.
The smallest negative biases in
Table 2 and
Table 3 are observed with the non-foundation products, with the DOISST showing the smallest bias (−0.08 °C) for SD1037, with the second smallest for SD1036 (−0.12 °C) and smallest negative bias with K10 ((−0.11 °C) for SD1036). The DOISST also has the smallest robust unbiased SST estimates (median of the residuals), relative to both saildrone deployments (−0.03 °C and −0.05 °C, respectively). The MWIR OI SSTs also have small residual differences (biased and unbiased (median)), but they are of the opposite sign, suggesting that these MWIR foundation SSTs are slightly warmer than the saildrone measurements (mean biases of 0.05 °C and 0.11 °C, for SD1037 and SD1037, and a median of 0.08 °C and 0.09 °C, respectively). Of the foundation SST products, CMC has the next smallest negative bias (−0.13 °C) for both saildrone deployments. Surprisingly, the GMPE median, established to be a more accurate unbiased estimate of foundation SST than the individual L4 foundation ensemble members (global bias = 0.03 K and SD = 0.4 K relative to Argo floats [
8]), had some of the largest mean and median differences, relative to the saildrone observations. This could be due to several factors, which will be discussed later.
It is interesting to note that, despite the fact that all the L4s used in this study are part of the global ensemble (GMPE), the smallest and the largest median error are both observed for SST analyses at the same 0.25°-resolution grid. The large distance between the median DOISST error, with respect to the saildrone and the middle value of the ordered statistics given by GMPE, suggests that the DOISST is more of an outlier in the ensemble. This was quite often the case for DOISST version 2.01, where there was a consistent cold bias for global SSTs and a warm bias for Arctic SSTs; however, existing biases in v.2.0 have been substantially reduced in DOISST v2.1 [
18]. The large difference between the DOISST and GMPE might be more in line with the fact that GMPE is an estimator of the foundation whereas the DOISST is a daily mean SST.
The DOISST minus saildrone SST differences have the smallest variation (SD = 0.74 °C) for SD1036 and the second smallest (SD = 0.88 °C), after the MWIR (SD = 0.84 °C), for SD1037. The SD of the foundation products tends to decrease as the spatial scale (pixel length or/grid spacing) increases (or equivalently, as the sample size/number of co-located pairs decreases with finer product resolution), up to about 9 km, when the SD increases again, as the spatial scale continues to increase (and the sample size continues to decrease), albeit at a slower rate. This issue is illustrated in
Figure 5, where the SDs for MUR (1 km), DMI (5 km), and OSTIA (6 km) decrease with scale up to the MWIR 9-km resolution, followed by an increase in SD for CMC, K10 (10 km), and GMPE (25 km). Interestingly, a scale of 9 km is comparable to the local internal Rossby radius of deformation [
24]. In the Arctic Ocean, the first Rossby radius increases from ~5–15 km for deep ocean basins, with a typical value of 9–10 km and ~1–7 km for shallow shelf seas [
24].
The analyzed pairs incorporate point-to-pixel differences that are influenced by multiple factors. While point to pixel differences can be larger for coarser scales, there is more inherent natural variability at finer spatial scales. It is known that the signal detected from the satellite corresponds to an integration of the surface-emitted radiation over the spatial domain, as determined by the product’s spatial resolution. The signal integration over larger spatial domains/coarser grids smooths out some of the natural variability within the pixel. As the SDE vs. scale trend, shown in
Figure 5, suggests, more is not necessarily better for scales < 9 km, as better precision in the estimates (L4 with smaller SDEs) are achieved with smaller sample sizes. This point suggests that caution must be used in interpreting variability at scales less than 10 km, as the noise could be the dominant factor. It is also important to mention that it could also be a natural consequence of increased averaging over the larger spatial scales and thus smoother results. The effects of natural variability and sample variability (sample size) reach a balance at about 9–10 km-spatial resolutions. For scales greater than 9–10 km, the natural smoothing of the gridding process dampens some of the variability and ‘less becomes more’ or at least enough, as the SDEs increase again but at a much slower rate.
The SDE is particularly sensitive to outliers, as large errors are amplified when they are squared in the SDE computation. This tendency is not present in the RD, which is expected, given that this parameter is more effective at handling variability. It is interesting to note that for spatial scales greater than or equal than 10 km, the difference between the SDE and the RD gets smaller (see
Table 3). Once again, the convergence of the SDE and the RD at larger scales suggests that the spatial averaging that occurs from increasing the spatial domain/grid resolution of the L4 SSTs is effective at damping the noise (outliers) resulting from natural variability. However, it is important that footprint size alone is not a determining factor in the noise level of satellite products. Other sources of errors exist, including cloud cover, ice contamination (for the Arctic), and possible land contamination in the passive microwave. The L4s with the smallest RD are OSTIA, DOISST, and CMC (with RD of 0.72 °C, 0.73 °C, and 0.80 °C, respectively, for SD1036 and 0.80 °C, 0.87 °C, 0.87 °C, respectively, for SD1037).
The RMSE, while conceptually similar to the SDE, removes some of the randomness in the error estimates and is the standard measure of the accuracy of satellite SST products. Once again, DOISST, MWIR, and CMC are among the products with the smallest RMSE (DOISST: 0.56, MWIR: 0.60, CMC: 0.74 for SD1036, and MWIR: 0.72, DOISST: 0.78, CMC: 0.87 for SD1037). Note that the two products with the better accuracies, DOISST and MWIR, correspond to an SST-at-Depth product and a foundation SST product, respectively. This point suggests that a good precision foundation SST product can perform similarly to a daily mean SST-at-depth product when estimating the Arctic summer SST-at-depth observed from the saildrone.
This result suggests that diurnal variability, although a source of uncertainty, must be considered carefully with respect to other sources of error. Spatial variability, however, seems to have a more substantial effect on L4 foundation accuracy, as the RMSE gets smaller with increasing product spatial resolution, up to a scale of ~9–10 km, after which the RMSE increases, but at a slower rate (see
Figure 5). The curves for the two saildrone deployments seem to converge for spatial scales of ~6 km. The separation in mean RMSE amplitudes barely changes as the sample size diminishes from spatial lengths of 10 to 25 km, suggesting that there is a critical scale where the statistical power is associated with the variability of the data and the sample density balances out. The accuracy of the non-foundation products (i.e., DOISST and K10) does seem to follow this trend, as well. This trend is not surprising after the similar behavior observed with the SDs and the known fact that the RMSE is dependent on the scale of the values used. However,
Figure 5 shows that, while the SDE dependence on scale appears linear for scales < 10 km, the RMSE dependence, over the same scales, seems to be non-linear convex in shape. Recall from Equations (2) and (3) that the SDE has the mean bias error removed, but the RMSE does not. The nonlinearity of the RMSE curve in
Figure 5, hence, is capturing the portion corresponding to the systematic error that is excluded from the SDE and, as is evident in this figure, the RMSE is giving more weight to the largest errors observed at the finest scales. While this newly identified dependence has important implications for gridded satellite products, it remains to be proven that it is universal and is upheld for other products and conditions.
Except for those with the finest resolution, most SST products have an SNR > 2.5. The L4 with the largest SNR is DOISST, with SNR = 3.29 and 3.15 for SD1036 and SD1037, respectively. The statistical correlation between the time series of L4 and saildrone SSTs (final column in
Table 2 and
Table 3) is very high for all products (>0.90), i.e., the L4 SST products are performing quite well in this region but, once again, the DOISST seems to slightly outperform the others, when it comes to estimating saildrone SSTs.
A possible explanation for the good agreement between the Arctic saildrone-borne SSTs and DOISST retrievals is that the DOISST is highly tied to the available buoy data, which serves as the primary bias correction and calibration of this product. This was made evident, displayed by the DOISST version 2.10, when they stopped feeding a significant percentage of drifting buoys into their system, as the buoy transmissions changed from alpha-numerical to binary form [
18]. In-situ measurements, while ingested in some of the other L4 analyses, potentially do not play as critical a role, as they rely more on the multisensor blending aspect of the satellite retrievals.
The DOISST implicitly adjusts all the input data streams that enter into their OI system to coincide with the buoy measurements at approximately 20 cm-depth. It is important to point out, however, that the saildrone is not incorporated in the DOISST correction and, thus, these are truly independent measurements. Both the saildrone and the buoys use sea bird-type thermistors to measure the SST-at-depth.
3.2. Taylor Diagrams
It is clear from the above analysis that the statistics in
Table 2 and
Table 3 are simultaneously constrained by both the disparity in sample sizes of the L4 vs. saildrone SST matchups and the variability of the data itself. In order to facilitate comparisons of L4 products with different scales, normalized statistics were computed using the background variability or SD of the reference SST (i.e., the SDSAIL) as the normalization variable. By using the SDSAIL (via Equation (5)) as the standardizing criterion, we are removing the impact of the variability in the saildrone observations from the interdependence of the statistical measures. We then looked at the simultaneous behavior of the normalized SDs, from both the L4 and observations (i.e., NSDSAT = SDSAT/SDSAIL; NSDSAIL = SDSAIL/SDSAIL = 1), the normalized RMSE (i.e., NRMSE = RMSE/SDSAIL), and their serial correlation, through a normalized Taylor diagram. These are shown in
Figure 6a,b for SD1036 and SD1037, respectively. A detailed explanation of how to interpret these diagrams for comparing the performance of different L4 SST products can be found at [
10].
The normalized standard deviation (NSD) of the observations is represented in the diagram by the point where the x-axis equals 1, labeled “observed.”. The NSDSAT for the different L4s is given in the y-axis. The dashed circle of unit radius also gives an indication of where the products being compared stand, in relation to the ‘denoised’ observations. The NRMSE is represented by the concentric circles, centered at the observation point (x = 1). The correlations are given by the radial lines departing from the origin (x = 0). The objective is to quickly determine which products, represented by the dots labeled A through H, are closer to the point/dash circle representing the observations. The closer an L4 is to the observations, the smaller the SD and the RMSE and the higher the correlation.
As it can be seen from these diagrams that all the L4 products, represented by the dots, labeled A: CMC, B: DMI, C: GMPE, D: trimmed MUR, E: K10, F: OSTIA, and G: MWIR, H: DOISST, have similar performances and are in overall good agreement with the saildrone, given that all the dots cluster together close to the observations and there is no spread in the radial direction. The products less affected by the variability/noise in the observations, i.e., closer to the dashed circle of the denoised observations, are GMPE, trimmed MUR, and DMI (C, D, and B). Products more affected by systematic errors (i.e., farther from the unit circle) are K10 and MWIR (E and G). The products with better accuracy (closer to the smallest NRMSE circle), and the highest correlations (smallest azimuthal angle between the L4 dot and the x-axis), are the DOISST and the trimmed MUR (H and D) for SD1036 and DOISST and GMPE (H and C) for SD1037. The products with degraded accuracy are K10 for SD1036 and DMI for SD1036 and SD1037. The fact that DMI is closest to the dashed unit circle but has the largest azimuthal spread (correlation less than 0.9) suggests the product is getting the right SST amplitudes but has issues with the phasing of the SST patterns.
The products that have the best overall performance, based on the smallest absolute distance to the observations, are GMPE, DOISST, and the trimmed MUR (C, D, and H). As the Taylor diagram illustrates, the DOISST remains a top performer, regardless of the normalization of the statistics, but two of the L4 products that were more impacted by noise in the saildrone observations before (e.g., GMPE and the untrimmed MUR in
Table 2 and
Table 3), perform substantially better relative to the saildrone observations. The GMPE result confirms previous analyses reported in the literature [
8], indicating that it was the noise in the saildrone observations driving the spread in the statistics. When nighttime data are available, the MUR L4 could be a leading performer. The MUR product is currently being analyzed to include daytime observations for the estimation of the foundation SST, which will take effect in the next version of MUR (M. Chin, personal communication, 2021).
Among the products with slightly diminished skill after the normalization are DMI, K10, and MWIR (C, E, and G). After taking the saildrone variability out, the K10 and the MWIR, which had a leading edge according to the statistics of
Table 2 and
Table 3, are now further to the left from the actual SD given by the unit circle, NSDSAIL = 1. In other words, the NSD is decreasing with noise in these two products, which suggests that they are under-predicting the observed saildrone variability (i.e., they are a bit smooth). The K10 in particular was singled out before as being the same type of SST as the SBE37 SST, which was thought to be advantageous for comparisons with the saildrone. It is known that the lack of an ice mask slightly undermines the K10 predictions, when in close proximity to the ice edge. The K10 product is currently being modified to include an ice mask in a new future version [J.F. Cayula, personal communication, 2021]. In previous comparisons involving the MWIR SST, the product appeared to have too much small-scale noise [
10]. In its current version (version 5), however,
Figure 6 suggests that this analysis is under-predicting the actual saildrone variability. The NRMSE and correlation, however, are not perturbed enough by the noise, since the MWIR dot is part of the general cluster.
3.3. Wavelength Spectra
In order to further explore the dependence of spatial variability on spatial scales, spectral analysis was performed on each of the L4 products and the saildrone SSTs. Wavelength spectra were calculated based on the co-located data, which means that there is a saildrone power spectrum for each of the satellite products (only the grid resolution varies). The entire time series of the products were used, DOY 135–283. Thus, the saildrone power spectra are reflective of the resolution of the GHRSST L4 product. For the MUR product, the whole length of the time series was considered in the spectral analysis. The resulting plots are shown in
Figure 7 for both SD1036 and SD1037 with the saildrone Fourier autospectra on the left panel, and the L4 SST on the right.
The saildrone SST spectra shown on the left were computed from the SBE37 collocations with the different SST analyses. That is, the only thing that is changing is the spatial resolution of the subsampling of the saildrone SBE37 SSTs. The spectra are plotted only for wavelengths greater than 50 km to reflect the Nyquist wavelength associated with the DOISST and GMPE products, which have the coarser spatial resolution of the L4s used in this spectral analysis. The saildrone-derived power spectral density, shown in black with the L4 autospectra of
Figure 7b,d, is based on the co-locations with OSTIA. This particular subsampling of the saildrone spectrum was chosen because, as it will be explained in more detail in the analysis of spectral slope below, only OSTIA appears to have the same scaling relation observed with the saildrone-derived SSTs.
The most visible feature of the spectra shown in
Figure 7 is the power law behavior (i.e., the log-log linearity as the log of the spectral power decreases with the log of the decreasing wavelength) exhibited by all the autospectra over the whole range of measurement scales (between 2000 km and 50 km). Additionally, the rate of decrease (given by the spectral slope or, in this case, the scaling exponent) appears quite similar for the individual autospectra, suggesting scale invariance. The saildrone spectra in
Figure 7a,c show peaks at approximately 1000 and 500 km. One possible explanation is these arise when a saildrone changes trajectory. However, this would require further research to confirm and is only speculative.
Overall, for wavelengths < 100 km, the spectral densities of the L4s are lower than those derived from the SBE37 SSTs, reflective of the higher spatial sampling of the in-situ instruments deployed on the saildrone. It is important to note that spectra < 100 km were found to be statistically different from zero, based on the derivation of error bars. Note that for this mesoscale regime, only OSTIA matches saildrone, with the others showing a slight drop in power density.
For scales > 200 km, the saildrone spectra flattened slightly, indicating white noise. The saildrone deployment takes place over several months and, thus, over the larger spatial scales the assumption of a synoptic scale is not valid. The L4 power density spectra in general show increasing power for scales > 200 km, indicating that the satellite products are resolving the large-scale fluctuations better than saildrone. However, this must be interpreted with caution as the spectra were derived assuming a synoptic-scale over the entire saildrone deployment. Overall, results are encouraging indicating that the GHRSST L4 SST products are replicating the power spectral density associated with the saildrone SBE37 SSTs.
3.4. Spectral Slopes
The power spectral density slopes (or scaling exponent of the power-law suggested by the log-log linearity of the Fourier power spectra) were determined for each of the individual autospectrum shown in
Figure 7. The slope was determined by a simple linear regression fit to the log(power spectral density) versus the log(wavelengths). Slopes for the SBE37 SST autospectra from both the SD1036 and the SD1037, sampled on the different L4 grids, are shown on the left column of
Table 4. Slopes for the GHRSST L4 autospectra are shown on the right.
Spectral slopes are tabulated and sorted by the size of the L4 grid. It can be seen from
Table 4 that the saildrone slope becomes increasingly negative (i.e., the drop in power becomes slightly steeper) with increasing spatial resolution of the L4 product in which it is subsampled. In fact, the increase in negative slope appears to be roughly 0.01 °C 2 km
−1 per kilometer increase in satellite grid length used to subsample the saildrone-derived SSTs. This appears to be the case for both saildrone deployments, but with SD1037 showing more transparently the dependence just described. Taking DMI as the reference, L4 slope = −1.76 + 0.01 × (5 km − grid size [in km]).
Overall, the log-log negative slopes associated with the co-located saildrone data are less negative (shallower) than those associated with the GHRSST L4 SST products, with an average slope of −1.84 (
Table 4, left column). This is in very good agreement with the SST scaling exponent of −1.80 reported by [
25] using a 2-D power spectrum and a direct scaling moment function on MODIS Aqua SST images to characterize fluctuations of velocity and SST [
25]. The log-log slopes of the different L4 wavelength spectra (
Table 4, right column), on the other hand, vary approximately between −2.12 for SD1036 and −2.23 for SD1037. These values are also in good agreement with previous slopes of Fourier power spectrum of satellite-derived SSTs reported in the literature. [
25,
26] reported a slope of −2.44. Note that the DOISST had a slope of −2.39 for the SD1037). This difference between the saildrone and L4 spectra is seen across all the grids in which the saildrone spectrum is subsampled, with the exception of OSTIA. The OSTIA spectral slope is the only one that coincides with that of the saildrone when subsampled on its grid (see
Table 4. OSTIA slope ~1.8 vs. saildrone on OSTIA grid ~1.78). This result suggests that only the OSTIA SST product is reproducing the small-scale spatial variability observed from in situ instruments more accurately than the other satellite products.
The saildrone exponent of −1.8 is slightly steeper but closer to the −5/3 spectral slope of the Kolmogorov power law for temperature fluctuations in the inertial range, displaying characteristics of passive scalar (temperature is advected with the flow) fully developed turbulence. The SST spectral slopes of −2 are consistent with the presence of submesoscale processes at the ocean surface in the Arctic Ocean and other oceanic regions [
27,
28,
29].