Fractional Fourier Transform-Based Tensor RX for Hyperspectral Anomaly Detection
Abstract
:1. Introduction
- Through improved mining of the spatial characteristics of HSI, tensor RX (TRX)—an improved version of LRX—is proposed. TRX uses the test point tensor, instead of the test point vector.
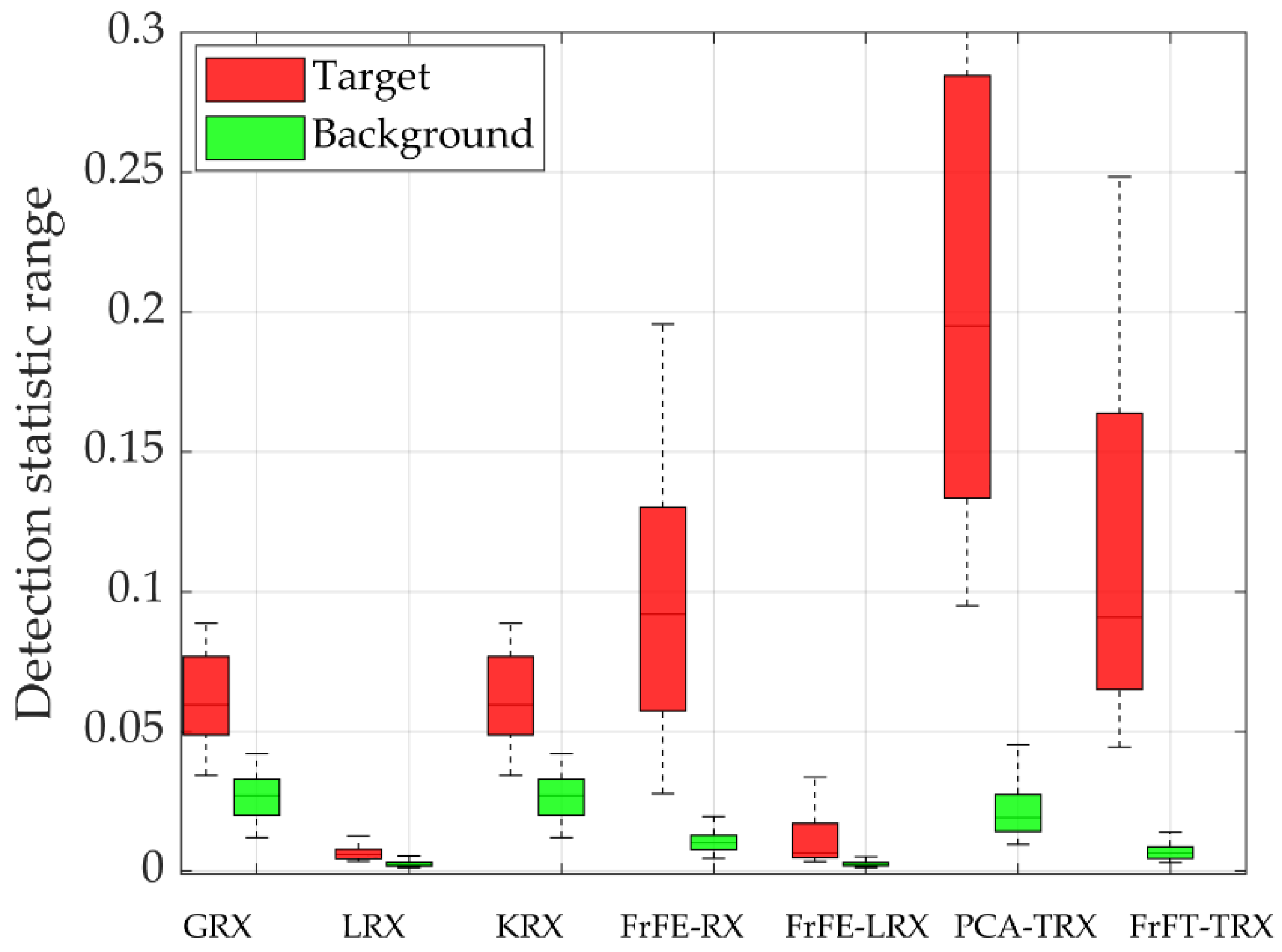
- The proposed TRX is combined with FrFT, which can handle non-stationary noise better than the traditional Fourier transform (FT). In the FrFD, discrimination between anomalies and the background is enhanced.
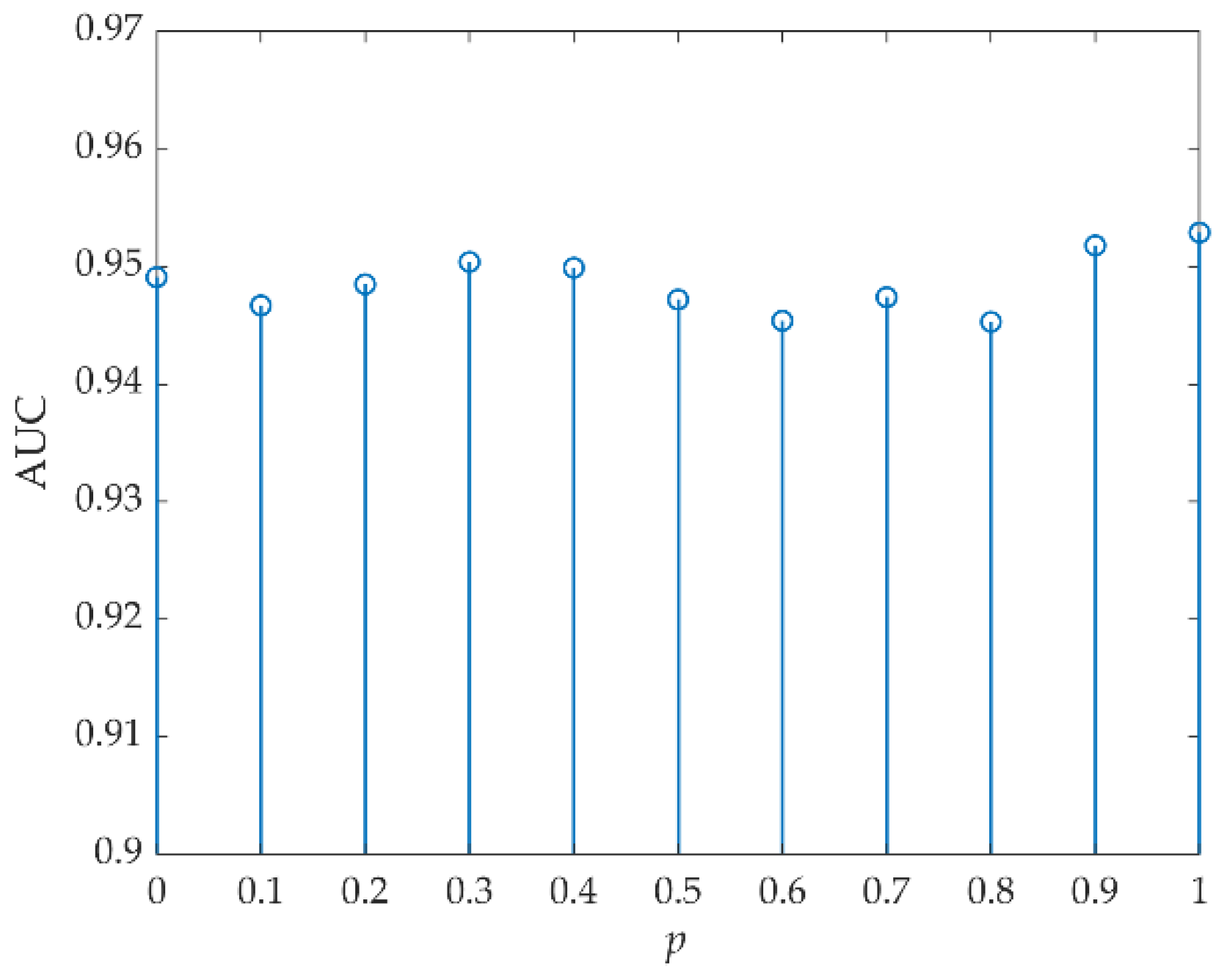
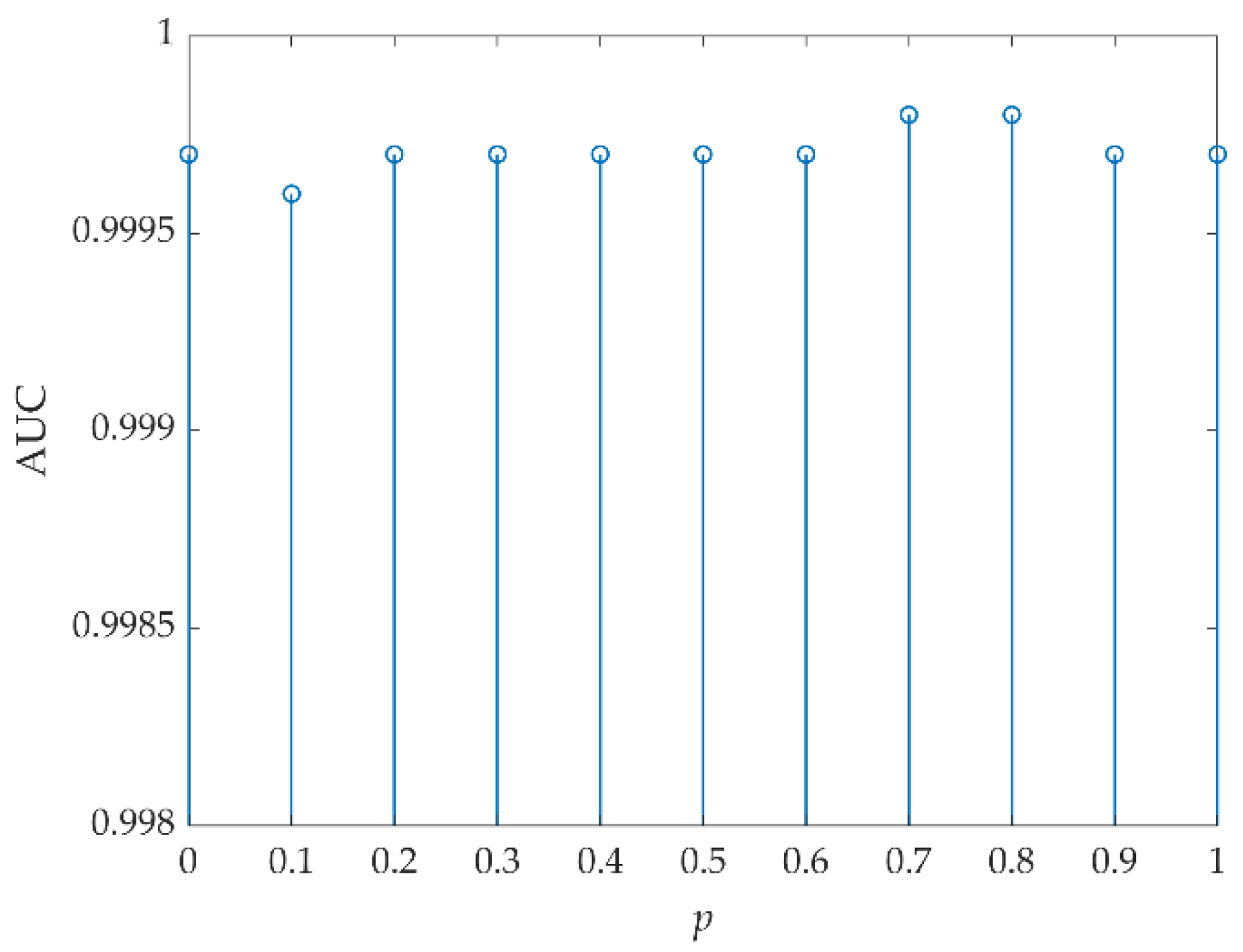
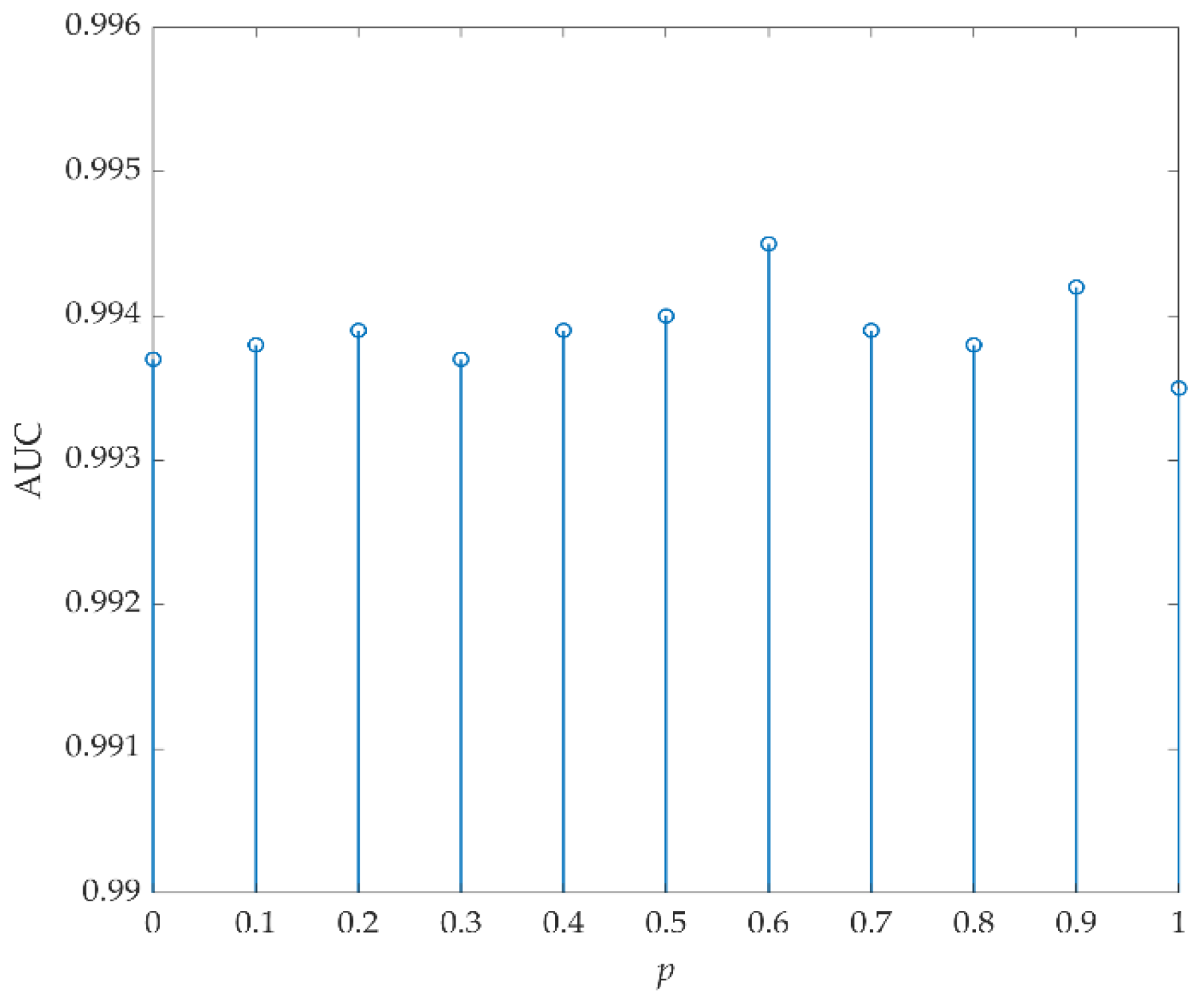
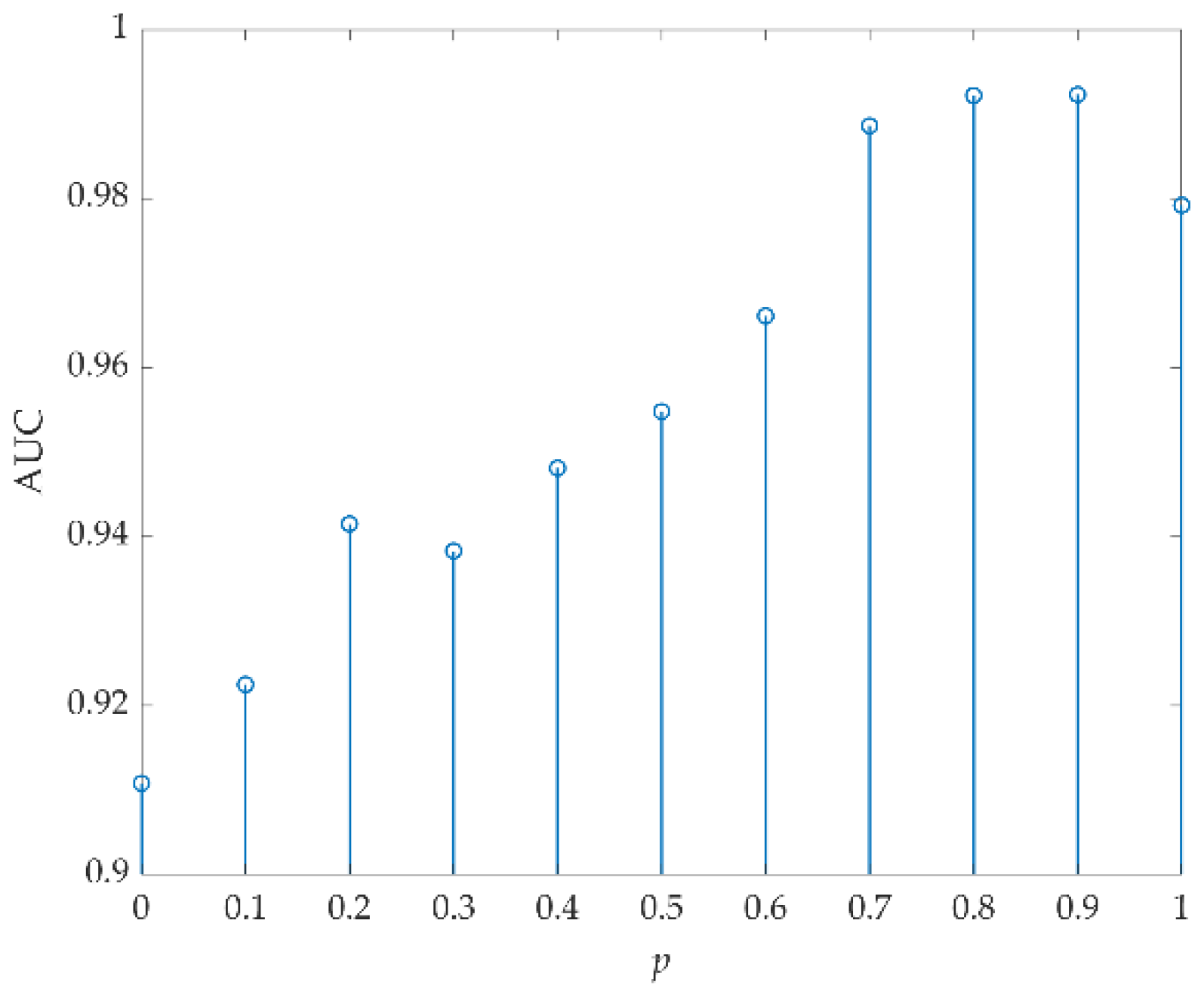
- The optimal fractional order, p, of FrFT in the proposed FrFT-TRX does not correspond to FrFE maximization but is obtained by reverse adjustment. That is, p is first selected by FrFE maximization and TRX is employed in the FrFD. According to the optimal spatial dimensions of the target and background tensors, the optimal AD result is achieved by adjusting the p value, such that the optimal p is obtained.
2. Proposed Method
2.1. Fractional Fourier Transform for HSI
2.2. Tensor RX for HSI
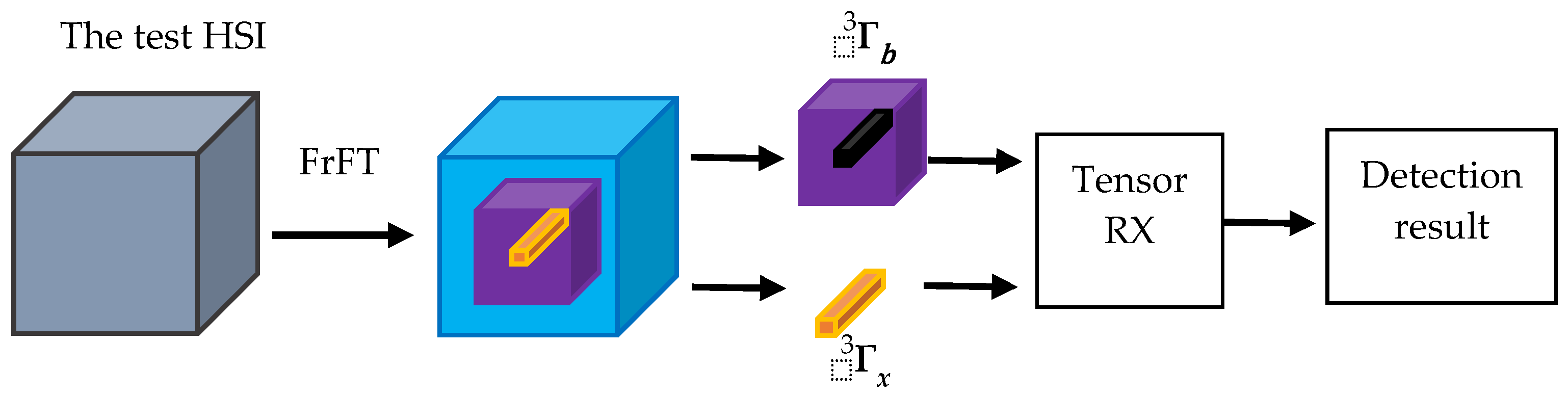
2.3. FrFT-TRX for HSI
| Algorithm 1: Proposed FrFT-TRX method. |
Input: HSI , fractional order of FrFT p, test tensor , and background tensor
|
3. Experimental Results
3.1. Datasets
3.2. Experiment
3.3. Parameter Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent Advances in Techniques for Hyperspectral Image Processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A Review of Nonlinear Hyperspectral Unmixing Methods. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Fang, L.; Li, M.; Benediktsson, J.A. Extended Random Walker-based Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 144–153. [Google Scholar] [CrossRef]
- Chang, C.-I.; Chiang, S.-S. Anomaly Detection and Classification for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef] [Green Version]
- Stein, D.W.J.; Beaven, S.G.; Hoff, L.E.; Winter, E.M.; Schaum, A.P.; Stocker, A.D. Anomaly Detection from Hyperspectral Imagery. IEEE Signal Process. Mag. 2002, 19, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Manolakis, D.; Shaw, G.S. Detection Algorithms for Hyperspectral Imaging Applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral Anomaly Detection by the Use of Background Joint Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Ling, Q.; Guo, Y.; Lin, Z.; An, W. A Constrained Sparse Representation Model for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2358–2371. [Google Scholar] [CrossRef]
- Yang, X.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly Detection in Hyperspectral Images based on Low-rank and Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Zhu, L.; Wen, G. Hyperspectral Anomaly Detection via Background Estimation and Adaptive Weighted Sparse Representation. Remote Sens. 2018, 10, 272. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Du, B.; Zhang, L. Hyperspectral Anomaly Detection via a Sparsity Score Estimation Framework. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3208–3222. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive Multiple-band CFAR Detection of an Optical Pattern with Unknown Spectral Distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Yu, X.; Reed, I.S.; Stocker, A.D. Comparative Performance Analysis of Adaptive Multispectral Detectors. IEEE Trans. Signal Process. 1993, 41, 2639–2656. [Google Scholar] [CrossRef]
- Borghys, D.; Kåsen, I.; Achard, V.; Perneel, C. Comparative Evaluation of Hyperspectral Anomaly Detectors in Different Types of Background. In Proceedings of the SPIE Defense, Security, and Sensing, Baltimore, MD, USA, 23–27 April 2012; Volume 83902. [Google Scholar]
- Molero, J.M.; Garzon, E.M.; Garcia, I.; Plaza, A. Analysis and Optimizations of Global and Local Versions of the RX Algorithm for Anomaly Detection in Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 801–814. [Google Scholar] [CrossRef]
- Fowler, J.E.; Du, Q. Anomaly Detection and Reconstruction from Random Projections. IEEE Trans. Image Process. 2012, 21, 184–195. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Hou, Z.; Li, W.; Tao, R.; Orlando, D.; Li, H. Multipixel Anomaly Detection with Unknown Patterns for Hyperspectral Imagery. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Qu, Y.; Guo, R.; Wang, W.; Qi, H.; Ayhan, B.; Kwan, C.; Vance, S. Anomaly Detection in Hyperspectral Images through Spectral Unmixing and Low Rank Decomposition. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar] [CrossRef]
- Song, S.; Yang, Y.; Zhou, H.; Chan, J. Hyperspectral Anomaly Detection via Graph Dictionary-Based Low Rank Decomposition with Texture Feature Extraction. Remote Sens. 2020, 12, 3966. [Google Scholar] [CrossRef]
- Li, S.; Wang, W.; Qi, H.; Ayhan, B.; Kwan, C.; Vance, S. Low-rank Tensor Decomposition based Anomaly Detection for Hyperspectral Imagery. In Proceedings of the IEEE International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015. INSPEC Accession Number: 15654639. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, G.J.; Dai, W. A Tensor Decomposition-Based Anomaly Detection Algorithm for Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5801–5820. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, B.; Deng, Y. A Tensor-based Adaptive Subspace Detector for Hyperspectral Anomaly Detection. Int. J. Remote Sens. 2018, 39, 2366–2382. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. R-VCANet: A New Deep-Learning-Based Hyperspectral Image Classification Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 10, 1975–1986. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Du, Q. Transferred Deep Learning for Anomaly Detection in Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 597–601. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification with Transformers. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A Nonlinear Anomaly Detector for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Tao, R.; Zhao, X.; Li, W.; Li, H.; Du, Q. Hyperspectral Anomaly Detection by Fractional Fourier Entropy. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 4920–4929. [Google Scholar] [CrossRef]
- Candan, C.; Kutay, M.A.; Ozaktas, H. The Discrete Fractional Fourier Transform. IEEE Trans. Signal Process. 2000, 48, 1329–1337. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Zhang, S.; Zhao, H.; Chen, Y. A New Chirp Scaling Algorithm for Highly Squinted Missile-borne SAR based on FrFT. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 3977–3987. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, B. Fractional Fourier Transform and Transferred CNN based on Tensor for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5505505. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985; p. 176. [Google Scholar]








| Data | Capture Location | Resolution | Sensor | Experimental Size | Flight Date |
|---|---|---|---|---|---|
| data L | Los Angeles | 7.1 m | AVIRIS | 100 × 100 × 205 | 11/9/2011 |
| data C | Cat Island | 17.2 m | AVIRIS | 150 × 150 × 189 | 9/12/2010 |
| data P | Pavia | 1.3 m | ROSIS-03 | 150 × 150 × 102 | Unknown |
| data T | Texas Coast | 17.2 m | AVIRIS | 100 × 100 × 204 | 8/29/2010 |
| data S | San Diego | 3.5 m | AVIRIS | 120 × 120 × 126 | Unknown |
| Data | LRX (Win, Wout) | KRX (c, Win, Wout) | FrFE-RX p | FrFE-LRX (p, Win, Wout) | PCA-TRX (d, Wt, Wb) | FrFT-TRX (p, Wt, Wb) |
|---|---|---|---|---|---|---|
| data L | (7, 9) | (10−5, 5, 9) | 0.2 | (0.2, 7, 9) | (10, 7, 9) | (1, 7, 9) |
| data C | (25, 77) | (10−2, 5, 7) | 0.2 | (0.2, 25, 77) | (10, 3, 37) | (0.2, 3, 37) |
| data P | (25, 81) | (10−1, 25, 29) | 1 | (1, 25, 77) | (20, 3, 37) | (1, 3, 37) |
| data T | (7, 9) | (10−2, 7, 9) | 1 | (1, 5, 7) | (8, 7, 9) | (0.2, 7, 9) |
| data S | (7, 9) | (10−2, 7, 9) | 0.9 | (0.9, 7, 9) | (9, 3, 31) | (0.9, 3, 31) |
| Data | GRX | LRX | KRX | FrFE-RX | FrFE-LRX | PCA-TRX | FrFT-TRX |
|---|---|---|---|---|---|---|---|
| data L | 1.43 | 27.79 | 56.67 | 11.35 | 39.08 | 4.97 | 32.54 |
| data C | 0.71 | 421.21 | 25.87 | 22.35 | 430.72 | 2.92 | 140.65 |
| data P | 0.63 | 236.19 | 1418.01 | 11.86 | 218.95 | 5.56 | 44.78 |
| data T | 0.58 | 26.95 | 20.92 | 10.96 | 38.06 | 5.64 | 33.13 |
| data S | 0.59 | 15.05 | 26.21 | 9.37 | 24.89 | 1.80 | 33.61 |
| Wt | Wb | |||||
|---|---|---|---|---|---|---|
| 5 | 7 | 9 | 11 | 13 | 15 | |
| 3 | 0.8812 | 0.8898 | 0.8790 | 0.8484 | 0.8041 | 0.6838 |
| 5 | 0.9314 | 0.9356 | 0.9056 | 0.8655 | 0.7733 | |
| 7 | 0.9485 | 0.9410 | 0.9135 | 0.8449 | ||
| 9 | 0.9493 | 0.9144 | 0.8744 | |||
| Wt | Wb | ||||||
|---|---|---|---|---|---|---|---|
| 15 | 17 | 19 | 21 | 23 | 25 | 27 | |
| 3 | 0.9923 | 0.9992 | 0.9865 | 0.9994 | 0.9997 | 0.9997 | 0.9997 |
| 5 | 0.9994 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 |
| 7 | 0.998 | 0.9994 | 0.9995 | 0.9995 | 0.9995 | 0.9995 | 0.9995 |
| 9 | 0.9994 | 0.9994 | 0.9995 | 0.9995 | 0.9995 | 0.9995 | 0.9995 |
| Wt | Wb | ||||||
|---|---|---|---|---|---|---|---|
| 31 | 33 | 35 | 37 | 39 | 41 | 43 | |
| 1 | 0.9697 | 0.9714 | 0.9725 | 0.9732 | 0.9738 | 0.9741 | 0.9746 |
| 3 | 0.9955 | 0.9958 | 0.9959 | 0.9960 | 0.9954 | 0.9957 | 0.9958 |
| 5 | 0.9941 | 0.9945 | 0.9948 | 0.9945 | 0.9942 | 0.9942 | 0.9945 |
| 7 | 0.9853 | 0.9864 | 0.9874 | 0.9868 | 0.9855 | 0.9845 | 0.9849 |
| Wt | Wb | ||||||
|---|---|---|---|---|---|---|---|
| 5 | 7 | 9 | 11 | 13 | 15 | 17 | |
| 3 | 0.9315 | 0.9736 | 0.9832 | 0.7310 | 0.9645 | 0.9440 | 0.9537 |
| 5 | 0.9916 | 0.9934 | 0.9917 | 0.9400 | 0.9487 | 0.9574 | |
| 7 | 0.9935 | 0.9904 | 0.9160 | 0.9277 | 0.9159 | ||
| 9 | 0.9750 | 0.9476 | 0.8347 | 0.8363 | |||
| Wt | Wb | ||||||
|---|---|---|---|---|---|---|---|
| 25 | 27 | 29 | 31 | 33 | 35 | 37 | |
| 1 | 0.9747 | 0.9797 | 0.9808 | 0.9798 | 0.9782 | 0.9742 | 0.9723 |
| 3 | 0.9899 | 0.9914 | 0.9921 | 0.9923 | 0.9920 | 0.9900 | 0.9876 |
| 5 | 0.9874 | 0.9893 | 0.9901 | 0.9903 | 0.9896 | 0.9873 | 0.9825 |
| 7 | 0.9881 | 0.9896 | 0.9901 | 0.9896 | 0.9884 | 0.9842 | 0.9802 |
| 9 | 0.9907 | 0.9913 | 0.9907 | 0.989 | 0.9863 | 0.9795 | 0.9740 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Ma, J.; Cheng, B.; Lin, F. Fractional Fourier Transform-Based Tensor RX for Hyperspectral Anomaly Detection. Remote Sens. 2022, 14, 797. https://doi.org/10.3390/rs14030797
Zhang L, Ma J, Cheng B, Lin F. Fractional Fourier Transform-Based Tensor RX for Hyperspectral Anomaly Detection. Remote Sensing. 2022; 14(3):797. https://doi.org/10.3390/rs14030797
Chicago/Turabian StyleZhang, Lili, Jiachen Ma, Baozhi Cheng, and Fang Lin. 2022. "Fractional Fourier Transform-Based Tensor RX for Hyperspectral Anomaly Detection" Remote Sensing 14, no. 3: 797. https://doi.org/10.3390/rs14030797
APA StyleZhang, L., Ma, J., Cheng, B., & Lin, F. (2022). Fractional Fourier Transform-Based Tensor RX for Hyperspectral Anomaly Detection. Remote Sensing, 14(3), 797. https://doi.org/10.3390/rs14030797





