Microtopographic Controls on Erosion and Deposition of a Rilled Hillslope in Eastern Tennessee, USA
Abstract
:1. Introduction
2. Study Area
3. Materials and Methods
3.1. Data Acquisition
3.2. Preprocessing and DEM Generation
3.3. DEM of Difference
3.4. Microtopographic Factors
3.5. Correlation and Regression Analysis
4. Results
4.1. DEM of Difference
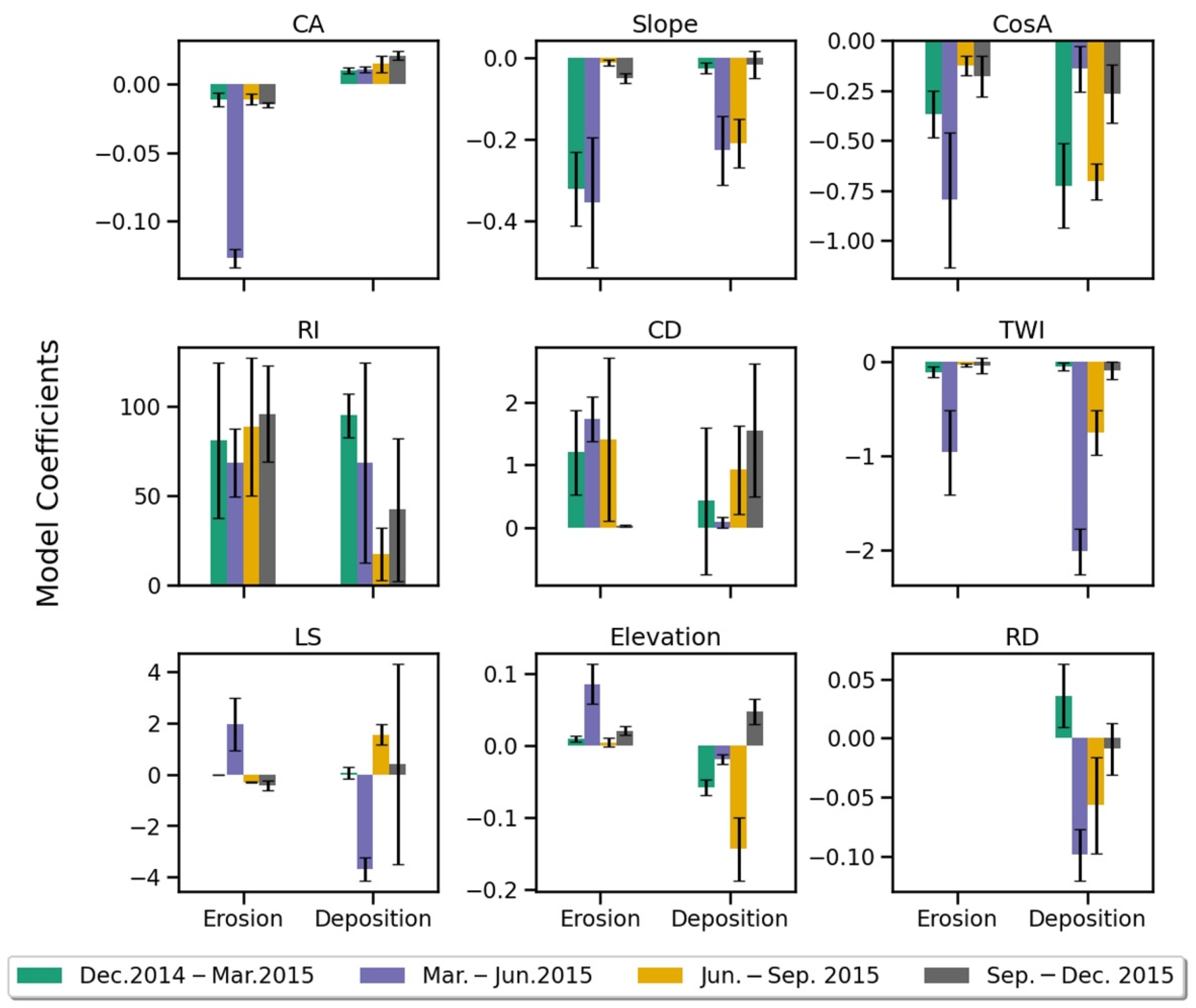
4.2. Correlation and Regression Analyses
5. Discussion
5.1. Seasonal Variation of Erosion and Deposition
5.2. Factors Controlling Erosion and Deposition
5.3. Limitations of This Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Neal, A.L.; Mendoza, G.F.; Todd, W.M. Incorporating variable source area hydrology into a curve-number-based watershed model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses-A Guide to Conservation Planning; United States Department of Agriculture: Hyattsville, MA, USA, 1978. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.; McCool, D.; Yoder, D. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); US Department of Agriculture: Washington, DC, USA, 1997. [Google Scholar]
- Nearing, M.; Foster, G.; Lane, L.; Finkner, S. A process-based soil erosion model for USDA-Water Erosion Prediction Project technology. Trans. ASAE 1989, 32, 1587–1593. [Google Scholar] [CrossRef]
- Liu, B.; Nearing, M.; Shi, P.; Jia, Z. Slope length effects on soil loss for steep slopes. Soil. Sci. Soc. Am. J. 2000, 64, 1759–1763. [Google Scholar] [CrossRef] [Green Version]
- McCool, D.; Foster, G.; Weesies, G. Slope length and steepness factor (LS). In Predicting Soil Erosion by Water–A Guide to Conservation Planning with Revised Universal Soil Loss Equation (RUSLE); Renard, K.G., Foster, G.R., Weesies, G., McCool, D., Yoder, D., Eds.; USDA: Washington, DC, USA, 1997; Chapter 4; pp. 101–142. [Google Scholar]
- Desmet, P.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Montgomery, D.R.; Brandon, M.T. Topographic controls on erosion rates in tectonically active mountain ranges. Earth Planet. Sci. Lett. 2002, 201, 481–489. [Google Scholar] [CrossRef]
- Tarolli, P.; Sofia, G.; Dalla, F.G. Geomorphic features extraction from high-resolution topography: Landslide crowns and bank erosion. Nat. Hazards 2012, 61, 65–83. [Google Scholar] [CrossRef]
- Lu, X.; Li, Y.; Washington-Allen, R.A.; Li, Y.; Li, H.; Hu, Q. The effect of grid size on the quantification of erosion, deposition, and rill network. Int. Soil Water Cons. Res. 2017, 5, 241–251. [Google Scholar] [CrossRef]
- Lu, X.; Li, Y.; Washington-Allen, R.A.; Li, Y. Structural and sedimentological connectivity on a rilled hillslope. Sci. Total Environ. 2019, 655, 1479–1494. [Google Scholar] [CrossRef]
- Eltner, A.; Baumgart, P.; Maas, H.G.; Faust, D. Multi-temporal UAV data for automatic measurement of rill and interrill erosion on loess soil. Earth Surf. Process. Landf. 2015, 40, 741–755. [Google Scholar] [CrossRef]
- Vinci, A.; Brigante, R.; Todisco, F.; Mannocchi, F.; Radicioni, F. Measuring rill erosion by laser scanning. Catena 2015, 124, 97–108. [Google Scholar] [CrossRef]
- Brubaker, K.M.; Myers, W.L.; Drohan, P.J.; Miller, D.A.; Boyer, E.W. The use of LiDAR terrain data in characterizing surface roughness and microtopography. Appl. Environ. Soil Sci. 2013, 891534. [Google Scholar] [CrossRef]
- Eitel, J.U.; Williams, C.J.; Vierling, L.A.; Al-Hamdan, O.Z.; Pierson, F.B. Suitability of terrestrial laser scanning for studying surface roughness effects on concentrated flow erosion processes in rangelands. Catena 2011, 87, 398–407. [Google Scholar] [CrossRef]
- Hancock, G.; Crawter, D.; Fityus, S.; Chandler, J.; Wells, T. The measurement and modelling of rill erosion at angle of repose slopes in mine spoil. Earth Surf. Process. Landf. 2008, 33, 1006–1020. [Google Scholar] [CrossRef]
- Lucieer, A.; Turner, D.; King, D.H.; Robinson, S.A. Using an Unmanned Aerial Vehicle (UAV) to capture micro-topography of Antarctic moss beds. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.W.; Vericat, D. From experimental plots to experimental landscapes: Topography, erosion and deposition in sub-humid badlands from Structure-from-Motion photogrammetry. Earth Surf. Process. Landf. 2015, 40, 1656–1671. [Google Scholar] [CrossRef] [Green Version]
- Neugirg, F.; Stark, M.; Kaiser, A.; Vlacilova, M.; Della Seta, M.; Vergari, F.; Schmidt, J.; Becht, M.; Haas, F. Erosion processes in calanchi in the Upper Orcia Valley, Southern Tuscany, Italy based on multitemporal high-resolution terrestrial LiDAR and UAV surveys. Geomorphology 2016, 269, 8–22. [Google Scholar] [CrossRef]
- Di Stefano, C.; Ferro, V.; Palmeri, V.; Pampalone, V. Measuring rill erosion using structure from motion: A plot experiment. Catena 2017, 156, 383–392. [Google Scholar] [CrossRef]
- Llena, M.; Vericat, D.; Smith, M.W.; Wheaton, J.M. Geomorphic process signatures reshaping sub-humid Mediterranean badlands: 1. Methodological development based on high-resolution topography. Earth Surf. Process. Landf. 2020, 45, 1335–1346. [Google Scholar] [CrossRef]
- Llena, M.; Smith, M.W.; Wheaton, J.M.; Vericat, D. Geomorphic process signatures reshaping sub-humid Mediterranean badlands: 2. Application to 5-year dataset. Earth Surf. Process. Landf. 2020, 45, 1292–1310. [Google Scholar] [CrossRef]
- Luffman, I.E.; Nandi, A.; Spiegel, T. Gully morphology, hillslope erosion, and precipitation characteristics in the Appalachian Valley and Ridge province, southeastern USA. Catena 2015, 133, 221–232. [Google Scholar] [CrossRef]
- Harden, C.P.; Mathews, L. Rainfall response of degraded soil following reforestation in the Copper Basin, Tennessee, USA. Environ. Manag. 2000, 26, 163–174. [Google Scholar] [CrossRef]
- Turnage, K.; Lee, S.; Foss, J.; Kim, K.; Larsen, I. Comparison of soil erosion and deposition rates using radiocesium, RUSLE, and buried soils in dolines in East Tennessee. Environ. Geol. 1997, 29, 1–10. [Google Scholar] [CrossRef]
- Boix-Fayos, C.; Martínez-Mena, M.; Arnau-Rosalén, E.; Calvo-Cases, A.; Castillo, V.; Albaladejo, J. Measuring soil erosion by field plots: Understanding the sources of variation. Earth Sci. Rev. 2006, 78, 267–285. [Google Scholar] [CrossRef]
- Pesci, A.; Teza, G.; Bonali, E. Terrestrial laser scanner resolution: Numerical simulations and experiments on spatial sampling optimization. Remote Sens. 2011, 3, 167–184. [Google Scholar] [CrossRef] [Green Version]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change detection on points cloud data acquired with a ground laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, W19. [Google Scholar]
- Chetverikov, D.; Svirko, D.; Stepanov, D.; Krsek, P. The trimmed iterative closest point algorithm. In Proceedings of the 16th International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002; Volume 3, pp. 545–548. [Google Scholar]
- Li, Y.; McNelis, J.J.; Washington-Allen, R.A. Quantifying short-term erosion and deposition in an active gully using terrestrial laser scanning: A case study from west Tennessee, USA. 2020. Front. Earth Sci. 2020, 8, 481. [Google Scholar] [CrossRef]
- Kidner, D.; Dorey, M.; Smith, D. What’s the point? Interpolation and extrapolation with a regular grid DEM. In Proceedings of the Fourth International Conference on GeoComputation, Fredericksburg, VA, USA, 25–28 July 1999. [Google Scholar]
- Cobby, D.M.; Mason, D.C.; Davenport, I.J. Image processing of airborne scanning laser altimetry data for improved river flood modelling. ISPRS J. Photogramm. Remote Sens. 2001, 56, 121–138. [Google Scholar] [CrossRef]
- Rees, W. The accuracy of digital elevation models interpolated to higher resolutions. Int. J. Remote Sens. 2000, 21, 7–20. [Google Scholar] [CrossRef]
- Smith, S.; Holland, D.; Longley, P. The importance of understanding error in lidar digital elevation models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 996–1001. [Google Scholar]
- Kennedy, M.; Kopp, S. Understanding map projections. In ESRI: Manual of ArcGIS; ESRI: Redlands, CA, USA, 2002. [Google Scholar]
- Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for uncertainty in DEMs from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
- Wilson, J.P.; Gallant, J.C. Digital terrain analysis. In Terrain Analysis Principles and Applications; Wilson, J.P., Gallant, J.C., Eds.; John Wiley & Sons Inc.: New York, NY, USA, 2000; Chapter 1; pp. 1–27. [Google Scholar]
- Abrahams, A.D.; Parsons, A.J. Resistance to overland flow on desert pavement and its implications for sediment transport modeling. Water Resour. Res. 1991, 27, 1827–1836. [Google Scholar] [CrossRef]
- Römkens, M.; Wang, J. Effect of tillage on surface roughness. Trans. ASAE 1986, 29, 429–433. [Google Scholar] [CrossRef]
- Darboux, F.; Huang, C. Does soil surface roughness increase or decrease water and particle transfers? Soil. Sci. Soc. Am. J. 2005, 69, 748–756. [Google Scholar] [CrossRef] [Green Version]
- Gómez, J.; Nearing, M. Runoff and sediment losses from rough and smooth soil surfaces in a laboratory experiment. Catena 2005, 59, 253–266. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Gr. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. On the extraction of channel networks from digital elevation data. Hydrol. Process. 1991, 5, 81–100. [Google Scholar] [CrossRef]
- Desmet, P.J.J.; Govers, G. GIS-based simulation of erosion and deposition patterns in an agricultural landscape: A comparison of model results with soil map information. Catena 1995, 25, 389–401. [Google Scholar] [CrossRef]
- Tucker, G.E.; Bras, R.L. Hillslope processes, drainage density, and landscape morphology. Water Resour. Res. 1998, 34, 2751–2764. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.; Sun, L.; Tang, Z. Effects of rainfall and slope on runoff, soil erosion and rill development: An experimental study using two loess soils. Hydrol. Process. 2015, 29, 2649–2658. [Google Scholar] [CrossRef]
- Shen, H.; Zheng, F.; Wen, L.; Lu, J.; Jiang, Y. An experimental study of rill erosion and morphology. Geomorphology 2015, 231, 193–201. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E.; Minasny, B.; Kheir, R.B.; Greve, M.B.; Greve, M.H. Digital mapping of soil organic carbon contents and stocks in Denmark. PLoS ONE 2014, 9, e105519. [Google Scholar] [CrossRef] [PubMed]
- Feuillet, T.; Mercier, D.; Decaulne, A.; Cossart, E. Classification of sorted patterned ground areas based on their environmental characteristics (Skagafjörður, Northern Iceland). Geomorphology 2012, 139, 577–587. [Google Scholar] [CrossRef]
- Beven, K.; Kirkby, M. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Barling, R.D.; Moore, I.D.; Grayson, R.B. A quasi-dynamic wetness index for characterizing the spatial distribution of zones of surface saturation and soil water content. Water Resour. Res. 1994, 30, 1029–1044. [Google Scholar] [CrossRef]
- Burt, T.; Butcher, D. Topographic controls of soil moisture distributions. Eur. J. Soil Sci. 1985, 36, 469–486. [Google Scholar] [CrossRef]
- Hancock, G.; Wells, T.; Martinez, C.; Dever, C. Soil erosion and tolerable soil loss: Insights into erosion rates for a well-managed grassland catchment. Geoderma 2015, 237, 256–265. [Google Scholar] [CrossRef]
- Western, A.W.; Zhou, S.L.; Grayson, R.B.; McMahon, T.A.; Blöschl, G.; Wilson, D.J. Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes. J. Hydrol. 2004, 286, 113–134. [Google Scholar] [CrossRef]
- McCool, D.K.; Foster, G.R.; Mutchler, C.; Meyer, L. Revised slope length factor for the Universal Soil Loss Equation. Trans. ASAE 1989, 32, 1571–1576. [Google Scholar] [CrossRef]
- Schmidt, S.; Tresch, S.; Meusburger, K. Modification of the RUSLE slope length and steepness factor (LS-factor) based on rainfall experiments at steep alpine grasslands. MethodsX 2019, 6, 219–229. [Google Scholar] [CrossRef]
- Tarboton, D.G. Terrain Analysis Using Digital Elevation Models (TauDEM). Available online: http://hydrology.usu.edu/taudem/taudem5/ (accessed on 5 March 2022).
- Böhner, J.; McCloy, K.R.; Strobl, J. SAGA: Analysis and Modelling Applications; Number 115; Goltze: Gottingen, Germany, 2006. [Google Scholar]
- Koenker, R.; Hallock, K.F. Quantile regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Legendre, P. Spatial autocorrelation: Trouble or new paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar] [CrossRef]
- Kuhn, M. Caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar]
- Ambroise, C.; McLachlan, G.J. Selection bias in gene extraction on the basis of microarray gene-expression data. Proc. Natl. Acad. Sci. USA 2002, 99, 6562–6566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barnes, N.; Luffman, I.; Nandi, A. Gully erosion and freeze-thaw processes in clay-rich soils, northeast Tennessee, USA. GeoResJ 2016, 9, 67–76. [Google Scholar] [CrossRef]
- Gatto, L.W. Soil freeze–thaw-induced changes to a simulated rill: Potential impacts on soil erosion. Geomorphology 2000, 32, 147–160. [Google Scholar] [CrossRef]
- Gessesse, G.D.; Fuchs, H.; Mansberger, R.; Klik, A.; Rieke-Zapp, D.H. Assessment of erosion, deposition and rill development on irregular soil surfaces using close range digital photogrammetry. Photogramm. Rec. 2010, 25, 299–318. [Google Scholar] [CrossRef]
- Nouwakpo, S.K.; Weltz, M.A.; McGwire, K.C.; Williams, J.C.; Osama, A.H.; Green, C.H. Insight into sediment transport processes on saline rangeland hillslopes using three-dimensional soil microtopography changes. Earth Surf. Process. Landf. 2017, 42, 681–696. [Google Scholar] [CrossRef]
- Mah, M.; Douglas, L.; Ringrose-Voase, A. Effects of crust development and surface slope on erosion by rainfall. Soil Sci. 1992, 154, 37–43. [Google Scholar] [CrossRef]

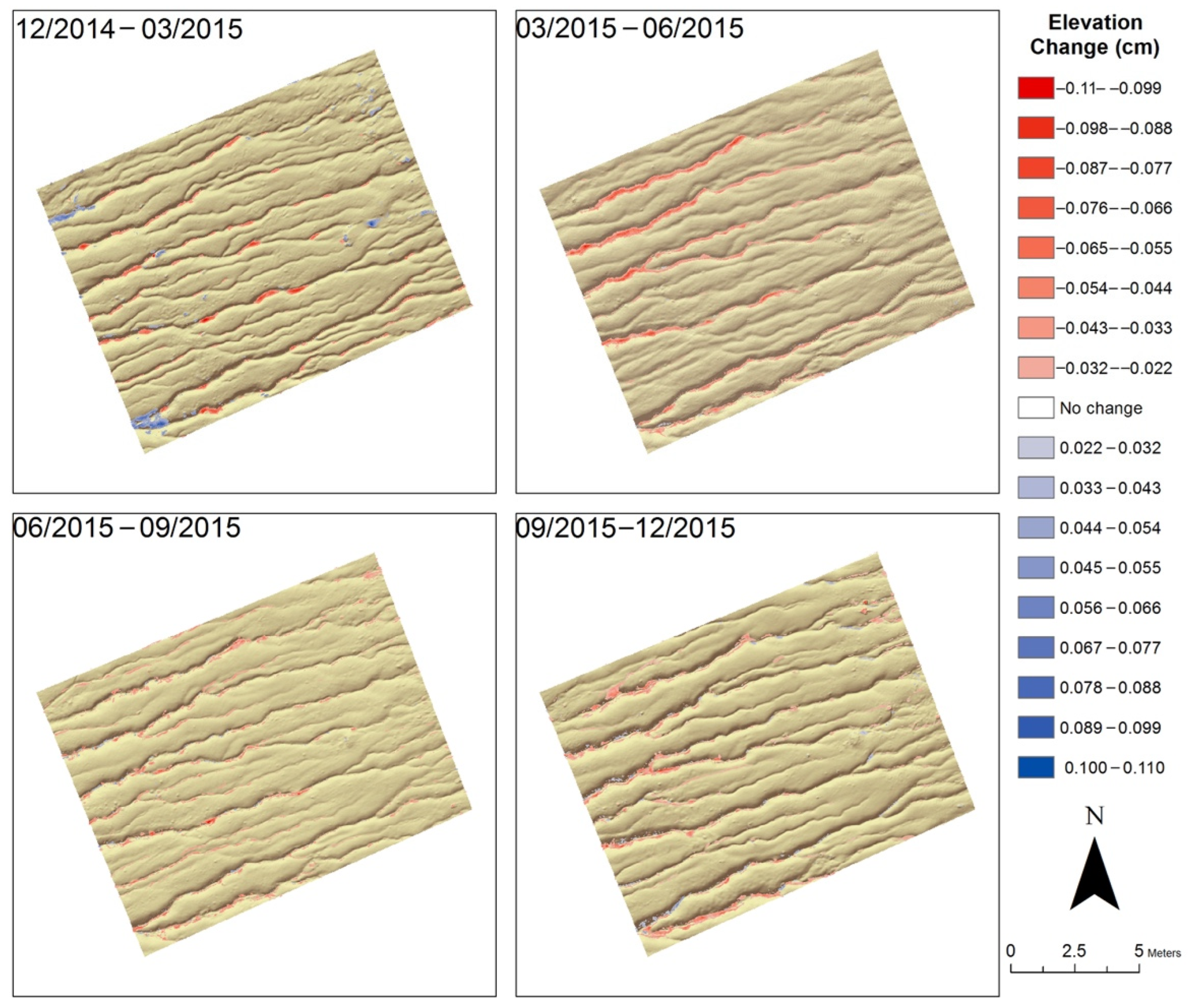



| Survey Date | Number of Return Points | Average Point Density (pts/cm2) | Intra-Survey RMSE (cm) | Between-Survey RMSE (cm) |
|---|---|---|---|---|
| 10 December 2014 | 7,671,276 | 1.91 | 0.35 ± 0.11 | (reference) |
| 7 March 2015 | 8,983,232 | 2.25 | 0.35 ± 0.13 | 0.53 ± 0.08 |
| 11 June 2015 | 8,223,775 | 2.06 | 0.34 ± 0.11 | 0.41 ± 0.08 |
| 13 September 2015 | 8,059,708 | 2.02 | 0.33 ± 0.12 | 0.44 ± 0.05 |
| 16 December 2015 | 7,931,839 | 1.99 | 0.35 ± 0.14 | 0.40 ± 0.07 |
| December 2014–March 2015 | March 2015–June 2015 | June 2015–September 2015 | September 2015–December 2015 | Total | |
|---|---|---|---|---|---|
| Areal change | |||||
| Total detectable change (m2) | 5.83 | 8.73 | 6.86 | 8.75 | - |
| Total change percentage (%) | 3.76 | 5.63 | 4.42 | 5.65 | - |
| Erosion (m2) | 3.80 | 8.59 | 6.35 | 7.37 | - |
| Deposition (m2) | 2.03 | 0.14 | 0.52 | 1.38 | - |
| Volumetric change | |||||
| Erosion (m3) | 0.18 ± 0.07 | 0.38 ± 0.16 | 0.27 ±0.10 | 0.36 ± 0.13 | 1.19 ± 0.46 |
| Deposition (m3) | 0.05 ± 0.03 | 0.03 ± 0.01 | 0.04 ± 0.02 | 0.05 ±0.02 | 0.17 ± 0.08 |
| Net change (m3) | 0.13 ± 0.10 | 0.35 ± 0.17 | 0.23 ± 0.12 | 0.31 ±0.15 | 1.02 ± 0.54 |
| Erosion | Deposition | Elevation | Slope | LS | CA | CD | CosA | SinA | RD | RI | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Deposition | −0.11 | ||||||||||
| Elevation | 0.38 ** | −0.17 *** | |||||||||
| Slope | −0.30 *** | 0.23 *** | −0.36 *** | ||||||||
| LS | −0.37 *** | 0.25 | −0.50 ** | 0.83 *** | |||||||
| CA | −0.43 *** | 0.31 ** | −0.55 *** | 0.53 *** | 0.73 *** | ||||||
| CD | 0.27 ** | −0.12 | −0.10 * | −0.01 | 0.03 | 0.15 ** | |||||
| CosA | 0.04 | −0.09 * | 0.01 | −0.06 | −0.07 | −0.01 | 0.07 | ||||
| SinA | 0.03 | −0.09 * | 0.01 | −0.06 | −0.07 | −0.01 | 0.07 | 0.99 *** | |||
| RD | −0.01 | 0.04 | 0.06 | 0.04 *** | 0.25 ** | 0.15 | −0.07 ** | −0.11 *** | 0.10 *** | ||
| RI | −0.31 *** | 0.24 *** | −0.37 *** | 0.97 *** | 0.84 *** | 0.58 *** | −0.02 ** | −0.09 | −0.08 | 0.04 ** | |
| TWI | 0.02 ** | 0.01 | −0.07 *** | −0.52 *** | −0.05 | 0.00 | 0.10 | 0.00 | 0.00 | 0.31 *** | −0.50 *** |
| Variable Rank | Erosion | Deposition | ||
|---|---|---|---|---|
| Variable * | MSE | Variable * | MSE | |
| 1 | CA | 0.286 | CA | 0.225 |
| 2 | Slope | 0.221 | Elevation | 0.179 |
| 3 | CosA | 0.208 | CD | 0.165 |
| 4 | CD | 0.197 | CosA | 0.159 |
| 5 | RI | 0.191 | TWI | 0.157 |
| 6 | TWI | 0.177 | LS | 0.152 |
| 7 | LS | 0.173 | Slope | 0.148 |
| 8 | Elevation ** | 0.171 | RD | 0.142 |
| 9 | RD | 0.172 | RI ** | 0.141 |
| 10 | SinA | 0.173 | SinA | 0.142 |
| Erosion Model * (τ = 0.56, n = 322) | Deposition Model (τ = 0.53, n = 297) | ||||||
|---|---|---|---|---|---|---|---|
| Variables | Coefficient | Std. Error | p-Value | Variables | Coefficient | Std. Error | p-Value |
| constant | −2.235 | 1.186 | 0.060 | constant | 16.454 | 2.903 | 0.000 |
| CA | −0.011 | 0.005 | 0.042 | CA | 0.010 | 0.002 | 0.000 |
| Slope | −0.322 | 0.090 | 0.000 | Slope | −0.025 | 0.013 | 0.065 |
| CosA | −0.367 | 0.116 | 0.002 | CosA | −0.726 | 0.213 | 0.001 |
| RI | 81.325 | 43.617 | 0.000 | RI | 95.151 | 12.201 | 0.000 |
| CD | 1.199 | 0.669 | 0.074 | RD | 0.036 | 0.027 | 0.185 |
| TWI | −0.115 | 0.055 | 0.035 | CD | 0.425 | 1.164 | 0.715 |
| LS | −0.012 | 0.005 | 0.021 | TWI | −0.056 | 0.042 | 0.188 |
| Elevation | 0.009 | 0.004 | 0.000 | LS | 0.068 | 0.228 | 0.767 |
| Elevation | −0.058 | 0.011 | 0.000 | ||||
| Erosion Model * (τ = 0.66, n = 255) | Deposition Model (τ = 0.59, n = 302) | ||||||
|---|---|---|---|---|---|---|---|
| Variables | Coefficient | Std. Error | p-Value | Variables | Coefficient | Std. Error | p-Value |
| constant | 6.454 | 2.525 | 0.011 | constant | 3.098 | 1.328 | 0.019 |
| CA | −0.127 | 0.007 | 0.000 | CA | 0.011 | 0.002 | 0.000 |
| Slope | −0.356 | 0.160 | 0.000 | Slope | −0.227 | 0.085 | 0.000 |
| CosA | −0.798 | 0.337 | 0.019 | CosA | −0.142 | 0.115 | 0.143 |
| RI | 68.499 | 19.014 | 0.000 | RI | 68.773 | 56.161 | 0.216 |
| CD | 1.727 | 0.353 | 0.001 | RD | −0.099 | 0.022 | 0.000 |
| TWI | −0.967 | 0.451 | 0.033 | CD | 0.085 | 0.081 | 0.299 |
| LS | 1.956 | 1.018 | 0.056 | TWI | −2.020 | 0.239 | 0.000 |
| Elevation | 0.085 | 0.028 | 0.003 | LS | −3.699 | 0.447 | 0.000 |
| Elevation | −0.019 | 0.007 | 0.002 | ||||
| Erosion Model * (τ = 0.63, n = 341) | Deposition Model (τ = 0.52, n = 169) | ||||||
|---|---|---|---|---|---|---|---|
| Variables | Coefficient | Std. Error | p-Value | Variables | Coefficient | Std. Error | p-Value |
| constant | −0.647 | 2.078 | 0.755 | constant | −1.816 | 4.472 | 0.685 |
| CA | −0.011 | 0.004 | 0.008 | CA | 0.015 | 0.006 | 0.000 |
| Slope | −0.012 | 0.007 | 0.113 | Slope | −0.210 | 0.059 | 0.000 |
| CosA | −0.124 | 0.049 | 0.012 | CosA | −0.705 | 0.091 | 0.000 |
| RI | 88.795 | 38.530 | 0.022 | RI | 17.169 | 14.803 | 0.256 |
| CD | 1.409 | 1.302 | 0.280 | RD | −0.057 | 0.041 | 0.162 |
| TWI | −0.039 | 0.016 | 0.015 | CD | 0.919 | 0.700 | 0.000 |
| LS | −0.305 | 0.027 | 0.000 | TWI | −0.759 | 0.237 | 0.002 |
| Elevation | 0.004 | 0.006 | 0.481 | LS | 1.565 | 0.408 | 0.000 |
| Elevation | −0.144 | 0.044 | 0.000 | ||||
| Erosion Model * (τ = 0.58, n = 290) | Deposition Model (τ = 0.66, n = 149) | ||||||
|---|---|---|---|---|---|---|---|
| Variables | Coefficient | Std. Error | p-Value | Variables | Coefficient | Std. Error | p-Value |
| constant | −5.791 | 1.452 | 0.000 | constant | −11.040 | 4.232 | 0.010 |
| CA | −0.015 | 0.002 | 0.000 | CA | 0.021 | 0.003 | 0.000 |
| Slope | −0.049 | 0.012 | 0.000 | Slope | −0.017 | 0.033 | 0.607 |
| CosA | −0.177 | 0.102 | 0.083 | CosA | −0.265 | 0.147 | 0.073 |
| RI | 95.925 | 26.975 | 0.000 | RI | 42.273 | 40.107 | 0.300 |
| CD | 0.034 | 0.014 | 0.012 | RD | −0.009 | 0.022 | 0.680 |
| TWI | −0.042 | 0.083 | 0.017 | CD | 1.553 | 1.065 | 0.147 |
| LS | −0.429 | 0.189 | 0.022 | TWI | −0.092 | 0.093 | 0.322 |
| Elevation | 0.020 | 0.006 | 0.000 | LS | 0.408 | 3.910 | 0.917 |
| Elevation | 0.047 | 0.018 | 0.009 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Lu, X.; Washington-Allen, R.A.; Li, Y. Microtopographic Controls on Erosion and Deposition of a Rilled Hillslope in Eastern Tennessee, USA. Remote Sens. 2022, 14, 1315. https://doi.org/10.3390/rs14061315
Li Y, Lu X, Washington-Allen RA, Li Y. Microtopographic Controls on Erosion and Deposition of a Rilled Hillslope in Eastern Tennessee, USA. Remote Sensing. 2022; 14(6):1315. https://doi.org/10.3390/rs14061315
Chicago/Turabian StyleLi, Yingkui, Xiaoyu Lu, Robert A. Washington-Allen, and Yanan Li. 2022. "Microtopographic Controls on Erosion and Deposition of a Rilled Hillslope in Eastern Tennessee, USA" Remote Sensing 14, no. 6: 1315. https://doi.org/10.3390/rs14061315
APA StyleLi, Y., Lu, X., Washington-Allen, R. A., & Li, Y. (2022). Microtopographic Controls on Erosion and Deposition of a Rilled Hillslope in Eastern Tennessee, USA. Remote Sensing, 14(6), 1315. https://doi.org/10.3390/rs14061315






