Joint Angle and Range Estimation in Monostatic FDA-MIMO Radar via Compressed Unitary PARAFAC
Abstract
:1. Introduction
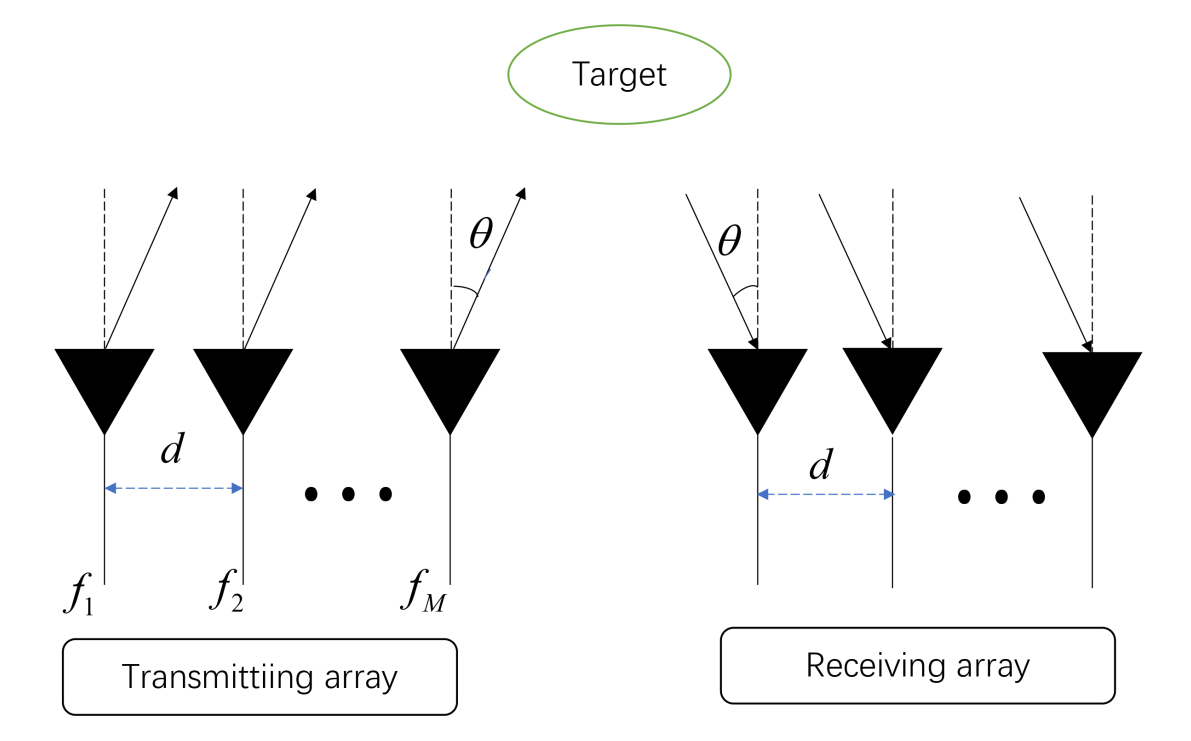
2. Tensor Data Model
3. Compressed Unitary PARAFAC Algorithm
3.1. The Real-Valued Signal Tensor
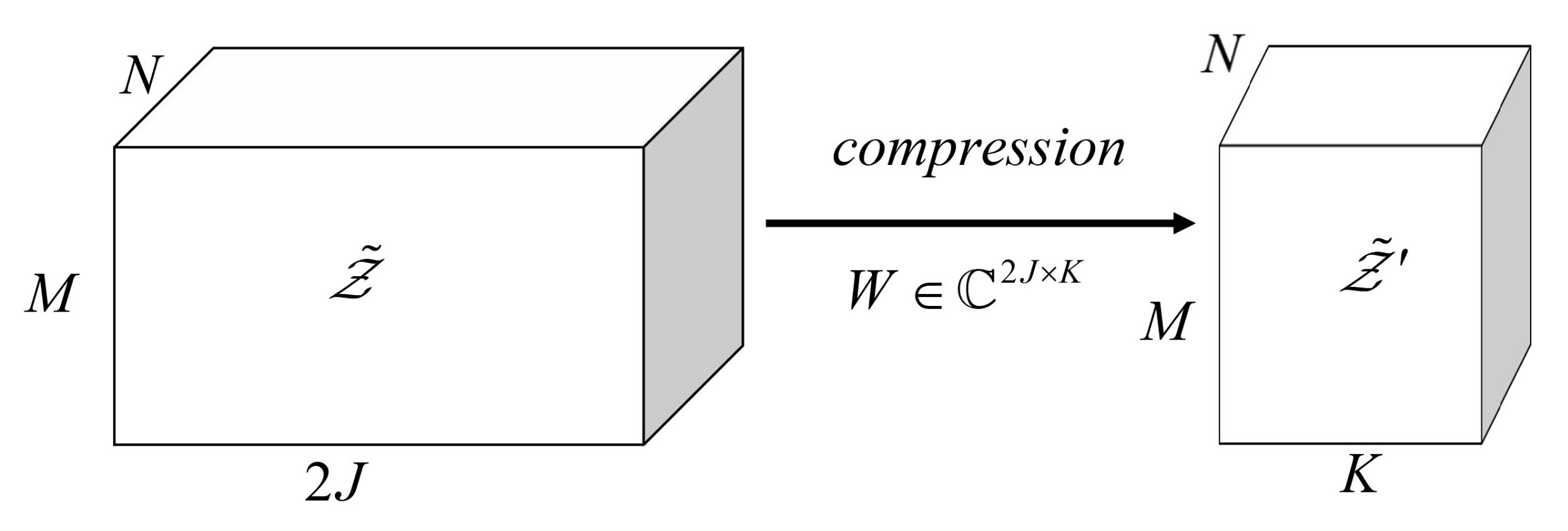
3.2. Tensor Model Compression
3.3. Trilinear Decomposition
3.4. Range and Angle Estimation
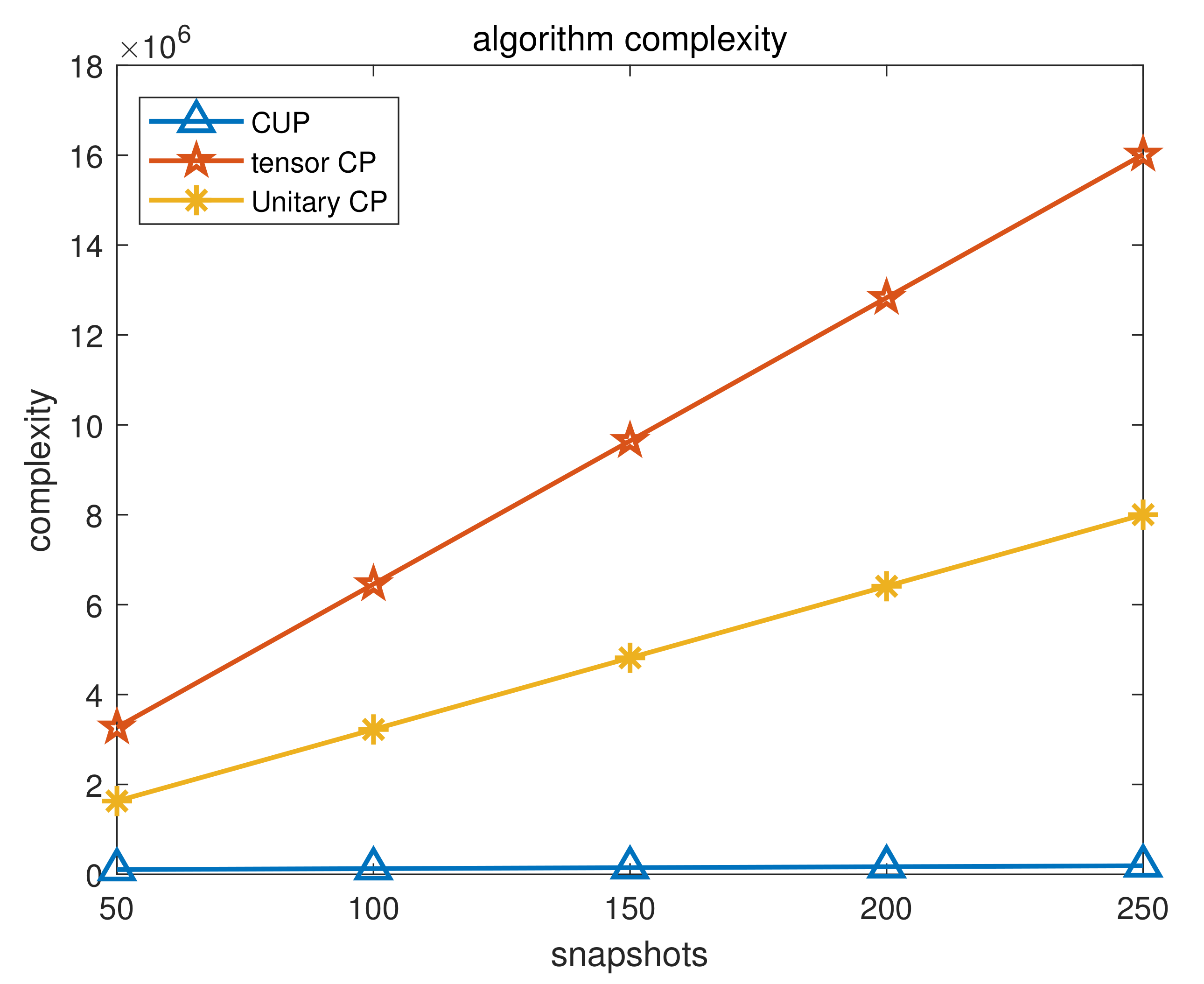
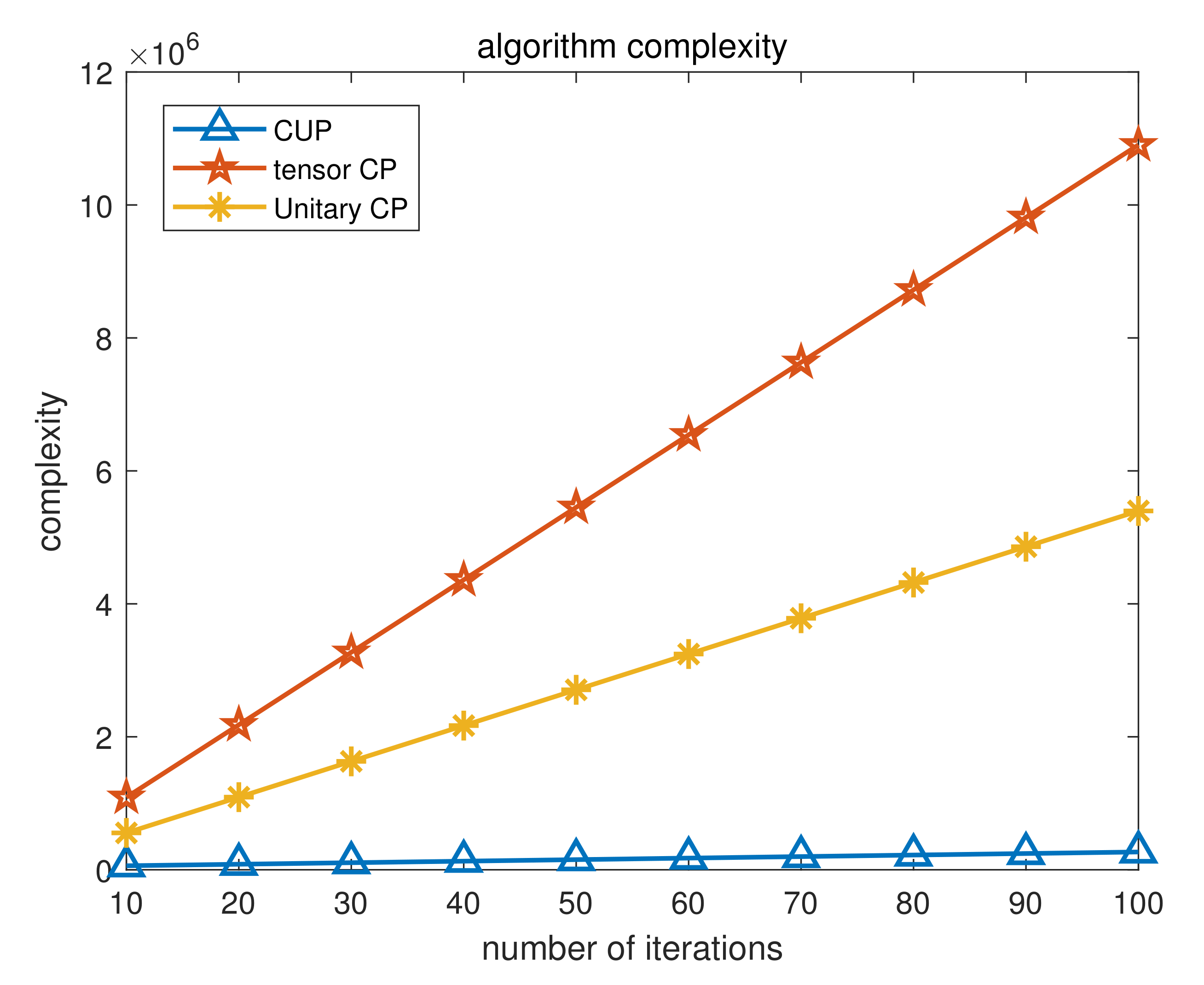
3.5. Complexity Analysis and Cramer-Rao Bound
4. Simulation Results
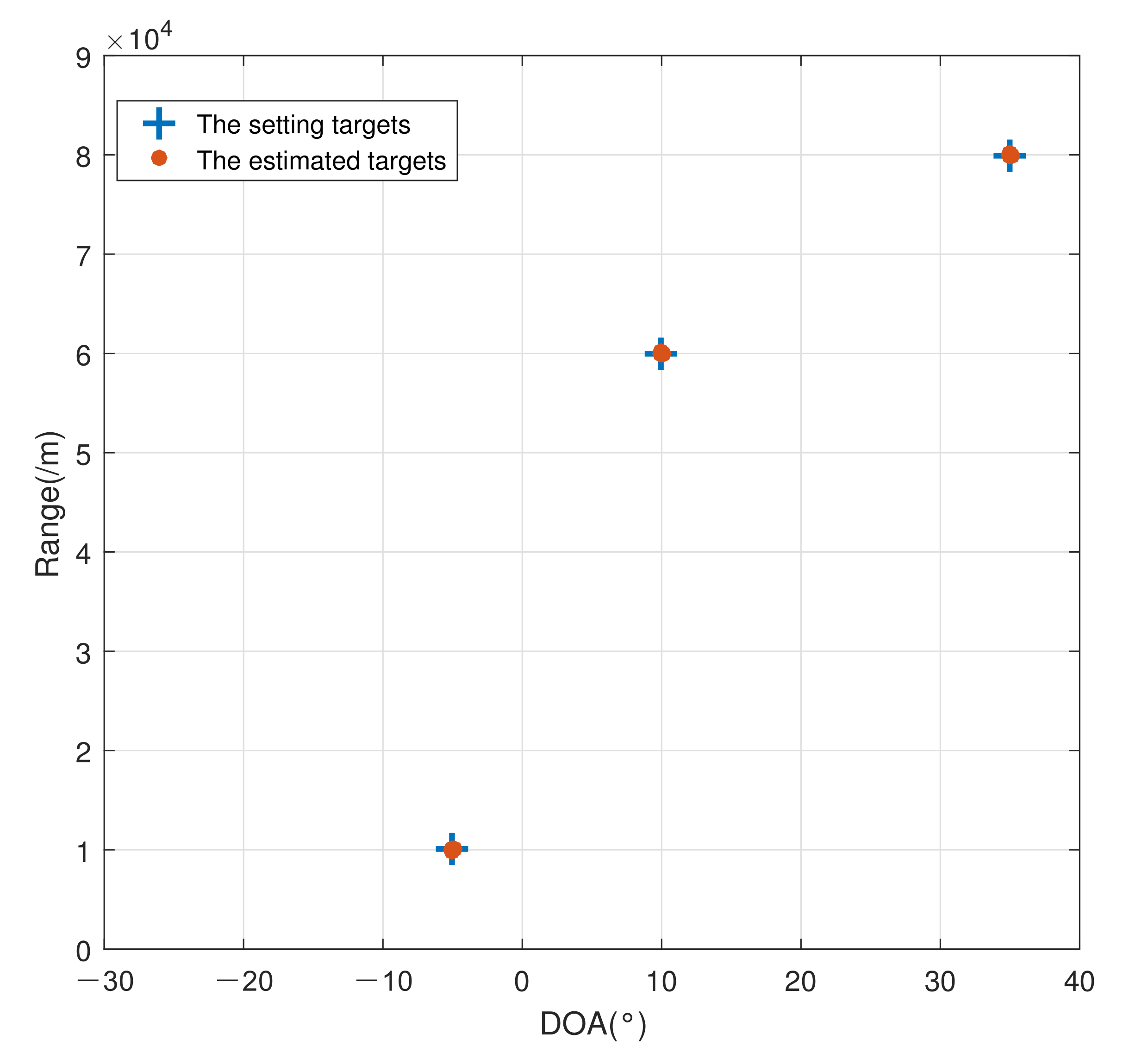
4.1. Stability Simulation
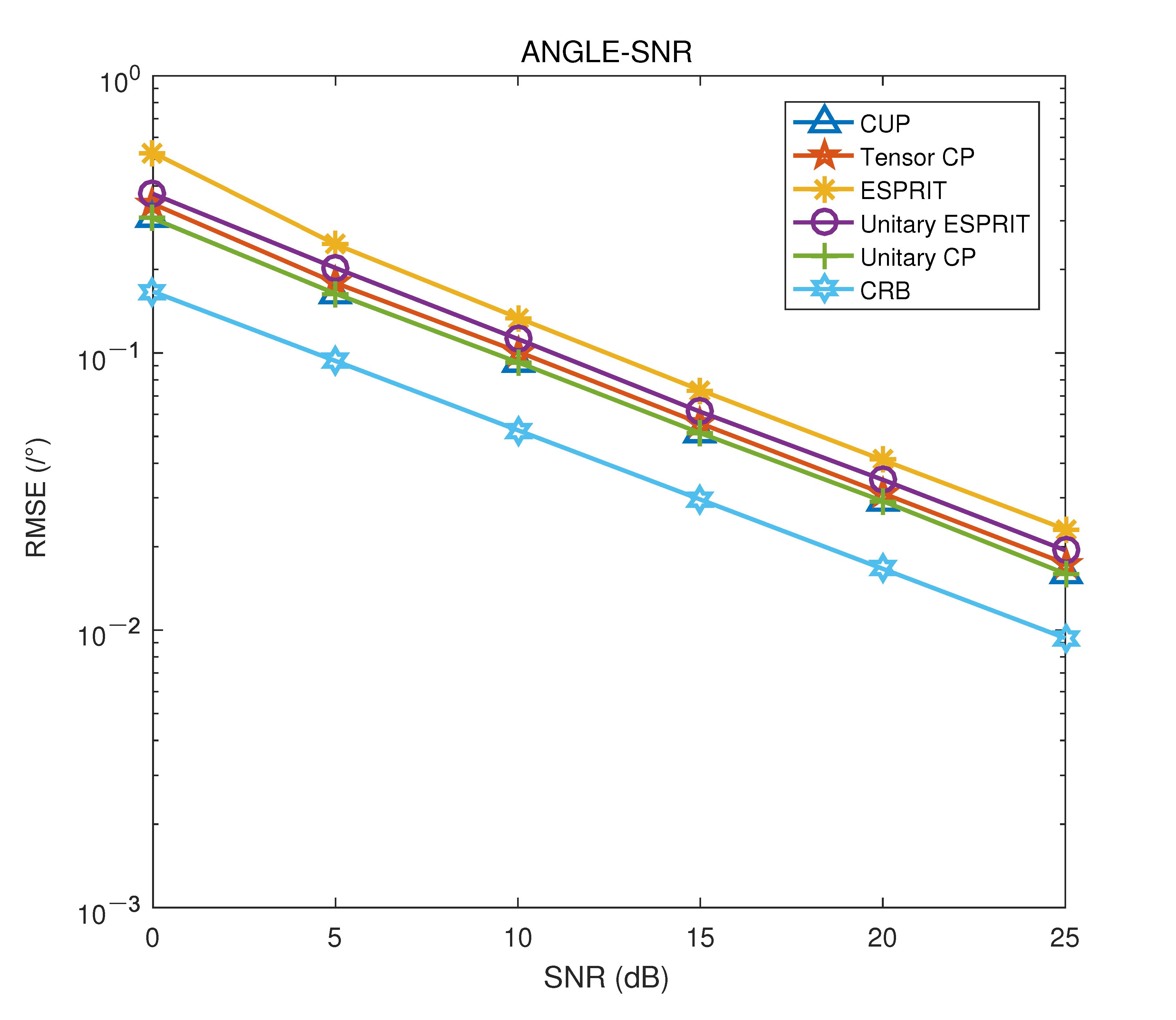
4.2. Simulation of Algorithm Performance with RMSE Changing with SNR
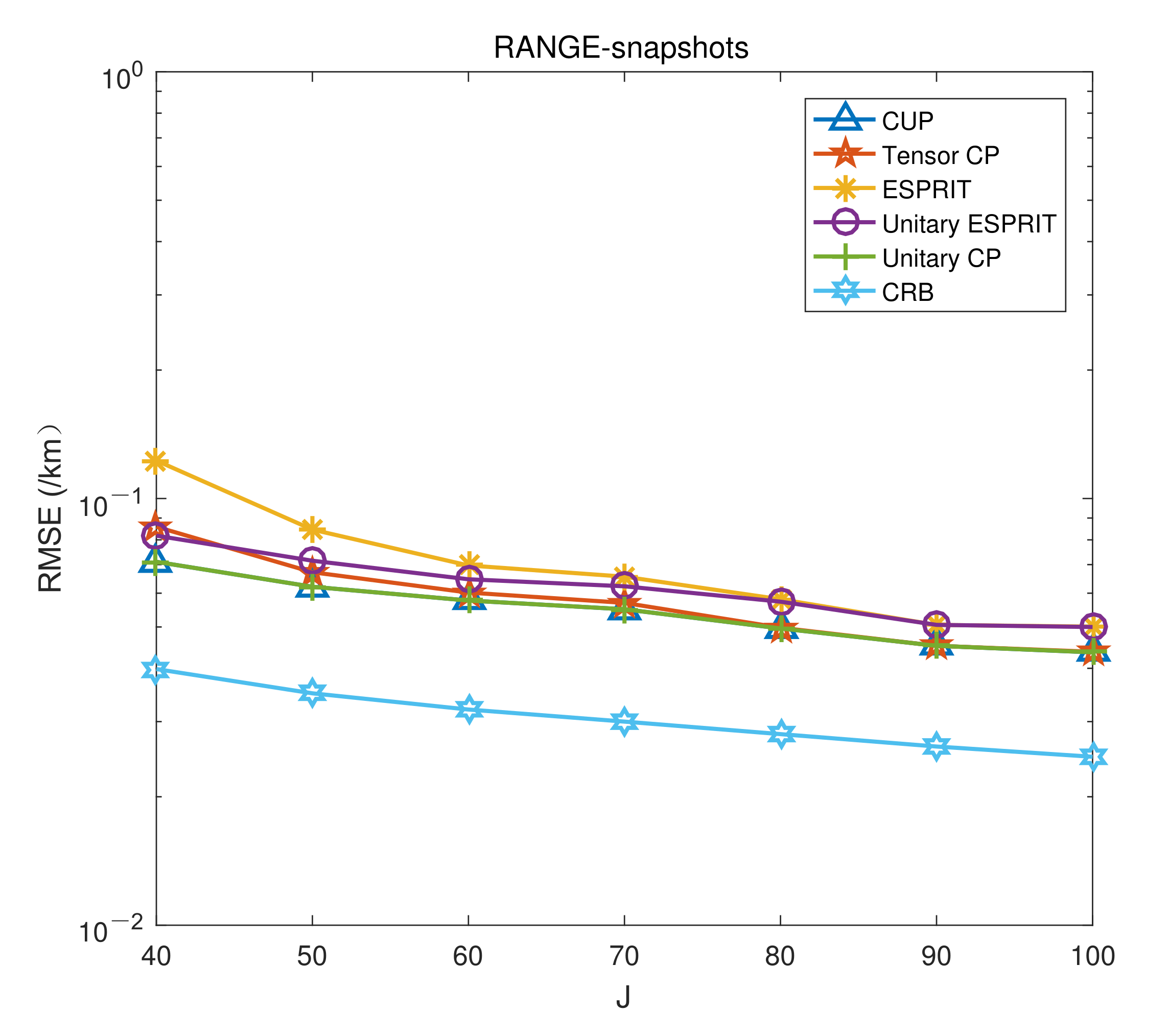
4.3. Simulation of Algorithm Performance with RMSE Changing with Snapshots
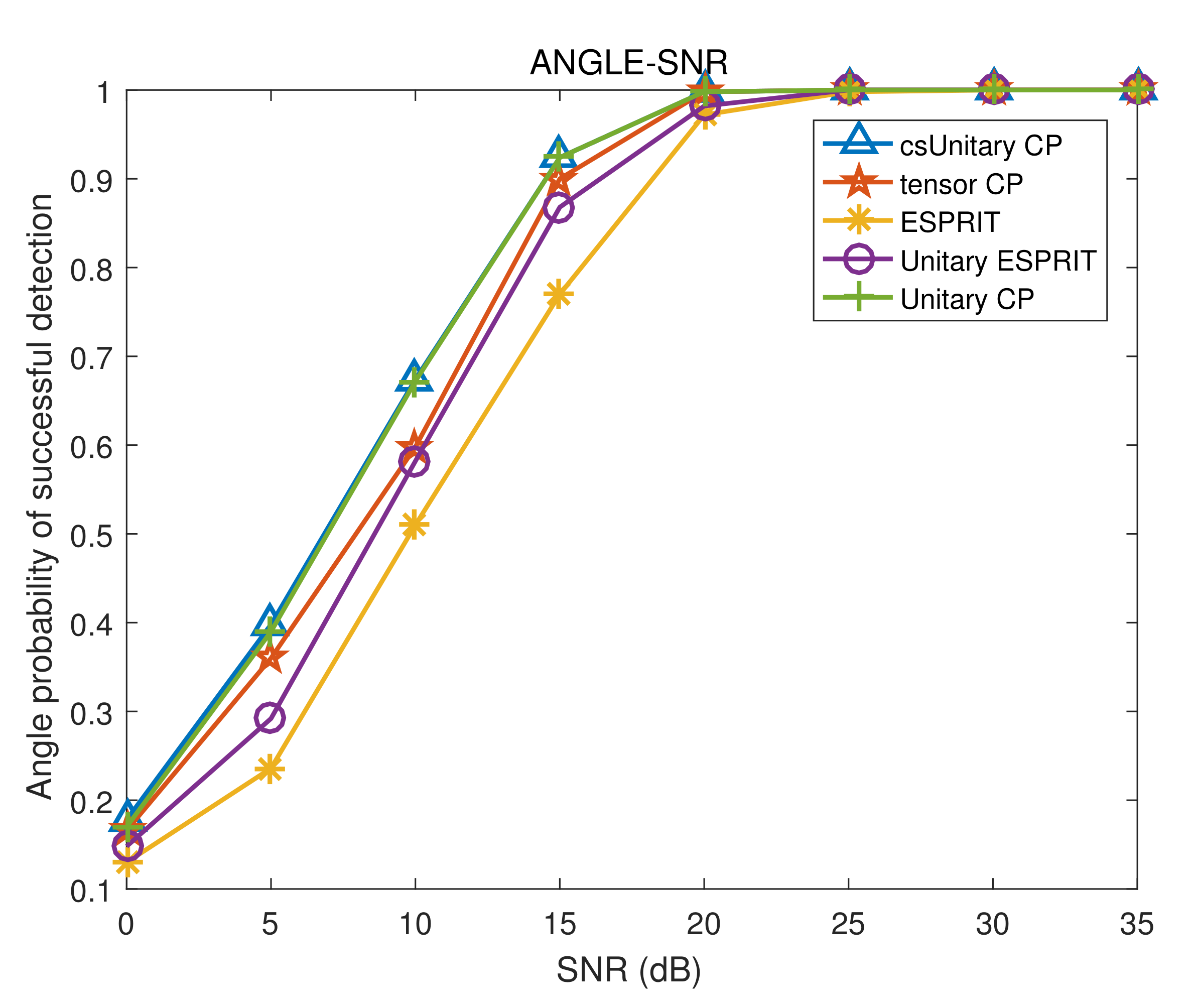
4.4. Simulation of Algorithm Performance with PSD Changing with SNR
4.5. Simulation of Algorithm Performance with PSD Changing with Snapshots
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coluccia, A.; Fascista, A.; Ricci, G. CFAR feature plane: A novel framework for the analysis and design of radar detectors. IEEE Trans. Signal Process. 2020, 68, 3903–3916. [Google Scholar] [CrossRef]
- Cao, Z.; Fang, W.; Song, Y.; He, L.; Song, C.; Xu, Z. DNN-Based Peak Sequence Classification CFAR Detection Algorithm for High-Resolution FMCW Radar. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Rabideau, D.J.; Parker, P. Ubiquitous MIMO multifunction digital array radar. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1057–1064. [Google Scholar]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the 2004 IEEE Radar Conference (IEEE Cat. No. 04CH37509), Philadelphia, PA, USA, 29–29 April 2004; pp. 71–78. [Google Scholar]
- Bliss, D.W.; Forsythe, K.W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 54–59. [Google Scholar]
- Wang, X.; Yang, L.T.; Meng, D.; Dong, M.; Ota, K.; Wang, H. Multi-UAV cooperative localization for marine targets based on weighted subspace fitting in SAGIN environment. IEEE Internet Things J. 2021, in press. [Google Scholar] [CrossRef]
- Antonik, P.; Wicks, M.C.; Griffiths, H.D.; Baker, C.J. Frequency diverse array radars. In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, 24–27 April 2006; p. 3. [Google Scholar]
- Wang, W.Q. Subarray-based frequency diverse array radar for target range-angle estimation. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3057–3067. [Google Scholar] [CrossRef]
- Chen, H.; Shao, H.Z. Sparse reconstruction based target localization with frequency diverse array MIMO radar. In Proceedings of the 2015 IEEE China Summit and International Conference on Signal and Information Processing (ChinaSIP), Chengdu, China, 12–15 July 2015; pp. 94–98. [Google Scholar]
- Xu, J.; Liao, G.; Zhang, Y.; Ji, H.; Huang, L. An adaptive range-angle-Doppler processing approach for FDA-MIMO radar using three-dimensional localization. IEEE J. Sel. Top. Signal Process 2016, 11, 309–320. [Google Scholar] [CrossRef]
- Xu, J.; Wang, W.Q.; Cui, C.; Gui, R. Joint range, angle and doppler estimation for FDA-MIMO radar. In Proceedings of the 2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM), Sheffield, UK, 8–11 July 2018; pp. 499–503. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Xu, L.; Xu, D. Trilinear decomposition-based transmit angle and receive angle estimation for multiple-input multiple-output radar. IET Radar Sonar Navig. 2011, 5, 626–631. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, Y.; Cheng, Z.; Li, H. A novel unitary PARAFAC method for DOD and DOA estimation in bistatic MIMO radar. Signal Process. 2017, 138, 273–279. [Google Scholar] [CrossRef]
- Xu, L.; Wen, F.; Zhangm, X. A novel unitary PARAFAC algorithm for joint DOA and frequency estimation. IEEE Commun. Lett. 2019, 23, 660–663. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, Y. Transmit beamspace-based unitary parallel factor method for DOD and DOA estimation in bistatic MIMO radar. IEEE Access 2018, 6, 65573–65581. [Google Scholar] [CrossRef]
- Xu, L.; Wu, R.; Zhang, X.; Shi, Z. Joint two-dimensional DOA and frequency estimation for L-shaped array via compressed sensing PARAFAC method. IEEE Access 2018, 6, 37204–37213. [Google Scholar] [CrossRef]
- Li, S.; Sun, Z.; Zhang, X.; Chen, W.; Xu, D. Joint DOA and frequency estimation for linear array with compressed sensing PARAFAC framework. J. Circuits Syst. Comput. 2017, 26, 1750136. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, X.; Chen, W. Compressed sensing parallel factor analysis-based joint angle and Doppler frequency estimation for monostatic multiple-input–multiple-output radar. IET Radar Sonar Navig. 2014, 8, 597–606. [Google Scholar] [CrossRef]
- Li, S.; Zhang, X.F. Study on the compressed matrices in compressed sensing trilinear model. Appl. Mech. Mater. 2014, 556, 3380–3383. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; Kyrillidis, A. Multi-way compressed sensing for sparse low-rank tensors. IEEE Signal Process. Lett. 2012, 19, 757–760. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Bai, W.; Zheng, G. Successive ESPRIT algorithm for joint DOA-range-polarization estimation with polarization sensitive FDA-MIMO radar. IEEE Access 2018, 6, 36376–36382. [Google Scholar] [CrossRef]
- Xu, T.; Yang, Y.; Huang, M.; Wang, H.; Wu, D.; Yi, Q. Tensor-based angle and range estimation method in monostatic FDA-MIMO radar. Math. Probl. Eng. 2020, 2020, 5720189. [Google Scholar] [CrossRef]
- Liu, F.; Wang, X.; Huang, M.; Wan, L.; Wang, H.; Zhang, B. A novel unitary ESPRIT algorithm for monostatic FDA-MIMO radar. Sensors 2020, 20, 827. [Google Scholar] [CrossRef] [Green Version]
- Haardt, M.; Roemer, F.; Del Galdo, G. Higher-order SVD-based subspace estimation of improve the parameter estimation accuracy in multidimensional harmonic retrieval problems. IEEE Trans. Signal Process. 2008, 56, 3198–3213. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Liu, J.; Liu, Q.; Wang, B. Tensor-based real-valued subspace approach for angle estimation in bistatic MIMO radar with unknown mutual coupling. Signal Process. 2015, 116, 152–158. [Google Scholar] [CrossRef]
- Andersson, C.A.; Bro, R. Improving the speed of multi-way algorithms: Part I. Tucker3. Chemom. Intell. Lab. Syst. 1998, 42, 93–103. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, W.Q.; Gao, K. FDA-MIMO radar range-angle estimation: CRLB, MSE, and resolution analysis. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 284–294. [Google Scholar] [CrossRef]



| Notations | Definitions |
|---|---|
| conjugate-transpose | |
| transpose | |
| conjugate | |
| pseudo-inverse | |
| inverse | |
| ⊙ | Khatri–Rao product operator |
| ⊗ | Kronecker product operator |
| the Frobenius norm operator | |
| the diagonal matrix composed of the n-th row of . | |
| the real part operator | |
| ∘ | identity matrix the vector outer product operator |
| identity matrix |
| Targets | 10 km | 60 km | 80 km | ||||
|---|---|---|---|---|---|---|---|
| Time | |||||||
| 1 | km | km | km | ||||
| 2 | km | km | km | ||||
| 3 | km | km | km | ||||
| 4 | km | km | km | ||||
| 5 | km | km | km | ||||
| 6 | km | km | km | ||||
| 7 | km | km | km | ||||
| 8 | km | km | km | ||||
| 9 | km | km | km | ||||
| 10 | km | km | km | ||||
| 11 | km | km | km | ||||
| 12 | km | km | km | ||||
| 13 | km | km | km | ||||
| 14 | km | km | km | ||||
| 15 | km | km | km | ||||
| 16 | km | km | km | ||||
| 17 | km | km | km | ||||
| 18 | km | km | km | ||||
| 19 | km | km | km | ||||
| 20 | km | km | km | ||||
| Algorithm | SNR = 0 | SNR = 5 | SNR = 10 | SNR = 15 | SNR = 20 | SNR = 25 |
|---|---|---|---|---|---|---|
| CRB | ||||||
| CUP | ||||||
| unitary CP | ||||||
| tensor CP | ||||||
| unitary ESPRIT | ||||||
| ESPRIT |
| Algorithm (km) | SNR = 0 | SNR = 5 | SNR = 10 | SNR = 15 | SNR = 20 | SNR = 25 |
|---|---|---|---|---|---|---|
| CRB (km) | ||||||
| CUP (km) | ||||||
| unitary CP (km) | ||||||
| tensor CP (km) | ||||||
| unitary ESPRIT (km) | ||||||
| ESPRIT (km) |
| Algorithm | J = 40 | J = 50 | J = 60 | J = 70 | J = 80 | J = 90 | J = 100 |
|---|---|---|---|---|---|---|---|
| CRB | |||||||
| CUP | |||||||
| unitary CP | |||||||
| tensor CP | |||||||
| unitary ESPRIT | |||||||
| ESPRIT |
| Algorithm | J = 40 | J = 50 | J = 60 | J = 70 | J = 80 | J = 90 | J = 100 |
|---|---|---|---|---|---|---|---|
| CRB (km) | |||||||
| CUP (km) | |||||||
| unitary CP (km) | |||||||
| tensor CP (km) | |||||||
| unitary ESPRIT (km) | |||||||
| ESPRIT (km) |
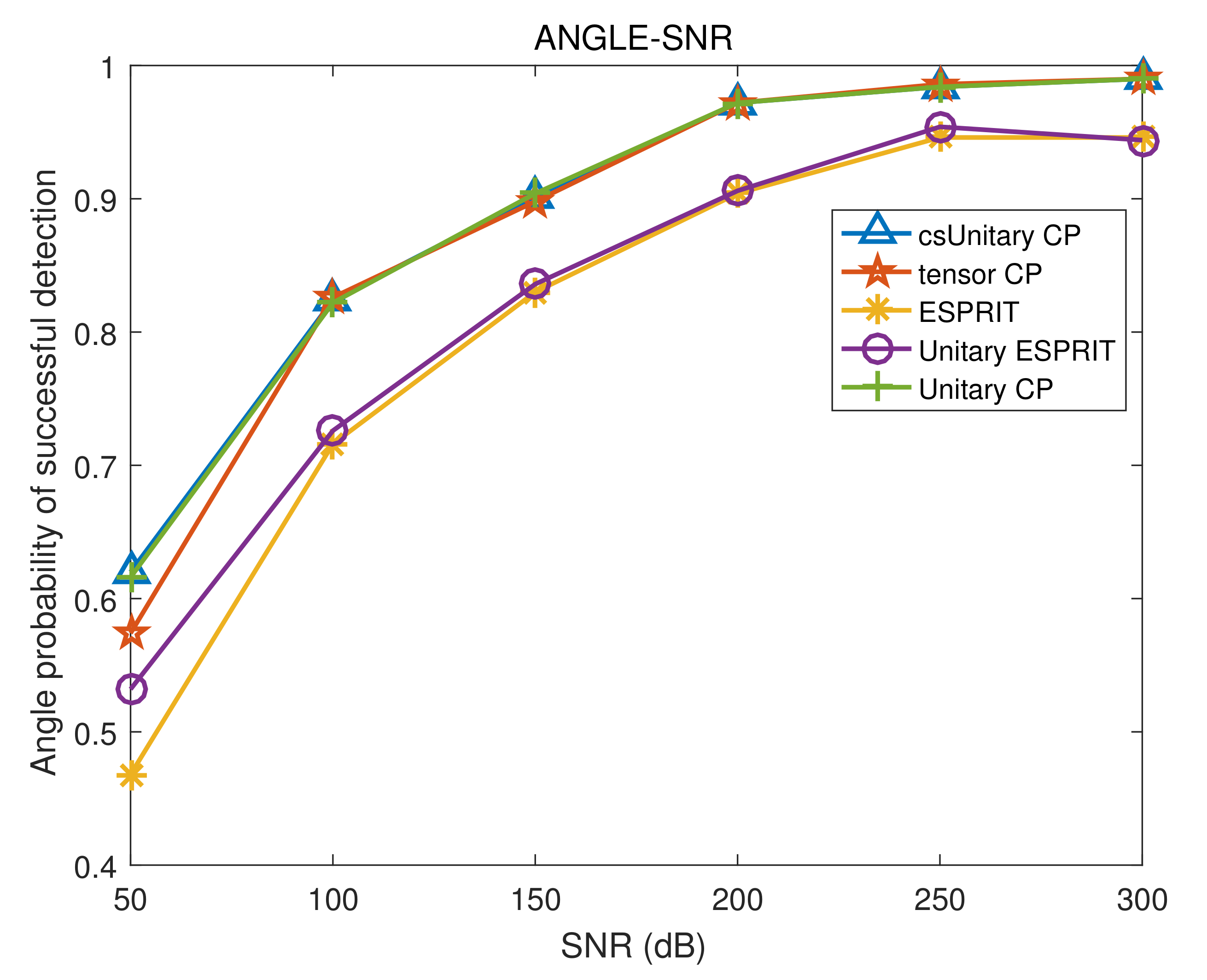
| Algorithm | SNR = 0 | SNR = 5 | SNR = 10 | SNR = 15 | SNR = 20 | SNR = 25 | SNR = 30 |
|---|---|---|---|---|---|---|---|
| CUP | 20.2% | 40.6% | 63.2% | 92.3% | 100% | 100% | 100% |
| unitary CP | 20.6% | 41.0% | 63.4% | 92.4% | 100% | 100% | 100% |
| tensor CP | 18.6% | 34.8% | 59.0% | 90.6% | 99.6% | 100% | 100% |
| unitary ESPRIT | 16.6% | 30.2% | 55.0% | 83.8% | 99.0% | 100% | 100% |
| ESPRIT | 13.8% | 25.0% | 45.6% | 75.4% | 96.8% | 99.8% | 100% |
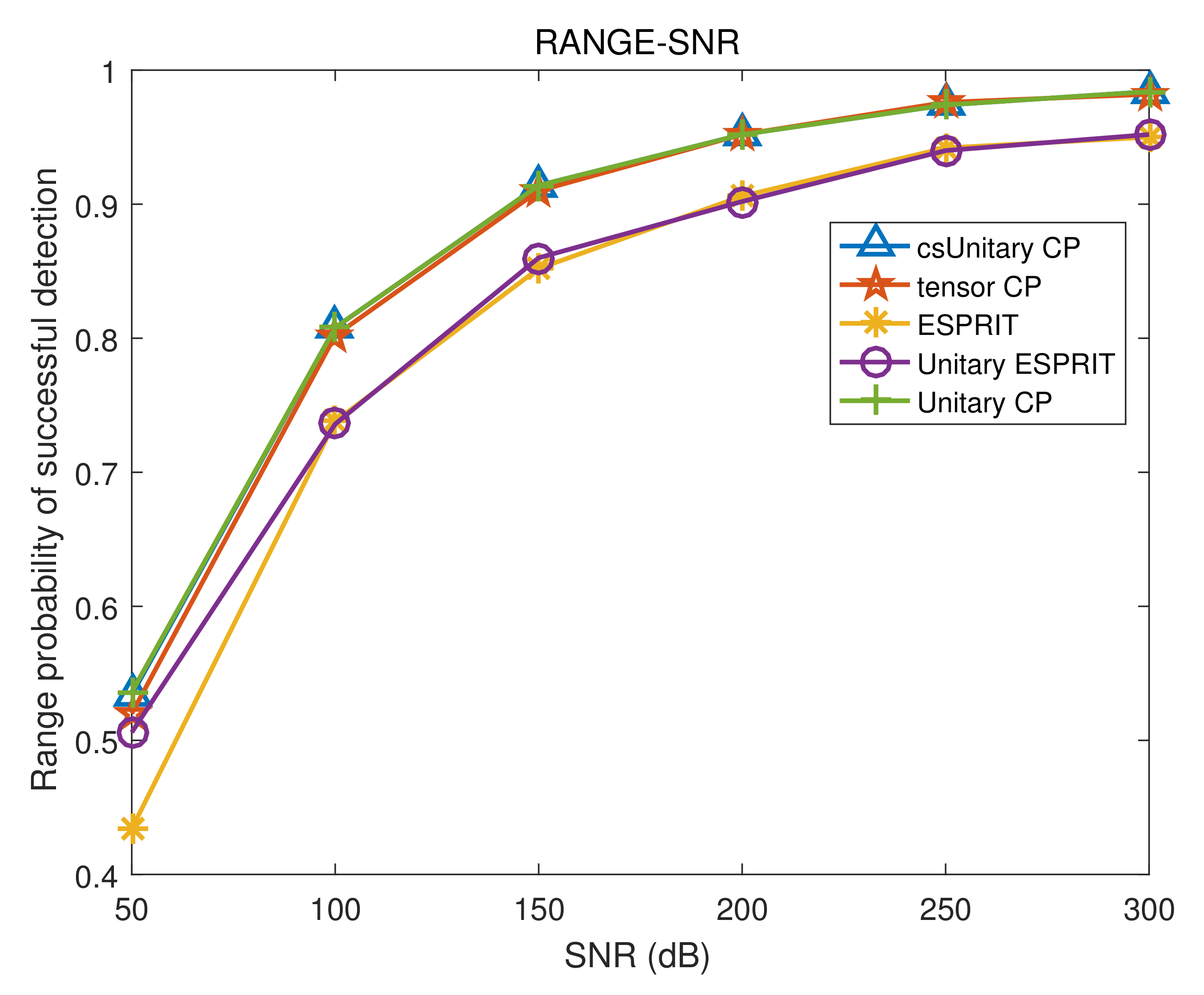
| Algorithm | SNR = 0 | SNR = 5 | SNR = 10 | SNR = 15 | SNR = 20 | SNR = 25 | SNR = 30 |
|---|---|---|---|---|---|---|---|
| CUP | 18.0% | 38.6% | 56.4% | 88.8% | 99.8% | 100% | 100% |
| unitary CP | 17.8% | 38.6% | 56.4% | 88.8% | 99.8% | 100% | 100% |
| tensor CP | 14.2% | 33.0% | 52.8% | 87.6% | 98.8% | 100% | 100% |
| unitary ESPRIT | 15.4% | 33.0% | 49.8% | 83.0% | 99.0% | 100% | 100% |
| ESPRIT | 14.0% | 26.0% | 44.2% | 73.6% | 96.6% | 100% | 100% |
| Algorithm | J = 50 | J = 100 | J = 150 | J = 200 | J = 250 | J = 300 |
|---|---|---|---|---|---|---|
| CUP | 67.8% | 84.2% | 88.2% | 95.6% | 97.6% | 98.8% |
| unitary CP | 67.4% | 84.2% | 88.2% | 95.6% | 97.6% | 98.8% |
| tensor CP | 63.0% | 84.0% | 88.4% | 95.6% | 97.8% | 98.6% |
| unitary ESPRIT | 56.6% | 71.8% | 82.2% | 88.8% | 93.0% | 97.6% |
| ESPRIT | 47.4% | 71.8% | 80.6% | 87.6% | 91.8% | 97.6% |
| Algorithm | J = 50 | J = 100 | J = 150 | J = 200 | J = 250 | J = 300 |
|---|---|---|---|---|---|---|
| CUP | 63.0% | 79.8% | 88.0% | 94.4% | 96.2% | 98.4% |
| unitary CP | 63.0% | 79.8% | 88.0% | 94.4% | 96.2% | 98.4% |
| tensor CP | 60.0% | 80.0% | 87.4% | 95.0% | 96.0% | 98.4% |
| unitary ESPRIT | 54.8% | 72.8% | 82.0% | 87.8% | 92.8% | 96.4% |
| ESPRIT | 49.4% | 72.6% | 80.2% | 87.6% | 92.8% | 96.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, X.; Shi, J.; Lan, X. Joint Angle and Range Estimation in Monostatic FDA-MIMO Radar via Compressed Unitary PARAFAC. Remote Sens. 2022, 14, 1398. https://doi.org/10.3390/rs14061398
Wang W, Wang X, Shi J, Lan X. Joint Angle and Range Estimation in Monostatic FDA-MIMO Radar via Compressed Unitary PARAFAC. Remote Sensing. 2022; 14(6):1398. https://doi.org/10.3390/rs14061398
Chicago/Turabian StyleWang, Wenshuai, Xianpeng Wang, Jinmei Shi, and Xiang Lan. 2022. "Joint Angle and Range Estimation in Monostatic FDA-MIMO Radar via Compressed Unitary PARAFAC" Remote Sensing 14, no. 6: 1398. https://doi.org/10.3390/rs14061398
APA StyleWang, W., Wang, X., Shi, J., & Lan, X. (2022). Joint Angle and Range Estimation in Monostatic FDA-MIMO Radar via Compressed Unitary PARAFAC. Remote Sensing, 14(6), 1398. https://doi.org/10.3390/rs14061398






