Distributed Feedback Interband Cascade Laser Based Laser Heterodyne Radiometer for Column Density of HDO and CH4 Measurements at Dunhuang, Northwest of China
Abstract
:1. Introduction
2. Materials and Methods
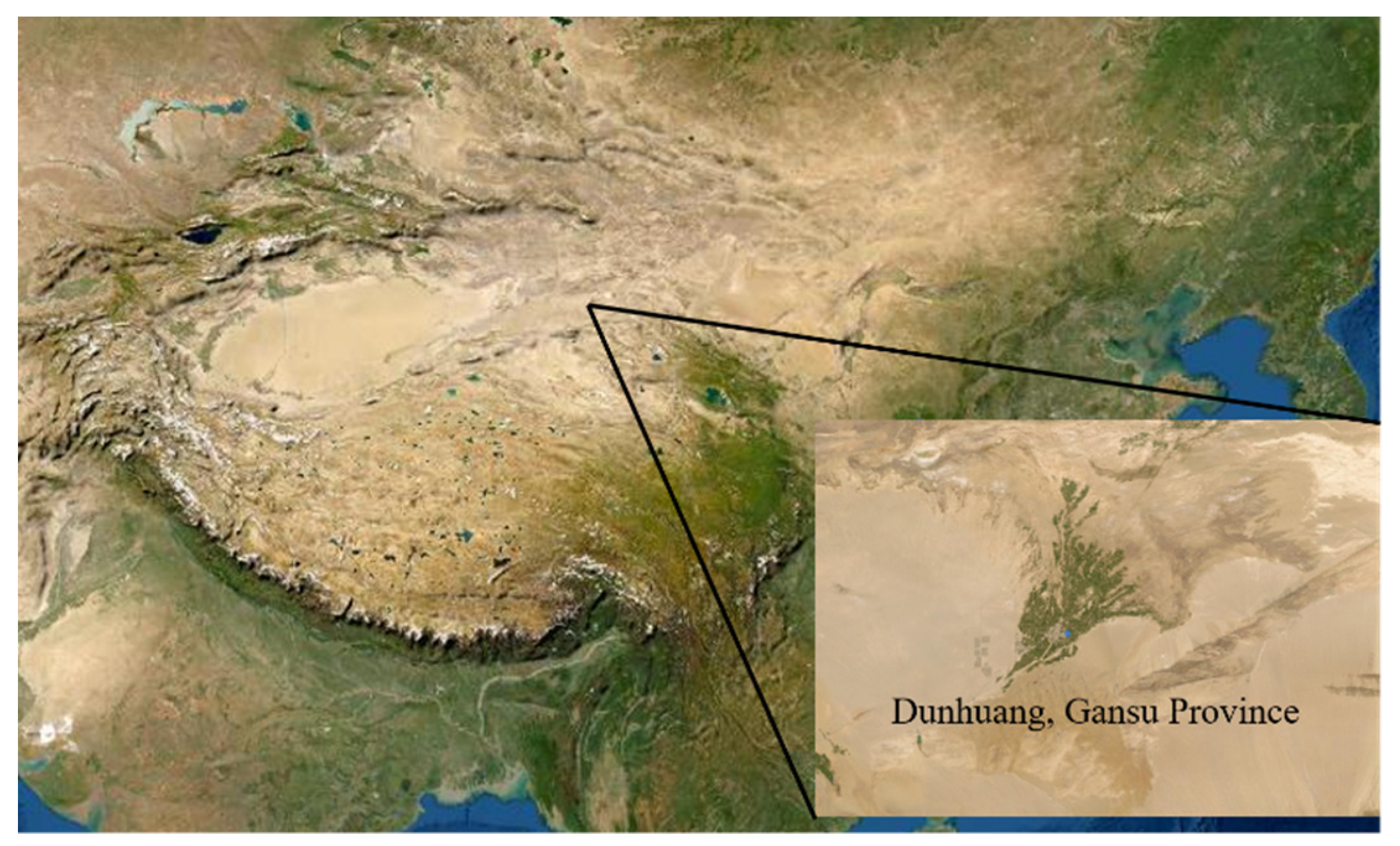
2.1. Measurement Site
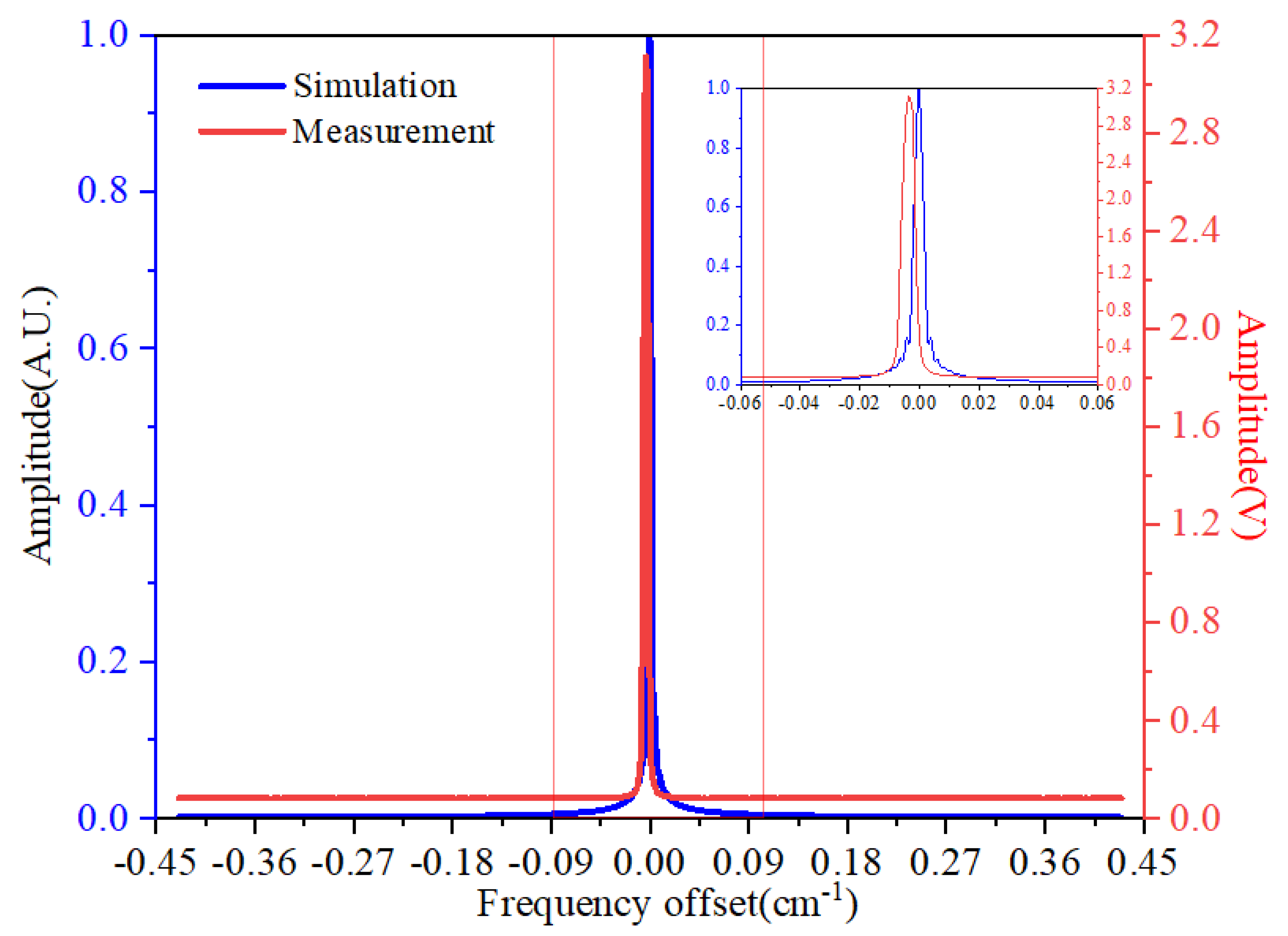
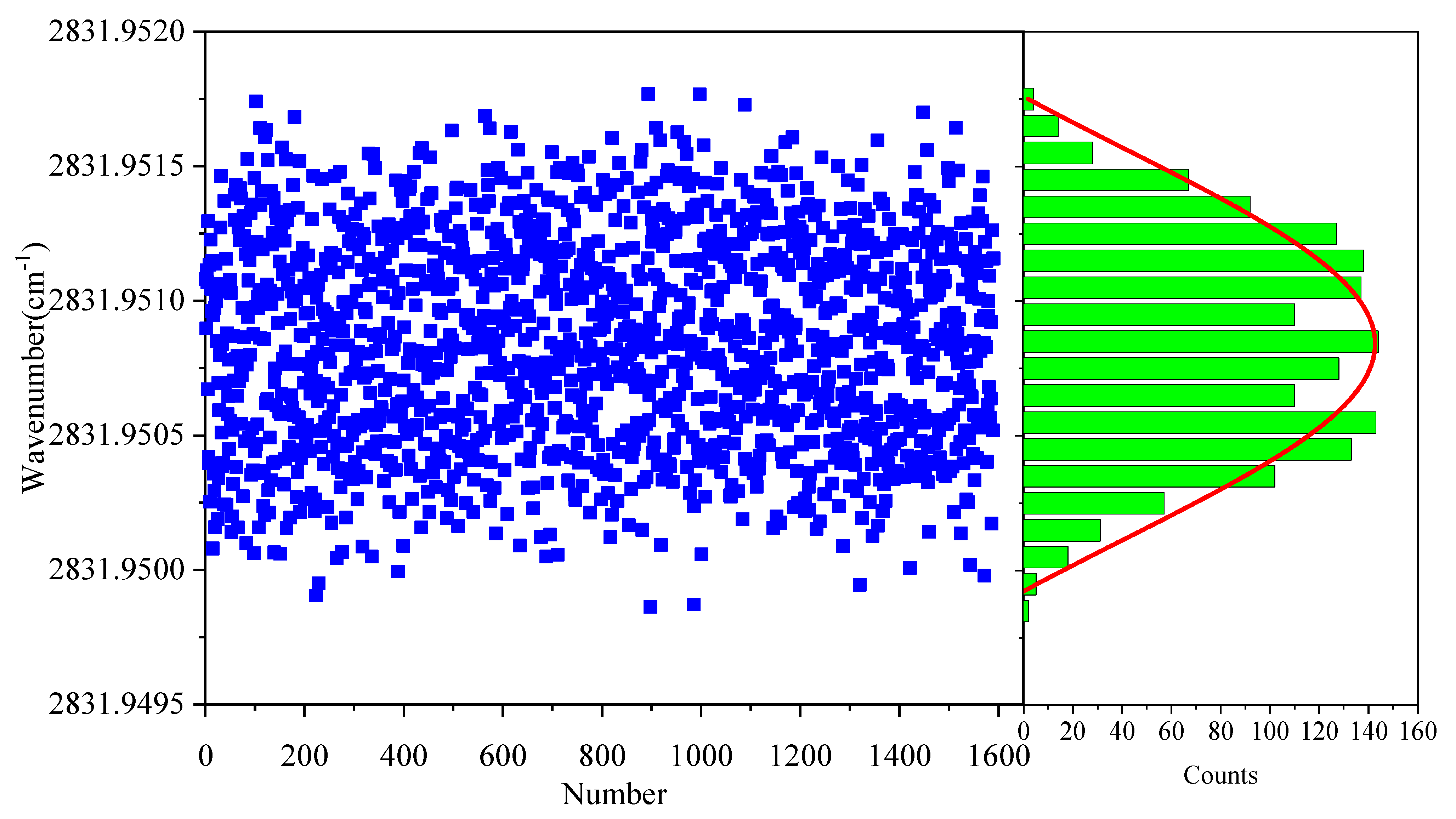
2.2. Laser Heterodyne Radiometer
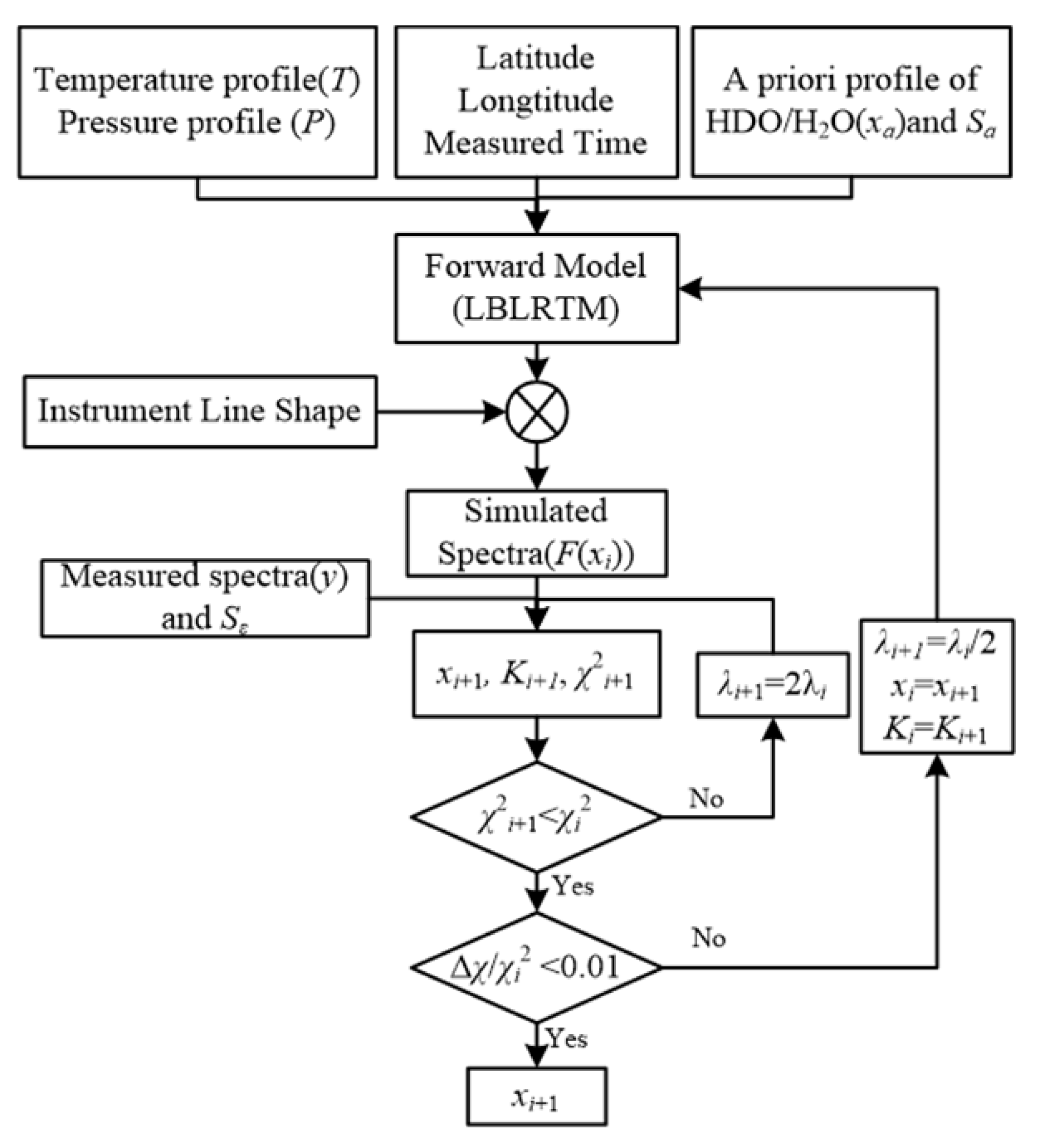
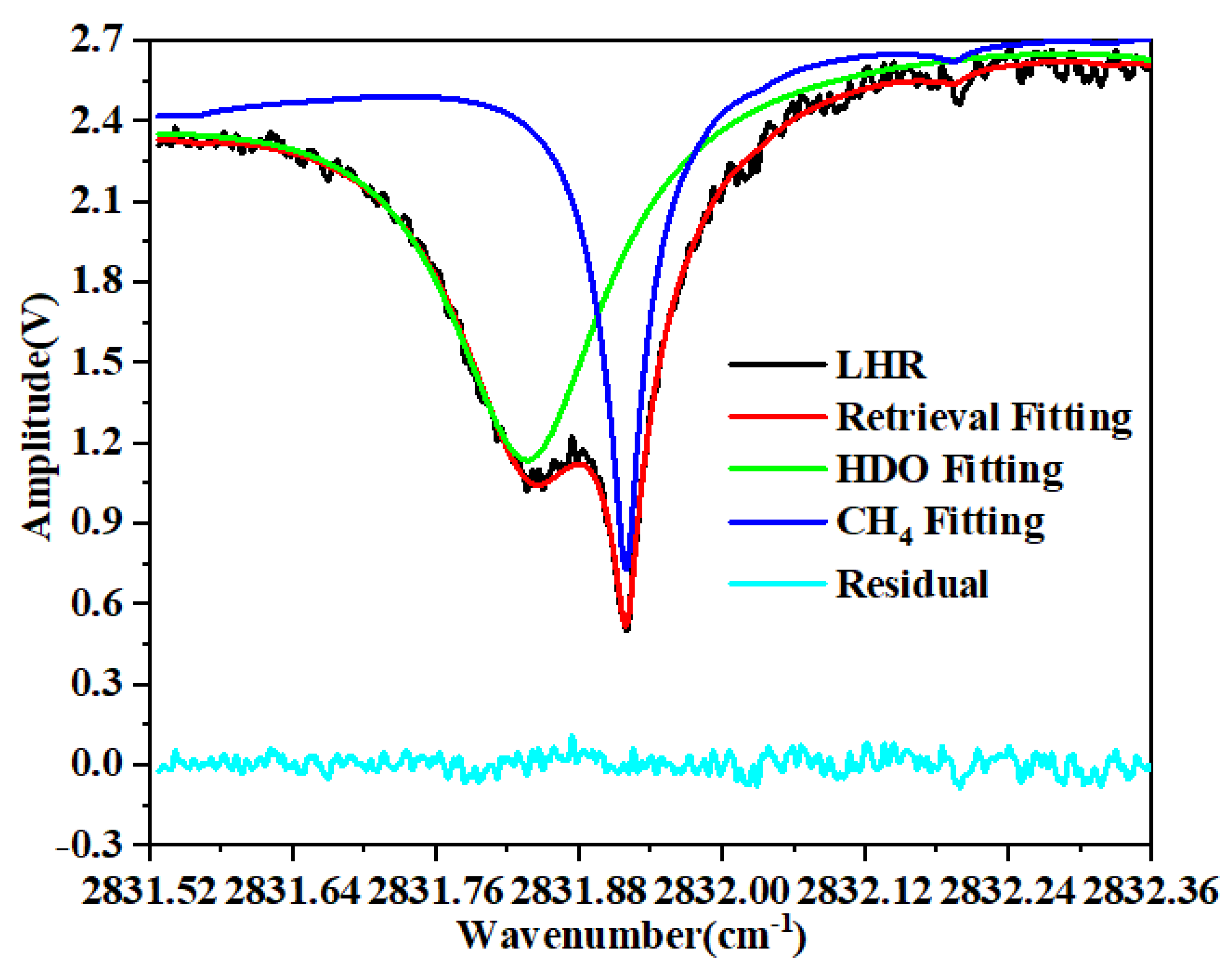
2.3. Retrieval Method
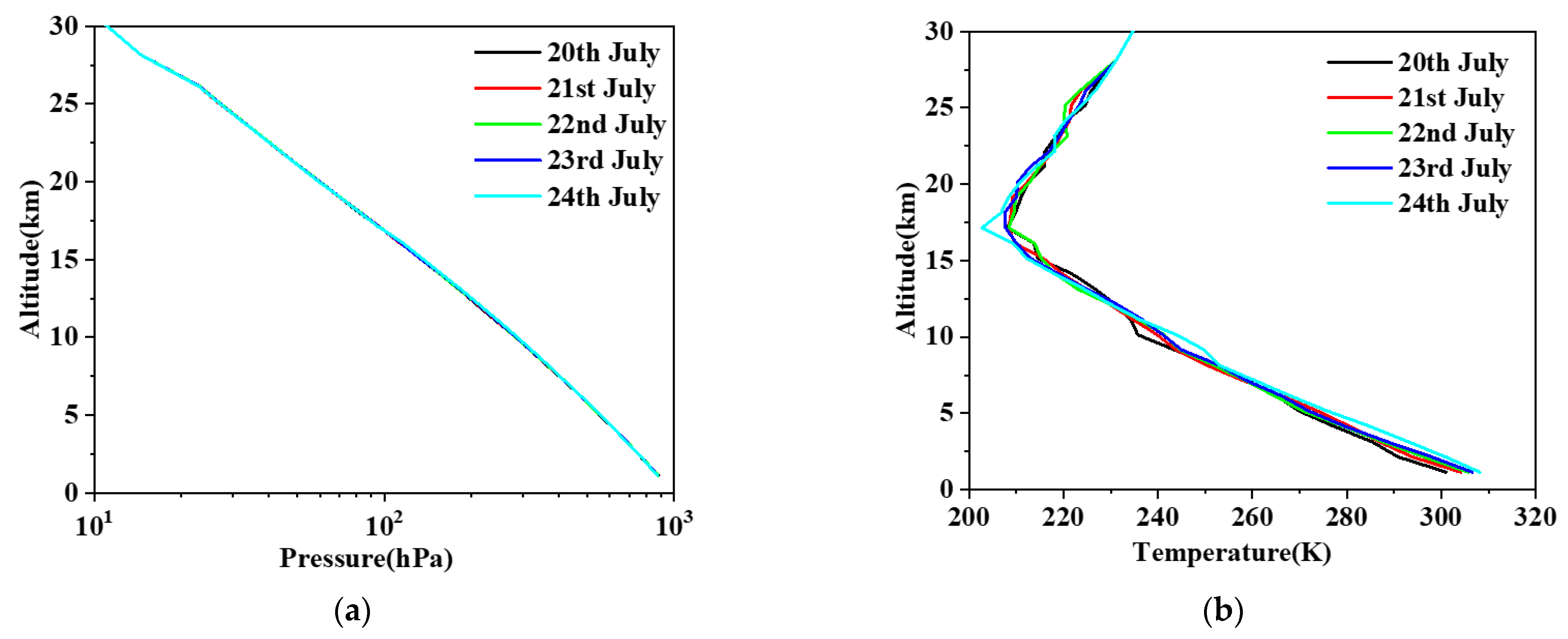
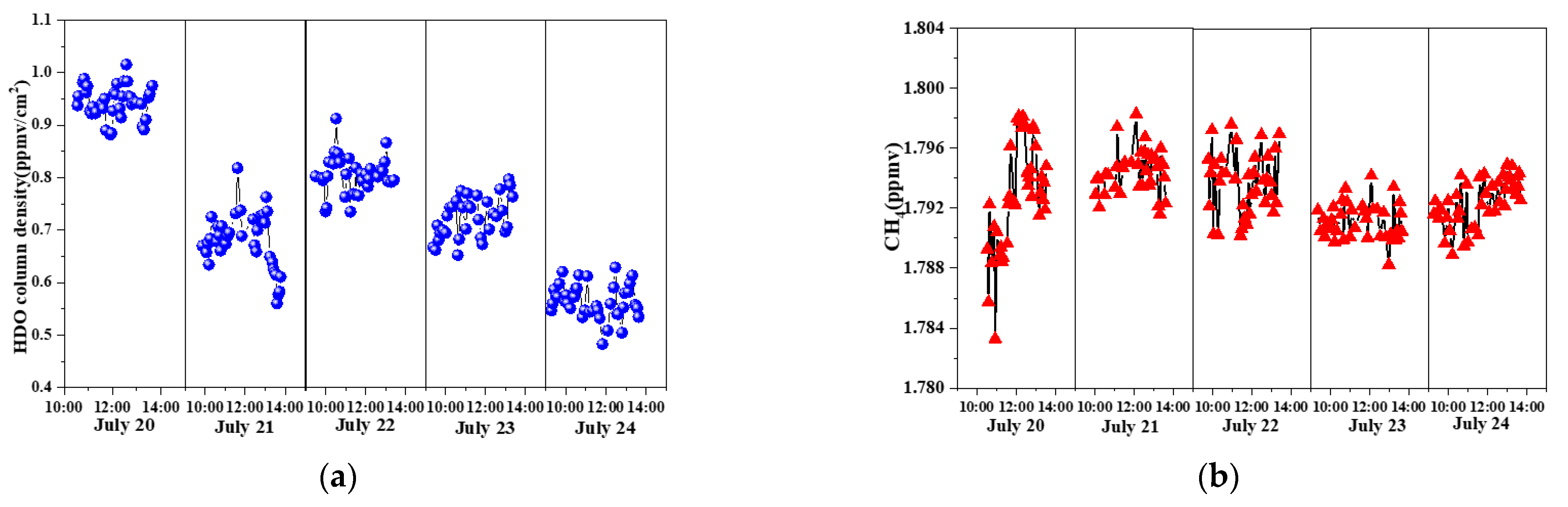
3. Results
4. Discussion
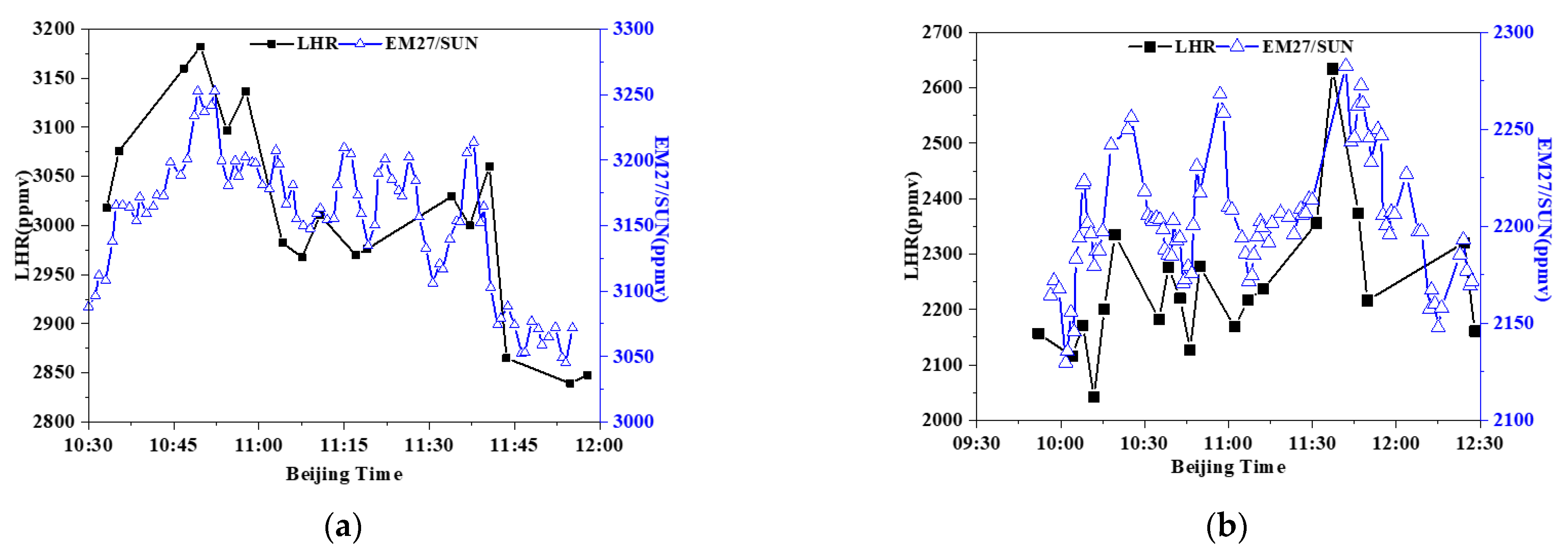
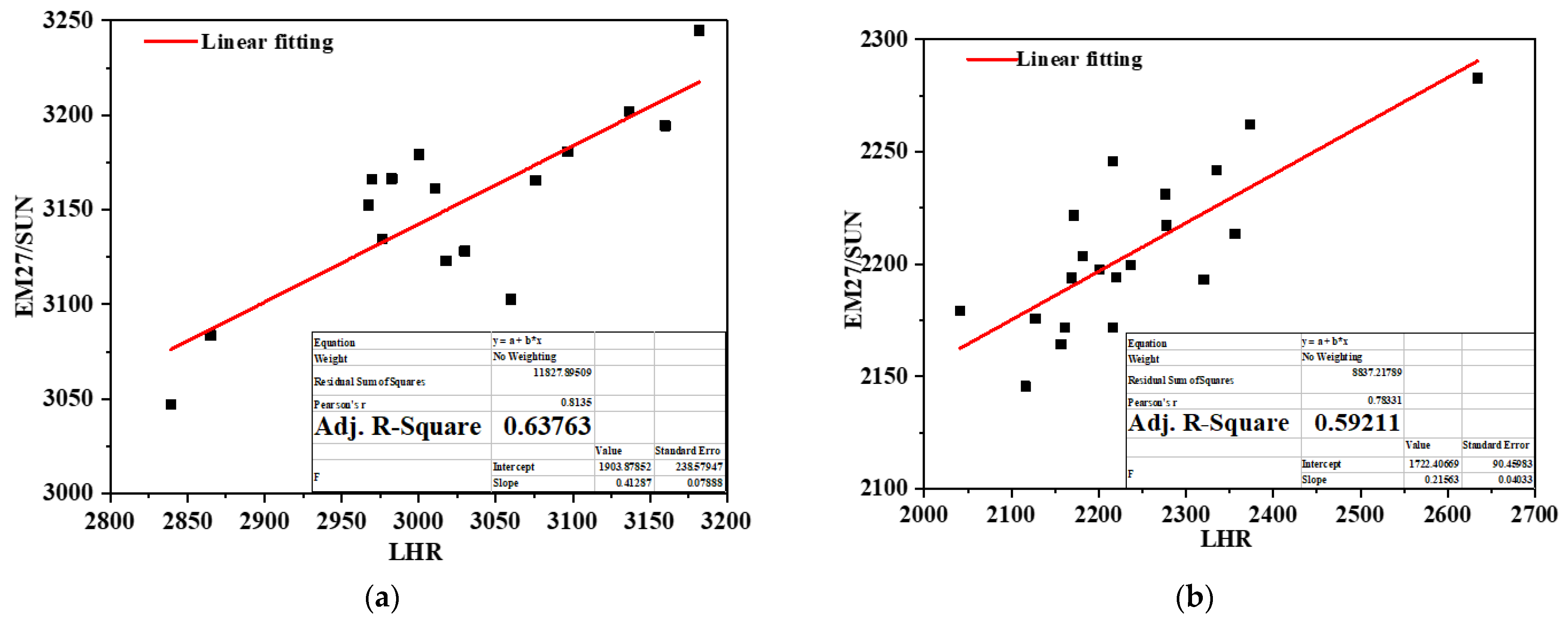
4.1. Comparison of LHR and FTIR
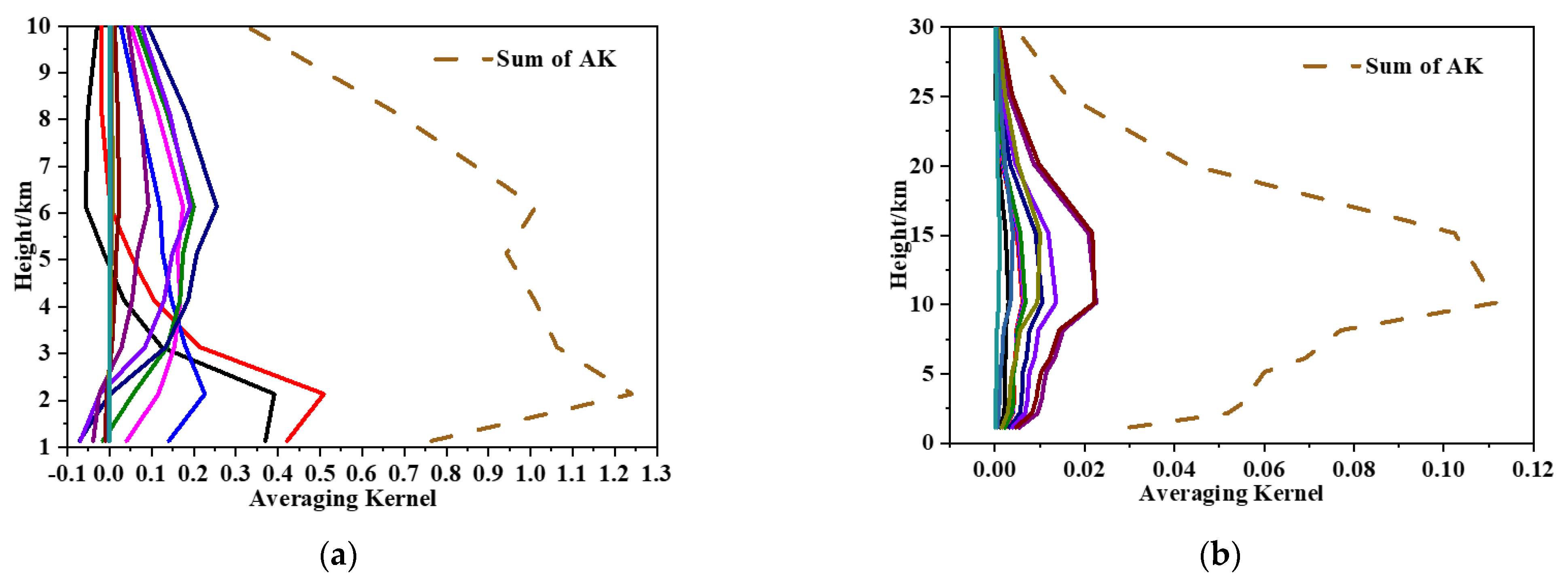
4.2. Analysis of the Jacobian and Averaging Kernel
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheng, F.X.; Mao, J.T.; Li, J.G.; Ge, Z.; Zhang, A.C.; Sang, J.G.; Pan, N.; Zhang, H. Radiation processes in the ground and atmosphere. In Atmospheric Physics, 2nd ed.; Peking University Press: Beijing, China, 2013; Volume 2, pp. 6–25. [Google Scholar]
- Held, I.M.; Soden, B.J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef] [Green Version]
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC). Comput. Geom. 2007, 18, 95–123. [Google Scholar] [CrossRef] [Green Version]
- Michel, A.P.M.; Wang, W.E.; Wang, L.; Nikodem, M.; Tsai, T.; Baeck, M.L.; Smith, J.; Wysocki, G. A Quantum Cascade Laser Spectrometer for Measurement of Water Vapor Isotopes in the Urban Environment. In CLEO: Applications and Technology; Optical Society of America: Washington, DC, USA, 2012. [Google Scholar]
- Chang, A.; Visser, A.; Oerter, E.; Bond, T. Detection of O18 and D Isotopes in Water Vapor using a Fiber-Coupled Tunable Diode Laser Absorption Spectroscopy Multi-Pass Cell. In CLEO: QELS_Fundamental; Optical Society of America: Washington, DC, USA, 2018. [Google Scholar]
- Liu, J.; Zhao, G.; Ma, W.; Axner, O. Development of a Doppler-bradened NICE-OHMS system for trace gas detection based on a single sideband phase modulator. Opt. Express 2021, 29, 42411–42419. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, G.; Liu, J.; Zhou, Y.; Yan, X.; Li, Z.; Ma, W.; Jia, S. Fiber pigtailed DFB laser-based optical feedback cavity enhanced absorption spectroscopy with a fiber-coupled EOM for phase correction. Opt. Express 2022, 30, 6332–6340. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, Y.; Qiao, S.; Lang, Z.; Liu, X. H-shaped acoustic micro-resonator-based quartz-enhaced photoacoustic spectroscopy. Opt. Lett. 2022, 47, 601–604. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, Y.; Qiao, S.; Lang, Z.; Liu, X.; He, Y.; Spagnolo, V. Quartz tuning forks resonance frequency matching for laser spectroscopy sensing. Photoacoustics 2022, 25, 1003291–1003297. [Google Scholar] [CrossRef]
- Qiao, S.; Ma, Y.; He, Y.; Patimisco, P.; Sampaolo, A.; Spagnolo, V. Ppt level carbon monoxide detection based on light-induced thermoelastic spectroscopy exploring custom quartz tuning forks and a mid-infrared QCL. Opt. Express 2021, 29, 25100–25108. [Google Scholar] [CrossRef]
- Liu, X.; Qiao, S.; Ma, Y. Highly sensitive methane detection based on light-induced thermoelastic spectroscopy with a 2.33 µm diode laser and adaptive Savitzky-Golay filtering. Opt. Express 2022, 30, 1304–1313. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Y. Sensitive carbon monoxide detection based on light-induced thermoelastic spectroscopy with a fiber-coupled multipass cell. Chin. Opt. Lett. 2022, 20, 0312011–0312015. [Google Scholar] [CrossRef]
- Toptygin, A.Y.; Gribanov, K.G.; Zakharov, V.I.; Kasai, Y.; Kagawa, A.; Murayama, Y.; Imasu, R.; Schmidt, G.; Hoffmann, G.W.; Jouzel, J. Method and results of retrieval of HDO/H2O in atmosphere from IMG/ADEOS and FTIR data. In Proceedings of the 15th Symposium on High-Resolution Molecular Spectroscopy, Nizhny Novgorod, Russia, 12 December 2006; Volume 6580, p. 65800X. [Google Scholar] [CrossRef]
- Worden, J.; Noone, D.; Galewsky, J.; Bailey, A.; Bowman, K.; Brown, D.; Hurley, J.; Kulawik, S.; Lee, J.; Strong, M. Estimate of bias in Aura TES HDO/H2O profiles from comparison of TES and in situ HDO/H2O measurements at the Mauna Loa observatory. Atmos. Chem. Phys. 2011, 11, 4491–4503. [Google Scholar] [CrossRef] [Green Version]
- Lacour, J.L.; Clarisse, L.; Worden, J.; Schneider, M.; Barthlott, S.; Hase, F.; Risi, C.; Clerbaux, C.; Hurtmans, D.; Coheur, P.-F. Cross-validation of IASI/MetOp derived tropospheric δD with TES and ground-based FTIR observations. Atmos. Chem. Phys. 2015, 8, 1447–1466. [Google Scholar] [CrossRef] [Green Version]
- Scheepmaker, R.A.; Frankenberg, C.; Galli, A.; Butz, A.; Schrijver, H.; Deutscher, N.M.; Wunch, D.; Warneke, T.; Fally, S.; Aben, I. Improved water vapour spectroscopy in the 4174–4300 cm−1 region and its impact on SCIAMACHY HDO/H2O measurements. Atmos. Meas. Tech. Discuss. 2013, 5, 8539–8578. [Google Scholar] [CrossRef]
- Boesch, H.; Deutscher, N.M.; Warneke, T.; Byckling, K.; Cogan, A.J.; Griffith, D.W.T.; Notholt, J.; Parker, R.J.; Wang, Z. HDO/H2O ratio retrievals from GOSAT. Atmos. Meas. Tech. 2013, 6, 599–612. [Google Scholar] [CrossRef] [Green Version]
- Frankenberg, C.; Wunch, D.; Toon, G.; Risi, C.; Scheepmaker, R.; Lee, J.-E.; Wennberg, P.; Worden, J. Water vapor isotopologue retrievals from high-resolution GOSAT shortwave infrared spectra. Atmos. Meas. Tech. 2013, 6, 263–274. [Google Scholar] [CrossRef] [Green Version]
- Herman, R.L.; Worden, J.; Noone, D.; Henze, D.; Bowman, K.; Pereira, K.C.; Payne, V.H.; Kulawik, S.S.; Fu, D.J. Comparison of Optimal Estimation HDO/H2O Retrievals from AIRS with ORACLES measurements. Atmos. Meas. Tech. Discuss. 2019. [Google Scholar] [CrossRef]
- Schneider, A.; Borsdorff, T.; De Brugh, J.A.; Aemisegger, F.; Feist, D.G.; Kivi, R.; Hase, F.; Schneider, M.; Landgraf, J. First data set of H2O/HDO columns from the Tropospheric Monitoring Instrument (TROPOMI). Atmos. Meas. Tech. 2020, 13, 85–100. [Google Scholar] [CrossRef] [Green Version]
- Fukunishi, H.; Okano, S.; Taguchi, M.; Ohnuma, T. Laser heterodyne spectrometer using a liquid nitrogen cooled tunable diode laser for remote measurements of atmospheric O3 and N2O. Appl. Opt. 1990, 29, 2722–2728. [Google Scholar] [CrossRef]
- Taguchi, M.; Okano, S.; Fukunishi, H.; Sasano, Y. Comparison of ozone profiles from ground-based laser heterodyne spectrometer and ozonesonde measurements. Geo. Res. Lett. 1990, 17, 2349–2352. [Google Scholar] [CrossRef]
- Weidmann, D.; Reburn, W.J.; Smith, K.M. Retrieval of atmospheric ozone profiles from an infrared quantum cascade laser heterodyne radiometer: Results and analysis. Appl. Opt. 2007, 46, 7162–7171. [Google Scholar] [CrossRef]
- Tsai, T.R.; Rose, R.A.; Weidmann, D.; Wysocki, G. Atmospheric vertical profiles of O3, N2O, CH4, CCl2F2, and H2O retrieved from external-cavity quantum-cascade laser heterodyne radiometer measurements. Appl. Opt. 2012, 51, 8779–8792. [Google Scholar] [CrossRef] [Green Version]
- Melroy, H.R.; Wilson, E.L.; Clarke, G.B.; Ott, L.E.; Mao, J.; Ramanathan, A.K.; McLinden, M.L. Autonomous field measurements of CO2 in the atmospheric column with the miniaturized laser heterodyne radiometer (Mini-LHR). Appl. Phys. B 2015, 120, 609–615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Protopopov, V.V. Principles of optical heterodyning. In Laser Heterodyning; Rhodes, W.T., Ed.; Springer: Berlin, Germany, 2009; Volume 1, pp. 1–47. [Google Scholar]
- Tan, T.; Cao, Z.S.; Wang, G.S.; Wang, L.; Liu, K.; Huang, Y.B.; Chen, W.D.; Gao, X.M. Study on the technology of the 4.4 μm mid-infrared laser heterodyne spectrum. Spectrosc. Spect. Anal. 2015, 35, 60–63. [Google Scholar] [CrossRef]
- Lu, X.J.; Cao, Z.S.; Huang, Y.B.; Gao, X.M.; Rao, R.Z. Laser heterodyne spectrometer for solar spectrum measurement in the 3.53 μm region. Opt. Precis. Eng. 2019, 26, 16–24. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, G.S.; Tan, T.; Zhu, G.; Sun, C.Y.; Cao, Z.S.; Chen, W.D.; Gao, X.M. Mid-infrared laser heterodyne radiometer (LHR) based on a 3.53 μm room-temperature interband cascade laser. Opt. Express 2019, 27, 9610–9619. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding, 2nd ed.; World Scientific: London, UK, 2004; Volume 4–5, pp. 65–100. [Google Scholar]
- Hase, F.; Hannigan, J.W.; Coffey, M.T.; Goldman, A.; Pfner, M.H.; Jones, N.B.; Rinsland, C.P.; Wood, S.W. Intercomparison of retrieval codes used for the analysis of high-resolution, ground-based FTIR measurements. J. Quant. Spectrosc. Radiat. Transf. 2004, 87, 25–52. [Google Scholar] [CrossRef]





| Parameter | Value | Unit |
|---|---|---|
| Line-width of LO | <10 | MHz |
| Frequency coverage | 2831.5~2832.4 | cm−1 |
| Scanning period | 12 | s |
| Radiofilter band | 8~35 | MHz |
| Integral time | 10 | ms |
| Target species | HDO, CH4 | -- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Huang, Y.; Wu, P.; Liu, D.; Ma, H.; Wang, G.; Cao, Z. Distributed Feedback Interband Cascade Laser Based Laser Heterodyne Radiometer for Column Density of HDO and CH4 Measurements at Dunhuang, Northwest of China. Remote Sens. 2022, 14, 1489. https://doi.org/10.3390/rs14061489
Lu X, Huang Y, Wu P, Liu D, Ma H, Wang G, Cao Z. Distributed Feedback Interband Cascade Laser Based Laser Heterodyne Radiometer for Column Density of HDO and CH4 Measurements at Dunhuang, Northwest of China. Remote Sensing. 2022; 14(6):1489. https://doi.org/10.3390/rs14061489
Chicago/Turabian StyleLu, Xingji, Yinbo Huang, Pengfei Wu, Dandan Liu, Hongliang Ma, Guishi Wang, and Zhensong Cao. 2022. "Distributed Feedback Interband Cascade Laser Based Laser Heterodyne Radiometer for Column Density of HDO and CH4 Measurements at Dunhuang, Northwest of China" Remote Sensing 14, no. 6: 1489. https://doi.org/10.3390/rs14061489





