Quantifying Post-Fire Changes in the Aboveground Biomass of an Amazonian Forest Based on Field and Remote Sensing Data
Abstract
:1. Introduction
2. Materials and Methods
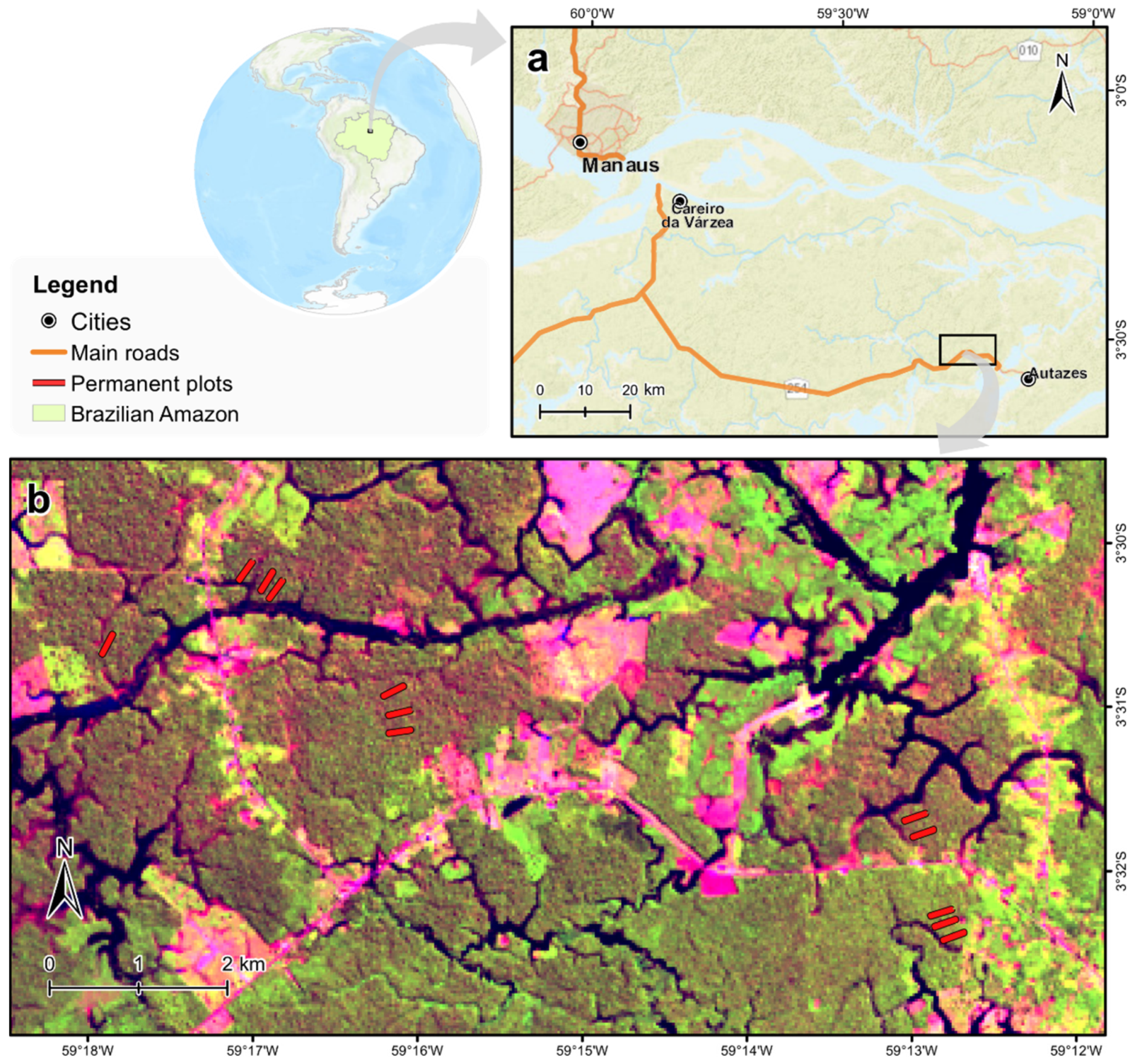
2.1. Study Area
2.2. Data
2.2.1. Field Dataset
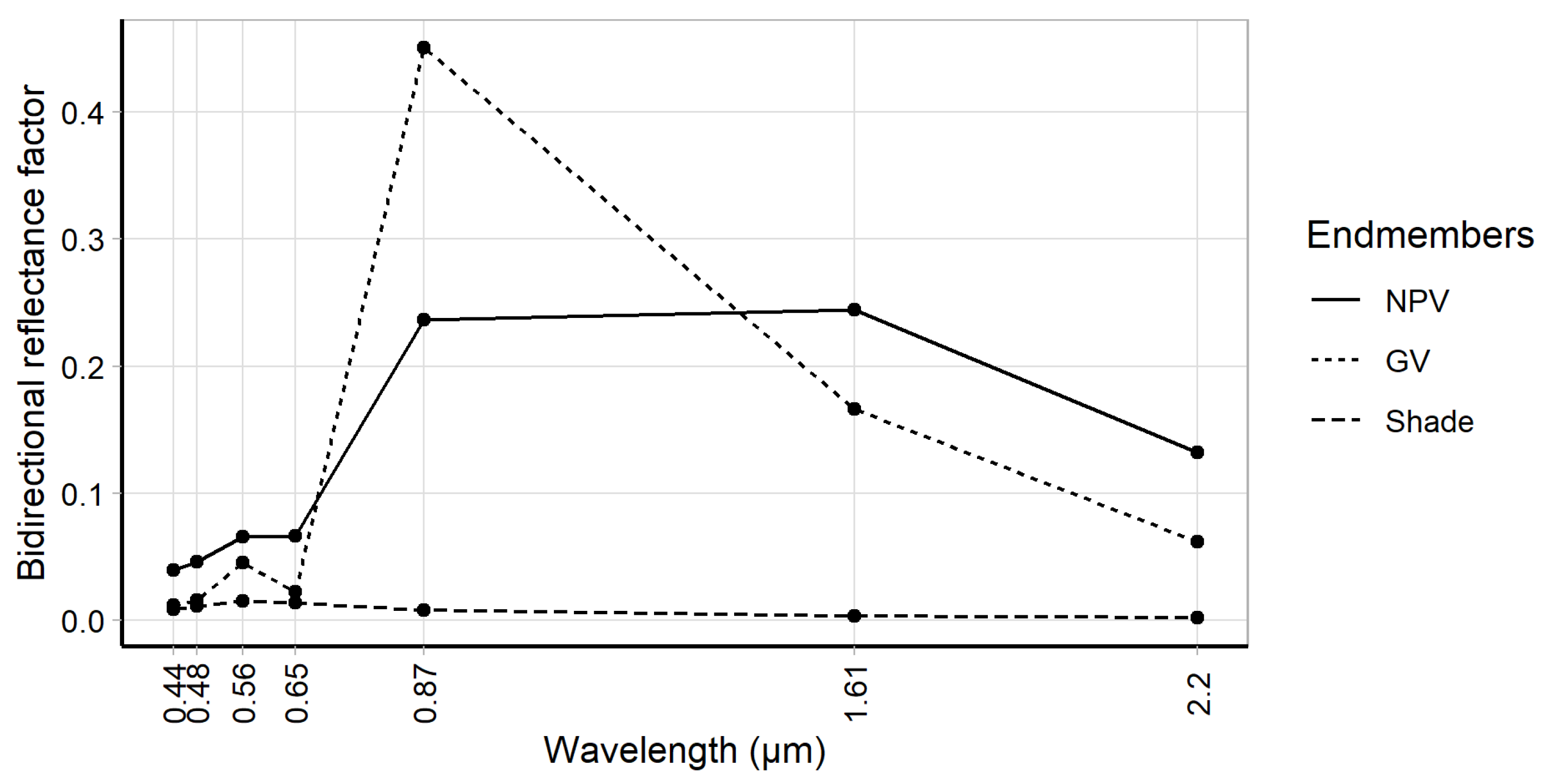
2.2.2. Remote Sensing Dataset
2.3. Data Analyses
3. Results
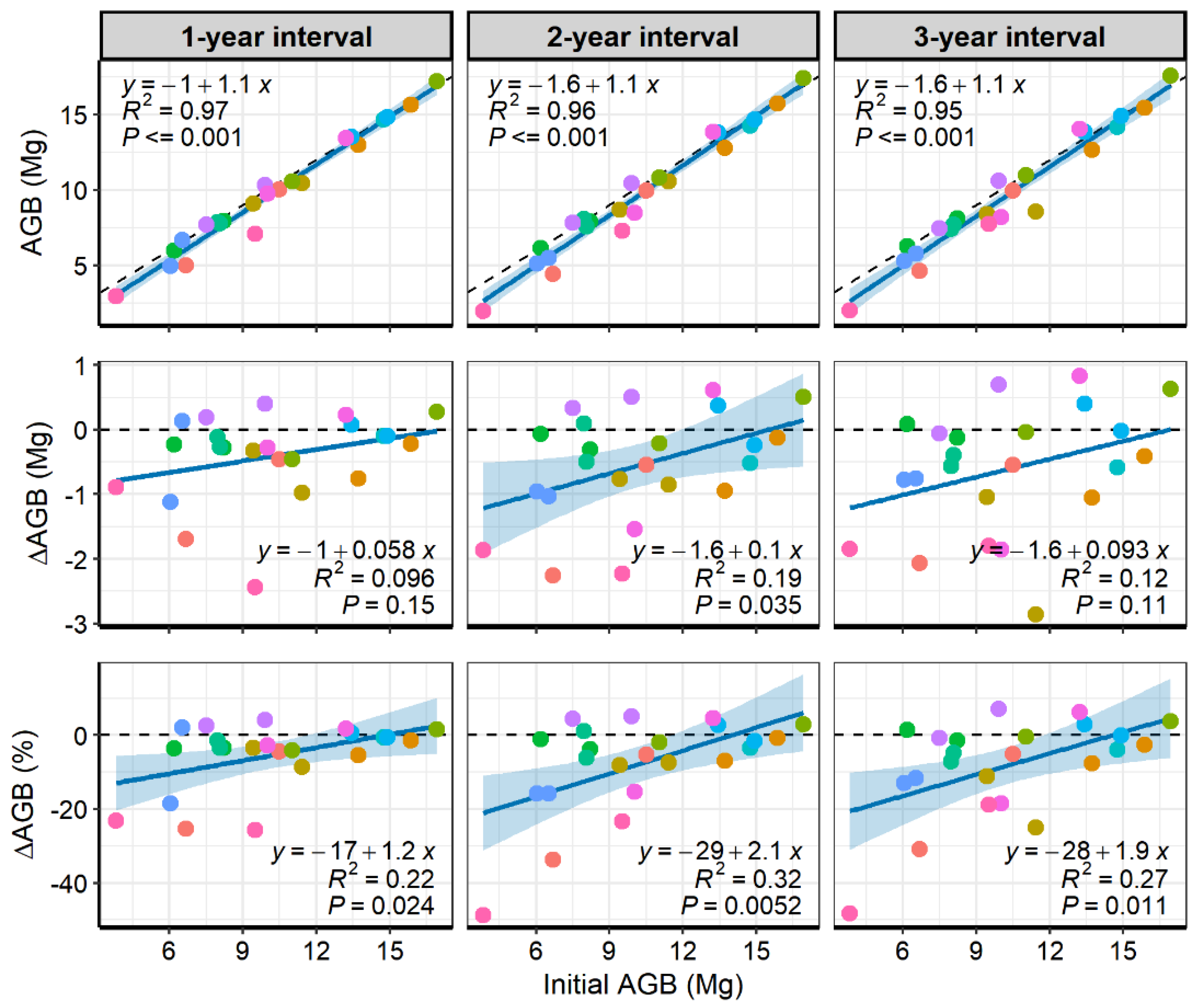
3.1. Relationships between Initial and Post-Fire Biomass Stocks
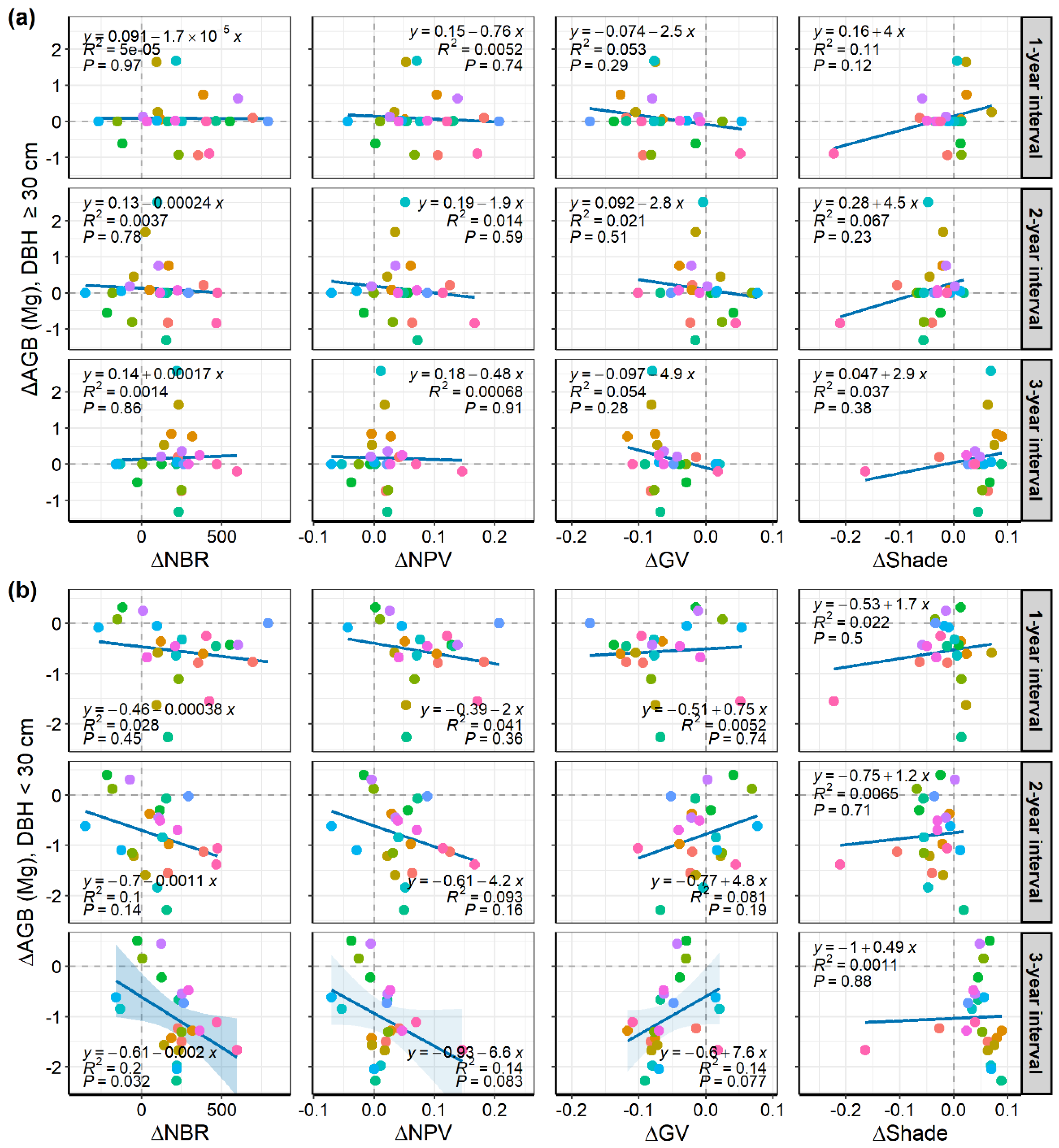
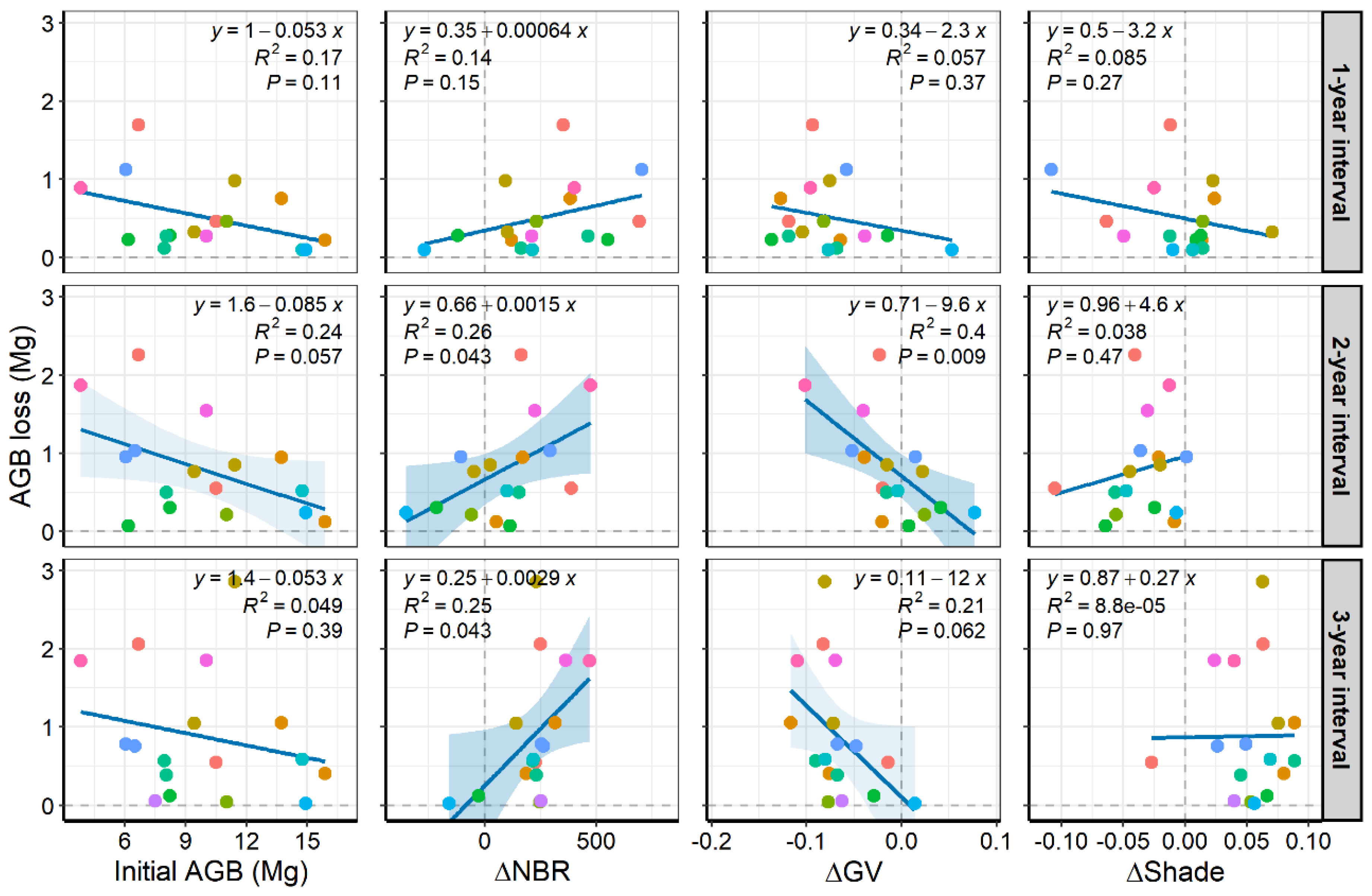
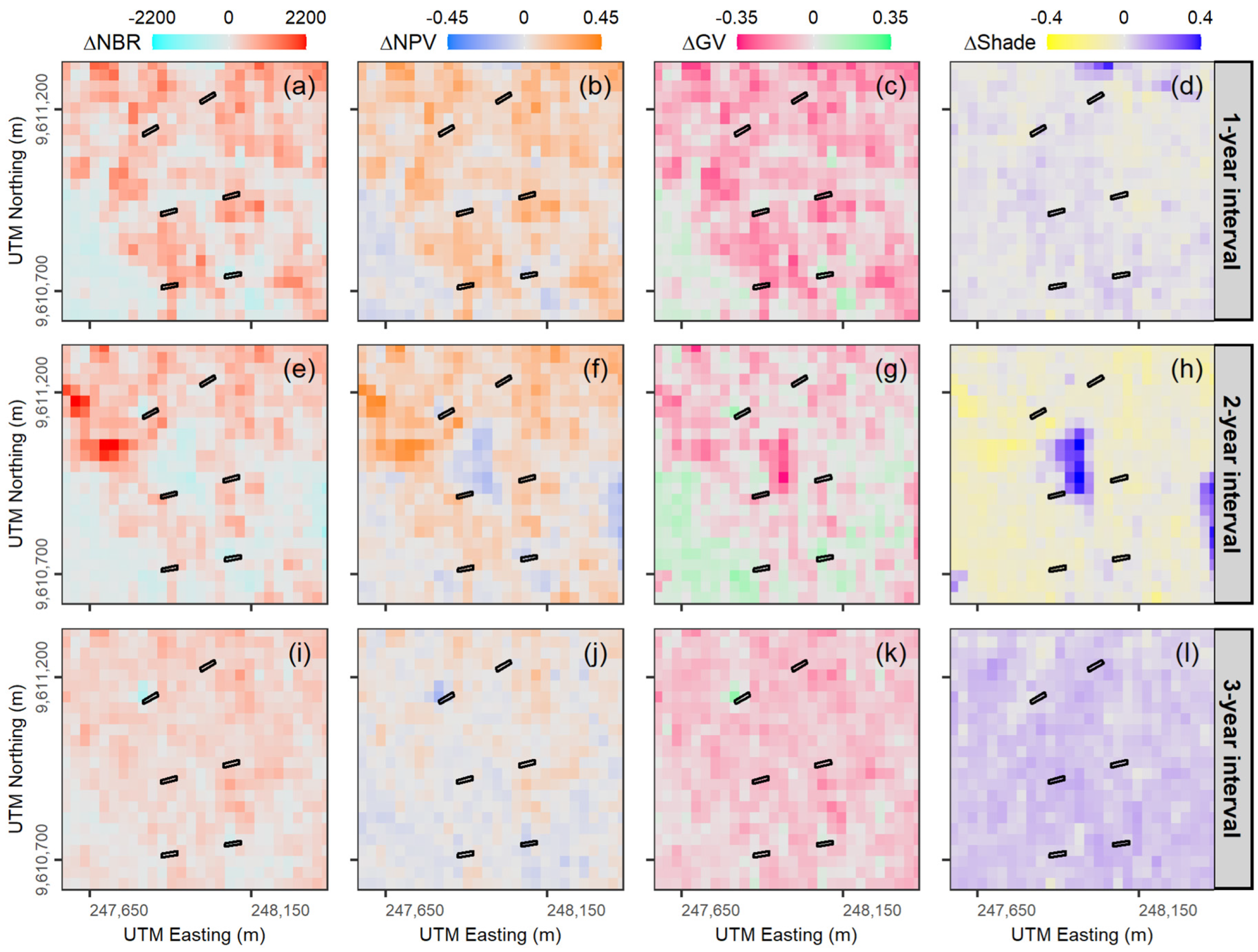
3.2. Relationships between Spectral Indices and Structural Changes
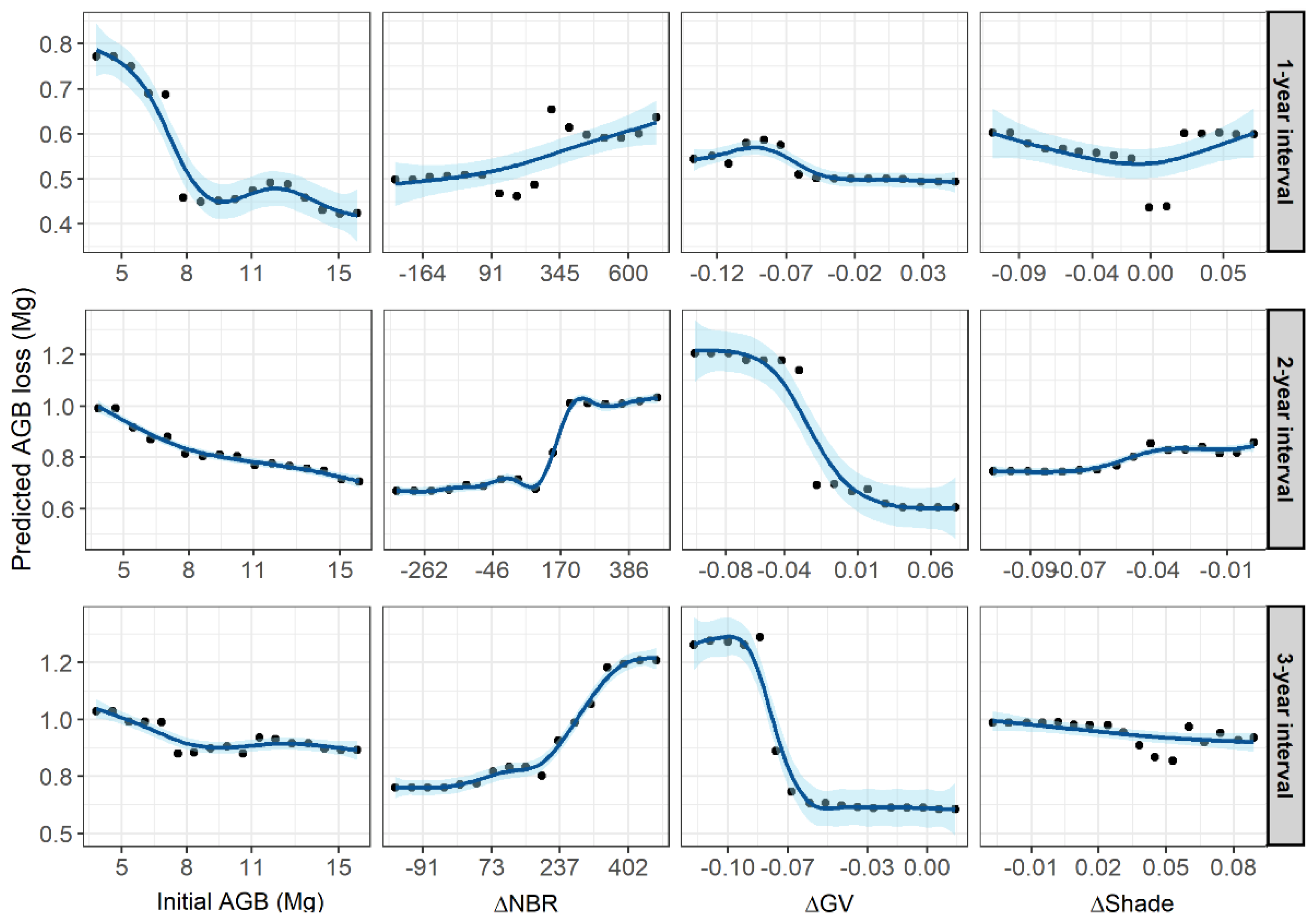
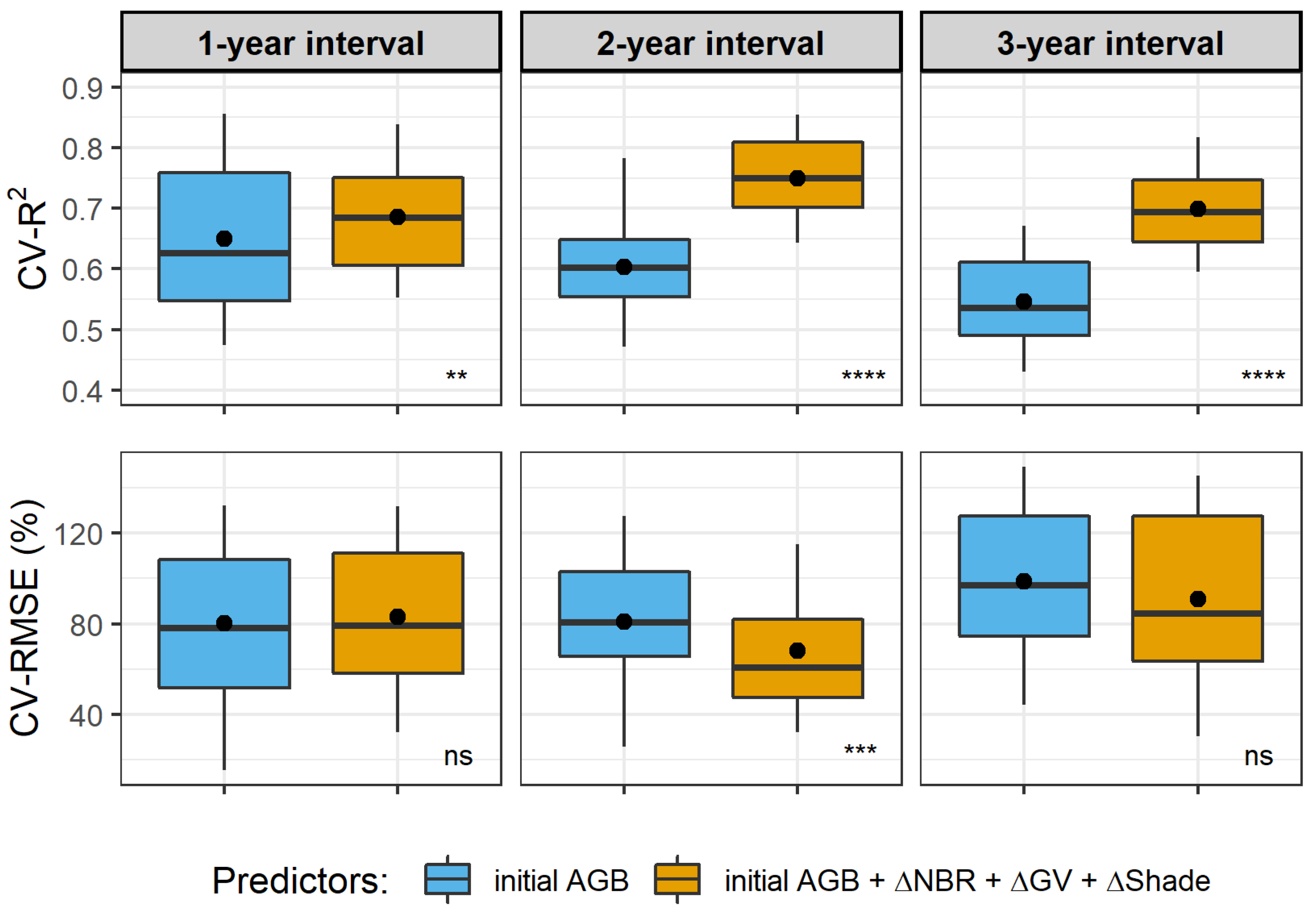
3.3. Biomass Loss Modelling
4. Discussion
4.1. Post-Fire Biomass Losses Accounting for Spatial Variability
4.2. Spectral Indices Are Sensitive to Accumulated Tree Mortality
4.3. Spectral Indices’ Changes for Predicting Biomass Losses
4.4. Limitations of This Study
4.5. Implications for Future Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Tree State | Size Class (DBH) | Mean BA (± s.d.) (m2 ha−1) | p-Value | ||
|---|---|---|---|---|---|
| Burned | Unburned | Welch’s t Test | Mann-Whitney U Test | ||
| dead | 10− | 0.49 (±0.26) | 0.26 (±0.21) | 0.181 ns | 0.053 m |
| 20− | 0.32 (±0.31) | 0.33 (±0.28) | - | 0.888 ns | |
| 30− | 0.47 (±0.57) | 0.7 (±0.7) | - | 0.538 ns | |
| 40− | 0.16 (±0.29) | 1.3 (±0.37) | - | 0.001 * | |
| 50+ | 0.53 (±0.87) | 0.38 (±0.62) | - | 0.867 ns | |
| all | 1.97 (±0.82) | 2.97 (±1) | 0.048 * | 0.067 m | |
| live | 10− | 4.68 (±0.67) | 4.39 (±0.57) | 0.440 ns | 0.553 ns |
| 20− | 4.77 (±0.88) | 4.68 (±0.62) | 1.000 ns | 1.000 ns | |
| 30− | 4.2 (±1.41) | 4.5 (±1.49) | 0.665 ns | 0.682 ns | |
| 40− | 3.08 (±1.21) | 2.26 (±0.36) | 0.061 m | 0.083 m | |
| 50+ | 6.84 (±5.24) | 4.56 (±3.55) | - | 0.494 ns | |
| all | 23.56 (±5.23) | 20.39 (±2.86) | - | 0.151 ns | |
| Post-Fire Interval | Predictors | R2 | RMSE | RMSE(%) |
|---|---|---|---|---|
| 1-year | initial AGB | 0.65 | 0.42 | 80.3 |
| initial AGB + ∆NBR + ∆GV + ∆Shade | 0.69 | 0.43 | 82.9 | |
| initial AGB + ∆NPV + ∆GV + ∆Shade | 0.68 | 0.44 | 84.1 | |
| ∆NBR + ∆GV + ∆Shade | 0.65 | 0.44 | 84.2 | |
| ∆NBR + ∆NPV + ∆GV + ∆Shade | 0.65 | 0.44 | 85.0 | |
| ∆NPV + ∆GV + ∆Shade | 0.63 | 0.45 | 86.9 | |
| 2-year | initial AGB + ∆NBR + ∆GV + ∆Shade | 0.75 | 0.54 | 67.9 |
| initial AGB + ∆NPV + ∆GV + ∆Shade | 0.75 | 0.54 | 68.1 | |
| ∆NBR + ∆GV + ∆Shade | 0.74 | 0.55 | 69.6 | |
| ∆NPV + ∆GV + ∆Shade | 0.74 | 0.55 | 69.7 | |
| ∆NBR + ∆NPV + ∆GV + ∆Shade | 0.74 | 0.57 | 71.0 | |
| initial AGB | 0.60 | 0.64 | 81.0 | |
| 3-year | ∆NBR + ∆NPV + ∆GV + ∆Shade | 0.71 | 0.76 | 86.4 |
| ∆NBR + ∆GV + ∆Shade | 0.71 | 0.77 | 87.3 | |
| ∆NPV + ∆GV + ∆Shade | 0.71 | 0.78 | 88.1 | |
| initial AGB + ∆NBR + ∆GV + ∆Shade | 0.70 | 0.80 | 90.9 | |
| initial AGB + ∆NPV + ∆GV + ∆Shade | 0.71 | 0.81 | 91.8 | |
| initial AGB | 0.55 | 0.87 | 98.8 |
References
- Bullock, E.L.; Woodcock, C.E.; Souza, C.; Olofsson, P. Satellite-based estimates reveal widespread forest degradation in the Amazon. Glob. Chang. Biol. 2020, 26, 2956–2969. [Google Scholar] [CrossRef] [PubMed]
- Matricardi, E.A.T.; Skole, D.L.; Costa, O.B.; Pedlowski, M.A.; Samek, J.H.; Miguel, E.P. Long-term forest degradation surpasses deforestation in the Brazilian Amazon. Science 2020, 369, 1378–1382. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Xiao, X.; Wigneron, J.-P.; Ciais, P.; Brandt, M.; Fan, L.; Li, X.; Crowell, S.; Wu, X.; Doughty, R.; et al. Carbon loss from forest degradation exceeds that from deforestation in the Brazilian Amazon. Nat. Clim. Chang. 2021, 11, 442–448. [Google Scholar] [CrossRef]
- Fu, R.; Yin, L.; Li, W.; Arias, P.A.; Dickinson, R.E.; Huang, L.; Chakraborty, S.; Fernandes, K.; Liebmann, B.; Fisher, R.; et al. Increased dry-season length over southern Amazonia in recent decades and its implication for future climate projection. Proc. Natl. Acad. Sci. USA 2013, 110, 18110–18115. [Google Scholar] [CrossRef] [Green Version]
- Le Page, Y.; Morton, D.; Hartin, C.; Bond-Lamberty, B.; Pereira, J.M.C.; Hurtt, G.; Asrar, G. Synergy between land use and climate change increases future fire risk in Amazon forests. Earth Syst. Dyn. 2017, 8, 1237–1246. [Google Scholar] [CrossRef] [Green Version]
- Barni, P.; Fearnside, P.M.; Graça, P. Simulating Deforestation and Carbon Loss in Amazonia: Impacts in Brazil’s Roraima State from Reconstructing Highway BR-319 (Manaus-Porto Velho). Environ. Manag. 2014, 55, 259–278. [Google Scholar] [CrossRef]
- Ferrante, L.; Fearnside, P.M. The Amazon’s road to deforestation. Science 2020, 369, 634. [Google Scholar] [CrossRef]
- Aragão, L.E.O.C.; Anderson, L.O.; Fonseca, M.G.; Rosan, T.M.; Vedovato, L.B.; Wagner, F.H.; Silva, C.V.J.; Silva Junior, C.H.L.; Arai, E.; Aguiar, A.P.; et al. 21st Century drought-related fires counteract the decline of Amazon deforestation carbon emissions. Nat. Commun. 2018, 9, 536. [Google Scholar] [CrossRef]
- Mitchard, E.T.A. The tropical forest carbon cycle and climate change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef]
- Silva, C.V.J.; Aragão, L.E.O.C.; Young, P.J.; Espirito-Santo, F.; Berenguer, E.; Anderson, L.O.; Brasil, I.; Pontes-Lopes, A.; Ferreira, J.; Withey, K.; et al. Estimating the multi-decadal carbon deficit of burned Amazonian forests. Environ. Res. Lett. 2020, 15, 114023. [Google Scholar] [CrossRef]
- Brando, P.M.; Oliveria-Santos, C.; Rocha, W.; Cury, R.; Coe, M.T. Effects of experimental fuel additions on fire intensity and severity: Unexpected carbon resilience of a neotropical forest. Glob. Chang. Biol. 2016, 22, 2516–2525. [Google Scholar] [CrossRef] [PubMed]
- Ray, D.; Nepstad, D.; Moutinho, P. Micrometeorological and Canopy Controls of Fire Susceptibility in a Forested Amazon Landscape. Ecol. Appl. 2005, 15, 1664–1678. [Google Scholar] [CrossRef]
- Alencar, A.; Nepstad, D.; Diaz, M.D.C.V. Forest understory fire in the Brazilian Amazon in ENSO and non-ENSO years: Area burned and committed carbon emissions. Earth Interact. 2006, 10, 1–17. [Google Scholar] [CrossRef]
- Pontes-Lopes, A.; Silva, C.V.J.; Barlow, J.; Rincón, L.M.; Campanharo, W.A.; Nunes, C.A.; De Almeida, C.T.; Silva Júnior, C.H.L.; Cassol, H.L.G.; Dalagnol, R.; et al. Drought-driven wildfire impacts on structure and dynamics in a wet Central Amazonian forest. Proc. R. Soc. B Biol. Sci. 2021, 288, 20210094. [Google Scholar] [CrossRef]
- Morton, D.C.; DeFries, R.S.; Nagol, J.; Souza, C.M.; Kasischke, E.S.; Hurtt, G.C.; Dubayah, R. Mapping canopy damage from understory fires in Amazon forests using annual time series of Landsat and MODIS data. Remote Sens. Environ. 2011, 115, 1706–1720. [Google Scholar] [CrossRef] [Green Version]
- Barlow, J.; Peres, C.A. Ecological responses to El Niño–induced surface fires in central Brazilian Amazonia: Management implications for flammable tropical forests. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 2004, 359, 367–380. [Google Scholar] [CrossRef]
- Brando, P.M.; Balch, J.K.; Nepstad, D.C.; Morton, D.C.; Putz, F.E.; Coe, M.T.; Silvério, D.; Macedo, M.N.; Davidson, E.A.; Nóbrega, C.C.; et al. Abrupt increases in Amazonian tree mortality due to drought-fire interactions. Proc. Natl. Acad. Sci. USA 2014, 111, 6347–6352. [Google Scholar] [CrossRef] [Green Version]
- Silva, C.V.J.; Aragão, L.E.O.C.; Barlow, J.; Espirito-Santo, F.; Young, P.J.; Anderson, L.O.; Berenguer, E.; Brasil, I.; Foster Brown, I.; Castro, B.; et al. Drought-induced Amazonian wildfires instigate a decadal-scale disruption of forest carbon dynamics. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20180043. [Google Scholar] [CrossRef] [Green Version]
- Haugaasen, T.; Barlow, J.; Peres, C.A. Surface wildfires in central Amazonia: Short-term impact on forest structure and carbon loss. For. Ecol. Manag. 2003, 179, 321–331. [Google Scholar] [CrossRef]
- Barlow, J.; Peres, C.A.; Lagan, B.O.; Haugaasen, T. Large tree mortality and the decline of forest biomass following Amazonian wildfires. Ecol. Lett. 2003, 6, 6–8. [Google Scholar] [CrossRef]
- Aragão, L.E.O.C.; Malhi, Y.; Roman-Cuesta, R.M.; Saatchi, S.; Anderson, L.O.; Shimabukuro, Y.E. Spatial patterns and fire response of recent Amazonian droughts. Geophys. Res. Lett. 2007, 34, L07701. [Google Scholar] [CrossRef] [Green Version]
- Aragão, L.E.O.C.; Malhi, Y.; Barbier, N.; Lima, A.; Shimabukuro, Y.; Anderson, L.; Saatchi, S. Interactions between rainfall, deforestation and fires during recent years in the Brazilian Amazonia. Philos. Trans. R. Soc. 2008, 363, 1779–1785. [Google Scholar] [CrossRef] [PubMed]
- Silva Junior, C.H.L.; Anderson, L.O.; Silva, A.L.; Almeida, C.T.; Dalagnol, R.; Pletsch, M.A.J.S.; Penha, T.V.; Paloschi, R.A.; Aragão, L.E.O.C. Fire Responses to the 2010 and 2015/2016 Amazonian Droughts. Front. Earth Sci. 2019, 7, 97. [Google Scholar] [CrossRef]
- Armenteras, D.; Barreto, J.S.; Tabor, K.; Molowny-Horas, R.; Retana, J. Changing patterns of fire occurrence in proximity to forest edges, roads and rivers between NW Amazonian countries. Biogeosciences 2017, 14, 2755–2765. [Google Scholar] [CrossRef] [Green Version]
- Anderson, L.O.; Aragão, L.E.O.C.; Gloor, M.; Arai, E.; Adami, M.; Saatchi, S.S.; Malhi, Y.; Shimabukuro, Y.E.; Barlow, J.; Berenguer, E.; et al. Disentangling the contribution of multiple land covers to fire-mediated carbon emissions in Amazonia during the 2010 drought. Glob. Biogeochem. Cycles 2015, 29, 1739–1753. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Resende, A.F.; Nelson, B.W.; Flores, B.M.; Almeida, D.R. Fire damage in seasonally flooded and upland forests of the Central Amazon. Biotropica 2014, 46, 643–646. [Google Scholar] [CrossRef]
- Flores, B.M.; Holmgren, M. White-Sand Savannas Expand at the Core of the Amazon after Forest Wildfires. Ecosystems 2021, 24, 1624–1637. [Google Scholar] [CrossRef]
- Barlow, J.; Lagan, B.O.; Peres, C.A. Morphological correlates of fire-induced tree mortality in a central Amazonian forest. J. Trop. Ecol. 2003, 19, 291–299. [Google Scholar] [CrossRef] [Green Version]
- Brando, P.M.; Nepstad, D.C.; Balch, J.K.; Bolker, B.; Christman, M.C.; Coe, M.; Putz, F.E. Fire-induced tree mortality in a neotropical forest: The roles of bark traits, tree size, wood density and fire behavior. Glob. Chang. Biol. 2012, 18, 630–641. [Google Scholar] [CrossRef]
- Staver, A.C.; Brando, P.M.; Barlow, J.; Morton, D.C.; Paine, C.E.T.; Malhi, Y.; Araujo Murakami, A.; Pasquel, J. Thinner bark increases sensitivity of wetter Amazonian tropical forests to fire. Ecol. Lett. 2020, 23, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Campanharo, W.A.; Lopes, A.P.; Anderson, L.O.; Silva, T.F.M.R.; Arag, L.E.O.C. Translating Fire Impacts in Southwestern Amazonia into Economic Costs. Remote Sens. 2019, 11, 764. [Google Scholar] [CrossRef] [Green Version]
- Key, C.H.; Benson, N.C. Measuring and remote sensing of burn severity. In Proceedings Joint Fire Science Conference and Workshop; Neuenschwander, L.F., Ed.; University of Idaho and International Association of Wildland Fire: Moscow, Russia, 1999; p. 284. [Google Scholar]
- Bright, B.C.; Hudak, A.T.; Kennedy, R.E.; Braaten, J.D.; Henareh Khalyani, A. Examining post-fire vegetation recovery with Landsat time series analysis in three western North American forest types. Fire Ecol. 2019, 15, 8. [Google Scholar] [CrossRef] [Green Version]
- Key, C.H.; Benson, N.C. Landscape Assessment (LA). In MON: Fire Effects Monitoring and Inventory System; Lutes, D.C., Keane, R.E., Caratti, J.F., Key, C.H., Benson, N.C., Sutherland, S., Gangi, L.J., Eds.; Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; p. LA-1-55. [Google Scholar]
- Nelson, B.W.; Kapos, V.; Adams, J.B.; Oliveira, W.J.; Braun, O.P.G.; Do Amaral, I.L. Forest disturbance by large blowdowns in the Brazilian Amazon. Ecology 1994, 75, 853–858. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.I.; Chambers, J.Q.; Marra, D.M.; Ribeiro, G.H.P.M.; Rifai, S.W.; Higuchi, N.; Roberts, D. Detection of subpixel treefall gaps with Landsat imagery in Central Amazon forests. Remote Sens. Environ. 2011, 115, 3322–3328. [Google Scholar] [CrossRef]
- Numata, I.; Cochrane, M.A.; Galvão, L.S. Analyzing the impacts of frequency and severity of forest fire on the recovery of disturbed forest using landsat time series and EO-1 hyperion in the Southern Brazilian Amazon. Earth Interact. 2011, 15, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Almeida, D.R.A.; Walker, B.; Schietti, J.; Bastos, E.; Faria, A.; Stark, S.C.; Valbuena, R. Contrasting fire damage and fire susceptibility between seasonally flooded forest and upland forest in the Central Amazon using portable profiling LiDAR. Remote Sens. Environ. 2016, 184, 153–160. [Google Scholar] [CrossRef]
- Van Wagtendonk, J.W.; Root, R.R.; Key, C.H. Comparison of AVIRIS and Landsat ETM+ detection capabilities for burn severity. Remote Sens. Environ. 2004, 92, 397–408. [Google Scholar] [CrossRef]
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Rifai, S.W.; Urquiza Muñoz, J.D.; Negrón-Juárez, R.I.; Ramírez Arévalo, F.R.; Tello-Espinoza, R.; Vanderwel, M.C.; Lichstein, J.W.; Chambers, J.Q.; Bohlman, S.A. Landscape-scale consequences of differential tree mortality from catastrophic wind disturbance in the Amazon. Ecol. Appl. 2016, 26, 2225–2237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ximenes, A.C.; Amaral, S.; Monteiro, A.M.V.; Almeida, R.M.; Valeriano, D.M. Mapping the terrestrial ecoregions of the Purus-Madeira interfluve in the Amazon Forest using machine learning techniques. For. Ecol. Manag. 2021, 488, 118960. [Google Scholar] [CrossRef]
- Irion, G.; Junk, W.J.; De Mello, J.A.S.N. The Large Central Amazonian River Floodplains Near Manaus: Geological, Climatological, Hydrological and Geomorphological Aspects. In The Central Amazon Floodplain. Ecological Studies; Junk, W.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 23–46. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—a new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giglio, L.; Justice, C.; Boschetti, L.; Roy, D. MCD64A1 MODIS/Terra+Aqua Burned Area Monthly L3 Global 500 m SIN Grid V006 [Data Set]; NASA EOSDIS Land Processes DAAC: Washington, DC, USA, 2015. [Google Scholar] [CrossRef]
- Berenguer, E.; Malhi, Y.; Brando, P.; Cardoso Nunes Cordeiro, A.; Ferreira, J.; França, F.; Chesini Rossi, L.; Maria Moraes de Seixas, M.; Barlow, J. Tree growth and stem carbon accumulation in human-modified Amazonian forests following drought and fire. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20170308. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Goodman, R.C.; Phillips, O.L.; Del Castillo Torres, D.; Freitas, L.; Cortese, S.T.; Monteagudo, A.; Baker, T.R. Amazon palm biomass and allometry. For. Ecol. Manag. 2013, 310, 994–1004. [Google Scholar] [CrossRef]
- Gerwing, J.J.; Farias, D.L. Integrating liana abundance and forest stature into an estimate of total aboveground biomass for an eastern Amazonian forest. J. Trop. Ecol. 2000, 16, 327–335. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2020. [Google Scholar]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- USGS Landsat 8 Surface Reflectance Tier 1 (LANDSAT/LC08/C01/T1_SR). Available online: https://gee.stac.cloud/BJmBzK1uPSS1qPWphBuPHgfbcqSkzxvCWZ94q (accessed on 3 February 2022).
- Arai, E.; Shimabukuro, Y.E.; Dutra, A.C.; Duarte, V. Detection and Analysis of Forest Degradation by Fire Using Landsat/Oli Images in Google Earth Engine. Int. Geosci. Remote Sens. Symp. 2019, 1649–1652. [Google Scholar] [CrossRef]
- Shimabukuro, Y.E.; Smith, J.A. The least-squares mixing models to generate fraction images derived from remote sensing multispectral data. IEEE Trans. Geosci. Remote Sens. 1991, 29, 16–20. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Copernicus Sentinel Data 2021, Processed by ESA. Acessed on Google Earth Engine. Available online: https://developers.google.com/earth-engine/datasets/catalog/COPERNICUS_S2?hl=en#description (accessed on 10 March 2021).
- Gittleman, J.L.; Kot, M. Adaptation: Statistics and a Null Model for Estimating Phylogenetic Effects. Syst. Zool. 1990, 39, 227. [Google Scholar] [CrossRef]
- Paradis, E.; Schliep, K. ape 5.0: An environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 2019, 35, 526–528. [Google Scholar] [CrossRef] [PubMed]
- Kassambara, A. Ggpubr: “Ggplot2” Based Publication Ready Plots; Version 0.4.0; R Package: Vienna, Austria, 2020. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Hothorn, T.; Bretz, F.; Westfall, P. Simultaneous Inference in General Parametric Models. Biom. J. 2008, 50, 346–363. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28. [Google Scholar] [CrossRef] [Green Version]
- Greenwell, B.M. pdp: An R Package for Constructing Partial Dependence Plots. R J. 2017, 9, 421–436. [Google Scholar] [CrossRef] [Green Version]
- Souza, C.; Firestone, L.; Silva, L.M.; Roberts, D. Mapping forest degradation in the Eastern Amazon from SPOT 4 through spectral mixture models. Remote Sens. Environ. 2003, 87, 494–506. [Google Scholar] [CrossRef]
- Chambers, J.Q.; Asner, G.P.; Morton, D.C.; Anderson, L.O.; Saatchi, S.S.; Espírito-Santo, F.D.B.; Palace, M.; Souza, C. Regional ecosystem structure and function: Ecological insights from remote sensing of tropical forests. Trends Ecol. Evol. 2007, 22, 414–423. [Google Scholar] [CrossRef]
- Viana-Soto, A.; Aguado, I.; Salas, J.; García, M. Identifying Post-Fire Recovery Trajectories and Driving Factors Using Landsat Time Series in Fire-Prone Mediterranean Pine Forests. Remote Sens. 2020, 12, 1499. [Google Scholar] [CrossRef]
- Barlow, J.; Lennox, G.D.; Ferreira, J.; Berenguer, E.; Lees, A.C.; Mac Nally, R.; Thomson, J.R.; Ferraz, S.F.D.B.; Louzada, J.; Oliveira, V.H.F.; et al. Anthropogenic disturbance in tropical forests can double biodiversity loss from deforestation. Nature 2016, 535, 144–147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holdsworth, A.R.; Uhl, C. Fire in Amazonian selectively logged rain forest and the potential for fire reduction. Ecol. Appl. 1997, 7, 713–725. [Google Scholar] [CrossRef]
- De Vasconcelos, S.S.; Fearnside, P.; Graça, P.; Nogueira, E.M.; De Oliveira, L.C.; Figueiredo, E.O. Forest fires in southwestern Brazilian Amazonia: Estimates of area and potential carbon emissions. For. Ecol. Manag. 2013, 291, 199–208. [Google Scholar] [CrossRef]
- Berenguer, E.; Lennox, G.D.; Ferreira, J.; Malhi, Y.; Aragão, L.E.O.C.; Barreto, J.R.; Del Bon Espírito-Santo, F.; Figueiredo, A.E.S.; França, F.; Gardner, T.A.; et al. Tracking the impacts of El Niño drought and fire in human-modified Amazonian forests. Proc. Natl. Acad. Sci. USA 2021, 118, e2019377118. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.C.; Kennedy, M.C. Altered vegetation structure from mechanical thinning treatments changed wildfire behaviour in the wildland–urban interface on the 2011 Wallow Fire, Arizona, USA. Int. J. Wildland Fire 2019, 28, 216. [Google Scholar] [CrossRef]
- Wagner, F.; Rutishauser, E.; Blanc, L.; Herault, B. Effects of Plot Size and Census Interval on Descriptors of Forest Structure and Dynamics. Biotropica 2010, 42, 664–671. [Google Scholar] [CrossRef]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balance Manag. 2015, 10, 10. [Google Scholar] [CrossRef] [Green Version]
- De Almeida, C.T.; Galvão, L.S.; Aragão, L.E.D.O.C.E.; Ometto, J.P.H.B.; Jacon, A.D.; Pereira, F.R.D.S.; Sato, L.Y.; Pontes-Lopes, A.; Graça, P.; Silva, C.V.D.J.; et al. Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Keller, M.; Palace, M.; Hurtt, G. Biomass estimation in the Tapajos National Forest, Brazil. For. Ecol. Manag. 2001, 154, 371–382. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Mutanga, O.; Kumar, L. Google Earth Engine Applications. Remote Sens. 2019, 11, 591. [Google Scholar] [CrossRef] [Green Version]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Berenguer, E.; Carvalho, N.; Anderson, L.O.; Aragão, L.E.O.C.; França, F.; Barlow, J. Improving the spatial-temporal analysis of Amazonian fires. Glob. Chang. Biol. 2020, 27, 15425. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Da Silva, R.D.; Galvão, L.S.; Dos Santos, J.R.; Silva, C.V.D.J.; De Moura, Y.M. Spectral/textural attributes from ALI/EO-1 for mapping primary and secondary tropical forests and studying the relationships with biophysical parameters. GIScience Remote Sens. 2014, 51, 677–694. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Martins, F.S.R.; Santos, J.R.; Galvão, L.S.; Xaud, H.A.M. Sensitivity of ALOS/PALSAR imagery to forest degradation by fire in northern Amazon. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 163–174. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pontes-Lopes, A.; Dalagnol, R.; Dutra, A.C.; de Jesus Silva, C.V.; de Alencastro Graça, P.M.L.; de Oliveira e Cruz de Aragão, L.E. Quantifying Post-Fire Changes in the Aboveground Biomass of an Amazonian Forest Based on Field and Remote Sensing Data. Remote Sens. 2022, 14, 1545. https://doi.org/10.3390/rs14071545
Pontes-Lopes A, Dalagnol R, Dutra AC, de Jesus Silva CV, de Alencastro Graça PML, de Oliveira e Cruz de Aragão LE. Quantifying Post-Fire Changes in the Aboveground Biomass of an Amazonian Forest Based on Field and Remote Sensing Data. Remote Sensing. 2022; 14(7):1545. https://doi.org/10.3390/rs14071545
Chicago/Turabian StylePontes-Lopes, Aline, Ricardo Dalagnol, Andeise Cerqueira Dutra, Camila Valéria de Jesus Silva, Paulo Maurício Lima de Alencastro Graça, and Luiz Eduardo de Oliveira e Cruz de Aragão. 2022. "Quantifying Post-Fire Changes in the Aboveground Biomass of an Amazonian Forest Based on Field and Remote Sensing Data" Remote Sensing 14, no. 7: 1545. https://doi.org/10.3390/rs14071545
APA StylePontes-Lopes, A., Dalagnol, R., Dutra, A. C., de Jesus Silva, C. V., de Alencastro Graça, P. M. L., & de Oliveira e Cruz de Aragão, L. E. (2022). Quantifying Post-Fire Changes in the Aboveground Biomass of an Amazonian Forest Based on Field and Remote Sensing Data. Remote Sensing, 14(7), 1545. https://doi.org/10.3390/rs14071545







