Group-in-Group Relation-Based Transformer for 3D Point Cloud Learning
Abstract
:1. Introduction
- •
- We propose a new Transformer-based point cloud learning architecture GiG. By dividing a point cloud into a set of small groups, GiG can not only learn the relationship between groups to model global information but also model local semantic information by learning the relationship between points within each group. Therefore, it is possible to extract effective object-related global information as well as shape-related local information.
- •
- We propose a RFA module to enhance the representation of local semantic information by extracting radius-based density features to characterize the sparsity of local point clouds.
- •
- Extensive experiments demonstrate that our method achieves new state-of-the-art performance in object classification and part segmentation.
2. Related Work
2.1. Deep Learning on Point Clouds
2.1.1. Multi-View Based Methods
2.1.2. Voxel-Based Methods
2.1.3. Point-Based Methods
2.1.4. Hybrid-Data Based Methods
2.2. Transformer in Point Clouds
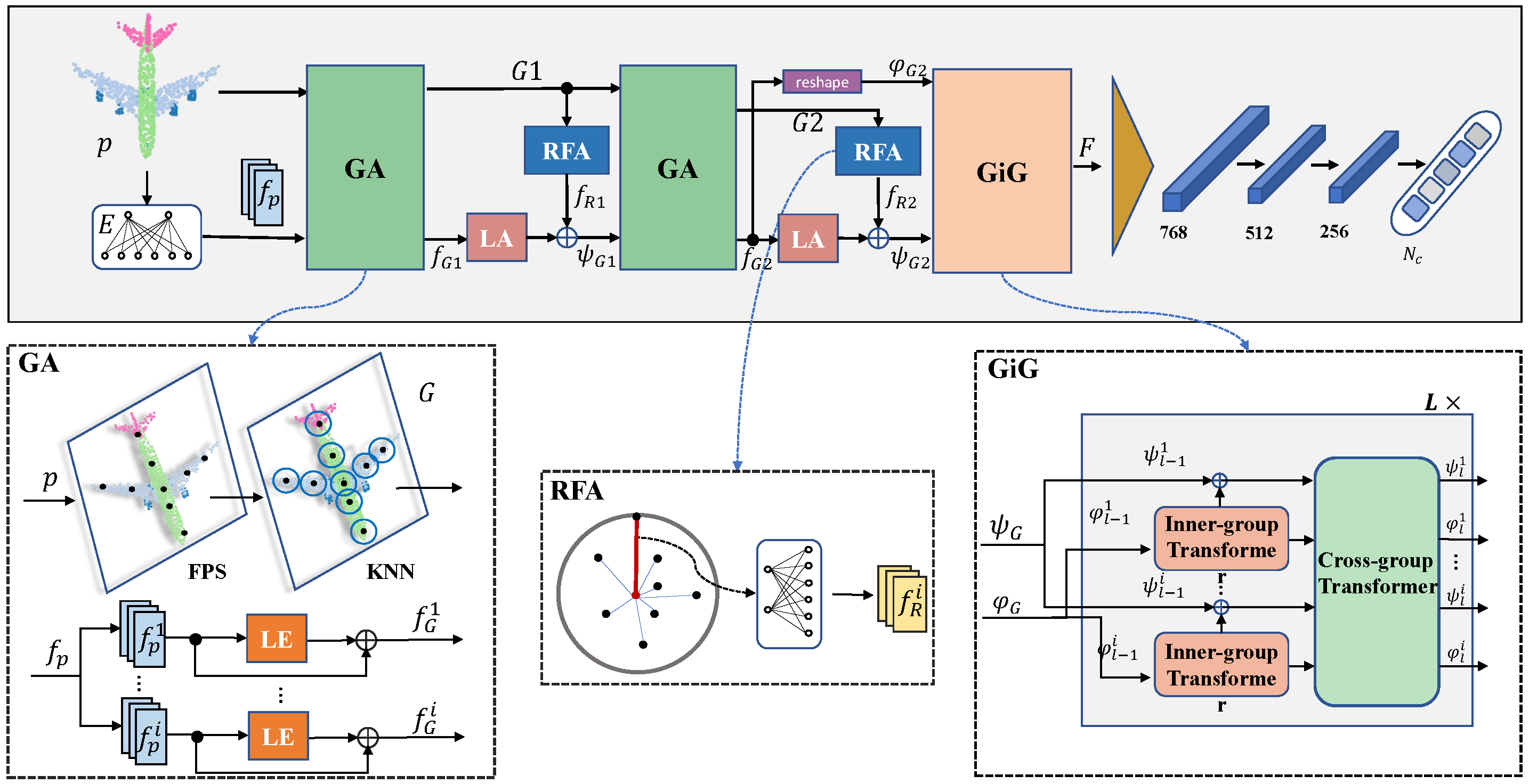
3. Methods
3.1. Preliminaries
3.2. Framework Overview
3.3. Group Abstraction (GA) and Radius-Based Feature Abstraction (RFA)
3.4. GiG (Group-in-Group Relation-Based Transformer)
4. Results
4.1. Classification on ModelNet40 Dataset
| Method | Input | #Points | Accuracy (%) |
|---|---|---|---|
| MVCNN [5] | multi-view | _ | 90.1 |
| OctNet [29] | octree | _ | 86.5 |
| PointwiseCNN [34] | points | 1K | 86.1 |
| PointNet [11] | points | 1K | 89.2 |
| PointNet++ [12] | points + normal | 5K | 91.9 |
| SpecGCN [47] | points + normal | 2K | 92.1 |
| PCNN [33] | points | 1K | 92.3 |
| SpiderCNN [47] | points + normal | 1K | 92.4 |
| DGCNN [16] | points | 1K | 92.9 |
| PointCNN [13] | points | 1K | 92.5 |
| PointWeb [30] | points + normal | 1K | 92.3 |
| PointConv [14] | points + normal | 1K | 92.5 |
| RS-CNN [32] w/o vot. | points | 1K | 92.4 |
| KPConv [22] | points | 1K | 92.9 |
| 3D-GCN [35] | points | 1K | 92.1 |
| FPConv [36] | points | 1K | 92.5 |
| PCT [21] | points | 1K | 93.2 |
| Ours w/o RFA | points | 1K | 93.4 |
| Ours | points | 1K | 93.9 |
4.2. Part Segmentation on ShapeNet Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wan, J.; Xie, Z.; Xu, Y.; Zeng, Z.; Yuan, D.; Qiu, Q. DGANet A Dilated Graph Attention-Based Network for Local Feature Extraction on 3D Point Clouds. Remote Sens. 2021, 13, 3484. [Google Scholar] [CrossRef]
- Wu, W.; Xie, Z.; Xu, Y.; Zeng, Z.; Wan, J. Point Projection Network: A Multi-View-Based Point Completion Network with Encoder-Decoder Architecture. Remote Sens. 2021, 13, 4917. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Nezhadarya, E.; Taghavi, E.; Razani, R.; Liu, B.; Luo, J. Adaptive hierarchical down-sampling for point cloud classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 12956–12964. [Google Scholar]
- Park, Y.; Lepetit, V.; Woo, W. Multiple 3d object tracking for augmented reality. In Proceedings of the 2008 7th IEEE/ACM International Symposium on Mixed and Augmented Reality, Cambridge, UK, 15–18 September 2008; pp. 117–120. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Han, Z.; Liu, Y.S.; Zwicker, M. Point2sequence: Learning the shape representation of 3d point clouds with an attention-based sequence to sequence network. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8778–8785. [Google Scholar]
- Duan, Y.; Zheng, Y.; Lu, J.; Zhou, J.; Tian, Q. Structural relational reasoning of point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 949–958. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view convolutional neural networks for 3d shape recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. arXiv 2017, arXiv:1706.02413. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31, 820–830. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9621–9630. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Phan, A.V.; Le Nguyen, M.; Nguyen, Y.L.H.; Bui, L.T. Dgcnn: A convolutional neural network over large-scale labeled graphs. Neural Netw. 2018, 108, 533–543. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Ma, X. Dynamic graph CNN with attention module for 3D hand pose estimation. In Proceedings of the International Symposium on Neural Networks, Moscow, Russia, 10–12 July 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 87–96. [Google Scholar]
- Pan, X.; Xia, Z.; Song, S.; Li, L.E.; Huang, G. 3d object detection with pointformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7463–7472. [Google Scholar]
- Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; Li, H. Pv-rcnn: Point-voxel feature set abstraction for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 10529–10538. [Google Scholar]
- Ye, M.; Xu, S.; Cao, T. Hvnet: Hybrid voxel network for lidar based 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1631–1640. [Google Scholar]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. PCT: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. arXiv 2020, arXiv:2005.14165. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. arXiv 2021, arXiv:2103.00112. [Google Scholar]
- Feng, Y.; Zhang, Z.; Zhao, X.; Ji, R.; Gao, Y. GVCNN: Group-view convolutional neural networks for 3D shape recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 264–272. [Google Scholar]
- Guo, H.; Wang, J.; Gao, Y.; Li, J.; Lu, H. Multi-view 3D object retrieval with deep embedding network. IEEE Trans. Image Process. 2016, 25, 5526–5537. [Google Scholar] [CrossRef] [PubMed]
- Gadelha, M.; Wang, R.; Maji, S. Multiresolution tree networks for 3d point cloud processing. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 103–118. [Google Scholar]
- Riegler, G.; Osman Ulusoy, A.; Geiger, A. Octnet: Learning deep 3d representations at high resolutions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3577–3586. [Google Scholar]
- Jiang, L.; Zhao, H.; Liu, S.; Shen, X.; Fu, C.W.; Jia, J. Hierarchical point-edge interaction network for point cloud semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 10433–10441. [Google Scholar]
- Yan, X.; Zheng, C.; Li, Z.; Wang, S.; Cui, S. Pointasnl: Robust point clouds processing using nonlocal neural networks with adaptive sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5589–5598. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8895–8904. [Google Scholar]
- Atzmon, M.; Maron, H.; Lipman, Y. Point convolutional neural networks by extension operators. ACM Trans. Graph. 2018, 37, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hua, B.S.; Tran, M.K.; Yeung, S.K. Pointwise convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 984–993. [Google Scholar]
- Lin, Z.H.; Huang, S.Y.; Wang, Y.C.F. Convolution in the cloud: Learning deformable kernels in 3d graph convolution networks for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1800–1809. [Google Scholar]
- Lin, Y.; Yan, Z.; Huang, H.; Du, D.; Liu, L.; Cui, S.; Han, X. Fpconv: Learning local flattening for point convolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4293–4302. [Google Scholar]
- Verma, N.; Boyer, E.; Verbeek, J. Feastnet: Feature-steered graph convolutions for 3d shape analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2598–2606. [Google Scholar]
- Wang, C.; Samari, B.; Siddiqi, K. Local spectral graph convolution for point set feature learning. In Proceedings of the European conference on computer vision, Munich, Germany, 8–14 September 2018; pp. 52–66. [Google Scholar]
- Te, G.; Hu, W.; Zheng, A.; Guo, Z. Rgcnn: Regularized graph cnn for point cloud segmentation. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Korea, 22–26 October 2018; pp. 746–754. [Google Scholar]
- Klokov, R.; Lempitsky, V. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 863–872. [Google Scholar]
- Li, J.; Chen, B.M.; Lee, G.H. So-net: Self-organizing network for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9397–9406. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A scalable active framework for region annotation in 3d shape collections. ACM Trans. Graph. 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 87–102. [Google Scholar]
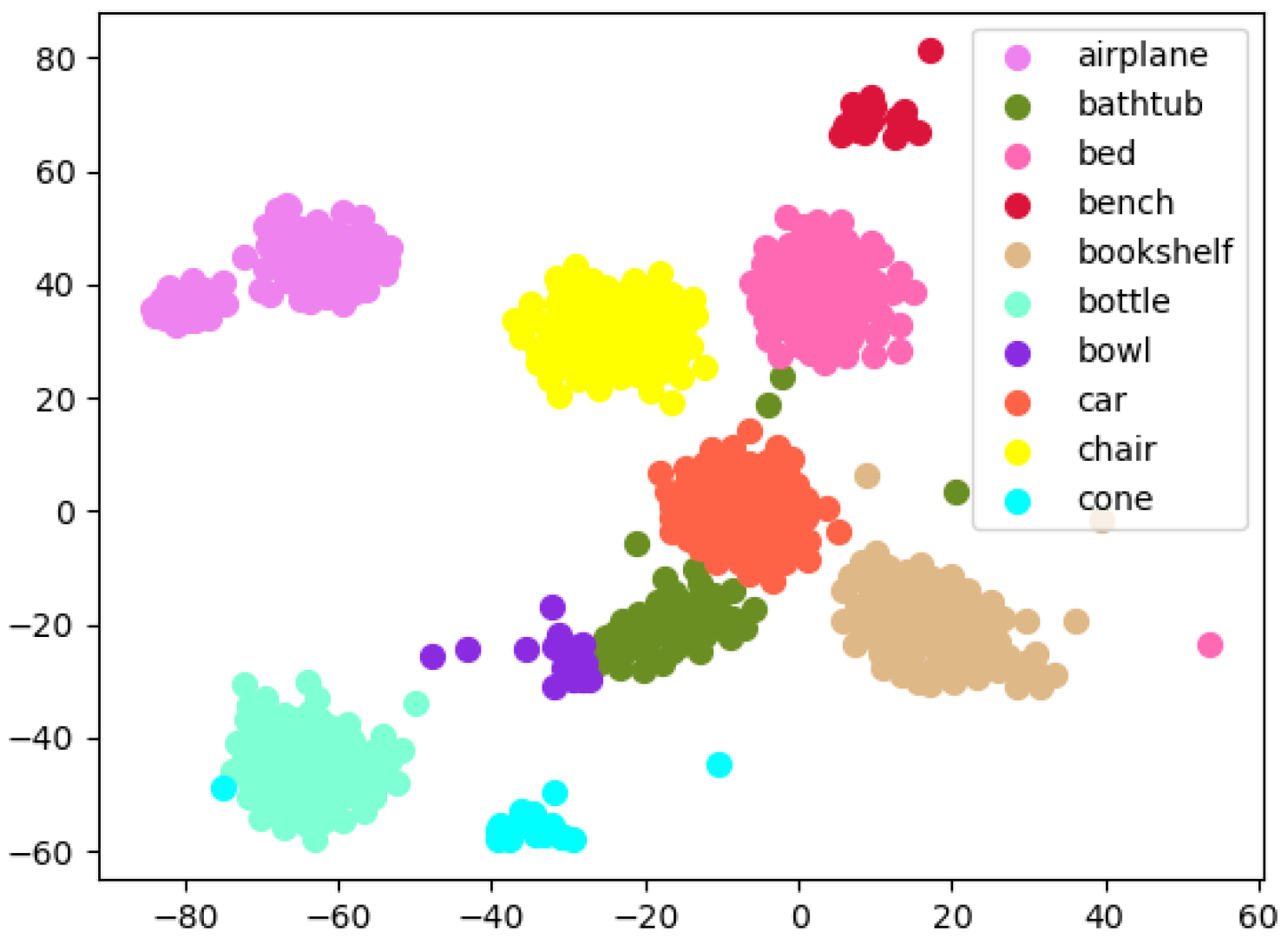

| Method | mIoU | Plane | Bag | Cap | Car | Chair | Earph- | Guitar | Knife | Lamp | Laptop | Motor | Mug | Pistol | Rocket | Skate | Table |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ShapeNet [45] | |||||||||||||||||
| PointNet [11] | |||||||||||||||||
| PointNet++ [12] | |||||||||||||||||
| KD-Net [40] | |||||||||||||||||
| SO-Net [41] | |||||||||||||||||
| RGCNN [39] | |||||||||||||||||
| PCNN [6] | |||||||||||||||||
| SRN [8] | |||||||||||||||||
| DGCNN [16] | |||||||||||||||||
| P2Sequence [7] | |||||||||||||||||
| PointConv [14] | − | − | − | − | − | − | − | − | − | − | − | − | − | − | − | − | |
| PointCNN [13] | |||||||||||||||||
| PointASNL [31] | |||||||||||||||||
| PCT [21] | |||||||||||||||||
| Ours |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Fu, K.; Wang, M.; Song, Z. Group-in-Group Relation-Based Transformer for 3D Point Cloud Learning. Remote Sens. 2022, 14, 1563. https://doi.org/10.3390/rs14071563
Liu S, Fu K, Wang M, Song Z. Group-in-Group Relation-Based Transformer for 3D Point Cloud Learning. Remote Sensing. 2022; 14(7):1563. https://doi.org/10.3390/rs14071563
Chicago/Turabian StyleLiu, Shaolei, Kexue Fu, Manning Wang, and Zhijian Song. 2022. "Group-in-Group Relation-Based Transformer for 3D Point Cloud Learning" Remote Sensing 14, no. 7: 1563. https://doi.org/10.3390/rs14071563
APA StyleLiu, S., Fu, K., Wang, M., & Song, Z. (2022). Group-in-Group Relation-Based Transformer for 3D Point Cloud Learning. Remote Sensing, 14(7), 1563. https://doi.org/10.3390/rs14071563








