Dynamic Harvest Index Estimation of Winter Wheat Based on UAV Hyperspectral Remote Sensing Considering Crop Aboveground Biomass Change and the Grain Filling Process
Abstract
:1. Introduction
2. Data Preparation and Processing
2.1. Study Area
2.2. Data Acquisition and Processing
2.2.1. Acquisition of Aboveground Biomass Data
2.2.2. Acquisition of the Dynamic Harvest Index (D-HI)
2.2.3. UAV Hyperspectral Data Acquisition and Processing
- (1)
- UAV data acquisition and preprocessing
- (2)
- Calculation of the normalized difference spectral index (NDSI)
3. Methodology
3.1. The Proposed Dynamic fG (D-fG) Parameter
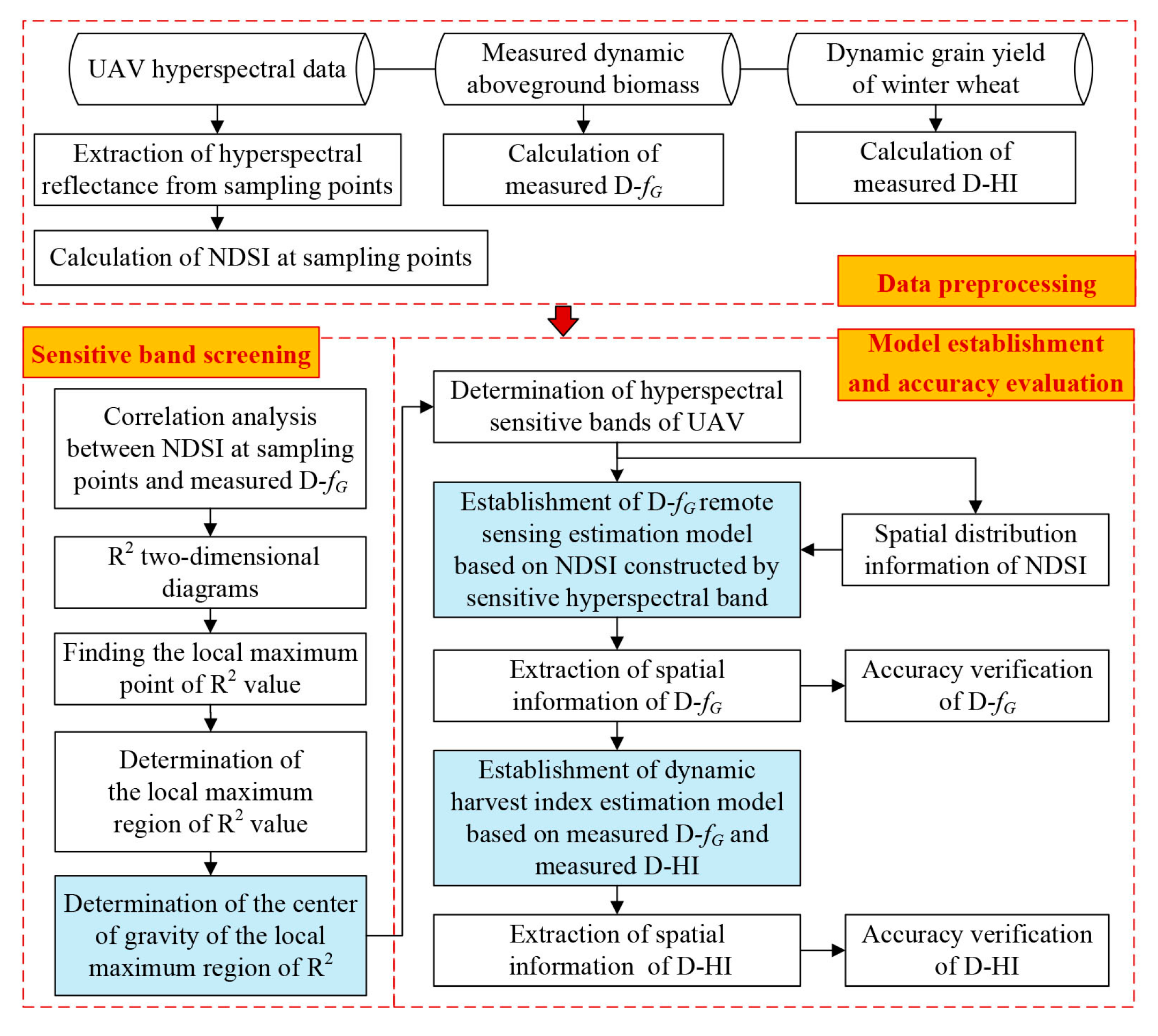
3.2. Overall Technical Process
3.3. D-fG Remote Sensing Estimation Based on the NDSI Constructed by Sensitive Hyperspectral Bands
3.3.1. Determination of the Sensitive Band Centers for D-fG Estimation
3.3.2. Establishment of the D-fG Estimation Model Based on Hyperspectral NDSI Data
3.4. Establishment of the D-HI Estimation Model Based on D-fG Remote Sensing Parameter
3.5. Accuracy Evaluation of the D-fG Estimation Model and D-HI Estimation Model
4. Results and Analysis
4.1. D-fG Remote Sensing Estimation Based on UAV Hyperspectral NDSI Data
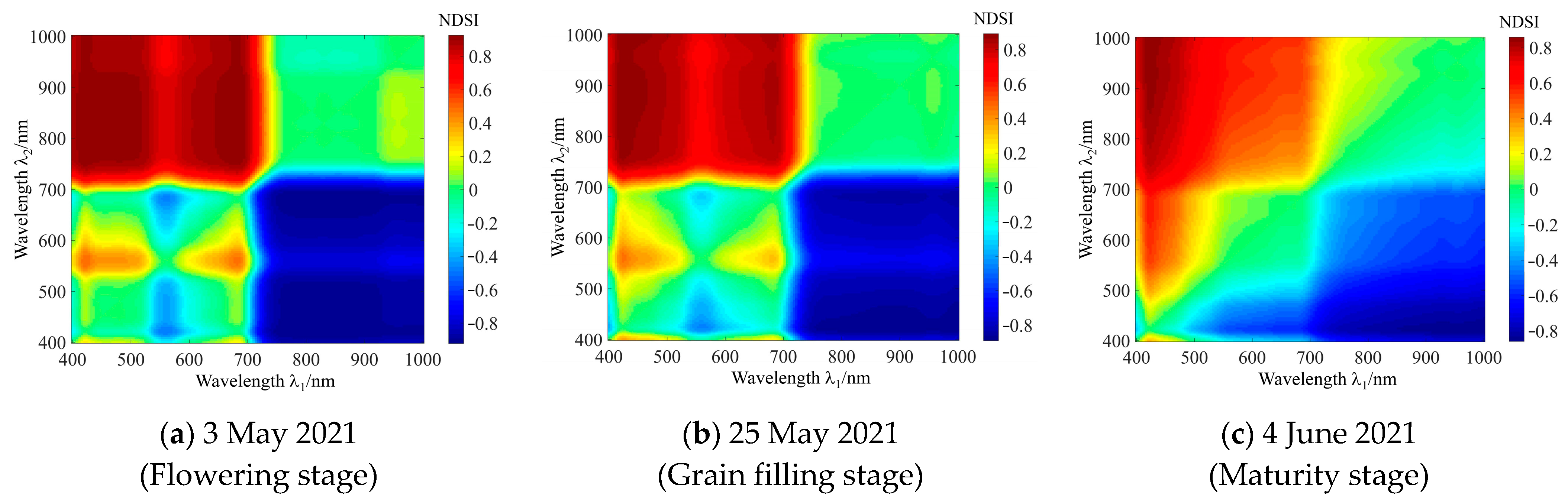
4.1.1. Hyperspectral NDSI Calculation Results at Ground Observation Points
4.1.2. Determination of Sensitive UAV Hyperspectral Band Centers for D-fG Estimation
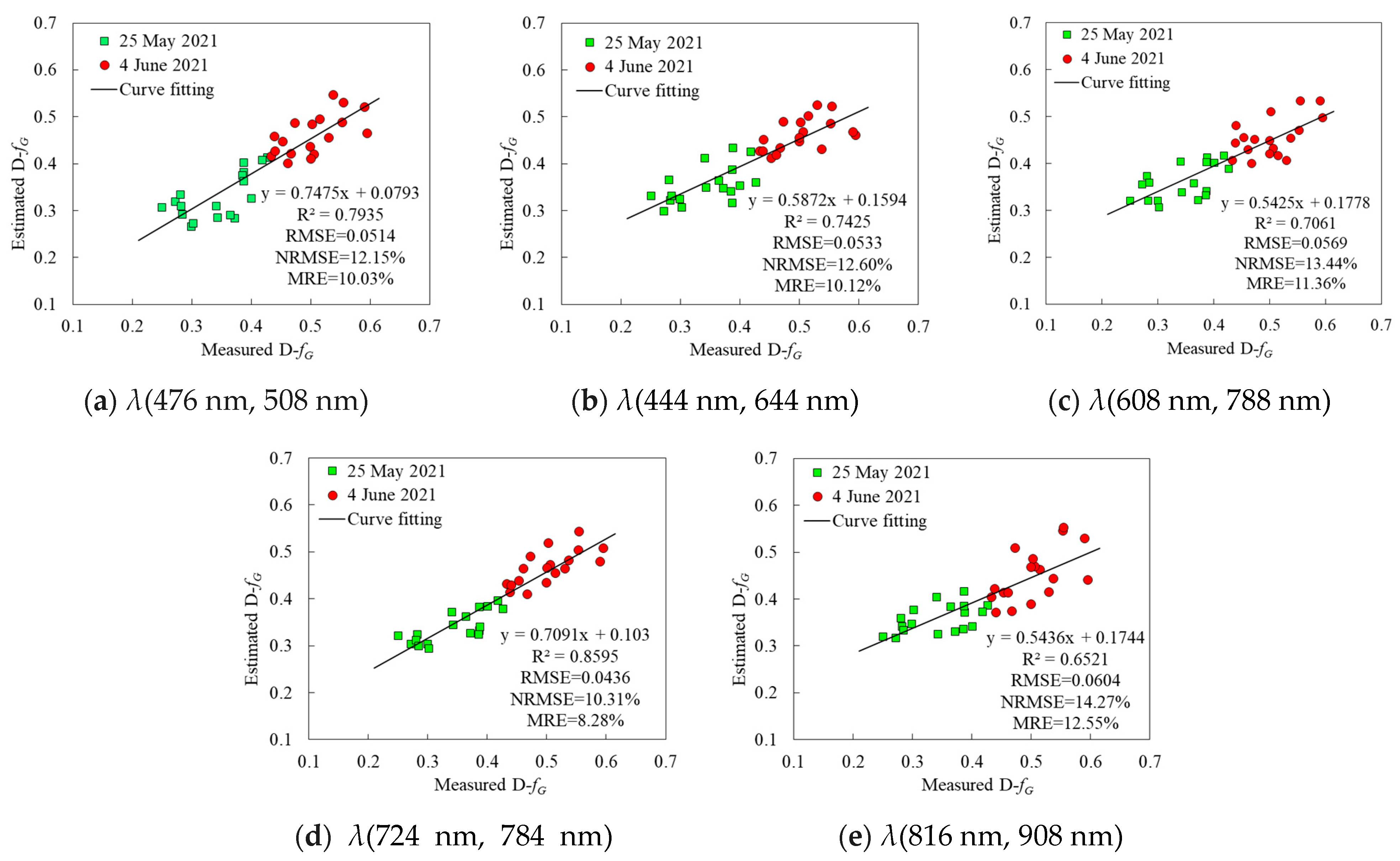
4.1.3. Remotely Sensed NDSI-Based D-fG Estimation and Its Verification
4.2. D-HI Estimation Based on UAV Remote Sensing Data
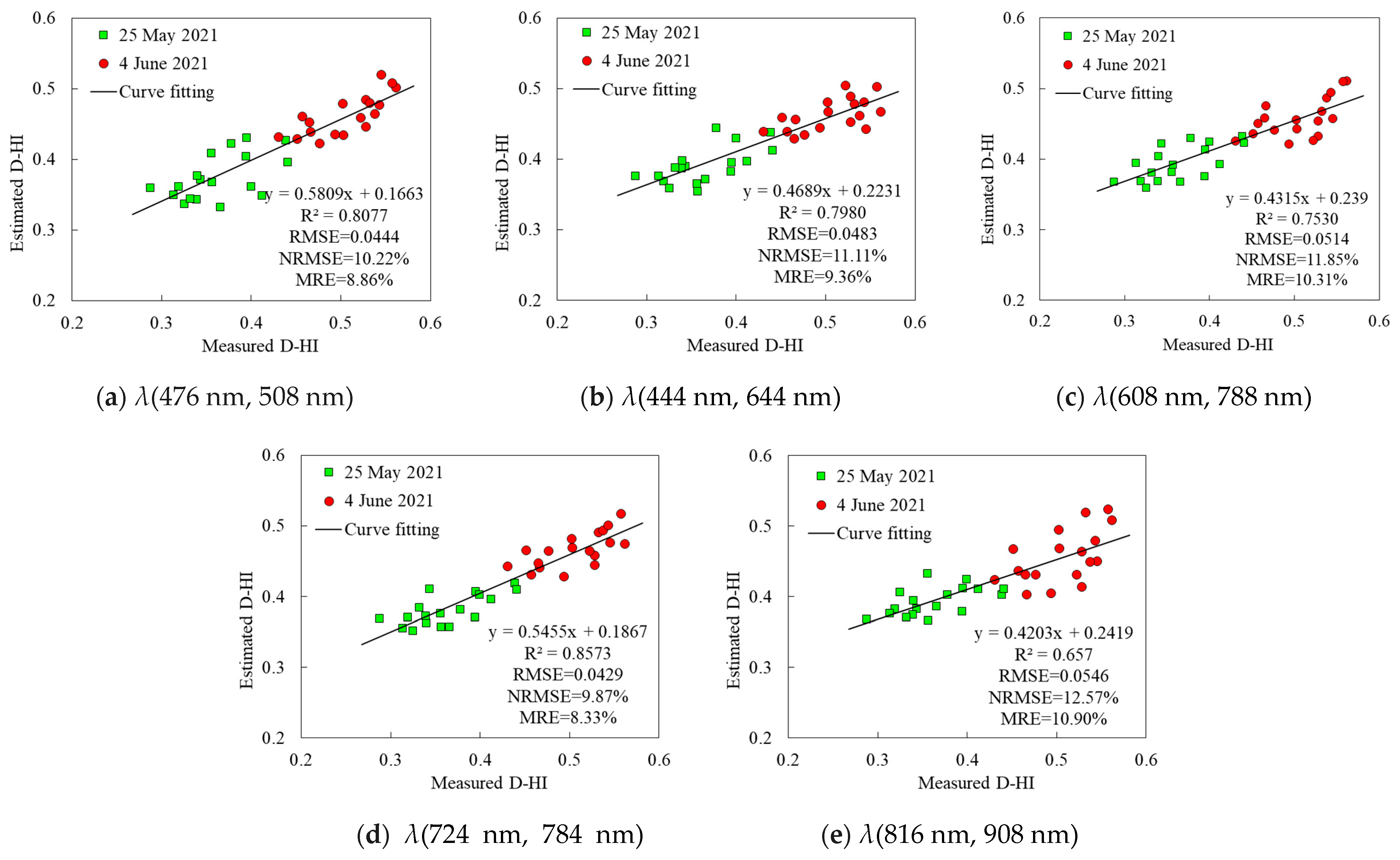
4.2.1. Establishment of a D-HI Estimation Model Based on D-fG
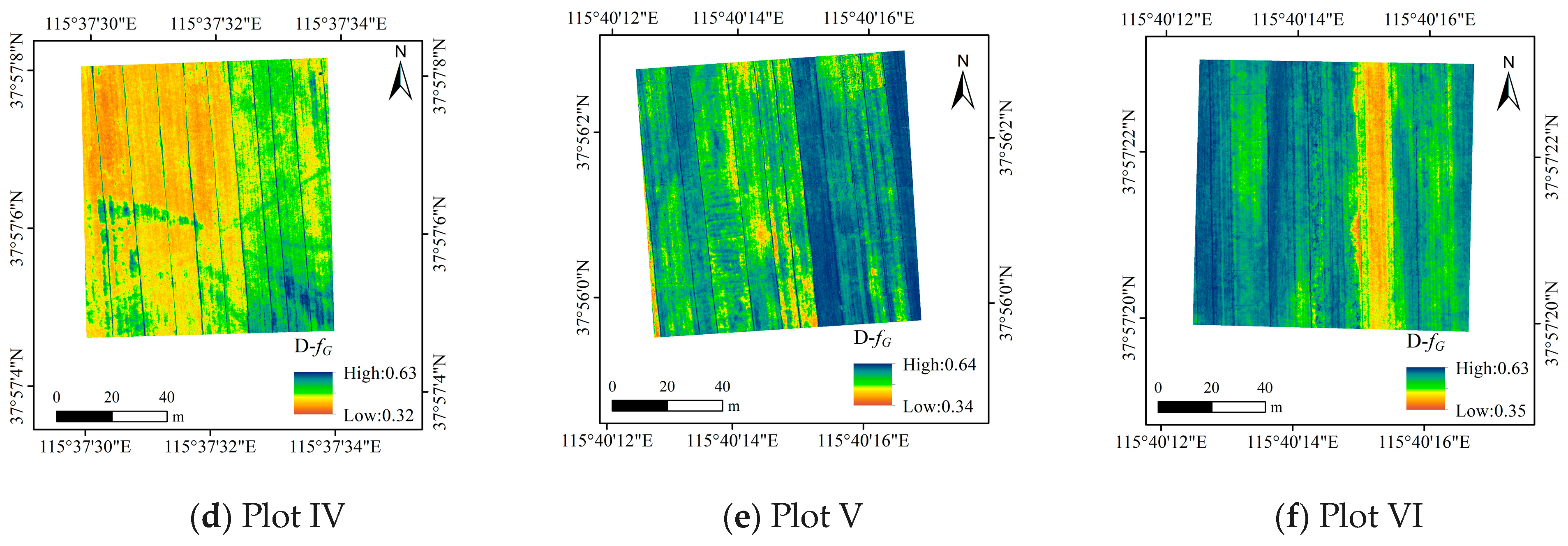
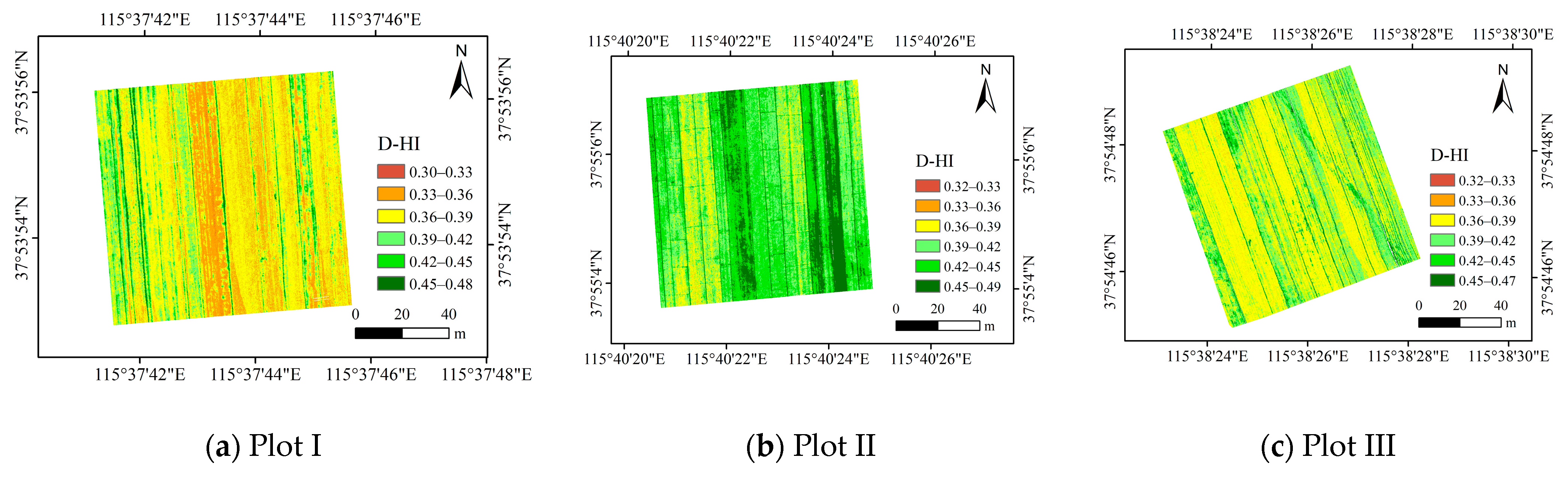
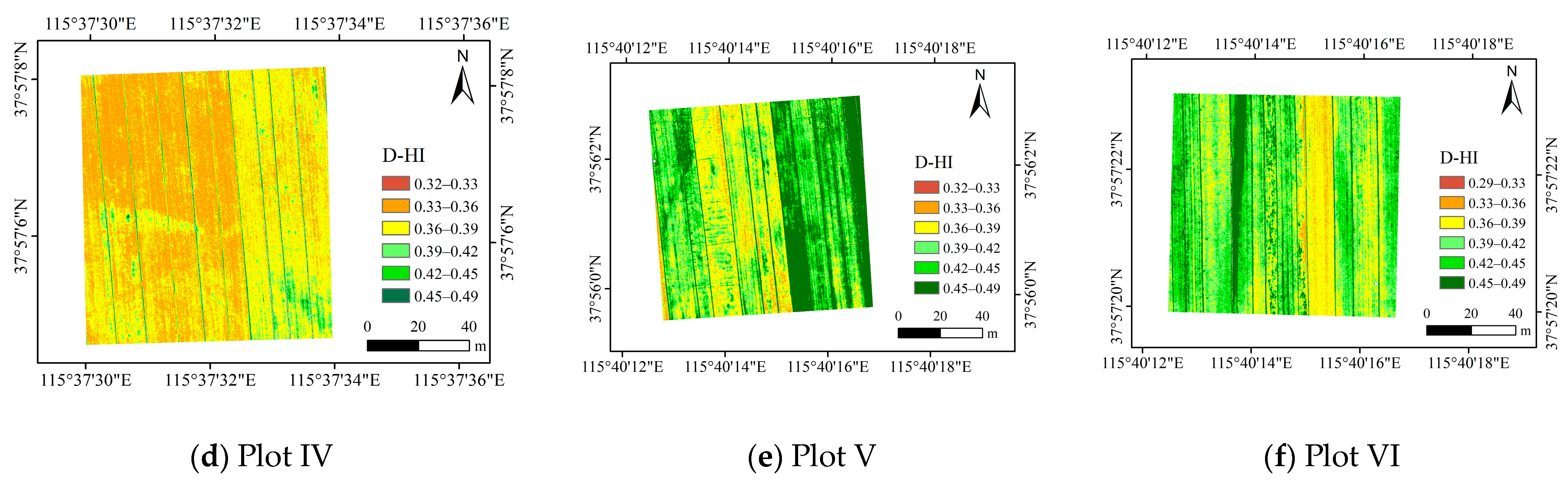
4.2.2. Acquisition and Verification of Spatial D-HI Information via Remote Sensing-Based D-fG Data
5. Discussion
5.1. The Characteristics and Application Potential of the Proposed Method
- (1)
- Full consideration of dynamic crop growth information
- (2)
- High-precision acquisition of D-fG based on optimal selection of sensitive bands
- (3)
- Spatial D-HI information acquisition based on D-fG remote sensing estimation
- (4)
- The potential application of spatial D-HI information acquisition in crops
5.2. Shortcomings and Improvements of the Proposed Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Long, S.; Marshall-Colon, A.; Zhu, X.G. Meeting the global food demand of the future by engineering crop photosynthesis and yield potential. Cell 2015, 161, 56–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donald, C.M. In search of yield. J. Aust. Inst. Agric. Sci. 1962, 28, 171–178. [Google Scholar]
- Donald, C.M.; Hamblin, J. The biological yield and harvest index of cereals as agronomic and plant breeding criteria. Adv. Agron. 1976, 28, 361–405. [Google Scholar]
- Fan, J.; Mcconkey, B.; Janzen, H.; Townley-Smith, L.; Wang, H. Harvest index–yield relationship for estimating crop residue in cold continental climates. Field Crop. Res. 2017, 204, 153–157. [Google Scholar] [CrossRef]
- Hu, C.; Sadras, V.O.; Lu, G.; Zhang, R.; Yang, X.; Zhang, S. Root pruning enhances wheat yield, harvest index and water-use efficiency in semiarid area. Field Crop. Res. 2019, 230, 62–71. [Google Scholar] [CrossRef]
- Lorenz, A.J.; Gustafson, T.J.; Coors, J.G.; Leon, N.D. Breeding maize for a bioeconomy: A literature survey examining harvest index and stover yield and their relationship to grain yield. Crop Sci. 2010, 50, 1–12. [Google Scholar] [CrossRef]
- Moser, S.B.; Feil, B.; Jampatong, S.; Stamp, P. Effects of pre-anthesis drought, nitrogen fertilizer rate, and variety on grain yield, yield components, and harvest index of tropical maize. Agric. Water Manag. 2006, 81, 41–58. [Google Scholar] [CrossRef]
- Soltani, A.; Galeshi, S.; Attarbashi, M.R.; Taheri, A.H. Comparison of two methods for estimating parameters of harvest index increase during seed growth. Field Crop. Res. 2004, 89, 369–378. [Google Scholar] [CrossRef]
- Soltani, A.; Torabi, B.; Zarei, H. Modeling crop yield using a modified harvest index-based approach: Application in chickpea. Field Crop. Res. 2005, 91, 273–285. [Google Scholar] [CrossRef]
- Fletcher, A.L.; Jamieson, P.D. Causes of variation in the rate of increase of wheat harvest index. Field Crop. Res. 2009, 113, 268–273. [Google Scholar] [CrossRef]
- Moriondo, M.; Maselli, F.; Bindi, M. A simple model of regional wheat yield based on NDVI data. Eur. J. Agron. 2007, 26, 266–274. [Google Scholar] [CrossRef]
- Richards, R.A.; Townley-Smith, T.F. Variation in leaf area development and its effect on water use, yield and harvest index of droughted wheat. Crop. Pasture Sci. 1987, 38, 983–992. [Google Scholar] [CrossRef]
- Sadras, V.O.; Connor, D.J. Physiological basis of the response of harvest index to the fraction of water transpired after anthesis: A simple model to estimate harvest index for determinate species. Field Crop. Res. 1991, 26, 227–239. [Google Scholar] [CrossRef]
- Du, X.; Wu, B.; Meng, J.; Li, Q. Estimation of harvest index of winter wheat based on remote sensing data. In Proceedings of the 33rd International Symposium on Remote Sensing of Environment (ISRSE 2009), Stresa, Italy, 4 May 2009. [Google Scholar]
- Ren, J.; Chen, Z.; Zhou, Q.; Tang, H. Retrieving the spatial-explicit harvest index for winter wheat from NDVI time series data. Trans. Chin. Soc. Agric. Eng. 2010, 26, 160–167. (In Chinese) [Google Scholar]
- Kemanian, A.R.; Stockle, C.O.; Huggins, D.R.; Viega, L.M. A simple method to estimate harvest index in grain crops. Field Crop. Res. 2007, 103, 208–216. [Google Scholar] [CrossRef]
- Li, H.; Luo, Y.; Xue, X.; Zhao, Y.; Zhao, H.; Li, F. A comparison of harvest index estimation methods of winter wheat based on field measurements of biophysical and spectral data. Biosyst. Eng. 2011, 109, 396–403. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. 2014, 92, 79–97. [Google Scholar] [CrossRef] [Green Version]
- Maes, W.H.; Steppe, K. Perspectives for remote sensing with unmanned aerial vehicles in precision agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef]
- Singh, K.K.; Frazier, A.E. A meta-analysis and review of unmanned aircraft system (UAS) imagery for terrestrial applications. Int. J. Remote Sens. 2018, 39, 5078–5098. [Google Scholar] [CrossRef]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Gao, L.; Yang, G.; Yu, H.; Xu, B.; Ma, Y. Retrieving winter wheat leaf area index based on unmanned aerial vehicle hyperspectral remote sensing. Trans. Chin. Soc. Agric. Eng. 2016, 32, 113–120. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.; Wang, W.; Chen, X.; Chang, Q. Monitoring of winter wheat nitrogen nutrition based on UAV hyperspectral images. Trans. Chin. Soc. Agric. Eng. 2020, 36, 31–39. (In Chinese) [Google Scholar]
- Pei, H.; Feng, H.; Li, C.; Jin, X.; Li, Z.; Yang, G. Remote sensing monitoring of winter wheat growth with UAV based on comprehensive index. Trans. Chin. Soc. Agric. Eng. 2017, 33, 74–82. (In Chinese) [Google Scholar]
- Deng, X.; Zhu, Z.; Yang, J.; Zheng, Z.; Huang, Z.; Yin, X.; Wei, S.; Lan, Y. Detection of Citrus Huanglongbing based on multi-input neural network model of UAV hyperspectral remote sensing. Remote Sens. 2020, 12, 2678. [Google Scholar] [CrossRef]
- Song, P.; Zheng, X.; Li, Y.; Zhang, K.; Huang, J.; Li, H.; Zhang, H.; Liu, L.; Wei, C.; Mansaray, L.R.; et al. Estimating reed loss caused by Locusta migratoria manilensis using UAV-based hyperspectral data. Sci. Total Environ. 2020, 719, 137519. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Wang, J.; Song, X.; Feng, H. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least squares regression using hyperspectral measurements. Comput. Electron. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Tao, H.; Xu, L.; Feng, H.; Yang, G.; Yang, X.; Miao, M.; Dai, Y. Estimation of plant height and biomass of winter wheat based on UAV digital image. Trans. Chin. Soc. Agric. Eng. 2019, 35, 107–116. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, B.; Zhang, M. Estimating the above ground biomass of winter wheat using the Sentinel-2 data. J. Remote Sens. 2017, 21, 318–328. (In Chinese) [Google Scholar] [CrossRef]
- Chen, H.; Huang, W.; Li, W.; Niu, Z.; Xing, S. Estimation of LAI in winter wheat from multi-angular hyperspectral VNIR data: Effects of view angles and plant architecture. Remote Sens. 2018, 10, 1630. [Google Scholar] [CrossRef] [Green Version]
- Inoue, Y.; Pe Uelas, J.; Miyata, A.; Mano, M. Normalized difference spectral indices for estimating photosynthetic efficiency and capacity at a canopy scale derived from hyperspectral and CO2 flux measurements in rice. Remote Sens. Environ. 2008, 112, 156–172. [Google Scholar] [CrossRef]
- Psomas, A.; Kneubühler, M.; Huber, S.; Itten, K.; Zimmermann, N.E. Hyperspectral remote sensing for estimating aboveground biomass and for exploring species richness patterns of grassland habitats. Int. J. Remote Sens. 2011, 32, 9007–9031. [Google Scholar] [CrossRef]
- Gaso, D.V.; Berger, A.G.; Ciganda, V.S. Predicting wheat grain yield and spatial variability at field scale using a simple regression or a crop model in conjunction with Landsat images. Comput. Electron. Agric. 2019, 159, 75–83. [Google Scholar] [CrossRef]
- Khan, A.; Stöckle, C.O.; Nelson, R.L.; Peters, T.; Adam, J.C.; Lamb, B.; Chi, J.; Waldo, S. Estimating Biomass and Yield Using METRIC Evapotranspiration and Simple Growth Algorithms. Agron. J. 2019, 111, 536–544. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Ren, J.; Chen, Z.; Tang, H.; Wu, S.; Li, H. Optimal selection of hyperspectral sensitive band for winter wheat fresh biomass estimation. Trans. Chin. Soc. Agric. Eng. 2016, 32, 125–134. (In Chinese) [Google Scholar]
- Dewenam, L.E.F.; Er-Raki, S.; Ezzahar, J.; Chehbouni, A. Performance evaluation of the WOFOST model for estimating evapotranspiration, soil water content, grain yield and total above-ground biomass of winter wheat in Tensift Al Haouz (Morocco): Application to yield gap estimation. Agronomy 2021, 11, 2480. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Z.; Ren, J.; Zhou, Q. Estimation of crop yield using CERES-Wheat model based on particle filter data assimilation method. Trans. Chin. Soc. Agric. Eng. 2012, 28, 138–146. (In Chinese) [Google Scholar]
- Rinaldi, M.; Losavio, N.; Flagella, Z. Evaluation and application of the OILCROP–SUN model for sunflower in southern Italy. Agric. Syst. 2003, 78, S0308–S0521. [Google Scholar] [CrossRef]
- Djaman, K.; Irmak, S.; Rathje, W.R.; Martin, D.L.; Eisenhauer, D.E. Maize Evapotranspiration, Yield Production Functions, Biomass, Grain Yield, Harvest Index, and Yield Response Factors under Full and Limited Irrigation. Trans. ASABE 2013, 56, 373–393. [Google Scholar] [CrossRef]
- Gajić, B.; Kresović, B.; Tapanarova, A.; Životić, L.; Todorović, M. Effect of irrigation regime on yield, harvest index and water productivity of soybean grown under different precipitation conditions in a temperate environment. Agric. Water Manag. 2018, 210, 224–231. [Google Scholar] [CrossRef]
- Cui, Z.; Kerekes, J.P. Potential of Red Edge Spectral Bands in Future Landsat Satellites on Agroecosystem Canopy Green Leaf Area Index Retrieval. Remote Sens. 2018, 10, 1458. [Google Scholar] [CrossRef] [Green Version]





| Parameter | Pika L |
|---|---|
| Spectral Range (nm) | 400–1000 |
| Spectral Resolution (nm) | 2.1 |
| Spectral Channels | 281 |
| Spectral Sampling (nm) | 1.07 |
| Spectral Pixels | 561 |
| Spatial Channels | 900 |
| Max Frame Rate (fps) | 249 |
| Bit Depth | 12 |
| Weight (lb/kg) | 1.3/0.6 |
| Dimensions (cm) | 10.0 × 12.5 × 5.3 |
| Sensitive Band Centers λ(λ1, λ2) for D-fG | Relationship between the NDSI (λ1, λ2) and D-fG (N = 72) | Estimation Accuracy of D-fG (N = 36) | |||||
|---|---|---|---|---|---|---|---|
| λ1/nm | λ2/nm | Regression Model | R2 | R2 | RMSE | NRMSE/% | MRE/% |
| 476 | 508 | y = 1.5113x + 0.2584 | 0.6627 ** | 0.7935 ** | 0.0514 | 12.15 | 10.03 |
| 444 | 644 | y = 0.7415x + 0.1803 | 0.6843 ** | 0.7425 ** | 0.0533 | 12.60 | 10.12 |
| 608 | 788 | y = −0.6847x + 0.8761 | 0.6047 ** | 0.7061 ** | 0.0569 | 13.44 | 11.36 |
| 724 | 784 | y = −0.6985x + 0.6995 | 0.6592 ** | 0.8595 ** | 0.0436 | 10.31 | 8.28 |
| 816 | 908 | y = 2.7589x + 0.3468 | 0.6062 ** | 0.6521 ** | 0.0604 | 14.27 | 12.55 |
| Indicator | Crop Growth Stage | Statistical Indicator | Statistics of the Estimation Results in Each Plot | |||||
|---|---|---|---|---|---|---|---|---|
| Plot I | Plot II | Plot III | Plot IV | Plot V | Plot VI | |||
| NDSI | Filling stage | Minimum | 0.31 | 0.29 | 0.33 | 0.30 | 0.29 | 0.30 |
| Maximum | 0.69 | 0.63 | 0.63 | 0.64 | 0.64 | 0.70 | ||
| Mean | 0.52 | 0.40 | 0.48 | 0.54 | 0.41 | 0.44 | ||
| Maturity stage | Minimum | 0.09 | 0.10 | 0.08 | 0.10 | 0.09 | 0.10 | |
| Maximum | 0.53 | 0.52 | 0.51 | 0.53 | 0.51 | 0.50 | ||
| Mean | 0.32 | 0.29 | 0.26 | 0.34 | 0.19 | 0.20 | ||
| D-fG | Filling stage | Minimum | 0.21 | 0.25 | 0.25 | 0.25 | 0.25 | 0.21 |
| Maximum | 0.49 | 0.50 | 0.47 | 0.49 | 0.50 | 0.49 | ||
| Mean | 0.33 | 0.41 | 0.35 | 0.32 | 0.41 | 0.39 | ||
| Maturity stage | Minimum | 0.32 | 0.33 | 0.34 | 0.32 | 0.34 | 0.35 | |
| Maximum | 0.64 | 0.63 | 0.65 | 0.63 | 0.64 | 0.63 | ||
| Mean | 0.47 | 0.49 | 0.51 | 0.46 | 0.56 | 0.55 | ||
| Sensitive Band Centers λ(λ1, λ2) for D-fG | Overall Verification Accuracy of the D-HI (N = 36) | ||||
|---|---|---|---|---|---|
| λ1/nm | λ2/nm | R2 | RMSE | NRMSE/% | MRE/% |
| 476 | 508 | 0.8077 ** | 0.0444 | 10.22 | 8.86 |
| 444 | 644 | 0.7980 ** | 0.0483 | 11.11 | 9.36 |
| 608 | 788 | 0.7530 ** | 0.0514 | 11.85 | 10.31 |
| 724 | 784 | 0.8573 ** | 0.0429 | 9.87 | 8.33 |
| 816 | 908 | 0.6570 ** | 0.0546 | 12.57 | 10.90 |
| Indicator | Crop Growth Stage | Statistical Indicator | Statistics of D-HI Estimation Results in Each Plot | |||||
|---|---|---|---|---|---|---|---|---|
| Plot I | Plot II | Plot III | Plot IV | Plot V | Plot VI | |||
| D-HI | Filling stage | Minimum | 0.30 | 0.32 | 0.32 | 0.32 | 0.32 | 0.29 |
| Maximum | 0.48 | 0.49 | 0.47 | 0.49 | 0.49 | 0.49 | ||
| Mean | 0.38 | 0.43 | 0.39 | 0.37 | 0.43 | 0.41 | ||
| Maturity stage | Minimum | 0.37 | 0.37 | 0.38 | 0.37 | 0.38 | 0.38 | |
| Maximum | 0.58 | 0.58 | 0.59 | 0.58 | 0.58 | 0.58 | ||
| Mean | 0.47 | 0.48 | 0.50 | 0.46 | 0.53 | 0.52 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Zhang, N.; Liu, X.; Wu, S.; Li, D. Dynamic Harvest Index Estimation of Winter Wheat Based on UAV Hyperspectral Remote Sensing Considering Crop Aboveground Biomass Change and the Grain Filling Process. Remote Sens. 2022, 14, 1955. https://doi.org/10.3390/rs14091955
Ren J, Zhang N, Liu X, Wu S, Li D. Dynamic Harvest Index Estimation of Winter Wheat Based on UAV Hyperspectral Remote Sensing Considering Crop Aboveground Biomass Change and the Grain Filling Process. Remote Sensing. 2022; 14(9):1955. https://doi.org/10.3390/rs14091955
Chicago/Turabian StyleRen, Jianqiang, Ningdan Zhang, Xingren Liu, Shangrong Wu, and Dandan Li. 2022. "Dynamic Harvest Index Estimation of Winter Wheat Based on UAV Hyperspectral Remote Sensing Considering Crop Aboveground Biomass Change and the Grain Filling Process" Remote Sensing 14, no. 9: 1955. https://doi.org/10.3390/rs14091955
APA StyleRen, J., Zhang, N., Liu, X., Wu, S., & Li, D. (2022). Dynamic Harvest Index Estimation of Winter Wheat Based on UAV Hyperspectral Remote Sensing Considering Crop Aboveground Biomass Change and the Grain Filling Process. Remote Sensing, 14(9), 1955. https://doi.org/10.3390/rs14091955







