Abstract
Previous ground-based, radar lunar imaging experiments have usually employed the Range-Doppler (RD) algorithm. This algorithm performs in the frequency domain and has high computational efficiency. However, in the case of a long coherent integration time, the defocus phenomenon will appear, and the image will be smeared. This study proposes the use of the back projection (BP) algorithm to obtain focused lunar images to solve this problem. The BP algorithm is a time-domain algorithm which is frequently employed in synthetic aperture radar (SAR) imaging and can theoretically achieve the focused imaging of each pixel in an arbitrarily long coherent integration time. However, the largest drawback of this algorithm is its high computational complexity. Therefore, this study only applies this method to map local regions of the moon. We select Sanya incoherent scatter radar (SYISR) as the transmitting and receiving device and utilize the linear frequency modulation chirp pulse to transmit right-hand, circularly polarized electromagnetic waves and to receive left-hand, circularly polarized echoes. RD and BP algorithms are simultaneously adopted to image the Pythagoras crater region, and a contrastive analysis is performed. The results show that the BP algorithm can be well applied to a ground-based, radar lunar imaging experiment and that it has a better focusing performance, but the effect is not as obvious as expected. Thus, the processing method needs to be further improved. In addition, the computational efficiency of BP is very low, and certain fast algorithms need to be applied to improve it.
1. Introduction
A commonly employed signal processing algorithm in ground-based, radar lunar imaging research is the range-Doppler (RD) algorithm. This algorithm was widely employed in synthetic aperture radar (SAR) imaging and was subsequently applied to ground-based, radar lunar imaging [1]. The algorithm obtains range resolution by pulse compression in the fast time dimension and azimuth resolution by discrete Fourier transform to coherently accumulate the Doppler signal in a slow time dimension within synthetic aperture, thereby realizing two-dimensional imaging. The advantage is that the discrete Fourier transform can obtain all azimuth information at the same range gate, so the imaging efficiency is high. However, the RD algorithm typically uses the move of the moon’s centroid instead of every point on the lunar surface to complete the motion compensation; thus, the acquired image is actually an unfocused image [2,3]. For unfocused images, when the coherent integration time is too long, smearing occurs when the target point on the lunar surface moves beyond the resolution cell, limiting the high resolution. Campbell et al. proposed a patch focusing method that divides the imaging area into several patches of appropriate size so that focused imaging can be achieved by compensating for the motion of the patch center instead of all the points in the patch [4]. This method works as expected but also uses an approximation to some extent.
Notably, many algorithms have been proposed for the signal processing of SAR imaging and are mainly divided into two categories, namely, frequency domain algorithms and time domain algorithms. The RD algorithm is a typical frequency domain algorithm. The most commonly employed time-domain algorithm is the back projection (BP) algorithm [5], which processes images pixel by pixel, separately corrects the range migration, and can achieve focused imaging. However, the disadvantage is that the computational complexity is high and varies with an increase in O(n3) (i.e., the time complexity of the BP algorithm increases with the cube of the problem size “n”). However, there are many ways to improve efficiency. First, the speed of the processor can be increased. Furthermore, since the BP algorithm can process data pixel by pixel, it is easy to parallelize. The algorithm has been implemented on graphics processing units (GPUs) [6] and central processing units (CPUs) [7] with multiple cores. Certain fast BP (FBP) algorithms have also been proposed [8].
The BP algorithm actually originated from computer-aided tomography (CAT) technology. To reduce the radiation dose of CAT to protect the health of patients while ensuring high diagnostic quality, several image reconstruction techniques have been developed and applied. As a relatively simple and practical analysis method, the BP algorithm has been widely employed in the reconstruction of CAT images [9]. Munson et al. revealed that the algorithms of CAT and spotlight SAR imaging are similar in principle, which allows the relatively mature CAT imaging technology to be applied to spotlight SAR imaging [10]. The convolution BP algorithm was first applied to SAR imaging in 1992 [11]. Subsequently, the BP algorithm has been widely utilized in SAR imaging because of its strong performance in compensating for any flight path and perfect focusing on any wide bandwidth and accumulation angle [8], and the science community has developed various methods for different situations [12,13,14,15,16,17,18]. The BP algorithm has even been used to image seismic sources [19]. Therefore, the BP algorithm is now an effective and mature image reconstruction technology.
We have done a previous study on lunar imaging using ground-based radar based on RD algorithm [20]. While in this study, it is proposed that the BP algorithm can be employed for lunar imaging. The main significance is that the algorithm can realize focusing imaging with an arbitrarily long integration time to achieve high azimuth resolution. A key point of the algorithm is that the time-varying position information of each target point needs to be applied as a known quantity to ensure accurate motion compensation, and the lunar ephemeris can just meet this requirement. However, due to the limitation of excessive computational complexity, which is the reason that we have not applied the fast optimization algorithm, this study only attempts to realize the BP imaging of local areas of the moon. The subsequent part of this study introduces the collection of lunar echo data and then discusses how to apply the BP algorithm to complete the signal processing and realize image reconstruction. The imaging results of the BP and RD algorithms are compared and analyzed.
2. Materials and Methods
We selected the Sanya Incoherent Scatter Radar (SYISR) as the transmitting and receiving device. SYISR is an active, phased array radar located in Sanya, Hainan Province, China (18.3°N, 109.6°E), with 4096 antenna units. The peak power can reach 2 MW, and the physical aperture of the antenna array is 32.5 m × 24.32 m.
We transmitted a right-hand, circularly polarized electromagnetic wave with a frequency of 430 MHz and a corresponding wavelength of approximately 70 cm. The waveform is a chirp pulse; the pulse length is 2 ms; the waveform bandwidth is 0.3 MHz; the corresponding range resolution after pulse compression is approximately 500 m; and the pulse repetition time (PRT) is adjusted within the range of 43 ms–60 ms to receive the lunar echo during the period that does not overlap the time of transmission. In addition, the selection of the pulse repetition frequency (PRF) should simultaneously meet the conditions of avoiding range and Doppler aliasing:
- (1)
- The PRF should meet the Nyquist sampling rate and exceed the Doppler broadening of the lunar echo. For a wavelength of 70 cm, the broadening is approximately 12 Hz [4];
- (2)
- The PRT is greater than the delay depth of the lunar echo, which corresponds to the time needed for the electromagnetic wave to pass through the diameter of the moon, which is approximately 11.59 ms.
Satisfying these two conditions means that . Therefore, the PRT applied in our experiment fully meets this requirement.
The reflected echoes were also received by SYISR with a sampling frequency of 0.4 MHz, which is slightly larger than the chirp bandwidth and satisfies the Nyquist sampling rate condition. The number of sampling points in one PRT is 8006, which corresponds to a range of approximately 3000 km. In addition, we only receive left-hand, circularly polarized echoes and do not receive right-hand, circularly polarized echoes, which means that we only obtain polarized echoes (echoes polarized in the opposite circular sense to that transmitted; they are termed “OC”) and do not obtain depolarized echoes (echoes polarized in the same circular sense as that transmitted; they are termed “SC”). Since the two echo scattering mechanisms differ [21], the information about the lunar surface or subsurface is usually investigated by the circular polarization ratio (SC/OC power) [2,4].
The half-power beam width of SYISR is approximately 1.4°, which is larger than the field angle (approximately 0.5°) corresponding to the diameter of the moon. As a result, when the central axis of the radar beam points to the moon’s center of mass, all areas on the front of the moon are illuminated, which will cause the Doppler “north–south ambiguity” problem [4]. This problem can be solved by adjusting the beam direction so that only the lunar echoes from the Doppler northern or southern hemisphere are received by the radar [3]. This method was adopted in our experiments to avoid the Doppler “north–south ambiguity” problem.
From December 2020 to March 2021, we conducted 21 lunar imaging experiments. Each of them tracked the Doppler northern and southern hemispheres of the Moon for 15 min, respectively, using the above experimental parameters. When the radar beam was tracking the Moon, the earth self-rotation and Moon orbiting around the earth were considered. We achieved this with the help of ephemeris data. A sequence of beam directions was generated with the time step of 5 s using ephemeris data before the experiment begin. These beam directions focused on the specific illuminating area, so that the echoes from the Doppler northern or southern hemispheres of the Moon were received constantly during the 15 min. The ephemeris data comprise the data published on the internet by Jet Propulsion Laboratory (JPL) of the National Aeronautics and Space Administration (NASA) (https://naif.jpl.nasa.gov/naif/data.html, accessed on 27 August 2020). The related ephemeris calculations are performed by SPICE software, also developed by JPL. During signal processing to generate images, a coherent integration time of 8 min was selected, and the azimuth resolution reached approximately 600 m. We utilized the RD algorithm to process all the data, from which we selected 8 experiments with a high signal-to-noise ratio (SNR) and good imaging quality and then carried out image reconstruction of these data based on the BP algorithm.
3. Signal Processing
RD and BP imaging algorithms were simultaneously performed on the raw data. The purpose is to compare and analyze the results of the two to verify the feasibility and reliability and to assess the performance after applying the BP algorithm to lunar imaging. Since the RD algorithm has been mentioned many times in previous studies [1,2,3,4,21], this study will not introduce it in detail. This section mainly introduces the BP algorithm that is applied in ground-based, radar lunar imaging experiments.
Generally speaking, the imaging process of the BP algorithm can be illustrated by the flowchart in Figure 1. The procedure is presented as follows: first, calculate the two-way delay between the radar position and the target point on the lunar surface at each PRT time; second, perform motion compensation on the signal samples at different PRT times corresponding to the delay; third, coherently integrate to obtain the target point scattering power; and last, cyclically process all target points in the whole imaging region to obtain an image. The BP algorithm does not have any theoretical approximation in principle, so the imaging effect is theoretically better than that of the RD algorithm. However, the pixel-by-pixel imaging calculation process renders this algorithm computationally expensive.
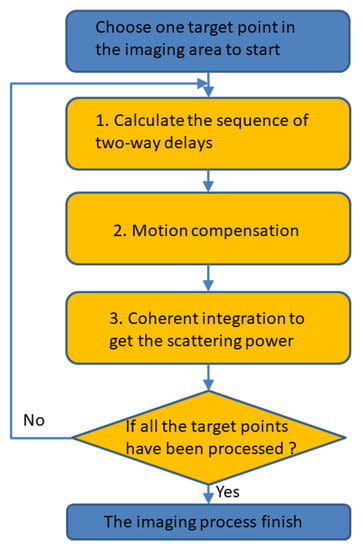
Figure 1.
The flowchart of BP algorithm. The steps indicated in yellow form a loop structure.
After pulse compression, the migration track of the echo signal of the lunar surface target point is curved. The degrees of curvature of different target point migration tracks vary, so different target points need different migration compensation focusing processing, and the BP algorithm just meets this need. In addition, the longer the coherent integration time is, the longer the migration track is, and the more obvious the distinction between the migration tracks of two adjacent target points on the lunar surface is. Thus, a higher resolution can be achieved.
The specific signal processing method is detailed as follows:
- Construct a two-dimensional raw data matrix
Construct the collected complex signals mixed to baseband into a two-dimensional, raw data matrix, consisting of a fast time dimension and slow time dimension, respectively. The fast time dimension is the delay that corresponds to the sequence of sampling times in one PRT, and the slow time dimension is the PRT sequence , where and are positive integers, representing discrete signals. We denote the raw data matrix as . The size of the raw data matrix is a range from to , where means the number of sampling points in one PRT and means the number of PRTs for each 15 min detection; it depends on the PRT value picked from 43 ms to 60 ms.
- 2.
- Pulse compression
We use the simulated chirp reference signal and the data of the fast time dimension in the raw data matrix to perform matched filtering to achieve pulse compression:
where is the data matrix after pulse compression; it has the same size as , represents the convolution operation, and is the complex conjugate of . Schematic (a) in Figure 2 shows a pulse-compressed data matrix.

Figure 2.
The back projection processing. (a) Data matrix after pulse compression. The red line represents the migration track of target imaging point A. The yellow dots represent the signal samples on the migration track of point A, which are obtained by interpolation. (b) Image obtained by back projection. The red dot denotes target imaging point A.
- 3.
- Calculate the two-way delay and interpolate
First, set the latitude and longitude grid of the target imaging area on the lunar surface, and then process all grid points in a loop. We focused on the Pythagoras crater region of the Moon. The longitude range is 70.37°W~55.37°W, the latitude range is 56.24°N~71.24°N, and the grid point step size is 0.02°. Schematic (b) in Figure 2 shows the latitude and longitude grid of an imaging area, assuming that the latitude and longitude coordinates of target grid point A (marked by the red dot) are . The ephemeris is used to calculate the two-way delay between grid point A and the radar. This two-way delay varies with the slow time, namely . Then, is converted to the LOS (line-of-sight) range , where is the speed of light in vacuum and the change in with constitutes the migration track of target grid point A.
Second, the complex signal data corresponding to the LOS range should be obtained at each , that is, we obtain the complex signal data corresponding to all the yellow dots on the red migration track of target point A in schematic (a) in Figure 2. Two problems need to be solved here:
The first problem is that the range is too large and exceeds the maximum unambiguous range determined by the PRT, so that the echo of one pulse will be received several PRTs later. Thus, the range of the target determined by the traditional equation cannot represent the real range, and we cannot directly obtain the track of target point A in data matrix using . To solve this problem, first, we correct the motion of the moon’s center of mass in the fast time dimension so that the lunar echoes in all PRTs are aligned with the first PRT.
where is the corrected data matrix, is the range from the moon’s center of mass to the radar platform, and is the start time of the first PRT that receives the lunar echo. Second, all aligned PRTs are averaged along the slow time dimension to obtain one-dimensional, fast time sampling, and the fast time coordinate of the maximum echo intensity is detected as , which is considered the echo of the subradar point (SRP) at time . Third, the moon-fixed coordinate vector from the moon’s center of mass pointing to the SRP at is obtained as from the ephemeris. The latitude and longitude of target grid point A are also converted to a moon-fixed coordinate vector . Fourth, calculate the fast time coordinate of the echo from point A at time according to the observation geometry (shown in Figure 3):
where is the average radius of the moon and is the angle between vector and vector . Last, calculate the range difference of target point A between times and , which is . According to this range difference, the fast time coordinates of target point A at other times can be calculated,
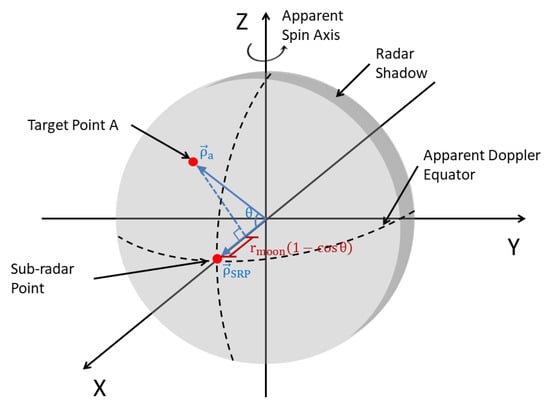
Figure 3.
Diagram showing the observation geometry. A Cartesian coordinate system whose original point is located at the Moon’s center of mass (COM) is employed. The X-axis points to the radar and it is the range direction, the Z-axis extends along the apparent spin axis toward the north, and the Y-axis follows the right-hand rule.
The second problem is that it is usually impossible to find a suitable value of so that . This is because the radar data are discrete sampling points, which means that , where is the sampling period and is a positive integer. While is a positive real number. Figure 2 shows that the yellow dots determined by usually cannot be exactly located at the intersection of the black lines determined by , so interpolation needs to be performed. The interpolation method that we selected is time domain function interpolation:
where , means rounding to the nearest integer; is the dataset on the migration track of target point A obtained after interpolation, that is, the dataset corresponding to all the yellow dots in Figure 2; the function is defined as ; and is used to limit the length of the interpolation window.
- 4.
- Migration compensation and coherent integration
During the coherent integration time, all the data (yellow dots in Figure 2) on the migration track (red line in Figure 2) of target point A are integrated after migration compensation (white arrow in Figure 2). The result is projected on the corresponding latitude and longitude grid point A (red dots in Figure 2),
where is the scattered echo intensity of target point A obtained by BP, is the number of PRTs to be integrated, and is the radar wavelength, for SYISR . The coherent integration after migration compensation can enhance the echo of target point A by in-phase superposition, while the echoes of other scattering points within the same range gate as target point A can be suppressed due to the existence of a phase difference.
- 5.
- Correction of echo power
The incident angle, scattering cell area, and antenna pattern will affect the echo power. To retain only the scattering information of the lunar surface and subsurface, we corrected these three influencing factors. We refer to the lunar polarized echo power detected by 68 cm wavelength variations with the incident angle summarized in the article [21] to correct the influence of the incident angle. We use the theoretically calculated area of the lunar surface scattering cells corresponding to each pixel in the imaging area to calculate the echo power per unit area, thereby correcting the effect of the scattering cell area. The projection of the antenna pattern on each pixel in the imaging area is calculated by theoretical simulation and ephemeris, and this effect is also corrected in the echo power. The calculation of the antenna pattern of phased array radar is discussed in the articles [22,23].
4. Results and Discussion
The BP algorithm is performed pixel by pixel, and the computational efficiency is very low, so this study only conducts the BP imaging experiment on a partial area of the lunar front side. The imaging area is selected as the Pythagoras crater region. In addition, to compare and verify the effect of the BP algorithm, we imaged the Pythagoras crater region using the RD algorithm. Figure 4 shows the imaging results of the RD algorithm (including coherent integration times of 4 min and 8 min, respectively) and the BP algorithm (coherent integration time of 8 min) of Pythagoras crater in the experiment on 23 January 2021. For either the RD algorithm or BP algorithm, the imaging resolution in this area is approximately 520 m × 1240 m with a coherent integration time of 4 min and approximately 520 m × 620 m with a coherent integration time of 8 min. A grid point step size of 0.02° corresponds to a lunar surface distance of approximately 600 m, which can well reflect the change in resolution. To better show the details and to facilitate comparative analysis, we magnified the smaller area of longitude range 64.5°W~61.5°W and latitude range 62.5°N~65°N. This area is marked with a red rectangle in Figure 4 and is shown in Figure 5.

Figure 4.
Imaging results of the Pythagoras crater region on the Doppler northern hemisphere of the front side of the moon. The imaging longitude range is 70.37°W~55.37°W. The latitude range is 56.24°N~71.24°N. The grid point step size is 0.02°. (a) Image obtained by the range-Doppler algorithm with a coherent integration time of 4 min. (b) Image obtained by the range-Doppler algorithm with a coherent integration time of 8 min. (c) Image obtained by the back projection algorithm with a coherent integration time of 8 min. The red rectangle on each image represents the magnified area shown in Figure 5.
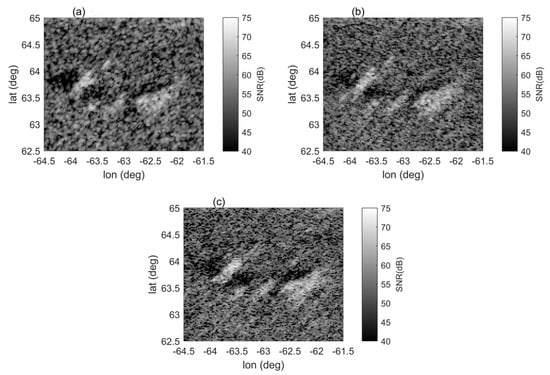
Comparing the RD algorithm imaging results of the coherent integration times of 4 min and 8 min, the longer integration time can show more details due to the higher resolution. However, the image with 8 min coherent integration time has defocusing phenomenon caused by the movement of the scattering points on the lunar surface exceeding the resolution cell during the coherent integration time. This causes the smearing of the image. Compared with the RD imaging results with a coherent integration time of 4 min, the BP imaging results with a coherent integration time of 8 min have higher resolution and more details. Compared with the RD imaging results with the same coherence integration time of 8 min, it is determined that the resolution is similar and that the defocusing phenomenon has been improved to a certain extent, but it is not as obvious as expected. Based on this finding, it can be preliminarily summarized that the application of the BP algorithm in the ground-based, radar lunar imaging experiment has feasibility and reliability. The focusing performance of the BP algorithm can solve the defocusing problem of the RD algorithm to a certain extent. However, the results of this study reveal that the focusing performance is not obvious, which may be attributed to certain errors introduced from the calculation process, such as the error of the ephemeris, the lunar sphere approximation, and the effect of disregarding parallax. The resulting impact and how to improve these results needs further exploration. In addition, the computational efficiency of the BP algorithm is very low, which will greatly increase the time cost of calculation, and certain fast algorithms need to be applied to improve the efficiency.
Figure 5 shows that the noise speckle is obvious. The method of averaging multiple images in the same imaging area is usually adopted to suppress noise [4]. However, we did not adopt this method because the experiments were distributed on different days from January to March 2021 and the observation geometry of each imaging was different. As a result, for the same area of the lunar surface, such as the Pythagoras crater area, the resolution of the lunar surface for each imaging varies, which influences the averaging effect. Figure 6 can explain the problem more clearly and intuitively. Subfigures (a) and (b) show the results of the experiment on 23 January 2021, and subfigures (c) and (d) show the results of the experiment on 7 February 2021. The distribution of the lunar, front-side Northern Hemisphere image obtained by the RD algorithm on the Doppler equatorial plane is a semicircle, and the arc line is the Doppler equator. The closer the distance to the Doppler equator, the lower the resolution. The position of the Pythagoras crater on the Doppler equatorial plane (marked with a red rectangle) was significantly different between 23 January and 7 February and was closer to the Doppler equator on 7 February, which reduced the resolution of the crater image. This conclusion is evident from the comparison of the BP images of subfigures (b) and (d). Therefore, the averaging of images of different dates means the averaging of images of different resolutions. This averaging causes smearing and in turn affects the judgment of the imaging performance of the BP algorithm.
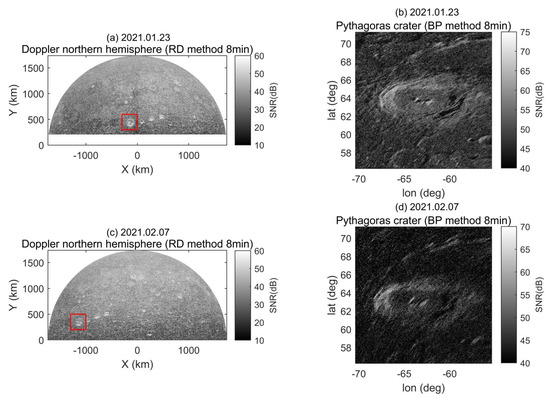
Figure 6.
Imaging results used to explain why not to average multiple images obtained from the experiments on different dates. (a,b) are the results of the experiment on 23 January 2021. (c,d) are the results of the experiment on 7 February 2021. (a,c) are the images of the Doppler Northern Hemisphere of the front side of the moon. These images are obtained by the range-Doppler algorithm with a coherent integration time of 8 min. (b,d) are the images of the Pythagoras crater region obtained by the back projection algorithm with a coherent integration time of 8 min. The red rectangles represent the position of the Pythagoras crater region on the Doppler northern hemisphere of the front side of the moon.
5. Conclusions
We propose applying the BP algorithm in the SAR imaging technique to the signal processing of ground-based, radar lunar imaging experiments. The purpose is to solve the defocusing problem of the RD algorithm in the case of a long coherent integration time and thus to improve the imaging quality. We performed many monostatic lunar imaging experiments using SYISR and implemented the BP algorithm. The imaging results show that applying the BP algorithm in ground-based, radar lunar imaging experiments has a certain feasibility and reliability. The results also show a certain focusing performance. However, the comparison between the imaging results obtained by the RD and BP algorithms indicated that the focusing performance of BP is not obvious. According to the study in this article, we summarized some reasons for this issue. Firstly, the BP algorithm requires accurate migration correction, so the error involved in the experiments and processing procedure will affect the focusing performance. Secondly, the noise speckle is obvious in the images and it will affect the evaluation of the focusing performance. Future work may focus on these two aspects and make the improvement. In fact, some indicators, such as entropy and sharpness, can perhaps evaluate the image quality, so that the focusing performance of BP can be quantified. This will also be a part of the future work. In addition, certain fast algorithms need to be applied to improve the computational efficiency of the BP algorithm.
Author Contributions
Conceptualization, M.L. and X.Y.; methodology, M.L. and L.H.; software, M.L.; validation, M.L. and L.H.; formal analysis, X.Y.; investigation, M.L.; resources, M.L., Y.W., Z.W., J.W., N.Z. and J.L.; data curation, M.L., Y.W., Z.W., J.W., N.Z. and J.L.; writing—original draft preparation, M.L.; writing—review and editing, X.Y., F.D., B.N., J.W., N.Z. and L.H.; visualization, M.L.; supervision, X.Y.; project administration, X.Y.; funding acquisition, X.Y., F.D. and B.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the B-type Strategic Priority Program of the Chinese Academy of Sciences, grant number XDB4100000 and The Meridian Project and the National Natural Science Foundation of China, grant number 41427901.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pettengill, G.H.; Henry, J.C. Enhancement of radar reflectivity associated with the lunar crater Tycho. J. Geophys. Res. 1962, 67, 4881–4885. [Google Scholar] [CrossRef]
- Vierinen, J.; Tveito, T.; Gustavsson, B.; Kesaraju, S.; Milla, M. Radar images of the moon at 6-meter wavelength. Icarus 2017, 297, 179–188. [Google Scholar] [CrossRef] [Green Version]
- Vierinen, J.; Lehtinen, M.S. 32-cm wavelength radar mapping of the Moon. In Proceedings of the 2009 European Radar Conference, EuRAD, Rome, Italy, 30 September–2 October 2009. [Google Scholar]
- Campbell, B.A.; Campbell, D.B.; Margot, J.L.; Ghent, R.R.; Nolan, M.; Chandler, J.; Carter, L.M.; Stacy, N.J.S. Focused 70-cm wavelength radar mapping of the moon. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4032–4042. [Google Scholar] [CrossRef]
- Soumekh, M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Fasih, A.; Hartley, T. GPU-accelerated synthetic aperture radar backprojection in CUDA. In Proceedings of the 2010 IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010. [Google Scholar]
- Park, J.; Tang, P.T.P.; Smelyanskiy, M.; Kim, D.; Benson, T. Efficient backprojection-based synthetic aperture radar computation with many-core processors. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 11 October 2011; pp. 1–11. [Google Scholar]
- Yegulalp, A. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium, Waltham, MA, USA, 22 April 1999. [Google Scholar]
- Willemink, M.J.; Noël, P.B. The evolution of image reconstruction for CT—From filtered back projection to artificial intelligence. Eur. Radiol. 2019, 29, 2185–2195. [Google Scholar] [CrossRef] [Green Version]
- Munson, D.C.; O’Brien, J.D.; Jenkins, W.K. A tomographic formulation of spotlight-mode synthetic aperture radar. Proc. IEEE 1983, 71, 917–925. [Google Scholar] [CrossRef]
- Desai, M.D.; Jenkins, W.K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar. IEEE Trans. Image Process. A Publ. IEEE Signal Process. Soc. 1992, 1, 505–517. [Google Scholar] [CrossRef]
- Cho, Y.S.; Jung, H.K.; Cheon, C.; Chung, Y.S. Adaptive Back-Projection Algorithm Based on Climb Method (CM-ABP) for Microwave Imaging. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, X.; He, S.; Zhao, H.; Shi, J. A Less-Memory and High-Efficiency Autofocus Back Projection Algorithm for SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 890–894. [Google Scholar]
- Li, Z.; Wang, J.; Liu, Q.H. Frequency-Domain Backprojection Algorithm for Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 905–909. [Google Scholar]
- Lin, J.; Lv, X.; Li, R. Automatic registered back-projection approach based on object orientation for airborne repeat-track interferometric SAR. IET Radar Sonar Navig. 2018, 12, 1066–1076. [Google Scholar] [CrossRef]
- Meng, D.; Ding, C.; Hu, D.; Qiu, X.; Huang, L.; Han, B.; Liu, J.; Xu, N. On the Processing of Very High Resolution Spaceborne SAR Data: A Chirp-Modulated Back Projection Approach. IEEE Trans. Geosci. Remote Sens. 2017, 99, 1–11. [Google Scholar] [CrossRef]
- Meng, D.; Hu, D.; Ding, C. Precise Focusing of Airborne SAR Data with Wide Apertures Large Trajectory Deviations: A Chirp Modulated Back-Projection Approach. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2510–2519. [Google Scholar] [CrossRef]
- Ozsoy, S. Pencil back-projection method for SAR imaging. IEEE Trans. Image Process. 2009, 18, 573–581. [Google Scholar] [CrossRef] [PubMed]
- Kiser, E.; Ishii, M. Back-projection imaging of earthquakes. Annu. Rev. Earth Planet. Sci. 2017, 45, 271–299. [Google Scholar] [CrossRef]
- Li, M.; Yue, X.; Wang, Y.; Wang, J.; Ding, F.; Vierinen, J.; Zhang, N.; Wang, Z.; Ning, B.; Zhao, B.; et al. Moon imaging technique and experiments based on Sanya incoherent scatter radar. IEEE Trans. Geosci. Remote Sens. 2022. [Google Scholar] [CrossRef]
- Hagfors, T. Remote probing of the moon by infrared and microwave emissions and by radar. Radio Sci. 1970, 5, 189–227. [Google Scholar] [CrossRef]
- Li, M.; Yue, X.; Zhao, B.; Zhang, N.; Wang, J.; Zeng, L.; Hao, H.; Ding, F.; Ning, B.; Wan, W. Simulation of the Signal-to-Noise Ratio of Sanya Incoherent Scatter Radar Tristatic System. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2982–2993. [Google Scholar] [CrossRef]
- Swoboda, J.; Semeter, J.; Erickson, P. Space-time ambiguity functions for electronically scanned ISR applications. Radio Sci. 2015, 50, 415–430. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).