Precipitation Microphysics of Tropical Cyclones over Northeast China in 2020
Abstract
:1. Introduction
2. Data and Methods
3. Results
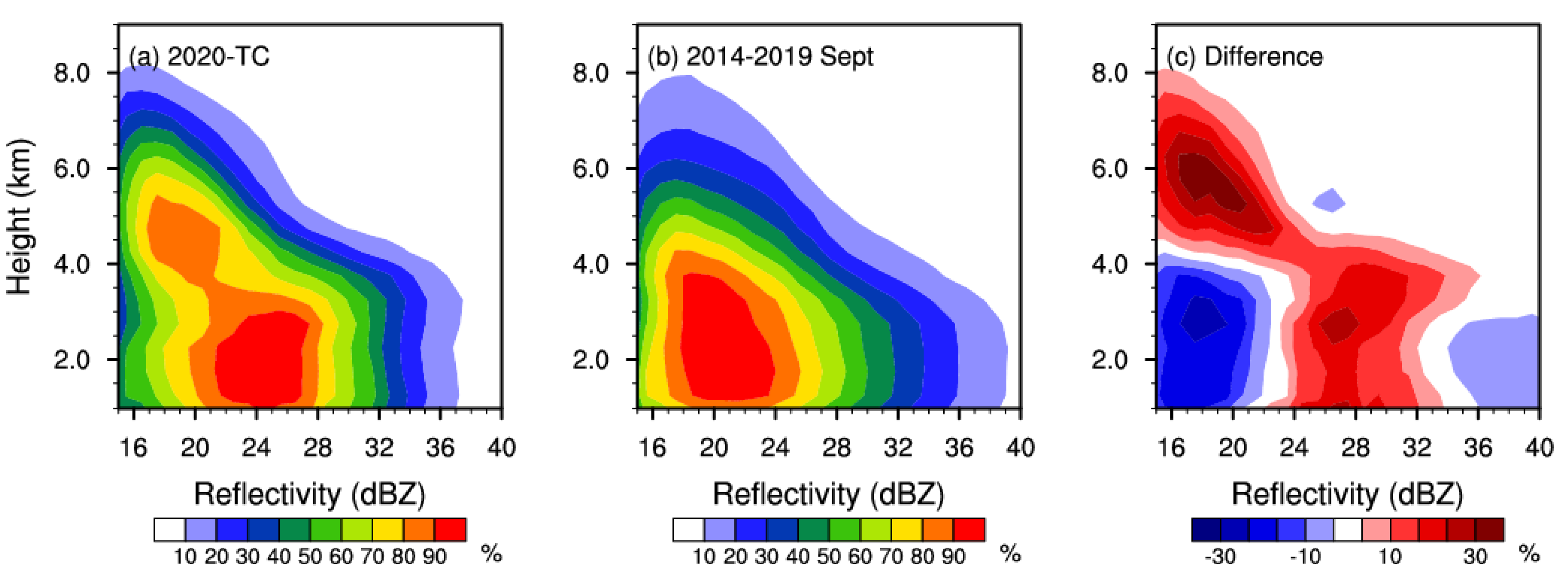
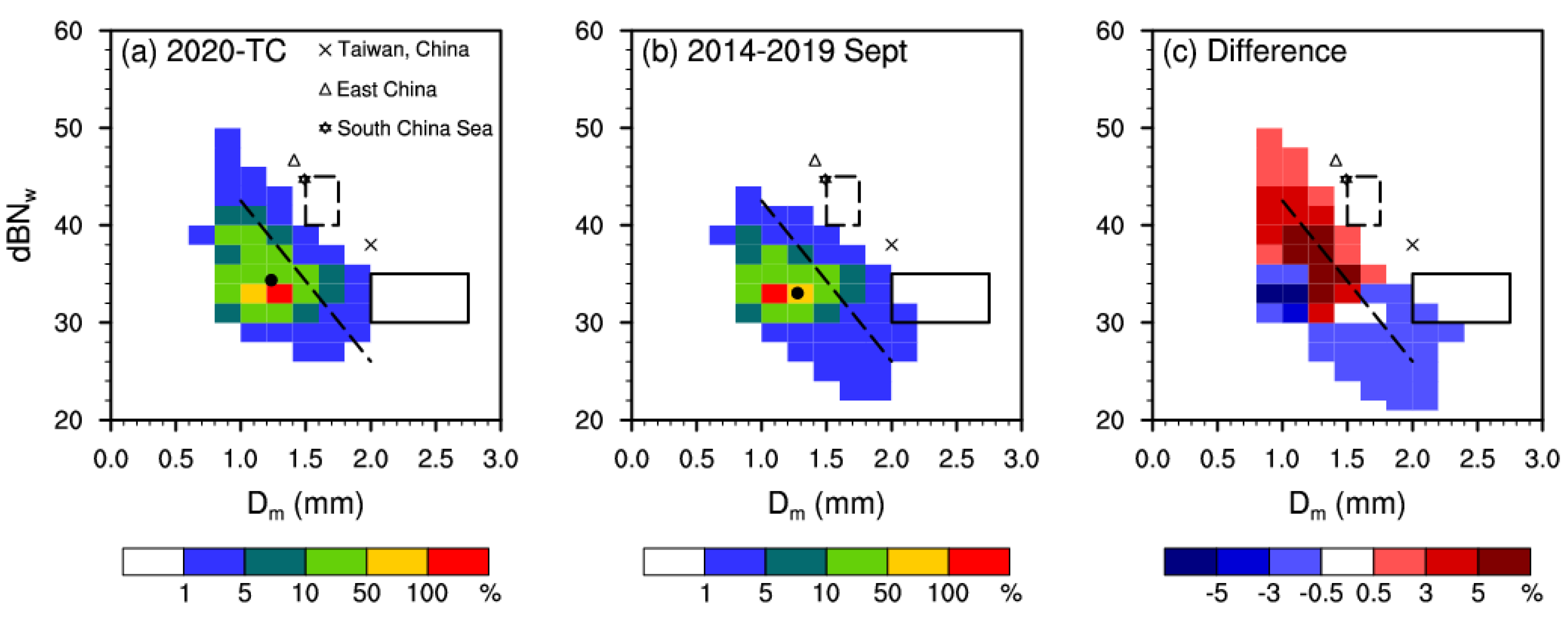
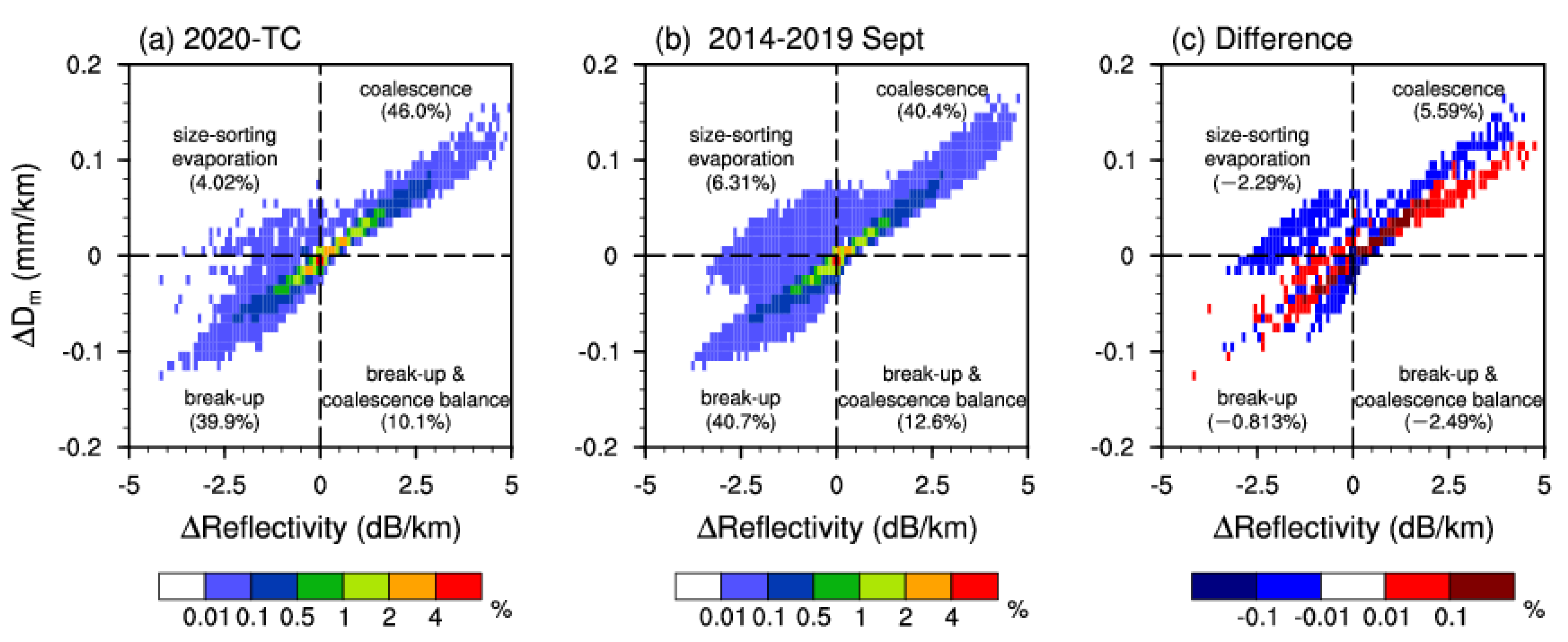
3.1. Differences in Precipitation Microphysics between 2020-TC and September 2014–September 2019
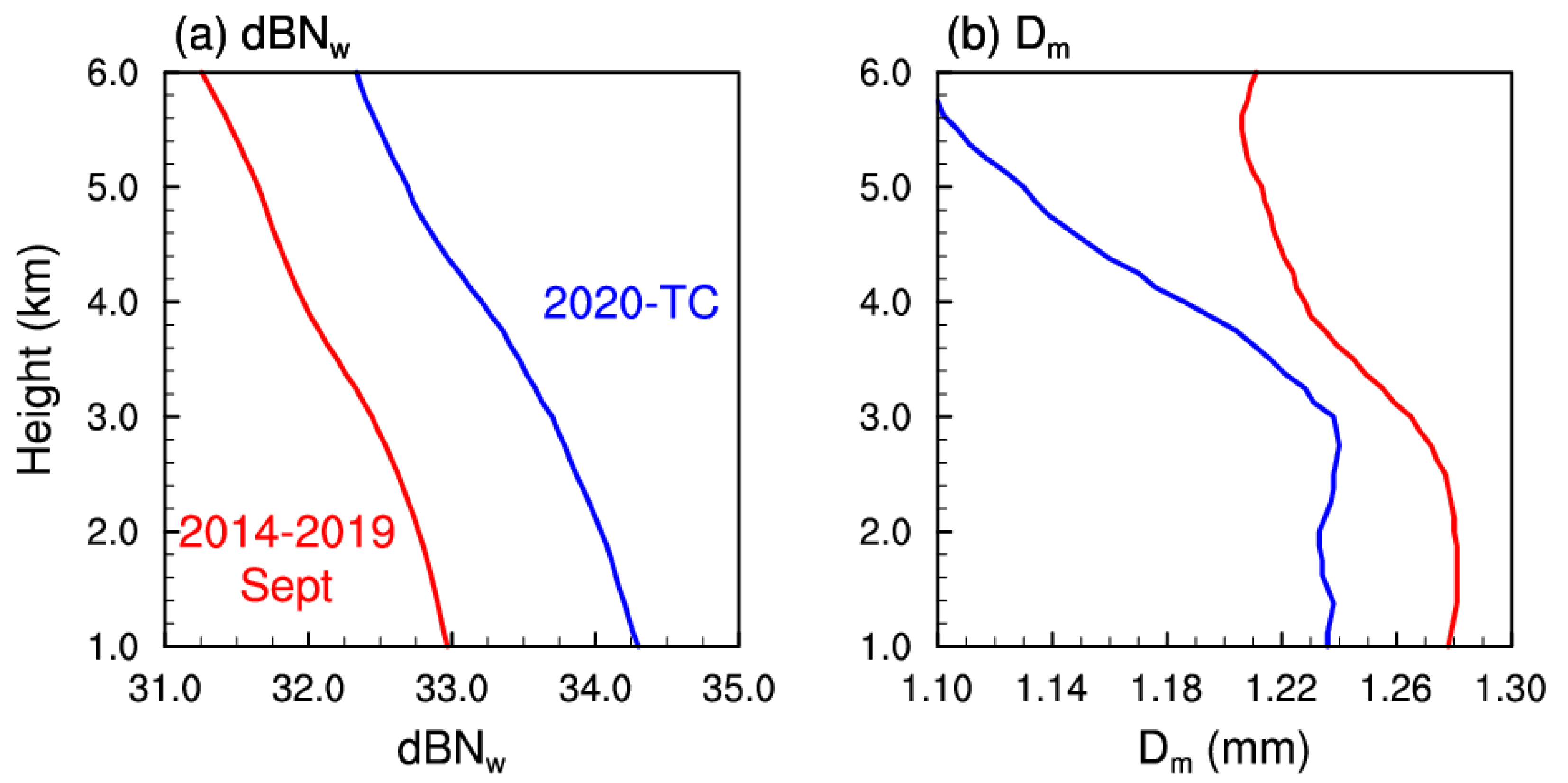
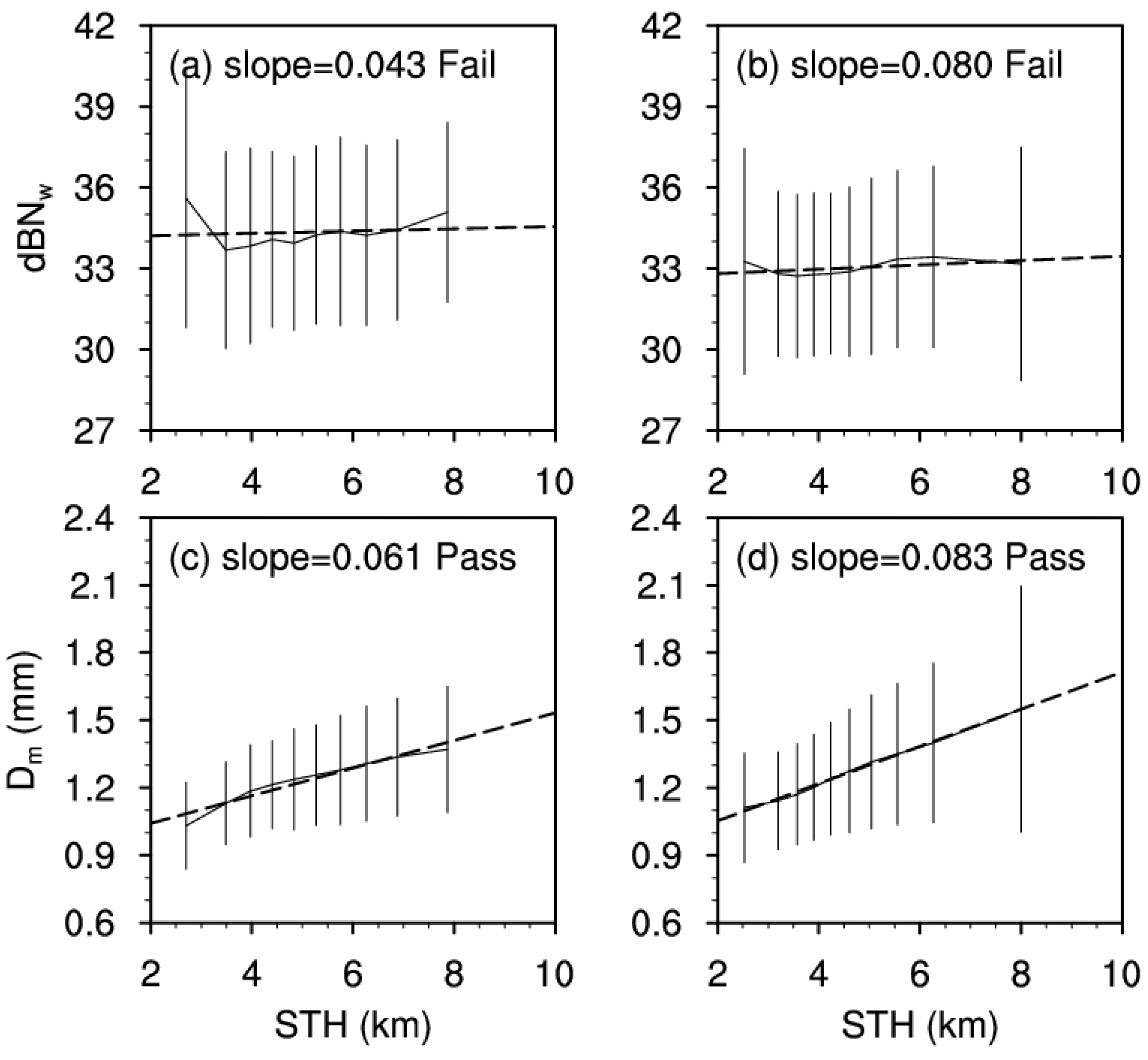
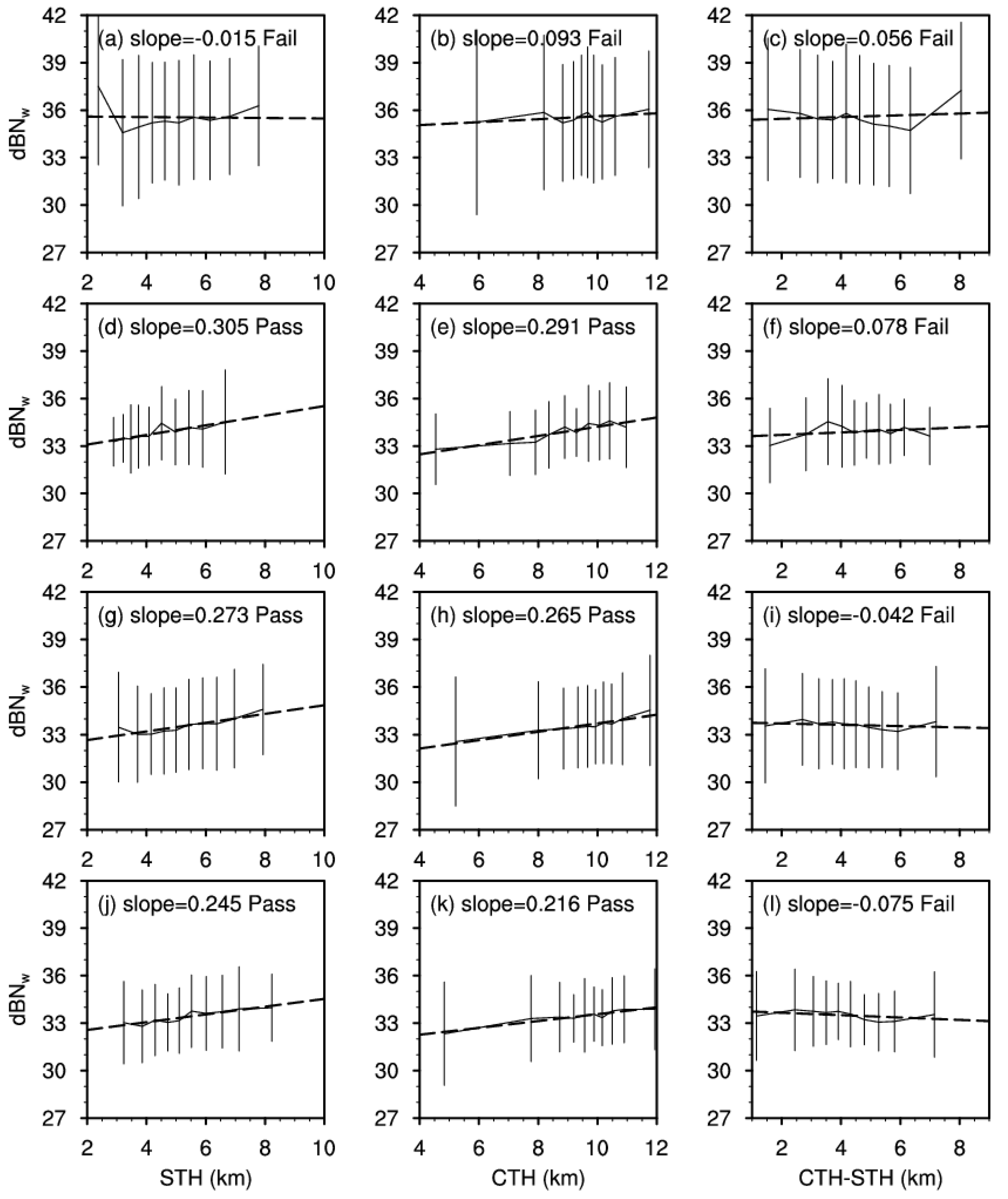
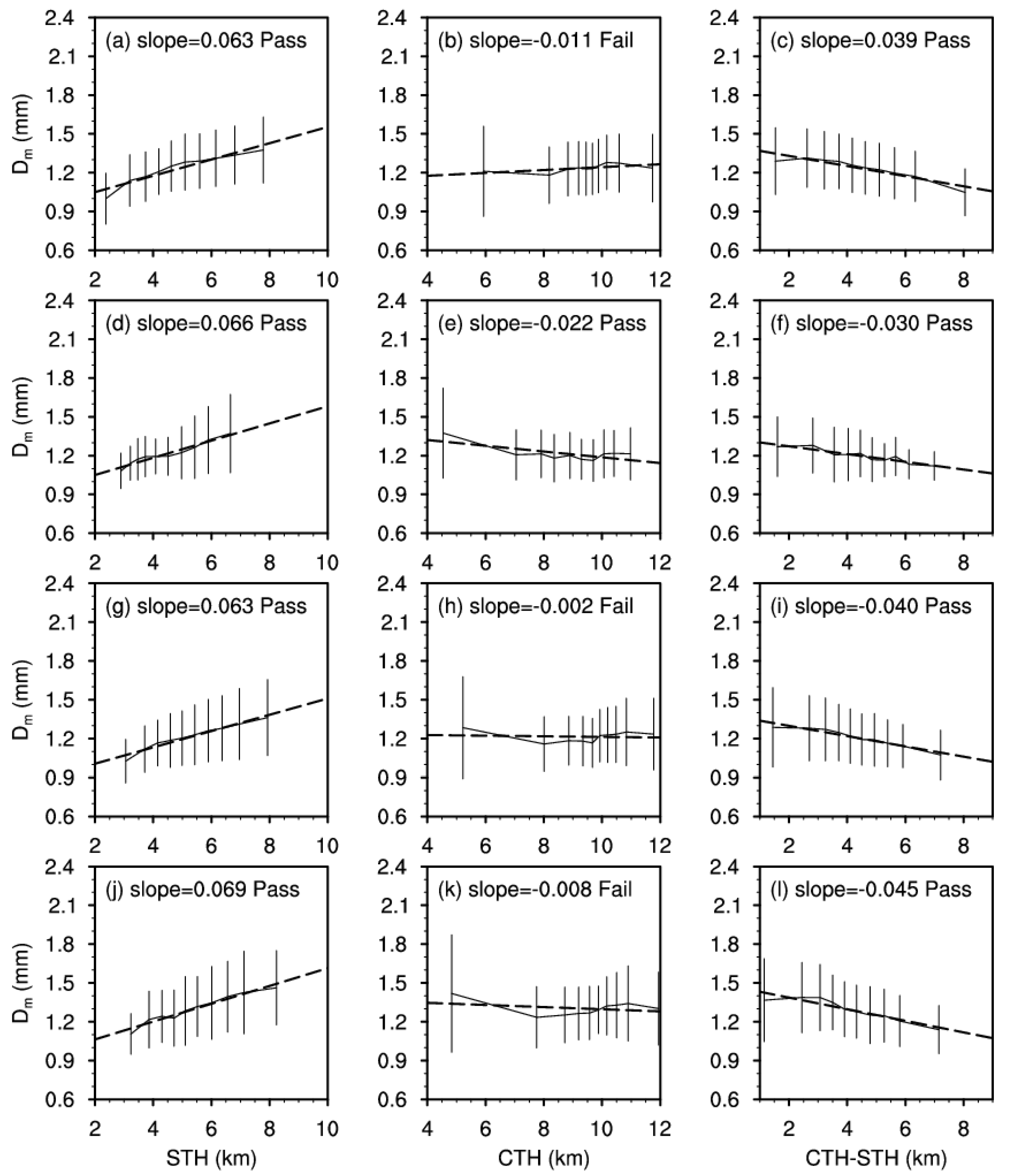
3.2. Relationship between Convective Intensity Indicators and DSDs
4. Discussion
- -
- Positive correlation between STH and Dm passes the test.
- -
- Positive correlation between CTH and dBNw passes the test.
- -
- Negative correlation between CTH-STH and Dm passes the test.
- -
- The other relationships all fail the test.
- -
- Positive correlations of STH (CTH) with dBNw pass the test (except coalescence).
- -
- The relationships between STH (CTH) and dBNw fail the test (coalescence dominant).
- -
- The relationships between STH and Dm pass the test (any conditions).
- -
- Negative correlation between CTH and Dm passes the test (size-sorting or evaporation).
- -
- The relationship between CTH-STH and DSD is the same as when liquid-phase processes are not distinguished.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, W.Y.; Wang, T.C.C.; Lin, P.L. Characteristics of the Raindrop Size Distribution and Drop Shape Relation in Typhoon Systems in the Western Pacific from the 2D Video Disdrometer and NCU C-Band Polarimetric Radar. J. Atmos. Ocean. Technol. 2009, 26, 1973–1993. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of Cloud Microphysics on the Development of Trailing Stratiform Precipitation in a Simulated Squall Line: Comparison of One- and Two-Moment Schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Duan, J.; An, J.; Liu, H. Raindrop Size Distribution Characteristics for Tropical Cyclones and Meiyu-Baiu Fronts Impacting Tokyo, Japan. Atmosphere 2019, 10, 391. [Google Scholar] [CrossRef] [Green Version]
- Janapati, J.; Seela, B.K.; Lin, P.-L.; Lee, M.-T.; Joseph, E. Microphysical features of typhoon and non-typhoon rainfall observed in Taiwan, an island in the northwestern Pacific. Hydrol. Earth Syst. Sci. 2021, 25, 4025–4040. [Google Scholar] [CrossRef]
- Wang, M.J.; Zhao, K.; Lee, W.C.; Zhang, F.Q. Microphysical and Kinematic Structure of Convective-Scale Elements in the Inner Rainband of Typhoon Matmo (2014) After Landfall. J. Geophys. Res.-Atmos. 2018, 123, 6549–6564. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.J.; Zhao, K.; Xue, M.; Zhang, G.F.; Liu, S.; Wen, L.; Chen, G. Precipitation microphysics characteristics of a Typhoon Matmo (2014) rainband after landfall over eastern China based on polarimetric radar observations. J. Geophys. Res.-Atmos. 2016, 121, 12415–12433. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, K.; Chen, G.; Wang, M.; Zhou, B.; Huang, H.; Hu, D.; Lee, W.-C.; Hu, H. Drop Size Distribution Characteristics of Seven Typhoons in China. J. Geophys. Res.-Atmos. 2018, 123, 6529–6548. [Google Scholar] [CrossRef]
- Zheng, H.P.; Zhang, Y.; Zhang, L.F.; Lei, H.C.; Wu, Z.H. Precipitation Microphysical Processes in the Inner Rainband of Tropical Cyclone Kajiki (2019) over the South China Sea Revealed by Polarimetric Radar. Adv. Atmos. Sci. 2021, 38, 65–80. [Google Scholar] [CrossRef]
- Duan, Y.H.; Wan, Q.L.; Huang, J.; Huang, J.; Zhao, K.; Yu, H.; Wang, Y.; Zhao, D.; Feng, J.; Tang, J.; et al. Landfalling Tropical Cyclone Research Project (LTCRP) in China. Bull. Am. Meteorol. Soc. 2019, 100, Es447–Es472. [Google Scholar] [CrossRef]
- Jones, S.C.; Harr, P.A.; Abraham, J.; Bosart, L.F.; Bowyer, P.J.; Evans, J.L.; Hanley, D.E.; Hanstrum, B.N.; Hart, R.E.; Lalaurette, F.; et al. The extratropical transition of tropical cyclones: Forecast challenges, current understanding, and future directions. Weather. Forecast. 2003, 18, 1052–1092. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.Q.; Wang, J.; Gong, D.L.; Zhang, D.G.; Zhang, L.; Zhang, Q.C. Rainfall Microphysical Properties of Landfalling Typhoon Yagi (201814) Based on the Observations of Micro Rain Radar and Cloud Radar in Shandong, China. Adv. Atmos. Sci. 2021, 38, 994–1011. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Huang, H.; Chen, F. Precipitation Microphysics of Tropical Cyclones Over the Western North Pacific Based on GPM DPR Observations: A Preliminary Analysis. J. Geophys. Res.-Atmos. 2019, 124, 3124–3142. [Google Scholar] [CrossRef]
- Chen, F.J.; Fu, Y.F.; Yang, Y.J. Regional Variability of Precipitation in Tropical Cyclones Over the Western North Pacific Revealed by the GPM Dual-Frequency Precipitation Radar and Microwave Imager. J. Geophys. Res.-Atmos. 2019, 124, 11281–11296. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, Y.; Zhang, Y.; Zhang, L.; Lei, H.; Zheng, H. Precipitation characteristics of typhoon Lekima (2019) at landfall revealed by joint observations from GPM satellite and S-band radar. Atmos. Res. 2021, 260, 105714. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, K.; Fu, P.L.; Chen, H.N.; Chen, G.; Zhang, Y. Validation of Precipitation Measurements from the Dual-Frequency Precipitation Radar Onboard the GPM Core Observatory Using a Polarimetric Radar in South China. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4104216. [Google Scholar] [CrossRef]
- Luo, Z.J.; Jeyaratnam, J.; Iwasaki, S.; Takahashi, H.; Anderson, R. Convective vertical velocity and cloud internal vertical structure: An A-Train perspective. Geophys. Res. Lett. 2014, 41, 723–729. [Google Scholar] [CrossRef]
- Huo, J.; Lu, D.R.; Duan, S.; Bi, Y.H.; Liu, B. Comparison of the cloud top heights retrieved from MODIS and AHI satellite data with ground-based Ka-band radar. Atmos. Meas. Tech. 2020, 13, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.Y.; Chiu, C.H.; Lin, P.H.; Min, M. Comparison of Cloud-Top Property Retrievals from Advanced Himawari Imager, MODIS, CloudSat/CPR, CALIPSO/CALIOP, and Radiosonde. J. Geophys. Res.-Atmos. 2020, 125, e2020JD032683. [Google Scholar] [CrossRef]
- Yang, X.; Ge, J.M.; Hu, X.Y.; Wang, M.H.; Han, Z.H. Cloud-Top Height Comparison from Multi-Satellite Sensors and Ground-Based Cloud Radar over SACOL Site. Remote Sens. 2021, 13, 2715. [Google Scholar] [CrossRef]
- Sun, L.X.; Tang, X.D.; Zhuge, X.Y.; Tan, Z.M.; Fang, J. Diurnal Variation of Overshooting Tops in Typhoons Detected by Himawari-8 Satellite. Geophys. Res. Lett. 2021, 48, e2021GL095565. [Google Scholar] [CrossRef]
- Masunaga, H.; Kummerow, C.D. Observations of tropical precipitating clouds ranging from shallow to deep convective systems. Geophys. Res. Lett. 2006, 33, L16805. [Google Scholar] [CrossRef] [Green Version]
- Masunaga, H.; L’Ecuyer, T.S.; Kummerow, C.D. Variability in the characteristics of precipitation systems in the tropical Pacific. Part 1: Spatial structure. J. Clim. 2005, 18, 823–840. [Google Scholar] [CrossRef] [Green Version]
- Masunaga, H.; Satoh, M.; Miura, H. A joint satellite and global cloud-resolving model analysis of a Madden-Julian Oscillation event: Model diagnosis. J. Geophys. Res.-Atmos. 2008, 113, D17210. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.T.; Zipser, E.J.; Nesbitt, S.W. Global distribution of tropical deep convection: Different perspectives from TRMM infrared and radar data. J. Clim. 2007, 20, 489–503. [Google Scholar] [CrossRef]
- Smalley, K.M.; Rapp, A.D. A-Train estimates of the sensitivity of the cloud-to-rainwater ratio to cloud size, relative humidity, and aerosols. Atmos. Chem. Phys. 2021, 21, 2765–2779. [Google Scholar] [CrossRef]
- Takayabu, Y.N. Spectral representation of rain profiles and diurnal variations observed with TRMM PR over the equatorial area. Geophys. Res. Lett. 2002, 29, 1584. [Google Scholar] [CrossRef] [Green Version]
- McFarquhar, G.M.; Jewett, B.F.; Gilmore, M.S.; Nesbitt, S.W.; Hsieh, T.L. Vertical Velocity and Microphysical Distributions Related to Rapid Intensification in a Simulation of Hurricane Dennis (2005). J. Atmos. Sci. 2012, 69, 3515–3534. [Google Scholar] [CrossRef]
- Chen, Y.L.; Zhang, A.Q.; Zhang, Y.H.; Cui, C.G.; Wan, R.; Wang, B.; Fu, Y.F. A Heavy Precipitation Event in the Yangtze River Basin Led by an Eastward Moving Tibetan Plateau Cloud System in the Summer of 2016. J. Geophys. Res.-Atmos. 2020, 125, e2020JD032429. [Google Scholar] [CrossRef]
- Dodson, J.B.; Taylor, P.C.; Branson, M. Microphysical variability of Amazonian deep convective cores observed by CloudSat and simulated by a multi-scale modeling framework. Atmos. Chem. Phys. 2018, 18, 6493–6510. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.Q.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, L. Western North Pacific Tropical Cyclone Database Created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Speirs, P.; Gabella, M.; Berne, A. A comparison between the GPM dual-frequency precipitation radar and ground-based radar precipitation rate estimates in the Swiss Alps and Plateau. J. Hydrometeorol. 2017, 18, 1247–1269. [Google Scholar] [CrossRef]
- Petracca, M.; D’Adderio, L.P.; Porcù, F. Validation of GPM dual-frequency precipitation radar (DPR) rainfall products over Italy. J. Hydrometeorol. 2018, 19, 907–925. [Google Scholar] [CrossRef]
- D’Adderio, L.P.; Vulpiani, G.; Porcù, F.; Tokay, A.; Meneghini, R. Comparison of GPM core observatory and ground-based radar retrieval of mass-weighted mean raindrop diameter at midlatitude. J. Hydrometeorol. 2018, 19, 1583–1598. [Google Scholar] [CrossRef]
- Ryu, J.; Song, H.J.; Sohn, B.J.; Liu, C. Global Distribution of Three Types of Drop Size Distribution Representing Heavy Rainfall From GPM/DPR Measurements. Geophys. Res. Lett. 2021, 48, e2020GL090871. [Google Scholar] [CrossRef]
- Seto, S.; Iguchi, T.; Meneghini, R.; Awaka, J.; Kubota, T.; Masaki, T.; Takahashi, N. The Precipitation Rate Retrieval Algorithms for the GPM Dual-frequency Precipitation Radar. J. Meteorol. Soc. Jpn. 2021, 99, 205–237. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Q.; Wang, Y.; Liang, X. Climatology of warm season cold vortices in East Asia: 1979–2005. Meteorol. Atmos. Phys. 2008, 100, 291–301. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.Q.; Wei, C.Y.; Lu, F.; Guo, Q. Introducing the New Generation of Chinese Geostationary Weather Satellites, Fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Min, M.; Wu, C.Q.; Li, C.; Liu, H.; Xu, N.; Wu, X.; Chen, L.; Wang, F.; Sun, F.; Qin, D.; et al. Developing the Science Product Algorithm Testbed for Chinese Next-Generation Geostationary Meteorological Satellites: Fengyun-4 Series. J. Meteorol. Res. 2017, 31, 708–719. [Google Scholar] [CrossRef]
- Chen, Y.L.; Li, W.B.; Chen, S.M.; Zhang, A.Q.; Fu, Y.F. Linkage Between the Vertical Evolution of Clouds and Droplet Growth Modes as Seen From FY-4A AGRI and GPM DPR. Geophys. Res. Lett. 2020, 47, e2020GL088312. [Google Scholar] [CrossRef]
- Xu, W.J.; Lyu, D.R. Evaluation of Cloud Mask and Cloud Top Height from Fengyun-4A with MODIS Cloud Retrievals over the Tibetan Plateau. Remote Sens. 2021, 13, 1418. [Google Scholar] [CrossRef]
- Zagrodnik, J.P.; McMurdie, L.A.; Houze, R.A.; Tanelli, S. Vertical Structure and Microphysical Characteristics of Frontal Systems Passing over a Three-Dimensional Coastal Mountain Range. J. Atmos. Sci. 2019, 76, 1521–1546. [Google Scholar] [CrossRef]
- Zagrodnik, J.P.; McMurdie, L.A.; Houze, R.A. Stratiform Precipitation Processes in Cyclones Passing over a Coastal Mountain Range. J. Atmos. Sci. 2018, 75, 983–1004. [Google Scholar] [CrossRef] [Green Version]
- Bao, X.W.; Wu, L.G.; Zhang, S.; Li, Q.; Lin, L.; Zhao, B.; Wu, D.; Xia, W.; Xu, B. Distinct Raindrop Size Distributions of Convective Inner- and Outer-Rainband Rain in Typhoon Maria (2018). J. Geophys. Res.-Atmos. 2020, 125, e2020JD032482. [Google Scholar] [CrossRef]
- Bao, X.W.; Wu, L.G.; Zhang, S.; Yuan, H.Z.; Wang, H.H. A Comparison of Convective Raindrop Size Distributions in the Eyewall and Spiral Rainbands of Typhoon Lekima (2019). Geophys. Res. Lett. 2020, 47, e2020GL090729. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Han, B.; Du, Y.; Wu, C.; Liu, X. Microphysical Characteristics of the Coexisting Frontal and Warm-Sector Heavy Rainfall in South China. J. Geophys. Res.-Atmos. 2021, 126, e2021JD035446. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Prat, O.P. The Impact of Raindrop Collisional Processes on the Polarimetric Radar Variables. J. Atmos. Sci. 2014, 71, 3052–3067. [Google Scholar] [CrossRef]
- Stephens, G.L.; Wood, N.B. Properties of tropical convection observed by millimeter-wave radar systems. Mon. Weather. Rev. 2007, 135, 821–842. [Google Scholar] [CrossRef]
- Hamada, A.; Takayabu, Y.N.; Liu, C.; Zipser, E.J. Weak linkage between the heaviest rainfall and tallest storms. Nat. Commun. 2015, 6, 6213. [Google Scholar] [CrossRef]
- Wang, T.C.; Tang, G.Q. Spatial Variability and Linkage between Extreme Convections and Extreme Precipitation Revealed by 22-Year Space-Borne Precipitation Radar Data. Geophys. Res. Lett. 2020, 47, e2020GL088437. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Chen, Y.; Pan, X.; Hu, Y.; Chen, S.; Li, W. Precipitation Microphysics of Tropical Cyclones over Northeast China in 2020. Remote Sens. 2022, 14, 2188. https://doi.org/10.3390/rs14092188
Zhang A, Chen Y, Pan X, Hu Y, Chen S, Li W. Precipitation Microphysics of Tropical Cyclones over Northeast China in 2020. Remote Sensing. 2022; 14(9):2188. https://doi.org/10.3390/rs14092188
Chicago/Turabian StyleZhang, Aoqi, Yilun Chen, Xiao Pan, Yuanyuan Hu, Shumin Chen, and Weibiao Li. 2022. "Precipitation Microphysics of Tropical Cyclones over Northeast China in 2020" Remote Sensing 14, no. 9: 2188. https://doi.org/10.3390/rs14092188
APA StyleZhang, A., Chen, Y., Pan, X., Hu, Y., Chen, S., & Li, W. (2022). Precipitation Microphysics of Tropical Cyclones over Northeast China in 2020. Remote Sensing, 14(9), 2188. https://doi.org/10.3390/rs14092188








