ERA5 Reanalysis for the Data Interpretation on Polarization Laser Sensing of High-Level Clouds
Abstract
1. Introduction
2. Materials and Methods
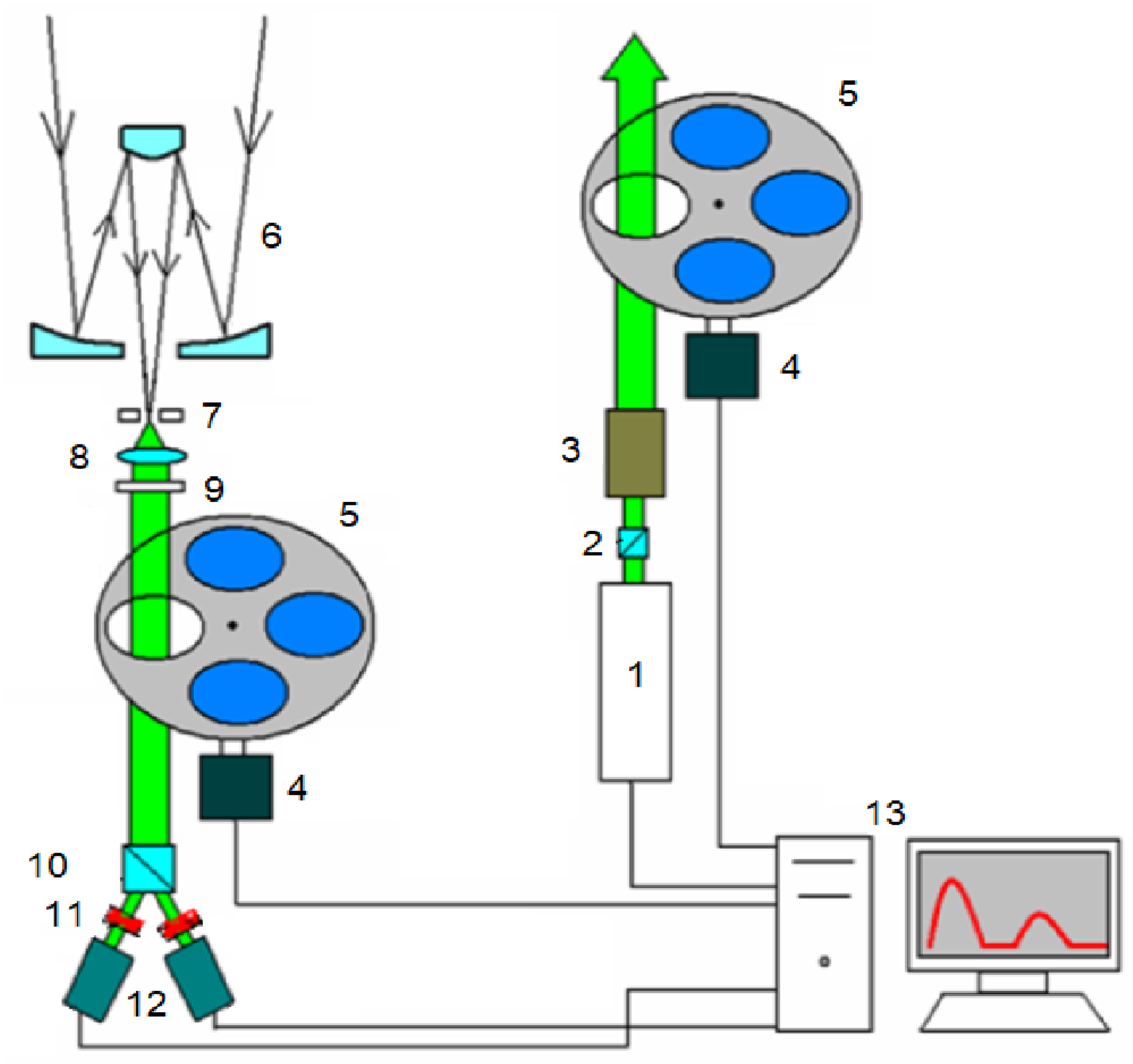
2.1. High-Altitude Matrix Polarization Lidar of National Research Tomsk State University
2.2. Use of Meteorological Data for the Interpretation of the Lidar Measurement Data
2.2.1. Radiosonde Observations and Conditions for the Formation of Specular Clouds
2.2.2. ERA5 Reanalysis
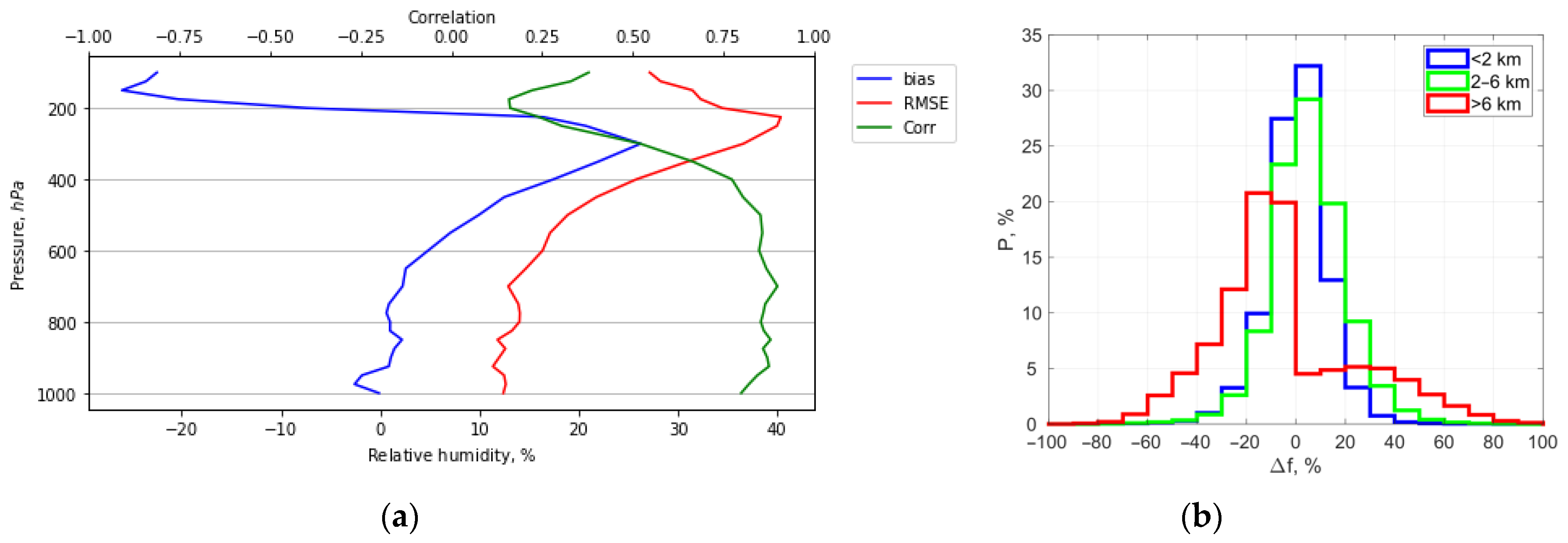
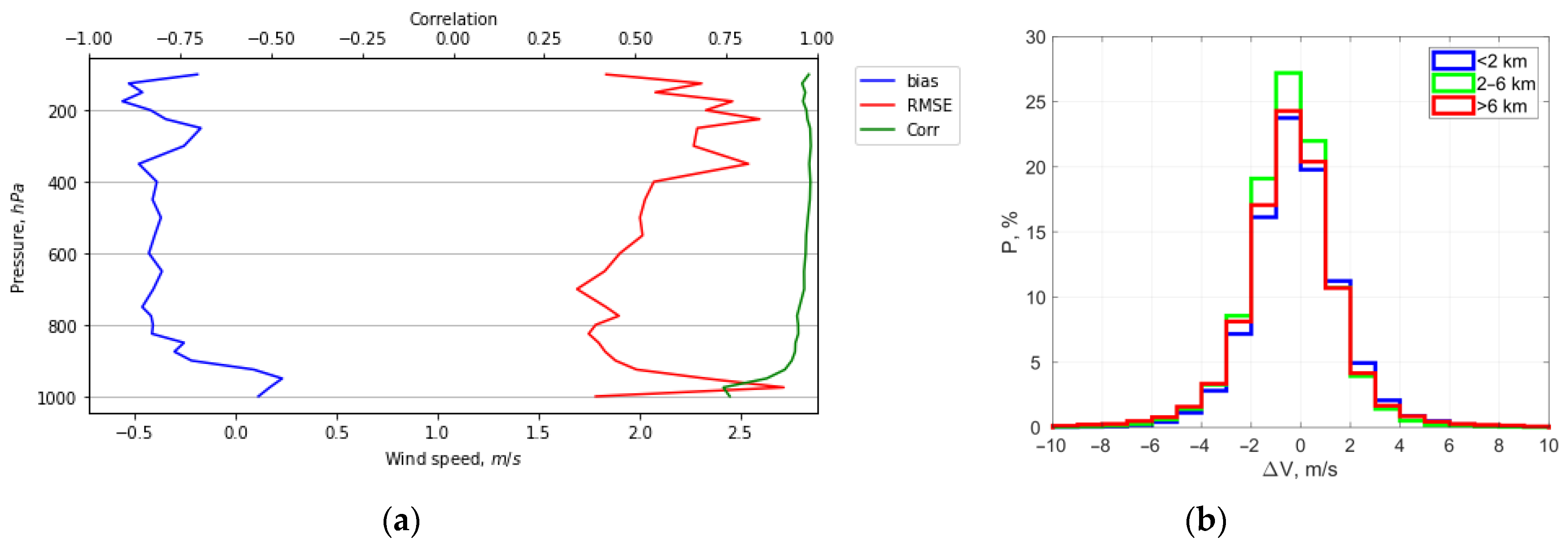
2.3. Evaluation of the Applicability of the ERA5 Reanalysis for Processing and Interpreting the Lidar Data
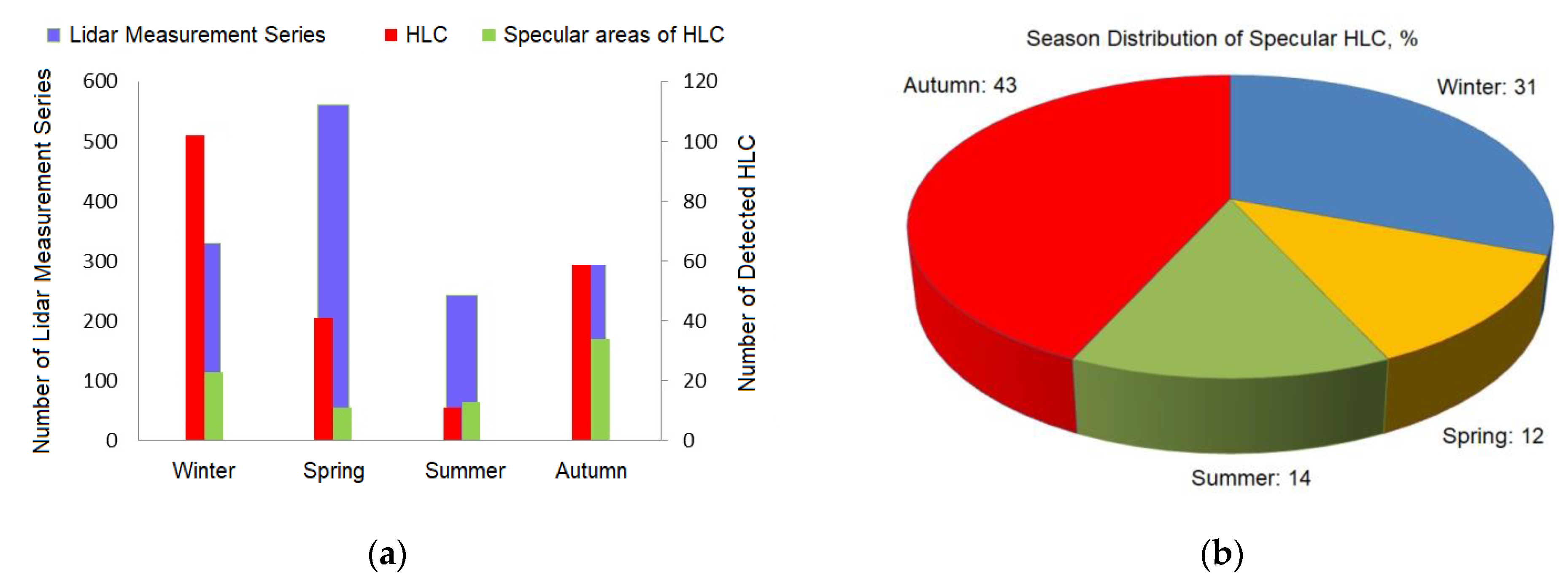
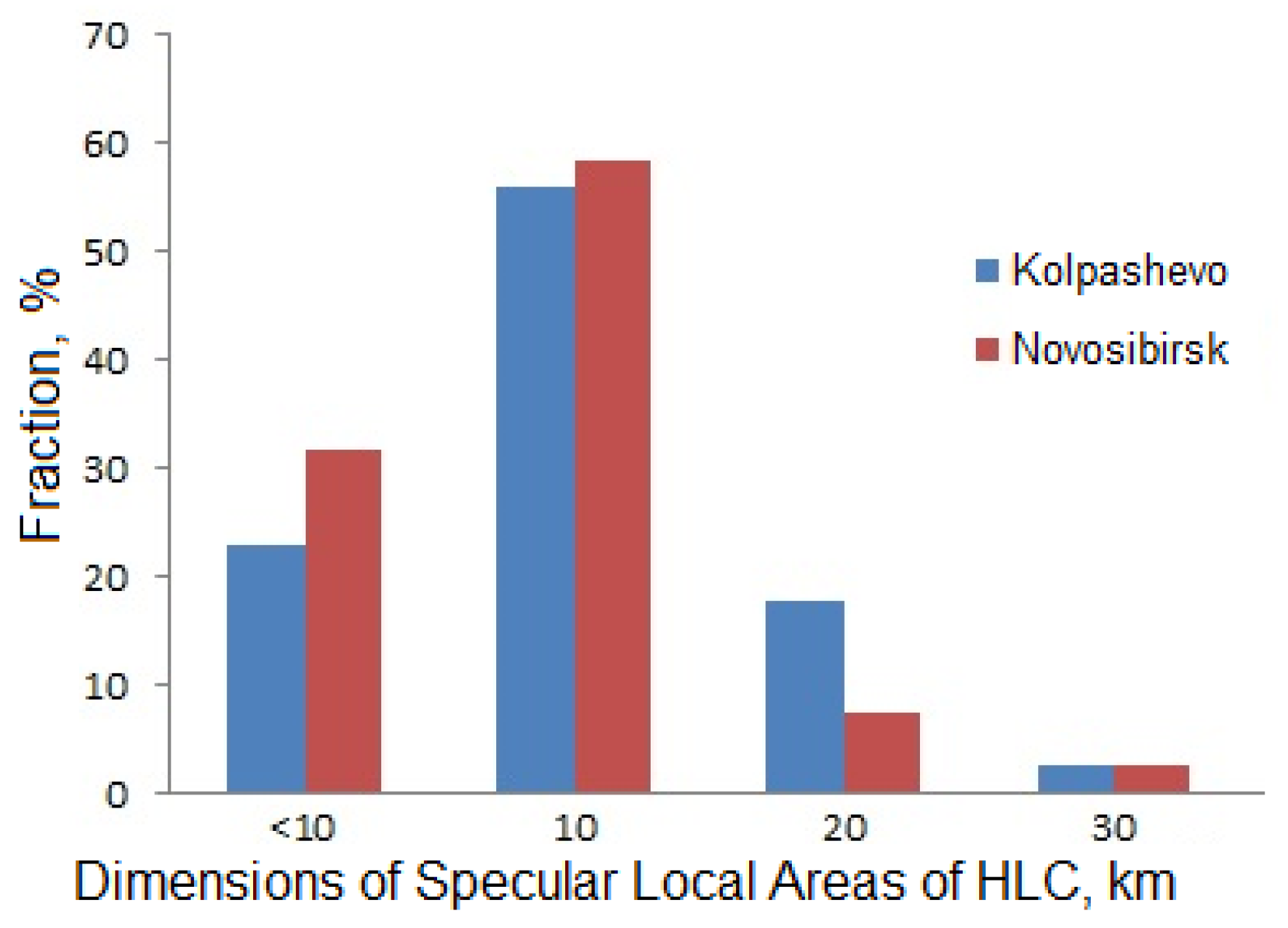
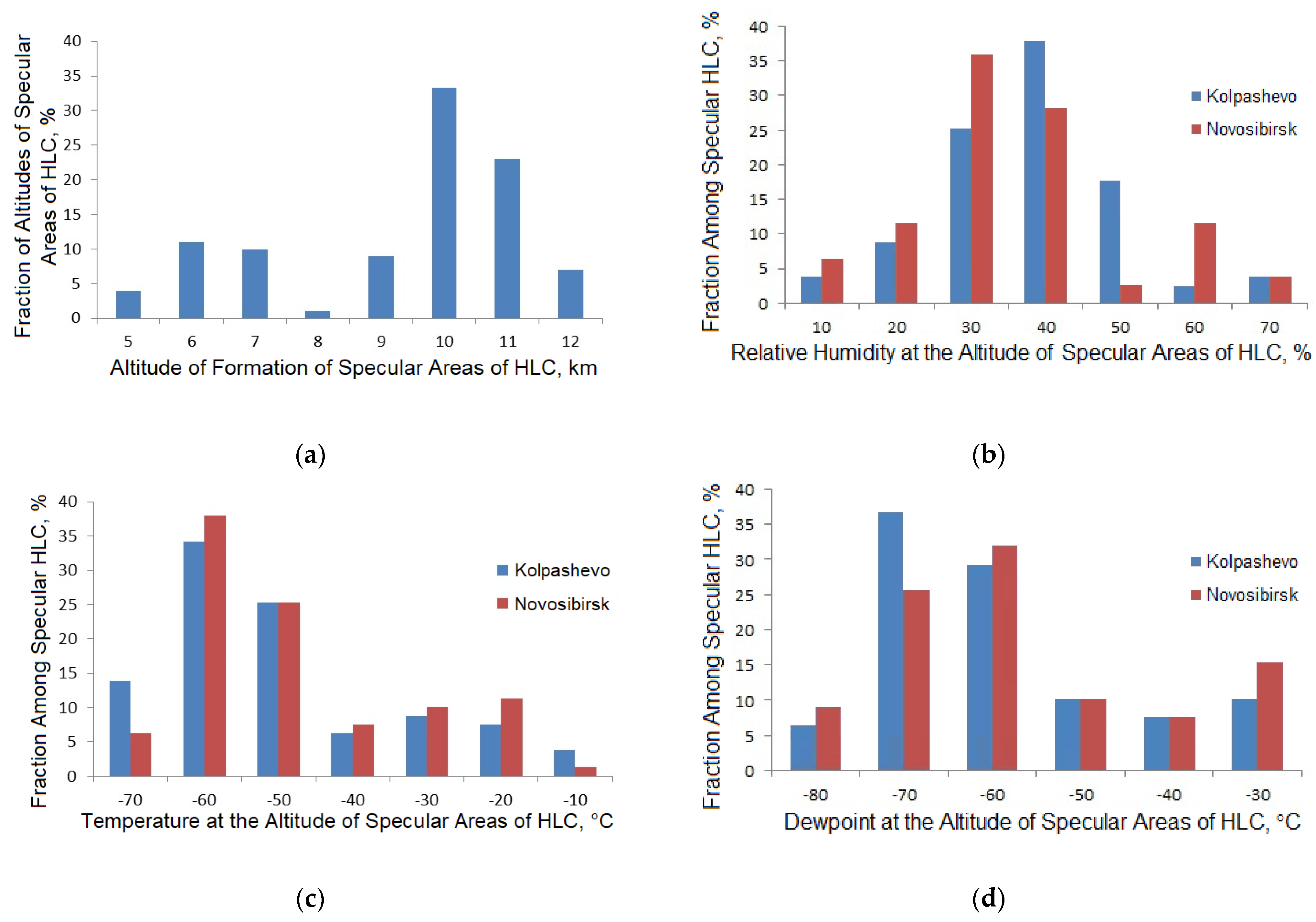
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dmitrieva-Arrago, L.R.; Trubina, M.A.; Tolstyh, M.A. Role of Phase Composition of Clouds in Forming High and Low Frequency Radiaion. Proc. Hydrometeorol. Res. Cent. Russ. Fed. 2017, 363, 19–34. (In Russian) [Google Scholar]
- Liou, K.N. Influence of Cirrus Clouds on Weather and Climate Processes: A Global Perspective. Mon. Weather. Rev. 1986, 114, 1167–1199. [Google Scholar] [CrossRef]
- Wylie, D.P.; Menzel, W.P.; Woolf, H.M.; Strabala, K.I. Four Years of Global Cirrus Cloud Statistics Using HIRS. J. Clim. 1994, 7, 1972–1986. [Google Scholar] [CrossRef]
- Reichardt, J.; Reichardt, S.; Lin, R.F.; Hess, M.; McGee, T.J.; Starr, D.O. Optical-Microphysical Cirrus Model. J. Geophys. Res. Atmos. 2008, 113, D22201:1–D22201:17. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) Climate Change 2013—The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Shanks, J.G.; Lynch, D.K. Specular Scattering in Cirrus Clouds. In Proceedings of the Passive Infrared Remote Sensing of Clouds and the Atmosphere III, Paris, France, 25–28 September 1995; Lynch, D.K., Shettle, E.P., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, DC, USA, 1995; Volume 2578, pp. 227–238. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Krämer, M.; Luebke, A.; Brown, P.; Cziczo, D.J.; Franklin, C.; Lawson, P.; Lohmann, U.; McFarquhar, G.; Ulanowski, Z.; et al. Cirrus Clouds. Meteorol. Monogr. 2017, 58, 2.1–2.26. [Google Scholar] [CrossRef]
- Mitchell, D.L.; Finnegan, W. Modification of Cirrus Clouds to Reduce Global Warming. Environ. Res. Lett. 2009, 4, 045102:1–045102:8. [Google Scholar] [CrossRef]
- Storelvmo, T.; Kristjansson, J.E.; Muri, H.; Pfeffer, M.; Barahona, D.; Nenes, A. Cirrus Cloud Seeding has Potential to Cool Climate. Geophys. Res. Lett. 2013, 40, 178–182. [Google Scholar] [CrossRef]
- Vorobyova, V.V.; Volodin, E.M. Numerical Simulation of Influence on Climate with the Help of Change of Properties of High-Level Clouds in Base of IVM RAS Model. Proc. Hydrometeorol. Res. Cent. Russ. Fed. 2017, 363, 5–18. (In Russian) [Google Scholar]
- Minnis, P.; Ayers, J.K.; Palikonda, R.; Phan, D. Contrails, Cirrus Trends, and Climate. J. Clim. 2004, 17, 1671–1685. [Google Scholar] [CrossRef]
- International Cloud Atlas. Available online: https://cloudatlas.wmo.int/en/homomutatus.html (accessed on 3 February 2022).
- Kärcher, B. Formation and Radiative Forcing of Contrail Cirrus. Nat. Commun. 2018, 9, 1824:1–1824:17. [Google Scholar] [CrossRef]
- Gierens, K.; Vázquez-Navarro, M. Statistical Analysis of Contrail Lifetimes from a Satellite Perspective. Meteorol. Z. 2018, 27, 183–193. [Google Scholar] [CrossRef]
- Rosenberg, G.V. Stokes Vector-Parameter. Adv. Phys. Sci. 1955, 56, 79–110. (In Russian) [Google Scholar]
- Samohvalov, I.V.; Kaul, B.V.; Nasonov, S.V.; Zhivotenyuk, I.V.; Bryukhanov, I.D. Backscattering Light Matrix of Reflecting High-Level Clouds Consisting of Crystal Mostly Horizontally-Oriented Particles. Atmos. Ocean. Opt. 2012, 25, 403–411. (In Russian) [Google Scholar]
- Guasta, M.D.; Vallar, E.; Riviere, O.; Castagnoli, F.; Venturi, V.; Morandi, M. Use of Polarimetric Lidar for the Study of Oriented Ice Plates in Clouds. Appl. Opt. 2006, 45, 4878–4887. [Google Scholar] [CrossRef] [PubMed]
- Hayman, M.; Spuler, S.; Morley, B.; VanAndel, J. Polarization Lidar Operation for Measuring Backscatter Phase Matrices of Oriented Scatterers. Opt. Express 2012, 20, 29553–29567. [Google Scholar] [CrossRef]
- Volkov, S.N.; Samokhvalov, I.V.; Cheong, H.D.; Kim, D. Investigation of East Asian Clouds with Polarization Light Detection and Ranging. Appl. Opt. 2015, 54, 3095–3105. [Google Scholar] [CrossRef] [PubMed]
- Kirillov, N.S.; Samokhvalov, I.V. Application of an Electro-Optical Shutter for Strobing of Lidar Signals. In Proceedings of the 20th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Novosibirsk, Russia, 23–27 June 2014; Romanovskii, O.A., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, DC, USA, 2014; Volume 9292, pp. 92922D:1–92922D:5. [Google Scholar] [CrossRef]
- Samokhvalov, I.V.; Bryukhanov, I.D.; Nasonov, S.V.; Zhivotenyuk, I.V.; Stykon, A.P. Investigation of the Optical Characteristics of Cirrus Clouds with Anomalous Backscattering. Russ. Phys. J. 2013, 55, 925–929. [Google Scholar] [CrossRef]
- Samokhvalov, I.V.; Bryukhanov, I.D.; Ni, E.V. Temporal Variability of the Specularity of High-Level Clouds According to the Data on Laser Polarization Sensing. In Proceedings of the 26th International Symposium on Atmospheric and Ocean Optics, Atmospheric Physics, Moscow, Russia, 29 June–3 July 2020; Matvienko, G.G., Romanovskii, O.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, DC, USA, 2020; Volume 11560, pp. 115604C:1–115604C:5. [Google Scholar] [CrossRef]
- Bryukhanov, I.D.; Zuev, S.V.; Samokhvalov, I.V. Effect of Specular High-Level Clouds on Scattered Solar Radiation Fluxes at the Zenith. Atmos. Ocean. Opt. 2021, 34, 327–334. [Google Scholar] [CrossRef]
- Chervyakov, M.Y. Zondirovanie Atmosfery: Uchebno-Metodicheskoe Posobie Dlya Studentov, Obuchayuschihsya po Napravleniyu 05.03.05 Prikladnaya Gidrometeorologiya; Nauka: Saratov, Russia, 2019. (In Russian) [Google Scholar]
- University of Wyoming. Available online: http://weather.uwyo.edu (accessed on 23 January 2022).
- Samokhvalov, I.V.; Bryukhanov, I.D.; Ni, E.V.; Zhivotenyuk, I.V.; Doroshkevich, A.A.; Stykon, A.P. Analysis of Occurrence Frequency and Forming Condition of Reflective High Level Clouds Using Polarized Laser Sensing Data. Trudy Voenno-Kosmicheskoy Akademii Imeni A. F. Mozhaiskogo 2021, 680, 342–345. (In Russian) [Google Scholar]
- Flightradar24: Live Air Traffic. Available online: https://www.flightradar24.com (accessed on 23 January 2022).
- Samokhvalov, I.V.; Bryukhanov, I.D.; Park, S.; Zhivotenyuk, I.V.; Ni, E.V.; Stykon, A.P. Optical Characteristics of Contrails According to Polarization Lidar Sensing Data. In Proceedings of the 24th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Tomsk, Russia, 2–5 July 2018; Matvienko, G.G., Romanovskii, O.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, DC, USA, 2018; Volume 10833, pp. 108335J:1–108335J:6. [Google Scholar] [CrossRef]
- Samokhvalov, I.V.; Bryukhanov, I.D.; Shishko, V.A.; Kustova, N.V.; Nie, E.V.; Konoshonkin, A.V.; Loktyushin, O.Y.; Timofeev, D.N. Estimation of Microphysical Characteristics of Contrails by Polarization Lidar Data: Theory and Experiment. Atmos. Ocean. Opt. 2019, 32, 400–409. [Google Scholar] [CrossRef]
- University of Wyoming. Description of Sounding Columns. Available online: http://weather.uwyo.edu/upperair/columns.html (accessed on 23 January 2022).
- The European Centre for Medium-Range Weather Forecasts. Available online: https://www.ecmwf.int (accessed on 23 January 2022).
- ECMWF Confluence Wiki. ERA5: Data Documentation. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation#ERA5:datadocumentation-Introduction (accessed on 23 January 2022).
- Gordov, E.; Schukin, G.G.; Itkin, D.M.; Karavaev, D.M.; Chichikova, E.F. Analysis of Regional Climatic Processes of Siberia: Approach, Data and Some Results. Vestnik Novosibirskogo Gosudarstvennogo Universiteta: Inf. Tehnol. 2011, 9, 56–66. (In Russian) [Google Scholar]
- Han, Y.; Yang, Q.; Nana, L.; Zhang, K.; Qing, C.; Li, X.; Wu, X.; Luo, T. Analysis of wind-speed profiles and optical turbulence above Gaomeigu and the Tibetan Plateau using ERA5 data. Mon. Not. R. Astron. Soc. 2021, 501, 4692–4702. [Google Scholar] [CrossRef]
- Mayer, J.; Mayer, M.; Haimberger, L. Consistency and homogeneity of atmospheric energy, moisture, and mass budgets in ERA5. J. Clim. 2021, 34, 3955–3974. [Google Scholar] [CrossRef]
- Zhu, J.; Xie, A.; Qin, X.; Wang, Y.; Xu, B.; Wang, Y. An assessment of ERA5 reanalysis for Antarctic near-surface air temperature. Atmosphere 2021, 12, 217. [Google Scholar] [CrossRef]
- Central Aerological Observatory (Scientific and Technical Center for Radio Sounding). Available online: http://cao-ntcr.mipt.ru/monitor/locator.htm (accessed on 23 January 2022).
- Um, J.; McFarquhar, G.M.; Hong, Y.P.; Lee, S.S.; Jung, C.H.; Lawson, R.P.; Mo, Q. Dimensions and Aspect Ratios of Natural Ice Crystals. Atmos. Chem. Phys. 2015, 15, 3933–3956. [Google Scholar] [CrossRef]
- Copernicus Climate Data Store. Available online: https://cds.climate.copernicus.eu (accessed on 23 January 2022).
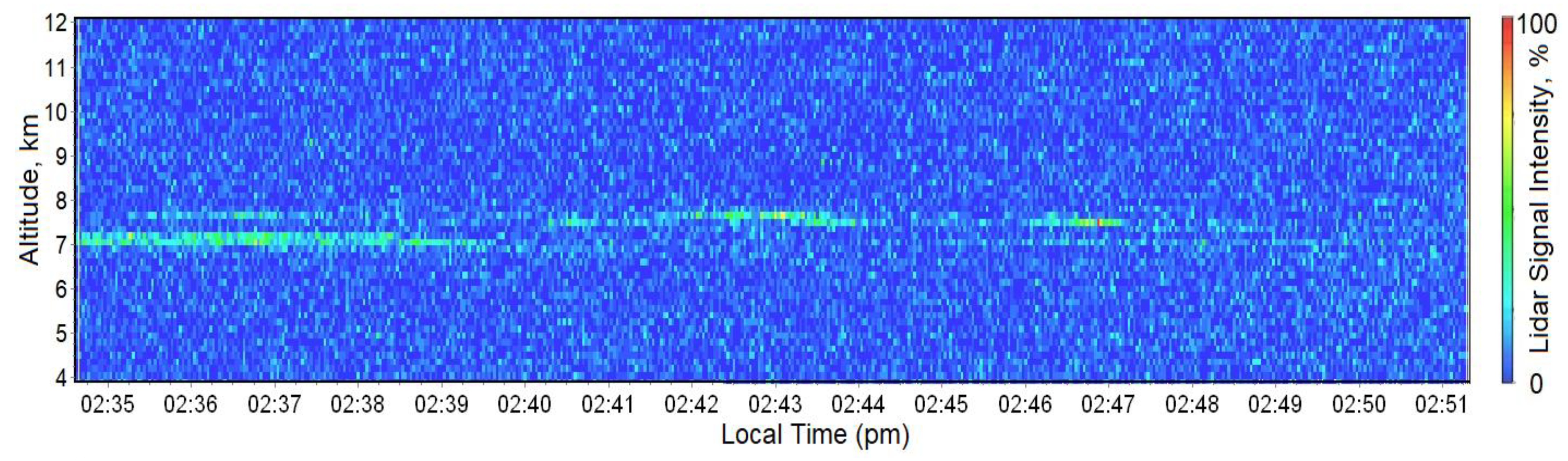
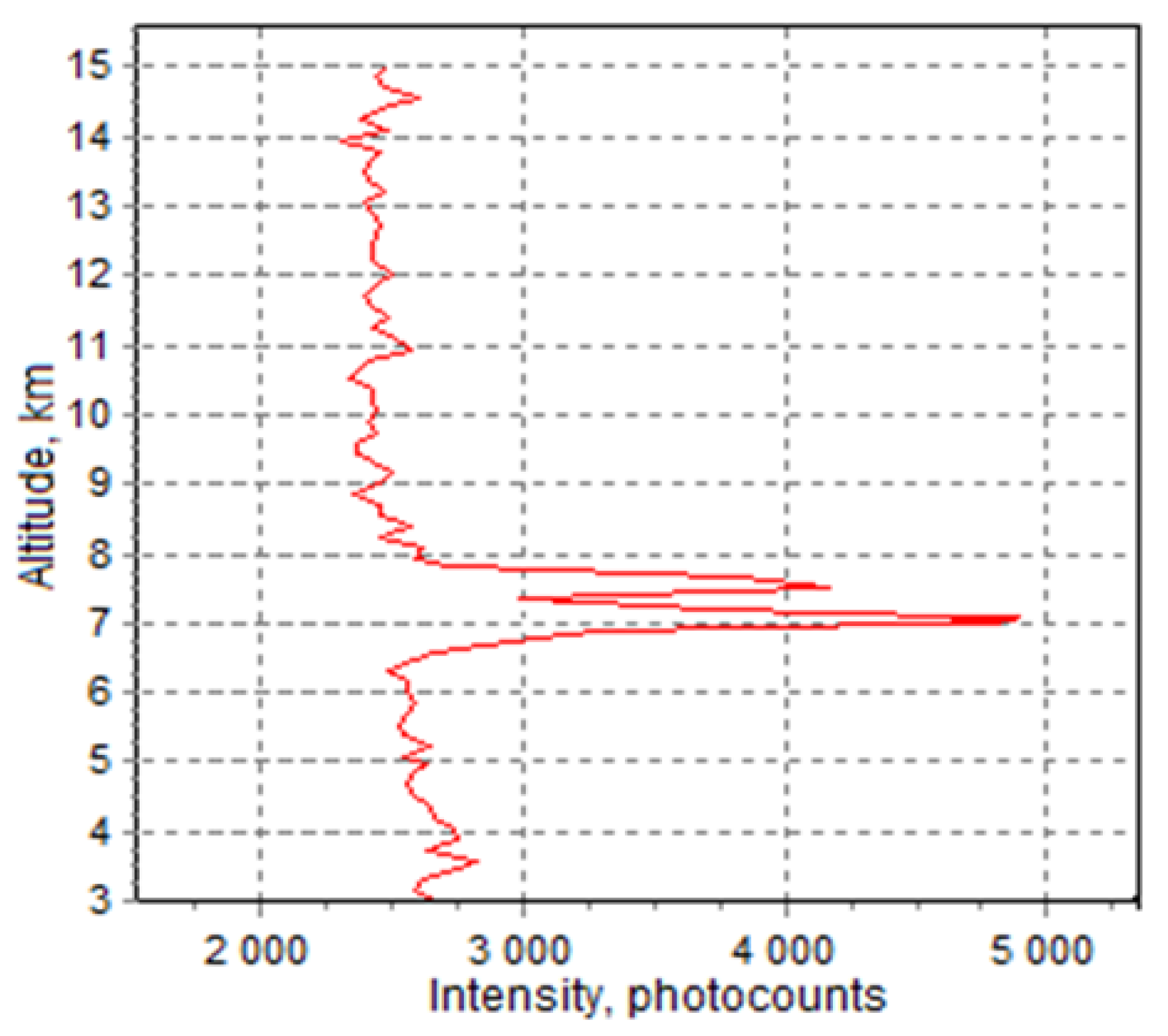




| Border Altitudes, km | Scattering Ratio R | Optical Thickness τ | BSPM in a Single Strobe (h, km) |
|---|---|---|---|
| 6.2–8.3 | 25.6 | 0.1 |
| Time | Station | PRES, hPa | HGHT, m | TEMP, °C | RELH, % | MIXR, g/kg | DRCT, ° | SKNT, kt |
|---|---|---|---|---|---|---|---|---|
| 7 a.m. | Kolp (29231) | 419 | 6979 | –24.8 | 49 | 0.61 | 260 | 27 |
| 7 a.m. | Nsk (29634) | 400 | 7340 | –26.5 | 19 | 0.20 | 315 | 21 |
| 7 p.m. | Kolp (29231) | 425 | 6857 | –25.0 | 40 | 0.48 | 265 | 37 |
| 7 p.m. | Nsk (29634) | 416 | 7104 | –22.1 | 33 | 0.52 | 269 | 14 |
| PRES, hPa | TEMP, °C | RELH, % | MIXR, g/kg | DRCT, ° | SKNT, kt | PRES, hPa | TEMP, °C | RELH, % | MIXR, g/kg | DRCT, ° | SKNT, kt |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 24 | 42 | 7.77 | 319 | 6 | 550 | −9 | 11 | 0.36 | 277 | 16 |
| 975 | 22 | 44 | 7.43 | 319 | 10 | 500 | −14 | 19 | 0.43 | 262 | 17 |
| 950 | 20 | 49 | 7.36 | 320 | 10 | 450 | −20 | 19 | 0.27 | 258 | 19 |
| 925 | 18 | 54 | 7.33 | 320 | 10 | 400 | −27 | 31 | 0.24 | 255 | 19 |
| 900 | 15 | 61 | 7.31 | 320 | 12 | 350 | −35 | 41 | 0.15 | 252 | 23 |
| 875 | 13 | 68 | 7.29 | 320 | 12 | 300 | −44 | 69 | 0.11 | 251 | 31 |
| 850 | 11 | 77 | 7.20 | 321 | 12 | 250 | −53 | 73 | 0.05 | 245 | 33 |
| 825 | 9 | 72 | 6.26 | 328 | 12 | 225 | −51 | 29 | 0.03 | 233 | 27 |
| 800 | 8 | 58 | 4.90 | 333 | 12 | 200 | −48 | 9 | 0.01 | 231 | 16 |
| 775 | 6 | 64 | 4.89 | 331 | 12 | 175 | −47 | 2 | 0.00 | 233 | 12 |
| 750 | 4 | 69 | 4.63 | 329 | 14 | 150 | −46 | 1 | 0.00 | 281 | 8 |
| 700 | 0 | 66 | 3.72 | 321 | 14 | 125 | −48 | 1 | 0.00 | 353 | 4 |
| 650 | −3 | 69 | 3.16 | 312 | 14 | 100 | −51 | 1 | 0.00 | 240 | 6 |
| 600 | −5 | 23 | 0.94 | 300 | 16 |
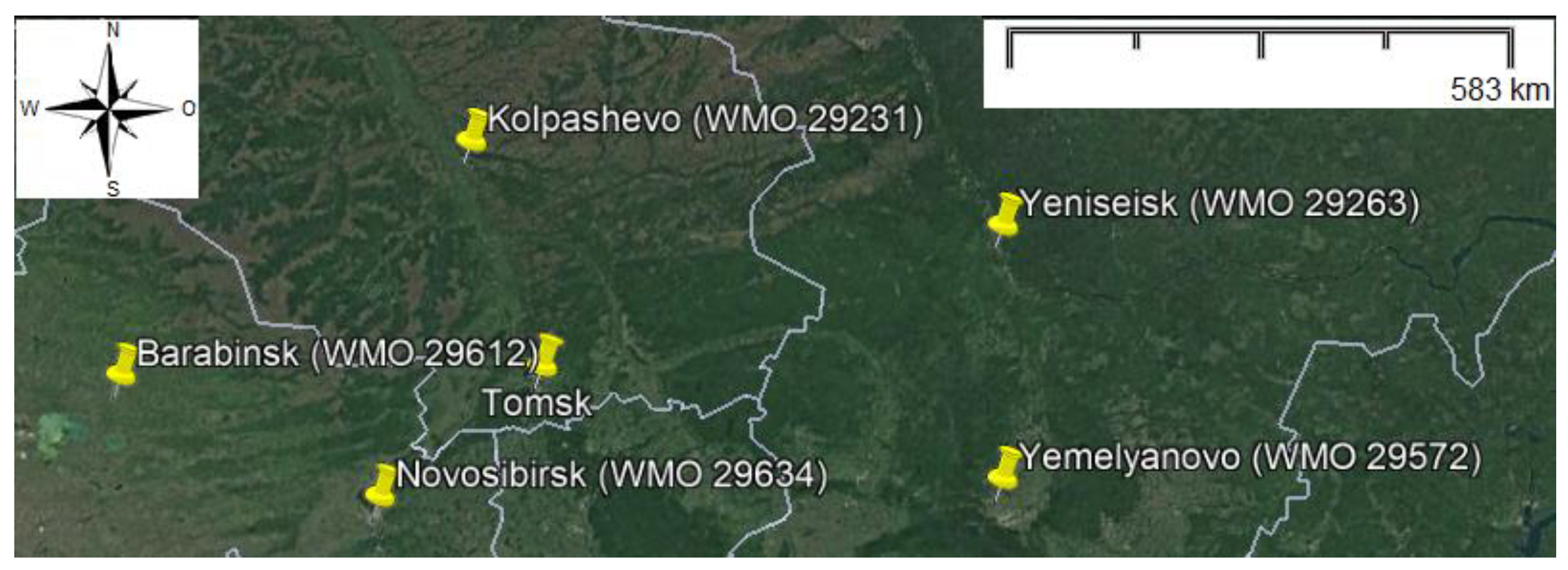
| Station Location | Station ID | Distance from the Station to Tomsk, km |
|---|---|---|
| Novosibirsk | WMO 29634 | 210 |
| Kolpashevo | WMO 29231 | 240 |
| Barabinsk | WMO 29612 | 430 |
| Yemelyanovo | WMO 29572 | 470 |
| Yeniseisk | WMO 29263 | 480 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuchinskaia, O.; Bryukhanov, I.; Penzin, M.; Ni, E.; Doroshkevich, A.; Kostyukhin, V.; Samokhvalov, I.; Pustovalov, K.; Bordulev, I.; Bryukhanova, V.; et al. ERA5 Reanalysis for the Data Interpretation on Polarization Laser Sensing of High-Level Clouds. Remote Sens. 2023, 15, 109. https://doi.org/10.3390/rs15010109
Kuchinskaia O, Bryukhanov I, Penzin M, Ni E, Doroshkevich A, Kostyukhin V, Samokhvalov I, Pustovalov K, Bordulev I, Bryukhanova V, et al. ERA5 Reanalysis for the Data Interpretation on Polarization Laser Sensing of High-Level Clouds. Remote Sensing. 2023; 15(1):109. https://doi.org/10.3390/rs15010109
Chicago/Turabian StyleKuchinskaia, Olesia, Ilia Bryukhanov, Maxim Penzin, Evgeny Ni, Anton Doroshkevich, Vadim Kostyukhin, Ignatii Samokhvalov, Konstantin Pustovalov, Iurii Bordulev, Valentina Bryukhanova, and et al. 2023. "ERA5 Reanalysis for the Data Interpretation on Polarization Laser Sensing of High-Level Clouds" Remote Sensing 15, no. 1: 109. https://doi.org/10.3390/rs15010109
APA StyleKuchinskaia, O., Bryukhanov, I., Penzin, M., Ni, E., Doroshkevich, A., Kostyukhin, V., Samokhvalov, I., Pustovalov, K., Bordulev, I., Bryukhanova, V., Stykon, A., Kirillov, N., & Zhivotenyuk, I. (2023). ERA5 Reanalysis for the Data Interpretation on Polarization Laser Sensing of High-Level Clouds. Remote Sensing, 15(1), 109. https://doi.org/10.3390/rs15010109






