Mid-Wave Infrared Snapshot Compressive Spectral Imager with Deep Infrared Denoising Prior
Abstract
:1. Introduction
2. A Compressive Spectral Imaging Model
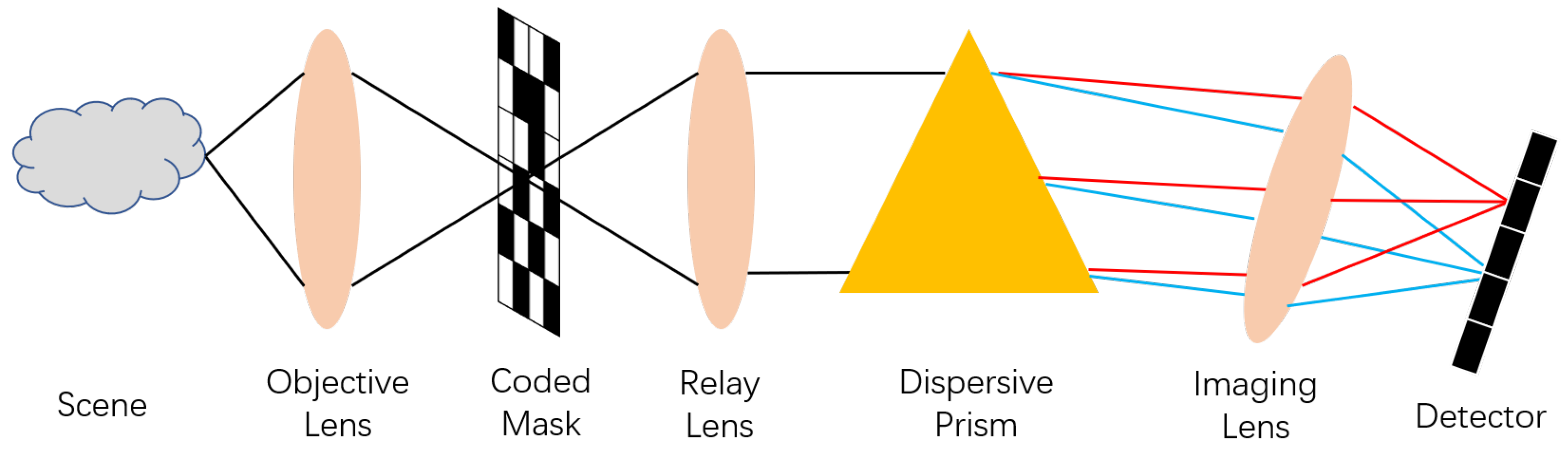
3. Optical Sensing and Reconstruction of the Proposed Architecture
4. A Deep Infrared Denoising Prior for Hyperspectral Image Reconstruction
5. Simulation Results
5.1. Training Details of the Infrared Denoising Network
5.2. Algorithm Evaluation
6. Experiment Results
6.1. MWIR Snapshot Compressive Spectral Imager Design
6.2. Spatial, Temporal, and Spectral Resolution
6.3. System Calibration
6.4. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sidran, M. Broadband reflectance and emissivity of specular and rough water surfaces. Appl. Opt. 1981, 20, 3176–3183. [Google Scholar] [CrossRef] [PubMed]
- Diener, R.; Tepper, J.; Labadie, L.; Pertsch, T.; Nolte, S.; Minardi, S. Towards 3D-photonic, multi-telescope beam combiners for mid-infrared astrointerferometry. Opt. Express 2017, 25, 19262–19274. [Google Scholar] [CrossRef]
- Amrania, H.; Antonacci, G.; Chan, C.H.; Drummond, L.; Otto, W.R.; Wright, N.A.; Phillips, C. Digistain: A digital staining instrument for histopathology. Opt. Express 2012, 20, 7290–7299. [Google Scholar] [CrossRef] [PubMed]
- Junaid, S.; Kumar, S.C.; Mathez, M.; Hermes, M.; Stone, N.; Shepherd, N.; Ebrahim-Zadeh, M.; Tidemand-Lichtenberg, P.; Pedersen, C. Video-rate, mid-infrared hyperspectral upconversion imaging. Optica 2019, 6, 702–708. [Google Scholar] [CrossRef] [Green Version]
- Elsner, A.E.; Weber, A.; Cheney, M.C.; VanNasdale, D.A.; Miura, M. Imaging polarimetry in patients with neovascular age-related macular degeneration. JOSA A 2007, 24, 1468–1480. [Google Scholar] [CrossRef] [Green Version]
- Dombrowski, M.S.; Willson, P.D. Video rate visible to LWIR hyperspectral image generation and exploitation. In Proceedings of the Internal Standardization and Calibration Architectures for Chemical Sensors, Boston, MA, USA, 20–22 September 1999; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3856, pp. 24–33. [Google Scholar]
- Schreer, O.; Zettner, J.; Spellenberg, B.; Schmidt, U.; Danner, A.; Peppermueller, C.; Saenz, M.L.; Hierl, T. Multispectral high-speed midwave infrared imaging system. In Proceedings of the Infrared Technology and Applications XXX, Orlando, FL, USA, 12–16 April 2004; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5406, pp. 249–257. [Google Scholar]
- Chamberland, M.; Farley, V.; Tremblay, P.; Legault, J.F. Performance model of imaging FTS as a standoff chemical agent detection tool. In Chemical and Biological Standoff Detection; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5268, pp. 240–251. [Google Scholar]
- Amenabar, I.; Poly, S.; Goikoetxea, M.; Nuansing, W.; Lasch, P.; Hillenbrand, R. Hyperspectral infrared nanoimaging of organic samples based on Fourier transform infrared nanospectroscopy. Nat. Commun. 2017, 8, 14402. [Google Scholar] [CrossRef] [Green Version]
- Gupta, N.; Dahmani, R.; Bennett, K.; Simizu, S.; Suhre, D.R.; Singh, N. Progress in AOTF hyperspectral imagers. In Proceedings of the Automated Geo-Spatial Image and Data Exploitation, Orlando, FL, USA, 24 April 2000; International Society for Optics and Photonics: Bellingham, WA, USA, 2000; Volume 4054, pp. 30–38. [Google Scholar]
- Zhao, H.; Ji, Z.; Jia, G.; Zhang, Y.; Li, Y.; Wang, D. MWIR thermal imaging spectrometer based on the acousto-optic tunable filter. Appl. Opt. 2017, 56, 7269–7276. [Google Scholar] [CrossRef]
- Dam, J.S.; Tidemand-Lichtenberg, P.; Pedersen, C. Room-temperature mid-infrared single-photon spectral imaging. Nat. Photonics 2012, 6, 788–793. [Google Scholar] [CrossRef] [Green Version]
- Junaid, S.; Tomko, J.; Semtsiv, M.P.; Kischkat, J.; Masselink, W.T.; Pedersen, C.; Tidemand-Lichtenberg, P. Mid-infrared upconversion based hyperspectral imaging. Opt. Express 2018, 26, 2203–2211. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Gehm, M.E.; John, R.; Brady, D.J.; Willett, R.M.; Schulz, T.J. Single-shot compressive spectral imaging with a dual-disperser architecture. Opt. Express 2007, 15, 14013–14027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wagadarikar, A.; John, R.; Willett, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt. 2008, 47, B44–B51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kittle, D.; Choi, K.; Wagadarikar, A.; Brady, D.J. Multiframe image estimation for coded aperture snapshot spectral imagers. Appl. Opt. 2010, 49, 6824–6833. [Google Scholar] [CrossRef]
- Arguello, H.; Arce, G.R. Colored coded aperture design by concentration of measure in compressive spectral imaging. IEEE Trans. Image Process. 2014, 23, 1896–1908. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Liu, Y.; Wu, J.; Dai, Q. Spatial-spectral encoded compressive hyperspectral imaging. ACM Trans. Graph. (TOG) 2014, 33, 1–11. [Google Scholar] [CrossRef]
- Yuan, X.; Tsai, T.H.; Zhu, R.; Llull, P.; Brady, D.; Carin, L. Compressive hyperspectral imaging with side information. IEEE J. Sel. Top. Signal Process. 2015, 9, 964–976. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Xiong, Z.; Gao, D.; Shi, G.; Wu, F. Dual-camera design for coded aperture snapshot spectral imaging. Appl. Opt. 2015, 54, 848–858. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Yu, Z.; Zheng, S.; Li, Y.; Tao, X.; Wu, F.; Xie, Q.; Sun, Y.; Wang, C.; Zheng, Z. Residual image recovery method based on the dual-camera design of a compressive hyperspectral imaging system. Opt. Express 2022, 30, 20100–20116. [Google Scholar] [CrossRef]
- Xie, H.; Zhao, Z.; Han, J.; Zhang, Y.; Bai, L.; Lu, J. Dual camera snapshot hyperspectral imaging system via physics-informed learning. Opt. Lasers Eng. 2022, 154, 107023. [Google Scholar] [CrossRef]
- Li, X.; Greenberg, J.A.; Gehm, M.E. Single-shot multispectral imaging through a thin scatterer. Optica 2019, 6, 864–871. [Google Scholar] [CrossRef]
- Saragadam, V.; DeZeeuw, M.; Baraniuk, R.G.; Veeraraghavan, A.; Sankaranarayanan, A.C. SASSI—Super-pixelated adaptive spatio-spectral imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2233–2244. [Google Scholar] [CrossRef] [PubMed]
- Arguello, H.; Pinilla, S.; Peng, Y.; Ikoma, H.; Bacca, J.; Wetzstein, G. Shift-variant color-coded diffractive spectral imaging system. Optica 2021, 8, 1424–1434. [Google Scholar] [CrossRef]
- Mahalanobis, A.; Shilling, R.; Murphy, R.; Muise, R. Recent results of medium wave infrared compressive sensing. Appl. Opt. 2014, 53, 8060–8070. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Ke, J.; Chi, S.; Hao, X.; Yang, T.; Cheng, D. High-resolution fast mid-wave infrared compressive imaging. Opt. Lett. 2021, 46, 2469–2472. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X. Focal plane array-based compressive imaging in medium wave infrared: Modeling, implementation, and challenges. Appl. Opt. 2019, 58, 8433–8441. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Wang, X. Non-uniformity correction for medium wave infrared focal plane array-based compressive imaging. Opt. Express 2020, 28, 8541–8559. [Google Scholar] [CrossRef] [PubMed]
- Russell, T.A.; McMackin, L.; Bridge, B.; Baraniuk, R. Compressive hyperspectral sensor for LWIR gas detection. In Compressive Sensing; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8365, p. 83650C. [Google Scholar]
- Dupuis, J.R.; Kirby, M.; Cosofret, B.R. Longwave infrared compressive hyperspectral imager. In Proceedings of the Next-Generation Spectroscopic Technologies VIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9482, p. 94820Z. [Google Scholar]
- Gattinger, P.; Kilgus, J.; Zorin, I.; Langer, G.; Nikzad-Langerodi, R.; Rankl, C.; Gröschl, M.; Brandstetter, M. Broadband near-infrared hyperspectral single pixel imaging for chemical characterization. Opt. Express 2019, 27, 12666–12672. [Google Scholar] [CrossRef]
- Yang, S.; Yan, X.; Qin, H.; Zeng, Q.; Liang, Y.; Arguello, H.; Yuan, X. Mid-Infrared Compressive Hyperspectral Imaging. Remote Sens. 2021, 13, 741. [Google Scholar] [CrossRef]
- Yuan, X.; Brady, D.J.; Katsaggelos, A.K. Snapshot compressive imaging: Theory, algorithms, and applications. IEEE Signal Process. Mag. 2021, 38, 65–88. [Google Scholar] [CrossRef]
- Sullenberger, R.; Milstein, A.; Rachlin, Y.; Kaushik, S.; Wynn, C. Computational reconfigurable imaging spectrometer. Opt. Express 2017, 25, 31960–31969. [Google Scholar] [CrossRef]
- Xiang, F.; Huang, Y.; Gu, X.; Liang, P.; Zhang, J. A restoration method of infrared image based on compressive sampling. In Proceedings of the 2016 8th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 27–28 August 2016; Volume 1, pp. 493–496. [Google Scholar]
- Emerson, T.H.; Olson, C.C.; Lutz, A. Image Recovery in the Infrared Domain via Path-Augmented Compressive Sampling Matching Pursuit. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Meng, Z.; Yu, Z.; Xu, K.; Yuan, X. Self-supervised neural networks for spectral snapshot compressive imaging. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 20–25 June 2021; pp. 2622–2631. [Google Scholar]
- Meng, Z.; Yuan, X. Perception inspired deep neural networks for spectral snapshot compressive imaging. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 2813–2817. [Google Scholar]
- Huang, T.; Dong, W.; Yuan, X.; Wu, J.; Shi, G. Deep gaussian scale mixture prior for spectral compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 16216–16225. [Google Scholar]
- Sun, Y.; Yang, Y.; Liu, Q.; Kankanhalli, M. Unsupervised Spatial–Spectral Network Learning for Hyperspectral Compressive Snapshot Reconstruction. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Yang, S.; Qin, H.; Yan, X.; Yuan, S.; Yang, T. Deep spatial-spectral prior with an adaptive dual attention network for single-pixel hyperspectral reconstruction. Opt. Express 2022, 30, 29621–29638. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wu, Z.; Zhong, Y.; Yuan, X. Snapshot spectral compressive imaging reconstruction using convolution and contextual Transformer. Photonics Res. 2022, 10, 1848–1858. [Google Scholar] [CrossRef]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Van Gool, L. Mask-guided spectral-wise transformer for efficient hyperspectral image reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 17502–17511. [Google Scholar]
- Zhang, X.; Zhang, Y.; Xiong, R.; Sun, Q.; Zhang, J. HerosNet: Hyperspectral Explicable Reconstruction and Optimal Sampling Deep Network for Snapshot Compressive Imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 17532–17541. [Google Scholar]
- Zhang, K.; Li, Y.; Zuo, W.; Zhang, L.; Van Gool, L.; Timofte, R. Plug-and-play image restoration with deep denoiser prior. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 6360–6376. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X. Generalized alternating projection based total variation minimization for compressive sensing. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2539–2543. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1874–1883. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef] [Green Version]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd Conference on Neural Information Processing System, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized assorted pixel camera: Postcapture control of resolution, dynamic range, and spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef] [Green Version]
- Choi, I.; Jeon, D.S.; Nam, G.; Gutierrez, D.; Kim, M.H. High-Quality Hyperspectral Reconstruction Using a Spectral Prior. ACM Trans. Graph. 2017, 36, 218. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, A.; Zickler, T. Statistics of real-world hyperspectral images. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 193–200. [Google Scholar]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [Green Version]
- Qiu, H.; Wang, Y.; Meng, D. Effective snapshot compressive-spectral imaging via deep denoising and total variation priors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9127–9136. [Google Scholar]
- Meng, Z.; Ma, J.; Yuan, X. End-to-end low cost compressive spectral imaging with spatial-spectral self-attention. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 187–204. [Google Scholar]
- Hu, X.; Cai, Y.; Lin, J.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Van Gool, L. Hdnet: High-resolution dual-domain learning for spectral compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 17542–17551. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Kruse, F.A.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]

















| Datasets | Index | TwIST | GAP-TV | GAP-3DTV | AutoEncoder | TSA-Net | HDNet | Ours |
|---|---|---|---|---|---|---|---|---|
| CAVE | PSNR | 23.74 | 29.07 | 29.15 | 32.46 | 26.10 | 32.18 | 33.03 |
| SSIM | 0.8523 | 0.9219 | 0.8866 | 0.9235 | 0.8105 | 0.9024 | 0.9257 | |
| SAM | 16.4033 | 11.5969 | 14.7321 | 4.7991 | 15.8743 | 13.7483 | 11.1254 | |
| KAIST | PSNR | 23.78 | 35.60 | 28.25 | 32.64 | 23.65 | 33.58 | 35.73 |
| SSIM | 0.8623 | 0.9468 | 0.8708 | 0.9475 | 0.7910 | 0.9428 | 0.9494 | |
| SAM | 15.2222 | 6.0389 | 12.3403 | 3.0663 | 14.2571 | 7.9834 | 5.8549 | |
| Harvard | PSNR | 22.84 | 30.23 | 28.19 | 31.84 | 23.28 | 32.02 | 32.73 |
| SSIM | 0.8346 | 0.9204 | 0.8739 | 0.9214 | 0.8043 | 0.9312 | 0.9345 | |
| SAM | 16.3466 | 11.9845 | 14.8793 | 5.2893 | 14.9385 | 12.3812 | 10.4895 |
| Index | TwIST | GAP-TV | GAP-3DTV | AutoEncoder | TSA-Net | HDNet | Ours |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.4749 | 0.4821 | 0.4892 | 0.4938 | 0.4873 | 0.4645 | 0.4921 |
| Precision | 0.6085 | 0.5599 | 0.8334 | 0.7792 | 0.7694 | 0.7812 | 0.7799 |
| Recall | 0.3090 | 0.2818 | 0.6889 | 0.8528 | 0.8498 | 0.8752 | 0.8787 |
| F1-score | 0.3968 | 0.2644 | 0.7454 | 0.8139 | 0.8123 | 0.8203 | 0.8209 |
| Algorithm | CAVE | KAIST | Harvard | Programming Language | Platform | |||
|---|---|---|---|---|---|---|---|---|
| CPU | GPU | CPU | GPU | CPU | GPU | |||
| TwIST | 441.4 | - | 111.8 | - | 1788.3 | - | Matlab | Intel Core i3-6100 CPU |
| GAP-TV | 49.3 | - | 12.7 | - | 210.5 | - | ||
| GAP-3DTV | 29.7 | - | 7.4 | - | 130.8 | - | ||
| AutoEncoder | - | 414.2 | - | 103.5 | - | 1639.5 | Python + TensorFlow | NVIDIA GTX 1080Ti GPU |
| TSA-Net | - | 48.6 | - | 12.4 | - | 201.4 | ||
| HDNet | - | 38.4 | - | 9.5 | - | 158.4 | Python + Pytorch | |
| Ours | - | 26.8 | - | 6.7 | - | 124.9 | ||
| Index | 3.7 m | 3.8 m | 3.9 m | 4.0 m | 4.1 m | 4.2 m | 4.3 m | 4.4 m | 4.5 m | 4.6 m | 4.7 m | 4.8 m |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.8453 | 0.8343 | 0.7984 | 0.8394 | 0.8473 | 0.8743 | 0.8323 | 0.8423 | 0.85023 | 0.8446 | 0.8564 | 0.8395 |
| Precision | 0.6574 | 0.6473 | 0.6473 | 0.7073 | 0.6378 | 0.6874 | 0.6594 | 0.5894 | 0.6058 | 0.6128 | 0.6392 | 0.6483 |
| Recall | 0.6673 | 0.6534 | 0.6889 | 0.7183 | 0.6483 | 0.6984 | 0.6639 | 0.5984 | 0.6139 | 0.6229 | 0.6432 | 0.6558 |
| F1-score | 0.6704 | 0.6606 | 0.6912 | 0.7291 | 0.6503 | 0.7049 | 0.6784 | 0.6084 | 0.6294 | 0.6384 | 0.6593 | 0.6639 |
| Mode | Coding Scheme | Spatial Resolution (Pixels) | Spectral Resolution | Spectral Channel | Acquisition Time (Second) | Reconstructed Time (Second) | Cost |
|---|---|---|---|---|---|---|---|
| Single-pixel | spatial | 64 × 48 | 2 | 100 | 4 | 2293 | low |
| Snapshot | spatial & spectral | 640 × 512 | 10 | 111 | 0.02 | 107 | high |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Qin, H.; Yan, X.; Yuan, S.; Zeng, Q. Mid-Wave Infrared Snapshot Compressive Spectral Imager with Deep Infrared Denoising Prior. Remote Sens. 2023, 15, 280. https://doi.org/10.3390/rs15010280
Yang S, Qin H, Yan X, Yuan S, Zeng Q. Mid-Wave Infrared Snapshot Compressive Spectral Imager with Deep Infrared Denoising Prior. Remote Sensing. 2023; 15(1):280. https://doi.org/10.3390/rs15010280
Chicago/Turabian StyleYang, Shuowen, Hanlin Qin, Xiang Yan, Shuai Yuan, and Qingjie Zeng. 2023. "Mid-Wave Infrared Snapshot Compressive Spectral Imager with Deep Infrared Denoising Prior" Remote Sensing 15, no. 1: 280. https://doi.org/10.3390/rs15010280
APA StyleYang, S., Qin, H., Yan, X., Yuan, S., & Zeng, Q. (2023). Mid-Wave Infrared Snapshot Compressive Spectral Imager with Deep Infrared Denoising Prior. Remote Sensing, 15(1), 280. https://doi.org/10.3390/rs15010280







