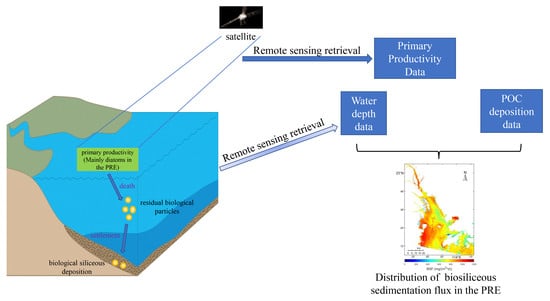
First Estimate Biosiliceous Sedimentation Flux in the Pearl River Estuary from 2000–2020 by Satellite Remote Sensing
Abstract
1. Introduction
2. Materials and Methods
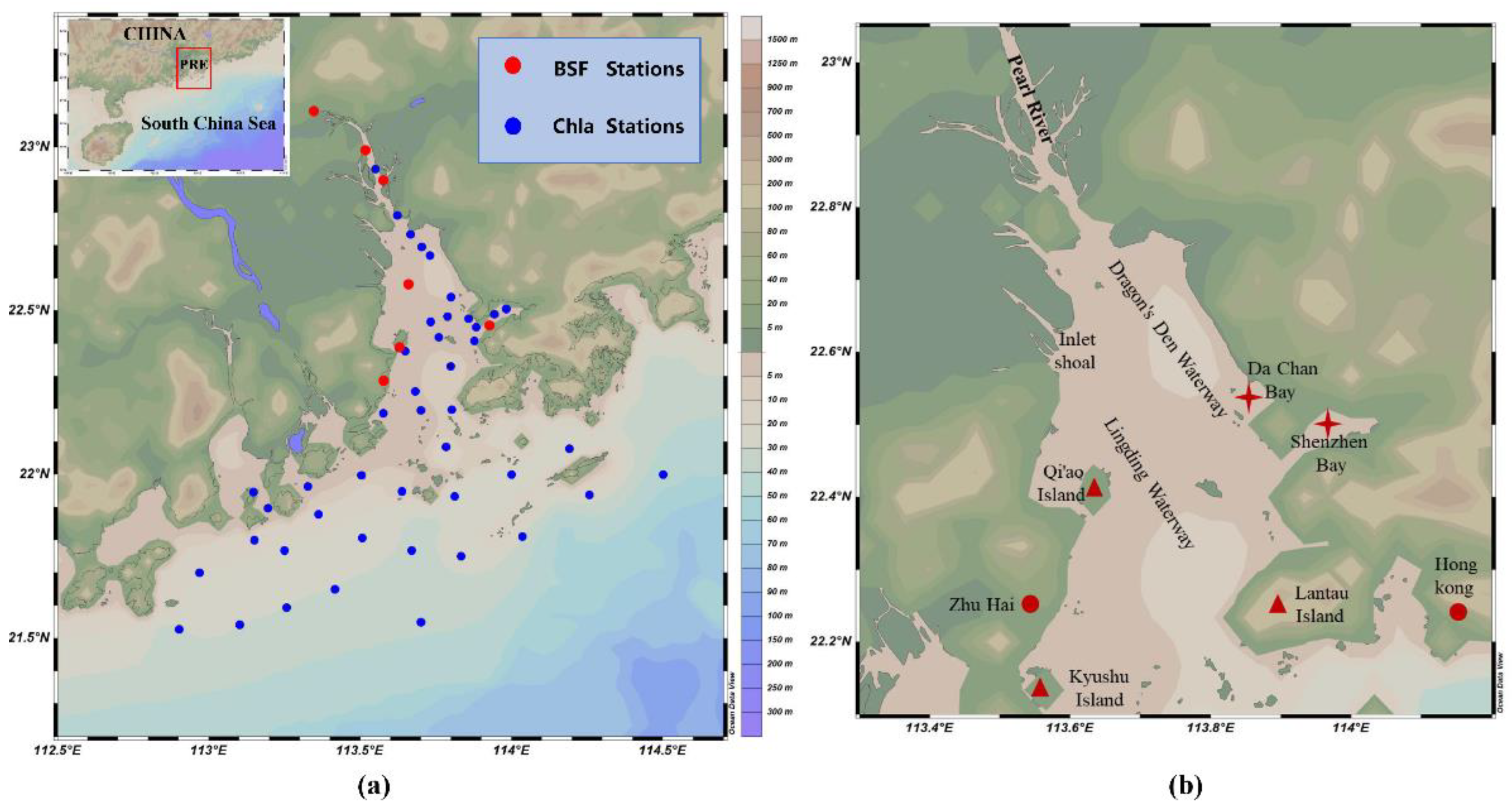
2.1. Study Area
2.2. Data Sources
2.2.1. In Situ Data
2.2.2. Satellite Data
2.2.3. Ancillary Data
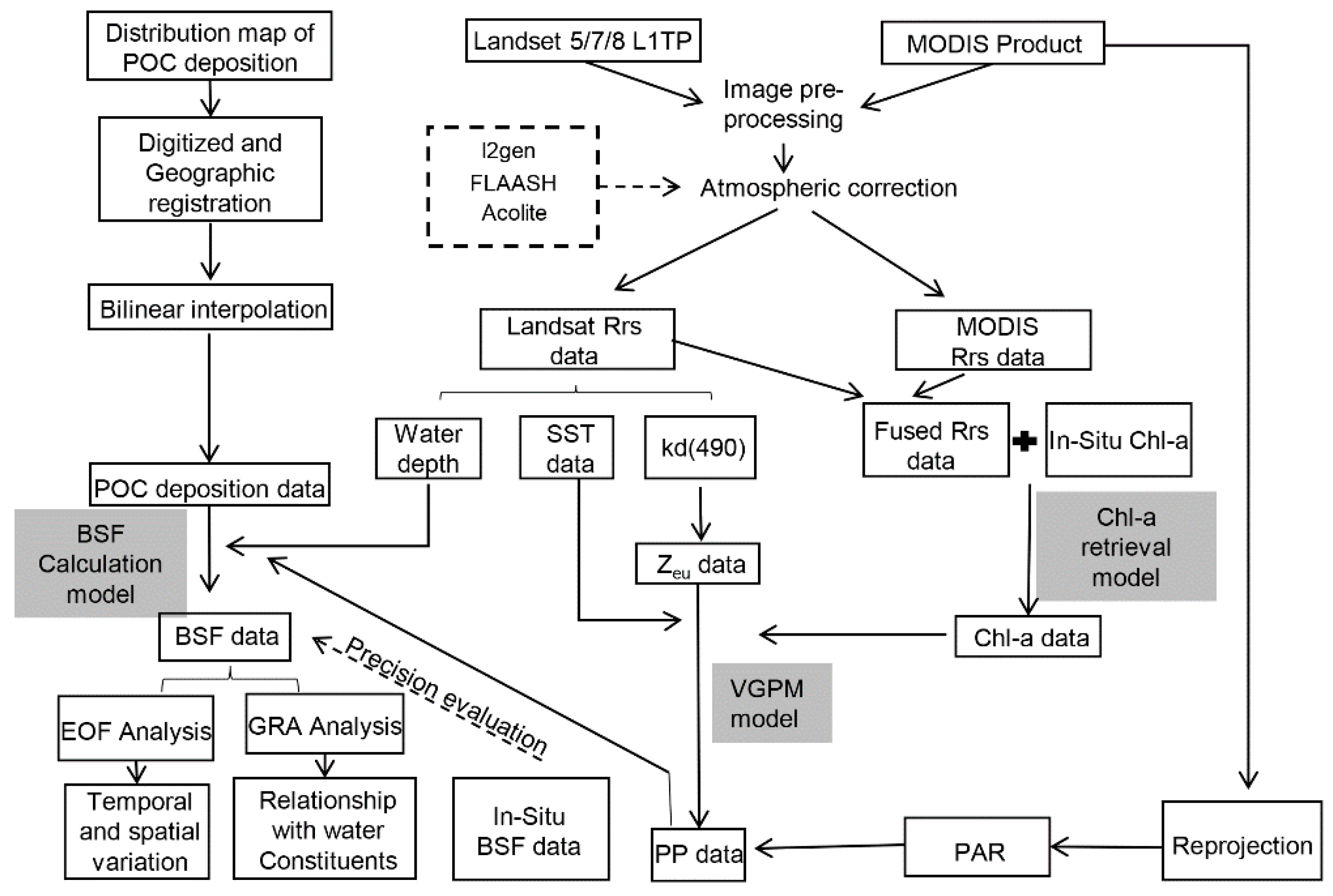
2.3. Methods and Process
2.4. Atmospheric Correction
2.5. Model Selection
2.5.1. Remote Sensing Spatiotemporal Fusion Model
2.5.2. Chlorophyll-a Retrieval Model Based on Landsat Imagery
2.5.3. Sea Surface Temperature Retrieval Model
2.5.4. Euphotic Depth Retrieval Model
2.5.5. Empirical Method for Bathymetry
2.5.6. Primary Productivity Estimation Model
2.5.7. BSF Estimation Model
3. Results
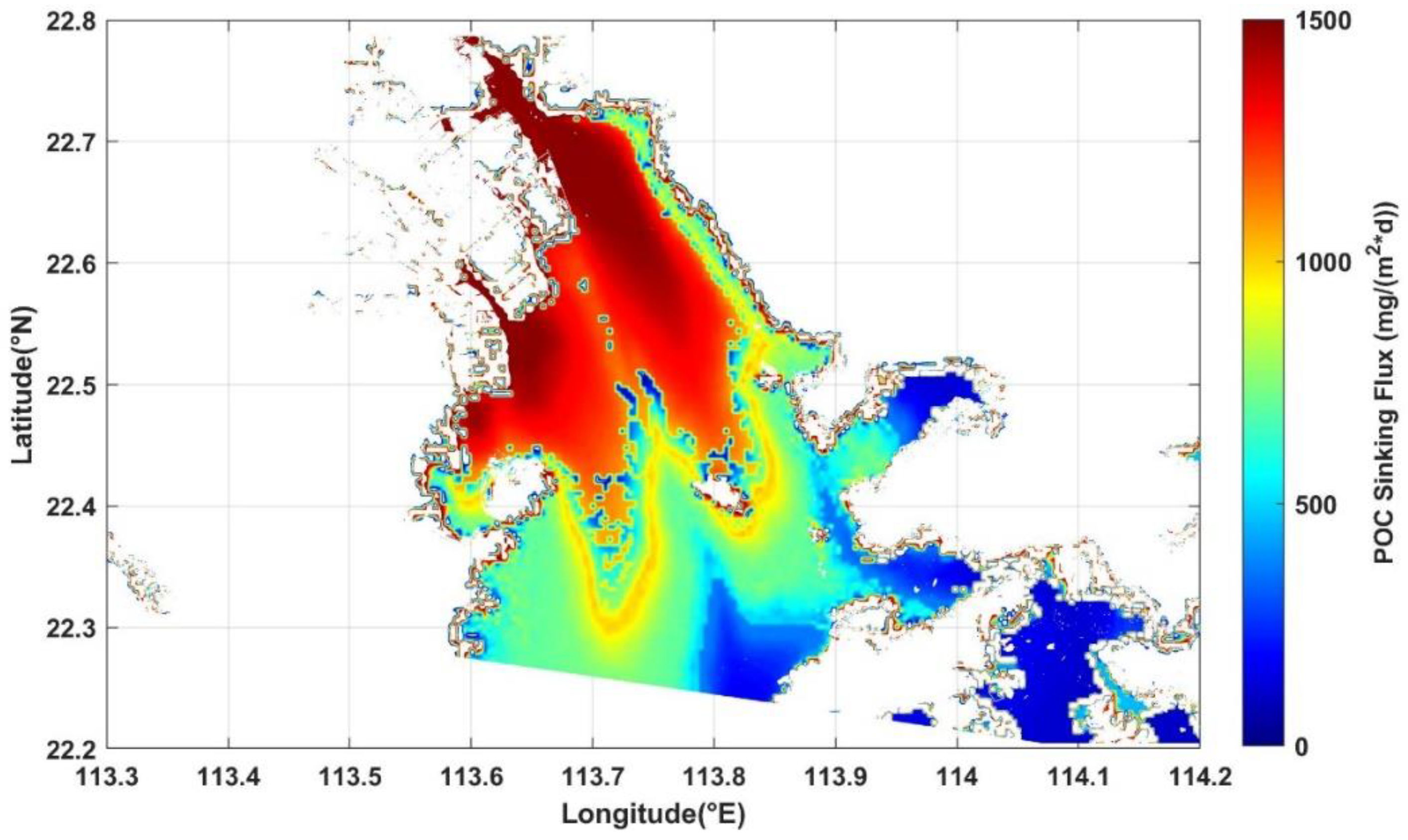
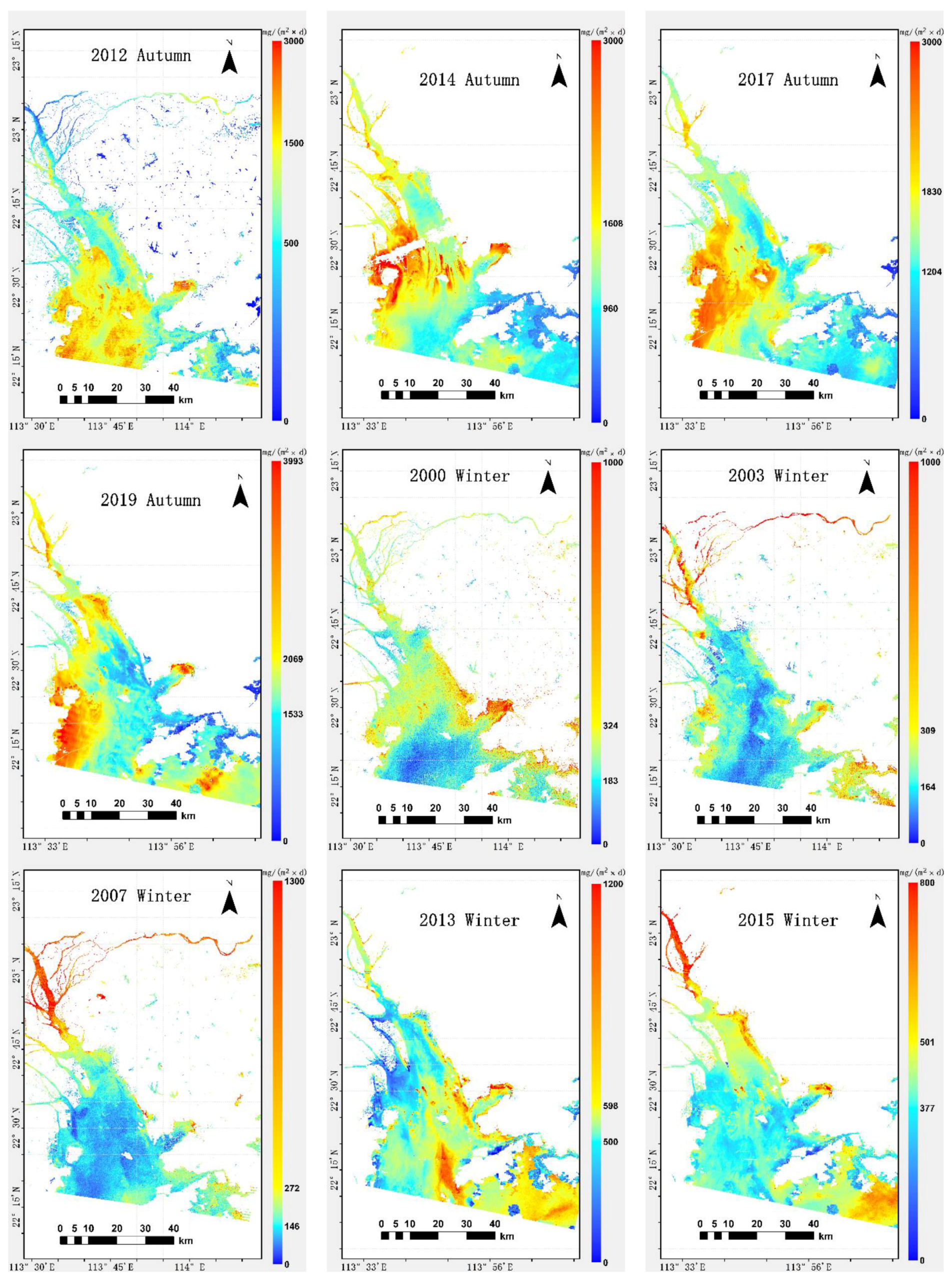
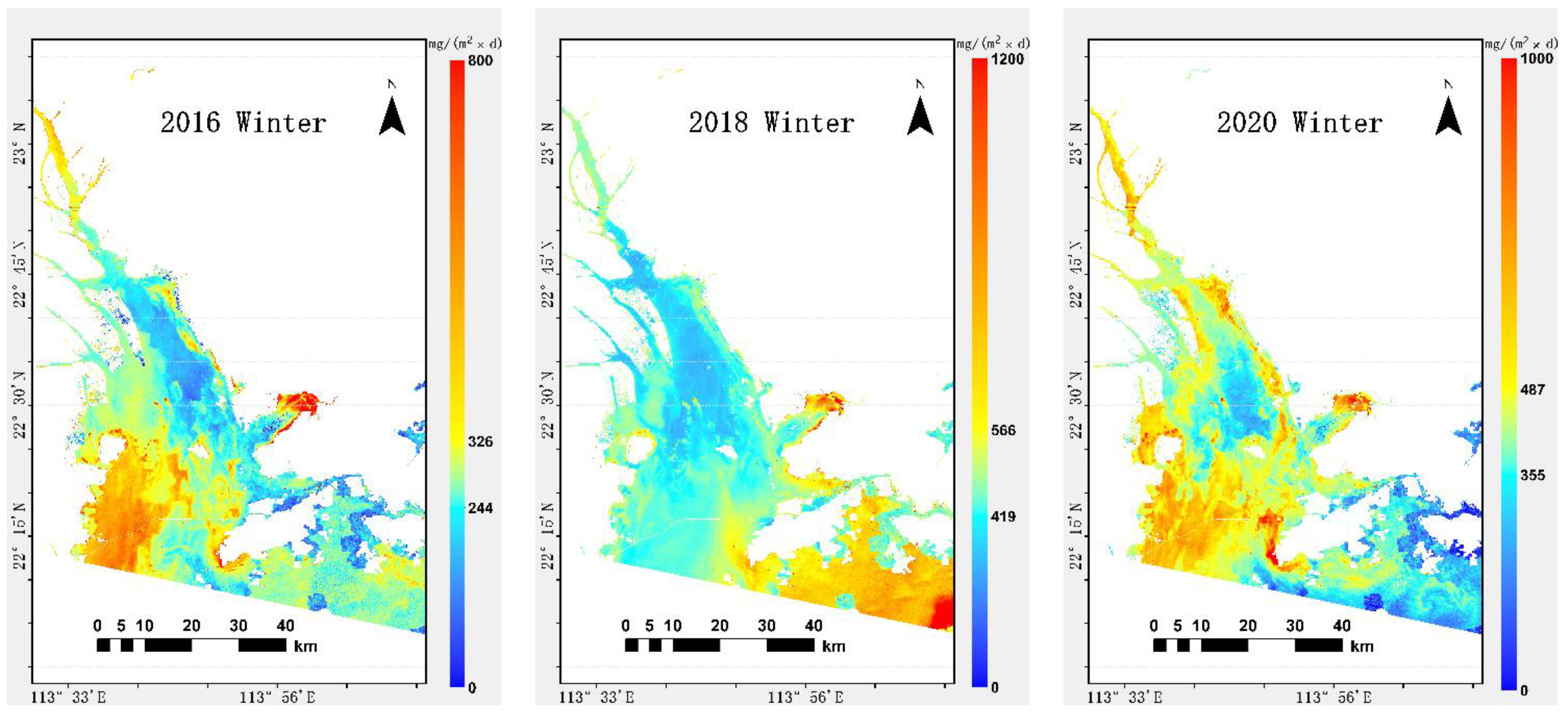
3.1. BSF Results
3.2. Accuracy Verification
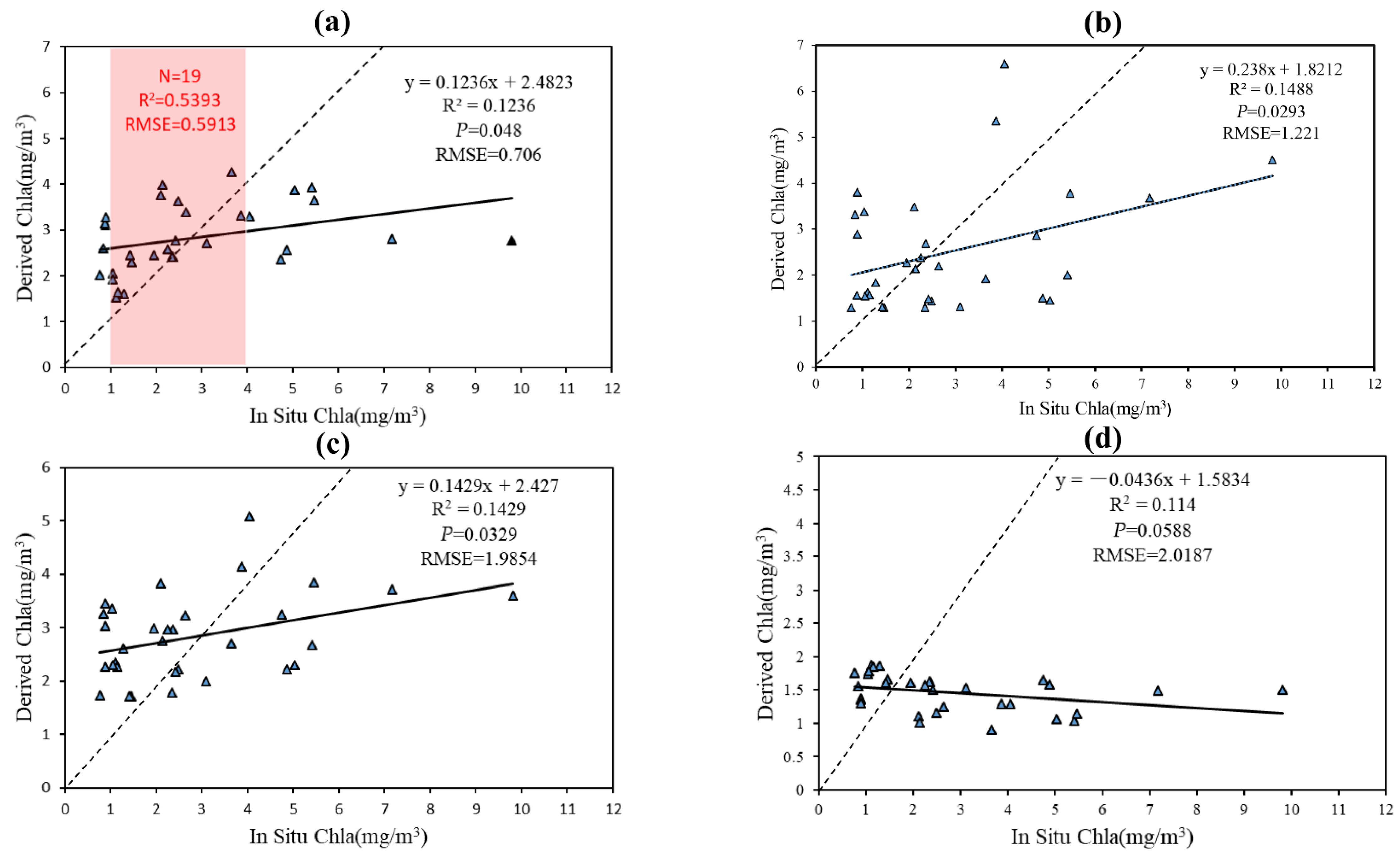
3.2.1. Chla Results Verification
3.2.2. Primary Productivity Results Verification
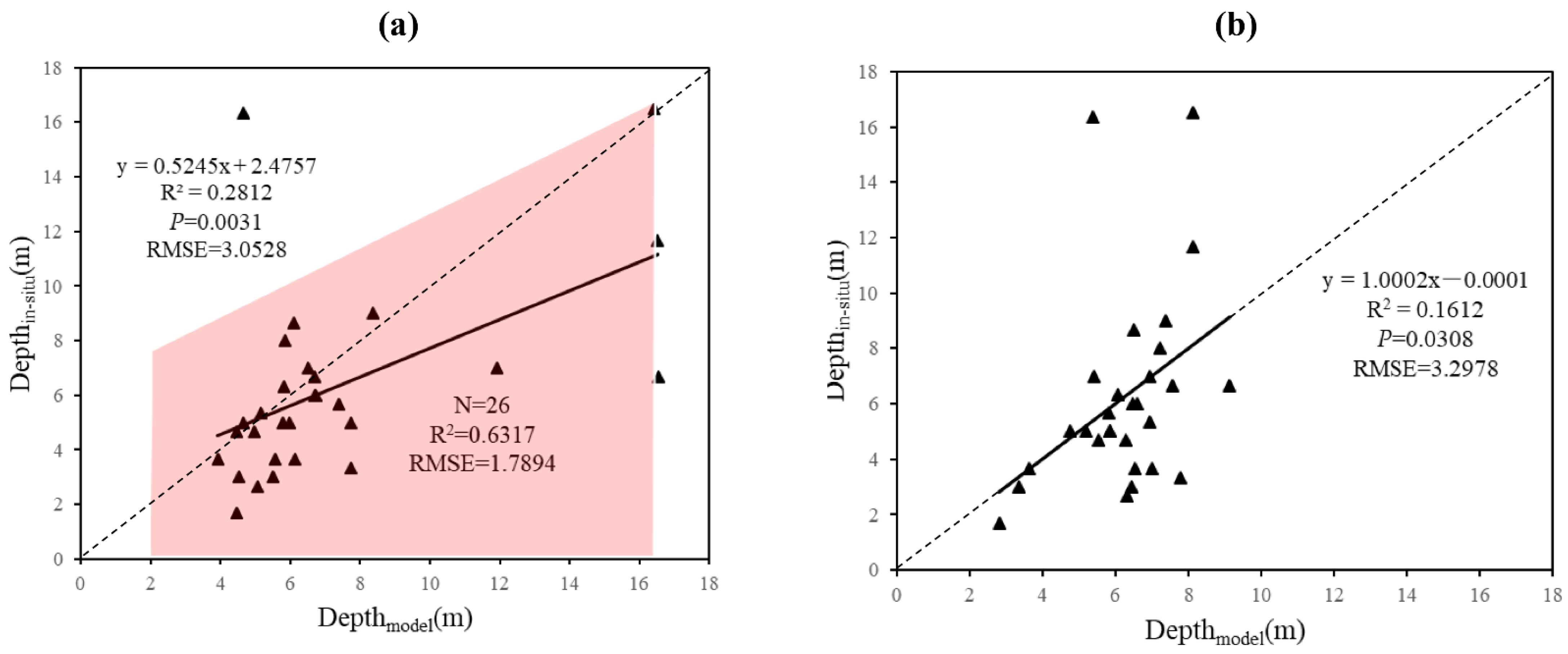
3.2.3. Validation of Water Depth Results
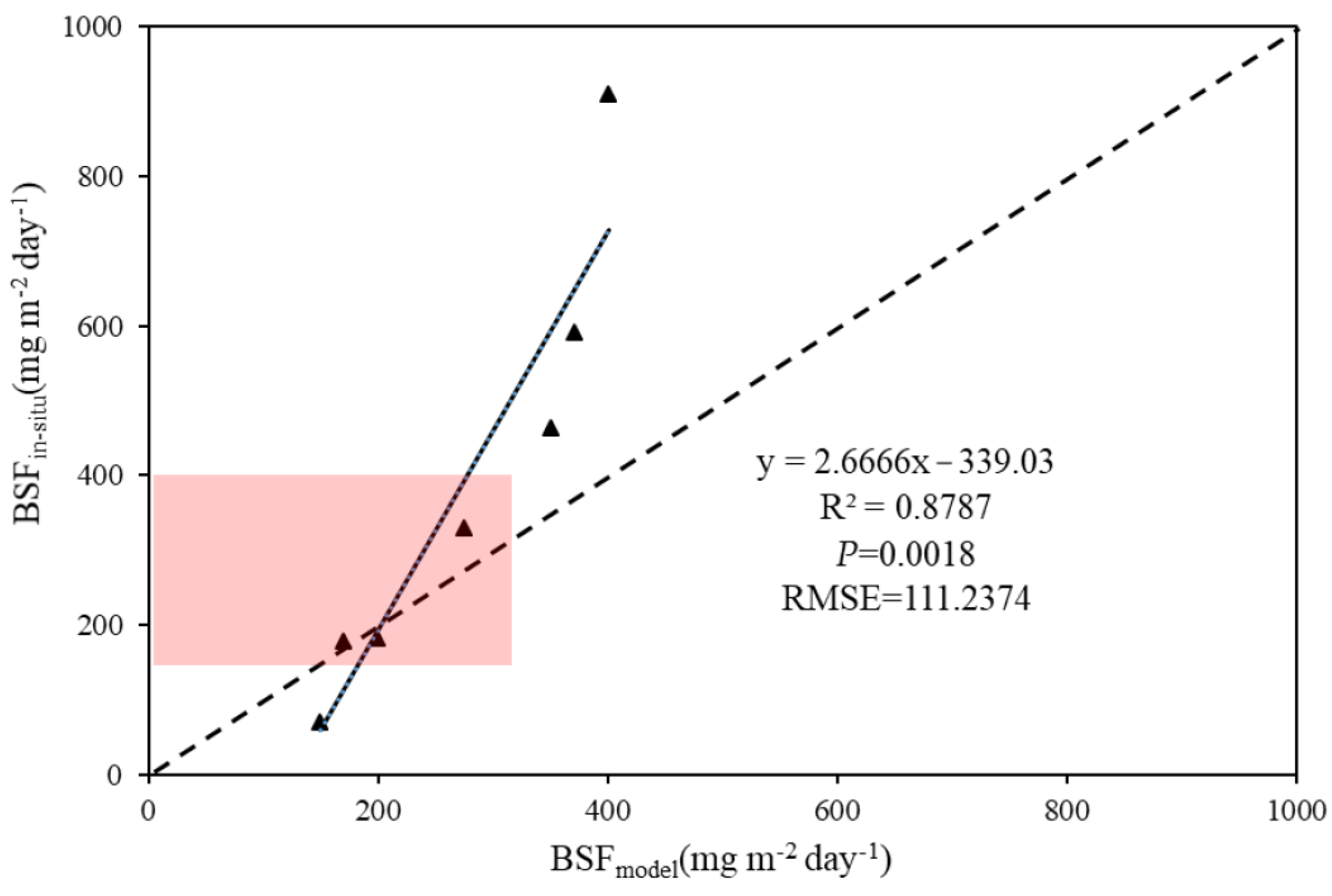
3.2.4. BSF Result Verification
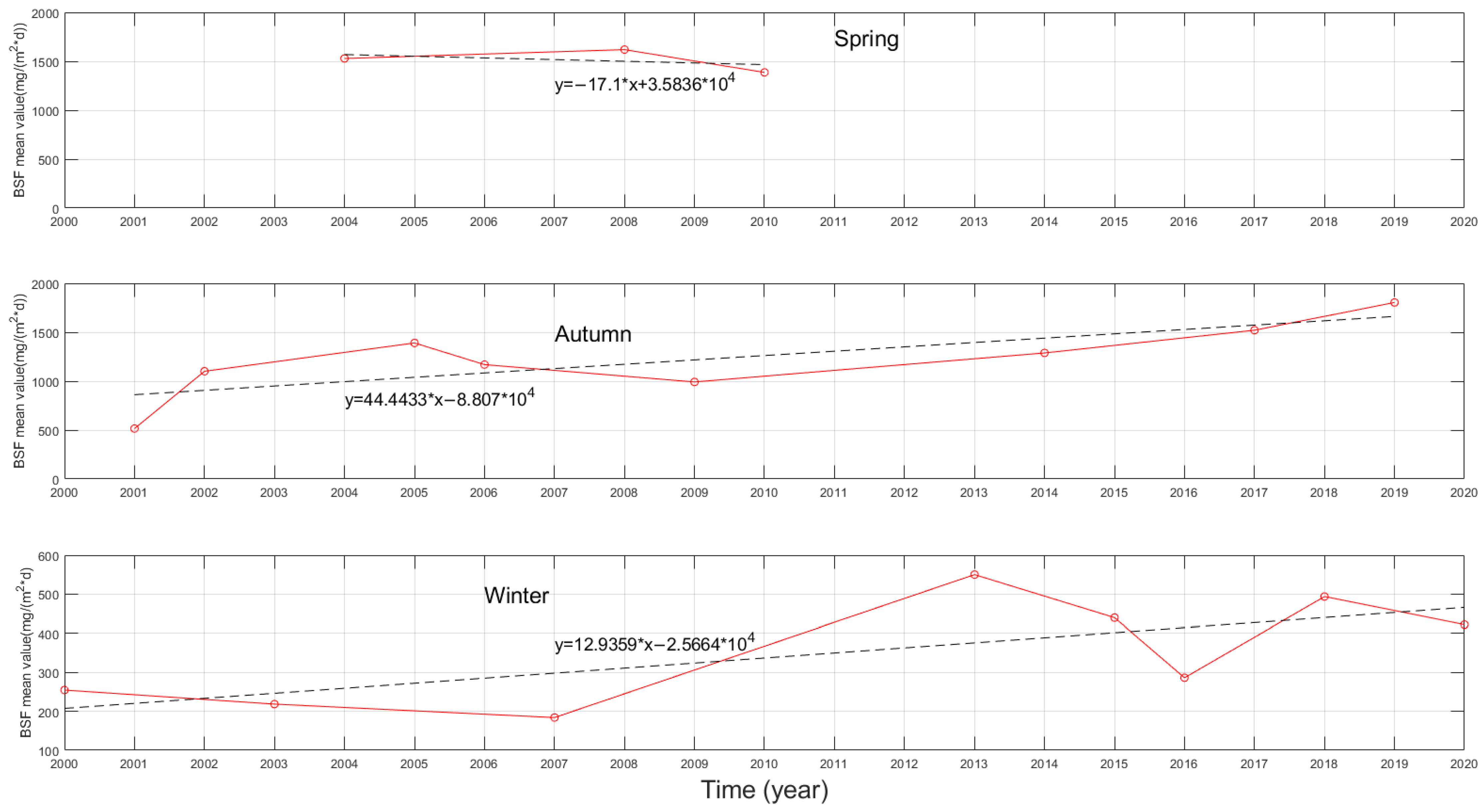
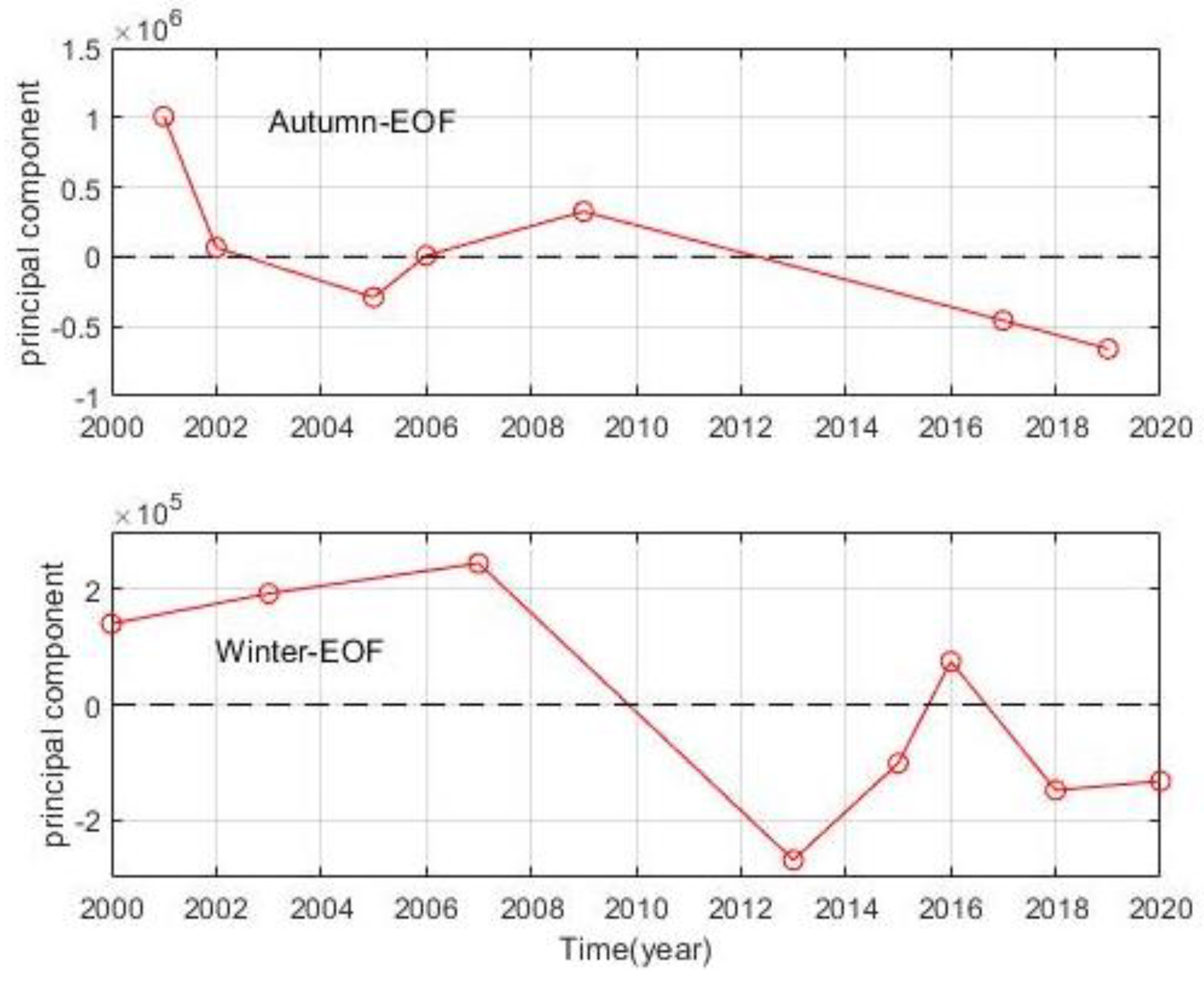
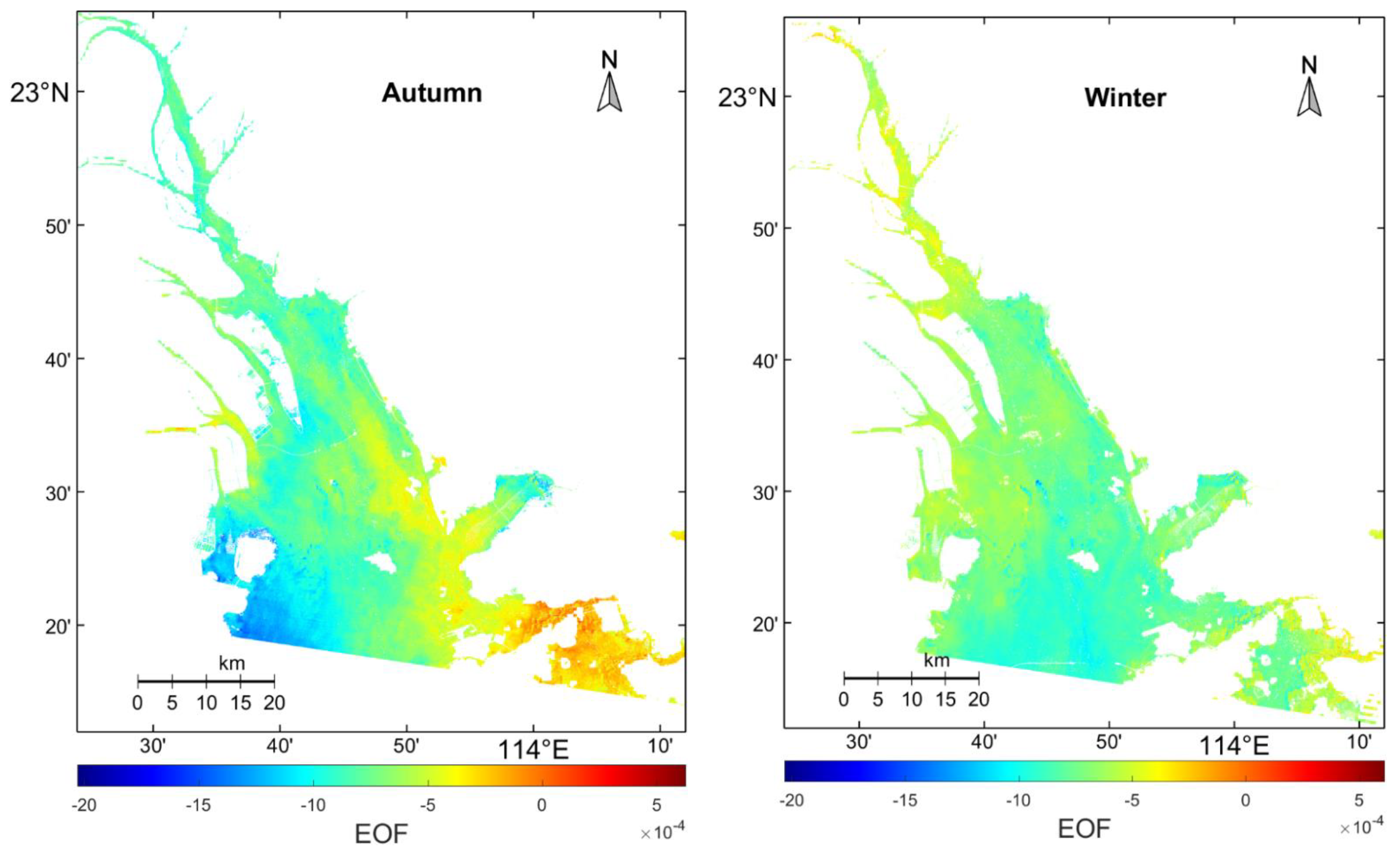
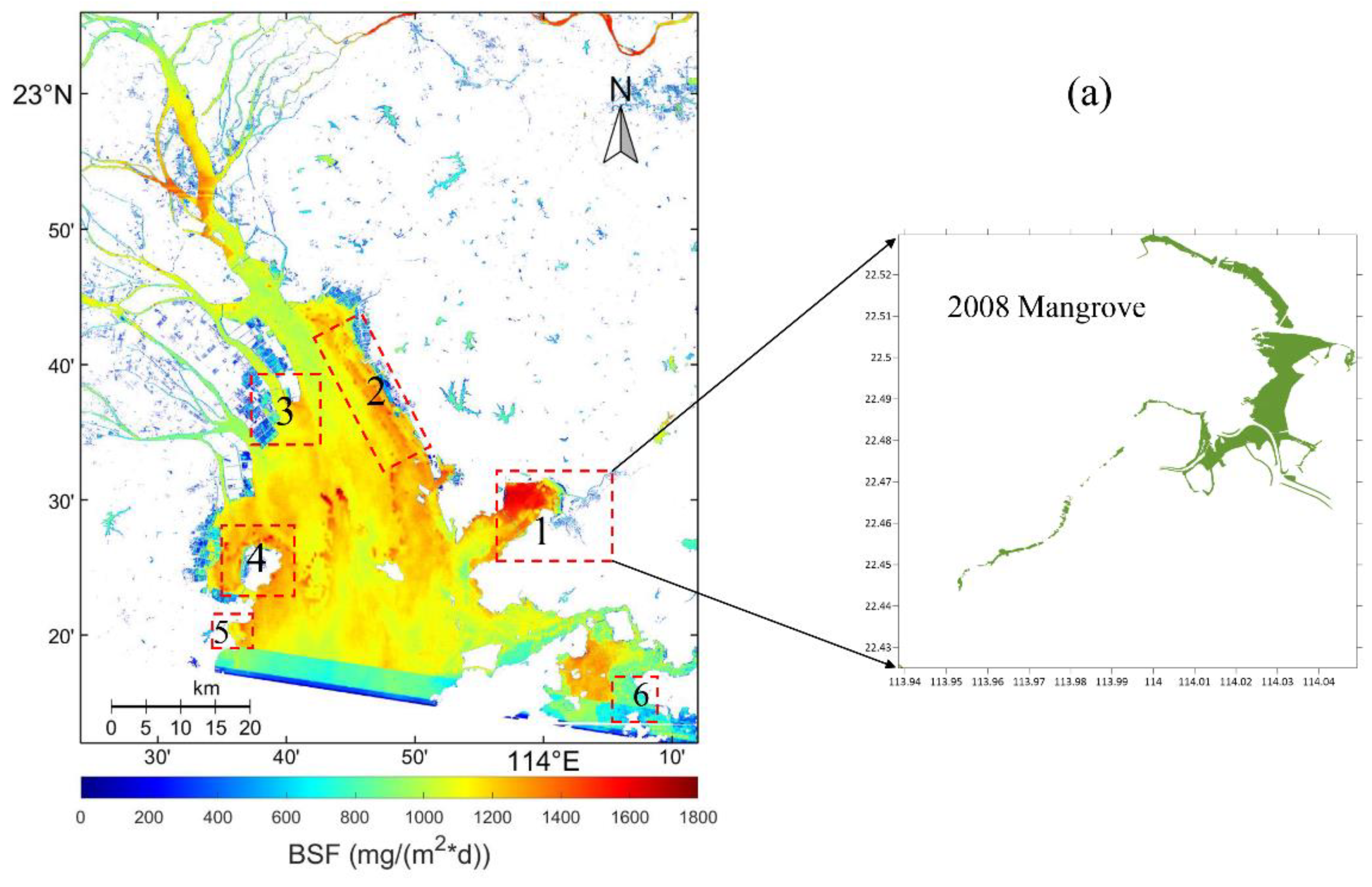
3.3. Temporal and Spatial Variation of BSF
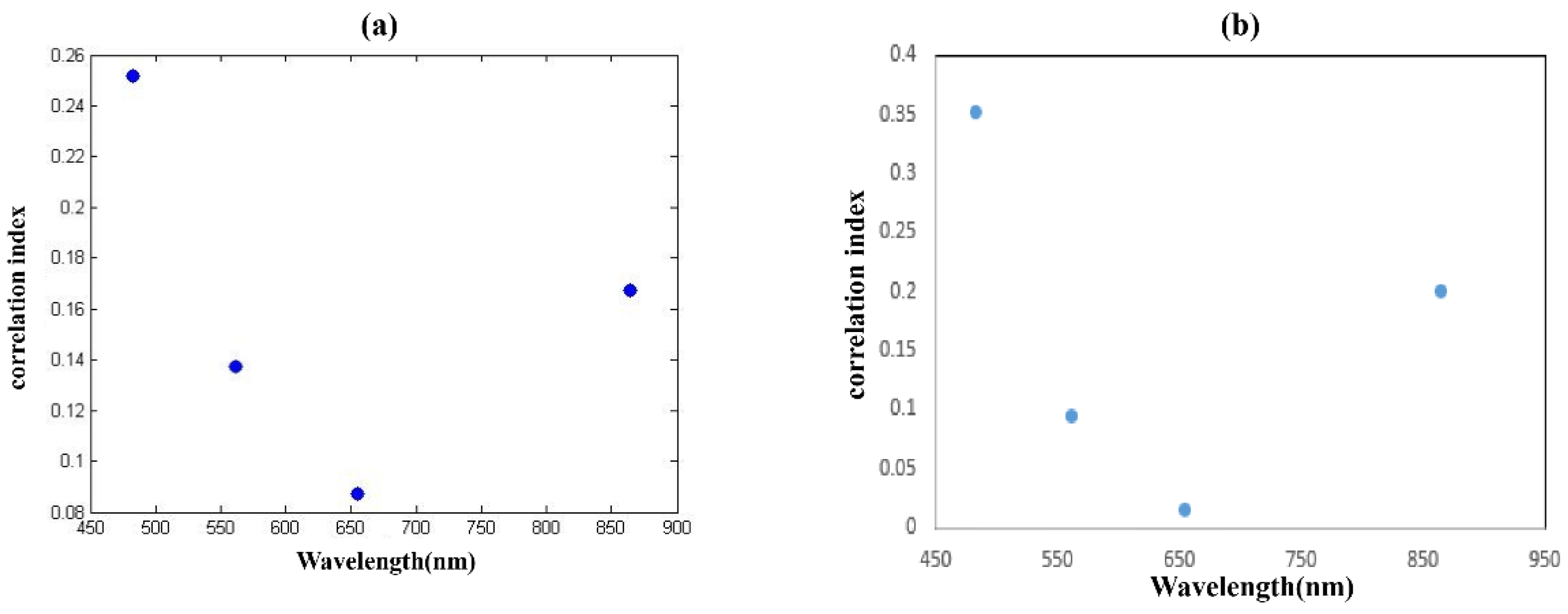
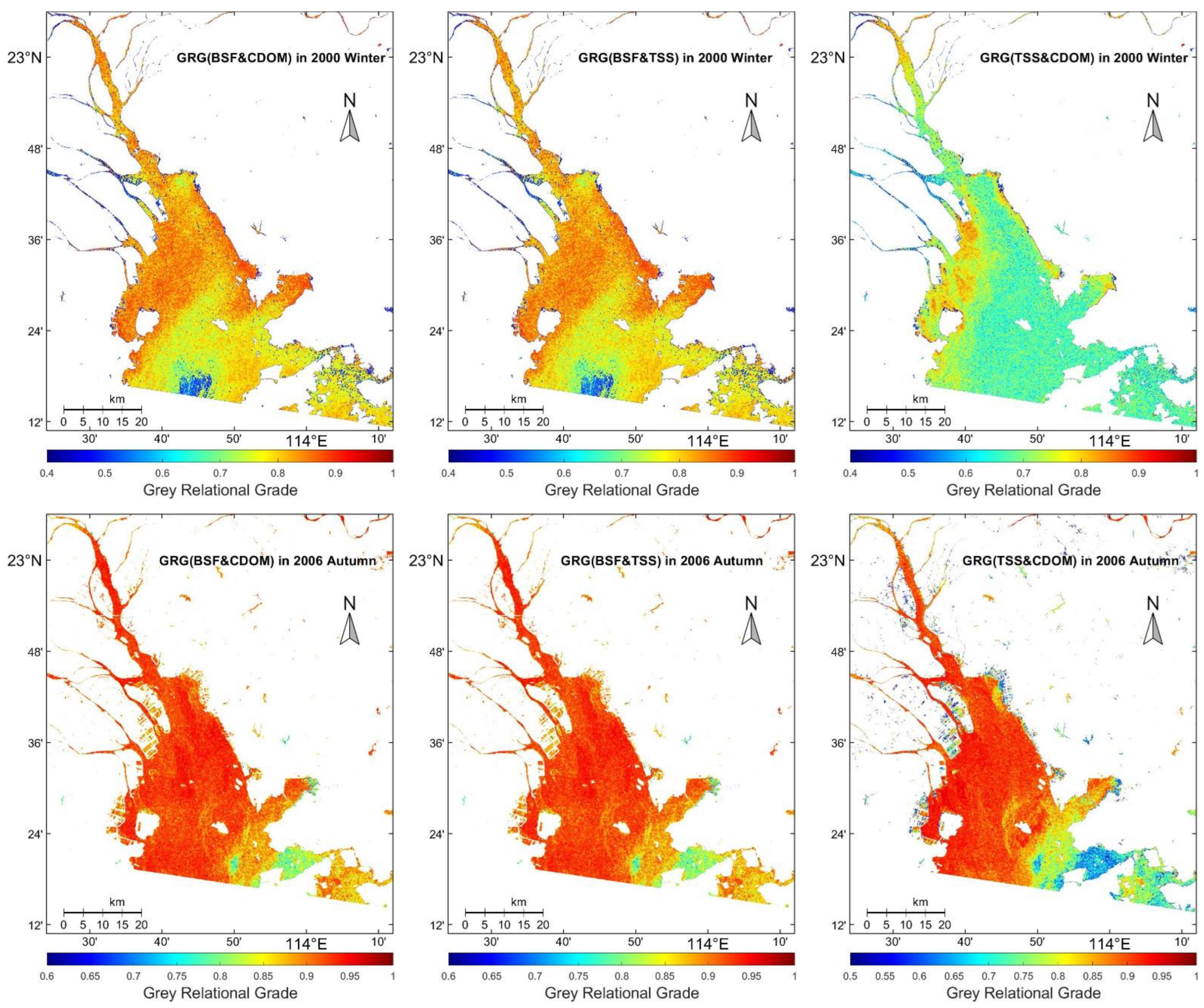
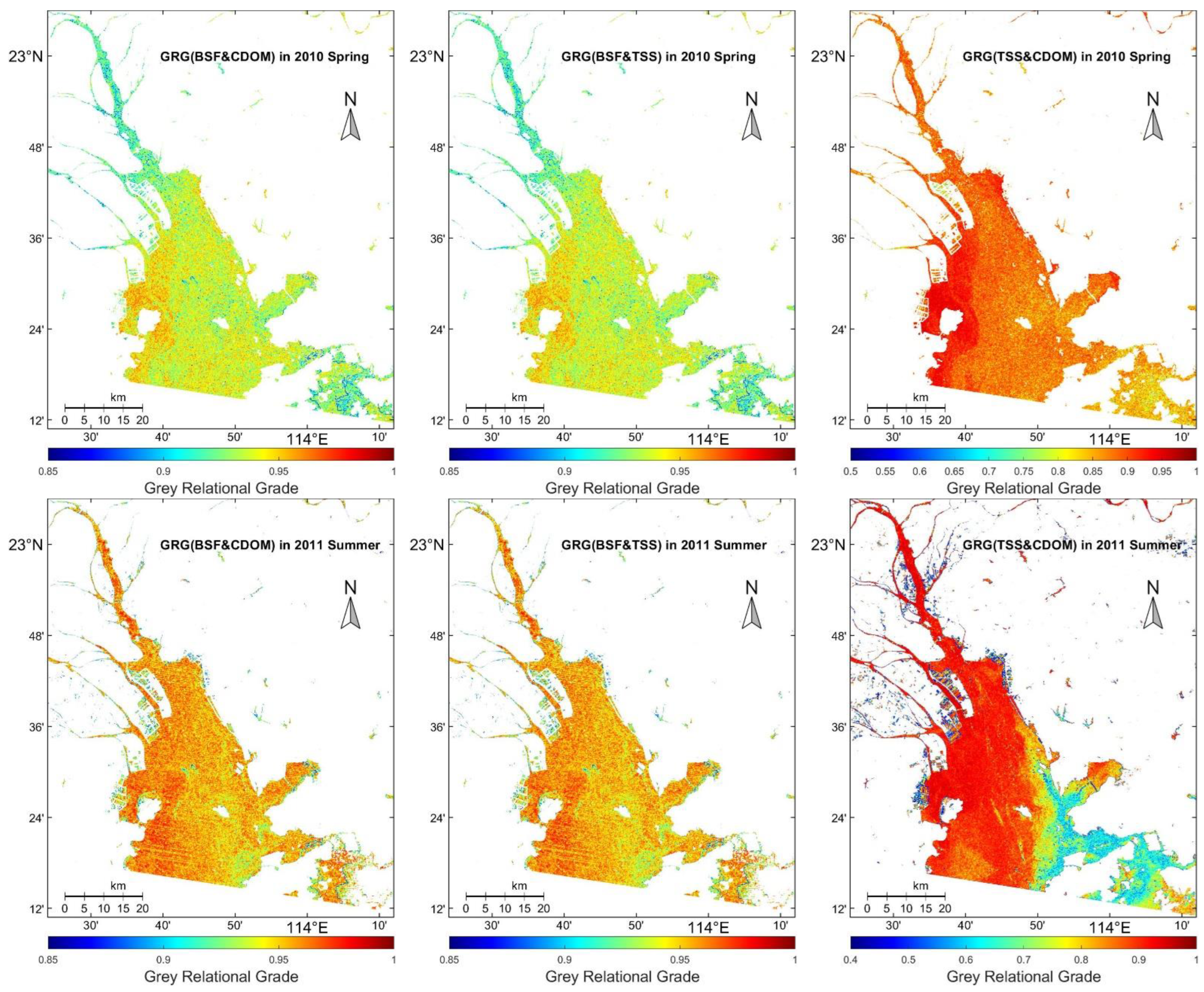
3.4. Results of Water Constituents Affecting BSF
4. Discussion
4.1. Evaluation of BSF Results
4.2. Relationship between BSF and Water Constituents
4.3. Influence of Environmental Factors on BSF
4.3.1. Ecosystem
4.3.2. Flow Field
4.3.3. Islands and Reefs
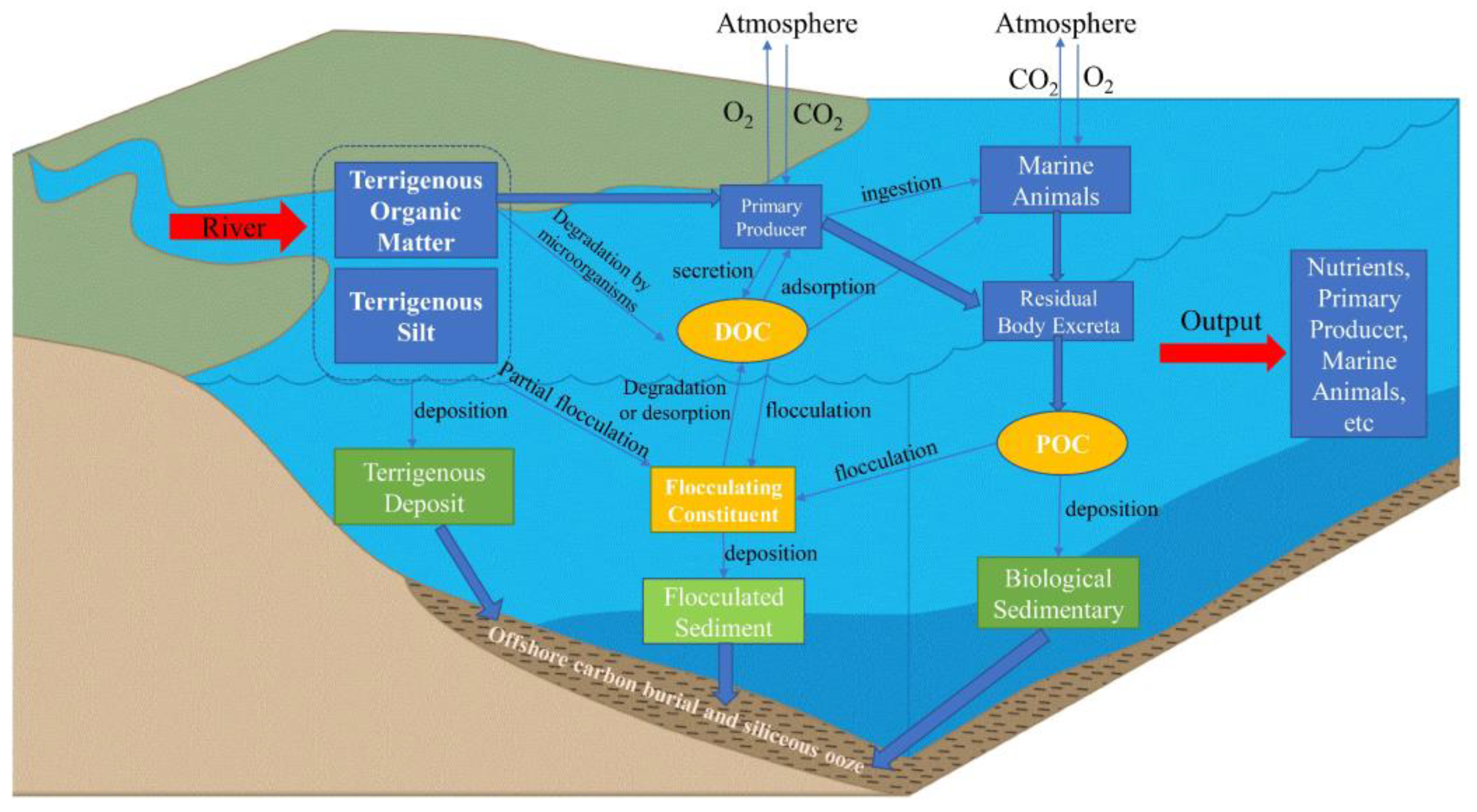
4.3.4. Flocculation
4.4. Prospect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Year | Remote Sensing Image ID | Remote Sensing Product ID |
|---|---|---|
| 2000 | LE71220442000002SGS00 | sw_par_1d_2018_0_1baa_6f01_82fa |
| 2001 | LE71220442001260SGS00 | sw_par_1d_2018_0_111d_563f_d732 |
| 2002 | LE71220442002311EDC00 | aqua_par_1d_2018_0_928a_f116_5fc4 |
| 2003 | LE71220442003058SGS00 | A2003059052000.L2_LAC_OC |
| 2004 | LT51220442004069BJC00 | A2004069052500.L2_LAC_OC |
| 2005 | LT51220442005295BJC00 | A2005295052500.L2_LAC_OC |
| 2006 | LT51220442006314BJC00 | A2006314052500.L2_LAC_OC |
| 2007 | LT51220442007029BJC00 | A2007029052500.L2_LAC_OC |
| 2008 | LT51220442008064BKT00 | A2008064052500.L2_LAC_OC |
| 2009 | LT51220442009290BJC00 | A2009290053000.L2_LAC_OC |
| 2010 | LT51220442010085BKT00 | A2010085053000.L2_LAC_OC |
| 2011 | LT51220442011152BKT00 | A2011152052500.L2_LAC_OC |
| 2012 | LE71220442012307EDC00 | A2012308052000.L2_LAC_OC |
| 2013 | LC81220442013365LGN01 | A2013365052500.L2_LAC_OC |
| 2014 | LC81220442014320LGN01 | A2014320052500.L2_LAC_OC |
| 2015 | LC81220442015003LGN01 | A2015003052500.L2_LAC_OC |
| 2016 | LC81220442016038LGN01 LC81220442016086LGN01 LC81220452016038LGN01 LC81220452016086LGN01 MYD02HKM.A2016038.0525.061.2018055133234 MOD02HKM.A2016059.0235.061.2017325012149 MOD02HKM.A2016060.0320.061.2017325013357 MYD02HKM.A2016086.0530.061.2018057053639 MYD02HKM.A2016086.0525.061.2018057053740 | A2016038052500.L2_LAC_OC |
| 2017 | LC81220442017296LGN00 | A2017296052500.L2_LAC_OC |
| 2018 | LC81220442018043LGN00 | A2018043052500.L2_LAC_OC |
| 2019 | LC81220442019318LGN00 | A2019318052500.L2_LAC_OC |
| 2020 | LC81220442020337LGN00 | A2020337052500.L2_LAC_OC |
Appendix B
Appendix C


Appendix D
Appendix E
References
- Trujillo, A.P.; Thurman, H.V. Essentials of Oceanography, 11th ed.; Pearson Education: Hoboken, NJ, USA, 2014; pp. 98–99. [Google Scholar]
- Yang, D.; Yin, X. Potential deposition of biogenic silica source sediment in the Paleo-Yangtze Grand Underwater Delta estimated with satellite remote sensing. Mar. Georesour. Geotechnol. 2017, 36, 245–252. [Google Scholar] [CrossRef]
- Klyuvitkin, A.A.; Novigatsky, A.N.; Politova, N.V.; Koltovskaya, E.V. Studies of Sedimentary Matter Fluxes along a Long-Term Transoceanic Transect in the North Atlantic and Arctic Interaction Area. Oceanology 2019, 59, 411–421. [Google Scholar] [CrossRef]
- Cai, J.; Zeng, X.; Wei, H.; Song, M.; Wang, X.; Liu, Q. From water body to sediments: Exploring the depositional processes of organic matter and their implications. J. Palaeogeogr. 2019, 21, 49–66. [Google Scholar]
- Wang, X.; Zhang, H.; Han, G. Carbon Cycle and Blue Carbon Potential in China’s Coastal Zone. Bull. Chin. Acad. Sci. 2016, 31, 1218–1225. [Google Scholar]
- He, M.Q.; Cai, L.L.; Xu, J.; Li, X.F.; Shi, Z.; Jiao, N.A.Z.; Zhang, R. Sedimentation of psbA Gene-Containing Cyanophages, Cyanobacteria, and Eukaryotes in Marine and Estuarine Sediments. J. Geophys. Res. Biogeosci. 2021, 126, 14. [Google Scholar] [CrossRef]
- Talavera, L.; Vila-Concejo, A.; Webster, J.M.; Smith, C.; Duce, S.; Fellowes, T.E.; Salles, T.; Harris, D.; Hill, J.; Figueira, W.; et al. Morphodynamic Controls for Growth and Evolution of a Rubble Coral Island. Remote Sens. 2021, 13, 1582. [Google Scholar] [CrossRef]
- Dam, G.; Van der Wegen, M.; Taal, M.; Van der Spek, A. Contrasting behaviour of sand and mud in a long-term sediment budget of the Western Scheldt estuary. Sedimentology 2022, 69, 2267–2283. [Google Scholar] [CrossRef]
- Bale, A.J.; Uncles, R.J.; Villena-Lincoln, A.; Widdows, J. An assessment of the potential impact of dredging activity on the Tamar Estuary over the last century: Bathymetric and hydrodynamic changes. Hydrobiologia 2007, 588, 83–95. [Google Scholar] [CrossRef]
- Xia, M.; Zhang, C.; Ma, Z.; Liang, Z.; Zhou, X. 210Pb-dating method and determination of sedimentation velocity in Pearl River Estuary and Jinzhou Bay in the Bohai Sea. Scientia 1983, 5, 291–295. [Google Scholar]
- Nasiha, H.J.; Shanmugam, P. Estimation of settling velocity of sediment particles in estuarine and coastal waters. Estuar. Coast. Shelf Sci. 2018, 203, 59–71. [Google Scholar] [CrossRef]
- Nasiha, H.J.; Shanmugam, P.; Sundaravadivelu, R. Estimation of sediment settling velocity in estuarine and coastal waters using optical remote sensing data. Adv. Space Res. 2019, 63, 3473–3488. [Google Scholar] [CrossRef]
- Wang, Y.S.; Liang, X.L.; Flener, C.; Kukko, A.; Kaartinen, H.; Kurkela, M.; Vaaja, M.; Hyyppa, H.; Alho, P. 3D Modeling of Coarse Fluvial Sediments Based on Mobile Laser Scanning Data. Remote Sens. 2013, 5, 4571–4592. [Google Scholar] [CrossRef]
- Duan, D.D.; Ran, Y.; Cheng, H.F.; Chen, J.A.; Wan, G.J. Contamination trends of trace metals and coupling with algal productivity in sediment cores in Pearl River Delta, South China. Chemosphere 2014, 103, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yin, K.D.; Wang, L.; Chen, F.R.; Zhang, D.R.; Yang, Y.Q. The sources and accumulation rate of sedimentary organic matter in the Pearl River Estuary and adjacent coastal area, Southern China. Estuar. Coast. Shelf Sci. 2009, 85, 190–196. [Google Scholar] [CrossRef]
- Zhou, P.; Li, D.; Li, H.; Zhao, L.; Zhao, F.; Zheng, Y.; Wu, M.; Yu, H. Biogenic silica contents and its distribution in the sediments of the west Daya Bay. J. Appl. Oceanogr. 2019, 38, 109–117. [Google Scholar]
- Suess, E. Particulate organic-carbon flux in the oceans—Surface productivity and oxygen utilization. Nature 1980, 288, 260–263. [Google Scholar] [CrossRef]
- Armstrong, R.A.; Lee, C.; Hedges, J.I.; Honjo, S.; Wakeham, S.G. A new, mechanistic model for organic carbon fluxes in the ocean based on the quantitative association of POC with ballast minerals. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2001, 49, 219–236. [Google Scholar] [CrossRef]
- Ye, H.B.; Chen, C.Q.; Sun, Z.H.; Tang, S.L.; Song, X.Y.; Yang, C.Y.; Tian, L.Q.; Liu, F.F. Estimation of the Primary Productivity in Pearl River Estuary Using MODIS Data. Estuaries Coasts 2015, 38, 506–518. [Google Scholar] [CrossRef]
- Zhang, Y.; Ghen, J.; Wang, J.; Han, Y.; Yi, L. Remote sensing inversion for net primary productivity and its spatial-temporal variability in Shenzhen coastal waters. J. Appl. Oceanogr. 2017, 36, 311–318. [Google Scholar]
- Dai, M.; Li, C.; Jia, X.; Zhang, H.; Chen, R. Ecological characteristics of phytoplankton in coastal area of Pearl River estuary. J. Appl. Ecol. 2004, 15, 1389–1394. [Google Scholar]
- Hu, X.Y.; Wang, Y.P. Coastline Fractal Dimension of Mainland, Island, and Estuaries Using Multi-temporal Landsat Remote Sensing Data from 1978 to 2018: A Case Study of the Pearl River Estuary Area. Remote Sens. 2020, 12, 2482. [Google Scholar] [CrossRef]
- Tang, S.; Cai, R.; Guo, H.; Wang, L. Response of phytoplankton in offshore China seas to climate change. J. Appl. Oceanogr. 2017, 36, 455–465. [Google Scholar]
- Chen, Y. Modern Sedimentary Velocity and Sedimentary Environment in the Pearl River Mouth. Acta Sci. Nat. Univ. Sunyatseni 1992, 31, 100. [Google Scholar]
- Chen, Y.; Luo, Z. Modern sedimentary velocity and their reflected sedimentary characteristics in the pearl river mouth. Trop. Oceanol. 1991, 10, 57. [Google Scholar]
- Liu, D.; Pan, D.L.; Bai, Y.; He, X.Q.; Wang, D.F.; Wei, J.A.; Zhang, L. Remote Sensing Observation of Particulate Organic Carbon in the Pearl River Estuary. Remote Sens. 2015, 7, 8683–8704. [Google Scholar] [CrossRef]
- Wang, Z.M.; Hu, S.B.; Li, Q.Q.; Liu, H.Z.; Liao, X.M.; Wu, G.F. A Four-Step Method for Estimating Suspended Particle Size Based on In Situ Comprehensive Observations in the Pearl River Estuary in China. Remote Sens. 2021, 13, 5172. [Google Scholar] [CrossRef]
- Yu, X.; Xu, J.; Long, A.; Zhong, W. Determination of suspended biogenic silica in the Pearl River Estuaryand its adjacent coastal waters in summer. J. Mar. Sci. 2018, 36, 67–75. [Google Scholar]
- Jia, G.; Peng, P.; Fu, J. Sedimentary records of accelerated eutrophication for the last 100 years at the pearl river estuary. Quat. Sci. 2002, 22, 158–165. [Google Scholar]
- Ye, H.B.; Chen, C.Q.; Yang, C.Y. Atmospheric Correction of Landsat-8/OLI Imagery in Turbid Estuarine Waters: A Case Study for the Pearl River Estuary. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 252–261. [Google Scholar] [CrossRef]
- Nukapothula, S.; Chen, C.Q.; Wu, J. Long-term distribution patterns of remotely sensed water quality variables in Pearl River Delta, China. Estuar. Coast. Shelf Sci. 2019, 221, 90–103. [Google Scholar] [CrossRef]
- Wong, L.A.; Chen, J.; Xue, H.; Dong, L.X.; Su, J.L.; Heinke, G. A model study of the circulation in the Pearl River Estuary (PRE) and its adjacent coastal waters: 1. Simulations and comparison with observations. J. Geophys. Res. Ocean. 2003, 108, 17. [Google Scholar] [CrossRef]
- Hu, J.T.; Li, S.Y.; Geng, B.X. Modeling the mass flux budgets of water and suspended sediments for the river network and estuary in the Pearl River Delta, China. J. Mar. Syst. 2011, 88, 252–266. [Google Scholar] [CrossRef]
- Li, H.T.; Xie, X.T.; Yang, X.K.; Cao, B.W.; Xia, X.N. An Integrated Model of Summer and Winter for Chlorophyll-a Retrieval in the Pearl River Estuary Based on Hyperspectral Data. Remote Sens. 2022, 14, 2270. [Google Scholar] [CrossRef]
- Chen, C.Q.; Pan, Z.L.; Shi, P.; Zhan, H.G.; Larson, M.; Jonsson, L. Application of satellite data for integrated assessment of water quality in the Pearl River Estuary, China. In Proceedings of the 25th IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2005), Seoul, Republic of Korea, 25–29 July 2005; pp. 2550–2553. [Google Scholar]
- Lin, R.; Min, Y.; Wei, K.; Zhang, G.; Yu, F.; Yu, Y. 210Pb-dating of sediment cores from the pearl river mouth and its environmental geochemistry implication. Geochimica 1998, 27, 401. [Google Scholar]
- Welschmeyer, N.A. Fluorometric analysis of chlorophyll-a in the presence of chlorophyll-b and pheopigments. Limnol. Oceanogr. 1994, 39, 1985–1992. [Google Scholar] [CrossRef]
- Shilin, T.; Chuqun, C.; Haigang, Z. Retrieval progress of ocean primary production by remote sensing. J. Oceanogr. Taiwan Strait 2006, 25, 591–598. [Google Scholar]
- Liu, G.; Hu, J.; Li, S.; Liang, B.; Huang, J. Simulation of organic carbon distribution and budgets during summer in the Pearl River Estuary. Acta Sci. Circumstantiae 2019, 39, 1123–1133. [Google Scholar]
- Wang, B.; Hu, J.T.; Li, S.Y.; Liu, D.H. A numerical analysis of biogeochemical controls with physical modulation on hypoxia during summer in the Pearl River estuary. Biogeosciences 2017, 14, 2979–2999. [Google Scholar] [CrossRef]
- Heng, Z.; Shi-yu, L.I. A numerical study on hypoxia and primary production in the Pearl River Estuary in summer using the modified RCA water quality model. J. Trop. Oceanogr. 2010, 29, 20–31. [Google Scholar]
- Liu, G.; Hu, J.; Li, S. Simulation of marine and terrestrial organic carbon in the Pearl River Estuary in summerdistribution characteristics, contribution rate and migration and transformation processes. China Environ. Sci. 2020, 40, 162–173. [Google Scholar]
- Wan, S.A.; Chang, S.H. Crop classification with WorldView-2 imagery using Support Vector Machine comparing texture analysis approaches and grey relational analysis in Jianan Plain, Taiwan. Int. J. Remote Sens. 2019, 40, 8076–8092. [Google Scholar] [CrossRef]
- Yang, C.Y.; Ye, H.B.; Tang, S.L. Seasonal Variability of Diffuse Attenuation Coefficient in the Pearl River Estuary from Long-Term Remote Sensing Imagery. Remote Sens. 2020, 12, 2269. [Google Scholar] [CrossRef]
- Liu, M.X.; Liu, X.N.; Dong, X.B.; Zhao, B.Y.; Zou, X.Y.; Wu, L.; Wei, H.J. An Improved Spatiotemporal Data Fusion Method Using Surface Heterogeneity Information Based on ESTARFM. Remote Sens. 2020, 12, 3673. [Google Scholar] [CrossRef]
- Liu, F.F.; Tang, S.L. Evaluation of Red-Peak Algorithms for Chlorophyll Measurement in the Pearl River Estuary. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8928–8936. [Google Scholar] [CrossRef]
- Martins, J.P.A.; Trigo, I.F.; Bento, V.A.; da Camara, C. A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms. Remote Sens. 2016, 8, 808. [Google Scholar] [CrossRef]
- Ermida, S.L.; Soares, P.; Mantas, V.; Gottsche, F.M.; Trigo, I.E. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Tiwari, S.P.; Shanmugam, P. A Robust Algorithm to Determine Diffuse Attenuation Coefficient of Downwelling Irradiance From Satellite Data in Coastal Oceanic Waters. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1616–1622. [Google Scholar] [CrossRef]
- Liu, Y.M.; Deng, R.R.; Qin, Y.; Cao, B.; Liang, Y.H.; Liu, Y.F.; Tian, J.L.; Wang, S.L. Rapid estimation of bathymetry from multispectral imagery without in situ bathymetry data. Appl. Opt. 2019, 58, 7538–7551. [Google Scholar] [CrossRef]
- Zhu, J.; Li, W.; Wang, G. Using remote sensing to define water depth in the pearl river estuary. Mar. Geol. Front. 2012, 28, 52–59. [Google Scholar]
- Carr, M.E.; Friedrichs, M.A.M.; Schmeltz, M.; Aita, M.N.; Antoine, D.; Arrigo, K.R.; Asanuma, I.; Aumont, O.; Barber, R.; Behrenfeld, M.; et al. A comparison of global estimates of marine primary production from ocean color. Deep. Sea Res. Part I Top. Stud. Oceanogr. 2006, 53, 741–770. [Google Scholar] [CrossRef]
- Sarnthein, M.; Winn, K.; Duplessy, J.C.; Fontugne, M.R. Global variations of surface ocean productivity in low and mid latitudes: Influence on CO2 reservoirs of the deep ocean and atmosphere during the last 21,000 years. Paleoceanography 1988, 3, 361–399. [Google Scholar] [CrossRef]
- Nazeer, M.; Bilal, M.; Nichol, J.E.; Wu, W.C.; Alsahli, M.M.M.; Shahzad, M.I.; Gayen, B.K. First Experiences with the Landsat-8 Aquatic Reflectance Product: Evaluation of the Regional and Ocean Color Algorithms in a Coastal Environment. Remote Sens. 2020, 12, 1938. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Tang, S.L.; Wu, J. A chlorophyll-a retrieval algorithm for the Coastal Zone Imager (CZI) onboard the HY-1C satellite in the Pearl River Estuary, China. Int. J. Remote Sens. 2021, 42, 8365–8379. [Google Scholar] [CrossRef]
- Mahasandana, S.; Tripathi, N.K.; Honda, K. Sea surface multispectral index model for estimating chlorophyll a concentration of productive coastal waters in Thailand. Can. J. Remote Sens. 2009, 35, 287–296. [Google Scholar] [CrossRef]
- Cai, Y.; Ning, X.; Liu, Z. Studies on primary production and new production of the Zhujiang Estuary, China. Acta Oceanol. Sin. 2002, 24, 101–111. [Google Scholar]
- Yin, K.D.; Zhang, J.L.; Qian, P.Y.; Jian, W.J.; Huang, L.M.; Chen, J.F.; Wu, M.C.S. Effect of wind events on phytoplankton blooms in the Pearl River estuary during summer. Cont. Shelf Res. 2004, 24, 1909–1923. [Google Scholar] [CrossRef]
- Wang, Y.J. Application of Remote Sensing Technology to Map Water Depth by Weakening the Influence of Suspended Sediment. Doctor Dissertation, Nanjing Normal University, Nanjing, China, 2006. [Google Scholar]
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Qin, Y.C. Study on the Biogeochemistry of Sedimentary Silica in the Pearl River Estuary, China. Doctor Dissertation, Zhejiang University, Hangzhou, China, 2006. [Google Scholar]
- Guo, J.; Ma, C.L.; Ai, B.; Xu, X.P.; Huang, W.; Zhao, J. Assessing the Effects of the Hong Kong-Zhuhai-Macau Bridge on the Total Suspended Solids in the Pearl River Estuary Based on Landsat Time Series. J. Geophys. Res. Ocean. 2020, 125, 13. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.N. Consistency evaluation of landsat-7 and landsat-8 for improved monitoring of colored dissolved organic matter in complex water. Geocarto Int. 2022, 37, 91–102. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.N.; Pang, S.N.; Cheng, Q. Applicability evaluation of Landsat-8 for estimating low concentration colored dissolved organic matter in inland water. Geocarto Int. 2022, 37, 1–15. [Google Scholar] [CrossRef]
- Liu, H.Z.; Zhou, Q.M.; Wu, G.F.; Hu, S.B.; Li, Q.Q. Adaptation and validation of the swire algorithm for sentinel-3 over complex waters of pearl river estuary. In Proceedings of the 38th IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 7933–7936. [Google Scholar]
- Xu, Y.; Feng, L.; Zhao, D.; Lu, J. Assessment of Landsat atmospheric correction methods for water color applications using global AERONET-OC data. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102192. [Google Scholar] [CrossRef]
- Wei, J.; Lee, Z.; Garcia, R.; Zoffoli, L.; Armstrong, R.A.; Shang, Z.; Sheldon, P.; Chen, R.F. An assessment of Landsat-8 atmospheric correction schemes and remote sensing reflectance products in coral reefs and coastal turbid waters. Remote Sens. Environ. 2018, 215, 18–32. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Ilori, C.; Pahlevan, N.; Knudby, A. Analyzing Performances of Different Atmospheric Correction Techniques for Landsat 8: Application for Coastal Remote Sensing. Remote Sens. 2019, 11, 469. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Adaptation of the dark spectrum fitting atmospheric correction for aquatic applications of the Landsat and Sentinel-2 archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Ye, H.B.; Yang, C.Y.; Tang, S.L.; Chen, C.Q. The phytoplankton variability in the Pearl River estuary based on VIIRS imagery. Cont. Shelf Res. 2020, 207, 104228. [Google Scholar] [CrossRef]
- Zhao, J.; Cao, W.X.; Xu, Z.T.; Ai, B.; Yang, Y.Z.; Jin, G.Z.; Wang, G.F.; Zhou, W.; Chen, Y.; Chen, H.Y.; et al. Estimating CDOM Concentration in Highly Turbid Estuarine Coastal Waters. J. Geophys. Res. Ocean. 2018, 123, 5856–5873. [Google Scholar] [CrossRef]
- Liu, R.Q.; Wang, Y.P.; Gao, J.H.; Wu, Z.Y.; Guan, W.B. Turbidity maximum formation and its seasonal variations in the Zhujiang (Pearl River) Estuary, southern China. Acta Oceanol. Sin. 2016, 35, 22–31. [Google Scholar] [CrossRef]
- He, Y.; Qin, Y.; Feng, Y.; Fu, Q.; Liu, C. Absorption characteristics of CDOM in the Pearl River Estuary at flood and ebb tides. Acta Sci. Nat. Univ. Sunyatseni 2018, 57, 22–31. [Google Scholar]
- Cheng, J.Y. Design and Production of Mangrove Remote Sensing Products and Data Sets in Guangdong-Hong Kong-Macao Greater Bay Area. Master Thesis, Jiangsu Ocean University, Lianyungang, China, 2022. [Google Scholar]
- Huang, X.P.; Jiang, Z.; Zhang, J.; Shi, Z.; Wang, F.; Ye, F.; Li, L. Newly discovered seagrass beds in the coastal seas of Guangdong Province. J. Trop. Oceanogr. 2010, 29, 132–135. [Google Scholar]
- Barcelona, A.; Serra, T.; Colomer, J. Fragmented Canopies Control the Regimes of Gravity Current Development. J. Geophys. Res. Ocean. 2018, 123, 1631–1646. [Google Scholar] [CrossRef]
- de Mendoza, F.P.; Fontolan, G.; Mancini, E.; Scanu, E.; Scanu, S.; Bonamano, S.; Marcelli, M. Sediment dynamics and resuspension processes in a shallow-water Posidonia oceanica meadow. Mar. Geol. 2018, 404, 174–186. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, Z.; Wu, Y.; Zhang, J.; Zhao, C.; Huang, X. Mechanisms of sediment carbon sequestration in seagrass meadows and its responses to eutrophication. Chin. Sci. Bull. 2017, 62, 3309–3318. [Google Scholar] [CrossRef][Green Version]
- Luan, H. Based on Landsat8 the Suspended Sediment Concentration and Chlorophyll a Concentration of the Pearl River Estuary Remote Sensing Inversion and Time and Spatial Change. Master Thesis, Guangdong Ocean University, Zhanjiang, China, 2016. [Google Scholar]
- Sun, Y.; Luo, L.; Wei, G.; Zhai, H.; Li, F. Species Composition and Seasonal Variation in Phytoplankton at Dashahe Reservoir. Resour. Sci. 2014, 36, 1732–1738. [Google Scholar]
- Chen, X.R. Observation and Dynamical Analysis of Hydrographic Characteristics in the Pearl River Estuary in Summer of 2015. Master Thesis, Xiamen University, Xiamen, China, 2017. [Google Scholar]
- Liang, W.; Tang, D. Distribution characteristics of phytoplankton size structure in the western South China Sea in summer. J. Trop. Oceanogr. 2017, 36, 93–101. [Google Scholar]
- He, Y.; Gao, S.; Xu, F.; Hu, X. Key issues of the numerical model for tidal current and sediment transport in the Pearl River Estuary. J. Sediment Res. 2014, 4, 60–66. [Google Scholar]
- Deng, Z.; He, Q.; Yang, Q.; Lin, J. Observations of in situ flocs characteristic in the Modaomen Estuary of the Pearl River. Acta Oceanol. Sin. 2015, 37, 152–161. [Google Scholar]
- Zhu, X.L.; Chen, J.; Gao, F.; Chen, X.H.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Huang, Y.G. Remote Sensing Inversion of Water Quality Parameters in Internal Lingding of Pearl River Estuary Based on Field Spectral Data and Landsat8 OLI Image. Master Thesis, Guangzhou University, Guangzhou, China, 2017. [Google Scholar]
- Hyde, K.J.W.; O’Reilly, J.E.; Oviatt, C.A. Evaluation and application of satellite primary production models in Massachusetts Bay. Cont. Shelf Res. 2008, 28, 1340–1351. [Google Scholar] [CrossRef]
- Kameda, T.; Ishizaka, J. Size-fractionated primary production estimated by a two-phytoplankton community model applicable to ocean color remote sensing. J. Oceanogr. 2005, 61, 663–672. [Google Scholar] [CrossRef]

| Model | Equation | Optimized Parameters | Citation |
|---|---|---|---|
| RTA20 | a = 0.19 | Nazeer et al., 2020 [54] | |
| b = 1.24 | |||
| c = 5 | |||
| SR | a = 0.2071 b = 4.7685 c = 3.7177 d = 1.2649 | Huang et al., 2021 [55] | |
| SSMI | a = 1.998 b = −23.74 | Mahasandana et al., 2009 [56] |
| Model | R2 | p | Slope | RMSE |
|---|---|---|---|---|
| Single-band | 0.1236 | 0.048 | 0.1236 | 0.706 |
| RTA20 | 0.1488 | 0.0293 | 0.238 | 1.221 |
| SR | 0.1429 | 0.0329 | 0.1429 | 1.9854 |
| SSMI | 0.114 | 0.0588 | 0.114 | 2.0187 |
| Date | Mean Values of PP in This Study (mg/m−2day−1) | Mean Values of PP in Other Study (mg/m−2day−1) | Period | Citation |
|---|---|---|---|---|
| March 2004 | 301.9 | 266.4 | Spring (2003 to 2011) | Ye et al., 2015 [19] |
| March 2008 | 358.2 | |||
| March 2010 | 305.2 | |||
| June 2011 | 95.3 | 302.9 | Summer (2003 to 2011) | Ye et al., 2015 [19] |
| 198.7 ± 119.1 | August 1997 | Cai et al., 2002 [57] | ||
| <100~400 | July 1999 | Yin et al., 2004b [58] | ||
| September 2001 | 124.8 | 344.6 | Autumn (2003 to 2011) | Ye et al., 2015 [19] |
| October 2005 | 301.7 | |||
| October 2009 | 268.8 | |||
| October 2017 | 431.1 | |||
| November 2006 | 267.2 | |||
| February 2003 | 59.8 | 224.5 | Winter (2003 to 2011) | Ye et al., 2015 [19] |
| Model | R2 | p | Slope | RMSE |
|---|---|---|---|---|
| This paper | 0.2812 | 0.0031 | 0.5245 | 3.0528 |
| Polynomial model | 0.1612 | 0.0308 | 1.0002 | 3.2978 |
| The BSF Value Retrieved in the Paper (mg × m−2d−1) | BSF Values Estimated in Other Literature (mg × m−2d−1) | Average Content of Biosiliceous in Sediment (μmol × g−1) | Coordinates or Location | Estimation Methods in Other Literature | Citation |
|---|---|---|---|---|---|
| 413.0~434.4 | 415.1~650.7 1 | - | The Northeast of Qi’ao Island | 210Pb dating | Zhang et al., 2009 [15] |
| 171.899673 204.402512 93.674751 277.018799 | - - - - | 55.49 63.96 68.56 164.06 | 22.4167°N, 113.7583°E 22.25°N, 113.8303°E 22.31°N, 113.7125°E 22.438°N, 113.894°E | three-step extraction | Qin, 2006 [61] |
| Coordinates | BSF in the Literature (mg/(m−2day−1)) | BSF in the Paper (mg/(m−2day−1)) |
|---|---|---|
| 22.898°N, 113.578°E | 70.03 | 149.57 |
| 22.454°N, 113.928°E | 178.96 | 169.56 |
| 23.109°N, 113.348°E | 182.85 | 198.74 |
| 22.990°N, 113.519°E | 330.69 | 274.42 |
| 22.581°N, 113.660°E | 462.96 | 349.79 |
| 22.286°N, 113.578°E | 591.34 | 370.35 |
| 22.388°N, 113.631°E | 910.36 | 400.26 |
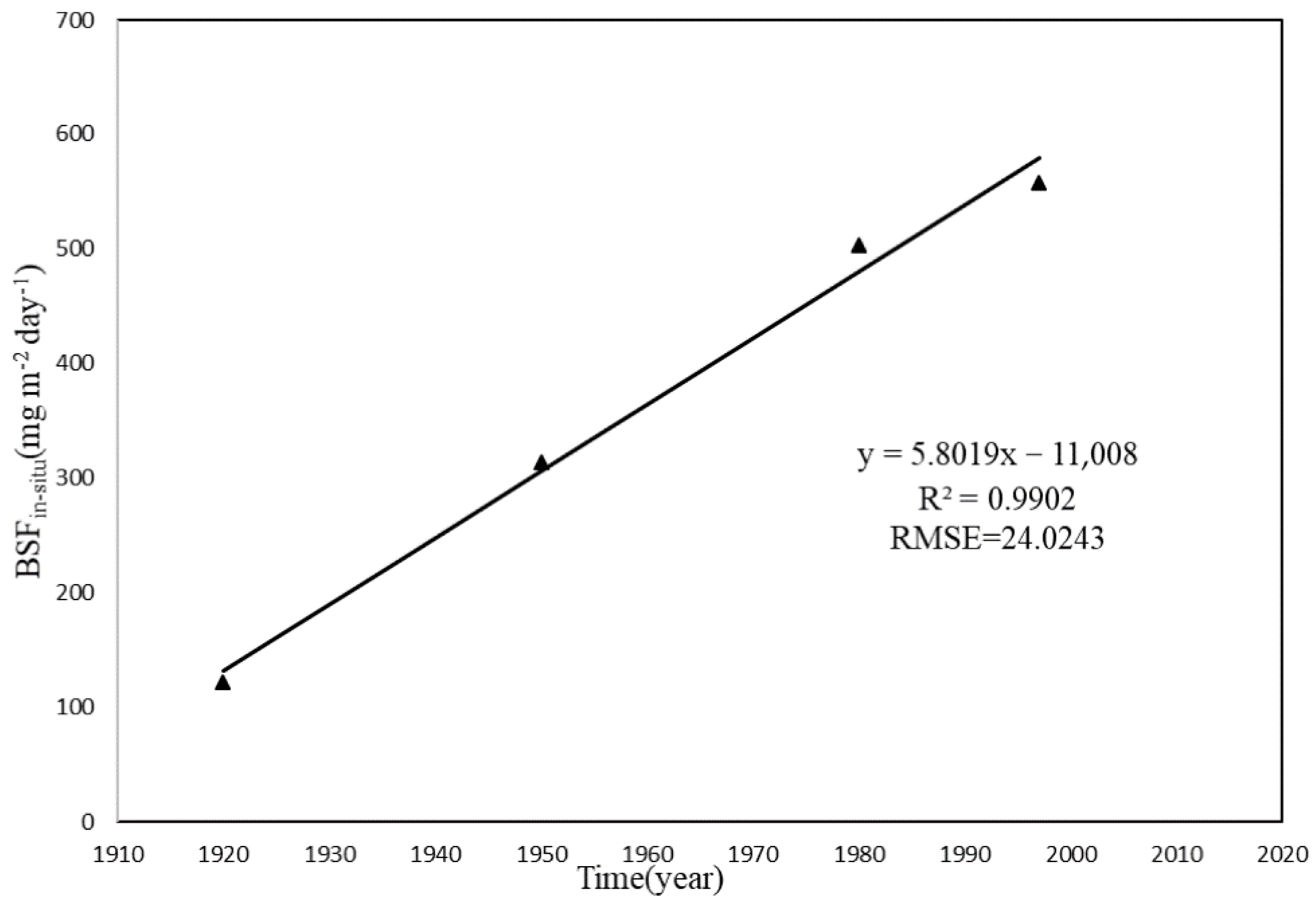
| Time (Year) | 1920 | 1950 | 1980 | 1997 | 2011 | Uncertainty Ratio |
|---|---|---|---|---|---|---|
| In situ BSF value Predicted BSF value | 122.1918 - | 313.6986 - | 503.5616 - | 557.5342 - | - 659.6209 | 35.99% |
| Retrieved BSF value | - | - | - | - | 422.1965 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, R.; Yang, D.; Zhao, L.; Yin, X. First Estimate Biosiliceous Sedimentation Flux in the Pearl River Estuary from 2000–2020 by Satellite Remote Sensing. Remote Sens. 2023, 15, 58. https://doi.org/10.3390/rs15010058
Zhong R, Yang D, Zhao L, Yin X. First Estimate Biosiliceous Sedimentation Flux in the Pearl River Estuary from 2000–2020 by Satellite Remote Sensing. Remote Sensing. 2023; 15(1):58. https://doi.org/10.3390/rs15010058
Chicago/Turabian StyleZhong, Rong, Dingtian Yang, Linhong Zhao, and Xiaoqing Yin. 2023. "First Estimate Biosiliceous Sedimentation Flux in the Pearl River Estuary from 2000–2020 by Satellite Remote Sensing" Remote Sensing 15, no. 1: 58. https://doi.org/10.3390/rs15010058
APA StyleZhong, R., Yang, D., Zhao, L., & Yin, X. (2023). First Estimate Biosiliceous Sedimentation Flux in the Pearl River Estuary from 2000–2020 by Satellite Remote Sensing. Remote Sensing, 15(1), 58. https://doi.org/10.3390/rs15010058