The Estimation of Maize Grain Protein Content and Yield by Assimilating LAI and LNA, Retrieved from Canopy Remote Sensing Data, into the DSSAT Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Experimental Section
2.3. Field Data Acquisition
2.3.1. Canopy Hyperspectral Reflectance Data
2.3.2. Plant Measurements
2.3.3. Fundamental Data
2.3.4. LAI and LNA Estimation with Canopy Hyperspectral Data
2.4. Description of the DSSAT CERES-Maize Model
2.5. The Data Assimilation Method
- (1)
- Assign the initial values to the position and velocity of the particle. The initial conditions sowing density (PPOP), the fertilization amount (FAMN) and the results of the parameter sensitivity analysis of the DSSAT-CERES-Maize model (Table 3) were used as parameters to be optimized;
- (2)
- Run the DSSAT executable using the Rstudio software and retrieve the Time series simulation values for the LAI and LNA;
- (3)
- Perform the remote sensing inversion of the LAI and LNA. The spectral parameter models of the LAI and LNA are constructed;
- (4)
- Construct the fitness function. The fitness function is established by the LAIs and LNAs simulated by the DSSAT model and the LAIm and LNAm retrieved by the vegetation index. This function is used to determine the optimal input parameters of the model. In the assimilation strategy with only one process variable (VLAI or VLNA), the cost function is constructed based on only one variable (LAI or LNA). In addition, the two variables are both considered for building the fitness function in the assimilation strategy, VLAI+LNA;
- (5)
- At each iteration, the Pobest and Pbest are updated by changing the speed and position of each particle. C1 and C2 are equal to 2, and ρ and η are set to a random number between 0 and 1 [61];
- (6)
- The iteration terminates or continues the loop. The position of each particle is updated, and if the number of iterations (100) is not reached, redo step (2). If the last iteration is reached, the maize LAI, LNA, yield and GPC results are output. Figure S1 showed the final distribution range of each optimization parameter.
3. Results
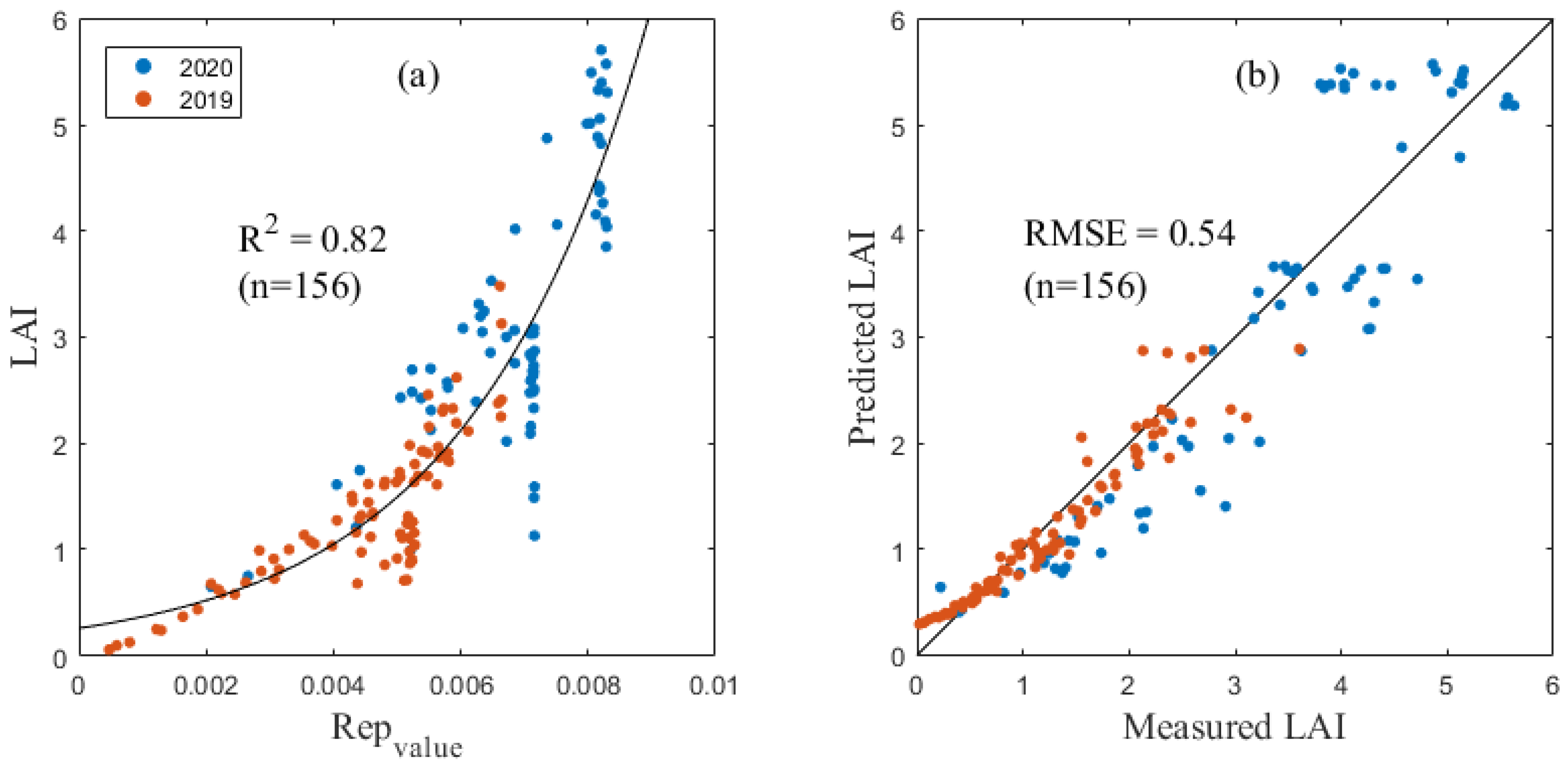
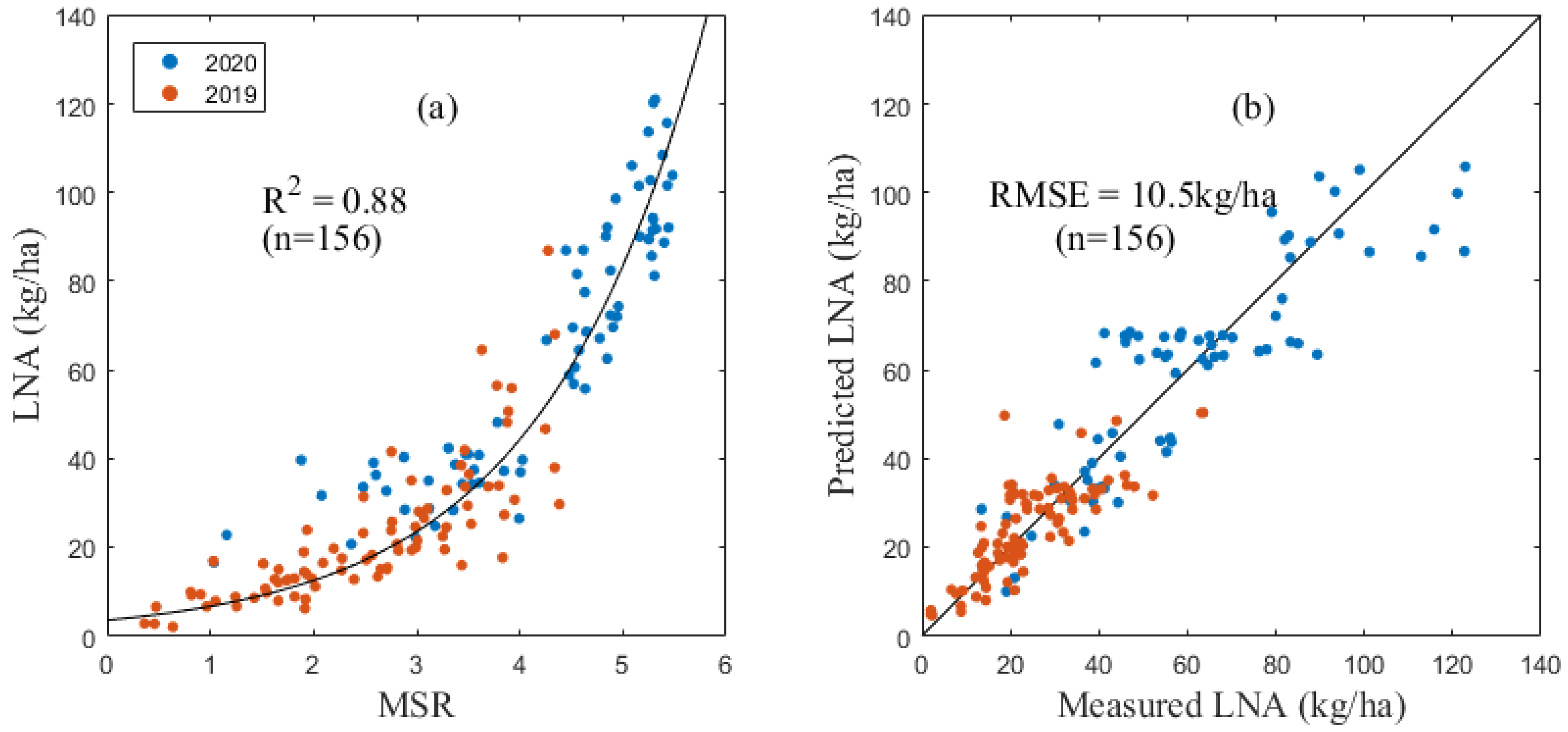
3.1. Estimating LAI and LNA Using Spectral Indices
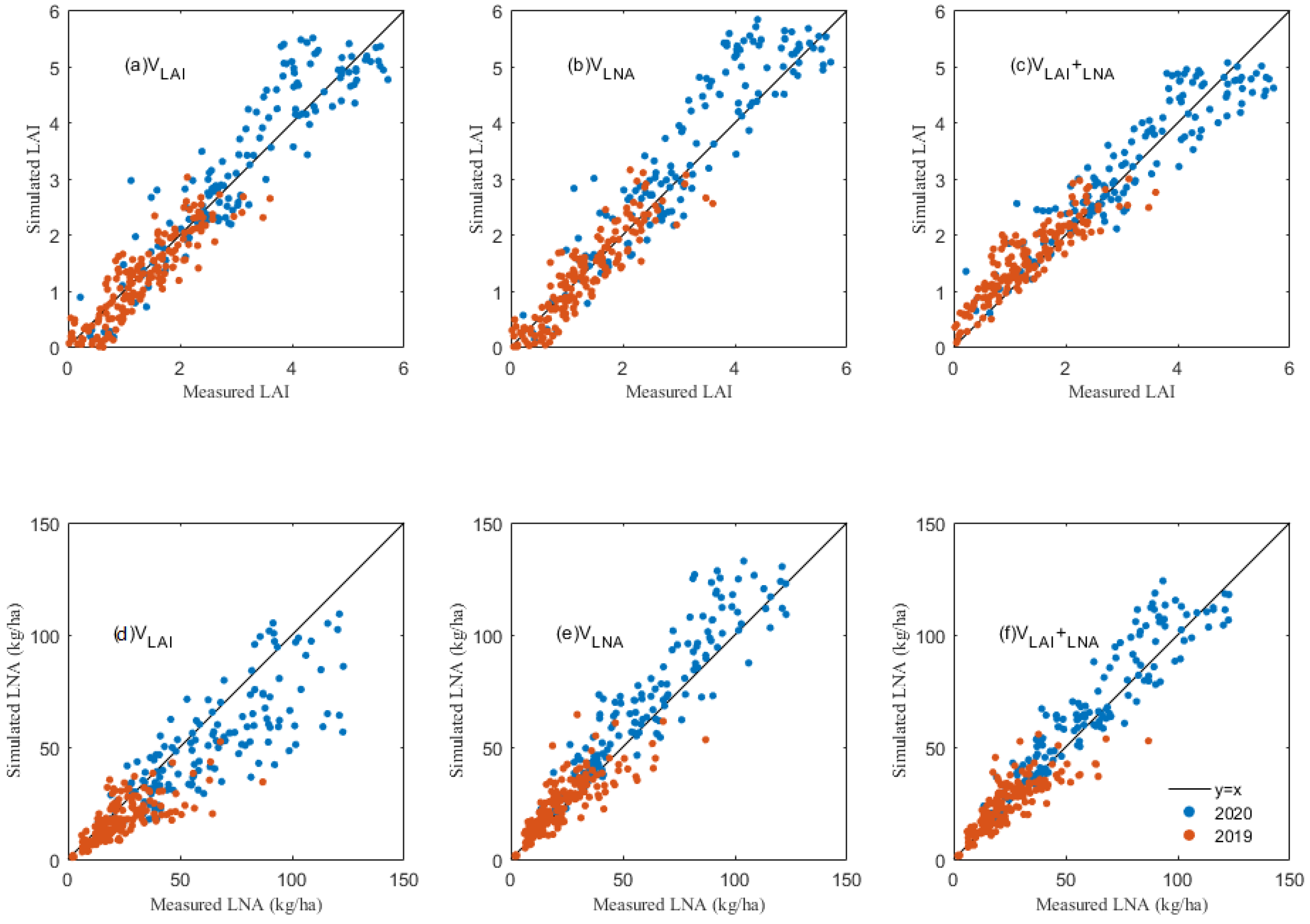
3.2. The LAI and LNA Simulation through Data Assimilating
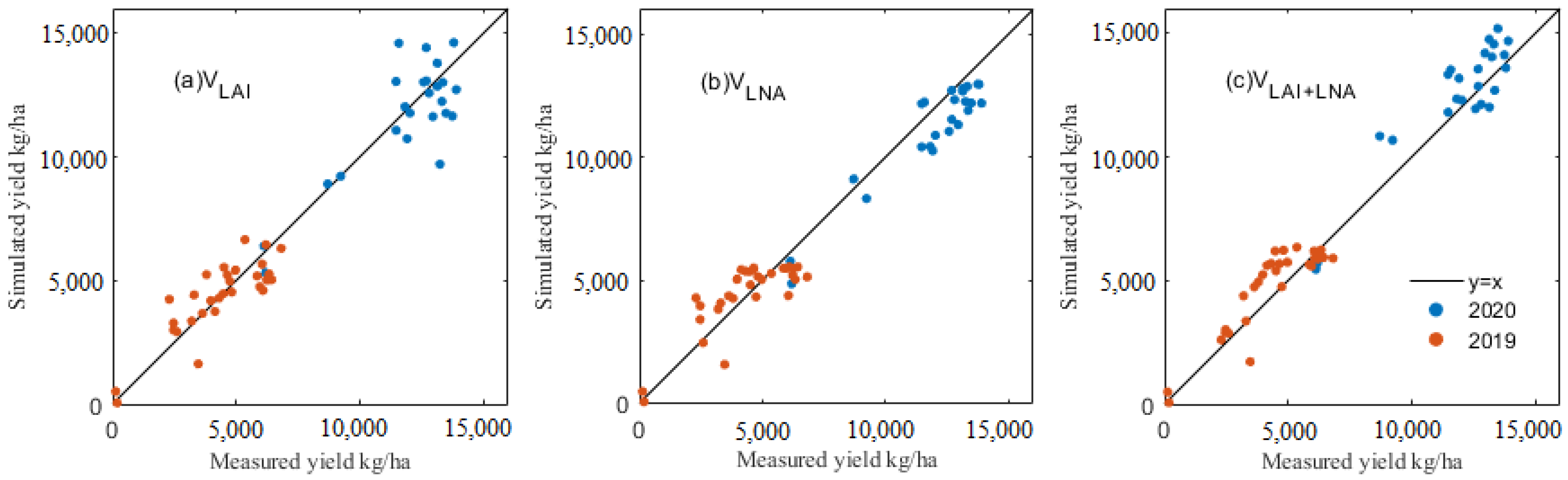
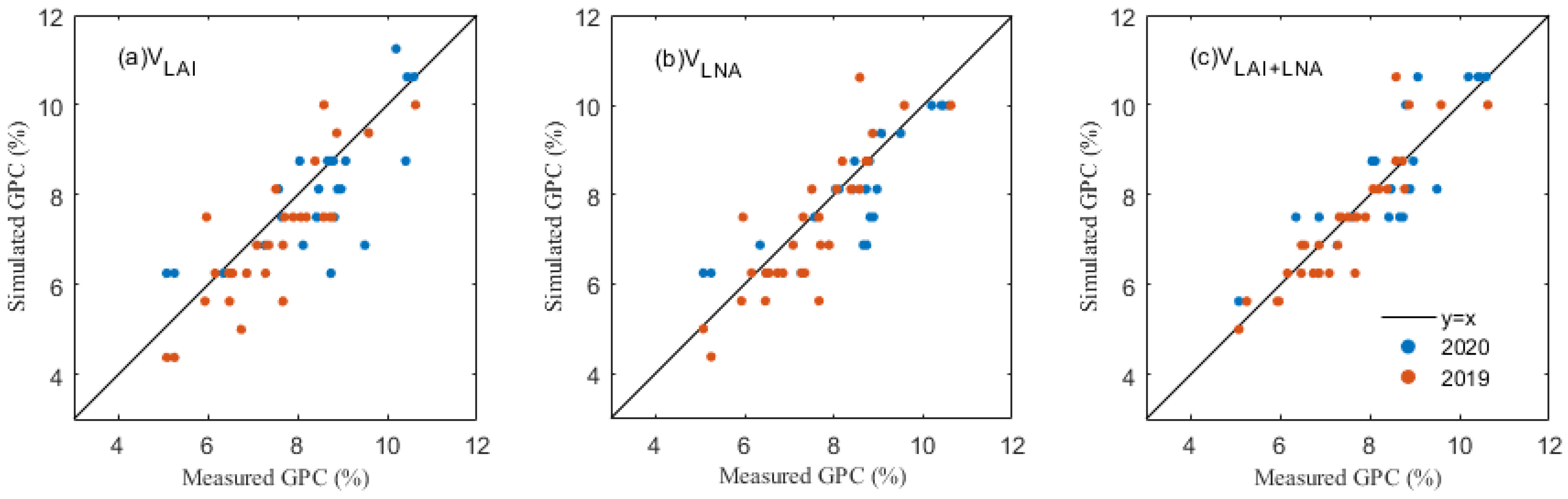
3.3. The Estimation of Yield and GPC
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erenstein, O.; Jaleta, M.; Sonder, K.; Mottaleb, K.; Prasanna, B.M. Global maize production, consumption and trade: Trends and R&D implications. Food Secur. 2022, 14, 1295–1319. [Google Scholar]
- Jin, Z.; Azzari, G.; You, C.; Di Tommaso, S.; Aston, S.; Burke, M.; Lobell, D.B. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 2019, 228, 115–128. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Estimation of maize yield by assimilating biomass and canopy cover derived from hyperspectral data into the AquaCrop model. Agric. Water Manag. 2020, 227, 105846. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, S.; Cao, Y.; Xu, Z.; Yu, Y.; Han, C. A regional maize yield hierarchical linear model combining landsat 8 vegetative indices and meteorological data: Case study in Jilin Province. Remote Sens. 2021, 13, 356. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăgu, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Chawla, I.; Mishra, A.K. A review of remote sensing applications in agriculture for food security: Crop growth and yield, irrigation, and crop losses. J. Hydrol. 2020, 586, 124905. [Google Scholar] [CrossRef]
- van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Su, W.; Zhang, X.; Huang, Y.; Fan, J.; Wu, W. Jointly Assimilating MODIS LAI and et Products into the SWAP Model for Winter Wheat Yield Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4060–4071. [Google Scholar] [CrossRef]
- Ban, H.Y.; Ahn, J.B.; Lee, B.W. Assimilating MODIS data-derived minimum input data set and water stress factors into CERES-Maize model improves regional corn yield predictions. PLoS ONE 2019, 14, e0211874. [Google Scholar] [CrossRef] [PubMed]
- Ines, A.V.M.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Hu, S.; Shi, L.; Huang, K.; Zha, Y.; Hu, X.; Ye, H.; Yang, Q. Field Crops Research Improvement of sugarcane crop simulation by SWAP-WOFOST model via data assimilation. Field Crop. Res. 2019, 232, 49–61. [Google Scholar] [CrossRef]
- Hansen, J.W.; Jones, J.W. Short Survey: Scaling-up crop models for climate variability. Agric. Syst. 2000, 65, 43–72. [Google Scholar] [CrossRef]
- Jiang, N.; Zha, L.; Hu, W.; Yang, C.; Meng, Y.; Chen, B.; Zhou, Z. Trade-offs between residue incorporation and K fertilizer on seed cotton yield and yield-scaled nitrous oxide emissions. Field Crop. Res. 2019, 244, 107630. [Google Scholar] [CrossRef]
- Fernandez, J.A.; DeBruin, J.; Messina, C.D.; Ciampitti, I.A. Late-season nitrogen fertilization on maize yield: A meta-analysis. Field Crop. Res. 2020, 247, 107586. [Google Scholar] [CrossRef]
- Ning, T.; Zheng, Y.; Han, H.; Jiang, G.; Li, Z. Nitrogen uptake, biomass yield and quality of intercropped spring- and summer-sown maize at different nitrogen levels in the North China Plain. Biomass Bioenergy 2012, 47, 91–98. [Google Scholar] [CrossRef]
- Serrano, L.; Filella, I.; Peñuelas, J. Remote sensing of biomass and yield of winter wheat under different nitrogen supplies. Crop. Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G.; Teasdale, J.; Cavigelli, M. Corn-yield estimation through assimilation of remotely sensed data into the CSM-CERES-Maize model. Int. J. Remote Sens. 2008, 29, 3011–3032. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Wu, S.; Yang, P.; Chen, Z.; Ren, J.; Li, H.; Sun, L. Estimating winter wheat yield by assimilation of remote sensing data with a four-dimensional variation algorithm considering anisotropic background error and time window. Agric. For. Meteorol. 2021, 301–302, 108345. [Google Scholar] [CrossRef]
- Chen, Y.; Tao, F. Improving the practicability of remote sensing data-assimilation-based crop yield estimations over a large area using a spatial assimilation algorithm and ensemble assimilation strategies. Agric. For. Meteorol. 2020, 291, 108082. [Google Scholar] [CrossRef]
- Ma, G.; Huang, J.; Wu, W.; Fan, J.; Zou, J.; Wu, S. Assimilation of MODIS-LAI into the WOFOST model for forecasting regional winter wheat yield. Math. Comput. Model. 2013, 58, 634–643. [Google Scholar] [CrossRef]
- Gumma, M.K.; Kadiyala, M.D.M.; Panjala, P.; Ray, S.S.; Akuraju, V.R.; Dubey, S.; Smith, A.P.; Das, R.; Whitbread, A.M. Assimilation of Remote Sensing Data into Crop Growth Model for Yield Estimation: A Case Study from India. J. Indian Soc. Remote Sens. 2022, 50, 257–270. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Wu, S.; Yang, P.; Ren, J.; Chen, Z.; Li, H. Regional winter wheat yield estimation based on the WOFOST model and a novel VW-4DEnSRF assimilation algorithm. Remote Sens. Environ. 2021, 255, 112276. [Google Scholar] [CrossRef]
- Maas, S.J. Using Satellite Data to Improve Model Estimates of Crop Yield. Agron. J. 1988, 80, 655–662. [Google Scholar] [CrossRef]
- Maas, S.J. Use of remotely-sensed information in agricultural crop growth models. Ecol. Modell. 1988, 41, 247–268. [Google Scholar] [CrossRef]
- Guérif, M.; Duke, C.L. Adjustment procedures of a crop model to the site specific characteristics of soil and crop using remote sensing data assimilation. Agric. Ecosyst. Environ. 2000, 81, 57–69. [Google Scholar] [CrossRef]
- Jongschaap, R.E.E. Run-time calibration of simulation models by integrating remote sensing estimates of leaf area index and canopy nitrogen. Eur. J. Agron. 2006, 24, 316–324. [Google Scholar] [CrossRef]
- de Wit, A.J.W.; van Diepen, C.A. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts. Agric. For. Meteorol. 2007, 146, 38–56. [Google Scholar] [CrossRef]
- Curnel, Y.; de Wit, A.J.W.; Duveiller, G.; Defourny, P. Potential performances of remotely sensed LAI assimilation in WOFOST model based on an OSS Experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Z.; Chen, J.; Ren, J.; Li, Z.; Sun, L. The estimation of regional crop yield using ensemble-based four-dimensional variational data assimilation. Remote Sens. 2014, 6, 2664–2681. [Google Scholar] [CrossRef]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G. Integration of MODIS LAI and vegetation index products with the CSM-CERES-Maize model for corn yield estimation. Int. J. Remote Sens. 2011, 32, 1039–1065. [Google Scholar] [CrossRef]
- Ren, J.; Yu, F.; Qin, J.; Chen, Z.; Tang, H. Integrating remotely sensed LAI with EPIC model based on global optimization algorithm for regional crop yield assessment. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2147–2150. [Google Scholar] [CrossRef]
- Thorp, K.R.; Wang, G.; West, A.L.; Moran, M.S.; Bronson, K.F.; White, J.W.; Mon, J. Estimating crop biophysical properties from remote sensing data by inverting linked radiative transfer and ecophysiological models. Remote Sens. Environ. 2012, 124, 224–233. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Xu, X.; Zhao, C.; Jin, X.; Yang, G.; Feng, H. Assimilation of two variables derived from hyperspectral data into the DSSAT-CERES model for grain yield and quality estimation. Remote Sens. 2015, 7, 12400–12418. [Google Scholar] [CrossRef]
- Qi, D.; Hu, T.; Liu, T. Biomass accumulation and distribution, yield formation and water use efficiency responses of maize (Zea mays L.) to nitrogen supply methods under partial root-zone irrigation. Agric. Water Manag. 2020, 230, 105981. [Google Scholar] [CrossRef]
- Silva, P.R.F.; Strieder, M.L.; Coser, R.P.S.; Rambo, L.; Sangoi, L.; Argenta, G.; Forsthofer, E.L.; Silva, A.A. Grain yield and kernel crude protein content increases of maize hybrids with late nitrogen side-dressing. Sci. Agric. 2005, 62, 487–492. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecol. Soc. Am. 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Blackburn, G.A. Quantifying chlorophylls and carotenoids at leaf and canopy scales: An evaluation of some hyperspectral approaches. Remote Sens. Environ. 1998, 66, 273–285. [Google Scholar] [CrossRef]
- Hunt, E.R.; Rock, B.N. Detection of changes in leaf water content using Near- and Middle-Infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Hao, X.; Hunt, E.R. Estimating dry matter content from spectral reflectance for green leaves of different species. Int. J. Remote Sens. 2011, 32, 7097–7109. [Google Scholar] [CrossRef]
- Daniel, A.; Sims, J.A.G. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Int. J. Remote Sens. 2002, 39, 4640–4662. [Google Scholar] [CrossRef]
- Datt, B. Visible/near infrared reflectance and chlorophyll content in eucalyptus leaves. Int. J. Remote Sens. 1999, 20, 2741–2759. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Pearson, R.L.; Miller, L.D. Remote mapping of standing crop biomass for estimation of the productivity of the short grass prairie. In Proceedings of the 8th International Symposium on Remote Sensing of the Environment, Ann Arbor, MI, USA, 2–6 October 1972; pp. 1355–1379. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT Cropping System Model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Thorp, K.R.; White, J.W.; Porter, C.H.; Hoogenboom, G.; Nearing, G.S.; French, A.N. Methodology to evaluate the performance of simulation models for alternative compiler and operating system configurations. Comput. Electron. Agric. 2012, 81, 62–71. [Google Scholar] [CrossRef]
- Jones, C.A.; Kiniry, J.R. CERES-Maize A Simulation Model; TEXAS A&M University Press: College Station, TX, USA, 1986. [Google Scholar]
- Ritchie, J.T.; Singh, U.; Godwin, D.C.; Bowen, W.T. Cereal Growth, Development and Yield. Underst. Opin. Agric. Prod. 1998, 7, 79–98. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New optimizer using particle swarm theory. In Proceedings of the MHS’95, the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Y.; Li, W.; Cao, W.; Tian, Y. Integrating remotely sensed leaf area index and leaf nitrogen accumulation with RiceGrow model based on particle swarm optimization algorithm for rice grain yield assessment. J. Appl. Remote Sens. 2014, 8, 083674. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Deep neural network algorithm for estimating maize biomass based on simulated Sentinel 2A vegetation indices and leaf area index. Crop. J. 2020, 8, 87–97. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; Gitelson, A.; Peng, Y.; Viña, A.; Arkebauer, T.; Rundquist, D. Green leaf area index estimation in maize and soybean: Combining vegetation indices to achieve maximal sensitivity. Agron. J. 2012, 104, 1336–1347. [Google Scholar] [CrossRef]
- Su, W.; Sun, Z.; Chen, W.H.; Zhang, X.; Yao, C.; Wu, J.; Huang, J.; Zhu, D. Joint retrieval of growing season corn canopy LAI and leaf chlorophyll content by fusing Sentinel-2 and MODIS images. Remote Sens. 2019, 11, 2409. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Zhang, J.; Fan, Y.; Cheng, Y.; Wang, B.; Wu, X.; Tan, X.; Tan, T.; Li, S.; et al. Predicting grain yield and protein content using canopy reflectance in maize grown under different water and nitrogen levels. Field Crop. Res. 2021, 260, 107988. [Google Scholar] [CrossRef]
- Liu, H.L.; Yang, J.Y.; Drury, C.F.; Reynolds, W.D.; Tan, C.S.; Bai, Y.L.; He, P.; Jin, J.; Hoogenboom, G. Using the DSSAT-CERES-Maize model to simulate crop yield and nitrogen cycling in fields under long-term continuous maize production. Nutr. Cycl. Agroecosystems 2011, 89, 313–328. [Google Scholar] [CrossRef]

| Spring Maize Cultivars | Planting Date | Nitrogen Level (kg/ha) | Phosphorus Level (kg/ha) | Potassic Level (kg/ha) | Plant Densities (Plants/ha) |
|---|---|---|---|---|---|
| XianYu335 | 29 May 2019 | 0, 110, 220, 330, 440 | 100 | 100 | potted test |
| XianYu335 | 29 May 2019 | 220 | 0, 50, 100, 150, 200 | 100 | potted test |
| XianYu335 | 29 May 2019 | 220 | 100 | 0, 50, 100, 150, 200 | potted test |
| Meilian158 | 8 May 2020 | 0, 110, 220, 330 | 100 | 100 | 62,500 |
| Meilian158 | 8 May 2020 | 220 | 0, 50, 100, 150 | 100 | 62,500 |
| Meilian158 | 8 May 2020 | 220 | 100 | 0, 50, 100, 150 | 62,500 |
| Vegetation Index | Name | Formula | Reference |
|---|---|---|---|
| REPvalue | REPvalue | dRREP/dλ | [43] |
| RVI | Ratio Vegetation Index | [44] | |
| MSR | Modified Simple Ratio index | [45] | |
| WDRVI | Wide Dynamic Range Vegetation Index | [46] | |
| NDCI | Normalized difference chlorophyll index | [47] | |
| SIPI | Structure insensitive pigment index | [48] | |
| PSDNa | Pigment-specific normalized difference-a | [49] | |
| PSDNb | Pigment-specific normalized difference-b | [49] | |
| PSDNc | Pigment-specific normalized difference-c | [49] | |
| NDII | Normalized difference infrared index | [50] | |
| NDMI | Normalized difference matter index | [51] | |
| mSR705 | Modified simple ratio 705 | [52] | |
| mND705 | Modified normalized difference 705 | [53] | |
| OSAVI | Optimized soil-adjusted vegetation index | [54] | |
| NDVI | Normalized difference vegetation index | [55] |
| Parameters | Initial Value | Range |
|---|---|---|
| PPOP (population of plant/m2) | 6.5 | 5.5–9.5 |
| FAMN (kg/ha) | 200 | 0–400 |
| P1 (°C) | 200.9 | 170–280 |
| P2 | 0.75 | 0.5–0.9 |
| P5 (°C) | 850.1 | 600–1100 |
| G2 | 850.2 | 400–1100 |
| G3 (mg/d) | 10.97 | 4–11.5 |
| PHINT (°C) | 44.58 | 30–90 |
| GDDE (day) | 6 | 4–9 |
| DSGFT (°C) | 110 | 85–225 |
| RUE | 4.92 | 2–5 |
| KCAN | 0.45 | 0.45–0.9 |
| SALB | 0.18 | 0.088–0.132 |
| SLUI (mm) | 6 | 3–12 |
| SLDR | 0.9 | 0.01–0.95 |
| SLRO | 66 | 61–94 |
| SLNF | 1 | 0.72–1.08 |
| SLPF | 0.96 | 0.72–1.08 |
| Spectral Indices | LAI Model | R2 | RMSE |
|---|---|---|---|
| REPvalue | y = 0.255e352.9x | 0.82 ** | 0.54 |
| NDII | y = 1.07e2.245x | 0.80 ** | 0.59 |
| NDCI | y = 75.96x + 9.12 | 0.79 ** | 0.63 |
| OSAVI | y = 0.015e7.07x | 0.77 ** | 0.76 |
| NDMI | y = 0.1324e76.21x | 0.72 ** | 0.81 |
| MSR | y = 0.28e0.52x | 0.72 ** | 0.81 |
| SIPI | y = 10.99x + 13.91 | 0.71 ** | 0.8 |
| WDRVI | y = 1.11e2.69x | 0.70 ** | 0.82 |
| RVI | y = 0.15x − 0.29 | 0.70 ** | 0.82 |
| Spectral Indices | LNA Model | R2 | RMSE (kg/ha) |
|---|---|---|---|
| MSR | y = 3.488e0.64x | 0.85 ** | 10.71 |
| OSAVI | y = 0.118e8.26x | 0.83 ** | 11.01 |
| WDRVI | y = 16.79e3.36x | 0.82 ** | 11.25 |
| PSDNc | y = 363.7x20.09 | 0.79 ** | 11.52 |
| PSDNa | y = 228.7e13.47x | 0.78 ** | 11.67 |
| TVI | y = 2.86e0.144x | 0.76 ** | 11.59 |
| mSR705 | y = 5.195x2.038 | 0.75 ** | 11.68 |
| mND705 | y = 330.4x4.575 | 0.74 ** | 11.83 |
| PSDNb | y = 173.3x8.02 | 0.71 ** | 12.03 |
| Year | n | R2 | RMSE | |
|---|---|---|---|---|
| VLAI | 2020 | 144 | 0.811 | 0.582 |
| 2019 | 168 | 0.761 | 0.363 | |
| VLNA | 2020 | 144 | 0.738 | 0.685 |
| 2019 | 168 | 0.787 | 0.343 | |
| VLAI+LNA | 2020 | 144 | 0.853 | 0.513 |
| 2019 | 168 | 0.699 | 0.408 |
| Year | n | R2 | RMSE (kg/ha) | |
|---|---|---|---|---|
| VLAI | 2020 | 144 | 0.455 | 20.442 |
| 2019 | 168 | 0.343 | 11.482 | |
| VLNA | 2020 | 144 | 0.720 | 14.646 |
| 2019 | 168 | 0.615 | 8.787 | |
| VLAI+LNA | 2020 | 144 | 0.824 | 11.618 |
| 2019 | 168 | 0.661 | 8.253 |
| Yield | Protein Content | |||||
|---|---|---|---|---|---|---|
| Methods | Year | n | R2 | RMSE (kg/ha) | R2 | RMSE (%) |
| VLAI | 2020 | 24 | 0.609 | 1339.339 | 0.466 | 1.048 |
| 2019 | 30 | 0.721 | 903.091 | 0.493 | 0.878 | |
| VLNA | 2020 | 24 | 0.754 | 1061.378 | 0.665 | 0.830 |
| 2019 | 30 | 0.674 | 976.681 | 0.577 | 0.802 | |
| VLAI+LNA | 2020 | 24 | 0.726 | 1120.934 | 0.711 | 0.771 |
| 2019 | 30 | 0.735 | 879.648 | 0.759 | 0.605 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Chen, S.; Xu, Z.; Ye, Y.; Han, C.; Lu, P.; Song, K. The Estimation of Maize Grain Protein Content and Yield by Assimilating LAI and LNA, Retrieved from Canopy Remote Sensing Data, into the DSSAT Model. Remote Sens. 2023, 15, 2576. https://doi.org/10.3390/rs15102576
Zhu B, Chen S, Xu Z, Ye Y, Han C, Lu P, Song K. The Estimation of Maize Grain Protein Content and Yield by Assimilating LAI and LNA, Retrieved from Canopy Remote Sensing Data, into the DSSAT Model. Remote Sensing. 2023; 15(10):2576. https://doi.org/10.3390/rs15102576
Chicago/Turabian StyleZhu, Bingxue, Shengbo Chen, Zhengyuan Xu, Yinghui Ye, Cheng Han, Peng Lu, and Kaishan Song. 2023. "The Estimation of Maize Grain Protein Content and Yield by Assimilating LAI and LNA, Retrieved from Canopy Remote Sensing Data, into the DSSAT Model" Remote Sensing 15, no. 10: 2576. https://doi.org/10.3390/rs15102576
APA StyleZhu, B., Chen, S., Xu, Z., Ye, Y., Han, C., Lu, P., & Song, K. (2023). The Estimation of Maize Grain Protein Content and Yield by Assimilating LAI and LNA, Retrieved from Canopy Remote Sensing Data, into the DSSAT Model. Remote Sensing, 15(10), 2576. https://doi.org/10.3390/rs15102576








