Next Article in Journal
Land Subsidence Monitoring and Building Risk Assessment Using InSAR and Machine Learning in a Loess Plateau City—A Case Study of Lanzhou, China
Next Article in Special Issue
Validation of FY-4A Temperature Profiles by Radiosonde Observations in Taklimakan Desert in China
Previous Article in Journal
Radar Observation of the Lava Tubes on the Moon and Mars
Previous Article in Special Issue
Spatiotemporal Variation of Hourly Scale Extreme Rainstorms in the Huang-Huai-Hai Plain and Its Impact on NDVI
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 11
10.3390/rs15112849
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

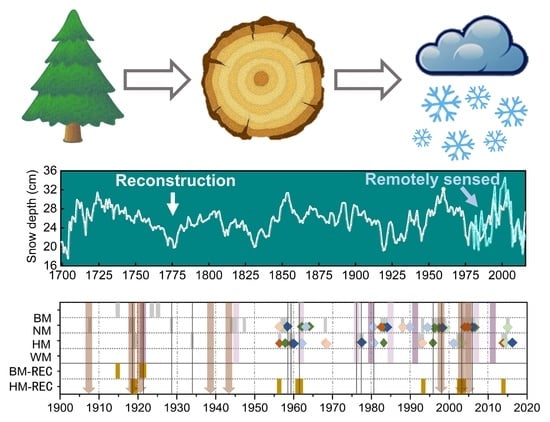
Snowpack Dynamics Influence Tree Growth and Signals in Tree Rings of Tianshan Mountain, Central Asia

by
Yuting Fan
1,2,3,
Qian Li
4,*,
Huaming Shang
1,2,3,
Shengxia Jiang
1,2,3,
Tongwen Zhang
1,2,3,
Ruibo Zhang
1,2,3,
Li Qin
1,2,3,
Shulong Yu
1,2,3 and
Heli Zhang
1,2,3
1
Institute of Desert Meteorology, China Meteorological Administration, Urumqi 830002, China
2
Key Laboratory of Tree Ring Physical and Chemical Research of China Meteorological Administration, Urumqi 830002, China
3
Xinjiang Key Laboratory for Tree Ring Ecology, Urumqi 830002, China
4
State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(11), 2849; https://doi.org/10.3390/rs15112849
Submission received: 12 April 2023 / Revised: 20 May 2023 / Accepted: 25 May 2023 / Published: 30 May 2023
(This article belongs to the Special Issue Understanding the Meteorological Environment in Arid Regions through the Integrative Analyses of Remote Sensing, Ground Observational Stations and Numerical Models)
Browse Figures
Versions Notes

Abstract

:
Snow is an important source of freshwater in the Tianshan Mountains of Central Asia. This study established 18 tree ring width chronologies and compound chronologies and analyzed the effects of snow depth, measured both by remote sensing and at meteorological stations, on the radial growth of spruce trees. The results showed that the established standard chronology of tree ring width is suitable for the analysis of tree ring climatology. The correlation coefficient of the ring width index (RWI) and the remote sensing snow depth was greater than that of the meteorological station snow depth. For the remote sensing snow depth, the correlation coefficients were greater in the winter and spring months compare to other periods, while the correlation coefficients of the meteorological stations were greater only in the winter. The nonlinear method (BRNN) showed good fitting in the reconstruction of the historical snow depth. The reconstructed snow depth exhibited a decreasing trend in the Bharakonu Mountains (BM), Narathi Mountains (NM), and Halke mountains (KM) sub-regions in the overall reconstructed period; however, the trends were inconsistent in both the historical and the observed periods, indicating the importance of reconstructing snow depth in the Tianshan Mountains.

Graphical Abstract

1. Introduction

Snowpack is an important component of the energy and water cycles. Freshwater from snowmelt is a major resource in mountainous areas, which feed the rivers of the populated downstream areas [1,2,3,4]. In addition, snow cover may inhibit the microbial decomposition of soil organic matter and the subsequent release of carbon dioxide in northern permafrost areas [5]. Earlier occurrences of snow cover in the past have positively influenced the carbon uptake and gross primary production in boreal forests [6].
Due to climate change, declines in snowfall, higher snowline elevations, and earlier snow melting in alpine regions have been reported in previous studies [1,7]. There have also been indications of considerable reductions in the continental-scale snow mass and snow cover during the past decades [8,9,10,11]. However, changes in regional snowpacks have exhibited different trends due to their high heterogeneity of distribution. A decreasing trend in snow mass was found in the Tibetan Plateau, but the opposite was observed in the Tianshan Mountains of Central Asia [12,13,14]. Many studies have focused on forecasting generalized future trends in snow cover and snow mass using the World Climate Research Program Coupled Model Intercomparison Project Phase 6 (CMIP6) [15,16,17]. However, clarifying the long-term variations in snow parameters on a regional scale is also of meteorological importance [18].
As a sensitive region for global climate change response and a fragile ecological environment, the spatial and temporal variability of water resources due to climate change in Central Asia is a destabilizing factor of breeding potential [19]. The resulting intra-regional conflicts and contradictions will have a direct impact on local resource security and ecological safety. The information provided by tree rings is widely used as an important proxy in studies on the radial growth climate response of trees, the reconstruction of climate hydrological series in historical periods, and the analysis of climate change patterns in Central Asia and beyond. Tree rings can be used for accurate dating, and have the advantages of strong continuity, high resolution, long life, and easy access to samples [20]. The use of the annual tree ring index to reconstruct snow data can provide important reference information for understanding the history of changes in snowfall and predicting future ones [21]. Existing studies have shown a correlation between radial tree growth and snowpack [22,23,24,25], and reconstructions of snowpack metrics, such as snow depth and snow days, have been performed based on these data [18,26,27,28,29,30,31]. However, only a limited number of studies have been conducted in Central Asia, and most of these studies were based on the results of analyses acquired from a relatively small number of sampling points and limited meteorological material. Thus, a more comprehensive understanding of historical snow dynamics must be made in order to predict the future trends in response to climate change.
In this study, four representative regions across the four mountains surrounded by the Ili River basin in the Tianshan Mountains Range were analyzed. They were classified according to their positions and slope directions. In total, 18 tree ring width chronologies and compound chronologies were established. In addition, the effects of snow depth, measured with remote sensing and at stations, on the radial growth of spruce trees were analyzed. In the current study, the relationships between tree rings, remote sensing snow depth, and meteorological station snow depth were investigated. In view of the problems related to adjacent points of grid data and climate data in tree ring research, the existence of a possible nonlinear relationship between tree growth and climate information was explored using mathematical analysis.

2. Materials and Methods

2.1. Study Area and Target Species

The study area was located in the mountainous region of the Tianshan Mountains, along the Ili Valley in Xinjiang, China, between 80°09′42″E–91°01′45″E and 40°14′16″N–49°10′45″N (Figure 1). This area shares borders with Kazakhstan in the northwest and Russia and Mongolia in the northeast. The region has a large geographical span and obvious natural geomorphological features [32]. It consists of four major mountain systems, the Bharakonu Mountains (BM), Narathi Mountains (NM), Halke mountains (KM) and Wusun Mountains (WM), as well as their water systems. The most important of these are the Ili River, the tributaries of which include three major rivers; the Turks River; the Kungas River; and the Kashi River. The climate types of the region include temperate continental and alpine. The typical climate condition in the study region is relatively mild, with an average annual temperature of 10.5 °C; a sunshine period of 2748.1 h; and a frost-free period of 149 days, especially in the rainy and humid mountainous regions. However, extreme conditions are to be expected in the dry plains of the study region, in which a maximum temperature of 42.8 °C and a minimum of −51 °C have been reported [33,34].
The Schrenk spruce (Picea schrenkiana Fisch. et Mey.) forests of the Tianshan Mountains belong to the Central Asian montane flora. They are the most dominant montane evergreen coniferous forests in the desert zone of Central Asia, as well as the most representative forest type in the montane coniferous forest zone of the Tianshan Mountains [33,35]. The Schrenk spruce forests in the studied area are widely distributed on the mid-mountain shaded slopes at altitudes of 1500–2800 m. The unique warm and humid climate conditions of the study region promote fast growth, high density, and high lumbering rates of Schrenk spruce. Environmental information extracted from the tree rings of spruce has become an important proxy for studying the system dynamics in this region [28,36,37].

2.2. Sample Collection and RWI Chronology Building

Core samples were collected from the trees according to the Sveriges Lantbruks Universitet (SLU, the Swedish national forest inventory, Department of Forest Resource Management) standards. Individual trees were subjected to a rigorous and objective selection process before sampling. Only isolated, mature, and healthy individuals were considered for sampling in order to avoid competition affecting plant structures [38]. Two cylindrical cores per tree were extracted along the approximate direction of the axis radius using an increment borer (Swedish Haglof, Stockholm, Sweden, 500 mm length, 12 mm internal diameter) between September and October (completion of the tree rings was achieved in the years 2006 and 2016). Subsequently, each of the sampled trees was tagged (determining location and elevation), and the characteristics of the tree and its immediate environment (species, numbers of trees and sample cores, aspect, slope, canopy density, etc.) were recorded. Of the 18 sampling sites at altitudes between 1542 and 2739 m, a total of 659 samples from 310 trees were collected. The information on the sampling sites is summarized in Table 1.
All cores were analyzed in the Key Laboratory of Tree Ring Physical and Chemical Research of the China Meteorological Administration, Institute of Desert Meteorology, China Meteorological Administration. This study followed normal dendrochronological techniques [20], and pre-processing was conducted prior to the measurement of the trees’ chronological widths (details in [39]). Tree ring width (TRW) was measured using a LINTAB measuring table with an accuracy of 0.001 mm, and cross-dating of the samples was carried out with the TSAP-Win™ dendrochronological software (http://www.rinntech.de, accessed on 11 April 2023). Cross-dating quality was controlled using COFECHA (program written by Richard Holmes, LTRR-University of Arizona) [40], and standardized ring width indices were converted via the ARSTAN_41d program [41]. The quality of the reliable chronology was evaluated by inter-series correlation (Rbar) and the expressed population signal (EPS ≥ 0.85) [42]. Ultimately, after checking the consistency of the TRW series among trees from the same site, tree ring series from 21 sites were successfully dated and used to establish chronologies (Table 2). The negative exponential curve (NEC) method was used to detrend the growth. By using principal component analysis (PCA) [43], the common variance of the regional RWI chronologies was explored. Based on the monthly snow depth data, different regression algorithms were compared during the reconstruction (REC). These include the Bayesian regularization training algorithm (BRNN), multiple linear regression (MLR), and random forests of regression trees (RF) [44]. The final visualization was performed using the dplR package of R [6].

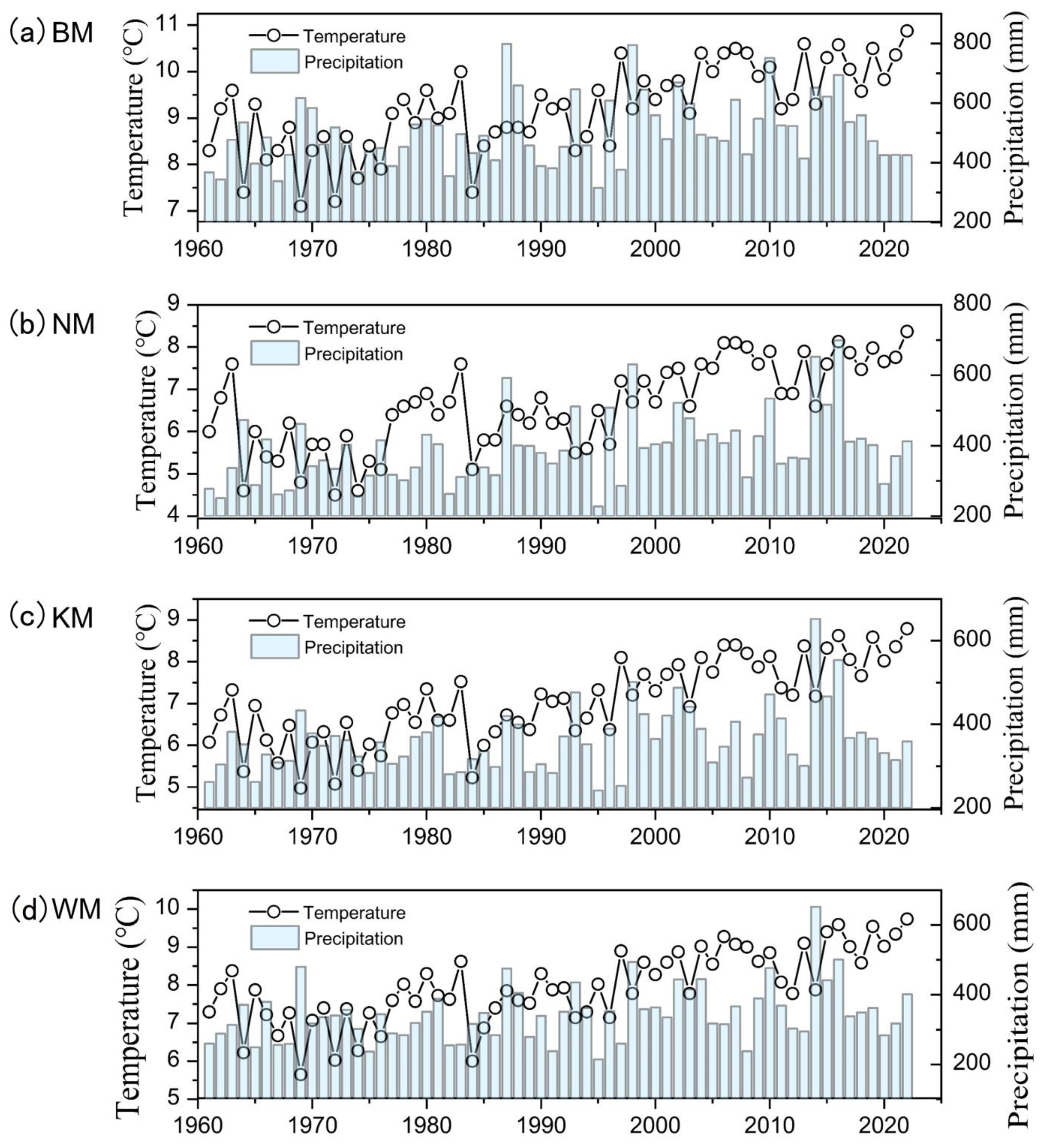
2.3. Remotely Sensed Snow Depth Data and Climate Response Analysis Data

A passive microwave snow depth dataset was retrieved from the scanning multichannel microwave radiometer (1979–1987), the special sensor microwave imager (SSM/I) (1987–2007), and the SSSMI sounder (SSMI/S) (2008–2019) [45,46]. This dataset was evaluated in the main snowy regions of China [47,48]. The instrumental climate records (snow depth, temperature, and precipitation) of 10 meteorological stations in the period of 1961–2016 near the sampling sites were obtained from the China National Climatic Data Center (http://data.cma.cn, accessed on 11 April 2023). Details of these stations are shown in Figure 1 and Table 2. Previous studies have reconstructed the historical snow water equivalent (SWE) series using the April 1 SWE, which was considered as the annual maximum SWE [49,50]. The November–April SWE was also confirmed for SWE reconstruction [51]. In the Tianshan Mountains, the maximum snow depth was mostly observed in the winter and early spring [13,14]. Different data sources (station data and satellite data), different time scales (monthly scale and seasonal scale), and different data types (mean value, maximum value, etc.) were analyzed in sequence to obtain the optimal solution for the reconstruction model. The monthly maximum remotely sensed snow depth values during 1979–2016 from the nearest grid cells to the tree ring sites were used for snow depth reconstruction (REC).

3. Results

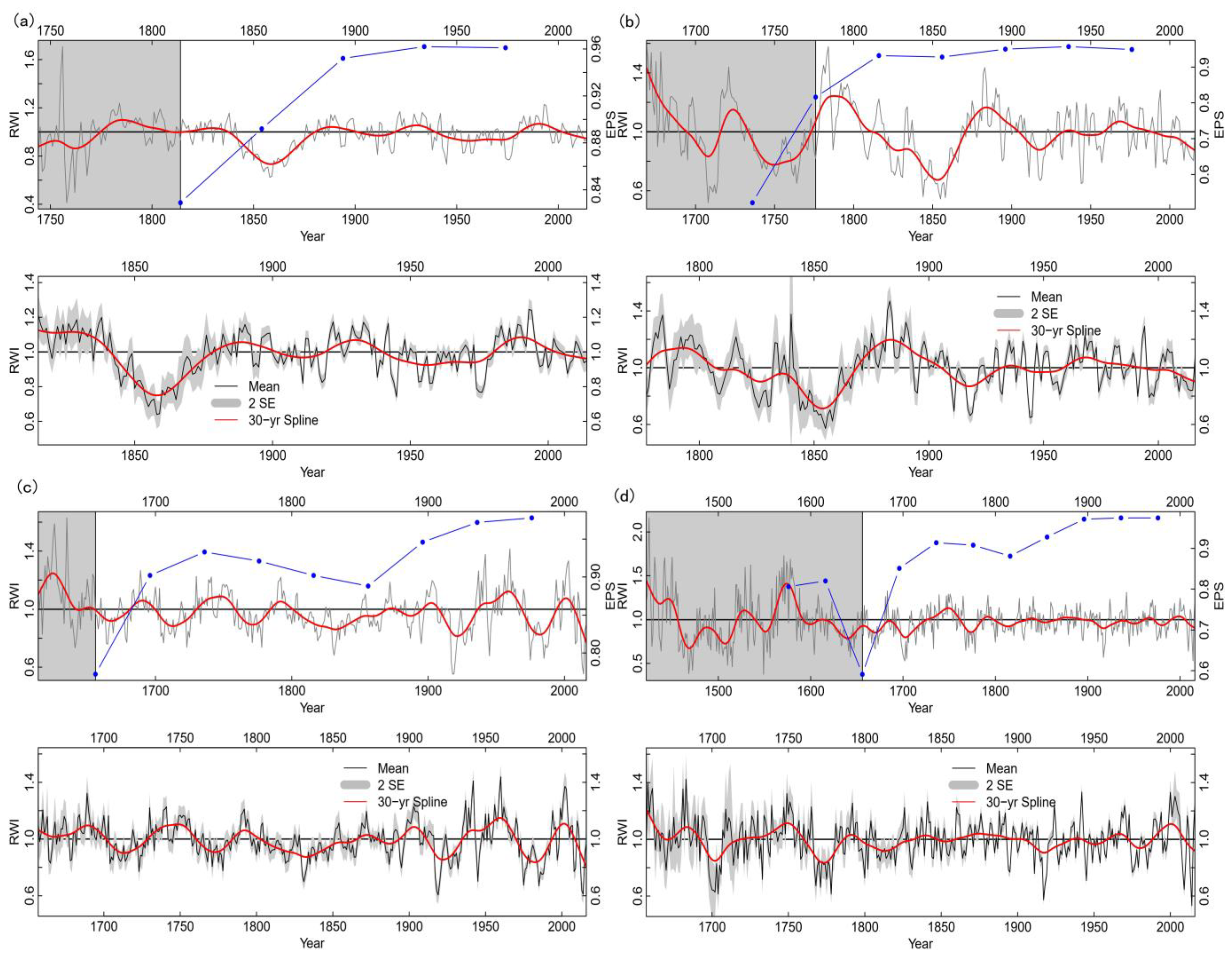
3.1. Statistical Characteristics of the RWI Chronologies

The subalpine ring width chronology of Schrenk spruce ranged from 1744 to 2016 (at BM), 1669 to 2016 (at NM), 1614 to 2016 (at KM), and 1422 to 2016 (WM) (Figure 2). According to some descriptive statistical results obtained by dendrochronology at each site, the average sensitivity was 0.216 and the signal-to-noise ratio was as high as 45.721, indicating that the standard chronology of the sampling sites retained ample climatic information. The standard error ranged from 0.01 to 0.72, and the Schrenk spruce showed a high mean inter-series correlation (Rbar-t, r ranges between 0.369 and 0.646, p ≤ 0.01) and a coherent effective signal (Rbar-e, r ranges between 0.269 and 0.466, p ≤ 0.01). The results showed that the sampling sites had good regional consistency and could represent the local Schrenk spruce growth situation. In addition, the first-order autocorrelation coefficient of chronologies was 0.48, suggesting that tree growth has a delayed response to changes in climate and hydrology. The total explanatory volume of the samples was between 0.944 and 0.979, far exceeding the threshold of 0.85, indicating that the samples were able to represent the basic characteristics of the ring width variation of spruce in this region. By analyzing the statistical parameters of the spruce samples, it can be seen that the established standard chronology of tree ring width was suitable for the analysis of tree ring climatology. The starting year of the reconstructed snow depth was determined by subsample signal intensity (EPS). Cross-dating was successfully performed for samples with an EPS value > 0.85. The width chronology met signal strength acceptance for the years after AD 1815 at BM, AD 1737 at NM, and AD 1657 at KM and WM, respectively. Consequently, four composite RWI chronologies of different typical regions were obtained (Figure 2). The results of some descriptive statistics of tree ring chronology from each site are illustrated in Table 3.

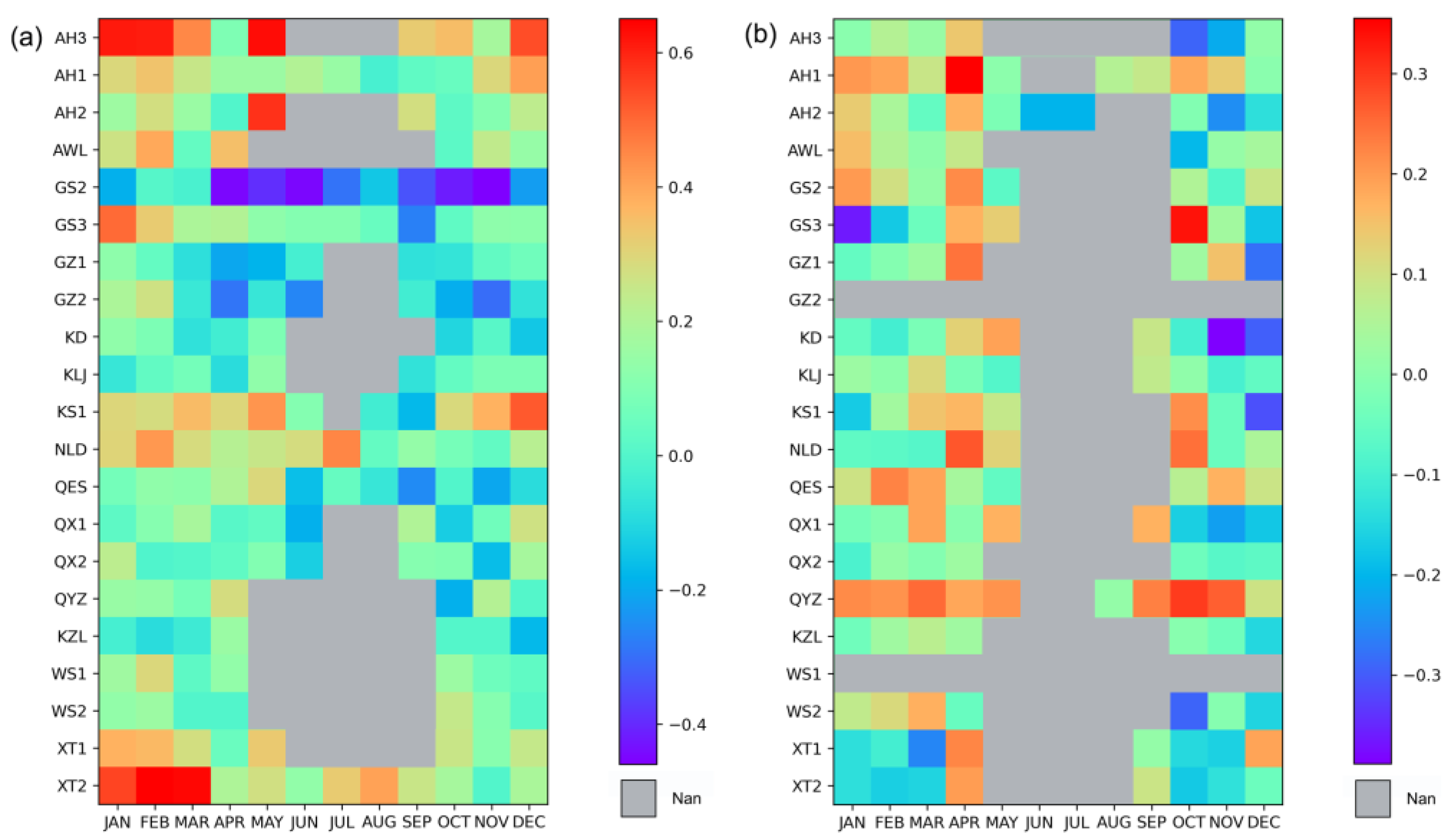
3.2. Response Analysis of Tree Ring Width to Snow Depth

Figure 3 illustrates the correlation coefficients between the RWI and the remote sensing and station-measured snow depth, respectively. Overall, the correlation coefficient between RWI and remote sensing snow depth was greater than that for the station-measured snow depth. The correlation coefficients for the remote sensing snow depth ranged from −0.46 to 0.65, and, for station-measured snow depth, ranged from −0.39 to 0.36. For the remote sensing snow depth, the correlation coefficients were greater in the winter and spring months compared to other periods, while those of the meteorological stations were greater only in the winter. The correlation coefficient was greater than 0.6 for the AH3 site in January and February and for the XT2 site in February. There were no significant relationships between the correlation coefficients and the elevations or slopes.

3.3. Model Statistical Analysis and Snow Depth Reconstruction

The BRNN, MLR, and RF methods were used to analyze the monthly climatic factors and spruce ring width chronology. It was found that the accuracy evaluation indices of the regression models established by the three methods showed certain differences (Table 4). The BRNN and MLR methods were superior to the RF methods. Compared with the MLR method, BRNN was less affected by the values of data boundary points, and was able to effectively fit the nonlinear relationship without assuming the functional form of the model in advance. Therefore, the nonlinear method (BRNN) has certain application potential. The method showed a good fitting for BM region, with little difference. However, the peak and trough values of the data fitted by the three methods were all lower than the actual SD data at the same time points. As a result, for either linear or nonlinear methods, the extreme values may have been underestimated because the explanatory variance was less than 1.
Based on the above-described correlation analysis results, the maximum snow depth values in April–June (in BM), October–December (in NM), and February–March (in KM) were the most appropriate seasonal predictions selected by the model for REC. The difference between the correlation coefficients of the calibration data set and validation data set of the three methods was very small, and the reduction in error (RE) and coefficient of efficiency (CE) were well above 0, indicating the high predictive capability of the model. Statistically significant data for calibration and verification supported the validity of the interval correction model, reconstructed from 1957 to 2016.
The snow depths at the three sub-regions exhibited a decreasing trend in their respective REC periods, but only the BM sub-region showed a significantly decreasing trend, with a value of −0.005 cm per year (Figure 4). During the overlapping period, the peaks and valleys of the reconstructed snow depths were similar to the observed snow depths, but with larger fluctuations. The reconstructed snow depths all showed a weak, non-significant, increasing trend during the overlapping periods in the three sub-regions. For the NM sub-region, the observed snow depth indicated a significantly increasing trend of 0.091 cm per year from 1961 to 2016. However, the observed snow depth in the BM sub-region showed a significantly decreasing trend from 1979 to 2016, with a rate of −0.148 cm per year. This might have been caused by mismatching of the averaged values from a 25 km × 25 km area to point values of the sampling locations.

4. Discussion

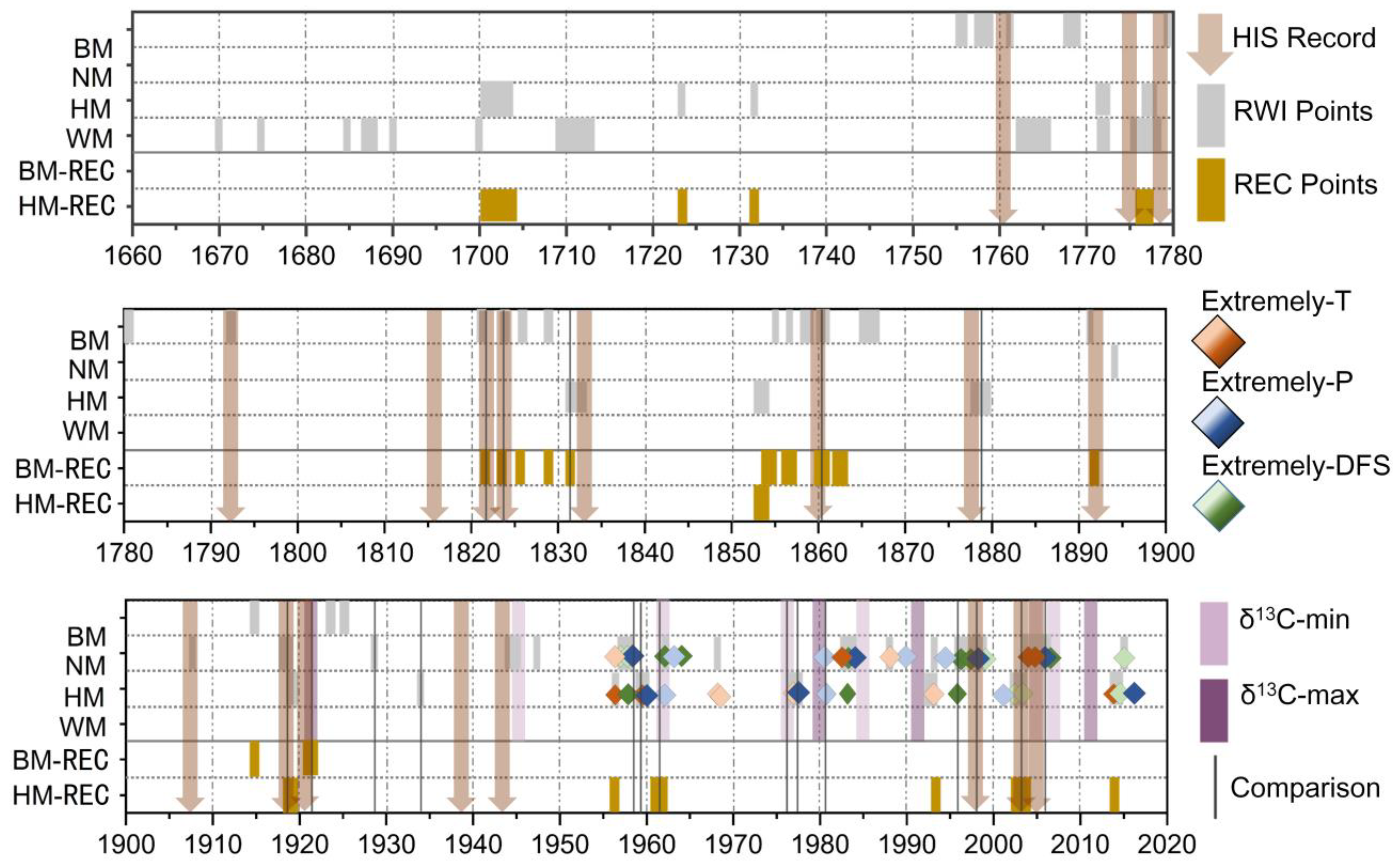
4.1. Historical Data Inspection

Records of climate disasters in the Ili region in the past were checked and compared with the chronological trends and REC sequences of the corresponding years (Figure 5). It was found that both the drought and flood years in the disaster records corresponded well with the data. For example, in 1877, the historical record showed that “Xinjiang suffered a great drought, with no harvest in summer and no replanting in autumn”. In 1917, it was recorded that “Ili was dry, food prices were high, people fled and houses empty”. In addition, the reconstructed series was consistent with the extreme values of temperature, precipitation, and frozen soil data recorded by meteorological stations in past decades, which indicates that the reconstructed sequence was able to represent the extreme values of these variables to a certain extent. On the other hand, the composite chronology of stable isotopes in this region showed a delayed response to the characterization ability of frozen soil depth [39], which requires further study. In view of the comparison of the records and historical data, the snow depth data reconstructed using tree ring data from the study area are considered to be reliable.

4.2. Attribution of the Snow Depth Variations

A significant downward trend in snow depth occurred only in BM sub-region, with a decrease of −0.005 cm per year during 1815–2016. However, the snow depth in the BM sub-region had a non-significantly decreasing trend in the historical period (1815–1979) and an opposite trend in the observed period (1979–2016). Compared with previous studies, the snow depth in NM and KM sub-regions exhibited similar trends in different periods, increasing during the observed period (1961–2016 for NM, 1979–2016 for KM) and the historical period (1737–1961 for NM, 1657–1979 for KM), but decreasing in the entire reconstructed period (1737–2016 for NM, 1657–2016 for KM) [18]. However, none of these trends were significant. Thus, it is useful to reconstruct the snow depth of the historical period to obtain a better understanding of the regional climate change, because the snow depth trends were different during the observed, historical, and reconstructed periods in the Tianshan Mountains.
The variations in annual temperature and precipitation in the four sub-regions during 1961 and 2016 are shown in Figure 6. Significant upward trends in both temperature and precipitation were found in the four sub-regions (p < 0.05). The most quickly increasing rate of temperature was observed in the NM sub-region, and the mostly slowly increasing rate was found in the BM sub-region, at 0.044 and 0.038 °C per year, respectively. The region with the greatest increase in precipitation was the NM region, while that with the lowest was the KM region, at 3.041 and 1.681 mm per year, respectively. Increased precipitation from the intensified North America Subtropical High and West Pacific Subtropical High has been shown to lead to more snow [13,52,53]. However, this increasing effect was limited due to the significant increase in temperature, which could lead to fewer days with snow cover [54].

5. Conclusions

In this study, the composite ring width chronology of four typical mountain ranges in the Tianshan Mountains was established. The effects of snow depth, assessed both by remote sensing and at meteorological stations, on the radial growth of spruce trees were analyzed. In addition, the snow depth data of BM, NM, and KM from both remote sensing and meteorological stations were employed in combination with tree ring data to reconstruct the historical snow depth using a nonlinear method (BRNN). The results showed that the established standard chronology of tree ring width was suitable for the analysis of tree ring climatology. The correlation coefficient between RWI and remote sensing snow depth was greater than that for station-measured snow depth. For the remote sensing snow depth, the correlation coefficients were greater in the winter and spring months, while those of the meteorological stations were greater only in the winter. By comparing the linear and nonlinear regression methods, it was found that the BRNN demonstrated better fitting than other methods due to the reduced model uncertainty brought about by the nonlinear relationship between tree growth and climate. The snow depth exhibited a decreasing trend in the BM, NM, KM sub-regions in the overall reconstructed period, but this trend was inconsistent in both the historical and observed periods, indicating the importance of reconstructing snow depth for the Tianshan Mountains.

Author Contributions

Conceptualization, Y.F. and Q.L.; methodology, Y.F. and Q.L.; software, S.Y.; validation, S.J.; formal analysis, H.Z.; investigation, H.S.; resources, R.Z.; data curation, Y.F.; writing—original draft preparation, Y.F. and Q.L.; review and editing, T.Z.; project administration, L.Q. All authors have read and agreed to the published version of the manuscript.

Funding

This research was sponsored by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (2022D01A365, 2022D01A350), the Key Laboratory Opening Subject of Xinjiang (2021D04004), and the Third Xinjiang Scientific Expedition Program (2021xjkk1400).

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Acknowledgments

We thank the anonymous reviewers for their useful comments to improve the manuscript. We thank Tong Li ([email protected]) for editing the English text of a draft of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Beniston, M.; Farinotti, D.; Stoffel, M.; Andreassen, L.M.; Coppola, E.; Eckert, N.; Fantini, A.; Giacona, F.; Hauck, C.; Huss, M.; et al. The European mountain cryosphere: A review of its current state, trends, and future challenges. Cryosphere 2018, 12, 759–794. [Google Scholar] [CrossRef]
  2. Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Mölg, T.; Bolch, T.; Vorogushyn, S.; Güntner, A. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
  3. Kraaijenbrink, P.D.A.; Stigter, E.E.; Yao, T.; Immerzeel, W.W. Climate change decisive for Asia’s snow meltwater supply. Nat. Clim. Chang. 2021, 11, 591–597. [Google Scholar] [CrossRef]
  4. Yao, T.; Xue, Y.; Chen, D.; Chen, F.; Thompson, L.; Cui, P.; Koike, T.; Lau, W.K.-M.; Lettenmaier, D.; Mosbrugger, V.; et al. Recent Third Pole’s Rapid Warming Accompanies Cryospheric Melt and Water Cycle Intensification and Interactions between Monsoon and Environment: Multidisciplinary Approach with Observations, Modeling, and Analysis. Bull. Am. Meteorol. Soc. 2019, 100, 423–444. [Google Scholar] [CrossRef]
  5. Natali, S.M.; Watts, J.D.; Rogers, B.M.; Potter, S.; Ludwig, S.M.; Selbmann, A.K.; Sullivan, P.F.; Abbott, B.W.; Arndt, K.A.; Birch, L.; et al. Large loss of CO2 in winter observed across the northern permafrost region. Nat. Clim. Chang. 2019, 9, 852–857. [Google Scholar] [CrossRef] [PubMed]
  6. Pulliainen, J.; Aurela, M.; Laurila, T.; Aalto, T.; Takala, M.; Salminen, M.; Kulmala, M.; Barr, A.; Heimann, M.; Lindroth, A.; et al. Early snowmelt significantly enhances boreal springtime carbon uptake. Proc. Natl. Acad. Sci. USA 2017, 114, 11081–11086. [Google Scholar] [CrossRef]
  7. Hu, Z.; Dietz, A.; Zhao, A.; Uereyen, S.; Zhang, H.; Wang, M.; Mederer, P.; Kuenzer, C. Snow Moving to Higher Elevations: Analyzing Three Decades of Snowline Dynamics in the Alps. Geophys. Res. Lett. 2020, 47, e2019GL085742. [Google Scholar] [CrossRef]
  8. Huning, L.S.; Agha Kouchak, A. Global snow drought hot spots and characteristics. Proc. Natl. Acad. Sci. USA 2020, 117, 19753–19759. [Google Scholar] [CrossRef]
  9. Mortimer, C.; Mudryk, L.; Derksen, C.; Luojus, K.; Brown, R.; Kelly, R.; Tedesco, M. Evaluation of long-term Northern Hemisphere snow water equivalent products. Cryosphere 2020, 14, 1579–1594. [Google Scholar] [CrossRef]
  10. Pulliainen, J.; Luojus, K.; Derksen, C.; Mudryk, L.; Lemmetyinen, J.; Salminen, M.; Ikonen, J.; Takala, M.; Cohen, J.; Smolander, T.; et al. Patterns and trends of Northern Hemisphere snow mass from 1980 to 2018. Nature 2020, 581, 294–298. [Google Scholar] [CrossRef]
  11. Notarnicola, C. Observing Snow Cover and Water Resource Changes in the High Mountain Asia Region in Comparison with Global Mountain Trends over 2000–2018. Remote Sens. 2020, 12, 3913. [Google Scholar] [CrossRef]
  12. Gao, Y.; Lu, N.; Dai, Y.; Yao, T. Reversal in snow mass trends on the Tibetan Plateau and their climatic causes. J. Hydrol. 2023, 620, 129438. [Google Scholar] [CrossRef]
  13. Li, Q.; Yang, T.; Zhou, H.; Li, L. Patterns in snow depth maximum and snow cover days during 1961–2015 period in the Tianshan Mountains, Central Asia. Atmos. Res. 2019, 228, 14–22. [Google Scholar] [CrossRef]
  14. Yang, T.; Li, Q.; Ahmad, S.; Zhou, H.; Li, L. Changes in Snow Phenology from 1979 to 2016 over the Tianshan Mountains, Central Asia. Remote Sens. 2019, 11, 499. [Google Scholar] [CrossRef]
  15. Mudryk, L.; Santolaria-Otín, M.; Krinner, G.; Ménégoz, M.; Derksen, C.; Brutel-Vuilmet, C.; Brady, M.; Essery, R. Historical Northern Hemisphere snow cover trends and projected changes in the CMIP6 multi-model ensemble. Cryosphere 2020, 14, 2495–2514. [Google Scholar] [CrossRef]
  16. Kouki, K.; Räisänen, P.; Luojus, K.; Luomaranta, A.; Riihelä, A. Evaluation of Northern Hemisphere snow water equivalent in CMIP6 models during 1982–2014. Cryosphere 2022, 16, 1007–1030. [Google Scholar] [CrossRef]
  17. Zhang, H.; Zhang, F.; Zhang, G.; Yan, W. Why Do CMIP6 Models Fail to Simulate Snow Depth in Terms of Temporal Change and High Mountain Snow of China Skillfully? Geophys. Res. Lett. 2022, 49, e2022GL098888. [Google Scholar] [CrossRef]
  18. Li, Q.; Yang, T.; Zhang, F.; Qi, Z.; Li, L. Snow depth reconstruction over last century: Trend and distribution in the Tianshan Mountains, China. Glob. Planet. Chang. 2019, 173, 73–82. [Google Scholar] [CrossRef]
  19. Zhang, R.; Ermenbaev, B.; Zhang, T.; Ali, M.; Qin, L.; Satylkanov, R. The Radial Growth of Schrenk Spruce (Picea schrenkiana Fisch. et Mey.) Records the Hydroclimatic Changes in the Chu River Basin over the Past 175 Years. Forests 2019, 10, 223. [Google Scholar] [CrossRef]
  20. Fritts, H.C. Dendrochronology and Dendroclimatology. In Tree Rings and Climate; Academic Press: Cambridge, MA, USA, 1976; Chapter 1. [Google Scholar]
  21. Coulthard, B.L.; Anchukaitis, K.J.; Pederson, G.T.; Cook, E.; Littell, J.; Smith, D.J. Snowpack signals in North American tree rings. Environ. Res. Lett. 2021, 16, 034037. [Google Scholar] [CrossRef]
  22. Dolanc, C.R.; Westfall, R.D.; Safford, H.D.; Thorne, J.H.; Schwartz, M.W. Growth–climate relationships for six subalpine tree species in a Mediterranean climate. Can. J. For. Res. 2013, 43, 1114–1126. [Google Scholar] [CrossRef]
  23. Shamir, E.; Meko, D.; Touchan, R.; Lepley, K.S.; Campbell, R.; Kaliff, R.N.; Georgakakos, K.P. Snowpack- and soil water content-related hydrologic indices and their association with radial growth of conifers in the Sierra Nevada, California. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005331. [Google Scholar] [CrossRef]
  24. Sanmiguel-Vallelado, A.; Camarero, J.J.; Gazol, A.; Morán-Tejeda, E.; Sangüesa-Barreda, G.; Alonso-González, E.; Gutiérrez, E.; Alla, A.Q.; Galván, J.D.; López-Moreno, J.I. Detecting snow-related signals in radial growth of Pinus uncinata mountain forests. Dendrochronologia 2019, 57, 125622. [Google Scholar] [CrossRef]
  25. Sanmiguel-Vallelado, A.; Camarero, J.J.; Morán-Tejeda, E.; Gazol, A.; Colangelo, M.; Alonso-González, E.; López-Moreno, J.I. Snow dynamics influence tree growth by controlling soil temperature in mountain pine forests. Agric. For. Meteorol. 2021, 296, 108205. [Google Scholar] [CrossRef]
  26. Falarz, M. Tree-Ring Widths and Snow Cover Depth in High Tauern. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2017; Volume 95. [Google Scholar]
  27. Liu, X.; Zhao, L.; Chen, T.; Shao, X.; Liu, Q.; Hou, S.; Qin, D.; An, W. Combined tree-ring width and δ13C to reconstruct snowpack depth: A pilot study in the Gongga Mountain, west China. Theor. Appl. Clim. 2011, 103, 133–144. [Google Scholar] [CrossRef]
  28. Qin, L.; Yuan, Y.; Zhang, R.; Wei, W.; Yu, S.; Fan, Z.; Chen, F.; Zhang, T.; Shang, H. Tree-Ring Response to Snow Cover and Reconstruction of Century annual Maximum Snow Depth for Northern Tianshan Mountains, China. Geochronometria 2016, 43, 9–17. [Google Scholar] [CrossRef]
  29. Wei, P.; Zhang, T.; Zhou, X.; Yi, G.; Li, J.; Wang, N.; Wen, B. Reconstruction of Snow Depth Data at Moderate Spatial Resolution (1 km) from Remotely Sensed Snow Data and Multiple Optimized Environmental Factors: A Case Study over the Qinghai-Tibetan Plateau. Remote Sens. 2021, 13, 657. [Google Scholar] [CrossRef]
  30. Song, Y.; Behrangi, A.; Blanchard-Wrigglesworth, E. Assessment of Satellite and Reanalysis Cold Season Snowfall Estimates Over Arctic Sea Ice. Geophys. Res. Lett. 2020, 47, e2020GL088970. [Google Scholar] [CrossRef]
  31. Ferrio, J.P.; Díez-Herrero, A.; Tarrés, D.; Ballesteros-Cánovas, J.A.; Aguilera, M.; Bodoque, J.M. Using stable isotopes of oxygen from tree-rings to study the origin of past flood events: First results from the iberian peninsula. Quaternaire 2015, 26, 67–80. [Google Scholar] [CrossRef]
  32. Panyushkina, I.P.; Meko, D.M.; Macklin, M.G.; Toonen, W.H.J.; Mukhamadiev, N.S.; Konovalov, V.G.; Ashikbaev, N.Z.; Sagitov, A.O. Runoff variations in Lake Balkhash Basin, Central Asia, 1779–2015, inferred from tree rings. Clim. Dyn. 2018, 51, 3161–3177. [Google Scholar] [CrossRef]
  33. Fan, Y.; Shang, H.; Wu, Y.; Li, Q. Tree-Ring Width and Carbon Isotope Chronologies Track Temperature, Humidity, and Baseflow in the Tianshan Mountains, Central Asia. Forests 2020, 11, 1308. [Google Scholar] [CrossRef]
  34. Mukhitdinov, A.; Nurtazin, S.; Alimova, S.; Ablaikhanova, N.; Yessimsiitova, Z.; Salmurzauly, R.; Margulan, I.; Mirasbek, Y. The transformation of ecosystems of the ili river delta (kazakhstan) under the flow regulation and climate change. Appl. Ecol. Environ. Res. 2020, 18, 2483–2498. [Google Scholar] [CrossRef]
  35. Qin, L.; Bolatov, K.; Yuan, Y.; Shang, H.; Yu, S.; Zhang, T.; Bagila, M.; Bolatova, A.; Zhang, R. The Spatially Inhomogeneous Influence of Snow on the Radial Growth of Schrenk Spruce (Picea schrenkiana Fisch. et Mey.) in the Ili-Balkhash Basin, Central Asia. Forests 2022, 13, 44. [Google Scholar] [CrossRef]
  36. Zhang, R.; Shang, H.; Yu, S.; He, Q.; Yuan, Y.; Bolatov, K.; Mambetov, B.T. Tree-ring-based precipitation reconstruction in southern Kazakhstan, reveals drought variability since A.D. 1770. Int. J. Clim. 2017, 37, 741–750. [Google Scholar] [CrossRef]
  37. Yuan, Y.; Shao, X.; Wei, W.; Yu, S.; Gong, Y.; Trouet, V. The Potential to Reconstruct Manasi River Streamflow in the Northern Tien Shan Mountains (NW China). Tree-Ring Res. 2007, 63, 81–93. [Google Scholar] [CrossRef]
  38. Fritts, H.; Swetnam, T. Dendroecology: A Tool for Evaluating Variations in Past and Present Forest Environments. Adv. Ecol. Res. 1989, 19, 111–188. [Google Scholar] [CrossRef]
  39. Fan, Y.; Shang, H.; Yu, S.; Wu, Y.; Li, Q. Understanding the Representativeness of Tree Rings and Their Carbon Isotopes in Characterizing the Climate Signal of Tajikistan. Forests 2021, 12, 1215. [Google Scholar] [CrossRef]
  40. Holmes, R. Computer-Assisted Quality Control in Tree-Ring Dating and Measurement. Tree-Ring Bull. 1983, 43, 51–67. [Google Scholar]
  41. Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Springer: Dordrecht, The Netherlands, 1990; 394p. [Google Scholar]
  42. Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the Average Value of Correlated Time Series with Applications in Dendroclimatology and Hydrometeorology. J. Clim. Appl. Meteorol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
  43. Yu, J.; Zhou, G.; Liu, Q. Tree-ring based summer temperature regime reconstruction in XiaoXing Anling Mountains, northeastern China since 1772 CE. Palaeogeogr. Palaeoclim. Palaeoecol. 2018, 495, 13–23. [Google Scholar] [CrossRef]
  44. Jevšenak, J.; Džeroski, S.; Zavadlav, S.; Levanič, T. A Machine Learning Approach to Analyzing the Relationship Between Temperatures and Multi-Proxy Tree-Ring Records. Tree-Ring Res. 2018, 74, 210–224. [Google Scholar] [CrossRef]
  45. Che, T.; Dai, L.; Zheng, X.; Li, X.; Zhao, K. Estimation of snow depth from passive microwave brightness temperature data in forest regions of northeast China. Remote Sens. Environ. 2016, 183, 334–349. [Google Scholar] [CrossRef]
  46. Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef]
  47. Dai, L.; Che, T.; Ding, Y. Inter-Calibrating SMMR, SSM/I and SSMI/S Data to Improve the Consistency of Snow-Depth Products in China. Remote Sens. 2015, 7, 7212–7230. [Google Scholar] [CrossRef]
  48. Huang, X.; Deng, J.; Ma, X.; Wang, Y.; Feng, Q.; Hao, X.; Liang, T. Spatiotemporal dynamics of snow cover based on multi-source remote sensing data in China. Cryosphere 2016, 10, 2453–2463. [Google Scholar] [CrossRef]
  49. Barandiaran, D.; Wang, S.-Y.S.; DeRose, R.J. Gridded Snow Water Equivalent Reconstruction for Utah Using Forest Inventory and Analysis Tree-Ring Data. Water 2017, 9, 403. [Google Scholar] [CrossRef]
  50. Anderson, S.; Moser, C.L.; Tootle, G.A.; Grissino-Mayer, H.D.; Timilsena, J.; Piechota, T. Snowpack Reconstructions Incorporating Climate in the Upper Green River Basin (Wyoming). Tree-Ring Res. 2012, 68, 105–114. [Google Scholar] [CrossRef]
  51. Yadav, R.R.; Bhutiyani, M.R. Tree-ring-based snowfall record for cold arid western Himalaya, India since A.D. 1460. J. Geophys. Res. Atmos. 2013, 118, 7516–7522. [Google Scholar] [CrossRef]
  52. Li, B.; Chen, Y.; Chen, Z.; Xiong, H.; Lian, L. Why does precipitation in northwest China show a significant increasing trend from 1960 to 2010? Atmos. Res. 2016, 167, 275–284. [Google Scholar] [CrossRef]
  53. Xu, M.; Kang, S.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
  54. Tang, Z.; Wang, X.; Wang, J.; Wang, X.; Li, H.; Jiang, Z. Spatiotemporal Variation of Snow Cover in Tianshan Mountains, Central Asia, Based on Cloud-Free MODIS Fractional Snow Cover Product, 2001–2015. Remote Sens. 2017, 9, 1045. [Google Scholar] [CrossRef]
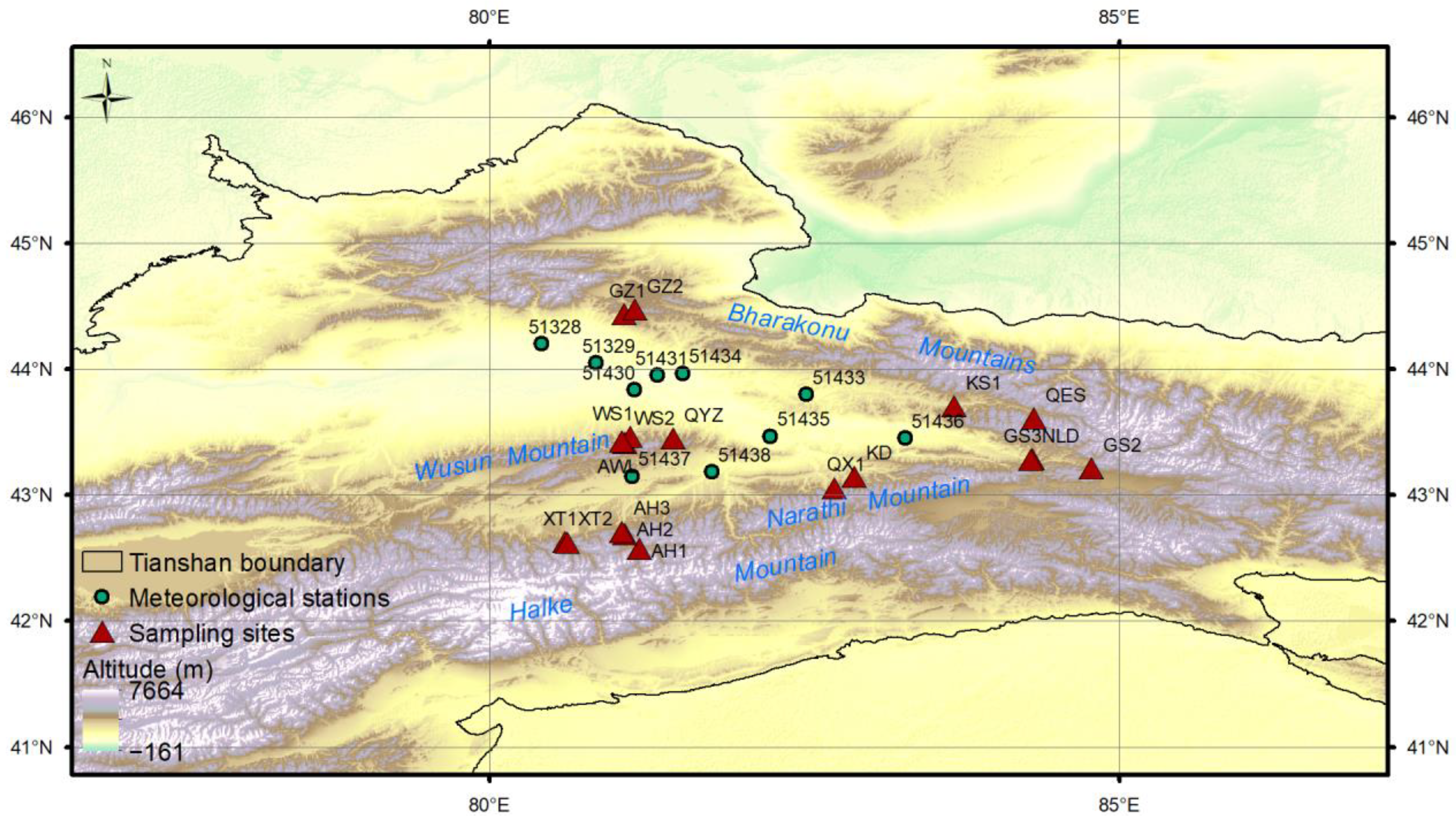
Remotesensing 15 02849 g001 550
Figure 1. Locations of the tree ring sampling sites (red triangle) and the meteorological stations (green circle) for the current study (black abbreviations represent the site ID of stations).
Figure 1. Locations of the tree ring sampling sites (red triangle) and the meteorological stations (green circle) for the current study (black abbreviations represent the site ID of stations).
Remotesensing 15 02849 g001
Remotesensing 15 02849 g002 550
Figure 2. The standard tree ring width chronology (STD), obtained using an EPS cutoff, and the residual chronology with two standard errors (SE) in the (a) Braconu Mountains (BM) of the eastern Ili Valley; (b) Narathi Mountains (NM) of the southeastern Ili Valley; (c) Khalk Mountains (KM) of the southern Ili Valley; and (d) Wusun Mountains (WM) in the middle of the Ili Valley. The negative exponential curve (NEC) method was used to detrend the growth. The 30-year smoothing splines were plotted for visualization. The blue dots represent the EPS cutoff. The shaded regions represent the truncated chronology.
Figure 2. The standard tree ring width chronology (STD), obtained using an EPS cutoff, and the residual chronology with two standard errors (SE) in the (a) Braconu Mountains (BM) of the eastern Ili Valley; (b) Narathi Mountains (NM) of the southeastern Ili Valley; (c) Khalk Mountains (KM) of the southern Ili Valley; and (d) Wusun Mountains (WM) in the middle of the Ili Valley. The negative exponential curve (NEC) method was used to detrend the growth. The 30-year smoothing splines were plotted for visualization. The blue dots represent the EPS cutoff. The shaded regions represent the truncated chronology.
Remotesensing 15 02849 g002
Remotesensing 15 02849 g003 550
Figure 3. Correlation coefficient between the RWI and (a) remote sensing and (b) meteorological monthly maximum snow depth at each sampling site.
Figure 3. Correlation coefficient between the RWI and (a) remote sensing and (b) meteorological monthly maximum snow depth at each sampling site.
Remotesensing 15 02849 g003
Remotesensing 15 02849 g004 550
Figure 4. Long-term variations of reconstructed snow depth and the actual observations for the three sub-regions.
Figure 4. Long-term variations of reconstructed snow depth and the actual observations for the three sub-regions.
Remotesensing 15 02849 g004
Remotesensing 15 02849 g005 550
Figure 5. Comparison of RWI of the four regions and the snow depth REC of BM (1815–2016) and HM (1657–2016) with other environmental factors. Arrows represent meteorological disaster events documented in the historical archives. Grey bands and orange bands represent years associated with RWI and REC extremes, as well as extreme temperatures (red), extreme precipitation (blue), and extreme depths of frozen soil (green). Purple bands represent chronological extremes of stable isotopes in the region. Vertical lines show reconstructed sequence extremes obtained from other literature (dark grey) [28].
Figure 5. Comparison of RWI of the four regions and the snow depth REC of BM (1815–2016) and HM (1657–2016) with other environmental factors. Arrows represent meteorological disaster events documented in the historical archives. Grey bands and orange bands represent years associated with RWI and REC extremes, as well as extreme temperatures (red), extreme precipitation (blue), and extreme depths of frozen soil (green). Purple bands represent chronological extremes of stable isotopes in the region. Vertical lines show reconstructed sequence extremes obtained from other literature (dark grey) [28].
Remotesensing 15 02849 g005
Remotesensing 15 02849 g006 550
Figure 6. Variations in annual mean temperature and annual precipitation in the four sub-regions from 1961 to 2016. (a) BM, (b) NM, (c) KM, and (d) WM.
Figure 6. Variations in annual mean temperature and annual precipitation in the four sub-regions from 1961 to 2016. (a) BM, (b) NM, (c) KM, and (d) WM.
Remotesensing 15 02849 g006
Table
Table 1. Coordinates and statistics of the sampling sites. The tree species was Schrenk spruce (Picea schrenkiana Fisch. et Mey).
Table 1. Coordinates and statistics of the sampling sites. The tree species was Schrenk spruce (Picea schrenkiana Fisch. et Mey).
SiteLongitude
(°N)		Latitude
(°E)		DateElevation
(m asl)		AspectSlope
(°)		Canopy DensityNOtreesNOsamples
AH142°34′34.24″81°11′47.15″September 20162266N100.51225
AH242°41′26.65″81°4′54.47″September 20161950NE350.51836
AH342°42′39.9″81°03′21.2″August 20062685EN-W350.32448
AWL43°24′54.6″81°04′35.7″August 20062739N-E450.12590
GS243°12′42.5″84°47′7.27″September 20162355N00.21836
GS343°17′13.72″84°18′47.16″September 20161698NW400.51530
GZ144°26′21.21″81°4′15.68″September 20161542NW500.259
GZ244°28′27.19″81°9′31.58″September 20162050N200.91836
KD43°8′53.1″82°53′57.7″September 20161813NE200.71225
KS143°42′23.29″83°41′44.56″September 20161809NW00.11835
GS143°17′84°18′June 20151770N300.12446
QES43°36′36.06″84°19′33.82″September 20162370W100.41836
QX143°3′30.97″82°44′33.8″September 20161894NE400.71225
QYZ43°27′04.5″81°27′40.0″August 20062322EN-N700.42550
WS143°27′43.38″81°7′16.84″September 20162150NE300.81530
WS243°25′40.17″81°3′25.47″September 20162552NW100.61836
XT142°37′43.68″80°36′20.44″September 20162049NW100.91530
XT242°37′27.22″80°37′11.33″September 20162066NNE100.91836
N, E, W, and S represents north, east, west, and south, respectively. The details of the site locations are shown in Figure 1.
Table
Table 2. Site coordinates and statistics for the meteorological stations.
Table 2. Site coordinates and statistics for the meteorological stations.
Site IDSiteLongitudeLatitudeElevationTimeData Type
51328HRGS44.2380.48713.31959–2016Temperature extreme (°C), precipitation extreme (mm), daily minimum temperature consecutive days (days), ground temperature extreme (°C), maximum frozen soil depth (mm), etc.
51329HC44.0480.84624.31959–2016
51430CBCR43.8381.15602.61959–2016
51431YN43.9581.33662.51951–2016
51433NLK43.882.561105.21958–2016
51434YNX43.9681.537701960–2016
51435GL43.4682.23774.91960–2016
51436XY43.4583.3928.21955–2016
51437ZS43.15 81.1318511954–2016
51438TKS43.1881.761239.61959–2016
Table
Table 3. Descriptive statistics of the standard tree ring chronologies.
Table 3. Descriptive statistics of the standard tree ring chronologies.
LocationSiteNcoresRbar-tRbar-eEPSSNRChronology Interval
BMKS1, QES, GS3, NLD, GS2,1430.4660.4660.96628.5551815–2016
NMQX1, KD510.3690.2690.94416.9121737–2016
KMXT1, XT2, AH1, AH2, AH3,1600.6460.3460.96527.3841657–2016
WMWS1, WS2, AWL, QYZ1560.3770.2770.97945.7211657–2016
The details of the site locations and their equivalent regions are shown in Figure 1. BM refers to the Bharakonu Mountains, NM refers to the Narathi Mountains, KM refers to the Halke mountains, and WM refers to the Wusun Mountains. Ncores is the number of sample cores; Rbar-t is the mean inter-series correlation between all series; Rbar-e is the effective signal; EPS is the expressed population signal; SNR is the signal-to-noise ratio; chronology interval shows the first year, with EPS > 0.85.
Table
Table 4. Statistics of the different regression models for the snow depth REC.
Table 4. Statistics of the different regression models for the snow depth REC.
LocationBRNNMLRRF
rRMSERRSEdRECErRMSERRSEdRECErRMSERRSEdRECE
BM0.790.680.820.650.560.560.800.820.760.670.320.320.760.570.660.820.380.38
NM0.650.800.920.770.490.420.626.450.940.710.370.280.725.640.770.810.510.45
KM0.850.750.710.860.490.480.882.940.520.930.730.730.853.530.620.920.620.61
r is the correlation coefficient; RMSE is the root mean squared error; RRSE is the root relative squared error; d is the index of agreement; RE is the reduction in error; and CE is the coefficient of efficiency. All of the results shown comprise the validation data set.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Fan, Y.; Li, Q.; Shang, H.; Jiang, S.; Zhang, T.; Zhang, R.; Qin, L.; Yu, S.; Zhang, H. Snowpack Dynamics Influence Tree Growth and Signals in Tree Rings of Tianshan Mountain, Central Asia. Remote Sens. 2023, 15, 2849. https://doi.org/10.3390/rs15112849

AMA Style

Fan Y, Li Q, Shang H, Jiang S, Zhang T, Zhang R, Qin L, Yu S, Zhang H. Snowpack Dynamics Influence Tree Growth and Signals in Tree Rings of Tianshan Mountain, Central Asia. Remote Sensing. 2023; 15(11):2849. https://doi.org/10.3390/rs15112849

Chicago/Turabian Style

Fan, Yuting, Qian Li, Huaming Shang, Shengxia Jiang, Tongwen Zhang, Ruibo Zhang, Li Qin, Shulong Yu, and Heli Zhang. 2023. "Snowpack Dynamics Influence Tree Growth and Signals in Tree Rings of Tianshan Mountain, Central Asia" Remote Sensing 15, no. 11: 2849. https://doi.org/10.3390/rs15112849

APA Style

Fan, Y., Li, Q., Shang, H., Jiang, S., Zhang, T., Zhang, R., Qin, L., Yu, S., & Zhang, H. (2023). Snowpack Dynamics Influence Tree Growth and Signals in Tree Rings of Tianshan Mountain, Central Asia. Remote Sensing, 15(11), 2849. https://doi.org/10.3390/rs15112849

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop