A Crustal Deformation Pattern on the Northeastern Margin of the Tibetan Plateau Derived from GPS Observations
Abstract
1. Introduction
2. Regional Tectonic Background
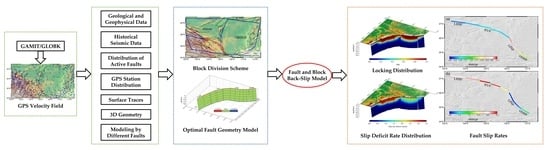
3. GPS Observation Data and Block Classification
3.1. GPS Data and Data Processing
3.2. Block Division Scheme
3.3. Fault Geometry Model
4. Inversion Principle
5. GPS Data Inversion Results
5.1. Fault Slip Rate
5.2. Fault Locking Slip Distribution
5.3. Block Motion
6. Discussion
6.1. Comparison of Modeling Results for Different Fault Participation
6.2. Optimal Model Parameter Settings
6.3. Distribution Characteristics of the Degree of Locking and Slip Deficit Rate in Different Segments of the Fault Zone
7. Conclusions
- (1)
- The LHSF is mainly controlled by a left-lateral strike-slip at a rate of ~3.5 mm/yr. The fault is completely locked within a 1 km depth and completely creeps below 5 km, so the locking degree of this fault is low. Combined with the slip deficit rate of 3.2–3.6 mm/yr, we considered that the seismic risk of this fault is low.
- (2)
- The HYF is mainly controlled by a left-lateral strike-slip at a rate of 3.0–3.2 mm/yr. The western and eastern sections of the fault are weakly locked, with strong locking at a depth of 5 km, and completely creeps at a depth of 10 km or less. The whole fault completely creeps below 13 km, and the overall locking degree showed the distribution characteristics of strong in the middle section and weak in the eastern and western sections. Combined with the slip deficit rate of 2.4–3.2 mm/yr, we believe that there is a certain amount of strain accumulation in the middle section, but combined with the regional geological and historical seismic data, we believe that this fault is still in the post-earthquake stress adjustment stage, the seismic risk is considered low.
- (3)
- The LPSF is mainly controlled by a thrust dip-slip at a rate of 1.7–1.9 mm/yr. The overall degree of locking in this fault is the strongest and uniformly distributed, it is completely locked at a depth of 5 km, there is still strong locking at a depth of 10 km, and the fault completely creeps at a depth of 15 km or less; the slip deficit rate of this fault is 1.7–1.9 mm/yr. Although its rate of strain accumulation is slow, when combining the analysis of geology, historical seismic data, and the activity characteristics, there is still a risk of a moderate to strong earthquake after a long period of strain accumulation, which should be continuously observed and analyzed.
- (4)
- The GGBJF has both left-lateral strike-slip and thrust dip-slip components, its strike-slip rate is 1.3–1.4 mm/yr and its dip-slip rate is 1.2–1.3 mm/yr, the locking fraction decreases gradually from north to south, locking is strong in the range of 5 km in depth, it completely creeps below 10 km, and is combined with a slip deficit rate of 1.8 mm/yr and decays to 0.2 mm/yr from west to east. The seismic risk of this fault is considered to be low.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, W.Q.; Jiao, D.C.; Zhang, P.Z. Displacement along the Haiyuan fault associated with the great 1920 Haiyuan, China, earthquake. Bull. Seismol. Soc. Am. 1987, 77, 117–131. [Google Scholar]
- Savage, J.C. Dislocation model of strain accumulation and release at a subduction zone. J. Geophys. Res. Atmos. 1983, 88, 4984–4996. [Google Scholar] [CrossRef]
- McClusky, S.; Balassanian, S.; Barka, A.; Demir, C.; Ergintav, S.; Georgiev, I.; Gurkan, O.; Hamburger, M.; Hurst, K.; Kahle, H.; et al. Global Positioning System constraints on plate kinematics and dynamics in the eastern Mediterranean and Caucasus. J. Geophys. Res. 2000, 105, 5695. [Google Scholar] [CrossRef]
- Müller, M.D.; Geiger, A.; Kahle, H.-G.; Veis, G.; Billiris, H.; Paradissis, D.; Felekis, S. Velocity and deformation fields in the North Aegean domain, Greece, and implications for fault kinematics, derived from GPS data 1993–2009. Tectonophysics 2013, 597–598, 34–49. [Google Scholar] [CrossRef]
- Lazos, I.; Sboras, S.; Pikridas, C.; Pavlides, S.; Chatzipetros, A. Geodetic analysis of the tectonic crustal deformation pattern in the North Aegean Sea, Greece. Mediterr. Geosci. Rev. 2021, 3, 79–94. [Google Scholar] [CrossRef]
- Nyst, M.; Thatcher, W. New constraints on the active tectonic deformation of the Aegean. J. Geophys. Res. Solid Earth 2004, 109, 1–23. [Google Scholar] [CrossRef]
- Institute of Geology; China Earthquake Administration; Ningxia Earthquake Administration. Haiyuan Active Fault Zone; Seismological Press: Beijing, China, 1990; (In Chinese).
- Zhang, P.Z.; Burchfiel, B.C.; Molnar, P. Amount and style of late Cenozoic deformation in the Liupanshan area, Ningxia autonomous region, China. Tectonics 1991, 10, 1111–1129. [Google Scholar] [CrossRef]
- Burchfiel, B.C.; Zhang, P.; Wang, Y.P. Geology of the Haiyuan fault Zone, Ningxia-Hui Autonomous Region, China, and its Relation to the Evolution of the Northeastern Margin of the Tibetan Plateau. Tectonics 1991, 10, 1091–1110. [Google Scholar] [CrossRef]
- Tian, Q.J.; Ding, G.Y.; Shen, X.H. Pull-apart Basins and the Totel Lateral Displacement along the Haiyuan Fault Zone in Cenozoic. Earthq. Res. China 2001, 17, 67–75. [Google Scholar] [CrossRef]
- Li, C.Y.; Zhang, P.Z.; Yin, J.H. Late Quaternary left-lateral slip rate of the Haiyuan Fault, northeastern margin of the Tibetan plateau. Tectonics 2009, 28, TC5010. [Google Scholar] [CrossRef]
- Wang, W.; Yang, S.; Wang, Q. Crustal block rotations in Chinese mainland revealed by GPS measurements. Earthq. Sci. 2009, 22, 639–649. [Google Scholar] [CrossRef]
- Hu, Y.X.; Cui, D.X.; Zhang, X.; Wang, X. Inversion and Analysis on the Active Characteristics of Subsections of Haiyuan Fault Belt Using GPS Data. Northwestern Seismol. J. 2009, 31, 227–230, 253. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=ZBDZ200903004&DbName=CJFQ2009 (accessed on 16 October 2021).
- Cui, D.X.; Hu, Y.X.; Wang, W.P.; Zhu, G.Z. Coulomb Stress Accumulation along Haiyuan Fault Zone. Earth Sci. J. China Univ. Geosci. 2009, 34, 641–650. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=DQKX200904011&DbName=CJFQ2009 (accessed on 16 October 2021).
- Duvall, A.R.; Clark, M.K. Dissipation of fast strike-slip faulting within and beyond northeastern Tibet. Geology 2010, 38, 223–226. [Google Scholar] [CrossRef]
- Loveless, J.P.; Meade, B.J. Partitioning of localized and diffuse deformation in the Tibetan Plateau from joint inversions of geologic and geodetic observations. Earth Planet. Sci. Lett. 2011, 303, 11–24. [Google Scholar] [CrossRef]
- Zhang, X.L.; Shi, Z.M.; Jiang, F.Y.; Zhu, L.Y.; Wang, X. Research on late tectonic deformation evolvement of Huayuan-Liupanshan Arc Fault and Iits surrounding area. J. Geod. Geodyn. 2011, 31, 20–24. [Google Scholar] [CrossRef]
- Ge, W.P.; Wang, M.; Shen, Z.K.; Yuan, D.Y.; Zheng, W.J. Intersiesmic kinematics and deformation patterns on the upper crust of Qaidam-Qilianshan block. Chin. J. Geophys. 2013, 56, 2994–3010. (In Chinese) [Google Scholar] [CrossRef]
- Li, Q.; Jiang, Z.S.; Wu, Y.Q.; Zhao, J.; Wei, W.X.; Liu, X.X. Present-day tectonic deformation characteristics of Haiyuan-Liupanshan fault zone. J. Geod. Geodyn. 2013, 33, 18–22. [Google Scholar] [CrossRef]
- Li, Y.H.; Cui, D.X.; Hao, M. GPS-Constrained Inversion of Slip Rate on Major Active Faults in the Northeastern Margin of Tibet Plateau. Earth Sci. J. China Univ. Geosci. 2015, 40, 1767–1780. [Google Scholar] [CrossRef]
- Li, Y.C.; Shan, X.J.; Qu, C.Y. Fault locking and slip rate deficit of the Haiyuan-Liupanshan fault zone in the northeastern margin of the Tibetan Plateau. J. Geodyn. 2016, 102, 47–57. [Google Scholar] [CrossRef]
- Ye, M.S.; Meng, G.J.; Su, X.N. Locking Characteristics and Slip Deficits of the Main Faults in the Northeast Margin of Tibetan Plateau. Earthquake 2018, 38, 1–12. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=DIZN201803001&DbName=CJFQ2018 (accessed on 24 October 2021).
- Qiao, X.; Qu, C.Y.; Shan, X.J.; Li, Y.C.; Zhu, C.H. Deformation Characteristics and kinematic Parameters Inversion of Haiyuan Fault Zone Based on Time Series InSAR. Seismol. Mology Geol. 2019, 41, 1481–1496. [Google Scholar] [CrossRef]
- Xu, H.C.; Wang, H.; Cao, J.L. Slip Rates of the Major faults in the Northeastern Tibetan Plateau and Their Geodynamic Implications. Earthquake 2018, 38, 13–23. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=DIZN201803002&DbName=CJFQ2018 (accessed on 18 November 2021).
- Sella, G.F.; Dixon, T.H.; Mao, A. A model for recent plate velocities from space geodesy. J. Geophys. Res. Solid Earth 2002, 107, 2081–2091. [Google Scholar] [CrossRef]
- Deng, Q.D.; Zhang, W.Q.; Zhang, P.Z. Haiyuan strike-slip fault zone and its compressional structures of the end. Seismol. Geol. 1989, 11, 1–14. (In Chinese) [Google Scholar] [CrossRef]
- Wang, W.T.; Zhang, P.Z.; Zheng, D.W.; Pang, J.Z. Late Cenozoic tectonic deformation of the Haiyuan fault zone in the northeastern margin of the Tibetan Plateau. Earth Sci. Front. 2014, 21, 266–274. [Google Scholar] [CrossRef]
- Yuan, D.Y.; Lei, Z.S.; Zhang, J.L.; Liu, B.C.; Liang, M.J. Textural research of 1219 A.D. Guyuan earthquake in Ningxia HuiAutonomous Region, China, and discussion on its causative structure. Acta Seismol. Sin. 2008, 30, 648–657. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=DZXB200806012&DbName=CJFQ2008 (accessed on 18 November 2021).
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual (Version 10.6); Massachusetts Institute of Technology: Cambridge, MA, USA, 2015; Available online: http://geoweb.mit.edu/gg/GAMIT_Ref.pdf (accessed on 16 June 2020).
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GLOBK Reference Manual (Version 10.6); Massachusetts Institute of Technology: Cambridge, MA, USA, 2015; Available online: http://geoweb.mit.edu/gg/GLOBK_Ref.pdf (accessed on 16 June 2020).
- Su, X.N.; Yao, L.B.; Wu, W.W.; Meng, G.J.; Su, L.N.; Xiong, R.W.; Hong, S.Y. Crustal Deformation on the Northeastern Margin of the Tibetan Plateau from Continuous GPS Observations. Remote Sens. 2019, 11, 34. [Google Scholar] [CrossRef]
- Zhang, P.Z.; Deng, Q.D.; Zhang, G.M. Strong Earthquake Activity and Active blocks in Chinese Mainland. Sci. Sin. 2003, 33, 12–20. (In Chinese). Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=JDXK2003S1001&DbName=CJFQ2003 (accessed on 18 November 2021).
- Wang, K.; Wells, R.; Mazzotti, S. A revised dislocation model of interseismic deformation of the Cascadia subduction zone. J. Geophys. Res. Atmos. 2003, 108, 327. [Google Scholar] [CrossRef]
- McCaffrey, R.; Qamar, A.I.; King, R.W. Fault locking, block rotation and crustal deformation in the Pacific Northwest. Geophys. J. Int. 2007, 169, 1315–1340. [Google Scholar] [CrossRef]
- McCaffrey, R. Crustal block rotations and plate coupling. In Plate Boundary Zones; Stein, S.C., Freymueller, J.T., Eds.; AGU: Washington, DC, USA, 2002; pp. 101–122. [Google Scholar] [CrossRef]
- McCaffrey, R. Block kinematics of the pacific–north America plate boundary in the southwestern United States from inversion of GPS, seismological, and geologic data. J. Geophys. Res. 2005, 110, 1–25. [Google Scholar] [CrossRef]
- Savage, J.C.; Gan, W.; Svarc, J.L. Strain accumulation and rotation in the Eastern California Shear Zone. J. Geophys. Res. Solid Earth 2001, 106, 21995–22007. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- McCaffrey, R.; Wallace, L.M. A Comparison of Geodetic and Paleomagnetic Estimates of Block Rotation Rates in Deforming Zones. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2004. [Google Scholar]
- Yuan, D.Y.; Liu, B.C.; Lv, T.Y.; He, W.G.; Liu, X.F.; Gan, W.J. The Study on Seismic SpatialCharacters by using the Self-Organized Critical phenomenom. Northeast. Seismol. J. 1998, 20, 27–34. Available online: https://kns.cnki.net/kcms2/article/abstract?v=2OF-LjPvQ9c0PiCsnwFA4jYVnFp1eiSIzRvhRnUS5yn7umIf8mPXJfcb-d37k2YKnWjzZglLBbBPTGwsYiPwC6otnihN5J-LAIBxqJC9naVDJRJV3JieCw==&uniplatform=NZKPT&language=CHS (accessed on 18 November 2021).
- Li, Q.; Jiang, Z.S.; Wu, Y.Q.; Zhao, J. Inversion of Locking and Distribution of Slip Deficit inHaiyuan-Liupanshan Fault Zone Using GPS Data. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 575–580. [Google Scholar] [CrossRef]
- Li, Y.C.; Qu, C.Y.; Shan, X.J. Deformation of the Haiyuan-Liupanshan fault zone inferred from the denser GPS observations. Earthq. Sci. 2015, 28, 319–331. [Google Scholar] [CrossRef]
- Meyer, B.; Tapponnier, P.; Bourjot, L. Crustal thickening in Gansu-Qinghai, lithospheric mantle subduction, and oblique, strike-slip controlled growth of the Tibet Plateau. Geophys. J. Int. 1998, 135, 1–47. [Google Scholar] [CrossRef]
- Wang, Y.P.; Shen, J.; Wang, Q. On the lateral contraction of Sichuan-Yunnan block (Chuandian block). Earth Sci. Front. 2003, 10, 188–192. (In Chinese) [Google Scholar]
- Hao, M.; Li, Y.H.; Qin, S.L. Spatial and Temporal Distribution of Slip Rate Deficit Across Haiyuan-Liupannshan Fault Zone Constrained by GPS Data. Seismol. Geol. 2017, 39, 471–484. [Google Scholar] [CrossRef]
- Zhao, J.; Niu, A.F.; Li, Q.; Yuan, Z.Y. Study on Dynamic Characteristics of Fault Locking and Fault Slip Deficit in the Faults around the Longxi Block. J. Seismol. Res. 2016, 31, 20–24. [Google Scholar]
- Zhang, X.; Jiang, Z.S.; Wang, Q.; Wang, X.X.; Cui, D.X.; Zhang, X.L. Invesion for negative dislocation on elastic block boundaries along the northeast margin of Qinghai-Xizang block and prediction for strong earthquake location. Acta Seismol. Sin. 2005, 27, 620–629. [Google Scholar] [CrossRef]
- Wan, Y.G.; Shen, Z.K.; Sheng, S.Z.; Xu, X.F. The influence of 2008 Wenchuan earthquake on surrounding faults. Acta Seismol. Sin. 2009, 31, 128–139. Available online: https://kns.cnki.net/kcms2/article/abstract?v=2OF-LjPvQ9eKuVkTgByJqbqBWmlnkjxJJDGs7mn47PGNiT_Iw8jEwCkr1Y25xQ_3cwmFszdefsuL_VtMZr5AnIIPbtC064G1KUzuPUjNPqxM9EOcj0rAqA==&uniplatform=NZKPT&language=CHS (accessed on 28 January 2022).
- Shi, W. The Analysis of the Developmental Characteristics and Activity about Fault Zone of Longxian-Baoji. Ph.D. Thesis, Chang’an University, Xi’an, China, 2011. Available online: https://kns.cnki.net/kcms2/article/abstract?v=2OF-LjPvQ9cFh1umQjfhDTBaw1FnlZyyQSXGbPPGumAtXPtDIGPvggWEGTC5THc7Y-WbtRDiqQDYk1vBcmm3lj39hg_t9QrTMsXd_vJs0ebFMNHYbZ8RTg==&uniplatform=NZKPT&language=CHS (accessed on 28 January 2022).
- Xu, W.J.; Gao, M.T. Statistical analysis of the completeness of earthquake catalogs in China mainland. Chin. J. Geophys. 2014, 57, 2802–2812. [Google Scholar] [CrossRef]
- Yang, Z.X.; Waldhuser, F.; Chen, Y.T.; Richards, P.G. Double-difference relocation of earthquakes in central-western China. J. Seismol. 2005, 9, 241–264. [Google Scholar] [CrossRef]
- Hao, M.; Wang, Q.L.; Shen, Z.K. Present-day crustal vertical movement inferred from precise leveling data in eastern margin of Tibetan plateau. Tectonophysics 2014, 632, 281–292. [Google Scholar] [CrossRef]
- Working Group of M7. Study on the Mid-to Long-Term Potential of Large Earthquakes on the Chinese Continent; Seismological Press: Beijing, China, 2012. [Google Scholar]








| Literature Sources | LHSF | HYF | LPSF | GGBJF | ||||
|---|---|---|---|---|---|---|---|---|
| Western | Middle | Eastern | Northern | Southern | ||||
| [7] | 3.3–9.2 | |||||||
| Geological results | [8] | Zhongwei section: 8–10, reduced eastward to 4–6 | ||||||
| [9] | ||||||||
| [10] | 5.8 | |||||||
| [11] | 4.5 ± 1.1 | |||||||
| [12] | 3.4 ± 0.2 | |||||||
| [13] | 8.25 | 5.49 | 5.97 | |||||
| [14] | 6.5 | 4.5 | 5.6 | 5.5 | ||||
| [15] | 2–4.5 | |||||||
| [16] | 4.6–4.7 | |||||||
| [17] | 2–5.5 | 1.0 | ||||||
| Terrestrial | [18] | 2.9–5.9 | ||||||
| measurement | [19] | 5.4 ± 0.1 | 5.0 ± 0.1 | 5.0 ± 0.2 | 1.3 ± 0.1 | 1.7 ± 0.1 | ||
| results | [20] | 7.8–8.4 | 3.2 | 3.9 | ||||
| [21] | 4.1 ± 0.4 | 3.9 ± 0.4 | 3.7 ± 0.4 | 3.6 ± 0.4 | 3.2 ± 0.3 | 3.1 ± 0.3 | ||
| [22] | 6.4 | 6.1 | 5.9 | 1.4 | 1.2 | 1.2 | ||
| [23] | 4.5–7.6 | 3.2–5.4 | ||||||
| [24] | 3.4 ± 0.2 | 3.2 ± 0.2 | 3.0 ± 0.2 | |||||
| This article | 3.5 | 3.2 | 3.0 | 3.1 | 1.9 | 1.8 | 1.3 | |
| Fault | Segment | Dip-Slip Rate (mm/yr) | Dip-Slip Rate (mm/yr) |
|---|---|---|---|
| LHSF | 3.5 | 0.0 | |
| HYF | West | 3.2 | 0.5 |
| Middle | 3.0 | 0.8 | |
| East | 3.2 | 0.4 | |
| LPSF | North | 0.3 | 1.9 |
| South | 0.6 | 1.8 | |
| GGBJF | 1.3 | 1.3 |
| Fault | Slip Rate (mm/yr) | Locking Depth (km) | Slip Deficit Rate (mm/yr) |
|---|---|---|---|
| LHSF | 3.5 | 5 | 3.2–3.6 |
| West section of HYF | 3.2 | 10 | 2.8–3.2 |
| Middle section of HYF | 3.0 | 13 | 2.4–2.8 |
| East section of HYF | 3.2 | 10 | ~2.4 |
| North section of LPSF | 0.3 | 15 | 1.7–1.8 |
| South section of LPSF | 0.6 | 15 | 1.8–1.9 |
| GGBJF | 1.3 | 10 | ~1.8 |
| Block Name | Eulerian Vector | Internal Strain Rate (Nanostrain/yr) | ||||
|---|---|---|---|---|---|---|
| Alxa Block | 110.4658 | 39.0087 | −0.4106 | −5.10 | 4.46 | 28.18 |
| Lanzhou block | 110.3636 | 32.0201 | −0.3731 | −14.34 | 6.05 | 50.04 |
| Block Name | Internal Strain Rate (Nanostrain/yr) | ||
|---|---|---|---|
| Alxa Block | 2.33 | −2.96 | −3.98 |
| Lanzhou block | −5.93 | −2.36 | −10.04 |
| Number | Faults | Data | Blocks | of the Alxa Block | of the Lanzhou Block | |
|---|---|---|---|---|---|---|
| 1 | HYF, LPSF | 526 stations | ORDOS, Alxa, Lanzhou | 1.633 | 0.629 | 0.892 |
| 2 | LHSF, HYF, LPSF | 538 stations | ORDOS, Alxa, Lanzhou | 1.599 | 0.589 | 0.872 |
| 3 | HYF, LPSF, GGBJF | 542 stations | ORDOS, Alxa, Lanzhou | 1.591 | 0.652 | 0.845 |
| 4 | LHSF, HYF, LPSF, GGBJF | 554 stations | ORDOS, Alxa, Lanzhou | 1.534 | 0.613 | 0.784 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Su, X. A Crustal Deformation Pattern on the Northeastern Margin of the Tibetan Plateau Derived from GPS Observations. Remote Sens. 2023, 15, 2905. https://doi.org/10.3390/rs15112905
Yu S, Su X. A Crustal Deformation Pattern on the Northeastern Margin of the Tibetan Plateau Derived from GPS Observations. Remote Sensing. 2023; 15(11):2905. https://doi.org/10.3390/rs15112905
Chicago/Turabian StyleYu, Sihan, and Xiaoning Su. 2023. "A Crustal Deformation Pattern on the Northeastern Margin of the Tibetan Plateau Derived from GPS Observations" Remote Sensing 15, no. 11: 2905. https://doi.org/10.3390/rs15112905
APA StyleYu, S., & Su, X. (2023). A Crustal Deformation Pattern on the Northeastern Margin of the Tibetan Plateau Derived from GPS Observations. Remote Sensing, 15(11), 2905. https://doi.org/10.3390/rs15112905