Examining the Consistency of Sea Surface Temperature and Sea Ice Concentration in Arctic Satellite Products
Abstract
:1. Introduction
2. Materials and Methods
2.1. L4 SST Analyses
2.1.1. OSTIA SST
2.1.2. C3S SST
2.1.3. Geo-Polar Blended SST v1.0
2.1.4. Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1
2.1.5. Canadian Meteorological Centre (CMC) SST Version 3.0
2.1.6. MWIR OI Version v05.0
2.2. In Situ Data
3. Results
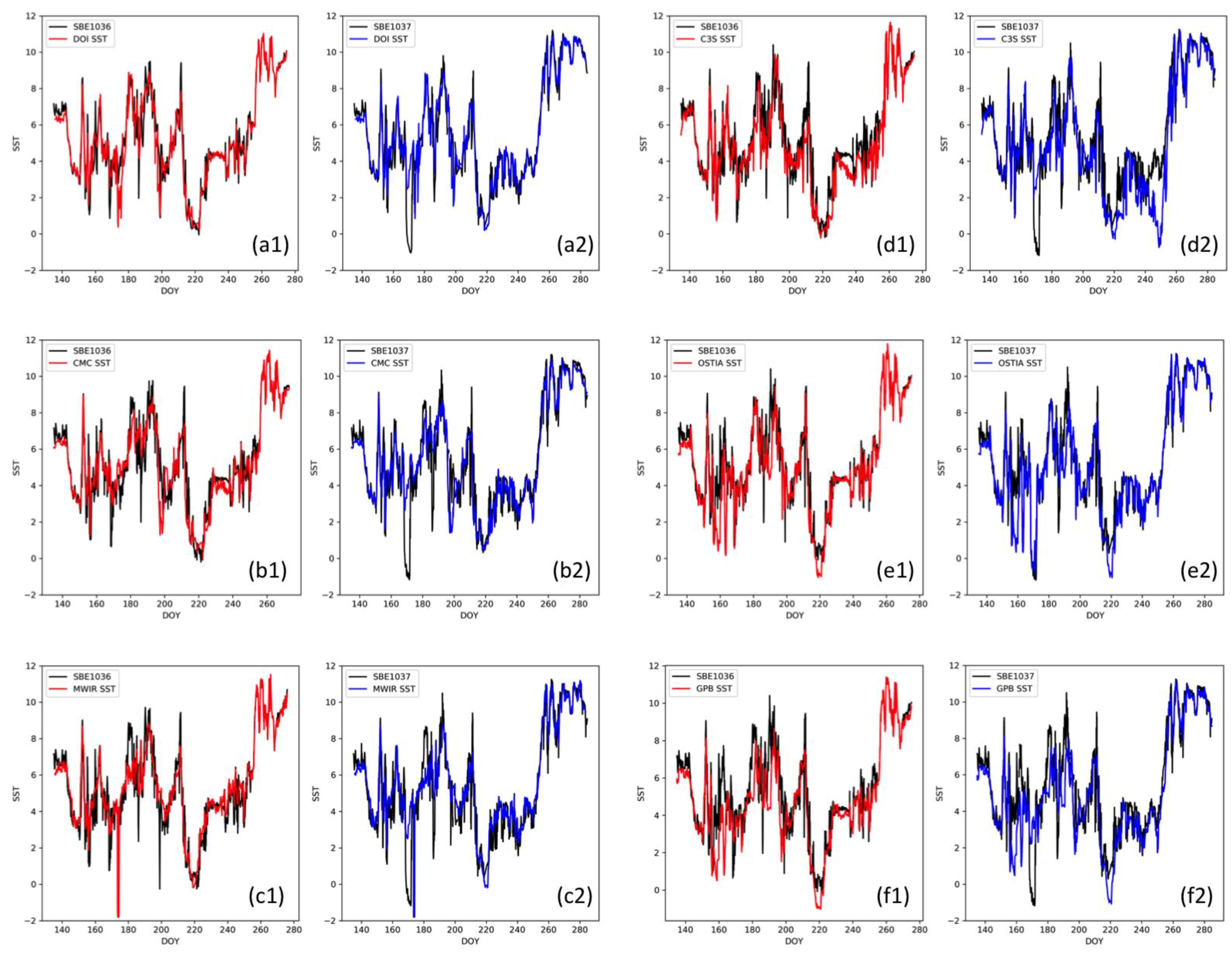
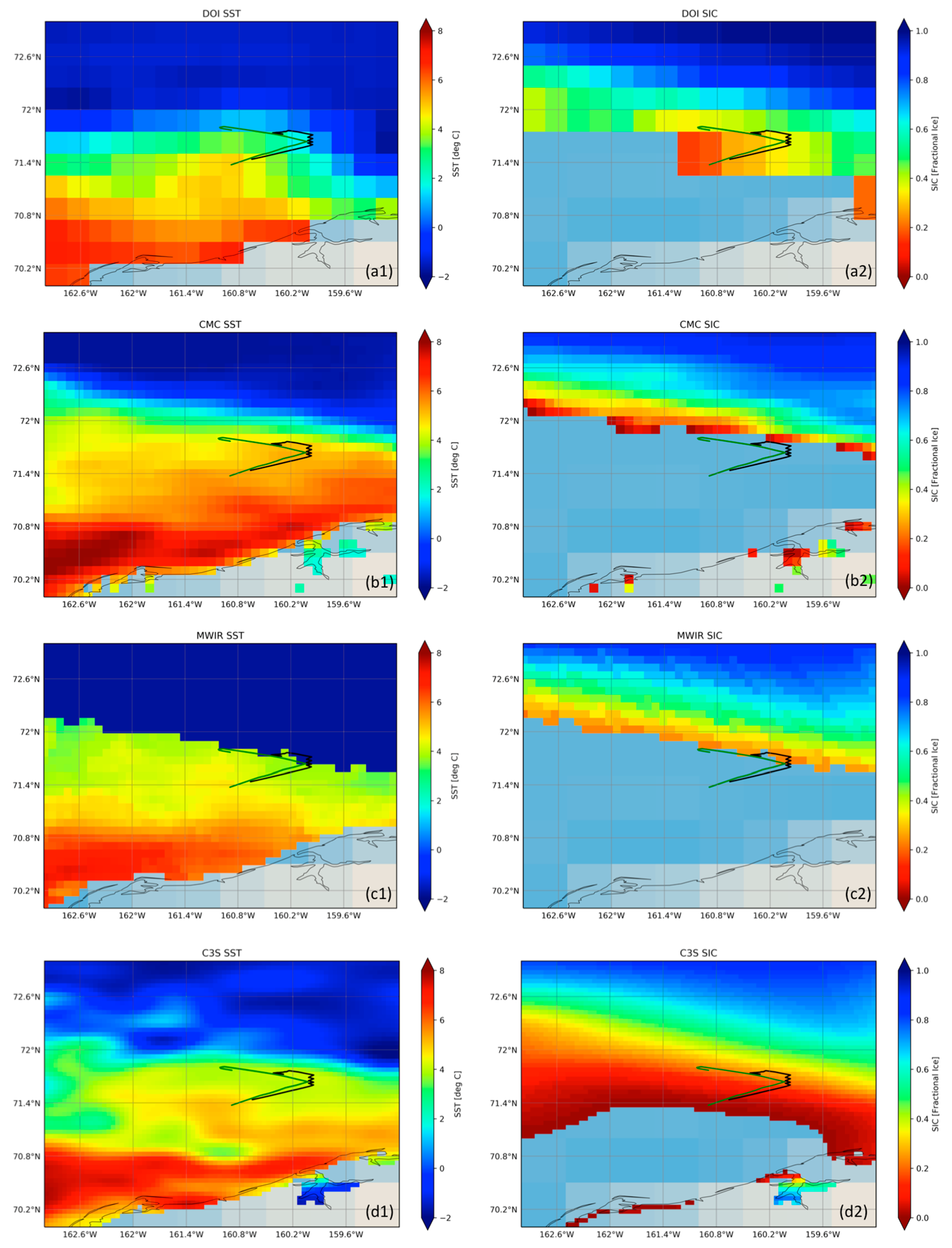
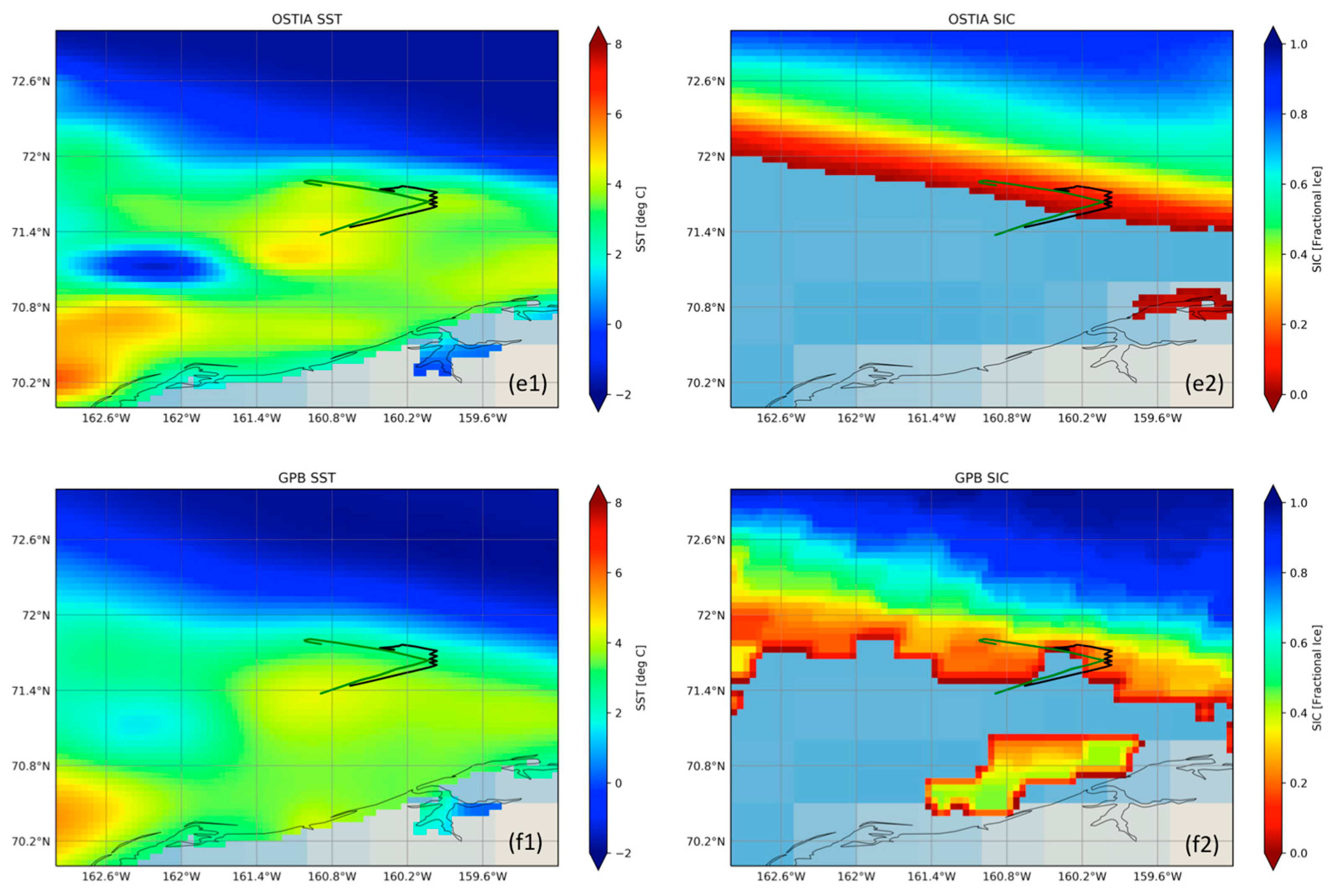
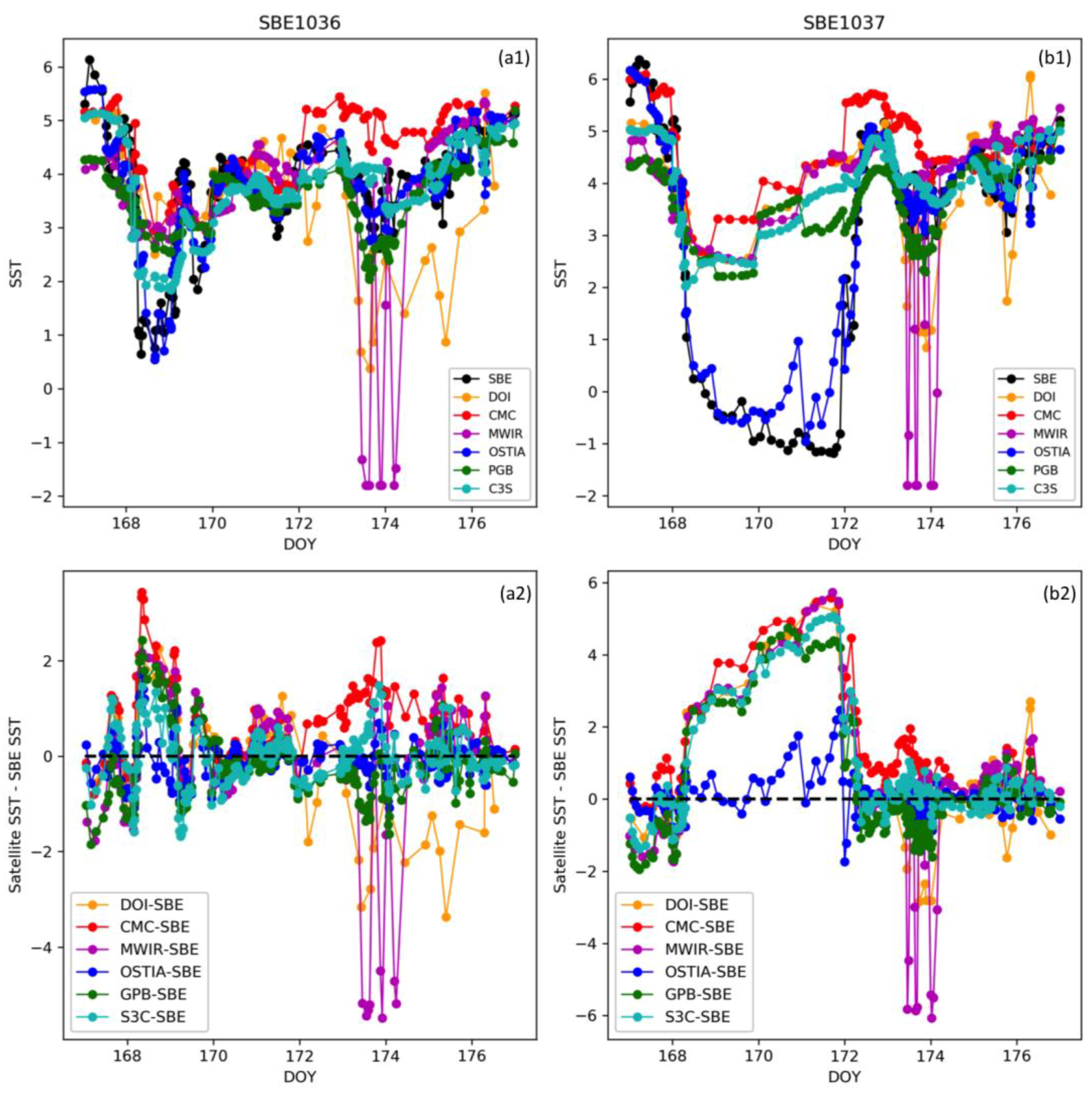
3.1. Near-Ice Comparison of L4 SST and SIC Combinations against Saildrones
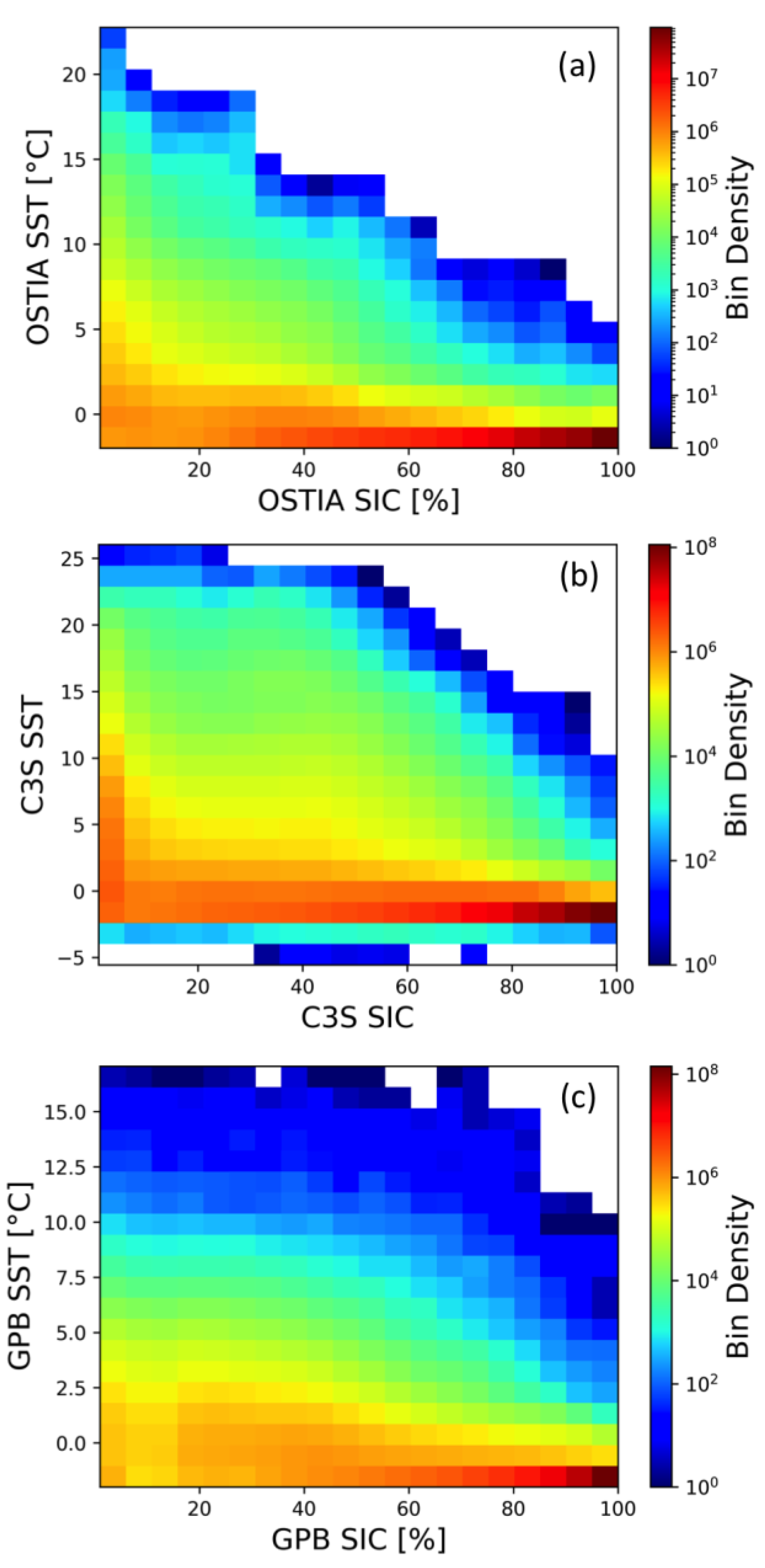
3.2. SST vs. SIC Interdependence in Mixed Water Ice Pixels of Gridded Satellite Products
3.3. Evaluation of the SST/SIC Interdependence in Mixed Water/Ice Pixels
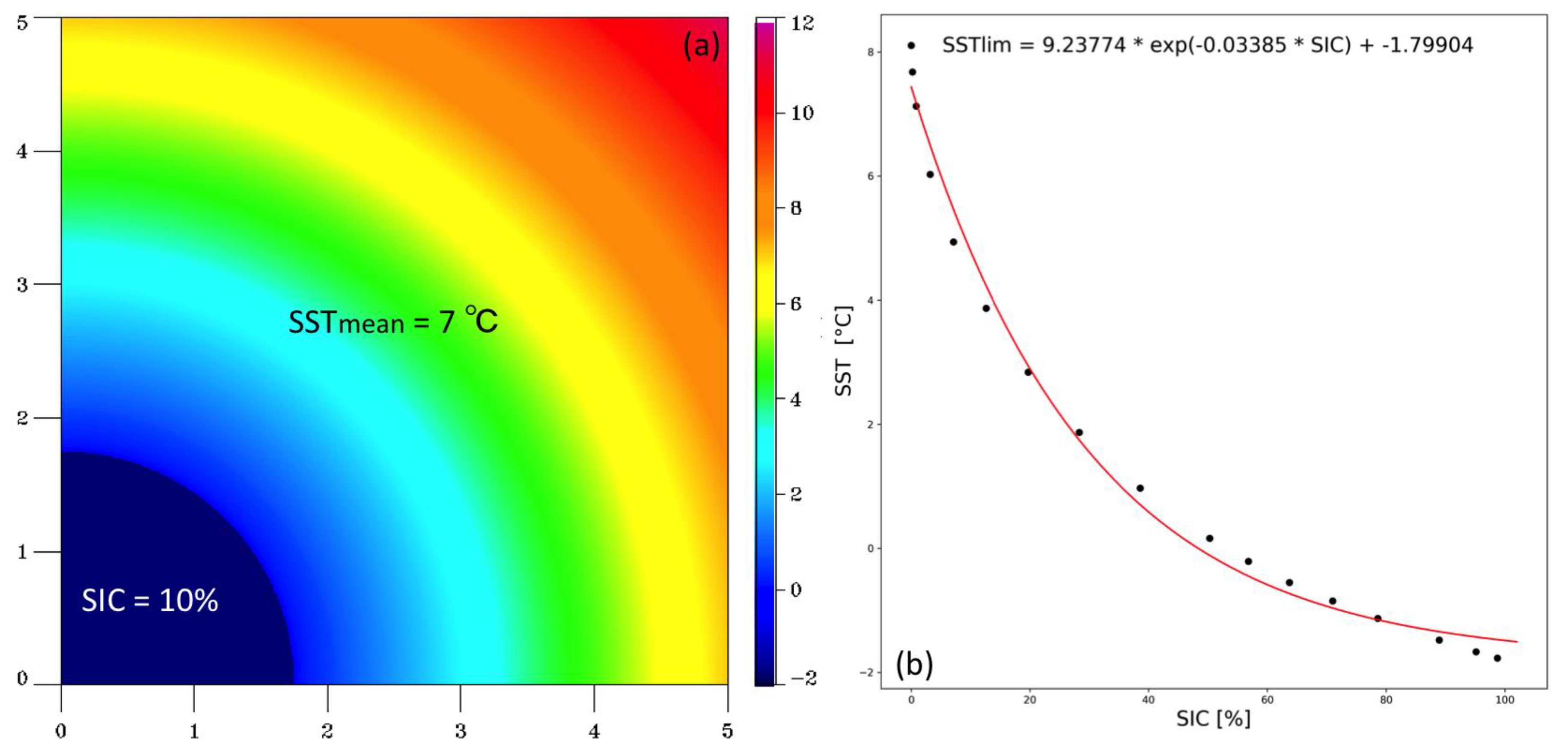
3.3.1. Theoretical Basis
3.3.2. Simulation Experiment
3.3.3. Initial Application of the of the SSTlim as a Post-Processing Joint (SST, SIC) Filter
3.3.4. Sensitivity of SSTlim to Specified Parameters
3.3.5. Further Evaluation of the Impact of the SSTlim Filter
4. Discussion and Conclusions
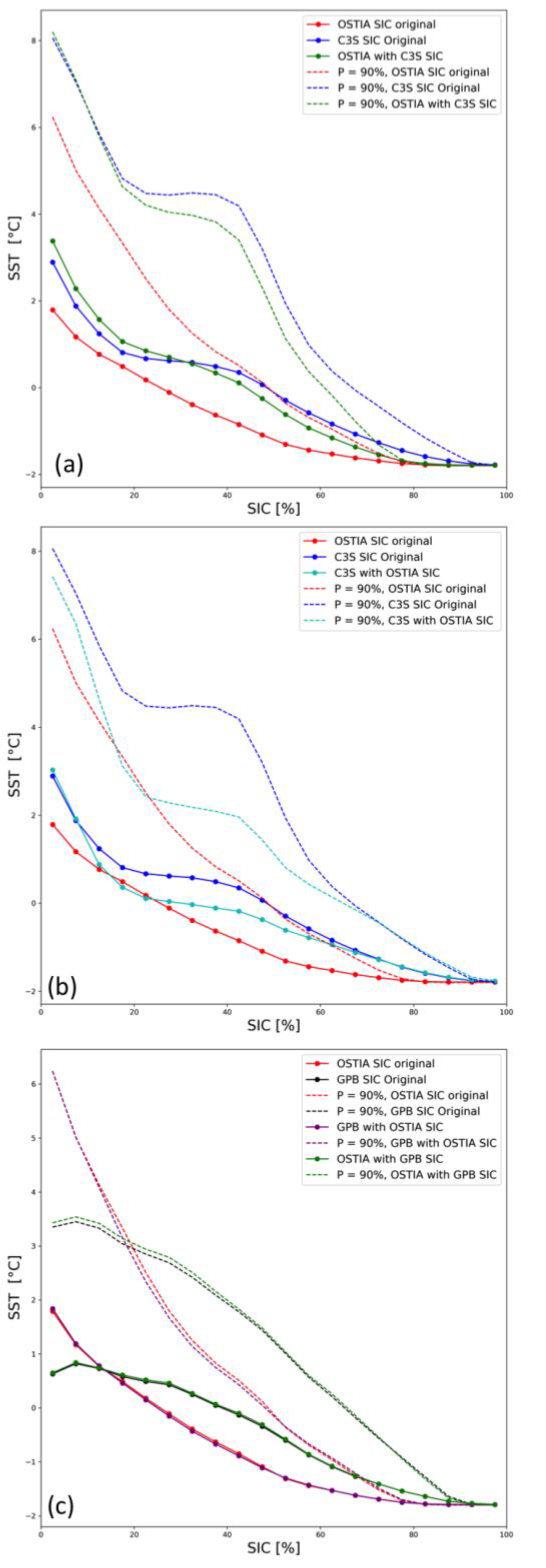
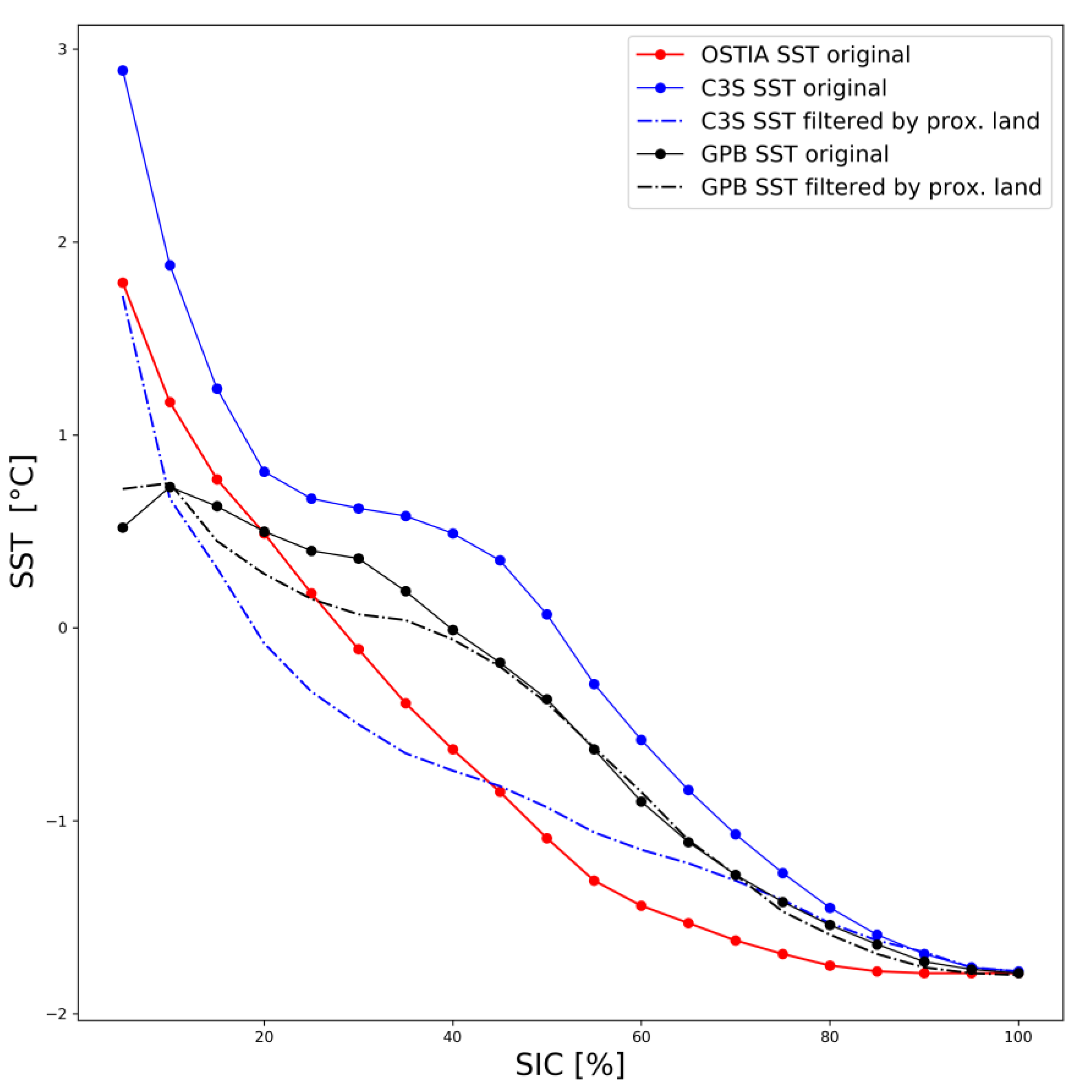
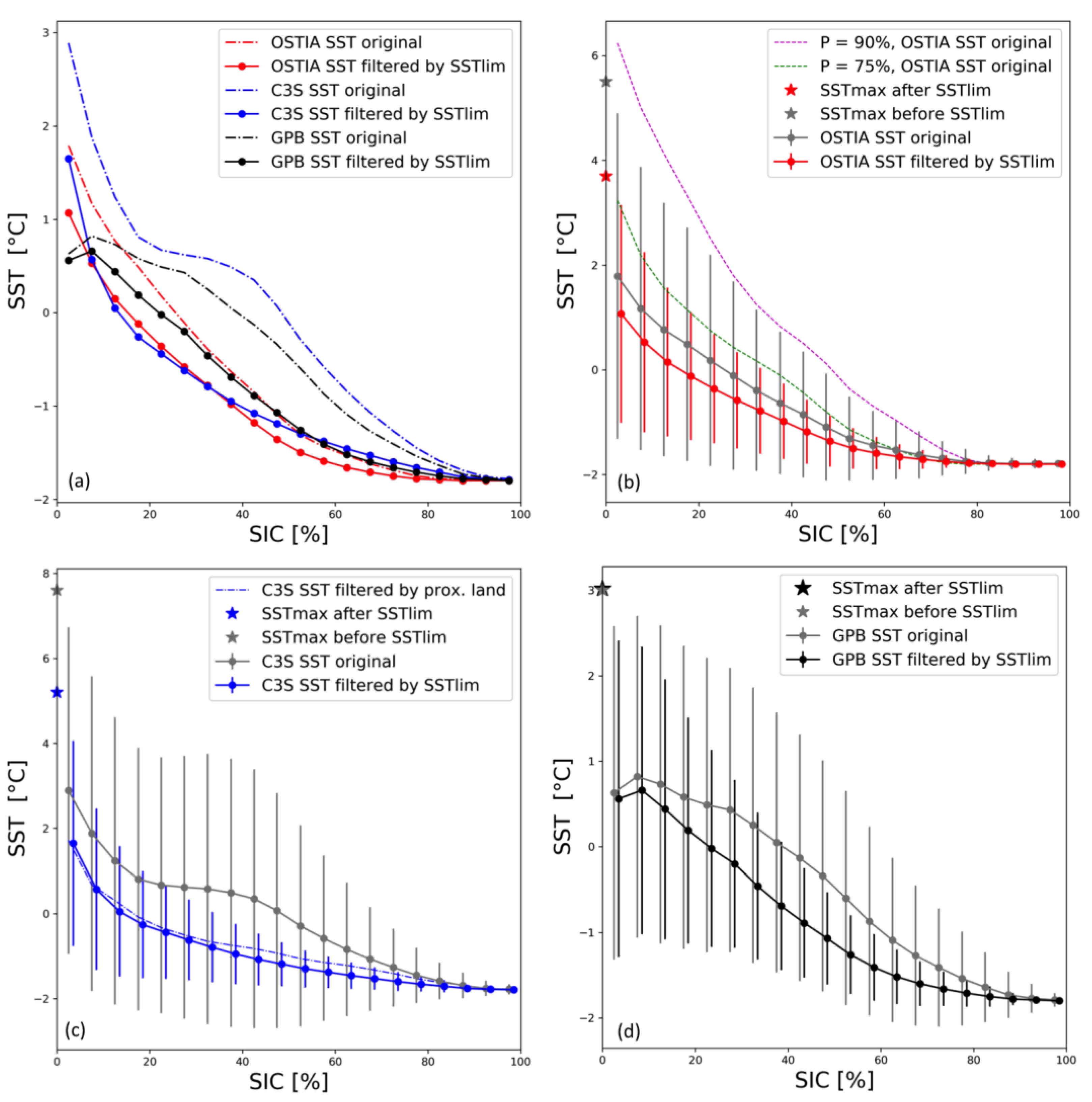
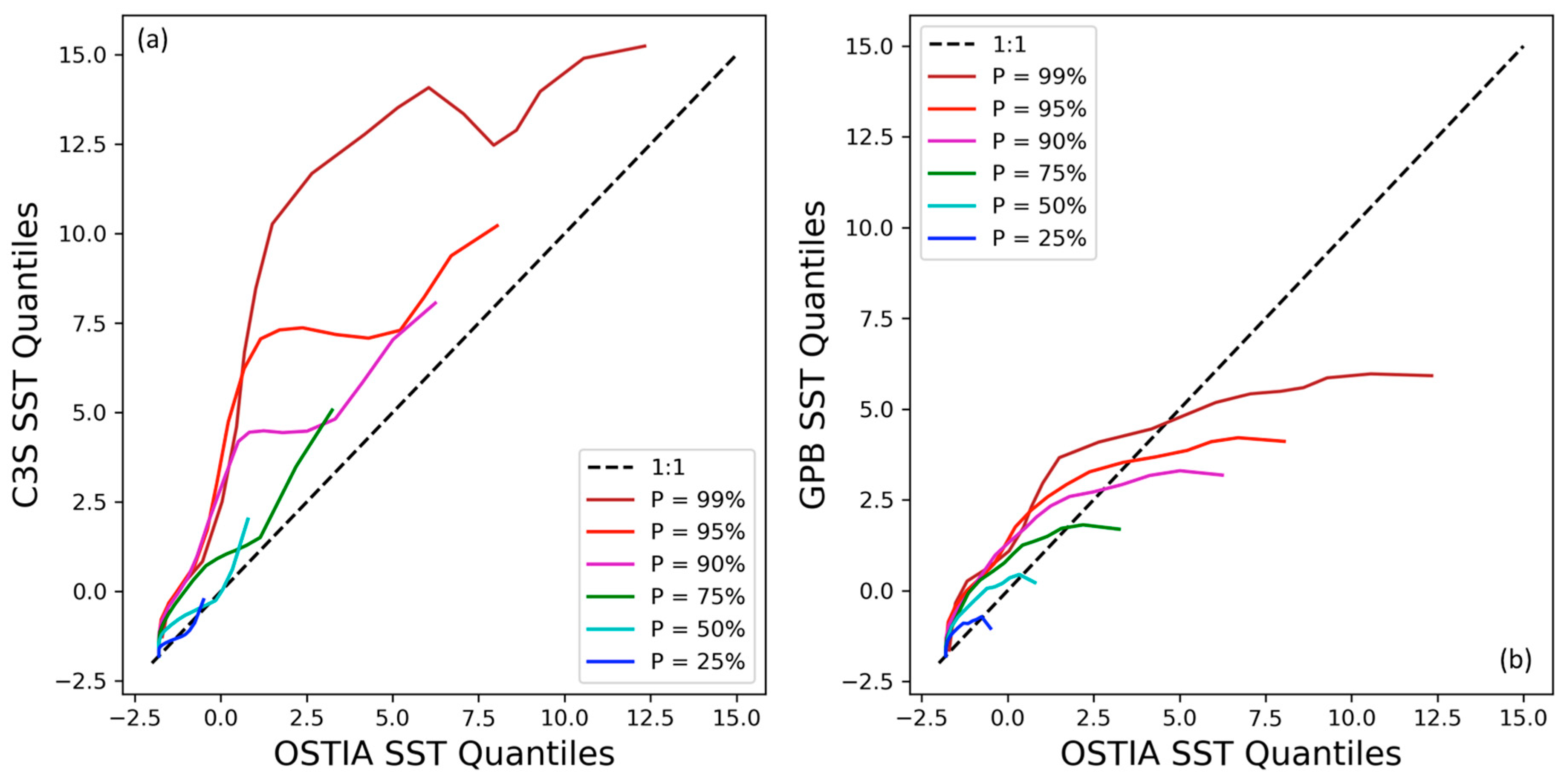
- The OSTIA SST vs. SIC interdependence appears to be exponential in nature with maximum SST of 6 °C for mixed pixels with very low ice concentrations (the maximum SST corresponds to a spatial average). We took the exponential shape of the OSTIA SST/SIC interdependence to be the model for mixed water/ice pixels, a fact later confirmed via numerical simulations;
- The C3S SSTs also appear to be exponential, with an SSTmax of 9 °C. The unfiltered SSTs appear to have a bump for 40–70%-SIC. This bump is artificially introduced into the OSTIA SST/SIC interdependence when the curve is reevaluated after switching the OSTIA SIC product with the C3S SIC product. When the C3S SIC is substituted by the OSTIA SIC, the bump is significantly reduced from the C3S SST/SIC curve, but not entirely eliminated, suggesting that the source of the errors introducing the bump affects both the C3S SST and corresponding SIC, but it affects the SSTs to a lesser degree. Further filtering of the C3S SSTs based on proximity to land suggests that the bump in C3S SST = f (SIC) is reduced by applying a more stringent filter for land contamination; and
- The GPB SST/SIC curve is significantly below the other two with a maximum SST of 3 °C for SIC ≈ 0%. This appears to be the result of the very restrictive open-water filter used by NCEP that eliminates all SIC retrievals with SST ≥ 2.15 °C. Furthermore, the curve has a different shape than the other two. The proximity-to-land filter has a minor impact on the shape of the SST/SIC distribution for the GPB product, most likely because the NCEP ice product only retrieves concentrations that are more than 100 km from land. The SIC used in this product combination, however, appears to be affected by grid projection errors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| ABI | Advanced Baseline Imager on the new generation of GOES R-Series (GOES-R) satellites. First ABI was launched on GOES16 (GOES-EAST-Atlantic Ocean) |
| ACSPO | NOAA/NESDIS/STAR Advanced Clear-Sky Processor for Oceans system |
| AVHRR | Advanced Very High Resolution Radiometer. This sensor is deployed on the NOAA and the MetOp series of satellites. |
| AMSR-E | Advanced Microwave Scanning Radiometer |
| AMSR2 | Advanced Microwave Scanning Radiometer 2 on the polar orbiting GCOM-W satellite. |
| ATBD | Algorithm Theoretical Basis Document |
| CCI | ESA’s Climate Change Initiative |
| CFSR | NCEP Climate Forecast System Reanalysis |
| CLASS | NCDC Comprehensive Large Array-data Stewardship System |
| CMEMS | Copernicus Marine Environment Monitoring Service; marine.copernicus.eu (accessed on 22 April 2023) |
| C3S | Copernicus Climate Change Service project SST |
| DMI | Danish Meteorological Institute |
| DMSP-F18 | US Defense Meteorological Satellite Program |
| ECMWF | European Centre for Medium-range Weather Forecasts |
| EMC | NOAA/NCEP Environmental Modeling Center |
| ESA | European Space agency |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites |
| GCOM-W | Global Change Observation Mission-Water satellite |
| GHRSST | Group for High Resolution Sea Surface Temperature |
| GMI | GPM Microwave Imager |
| GOES | NOAA Geostationary Operational Environmental Satellites, East (GOES16) and West (GOES15) |
| GPM | Global Precipitation Measurement satellite |
| GTS | WMO Global Telecommunications System |
| L2P | Level 2 Preprocessed. Refers to satellite retrievals in swath coordinates (orbit view). |
| L3U | Level 3 Uncollated. Refers to L2P data from an individual sensor remapped onto a regular grid. |
| L3C | Level 3 Collated. Refers to the daily combination of multiple L3U. |
| L4 | Level 4. Interpolated, spatially complete, gridded data. Lower level data from multiple sensors are merged via a data assimilation scheme and interpolated to fill gaps; also known as analyzed data. |
| Met Office | UK National Meteorological service; https://www.metoffice.gov.uk/ |
| MetOp A and B | EUMETSAT Meteorological Operational satellites A and B |
| MMAB | NOAA/NCEP/EMC Marine Modeling and Analysis Branch |
| MSG | EUMETSAT METEOSAT Second Generation geostationary orbiting satellite |
| NAVO | US Naval Oceanographic Office (NAVOCEANO); https://www.metoc.navy.mil/navo/ |
| NASA | US National Aeronautics and Space Administration |
| NESDIS | NOAA National Environmental Satellite Data and Information Service |
| NCDC | NOAA National Climatic Data Center |
| NCEI | NOAA/NCEP National Centers for Environmental Information; ncei.noaa.gov |
| NCEP | NOAA National Weather Service’s National Centers for Environmental Prediction |
| NIC | National Ice Center |
| NOAA | US National Oceanic and Atmospheric Administration |
| NPI | GOES N-P Imager on GOES15. SSTs computed with far-IR channels |
| OISST | NOAA/NCEP Optimal Interpolation Sea Surface Temperature analysis |
| OSI-SAF | EUMETSAT Ocean and Sea Ice Satellite Application Facility |
| OSPO | NOAA Office of Satellite and Product Operations |
| OSTIA | Met Office’s Operational Sea Surface Temperature and Sea Ice Analysis |
| PO.DAAC | NASA Physical Oceanography Distributed Active Archived Center |
| POES | NOAA Polar-orbiting Operational Environmental Satellites |
| REMSS | Remote Sensing Systems; www.remss.com |
| SAR | Synthetic Aperture Radar |
| SEVIRI | Spinning Enhanced Visible and Infrared Imager aboard the MSG satellites |
| SLSTR | Sea and Land Surface Temperature Radiometers on the polar orbiting Sentinel 3 (A and B) satellites. |
| SNPP | NOAA-NASA Suomi-National Polar Orbiting Partnership |
| STAR | NOAA/NESDIS Center for Satellite Applications and Research |
| SMMR | Scanning Multichannel Microwave Radiometer |
| SSMI | Special Sensor Microwave Imager |
| SSMI/S | Special Sensor Microwave Imager/Sounder on DMSP-F18 |
| VIIRS | Visible Infrared Imager Radiometer Suite. This sensor is deployed on the NOAA-20 and the SNPP satellite series. |
References
- Castro, S. Sea Surface Temperature Metrics for Evaluating OSI SAF Sea Ice Concentration Products, OSI SAF Visiting Scientist Program Report, OSI_AS19_04. October 2019, p. 67. Available online: https://osi-saf.eumetsat.int/sites/osi-saf.eumetsat.int/files/inline-files/OSI_VS19_04_DMI_VS_final_report_castro.pdf (accessed on 27 February 2023).
- Hurrell, J.W.; Hack, J.J.; Shea, D.; Caron, J.M.; Rosinski, J. A New Sea surface Temperature and Sea Ice Boundary Dataset for the community Atmosphere Model. J. Clim. 2008, 21, 5145–5153. [Google Scholar] [CrossRef]
- Ivanova, N.; Pedersen, L.T.; Tonboe, R.T.; Kern, S.; Heygster, G.; Lavergne, T.; Sørensen, A.; Saldo, R.; Dybkjær, G.; Brucker, L.; et al. Inter-comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations. Cryosphere 2015, 9, 1797–1817. [Google Scholar] [CrossRef] [Green Version]
- Lavergne, T.; Sørensen, A.M.; Kern, S.; Tonboe, R.; Notz, D.; Aaboe, S.; Bell, L.; Dybkjær, G.; Eastwood, S.; Gabarro, C.; et al. Version 2 of the EUMETSAT OSI SAF and ESA CCI sea-ice concentration climate data records. Cryosphere 2019, 13, 49–78. [Google Scholar] [CrossRef] [Green Version]
- Andersen, S.; Tonboe, R.; Kern, S.; Schyberg, H. Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using Numerical Weather Prediction model fields: An intercomparison of nine algorithms. Remote Sens. Environ. 2006, 104, 374–392. [Google Scholar] [CrossRef]
- Hwang, B.J.; Barber, D.J. Pixel-scale evaluation of SSM/I sea-ice algorithms in the marginal ice zone during early fall freeze-up. Hydrol. Process. 2006, 20, 1909–1927. [Google Scholar] [CrossRef]
- Tonboe, R.T.; Nandad, V.; Mäkynen, M.; Pederson, L.-T.; Kern, S.; Lavergne, T.; Øelund, J.; Dybkjær, G.; Saldo, R.; Huntemann, M. Simulated Geophysical Noise in Sea Ice Concentration Eestimates of Open Water and Snow-covered Sea Ice. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 15, 1309–1326. [Google Scholar] [CrossRef]
- Gloersen, P.; Cavalieri, D.J. Reduction of weather effects in the calculation of sea ice concentration from microwave radiances. J. Geophys. Res. 1986, 91, 3913–3919. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Crawford, J.P.; Drinkwater, M.R.; Emery, W.J.; Eppler, D.T.; Farmer, L.D.; Fowler, C.W.; Goodberlet, M.; Jentz, R.R.; Milman, A.; et al. NASA Sea Ice Validation Program for the Defense Meteorological Satellite Program Special Sensor Microwave Imager: Final Report. NASA-TM-104559 1992. National Aeronautics and Space Administration, Goddard Space Flight Center, Greenbelt, MD, 1992. p. 126. Available online: https://ntrs.nasa.gov/api/citations/19920015007 (accessed on 24 February 2023).
- Lavergne, T.; Tonboe, R.; Lavelle, J.; Eastwood, S. Algorithm Theoretical Basis Document for the OSI SAF Global Sea Ice Concentration Climate Data Record, OSI-450, OSI-430-b, Version 1.2, 14 March 2019, EUMETSAT Ocean and Sea Ice SAF High Latitude Processing Centre. 2019. Available online: https://osisaf-hl.met.no/sites/osisaf-hl/files/baseline_document/osisaf_cdop3_ss2_atbd_sea-ice-conc-climate-data-record_v1p2.pdf (accessed on 28 February 2023).
- Maaß, N.; Kalescke, L. Improving passive microwave sea ice concentration algorithms for coastal areas: Applications to the Baltic Sea. Tellus A 2010, 62, 393–410. [Google Scholar] [CrossRef] [Green Version]
- Parkinson, C.L.; Comiso, J.C.; Zwally, H.J.; Cavalieri, D.J.; Gloersen, P.; Campbell, W.J. Arctic Sea Ice, 1973–1976: Satellite Passive-Microwave Observations; NASA-SP-489 1987, National Aeronautics and Space Administration, Scientific and Technical Information Branch, Washington, DC. Available online: https://ntrs.nasa.gov/citations/19870015437 (accessed on 24 February 2023).
- Markus, T.; Cavalieri, D.J. The AMSR-E NT2 sea ice concentration algorithm: Its basis and implementation. J. Remote Sens. Soc. Jpn. 2009, 29, 216–225. [Google Scholar] [CrossRef]
- Meier, W.N.; Stroeve, J.; Fetterer, F.; Savoie, M.; Wilcox, H. Polar Stereographic Valid Ice Masks Derived from National Ice Center Monthly Sea Ice Climatologies, Version 1. User Guide. Boulder, CO, 2015, NASA National Snow and Ice Data Center Distributed Active Archive Center. Available online: https://doi.org/10.5067/M4PUJAQRI2DS (accessed on 24 February 2023).
- Grumbine, R.W. A Posteriori Filtering of Sea Ice Concentration Analyses. NOAA/NWS/NCEP/EMC MMAB Tech. Note 282. 2009; p. 7. Available online: https://polar.ncep.noaa.gov/mmab/papers/tn282/posteriori.pdf (accessed on 27 February 2023).
- Thiebaux, J.; Rogers, E.; Wang, W.; Katz, B. A New High-Resolution Blended Real-Time Global Sea Surface Temperature Analysis. Bull. Am. Meteor. Soc. 2003, 84, 645–656. [Google Scholar] [CrossRef] [Green Version]
- Baordo, F.; Vargas, L.F.; Howe, E. OSI SAF Product User Manual for Global Sea Ice Concentration Level 2 and Level 3, OSI-410-a, OSI-401-d, OSI-408-a. Version 1, 1/11/2022. Available online: https://osisaf-hl.met.no/sites/osisaf-hl/files/user_manuals/osisaf_pum_ice-conc_l2-3_v1p0.pdf (accessed on 8 March 2023).
- Nielsen-Englyst, P.; Høyer, J.L.; Kolbe, W.M.; Dybkjær, G.; Lavergne, T.; Tonboe, R.T.; Skarpalezoz, S.; Karagali, I. A combined sea and sea-ice surface temperature climate dataset of the Arctic, 1982–2021. Remote Sens. Environ. 2023, 284, 113331. [Google Scholar] [CrossRef]
- Castro, S.L.; Wick, G.A.; Steele, M. Validation of satellite sea surface temperature analyses in the Beaufort Sea using UpTempO buoys. Remote Sens. Environ. 2016, 187, 458–475. [Google Scholar] [CrossRef]
- Brasnett, B. The impact of satellite retrievals in a global sea-surface-temperature analysis. Q. R. Meteorol. Soc. 2008, 134, 1745–1760. [Google Scholar] [CrossRef]
- Caya, A.; Buehner, M.; Carrieres, T. Analysis and Forecasting of Sea Ice Conditions with Three-Dimensional Variational Data Assimilation and a Coupled Ice-Ocean Model. J. Atmos. Oceanic Technol. 2010, 27, 353–369. [Google Scholar] [CrossRef]
- GHRSST Science Team. The Recommended GHRSST Data Specification (GDS) 2.0, Document Revision 5; Available from the GHRSST International Project Office; 2012; p. 123. Available online: https://podaactools.jpl.nasa.gov/drive/files/OceanTemperature/ghrsst/docs/GDS20r5.pdf (accessed on 24 February 2023).
- Wick, G.A.; Jackson, D.L.; Castro, S.L. Assessing the ability of satellites to resolve spatial sea surface temperature variability-The Northwest Tropical Atlantic ATOMIC Region. Remote Sens. Environ. 2023, 284, 113377. [Google Scholar] [CrossRef]
- Vasquez-Cuervo, J.; Castro, S.L.; Steele, M.; Gentemann, C.; Gomez-Valdes, J.; Tang, W. Comparison of GHRSST SST Analysis in the Arctic Ocean and Alaskan Coastal Waters Using Saildrones. Remote Sens. 2022, 14, 692. [Google Scholar] [CrossRef]
- Good, S.; Fiedler, E.; Mao, C.; Martin, M.J.; Maycock, A.; Reid, R.; Robert-Jones, J.; Searle, T.; Waters, J.; While, J.; et al. The Current Configuration of the OSTIA System for Operational Production of Foundation Sea Surface Temperature and Ice Concentration Analyses. Remote Sens. 2020, 12, 720. [Google Scholar] [CrossRef] [Green Version]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Mogensen, K.S.; Alonso-Balmaseda, M.; Weaver, A. The NEMOVAR Ocean Data Assimilation System as Implemented in the ECMWF Ocean Analysis for System 4. ECMWF Tech. Memorandum 668, 2012, p. 59. ECMWF, Reading, UK. Available online: https://www.ecmwf.int/en/elibrary/75708-nemovar-ocean-data-assimilation-system-implemented-ecmwf-ocean-analysis-system-4 (accessed on 28 February 2023).
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily High-Resolution-Blended Analyses for Sea Surface Temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Tonboe, R.; Lavelle, J.; Pfiffer, R.-H.; Howe, E. Product User Manual for OSI SAF Global Sea Ice Concentration, Product OSI-401-b, Version 1.6. Tech. Rep. SAF/OSI/COP3/DMI_MET/TEC/MA/204. Danish Meteorological Institute. 2017, p. 25. Available online: https://osisaf-hl.met.no/sites/osisaf-hl/files/user_manuals/osisaf_cdop3_ss2_pum_ice-conc_v1p6.pdf (accessed on 28 February 2023).
- Robert-Jones, J.; Bovis, K.; Matthew, M.J.; McLaren, A. Estimating background error covariance parameters and assessing their impact in the OSTIA system. Remote Sens. Environ. 2016, 176, 117–138. [Google Scholar] [CrossRef]
- Fiedler, E.K.; Mao, C.; Good, S.A.; Waters, J.; Martin, M.J. Improvements to feature resolution in the OSTIA sea surface temperature analysis using the NEMOVAR assimilation scheme. Q. J. R. Meteorol. Soc. 2019, 145, 3609–3625. [Google Scholar] [CrossRef]
- Mirouze, I.; Blockley, E.W.; Lea, D.J.; Martin, M.J.; Bell, M.J. A multiple length scale correlation operator for ocean data assimilation. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 29744. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; Embury, O.; Roberts-Jones, J.; Fiedler, E.; Bulgin, C.E.; Corlett, G.K.; Good, S.; McLaren, A.; Rayner, N.; Morak-Bozzo, S.; et al. Sea surface temperature datasets for climate applications from Phase 1 of the European Space Agency Climate Change Initiative (SST CCI). Geosci. Data J. 2014, 1, 179–191. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite-based time-series of sea-surface temperature since 1981 for climate applications. Sci. Data 2019, 6, 223. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; The CCI SST Team. SST-CCI-Phase-II, SST CCI Algorithm Theoretical Basis Document (v2 Reprocessing). SST_CCI-ATBD-UOR-203, Issue 3. 6 May 2019. Available online: https://climate.esa.int/media/documents/SST_cci_ATBD_UOR_v3.pdf (accessed on 28 February 2023).
- Lu, J.; Heygster, G.; Spreen, G. Atmospheric correction of sea ice concentration retrievals for 89 GHz AMSR-E observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 5. [Google Scholar] [CrossRef]
- Maturi, E.; Harris, A.; Mittaz, J.; Sapper, J.; Wick, G.; Zhu, X.; Dash, P.; Koner, P. A New High-Resolution Sea Surface Temperature Blended Analysis. Bull. Am. Meteor. Soc. 2017, 98, 1015–1026. [Google Scholar] [CrossRef]
- Liu, G.; Heron, S.F.; Eakin, C.M.; Muller-Karger, F.E.; Vega-Rodriguez, M.; Guild, L.S.; De La Cour, J.L.; Geiger, E.F.; Skirving, W.J.; Burgess, T.F.R.; et al. Reef-Scale Thermal Stress Monitoring of Coral Ecosystems: New 5-km Global Products from NOAA Coral Reef Watch. Remote Sens. 2014, 6, 11579–11606. [Google Scholar] [CrossRef] [Green Version]
- Grumbine, R.W. Automated Sea Ice Concentration Analysis History at NCEP: 1996–2012. NOAA/NWS/NCEP/EMC MMAB Tech. Note 321. 2014; p. 39. Available online: https://polar.ncep.noaa.gov/mmab/papers/tn321/MMAB_321.pdf (accessed on 27 February 2023).
- Gemmill, W.; Katz, B.; Li, X. Daily Real-Time, Global Sea Surface Temperature High-Resolution Analysis: RTG_SST_HR. NOAA/NWS/NCEP/EMC/MMAB Tech. Note 260. 2007; p. 22. Available online: http://polar.ncep.noaa.gov/mmab/papers/tn260/MMAB260.pdf (accessed on 27 February 2023).
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.-M. Improvements of the Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Banzon, V.; Smith, T.M.; Chin, T.M.; Liu, C.; Hankins, W. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling, and environmental studies. Earth Syst. Sci. Data 2016, 8, 165–176. [Google Scholar] [CrossRef] [Green Version]
- Banzon, V.; Smith, T.M.; Steele, M.; Huang, B.; Zhang, H.-M. Improved Estimation of Proxy Sea Surface Temperature in the Arctic. J. Atmos. Oceanic Technol. 2020, 37, 341–349. [Google Scholar] [CrossRef]
- Brasnett, B.; Surcel-Colan, D. Assimilating Retrievals of Sea Surface Temperature from VIIRS and AMSR2. J. Atmos. Ocean. Technol. 2016, 33, 361–375. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 2003, 108, 4407. [Google Scholar] [CrossRef] [Green Version]
- Buehner, M.; Caya, A.; Pogson, L.; Carrieres, T.; Pestieau, P. A New Environment Canada Regional Ice Analysis System. Atmos. Ocean 2013, 51, 18–34. [Google Scholar] [CrossRef]
- Halliday, D.; Resnick, R. Fundamentals of Physics; Wiley: Hoboken, NJ, USA, 1974; p. 827. [Google Scholar]
- Charron, M.; Polavarapu, S.; Buehner, M.; Vaillancourt, P.A.; Charette, C.; Roch, M.; Morneau, J.; Garand, L.; Aparicio, J.M.; MacPherson, S.; et al. The Stratospheric Extension of the Canadian Global Deterministic Medium-Range Weather Forecasting System and Its Impact on Tropospheric Forecasts. Mon. Weather Rev. 2012, 140, 1924–1944. [Google Scholar] [CrossRef]
- Lavelle, J.; Tonboe, R.; Tian, T.; Pfeiffer, R.-H.; Howe, E. Product User Manual for the OSI SAF AMSR-2 Global Sea Ice Concentration, Product OSI-408, Version 1.1. Tech. Rep. SAF/OSI/COP2/DMI/TEC/265. The Danish Meteorological Institute. 2016, p. 28. Available online: https://osisaf-hl.met.no/sites/osisaf-hl/files/user_manuals/osisaf_cdop2_ss2_pum_amsr2-ice-conc_v1p1.pdf (accessed on 1 March 2023).
- Gentemann, C.L.; Scott, J.P.; Mazzini, P.L.F.; Pianca, C.; Akella, S.; Minnett, P.J.; Cornillon, P.; Fox-Kemper, B.; Cetinic, I.; Chin, T.M.; et al. Saildrone: Adaptively Sampling the Marine Environment. Bull. Am. Meteorol. Soc. 2020, 101, 744–762. [Google Scholar] [CrossRef] [Green Version]
- Chiodi, A.M.; Zhang, C.; Cokelet, E.D.; Yang, Q.; Mordy, C.W.; Gentemann, G.; Cross, J.N.; Lawrence-Slavas, N.; Meining, C.; Steele, M.; et al. Exploring the Pacific Arctic Seasonal Ice Zone with Saildrone USVs. Front. Mar. Sci. 2021, 8, 640690. [Google Scholar] [CrossRef]
- May, D.A.; Parmeter, M.M.; Olszewski, D.S.; McKenzie, B.D. Operational Processing of Satellite Sea Surface Temperature Retrievals at the Naval Oceanographic Office. Bull. Am. Meteor. Soc. 1998, 79, 397–407. [Google Scholar] [CrossRef]
- Richter-Menge, J.; Perovich, D.K.; Pegau, W.S. Summer ice dynamics during SHEBA and its effect on the ocean heat content. Ann. Glaciol. 2001, 33, 201–206. [Google Scholar] [CrossRef] [Green Version]
- Perovich, D.K.; Maykut, G.A. Solar heating of a stratified ocean in the presence of a static ice cover. J. Geophys. Res. 1990, 95, 18233–18245. [Google Scholar] [CrossRef]
- Perovich, D.K.; Tucker, W.B., III; Ligett, K.A. Aerial observations of the evolution of ice surface conditions during summer. J. Geophys. Res. 2002, 107, 8048. [Google Scholar] [CrossRef]






| L4 SST | SST Res (km) | SST Forcing | L4 SIC | SIC Res (km) | SIC Forcing |
|---|---|---|---|---|---|
| UK MetOffice OSTIA SST v.3.2 | 5 | IR_LEO IR_GEO MW In situ | UK Met Office OSTIA SIC v.3.2 | 5 | OSI-401-b (SSMIS) NOAA/NCEP (lakes) |
| ESA C3S C3S SST v.2.0 | 5 | IR_LEO | EUMETSAT OSI SAF OSI-430-b (complements OSI-450) | 25 | SSMIS (19, 37 GHz) |
| NOAA/NESDIS GPB v.1.0 | 5 | IR_LEO IR_GEO | NOAA/NCEP Global 1/12° | ~9 | SSMIS AMSR2 (85, 89 GHz) |
| NOAA/NESDIS DOISST v.2.1 | 25 | IR_LEO In situ | NOAA/NCEP Global 1/2° | 50 | SSM/IS AMSR2 (85, 89 GHz) |
| CMC CMC SST v.3.0 | 10 | IR_LEO MW In situ CMC SIC | CMC CMC SIC v.3.0 | 5 | SSM/I AMSR-E RADARSAT Ice Charts |
| REMSS MWIR v.05.0 | ~9 | IR_LEO MW | EUMETSAT OSI-SAF OSI-408 | 10 | AMSR2 (19, 37 GHz) |
| SSTmin = 0 °C | SSTmax = 3 °C | ||||
|---|---|---|---|---|---|
| Grid Res (km) | SSTmax (°C) | Gradient (K km−1) | Grid Res (km) | SSTmin (°C) | Gradient (K km−1) |
| 5 | 0.83 | 0.22 | 5 | −1.8 | 1.275 |
| 5 | 2 | 0.54 | 25 | −1.8 | 0.255 |
| 5 | 4 | 1.06 | 5 | 0 | 0.8 |
| 5 | 8 | 2.15 | 10 | 0 | 0.4 |
| 5 | 10 | 2.66 | 15 | 0 | 0.27 |
| 5 | 15 | 4.0 | 20 | 0 | 0.2 |
| 5 | 20 | 5.31 | 25 | 0 | 0.16 |
| Analysis | Region | Count | Mean | Median | SD | MAD | RMS | RRMS |
|---|---|---|---|---|---|---|---|---|
| OSTIA | OO | 7801 | −0.24 | −0.06 | 0.87 | 0.29 | 0.81 | 0.43 |
| MIZ | 96 | −0.13 | −0.11 | 0.33 | 0.30 | 0.13 | 0.46 | |
| MIZfilter | 80 | −0.10 | −0.11 | 0.31 | 0.28 | 0.10 | 0.41 | |
| C3S | OO | 7393 | −0.62 | −0.38 | 1.10 | 0.74 | 1.58 | 1.09 |
| MIZ | 504 | −0.44 | −0.24 | 0.80 | 0.63 | 0.83 | 0.93 | |
| MIZfilter | 420 | −0.53 | −0.34 | 0.79 | 0.62 | 0.91 | 0.91 | |
| GPB | OO | 7559 | −0.39 | −0.24 | 0.97 | 0.54 | 1.10 | 0.80 |
| MIZ | 338 | −0.63 | −0.32 | 1.18 | 0.85 | 1.80 | 1.27 | |
| MIZfilter | 226 | −0.69 | −0.33 | 1.26 | 0.78 | 2.06 | 1.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro, S.L.; Wick, G.A.; Eastwood, S.; Steele, M.A.; Tonboe, R.T. Examining the Consistency of Sea Surface Temperature and Sea Ice Concentration in Arctic Satellite Products. Remote Sens. 2023, 15, 2908. https://doi.org/10.3390/rs15112908
Castro SL, Wick GA, Eastwood S, Steele MA, Tonboe RT. Examining the Consistency of Sea Surface Temperature and Sea Ice Concentration in Arctic Satellite Products. Remote Sensing. 2023; 15(11):2908. https://doi.org/10.3390/rs15112908
Chicago/Turabian StyleCastro, Sandra L., Gary A. Wick, Steinar Eastwood, Michael A. Steele, and Rasmus T. Tonboe. 2023. "Examining the Consistency of Sea Surface Temperature and Sea Ice Concentration in Arctic Satellite Products" Remote Sensing 15, no. 11: 2908. https://doi.org/10.3390/rs15112908
APA StyleCastro, S. L., Wick, G. A., Eastwood, S., Steele, M. A., & Tonboe, R. T. (2023). Examining the Consistency of Sea Surface Temperature and Sea Ice Concentration in Arctic Satellite Products. Remote Sensing, 15(11), 2908. https://doi.org/10.3390/rs15112908






