Mitigation of Millimeter-Wave Radar Mutual Interference Using Spectrum Sub-Band Analysis and Synthesis
Abstract
:1. Introduction
- Compared with interference mitigation methods based on signal decomposition, the spectrum sub-band decomposition method used in this work provides more flexibility in sub-band processing, as it can flexibly control the bandwidth and number of sub-bands compared to EMD and wavelet decomposition. Meanwhile, the spectrum sub-band decomposition based on FFT has faster runtime compared to VMD, which is beneficial to real-time processing.
- For multi-target scenes, the signal is subjected to a sub-band decomposition that yields multiple bands with center frequencies that vary in value, meaning that the distance segments represented by each sub-band are approximately equal, effectively controlling the number of targets contained in each sub-band. These sub-bands exhibit orthogonality, indicating that they are mathematically independent of one another, thereby reducing the complexity of signal reconstruction.
- Compared with the time domain method, spectrum sub-band decomposition can utilize more information, resulting in improved interference mitigation performance. Compared with time–frequency domain methods, the proposed approach has the advantage of low complexity.
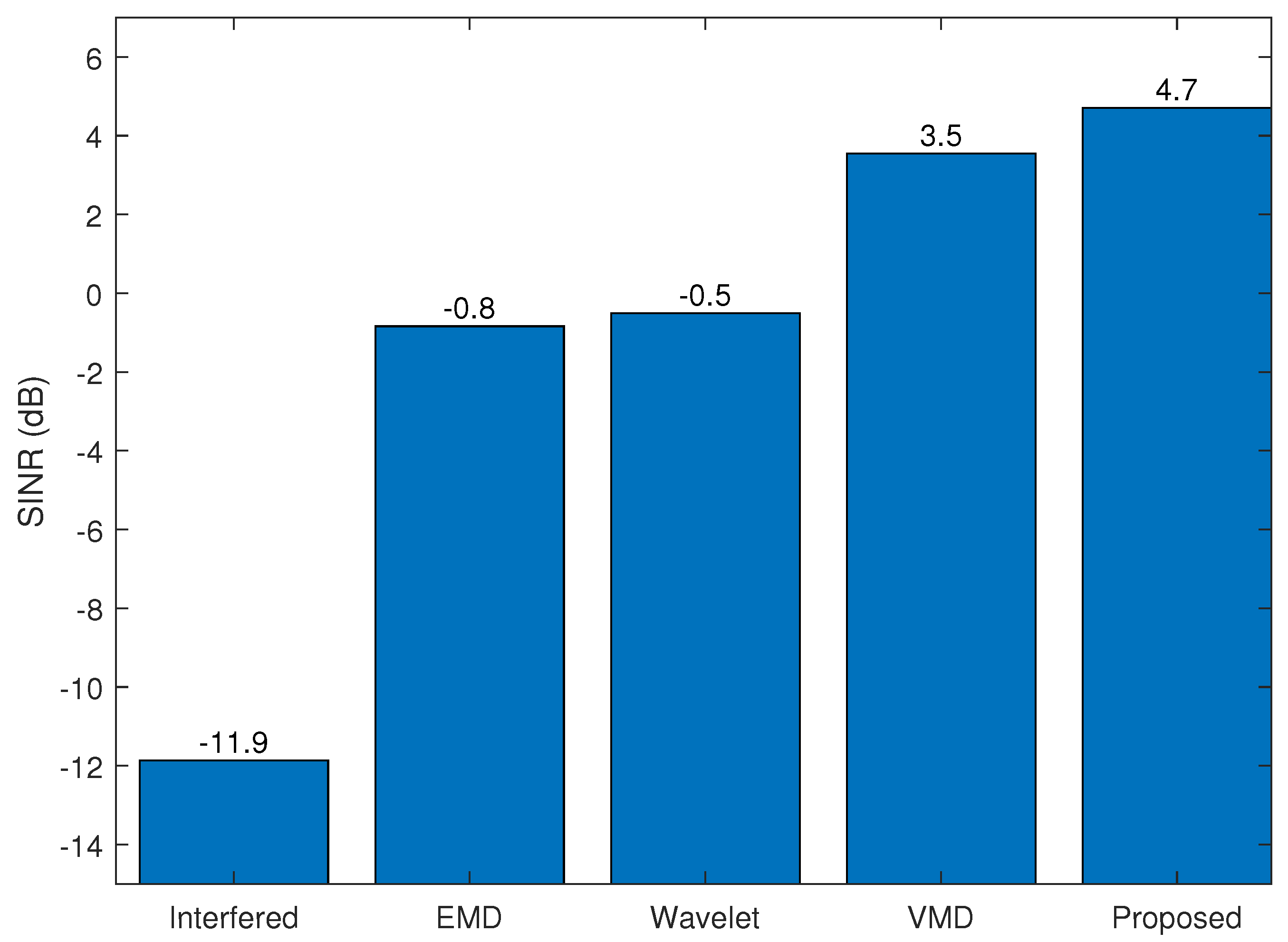
- The spectrum decomposition makes the interference power in the sub-bands lower, which in turn enhances the SIR and benefits interference detection.
- The interference signal in each sub-band has a small support area in the time domain, which is more favorable for subsequent interference detection and signal recovery.
2. Signal Model with Mutual Interference
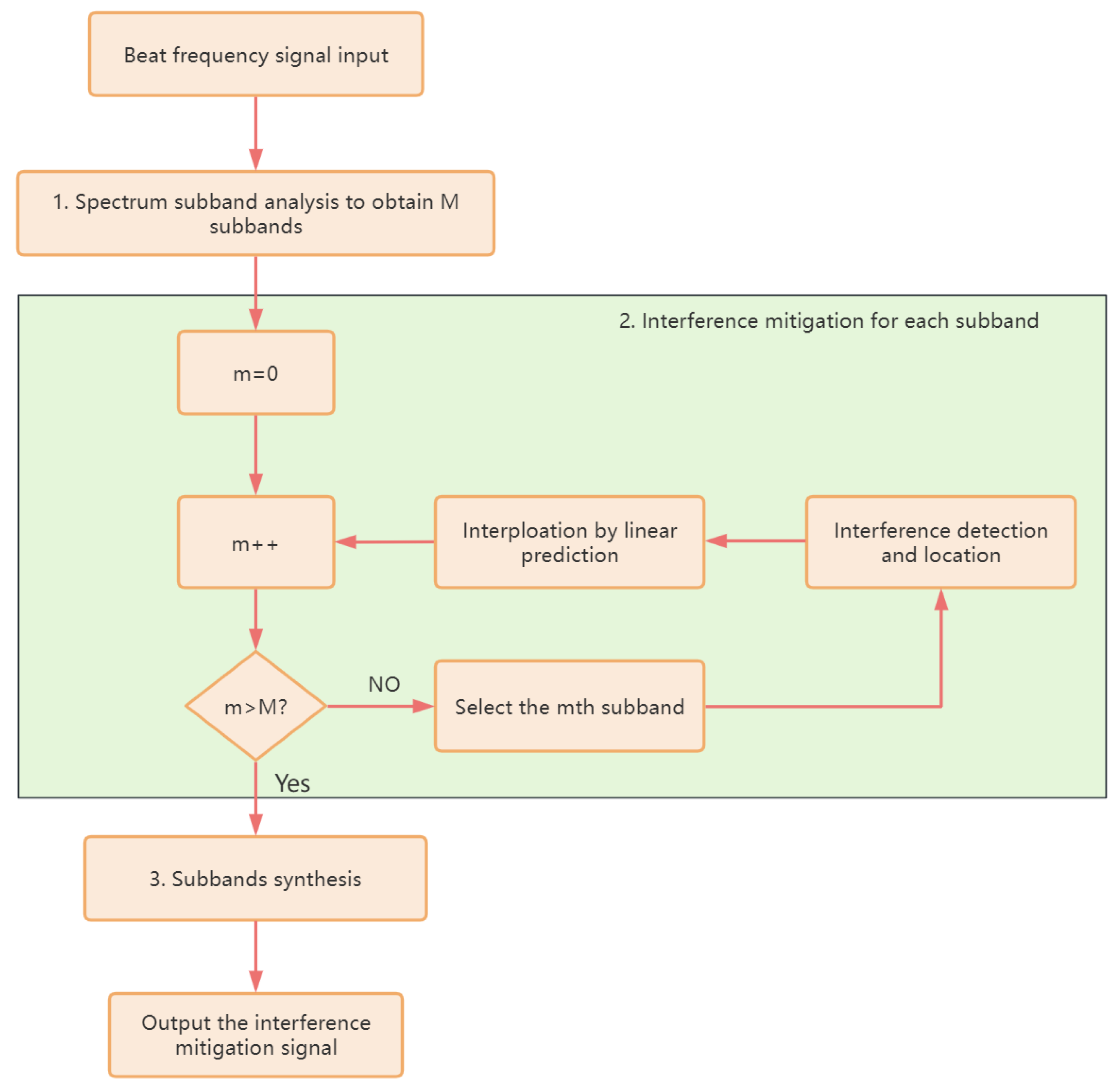
3. Interference Mitigation Method
- After obtaining the beat frequency signal via ADC sampling, the beat frequency signal is transformed to the frequency domain using FFT and the spectrum is divided uniformly to obtain different sub-bands. After that, the inverse FFT (IFFT) is used to transform the sub-bands to the time domain and the time domain signal corresponding to each sub-band is obtained. This is called the spectrum sub-band analysis process. After decomposition, a total of M sub-bands signals are obtained.
- For the mth decomposed sub-band signal, interference detection and mitigation are performed in the time domain. Meanwhile, the useful signal is recovered in the interference-detected region using the linear prediction technique.
- After traversing all the sub-band signals, i.e., the total M sub-band signals, the signals from the time domain undergo transformation into the frequency domain by means of FFT. The individual spectrum sub-bands are then meticulously combined to derive the complete spectrum of the beat frequency signal, then IFFT is performed to obtain the interference-mitigated time domain signal; this process is referred to as sub-band synthesis.
3.1. Spectrum Sub-Band Analysis of Beat Frequency Signal
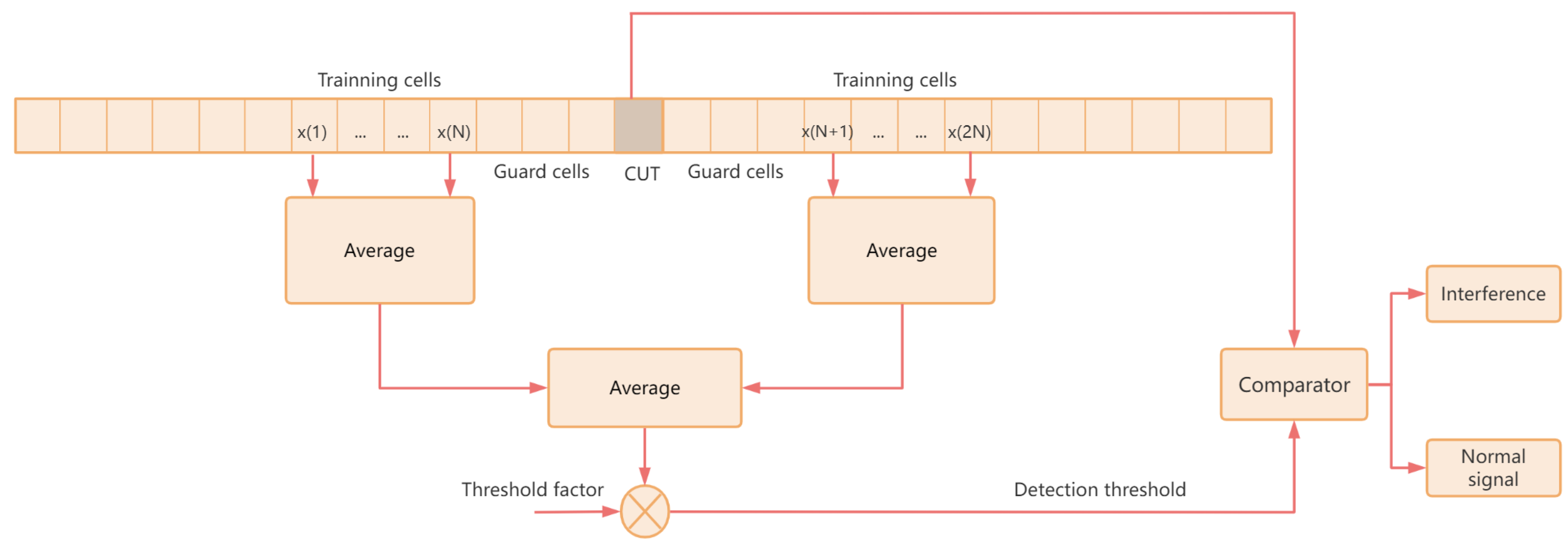
3.2. Interference Detection and Mitigation of Sub-Band Signals
3.3. Signal Reconstruction
4. Simulation Results
4.1. Simulation Setup
4.2. Performance Evaluation Methodology
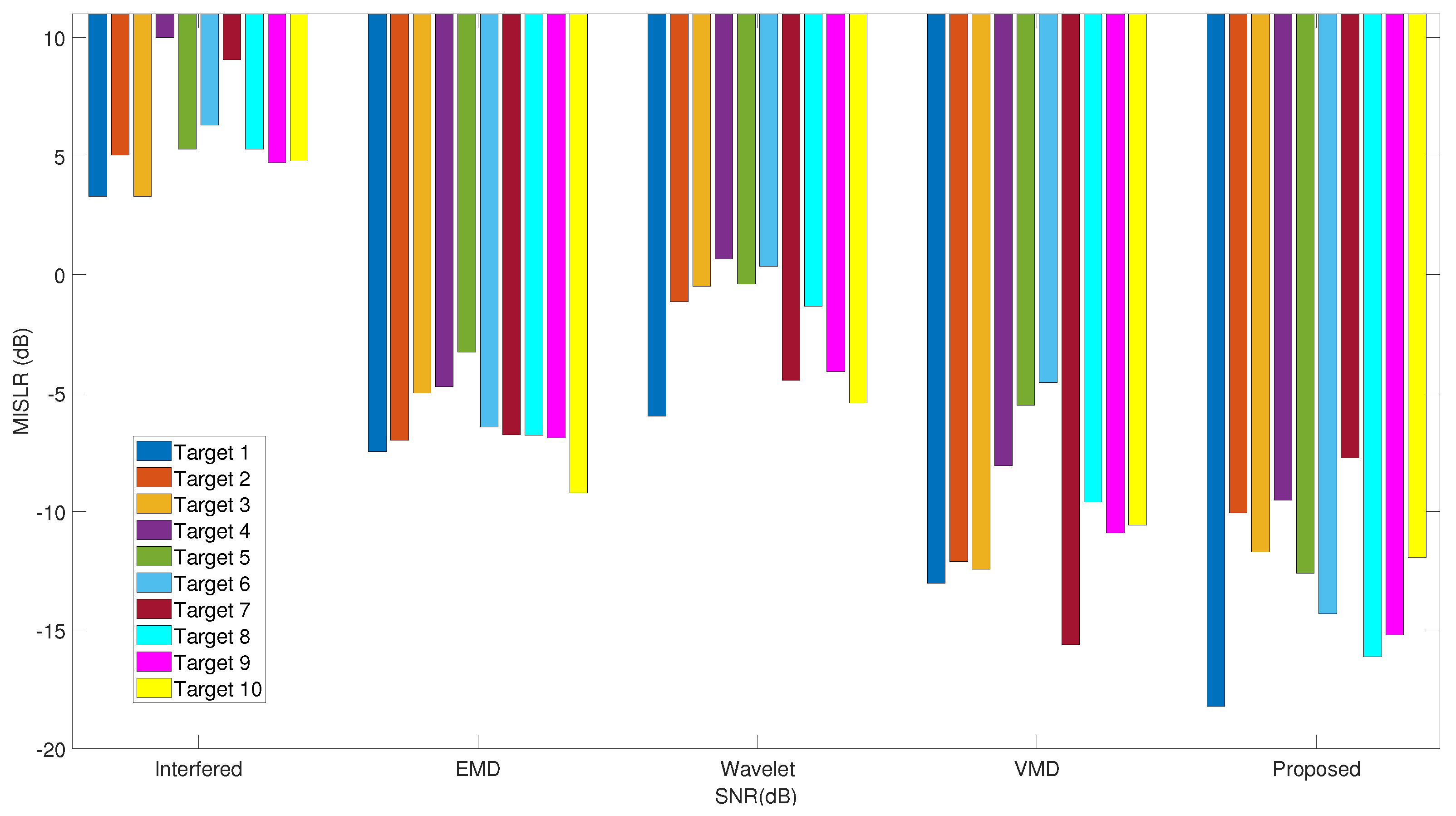
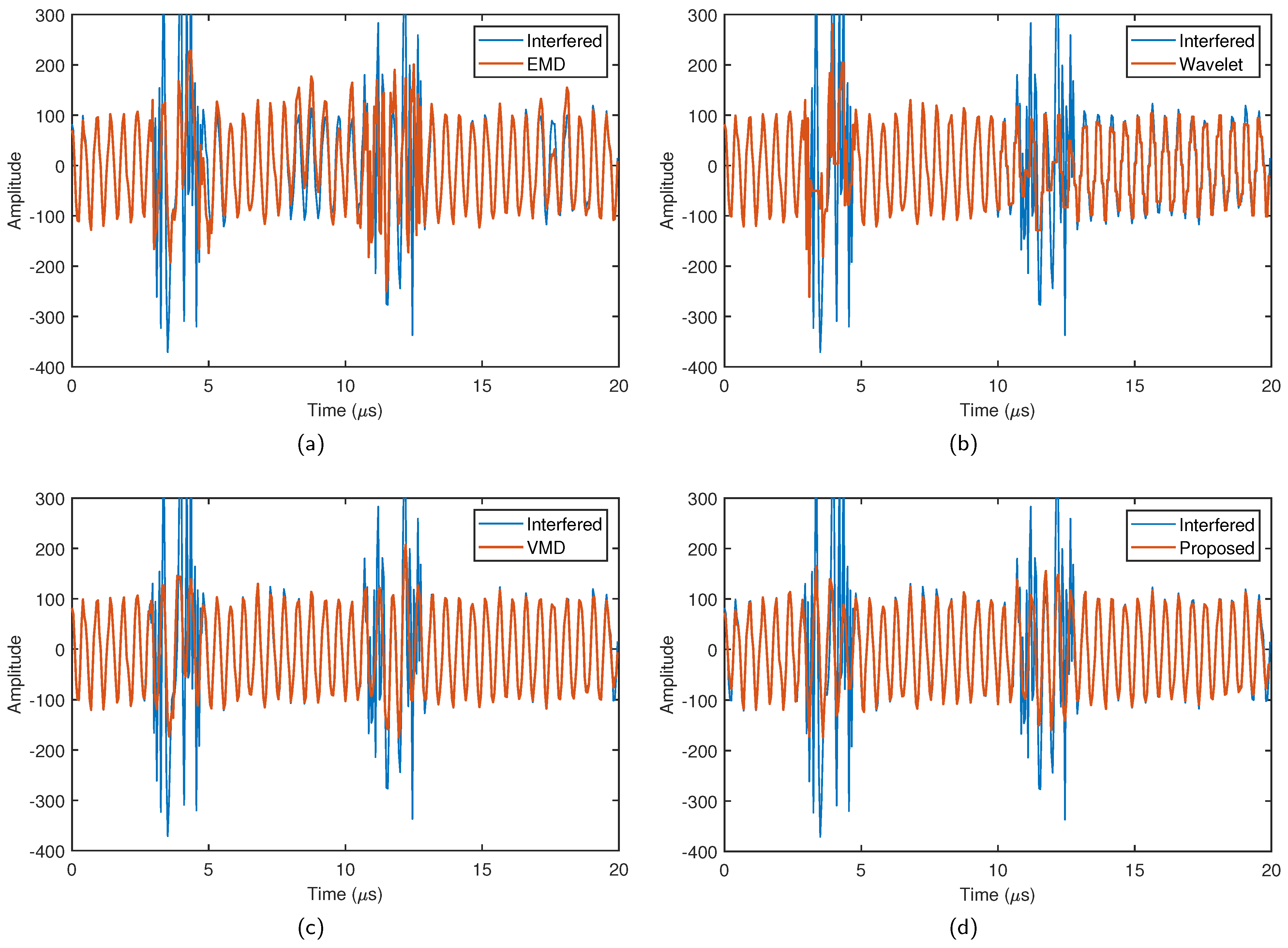
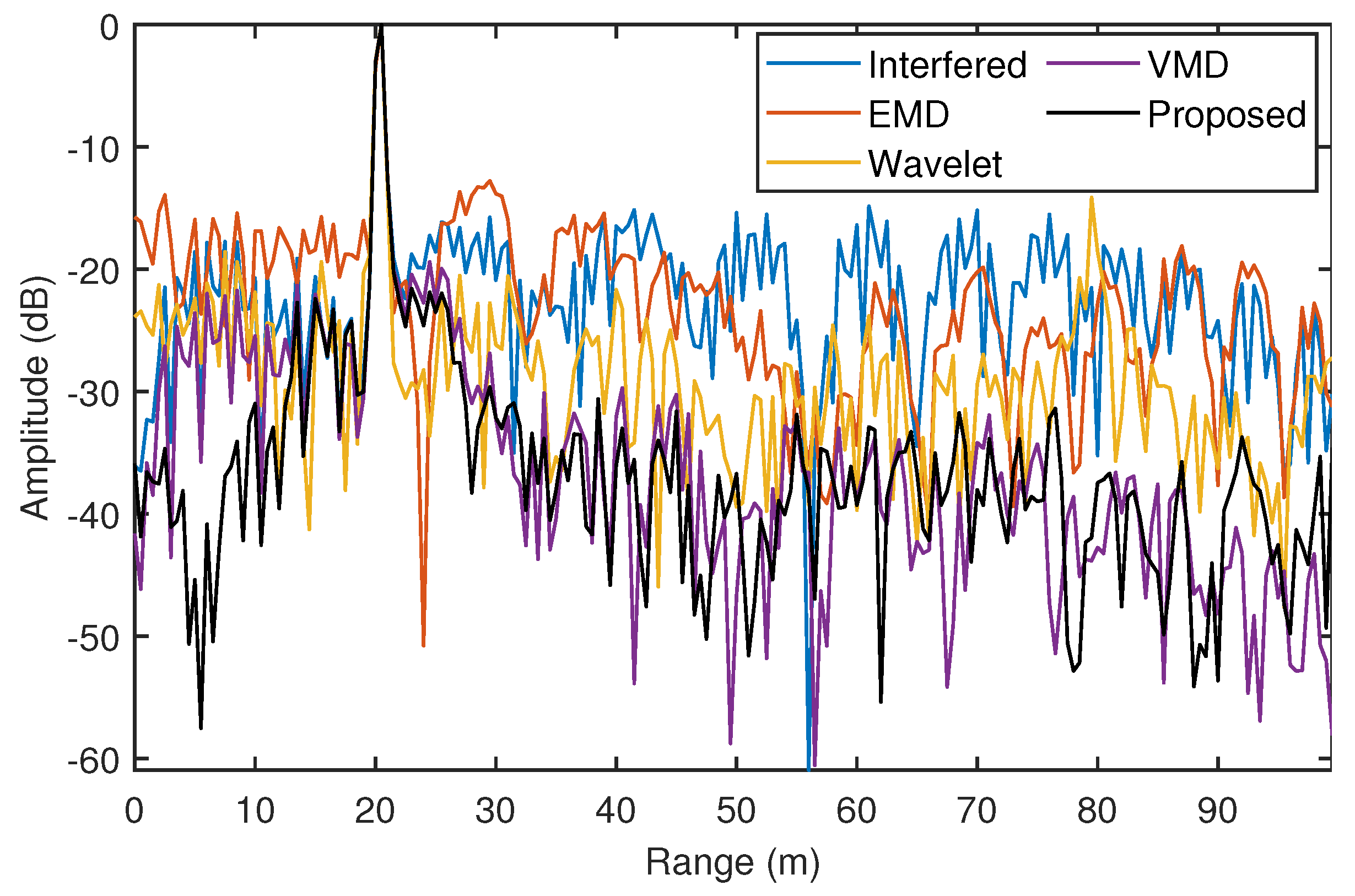
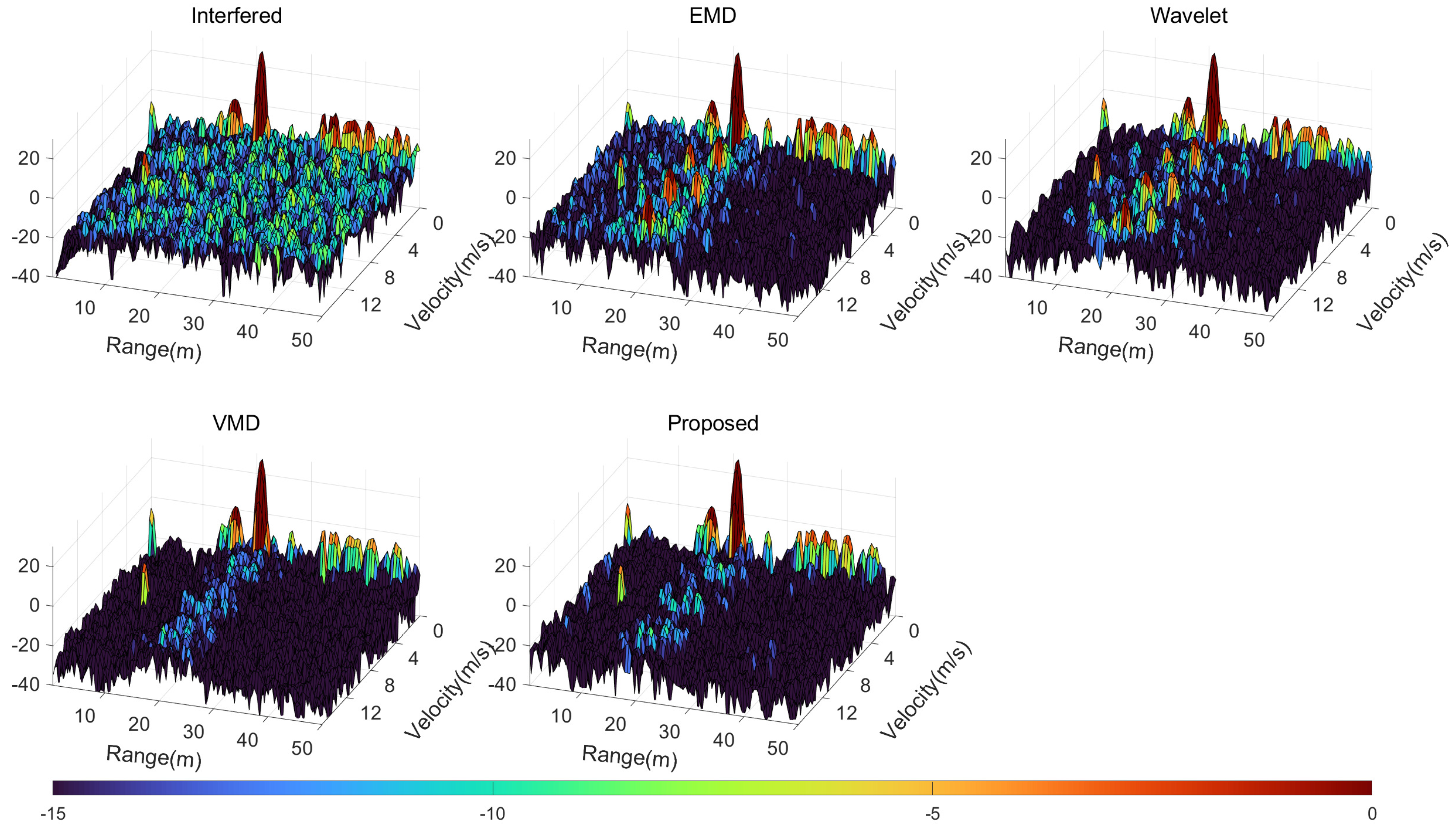
4.3. Simulation Results
5. Real Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dickmann, J.; Klappstein, J.; Hahn, M.; Appenrodt, N.; Bloecher, H.L.; Werber, K.; Sailer, A. Automotive radar the key technology for autonomous driving: From detection and ranging to environmental understanding. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Ziebinski, A.; Cupek, R.; Grzechca, D.; Chruszczyk, L. Review of advanced driver assistance systems (ADAS). AIP Conf. Proc. 2017, 1906, 120002. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Karam, L.; Katupitiya, J.; Milanés, V.; Pitas, I.; Ye, J. Autonomous Driving: Part 1-Sensing and Perception [From the Guest Editors]. IEEE Signal Process. Mag. 2020, 37, 11–13. [Google Scholar] [CrossRef]
- Li, Y.; Ibañez-Guzmán, J. Lidar for Autonomous Driving: The Principles, Challenges, and Trends for Automotive Lidar and Perception Systems. IEEE Signal Process. Mag. 2020, 37, 50–61. [Google Scholar] [CrossRef]
- Dabral, S.; Kamath, S.; Appia, V.; Mody, M.; Zhang, B.; Batur, U. Trends in camera based Automotive Driver Assistance Systems (ADAS). In Proceedings of the 2014 IEEE 57th International Midwest Symposium on Circuits and Systems (MWSCAS), College Station, TX, USA, 3–6 August 2014; pp. 1110–1115. [Google Scholar] [CrossRef]
- Roos, F.; Bechter, J.; Knill, C.; Schweizer, B.; Waldschmidt, C. Radar Sensors for Autonomous Driving: Modulation Schemes and Interference Mitigation. IEEE Microw. Mag. 2019, 20, 58–72. [Google Scholar] [CrossRef] [Green Version]
- Hasch, J.; Topak, E.; Schnabel, R.; Zwick, T.; Weigel, R.; Waldschmidt, C. Millimeter-Wave Technology for Automotive Radar Sensors in the 77 GHz Frequency Band. IEEE Trans. Microw. Theory Tech. 2012, 60, 845–860. [Google Scholar] [CrossRef]
- Dickmann, J.; Appenrodt, N.; Bloecher, H.L.; Brenk, C.; Hackbarth, T.; Hahn, M.; Klappstein, J.; Muntzinger, M.M.; Sailer, A. Radar contribution to highly automated driving. In Proceedings of the 2014 44th European Microwave Conference, Rome, Italy, 6–9 October 2014; pp. 1715–1718. [Google Scholar]
- Yamada, H.; Kobayashi, T.; Yamaguchi, Y.; Sugiyama, Y. High-resolution 2D SAR imaging by the millimeter-wave automobile radar. In Proceedings of the 2017 IEEE Conference on Antenna Measurements & Applications (CAMA), Tsukuba, Japan, 4–6 December 2017; pp. 149–150. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Huang, D.; Fang, X.; Zhou, M.; Zhang, Y. MRPT: Millimeter-Wave Radar-Based Pedestrian Trajectory Tracking for Autonomous Urban Driving. IEEE Trans. Instrum. Meas. 2022, 71, 8000117. [Google Scholar] [CrossRef]
- Jones, W. Keeping cars from crashing. IEEE Spectr. 2001, 38, 40–45. [Google Scholar] [CrossRef]
- Norouzian, F.; Pirkani, A.; Hoare, E.; Cherniakov, M.; Gashinova, M. Phenomenology of automotive radar interference. IET Radar Sonar Navig. 2021, 15, 1045–1060. [Google Scholar] [CrossRef]
- Hakobyan, G.; Armanious, K.; Yang, B. Interference-Aware Cognitive Radar: A Remedy to the Automotive Interference Problem. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2326–2339. [Google Scholar] [CrossRef]
- Goppelt, M.; Blöcher, H.L.; Menzel, W. Analytical investigation of mutual interference between automotive FMCW radar sensors. In Proceedings of the 2011 German Microwave Conference, Armstadt, Germany, 14–16 March 2011; pp. 1–4. [Google Scholar]
- Pirkani, A.A.; Norouzian, F.; Hoare, E.G.; Gashinova, M.S.; Cherniakov, M. Statistical Analysis of Automotive Radar Interference. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
- Brooker, G.M. Mutual interference of millimeter-wave radar systems. IEEE Trans. Electromagn. Compat. 2007, 49, 170–181. [Google Scholar] [CrossRef]
- Kim, G.; Mun, J.; Lee, J. A peer-to-peer interference analysis for automotive chirp sequence radars. IEEE Trans. Veh. Technol. 2018, 67, 8110–8117. [Google Scholar] [CrossRef]
- Fan, Y.; Bao, J.; Wu, K.; Li, H. Ghost Image Due to mmWave Radar Interference: Experiment, Mitigation and Leverage. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Yan, J.; Pu, W.; Zhou, S.; Liu, H.; Greco, M.S. Optimal Resource Allocation for Asynchronous Multiple Targets Tracking in Heterogeneous Radar Networks. IEEE Trans. Signal Process. 2020, 68, 4055–4068. [Google Scholar] [CrossRef]
- Yan, J.; Pu, W.; Zhou, S.; Liu, H.; Bao, Z. Collaborative detection and power allocation framework for target tracking in multiple radar system. Inf. Fusion 2020, 55, 173–183. [Google Scholar] [CrossRef]
- Yan, J.; Jiao, H.; Pu, W.; Shi, C.; Dai, J.; Liu, H. Radar sensor network resource allocation for fused target tracking: A brief review. Inf. Fusion 2022, 86-87, 104–115. [Google Scholar] [CrossRef]
- Toth, M.; Meissner, P.; Melzer, A.; Witrisal, K. Performance Comparison of Mutual Automotive Radar Interference Mitigation Algorithms. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Nozawa, T.; Makino, Y.; Takaya, N.; Umehira, M.; Takeda, S.; Wang, X.; Kuroda, H. An anti-collision automotive FMCW radar using time-domain interference detection and suppression. In Proceedings of the International Conference on Radar Systems (Radar 2017), Belfast, UK, 23–26 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Rameez, M.; Dahl, M.; Pettersson, M.I. Autoregressive Model-Based Signal Reconstruction for Automotive Radar Interference Mitigation. IEEE Sens. J. 2020, 21, 6575–6586. [Google Scholar] [CrossRef]
- Neemat, S.; Krasnov, O.; Yarovoy, A. An Interference Mitigation Technique for FMCW Radar Using Beat-Frequencies Interpolation in the STFT Domain. IEEE Trans. Microw. Theory Tech. 2019, 67, 1207–1220. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lee, J.Y.; Kim, S.C. Mutual Interference Suppression Using Wavelet Denoising in Automotive FMCW Radar Systems. IEEE Trans. Intell. Transp. Syst. 2021, 22, 887–897. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S.; Lu, W.; Liu, Z. Iterative modified threshold method based on EMD for interference suppression in FMCW radars. IET Radar Sonar Navig. 2020, 14, 1219–1228. [Google Scholar] [CrossRef]
- Zhou, F.; Xing, M.; Bai, X.; Sun, G.; Bao, Z. Narrow-Band Interference Suppression for SAR Based on Complex Empirical Mode Decomposition. IEEE Geosci. Remote Sens. Lett. 2009, 6, 423–427. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Zhang, W. Mutual Interference Mitigation of Millimeter-Wave Radar Based on Variational Mode Decomposition and Signal Reconstruction. Remote Sens. 2023, 15, 557. [Google Scholar] [CrossRef]
- Vetterli, M.; Herley, C. Wavelets and filter banks: Theory and design. IEEE Trans. Signal Process. 1992, 40, 2207–2232. [Google Scholar] [CrossRef] [Green Version]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef] [Green Version]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Miller, R. Fundamentals of Radar Signal Processing (Richards, M.A.; 2005) [Book review]. IEEE Signal Process. Mag. 2009, 26, 100–101. [Google Scholar] [CrossRef]
- Chan, Y.; Lavoie, J.; Plant, J. A parameter estimation approach to estimation of frequencies of sinusoids. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 214–219. [Google Scholar] [CrossRef]
- Chatzitheodoridi, M.E.; Taylor, A.; Rabaste, O. A Mismatched Filter for Integrated Sidelobe Level Minimization over a Continuous Doppler Shift Interval. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Davis, M.S.; Lanterman, A.D. Minimum integrated sidelobe ratio filters for MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 405–416. [Google Scholar] [CrossRef]



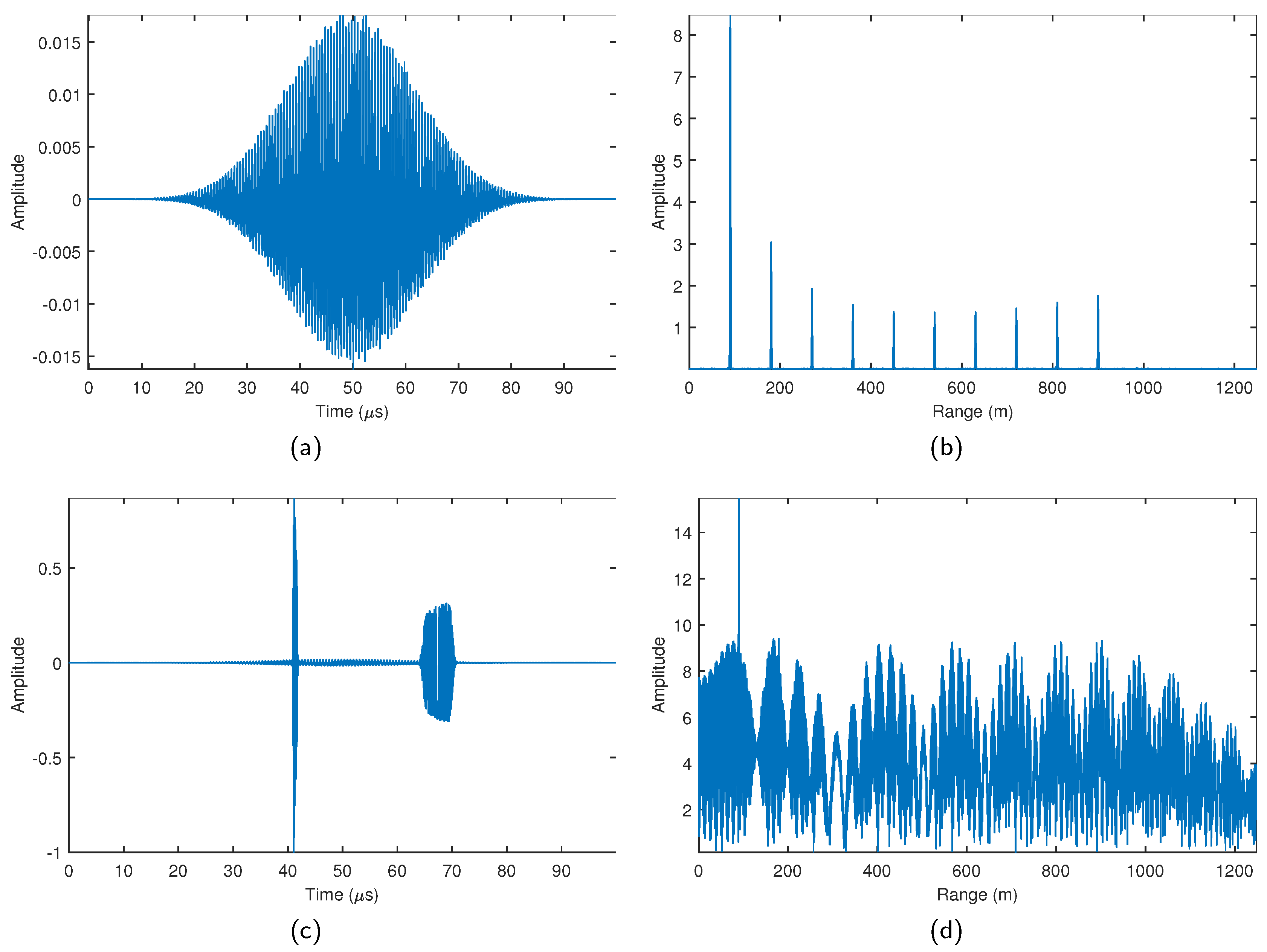

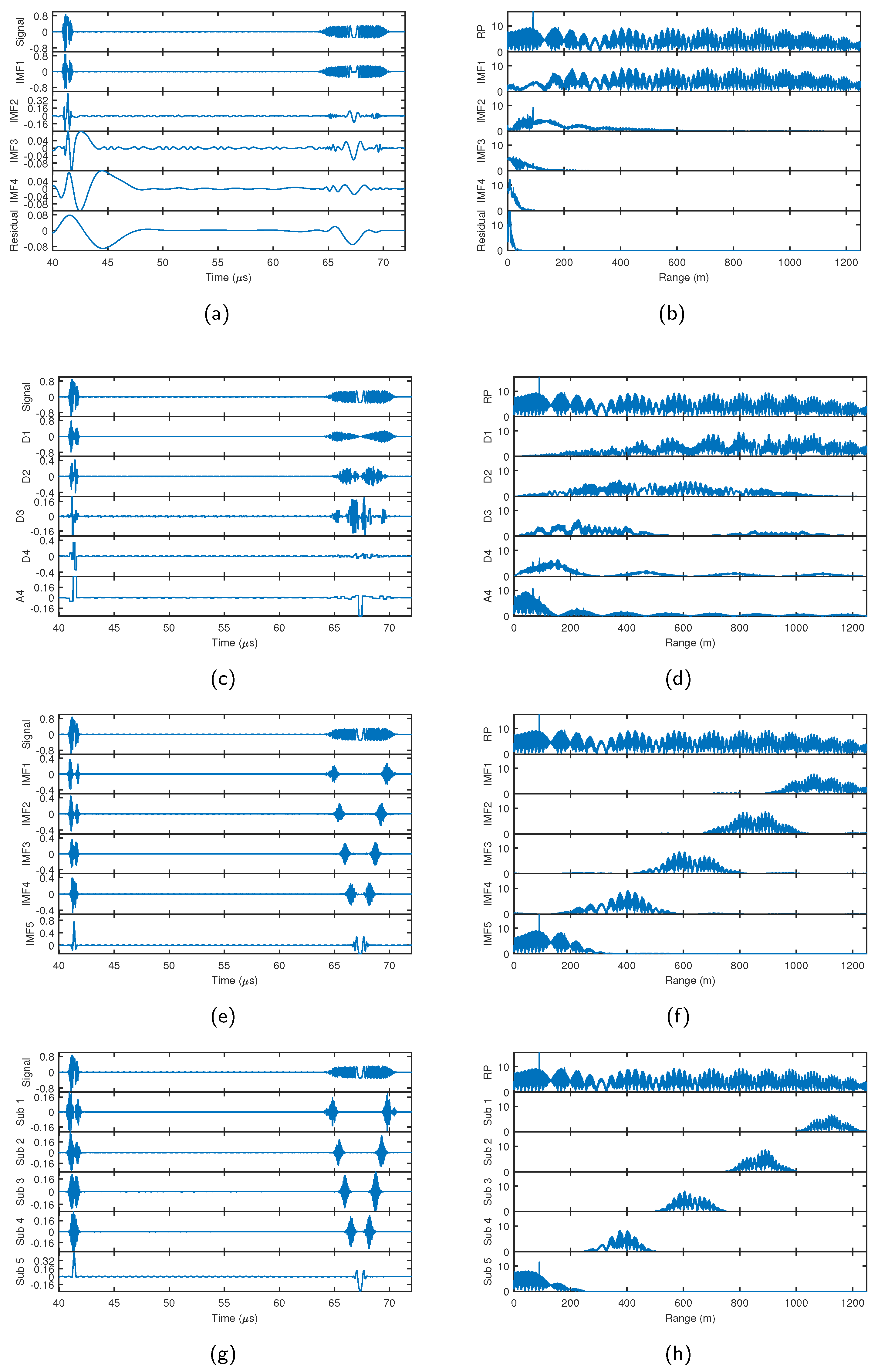






| Target Label | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Range (m) | 91 | 181 | 271 | 361 | 451 | 541 | 631 | 721 | 811 | 900 |
| Speed (m/s) | 2.8 | 2.9 | 3.2 | 3.5 | 3.8 | 4.1 | 4.6 | 4.8 | 5.1 | 5.4 |
| Rader Parameters | Victim | Interfere 1 | Interfere 2 |
|---|---|---|---|
| Carrier frequency (GHz) | 77 | 77 | 77 |
| Sweep bandwidth (MHz) | 300 | 600 | 600 |
| Pulse width (s) | 100 | 10 | 50 |
| Sweep direction | Up | Down | Up |
| Sampling frequency (MHz) | 50 | - | - |
| Method List | Runtime of Signal Decomposition (ms) | Runtime of Interference Detection and Mitigation (ms) | Total Runtime (ms) |
|---|---|---|---|
| EMD | 35.5 | 423.9 | 459.4 |
| Wavelet | 30.2 | 239.1 | 269.3 |
| VMD | 2973.6 | 628.8 | 3602.4 |
| Proposed | 605.3 | 627.5 | 1232.8 |
| Rader Configurations | Victim | Interferer 1 | Interferer 2 |
|---|---|---|---|
| Carrier frequency (GHz) | 77 | 77 | 77 |
| Sweep bandwidth (MHz) | 300 | 300 | 500 |
| Pulse width (s) | 20 | 20 | 20 |
| Sweep direction | Up | Down | Up |
| PRT (s) | 30 | 43 | 61 |
| Sampling frequency (MHz) | 20 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, M.; Feng, B.; Li, Y. Mitigation of Millimeter-Wave Radar Mutual Interference Using Spectrum Sub-Band Analysis and Synthesis. Remote Sens. 2023, 15, 3210. https://doi.org/10.3390/rs15133210
Yin M, Feng B, Li Y. Mitigation of Millimeter-Wave Radar Mutual Interference Using Spectrum Sub-Band Analysis and Synthesis. Remote Sensing. 2023; 15(13):3210. https://doi.org/10.3390/rs15133210
Chicago/Turabian StyleYin, Mingye, Bo Feng, and Yanbing Li. 2023. "Mitigation of Millimeter-Wave Radar Mutual Interference Using Spectrum Sub-Band Analysis and Synthesis" Remote Sensing 15, no. 13: 3210. https://doi.org/10.3390/rs15133210
APA StyleYin, M., Feng, B., & Li, Y. (2023). Mitigation of Millimeter-Wave Radar Mutual Interference Using Spectrum Sub-Band Analysis and Synthesis. Remote Sensing, 15(13), 3210. https://doi.org/10.3390/rs15133210






