MIMO DFRC Signal Design in Signal-Dependent Clutter
Abstract
1. Introduction
2. Methods
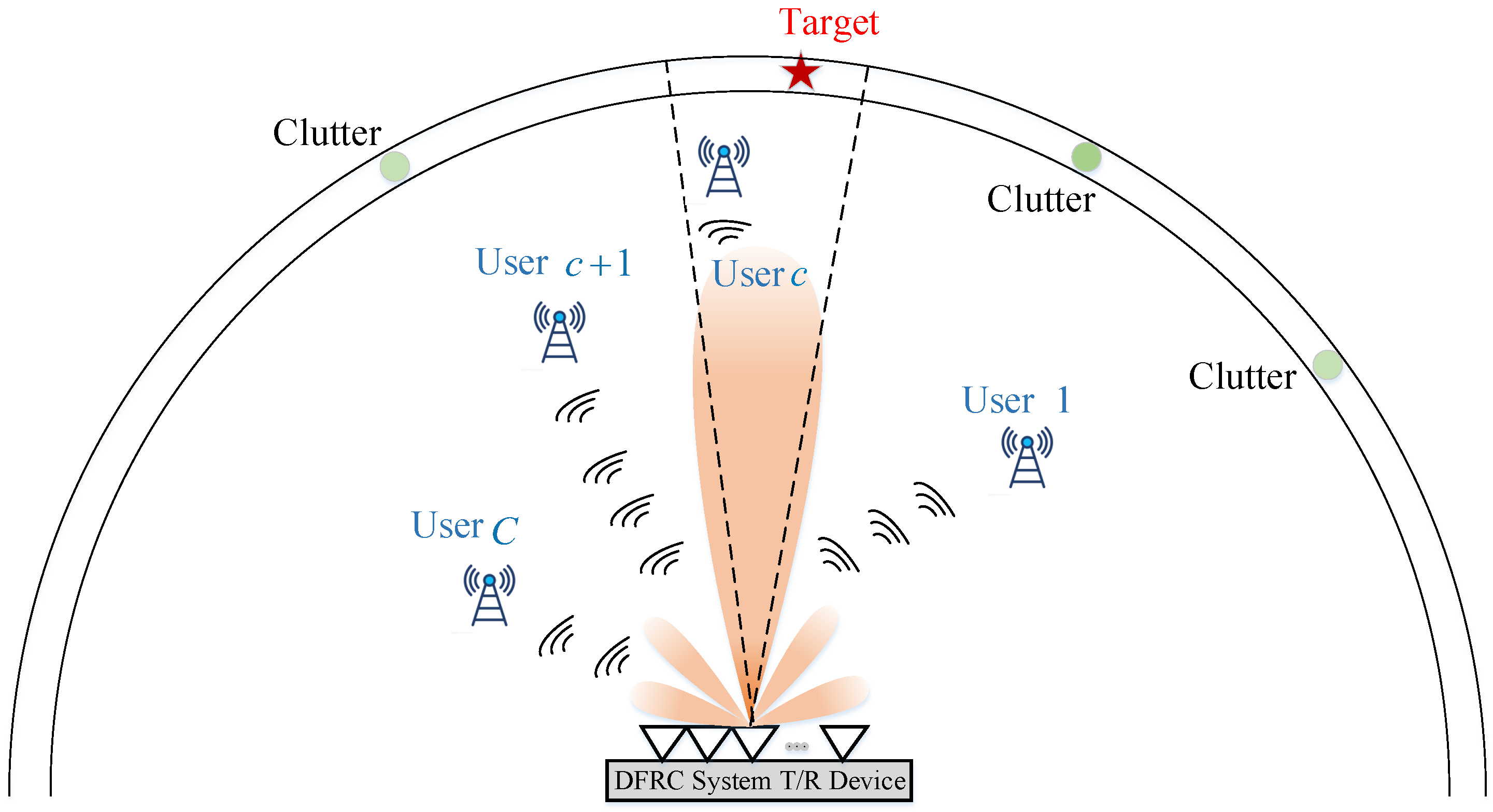
2.1. System Model
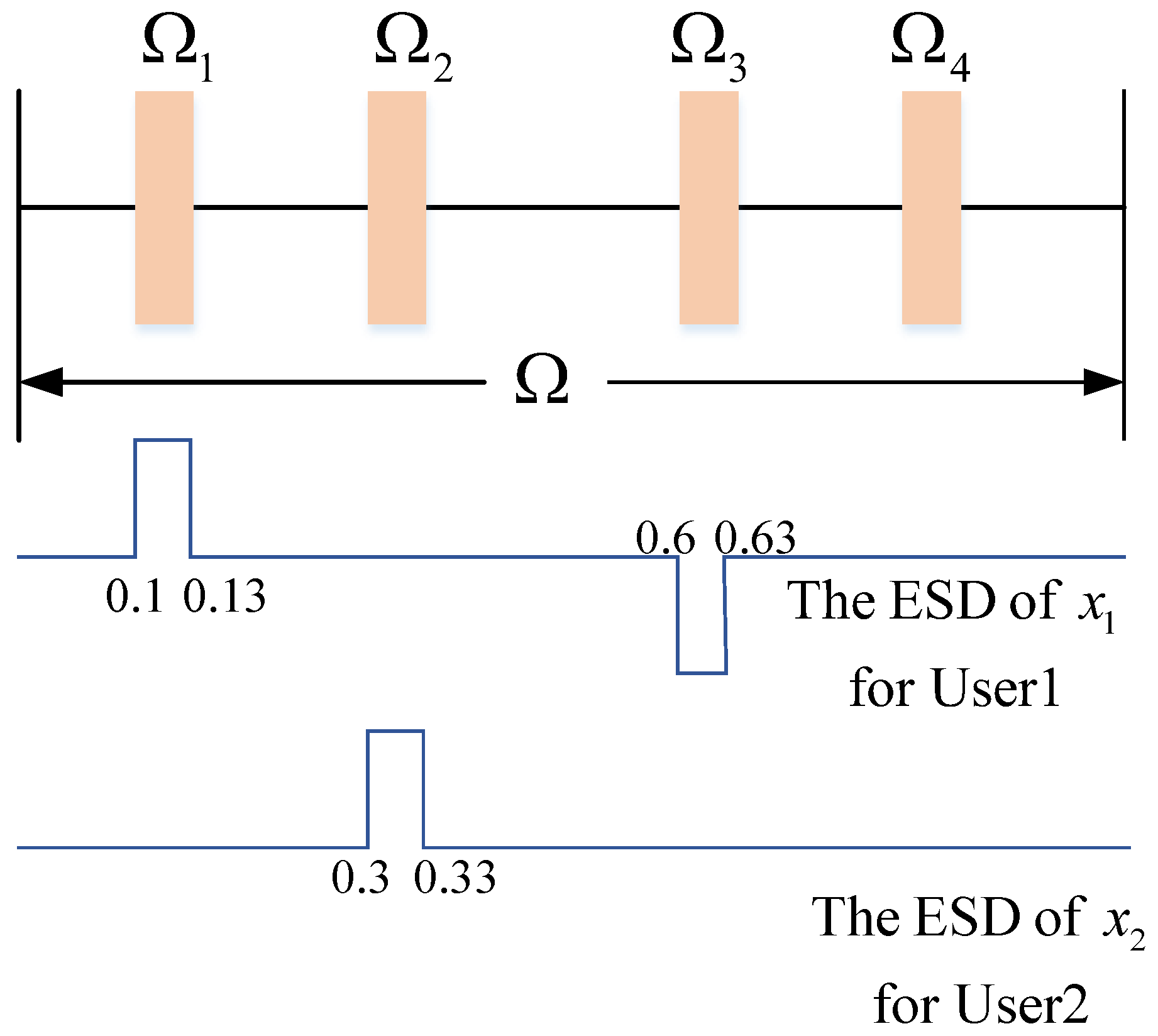
2.1.1. Spectral Position Index and Amplitude Modulation
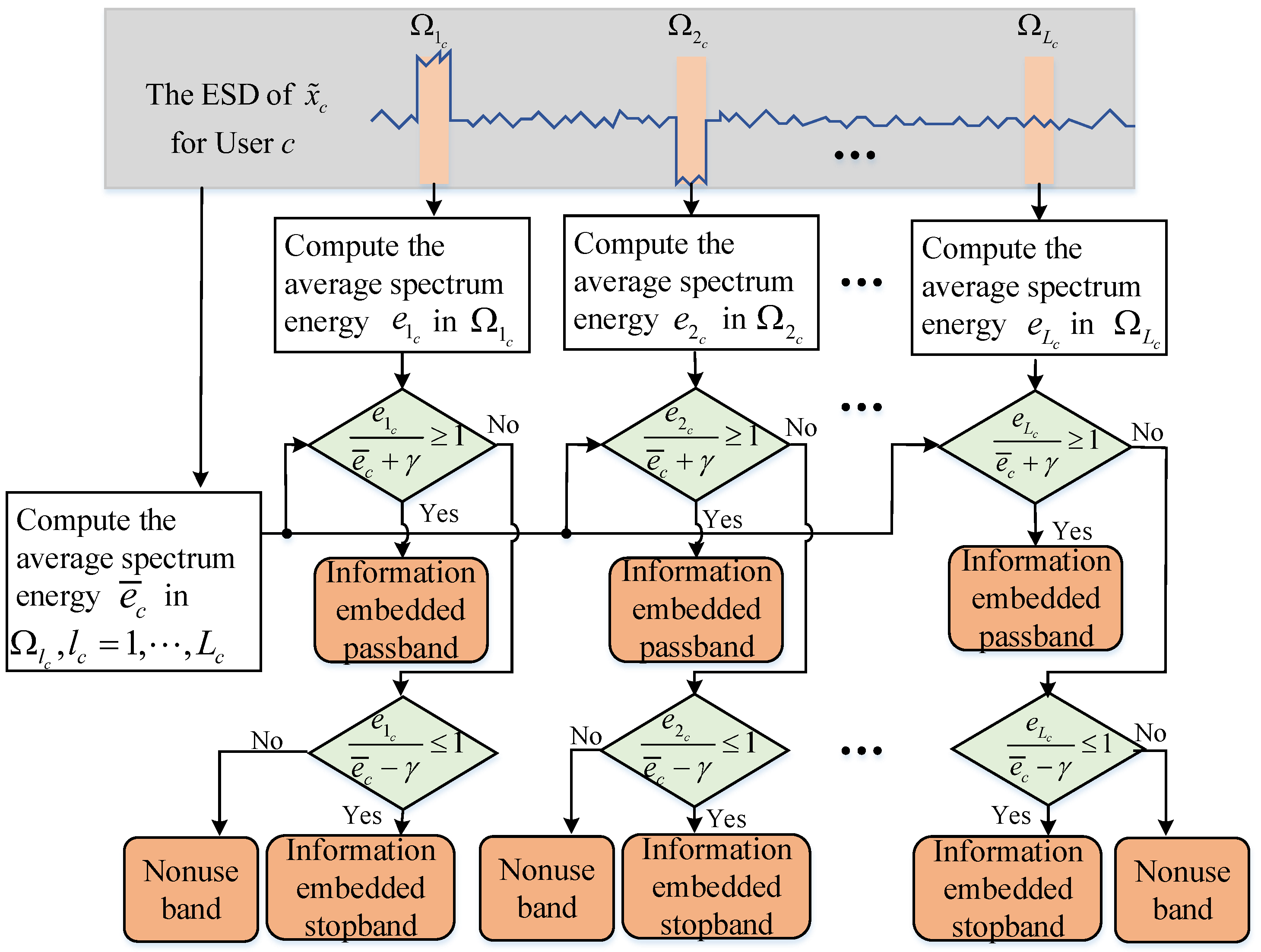
2.1.2. Spectral Position Index and Amplitude Demodulation
2.2. Problem Formulation
2.2.1. Waveform Design Metric
2.2.2. Waveform Constraints
2.2.3. Waveform Design Problem
2.3. Optimization Technique via IBE-DSADMM for Solving
2.3.1. IBE-DSADMM Algorithm
- Given and .
- Given , is updated by solving
- Repeat the above steps until convergence.
| Algorithm 1: IBE-DSADMM for |
| Input:
Feasible starting point ; Output: An optimized solution to ;
|
2.3.2. Algorithm Initialization
2.3.3. Computational Complexity
2.3.4. Convergence Analysis
3. Results
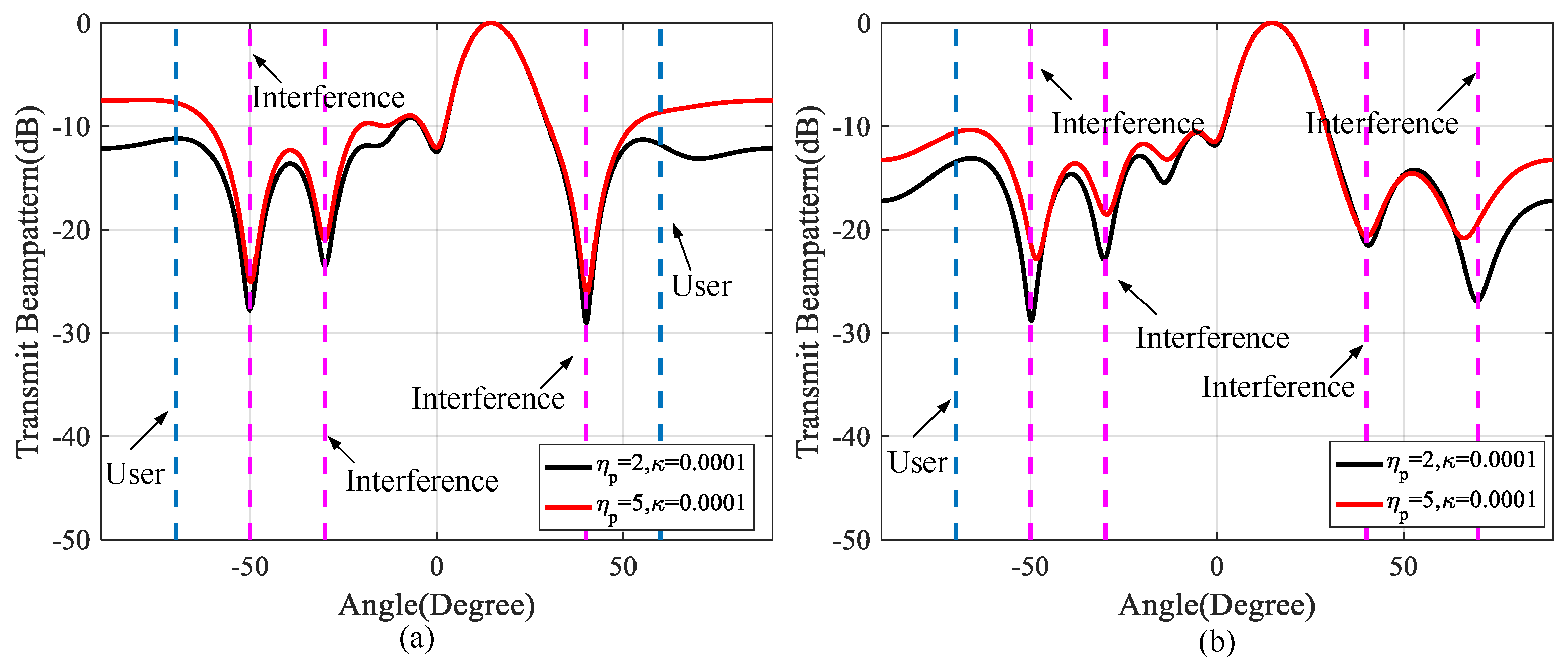
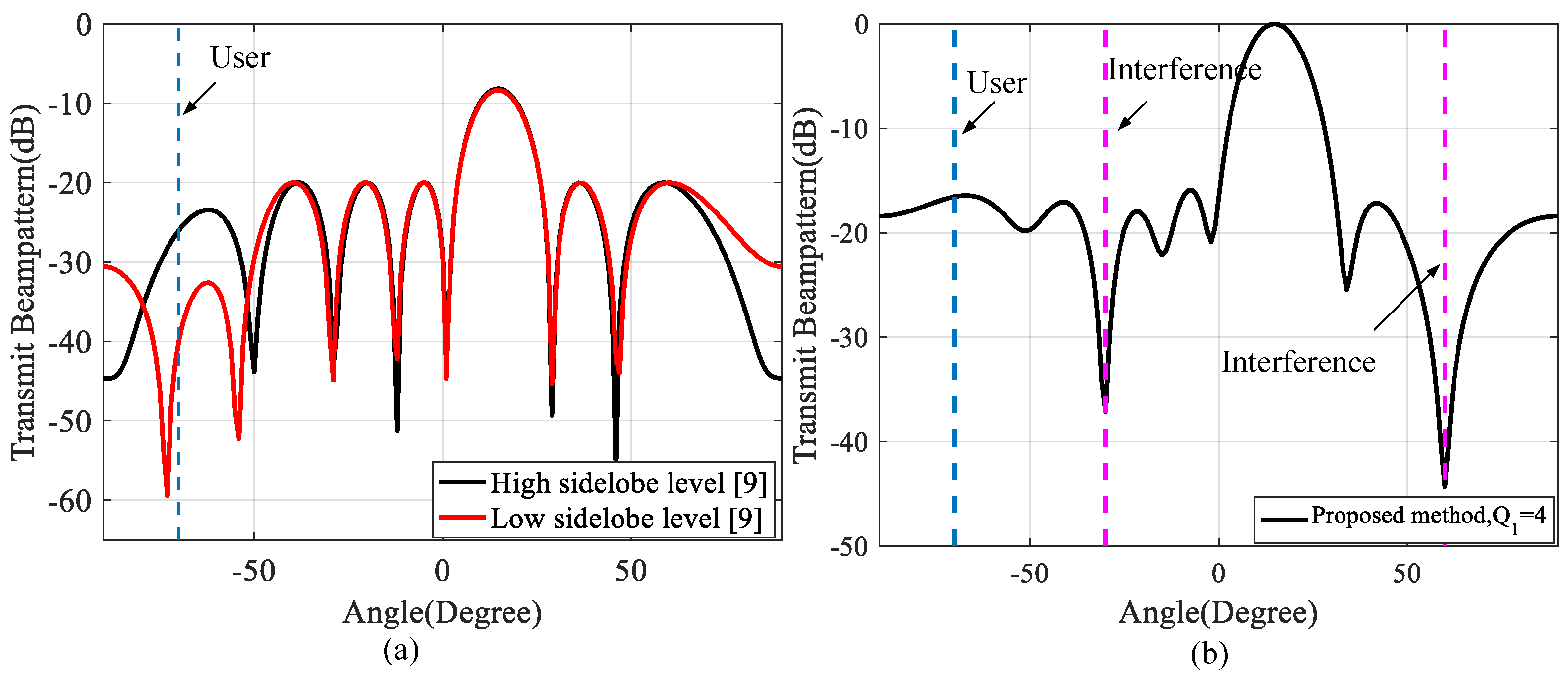
3.1. Beampattern Performance
3.2. Communication Performance
3.3. Performance Analysis for Different Application Scenarios
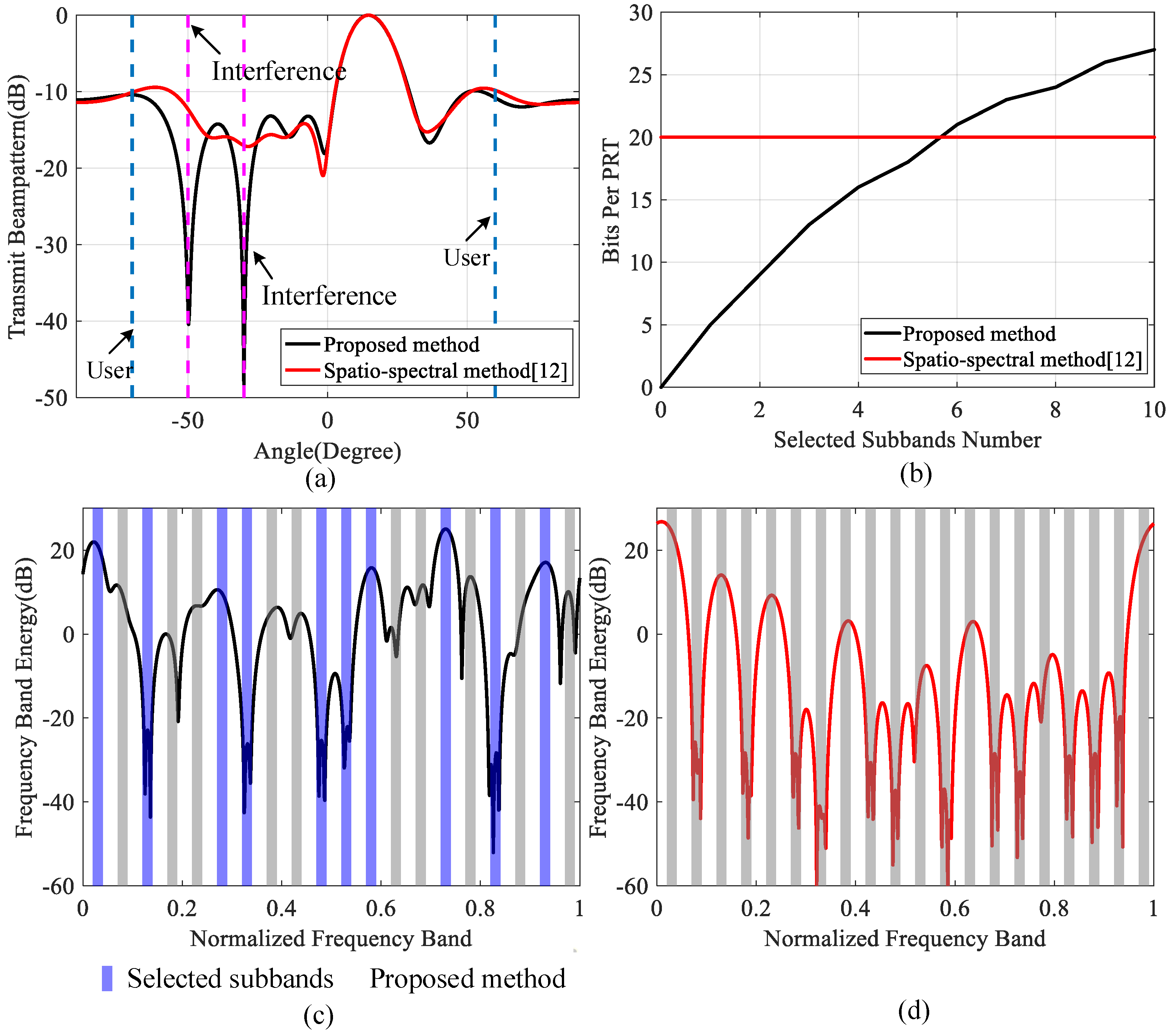
3.4. Comparison with Related Information Embedding Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| Algorithm A1: ADMM for solving |
| Input: ; Output: An optimized solution to ;
|
References
- Saddik, G.N.; Singh, R.S.; Brown, E.R. Ultra-wideband multifunctional communications/radar system. IEEE Trans. Microw. Theory Tech. 2007, 55, 1431–1437. [Google Scholar] [CrossRef]
- Liu, Z. Waveform Research on the Integration of Radar and Communication. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 12 June 2015. (In Chinese). [Google Scholar]
- Cui, G.; Yang, J.; Lu, S.; Yu, X.; Kong, L. Dual-use unimodular sequence design via frequency nulling modulation. IEEE Access 2018, 6, 62470–62481. [Google Scholar] [CrossRef]
- Yang, J.; Cui, G.; Yu, X.; Kong, L. Dual-use signal design for radar and communication via ambiguity function sidelobe control. IEEE Trans. Veh. Technol. 2020, 69, 9781–9794. [Google Scholar] [CrossRef]
- Yang, J.; Tan, Y.; Yu, X.; Cui, G.; Zhang, D. Waveform Design for Watermark Framework Based DFRC System With Application on Joint SAR Imaging and Communication. IEEE Trans. Geosci. Remote Sens. 2022, 61, 1–14. [Google Scholar] [CrossRef]
- Eedara, I.P.; Hassamien, A.; Amin, M.G. Performance analysis of dual-function multiple-input multiple-output radar-communications using frequency hopping waveforms and phase shift keying signalling. IET Radar Sonar Navig. 2021, 15, 402–418. [Google Scholar] [CrossRef]
- Eedara, I.P.; Amin, M.G.; Fabrizio, G.A. Target detection in frequency hopping MIMO dual-function radar-communication systems. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing, Toronto, ON, Canada, 6 June 2021; pp. 8458–8462. [Google Scholar]
- Eedara, I.P.; Amin, M.G.; Hoorfar, A.; Chalise, B.K. Dual-function frequency-hopping MIMO radar system with CSK signaling. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1501–1513. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity. IEEE Trans. Signal Process. 2016, 64, 2168–2181. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Signaling strategies for dual-function radar communications: An overview. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 36–45. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Phase-modulation based dual-function radar-communications. IET Radar Sonar Navig. 2016, 10, 1411–1421. [Google Scholar] [CrossRef]
- Yu, X.; Yao, X.; Yang, J.; Zhang, L.; Kong, L.; Cui, G. Integrated waveform design for MIMO radar and communication via spatio-spectral modulation. IEEE Trans. Signal Process. 2022, 70, 2293–2305. [Google Scholar] [CrossRef]
- Tang, B.; Stoica, P. MIMO multifunction RF systems: Detection performance and waveform design. IEEE Trans. Signal Process. 2022, 70, 4381–4394. [Google Scholar] [CrossRef]
- Hassanien, A.; Aboutanios, E.; Amin, M.G.; Fabrizio, G.A. A dual-function MIMO radar-communication system via waveform permutation. Digit. Signal Process. 2018, 83, 118–128. [Google Scholar] [CrossRef]
- Wang, X.; Hassanien, A.; Amin, M.G. Dual-function MIMO radar communications system design via sparse array optimization. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1213–1226. [Google Scholar] [CrossRef]
- Baxter, W.; Aboutanios, E.; Hassanien, A. Joint radar and communications for frequency-hopped MIMO systems. IEEE Trans. Signal Process. 2022, 70, 729–742. [Google Scholar] [CrossRef]
- Huang, T.; Shlezinger, N.; Xu, X.; Liu, Y.; Eldar, Y.C. MAJoRCom: A dual-function radar communication system using index modulation. IEEE Trans. Signal Process. 2020, 68, 3423–3438. [Google Scholar] [CrossRef]
- Ma, D.; Shlezinger, N.; Huang, T.; Liu, Y.; Eldar, Y.C. FRaC: FMCW-based joint radar-communications system via index modulation. IEEE J. Sel. Top. Signal Process. 2021, 15, 1348–1364. [Google Scholar] [CrossRef]
- Xu, J.; Wang, X.; Aboutanios, E.; Cui, G. Hybrid index modulation for dual-functional radar communications systems. IEEE Trans. Veh. Technol. 2022, 72, 3186–3200. [Google Scholar] [CrossRef]
- Wen, M.; Zheng, B.; Kim, K.; Di, R.M.; Tsiftsis, T.A.; Chen, K.C.; Al-Dhahir, N. A Survey on Spatial Modulation in Emerging Wireless Systems: Research Progresses and Applications. IEEE J. Sel. Areas Commun. 2019, 37, 1949–1972. [Google Scholar] [CrossRef]
- Li, J.; Dang, S.; Wen, M.; Li, Q.; Chen, Y.; Huang, Y.; Shang, W. Index Modulation Multiple Access for 6G Communications: Principles, Applications, and Challenges. IEEE Netw. 2023, 37, 52–60. [Google Scholar] [CrossRef]
- Wen, M.; Basar, E.; Li, Q.; Zheng, B.; Zhang, M. Multiple-Mode Orthogonal Frequency Division Multiplexing with Index Modulation. IEEE Trans. Commun. 2017, 65, 3892–3906. [Google Scholar] [CrossRef]
- Duly, A.J.; Love, D.J.; Krogmeier, J.V. Time-division beamforming for MIMO radar waveform design. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1210–1223. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Sun, Q.; Huang, G. Robust joint design of transmit waveform and receive filter for MIMO radar space-time adaptive processing with signal-dependent interferences. IET Radar Sonar Navig. 2017, 11, 1321–1332. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Kong, L.; Li, J.; Gui, G. Constrained waveform design for colocated MIMO radar with uncertain steering matrices. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 356–370. [Google Scholar] [CrossRef]
- Karbasi, S.M.; Aubry, A.; Carotenuto, V.; Naghsh, M.M.; Bastani, M.H. Knowledge-based design of space-time transmit code and receive filter for a multiple-input-multiple-output radar in signal-dependent interference. IET Radar Sonar Navig. 2015, 9, 1124–1135. [Google Scholar] [CrossRef]
- Cui, G.; Yu, X.; Carotenuto, V.; Kong, L. Space-time transmit code and receive filter design for colocated MIMO radar. IEEE Trans. Signal Process. 2017, 65, 1116–1129. [Google Scholar] [CrossRef]
- Yang, J.; Aubry, A.; De Maio, A.; Yu, X.; Cui, G. Multi-spectrally constrained transceiver design against signal-dependent interference. IEEE Trans. Signal Process. 2022, 70, 1320–1332. [Google Scholar] [CrossRef]
- Tang, B.; Tang, J. Joint design of transmit waveforms and receive filters for MIMO radar space-time adaptive processing. IEEE Trans. Signal Process. 2016, 64, 4707–4722. [Google Scholar] [CrossRef]
- Tang, B.; Tuck, J.; Stoica, P. Polyphase waveform design for MIMO radar space time adaptive processing. IEEE Trans. Signal Process. 2020, 68, 2143–2154. [Google Scholar] [CrossRef]
- Tang, B.; Stoica, P. Information-theoretic waveform design for MIMO radar detection in range-spread clutter. Signal Process. 2021, 182, 107961. [Google Scholar] [CrossRef]
- Wu, W.; Tang, B.; Tang, J. Waveform design for dual-function radar-communication systems in clutter. J. Radars 2022, 11, 570–580. (In Chinese) [Google Scholar]
- Tsinos, C.G.; Arora, A.; Chatzinotas, S.; Ottersten, B. Joint transmit waveform and receive filter design for dual-function radar-communication systems. IEEE J. Sel. Top. Signal Process. 2021, 15, 1378–1392. [Google Scholar] [CrossRef]
- Liu, R.; Li, M.; Liu, Q.; Swindlehurst, A.L. Joint waveform and filter designs for STAP-SLP-based MIMO-DFRC systems. IEEE J. Sel. Areas Commun. 2022, 40, 1918–1931. [Google Scholar] [CrossRef]
- Khalaj-Amirhosseini, M. Synthesis of linear and planar arrays with sidelobes of individually arbitrary levels. Int. J. RF Microw. Comput. Eng. 2019, 29. [Google Scholar] [CrossRef]
- Kang, M.; Baek, J. Efficient and Accurate Synthesis for Array Pattern Shaping. Sensors 2022, 22, 5537. [Google Scholar] [CrossRef]
- Dicandia, F.A.; Genovesi, S. Wide-Scan and Energy-Saving Phased Arrays by Exploiting Penrose Tiling Subarrays. IEEE Trans. Antennas Propag. 2022, 70, 7524–7537. [Google Scholar] [CrossRef]
- Raei, E.; Alaee-Kerahroodi, M.; Mysore Rand, B.S. Spatial- and Range- ISLR Trade-Off in MIMO Radar Via Waveform Correlation Optimization. IEEE Trans. Signal Process. 2021, 69, 3283–3298. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Farina, A.; Wicks, M. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 93–117. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Yang, J.; Li, J.; Kong, L. Quadratic optimization for unimodular sequence design via an ADPM framework. IEEE Trans. Signal Process. 2020, 68, 3619–3634. [Google Scholar] [CrossRef]
- He, H.; Li, J.; Stoica, P. Waveform Design for Active Sensing Systems: A Computational Approach; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Aubry, A.; De Maio, A.; Piezzo, M.; Farina, A. Radar waveform design in a spectrally crowded environment via nonconvex quadratic optimization. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1138–1152. [Google Scholar] [CrossRef]
- Yu, X.; Alhujaili, K.; Cui, G.; Monga, V. MIMO radar waveform design in the presence of multiple targets and practical constraints. IEEE Trans. Signal Process. 2020, 68, 1974–1989. [Google Scholar] [CrossRef]
- Seber, G.A.F. A Matrix Handbook for Statisticians; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Zhao, L.; Song, J.; Babu, P.; Palomar, D.P. A unified framework for low autocorrelation sequence design via majorization–minimization. IEEE Trans. Signal Process. 2017, 65, 438–453. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Yang, J.; Kong, L.; Li, J. Wideband MIMO radar waveform design. IEEE Trans. Signal Process. 2019, 67, 3487–3501. [Google Scholar] [CrossRef]
- Bertsekas, D.P.; Tsitsiklis, J.N. Parallel and Distributed Computation: Numerical Methods; Athena Scientific: New York, NY, USA, 1997. [Google Scholar]
- Mehanna, O.; Huang, K.; Gopalakrishnan, B.; Konar, A.; Sidiropoulos, N.D. Feasible point pursuit and successive approximation of non-convex QCQPs. IEEE Signal Process. Lett. 2015, 22, 804–808. [Google Scholar] [CrossRef]
- Yu, X.; Yao, X.; Qiu, H.; Cui, G. Integrated MIMO signal design via spatio-spectral modulation. In Proceedings of the 2022 30th European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 29 August 2022; pp. 1911–1915. [Google Scholar]
- Razaviyayn, M.; Hong, M.; Luo, Z.-Q. A unified convergence analysis of block successive minimization methods for nonsmooth optimization. SIAM J. Optimiz. 2013, 23, 1126–1153. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Zappone, A.; Razaviyayn, M.; Luo, Z. A new sequential optimization procedure and its applications to resource allocation for wireless systems. IEEE Trans. Signal Process. 2018, 66, 6518–6533. [Google Scholar] [CrossRef]
- Yu, X.; Qiu, H.; Yang, J.; Wei, W.; Cui, G.; Kong, L. Multispectrally constrained MIMO radar beampattern design via sequential convex approximation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2935–2949. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Guo, S.; Cui, G.; Wu, P.; Jia, C.; Kong, L. Joint estimation of NLOS building layout and targets via sparsity-driven approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Huang, K.; Sidiropoulos, N.D. Consensus-ADMM for general quadratically constrained quadratic programming. IEEE Trans. Signal Process. 2016, 64, 5297–5310. [Google Scholar] [CrossRef]



| Variable Name | Variable Setting |
|---|---|
| Transmitting array | Uniform linear array |
| Antenna spacing | half-wave |
| Antenna number | |
| Signal sample number | |
| Parameters of mainlobe width constraints | , , , and |
| Sidelobe region | |
| Upper limit of antenna pattern ISL | |
| Upper limit of stopband energy | |
| Number of stopband | |
| Exit condition value of IBE | |
| Exit condition value of DIP | |
| The location of communication user | |
| The location of target | |
| The power of target | |
| The location of two reference sources | and |
| The power of two reference sources | |
| Normalized available frequency subbands | , , , , , , , , |
| Number | SPIA Method | Number | Spatio-Spectral Method [12] |
|---|---|---|---|
| 1 | Two users positions | 1 | Two users positions |
| 2 | Lower bound of passband energies | 2 | Lower bound of passband energies |
| 3 | Upper bound of stopband energy | 3 | Upper bound of stopband energy |
| 4 | Two interference sources’ positions | 4 | Without this parameter |
| 5 | Power of two interference sources | 5 | Without this parameter |
| 6 | Power of target | 6 | Without this parameter |
| 7 | Ten frequency subbands are selected from the available frequency subbands using the spatio-spectral method [12] for information embedding | 7 | Frequency subbands for information embedding , , , , , , , , , , , , , , , , , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Pan, B.; Fan, T.; Yu, X.; Cui, G.; Nie, X. MIMO DFRC Signal Design in Signal-Dependent Clutter. Remote Sens. 2023, 15, 3256. https://doi.org/10.3390/rs15133256
Yao X, Pan B, Fan T, Yu X, Cui G, Nie X. MIMO DFRC Signal Design in Signal-Dependent Clutter. Remote Sensing. 2023; 15(13):3256. https://doi.org/10.3390/rs15133256
Chicago/Turabian StyleYao, Xue, Bunian Pan, Tao Fan, Xianxiang Yu, Guolong Cui, and Xiangfei Nie. 2023. "MIMO DFRC Signal Design in Signal-Dependent Clutter" Remote Sensing 15, no. 13: 3256. https://doi.org/10.3390/rs15133256
APA StyleYao, X., Pan, B., Fan, T., Yu, X., Cui, G., & Nie, X. (2023). MIMO DFRC Signal Design in Signal-Dependent Clutter. Remote Sensing, 15(13), 3256. https://doi.org/10.3390/rs15133256







